Multi-Strand RNA Secondary Structure Prediction and Nanostructure Design including Pseudoknots

Abstract

We are presenting NanoFolder, a method for the prediction of the base pairing of potentially pseudoknotted multi-strand RNA nanostructures. We show that the method outperforms several other structure prediction methods when applied to RNA complexes with non-nested base pairs. We extended this secondary structure prediction capability to allow RNA sequence design. Using native PAGE, we experimentally confirm that 4 in silico designed RNA strands corresponding to a triangular RNA structure form the expected stable complex.

RNA is an attractive molecule class for the design of nano-scale structures that potentially possess multiple biochemical functions. RNA-based molecular complexes have been designed to form shapes resembling squares,^{1, 2, 43} cubes,^{3, 4} an antiprism⁵, multimeric rings^{6–8, 44} and a tri-star.⁹ It is highly desirable to have computational tools that aid the structure prediction and design of such multi-strand RNA complexes. The secondary structure prediction problem considered here is to computationally predict the base pairing of one or several RNA strands such that the predicted structure coincides with the experimentally determined base pairing. We are particularly interested in developing a computational method for the fast and accurate prediction of multi-strand RNA nanostructures (tectoRNA).^{1, 10, 11}

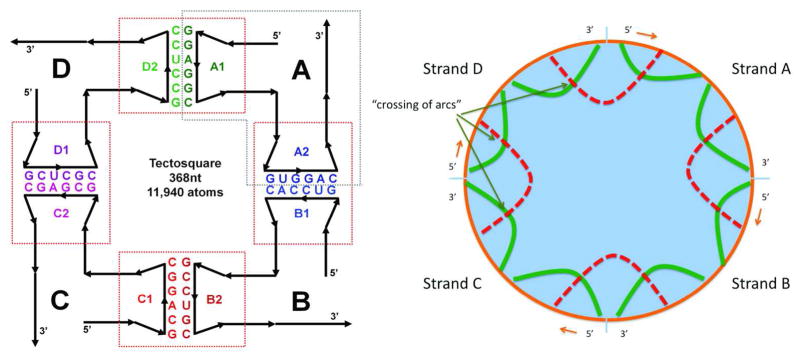
An example of a multi-strand RNA secondary structure is shown in Figure 1. In a circular diagram (Fig 1, right) sequences are laid out in a clockwise direction along the circumference of the circle: base pairs or helices are represented as arcs; non-nested base pairs correspond to “crossing arcs”. We also call RNA secondary structures with non-nested base pairs pseudoknotted. The computational prediction of RNA secondary structures is greatly simplified if RNA secondary structures are assumed to only consist of base pairs that are nested. In this case it is possible to find the minimum free energy (MFE) structure with the help of recursion relationships that can be computationally solved with the use of dynamic programming algorithms.^12–14 Much of recent work in this field has focused on considering subclasses of pseudoknots such that the minimum free energy structure can be found efficiently.^15–17 On the other hand, it has been mathematically proven that finding the minimum free energy RNA structure among the set of all (including non-nested) RNA secondary structures is equivalent to a class of problems for which no polynomial algorithm has yet been found.^{18, 19} For this case of unrestricted pseudoknot complexity, it will be desirable to develop heuristic algorithms (such as the one described in this paper) for the “search component” of RNA secondary structure prediction methods that are computationally efficient with the drawback that the solutions are not guaranteed to correspond to the minimum free energy structure.

Figure 1.

The internal representation of multi-strand secondary structures corresponds to non-nested basepairings. Left: schematic of one of the 4-strand RNA-square designs (also called tectosquare).¹ Right: Equivalent circular plot of the computer-internal representation of the RNA-square. Helices are represented as arcs. Non-nested base pairs correspond to crossing of arcs. A more detailed version of the circular representation of the RNA-square is part of the screenshot shown in Figure 5. The left part of the figure has been reprinted from Methods, 54(2), Kasprzak et al.: Use of RNA structure flexibility data in nanostructure modeling, 239–250, Copyright (2011), with permission from Elsevier.⁴¹

Most current RNA secondary structure prediction methods use a physics-based energy model that is derived from a nearest-neighbor base pair stacking model.^{14, 20, 21} Machine-learning techniques have, however, also been applied successfully to single-strand RNA secondary structure prediction as well as to the problem of predicting RNA secondary structure from a set of aligned homologous sequences. ^22–24

Methods for predicting the intra- and inter-strand base pairing of two RNA strands are available in the form of the RNAcofold program and the pairfold program.^{25, 26} Computational tools for the secondary structure prediction of three of more sequences were notably absent until recently. Programs that are able to predict secondary structures of multiple RNA sequences are multifold and NUPACK.^{16, 27} The NUPACK software considers pseudoknots for single RNA strands (the search space consists of all secondary structures that can be decomposed into two pseudoknot-free structures). This pseudoknot prediction capability is, however, currently not available for the prediction of two or more RNA strands. The inherent problem with not considering pseudoknotted structures (structures with non-nested base pairs) is shown for the example of an RNA-square (see Figure 1): the base pairing that corresponds to the correct secondary structure is highly non-nested. For dynamic programming algorithms that do not consider pseudoknots (or only a subclass of pseudoknots), this can lead to the situation, that the native secondary structure is not part of the search space and cannot be identified. This is the key motivation for the work presented here: the NanoFolder approach uses a very simple energy model, but has no restrictions on pseudoknot-complexity.

The ability to predict RNA base pairing from a given sequence prompts the problem of sequence design: given a desired RNA base pairing, what should the sequence of the RNA strands be? Several programs have been described that generate a novel sequence for a given pseudoknot-free single-strand RNA secondary structure. The RNAinverse program uses a Monte Carlo search in sequence space combined with dynamic programming that takes advantage of the fact that for a mutated sequence many energy terms from the previous sequence have not changed.¹⁴ RNA-SSD performs a stochastic local search of near-optimal substructures in order to find a sequence whose predicted secondary structure matches the target secondary structure as close as possible.^{28, 29} Busch and Backofen described the program INFO-RNA.^{30, 31} It uses dynamic programming to generate an initial sequence. The initial sequence is further optimized with a local stochastic search using structural decomposition for fast energy computation and a look-ahead for the determination of favorable next mutation steps. The NUPACK package performs sequence optimization by minimizing the ensemble defect (the ensemble-averaged number of incorrectly paired nucleotides of the RNA or DNA complex).^{16, 32}

This paper is organized as follows: First, our approaches for the prediction as well as the design of pseudoknotted, multi-strand RNA complexes are presented. We then evaluate the performance of the structure prediction approach using a test set of published RNA complexes. To demonstrate the viability of the RNA design approach, we lay out the steps involved in the design of a 4-strand RNA triangular structure. Using native PAGE, we then verify experimentally, that the in silico designed RNA sequences form the desired comp lex.

Results

Quality of Structure Prediction

We used several published RNA structures that consist of 3 or more strands as a test set to evaluate the quality of the RNA secondary structure predictions generated by NanoFolder. As a measure of how well the reference n×n base pair matrix is predicted (with n being the total number of residues in the RNA strands) we use the Matthews Correlation Coefficient (Materials and Methods). Note that MCC values can range between 1 and −1. An MCC of 1 corresponds to a “perfect prediction” (i.e. the predicted outcomes (base pairs) coincide with the correct result); an MCC of 0 corresponds to a random prediction with no correlation between prediction and the correct solution.

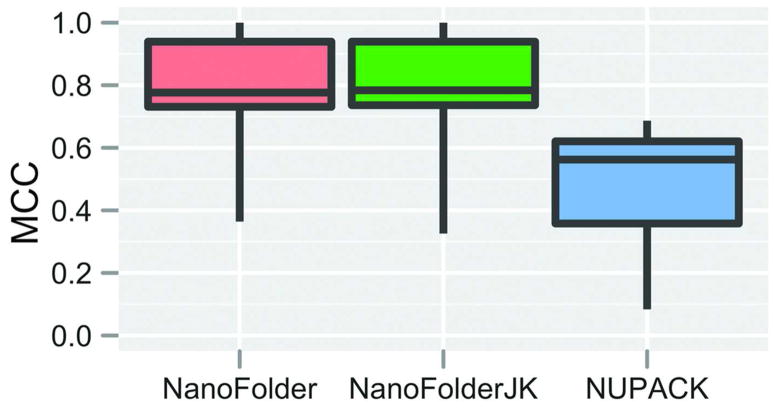
In Figure 2 we plot the Matthews Correlation Coefficient, comparing the programs NanoFolder and NUPACK. As one can see in the box-whisker plot, the median Matthews correlation coefficient (MCC) of the NanoFolder predictions is higher compared to NUPACK.

Figure 2.

Box-Whisker plot of achieved prediction qualities (Matthews correlation coefficients) for different methods applied to the set consisting of the nine multistrand RNA structures listed in Table 1. Each box-whisker element depicts the first quartile, median and third quartile in the form of a colored box; minimum and maximum scores are depicted as “whiskers” (vertical lines eminating from the colored box element). No data elements were considered “outliers”. The method NanoFolderJK corresponds to the leave-one-out (jack-knife) approach of training and testing the inter-strand interaction penalty parameter. For the method indicated as NanoFolder, this parameter was set to the median of the training results achieved in the jack-knife method.

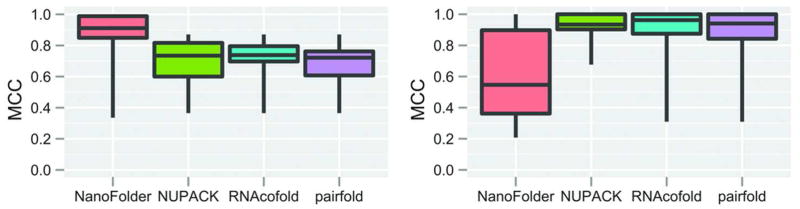
We also analyzed the performance of the program using a data set of 18 RNA hetero-duplexes. We compared the prediction quality of the programs NanoFolder, NUPACK (program pairs) RNAcofold, and pairfold.^{16, 25, 26} Figure 3 shows a box-whisker plot of the different approaches. Results for RNAs corresponding to the 8 non-nested secondary structures are shown on the left; results for RNAs corresponding to the 10 nested secondary structures are shown on the right. One can see that for non-nested RNA duplexes, NanoFolder has the highest median prediction quality (MCC) compared to the other approaches; for RNA duplexes with nested base pairings (essentially helices possibly containing bulges and internal loops) the median prediction quality of NanoFolder is lower compared to the other approaches.

Figure 3.

Box-Whisker plot of achieved prediction qualities (Matthews correlation coefficients) for different methods applied to a test set consisting of 18 RNA hetero-duplexes (Materials and Methods). Each box-whisker element depicts the first quartile, median and third quartile in the form of a colored box; minimum and maximum scores are depicted as “whiskers” (vertical lines eminating from the colored box element). No data elements were considered “outliers”. Left: accuracies of structure predictions corresponding to a data set of duplex structures with non-nested base pairs. Right: accuracies of structure predictions corresponding to a data set of duplex structures not containing non-nested base pairs.

The run-times of the NanoFolder program are shown in table 1. The RNA-square (368 residues) is computed in about 0.4s; the RNA-antiprism complex with 1008 residues is computed in less than 3s. This suggests that the structure prediction algorithm is sufficiently fast to be useful in many practical situtations.

Table 1.

Prediction results for RNA structures with 3 or more strands

Name	Ref.	Strands	Residues	NanoFolderJK	NanoFolder	Pairs	Time (s)
hairpin riboz. (2P7F)	42	4	60	0.82	0.82	0.56	0.053
nanosquare (3P59)	2	4	100	0.40	0.36	0.08	0.052
antiprism (lower half)	5	4	504	0.74	0.75	0.69	0.617
antiprism (upper half)	5	4	504	0.78	0.73	0.62	0.654
RNA-square	1	4	368	0.97	0.97	0.36	0.425
hexameric ring	7	6	264	0.33	0.63	0.10	0.199
antiprism	5	8	1008	0.78	0.78	0.63	2.913
6-stranded cube	3	6	288	1.00	1.00	0.53	0.233
10-stranded cube	3	10	332	0.94	0.94	0.57	0.252

Strands: number of input RNA sequences; Ref.: literature reference; Residues: total number of nucleotides; NanoFolerJK: NanoFolder results (Matthews correlation coefficient MCC) using Jack-knifing (such that current structure was not used during training); pairs results (MCC) from the NUPACK pairs program; NanoFolder: results (MCC) of NanoFolder using standard parameters. Time: run-time of the NanoFolder program (in seconds), evaluated using a Linux PC with a 3.0 GHz Intel Xeon processor.

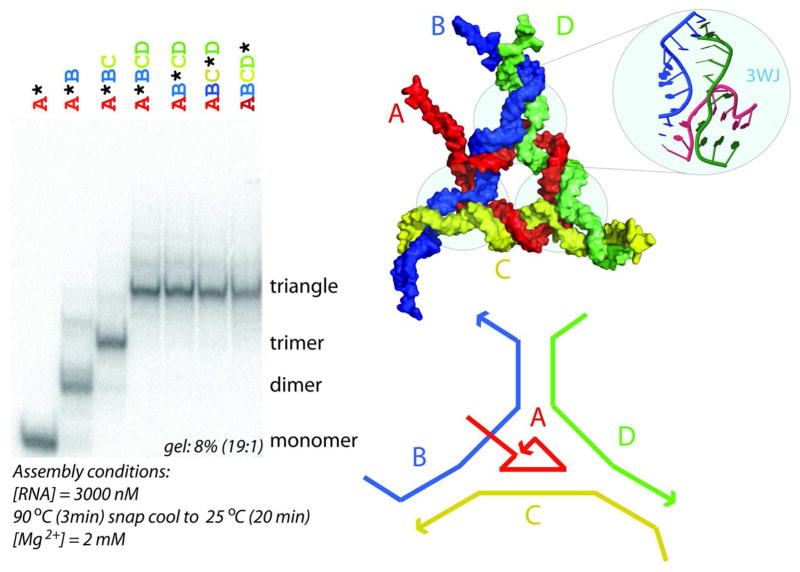
To demonstrate the utility of the design approach, we designed de novo an RNA nanoscale structure that forms a triangular shape and consists of 4 RNA strands (see Figure 4, top right and bottom right). The 3 corners of the triangular structure are formed by one type of three-way junction motif that was identified with the help of the RNAJunction database and the NanoTiler software.^{33, 34} The sequence segments corresponding to the corner motif as well as the 5′ ends were not modified during the sequence optimization; those residues are indicated in lower case in the sequences reported in the Materials and Methods section.

Figure 4.

Right: molecular model of 4-strand triangular RNA nanoscale structure. Shown is also the 3-way junction that was obtained from the RNAJunction database (RNAJunction database accession ID 11836). Each of the 3 “corners” of the designed triangular structure contains this three-way junction (3WJ) motif. We designed de novo an RNA nanoscale. Left: Native PAGE results for different strand combinations.

The formation of a 4-strand RNA complex was experimentally verified using non-denaturing polyacrylamide gel electrophoresis (native-PAGE). This electrophoretic separation technique is widely used for characterizations of RNA assemblies (Afonin et al., Nature Protocols, 2011). Major dark bands on the gel correspond to the products of the assemblies (see Figure 4, left). Assembled 4-strand RNA complexes are expected to migrate as a single band with the lowest mobility. Native-PAGE results presented in Figure 4 demonstrate the reproducible self-assembly of four (A–D) RNA strands, into the definite structure of a tetramer. Quantification of the bands reveals that the average yields of the RNA tetramer is greater than 90%. To verify that all four RNA strands participate in self-assembly, each of the four radio-labeled molecules (marked with “*”) was individually mixed with three other non-labeled molecules followed by the assembly protocol described in Methods. The results show identical gel shifts for all four tetramers with different labeled strands, suggesting the participation of all strands in the formation of the closed species.

Web Server

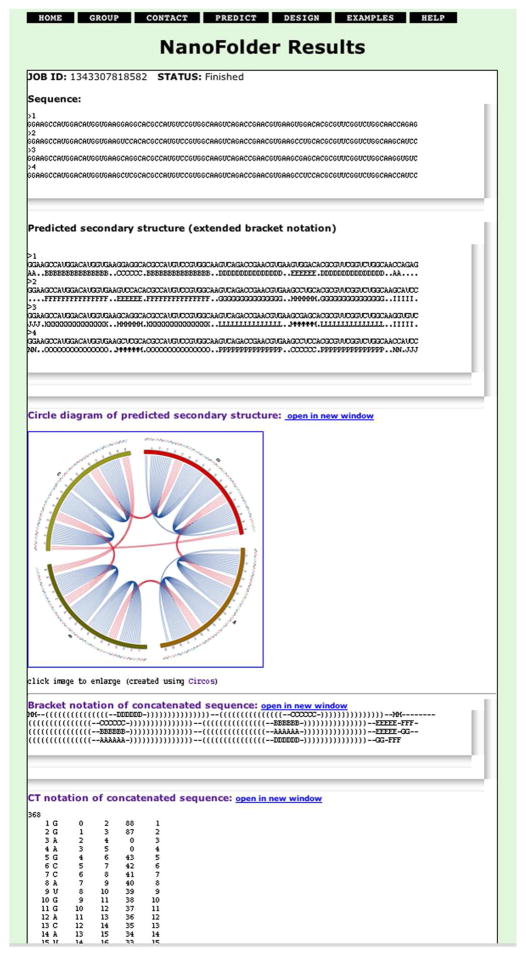
We implemented a publically available web server in order to provide a user-friendly interface to the structure prediction and sequence design methodology. Input for the secondary structure prediction is a set of RNA sequences in FASTA format. Figure 5 shows a screenshot of a secondary structure prediction result that one obtains after submitting 4 RNA sequences that correspond to the RNA-square.¹ The predicted base pairing is shown on the result-page in 3 different text formats as well as an image depicting a circular diagram.

Figure 5.

Screenshot of a secondary structure prediction result generated by the NanoFolder web server. The RNA sequences used as “input” for the web server (labeled in the screenshot as “Sequence”) correspond to an RNA-square.¹ The web server returns structure prediction results in 3 different text output formats (labeled in the screenshot as “Predicted secondary structure”, “Bracket notation of concatenated sequence” and “CT notation of concatenated sequence”). The predicted base pairing is depicted using a circular representation (labeled in the screenshot as “Circle diagram of predicted secondary structure”). The bottom part of the generated web page (containing the prediction result in tabular “CT” file format) is not shown in its entirety.

Input to the sequence design method is a set of RNA sequences combined with a descriptor for the desired target secondary structure (input format examples are given on the web page). Nucleotides that are represented as upper-case (lower-case) characters in the user-defined starting sequences will (not) be modified during sequence randomization and optimization, respectively. This effectively makes possible partial sequence optimization that can be useful for optimizing a set of sequence in stages as well as for keeping structural motifs unchanged. The user also can specify the number of iterations corresponding to the two stages of optimization. The URL of the web server is http://matchfold.abcc.ncifcrf.gov/.

Discussion

The secondary structure prediction algorithm of NanoFolder is strikingly simple: it proceeds by placing in a “greedy” fashion RNA helices in the order of their estimated free energy. This approach has the advantage that it is fast and that it is unrestricted in terms of pseudoknot complexity. Indeed, to the best of our knowledge, NanoFolder is currently the only computational method that considers non-nested base pairings for multi-strand secondary structure predictions. The computational multistrand predictions rely on the step of appending the multiple strands in a linear fashion, keeping track of the discontinuities between sequences.^{16, 25, 27} A circular representation reveals that this procedure effectively turns the multi-strand structure prediction problem into a single-sequence structure prediction problem with pseudoknots (see Figures 1 and 5). Only allowing a subclass of pseudoknots or not allowing pseudoknots at all potentially prohibits the target secondary structure from being part of the solution set. A sequence design algorithm with that restriction will then have to rely on a structure prediction methodology that only considers partially folded or misfolded structures.

The relative importance of considering pseudoknots versus the sophistication of the energy model becomes particularly apparent when considering the structure prediction results shown in Figure 3. The plot depicts structure prediction results of the various approaches (NanoFolder, NUPACK, RNAcofold, pairfold) to a set of RNA hetero-duplexes. When applied to a data set of RNA duplexes with non-nested base pairs (Fig. 3 left), NanoFolder outperforms the other methods, even though its energy model is much simpler. When applied to the data set of RNA duplexes not containing non-nested base pairs (Fig. 3 right), NanoFolder predictions are less accurate compared to the other methods. This is likely due to the simple energy model (essentially consisting of only two terms) employed by NanoFolder. Also apparent from Fig. 3 is that the structure prediction results of the 3 programs NUPACK, RNAcofold and pairfold are similar in quality. This is likely due to the similarity in the search algorithms (dynamic programming) and energy models. It would be desirable to develop a multi-strand RNA secondary structure prediction algorithm that is based on the energy model of the aforementioned programs and yet has no restriction in terms of pseudoknot-complexity.

This also suggests that designed architectonic RNAs possess different properties compared to natural RNAs. The key for tectoRNAs is robustness of folding (often implemented by using relatively long helices). Indeed, in the field of DNA nanoscale structure design, impressively complex DNA structures have been designed and experimentally verified using a set of heuristic rules without ever attempting a full minimum free energy DNA secondary structure prediction.

The NanoFolder design algorithm is specifically geared towards the design of tectoRNAs. It is a combination of RNA secondary structure prediction and sequence design rules. The demonstrated high secondary structure prediction accuracy combined with the shown experimental (native PAGE) confirmation of a designed RNA triangular structure make us confident that NanoFolder is an important addition to the toolkit of an RNA nanostructure designer.

Materials and Methods

RNA structure data sets

We developed two data sets for training and testing the multi-strand RNA secondary structure prediction algorithm. 18 RNA structures consisting of two RNA strands with nonidentical sequence (heteroduplexes) were obtained from the PDB data bank. Their PDB accession codes are for nested structures 1NTA, 2D1A, 2G5K, 2OE5, 2OEU, 2PN3, 2XEB, 3BNP, 3CJZ, and 429D; for non-nested structures the accession codes are: 1BJ2, 1F27, 1YKQ, 2GCS, 2JLT, 2P89, 2PCW, 3MJ3. We call this data set the hetero-duplex set. Another data set (called the multi-strand data set) consisting of 9 RNA structures (each possessing 3 or more RNA strands) was generated using the Protein Data Bank as well as the available literature. These structures and their literature references are listed in Table 1.

Multi-strand structure prediction including pseudoknots

A new program called NanoFolder performs the multi-strand RNA secondary structure prediction. The main characteristics of the implementation are fast execution times as well as no restriction in terms of pseudoknot complexity. The RNA secondary structure scoring function and the search algorithm used by NanoFolder are described below.

Scoring of RNA structures

The free energy contribution of an RNA double-helix is estimated using the sum of its base-pair stacking energies from a standard nearest neighbor energy model ²⁰ as well as an inter-strand penalty term that is zero for intra-strand helices and greater than zero for inter-strand helices. Instead of using a physical model with parameters that are unknown or hard to measure, the value of the inter-strand penalty term is determined using a training set (the inter-strand penalty can be viewed as an entropic penalty). Training has been performed in a jack-knife manner using the results corresponding to the 9 RNA structures reported in Table 1. In other words, for each predicted RNA structure, the trained value of the inter-strand penalty has been determined using the remaining 8 RNA structures. For a given “test-RNA”, the search for the optimal inter-strand penalty was an exhaustive enumeration of values between 0.0 kcal/mol and 2.0 kcal/mol in steps of 0.2 kcal/mol. The inter-strand penalty that led to the highest prediction accuracy of the training set was then applied to the prediction of the one RNA of the test set. This procedure was repeated 9 times corresponding to the 9 RNAs of the set shown in Table 1. The median of the 9 chosen inter-strand penalties was found to be 1.0 kcal/mol. This approach should be viewed as an empirical scoring function for RNA complexes rather than a physical energy function.

RNA folding algorithm

The structure prediction algorithm proceeds as follows: first, an exhaustive list of all possible helices consisting of two or more base pairs is generated. Each helix is scored as described in the previous section. To predict an RNA secondary structure, an RNA is folded in silico by placing the helices in ascending order of their scores, such that a newly placed helix is not overlapping with previously placed helices. If several unplaced helices have the same score contribution, a random choice is made to place one of them. The algorithm terminates, when there are no helices in the original helix list that have not been placed yet and that do not overlap with already placed helices.

RNA Sequence Design Algorithm

The sequence design algorithm has the task of generating a set of RNA sequences that fold into a secondary structure that is as close as possible to the folding pattern envisioned by the designer. In addition, there are “rules” that the designed sequences should obey. This lays out the general strategy for sequence design: Given an initial set of RNA sequences, the sequences are computationally mutated. Each set of RNA strands is scored using an objective function, that reflects how “good” the current set of sequences is. Using a Monte Carlo algorithm, the mutations of the sequences are accepted or rejected using a Metropolis criterion that depends on the difference in the values of the objective function as a consequence of the current mutation. The objective function consists of two components: a secondary structure similarity component and a sequence design rule component. Both terms are described in more detail in the following two sections.

Secondary structure similarity component

This score component reflects the similarity of the predicted multi-strand secondary structure and the desired target secondary structure. For the design of thermodynamically stable scaffold sequences, one wants the designed sequences to exhibit “robust” RNA folding. One can express this concept using an n × n matrix (with n being the total number of residues in all RNA strands) containing probabilities of base pairing between different residues. The desired secondary structure corresponds to a base pair probability matrix containing matrix elements that have a value of one for desired base pairs and a value of zero for undesired base pairs. This idealized probability of base pairing is then compared to the predicted base pair probability matrix. The more similar the predicted base pair probability matrix is to the idealized base pair probability matrix, the better the sequence design.

The base pair probability matrix is computed as follows: For a set of multi-strand RNA strands a secondary structure prediction is re-run 20 times, each time adding a Boltzmann-weighted noise term to the energy contribution of each helix that is part of the initial exhaustive list of all possible helices. This leads to a set of 20 predicted secondary structures. The average occupancy of each base pair is used to generate an estimated base pair probability matrix.

From the base pair probability matrix P, the reference secondary structure s, a total number of residues n, a similarity score d(P,s) is computed as follows:

$$d(P,s)=\sum _{i=1}^n{d}_i(P,s)$$

with

$$d_i(P,s)=\{\begin{array}{c}1-P(i,B(i,s)),\text{if }S(i)=1\\ \sum _{j=1}^{n}P(i,j),\text{if}S(i)=0\end{array}$$

The function S(i) is defined to be 1 if reference residue i participates in any base pairing and 0 otherwise. The function B(i,s) is defined to be equal to the index of the residue that participates in base pairing with residue i.

Sequence design rule component

This score component reflects how well the designed RNA sequences “obey” a set of sequence design rules. Several design rules can be formulated using the concept of same-length sequence fragments called “critons”: From a sequence of length N one can generate N-L+1 contiguous sequence fragments (critons) of length L. We choose the length L of the considered critons to be 6nt. Rules based on the concept of critons have been applied with great success to the design of DNA nanostructures.^{35, 36} Each “rule violation” is computationally modeled as a penalty term. For example, branch migration is a property that is usually not desired in designed nucleotide sequences, because it potentially leads to a variety of structurally and energetically similar folds. In order to bias designed RNA sequences to not exhibit branch migration, a branch migration penalty term is set equal to the number of RNA double-helix-ends that might contribute to branch migration. A subset of the employed set of rules has previously been used for the design of cubic RNA complexes.³

Here we present a list of the employed penalty scoring terms for the sequence design:

auViolation

Let k be the number of helical AU-regions (sequence regions that consist only of nucleotides A or U and correspond to nucleotides that are per design desired to participate in base pairing) with a length of 3 or more nucleotides. The penalty term is defined as $s_{AU}={\displaystyle \sum _{i=1}^k}(l_i-2)$ with l_i being the length of the i’th such AU region. The rationale for this term is to avoid designed helices that possess regions with too many consecutive A-U base pairs, which could result in helical regions with limited stability.

branchMigration

Count of the number of helix ends in the target secondary structure that could participate in branch-migration. Let i,j be the indices of two residues that are base-paired in the target structure. If residue pair i+1,j−1 (or i+1,j−1) is not part of the target secondary structure but is Watson-Crick complementary, the branch-migration counter is increased by one. The rationale for this term is to promote a unique native structure (being equal to the target design structure) without having energetically similar structures corresponding to migrated junctions or partially opened helices.

complement

Count of the number of critons, for which a reverse-complement criton exists that is not desired to base-pair according to the target structure. The key idea of “critons” is that each criton cannot form complete duplexes with any other criton forming base pairs that are not part of the target structure.

consecutive

Count of the number of adjacent Gs or non-G nucleotides of the same kind that exceed two or three respectively. A large number of adjacent nucleotides of the same type is not desirable, because it can potentially lead to a large set of structurally and energetically similar RNA folds.

duplicate

Count of the number of non-unique critons. If we denote the total number of generated critons from the input sequence(s) as n_c, and the number of unique sequence fragments obtained from these critons as n_u, we can express the scoring term as equal to n_c-n_u. Developing non-redundant sequences is the central idea of nucleic acid sequence design, and dates back to the work of Ned Seeman.³⁶ Duplicate critons can lead to ambiguities in the RNA folding process, potentially leading to a riboswitch-like structure.

gcFracViolation

If the target secondary structure consists of k helices, there are 2k helical strands in the target structure. Let $c_{\text{GCmin}}(i)=\lfloor f_{gc}{l}_i\rfloor$ be the minimum number of desired G or C bases in the i’th helical strand (l_i indicates the length of the i’th helical strand, the constant f_gc is set to 0.76, the square brackets indicates rounding to the nearest lower integer). Let c_GC (i) be the count of the number of G or C nucleotides in the i’th helical strand. The score is defined as:

$$s_{\mathit{GCfrac}}=\sum _{i=1}^{2k}\{\begin{array}{c}{c}_{\text{GC}min}(i)-c_{\text{GC}}(i),\text{if}{c}_{\text{GC}min}(i)>c_{\text{GC}}(i)\\ 0\text{otherwise}\end{array}$$

The rationale of this term is to promote a high G+C content in helices.

gcViolation

Let k be the number of helical GC-regions (sequence regions that consist only of nucleotides G or C and correspond to nucleotides that are per design desired to participate in base pairing) with a length of 2 or more nucleotides. The penalty term is defined as $s_{GC}={\displaystyle \sum _{i=1}^k}(l_i-1)$ with l_i being the length of the i’th GC region. The rationale for this term is to avoid helical regions that correspond to a long stretch of only G-C base pairs.

selfComplement

Count of the number of critons that are self-complementary. Self-complementary regions are not desirable because they can potentially lead to the formation of unwanted hairpin structures.

smallComplement

Count of the number of small critons (length 4), that cannot be matched with a reverse-complementary small criton. This term promotes the formation of some base pairing in order to avoid completely unstructured RNA strands. This is useful to allow slightly structured regions, which are presumably more stable compared to completely unfolded structures with regards to nuclease degradation.

zipper

Count of the number of non G-C base pairs at helix ends. The rationale for this term is to favor folded RNA structures whose helices are not “breathing” (temporarily partially unfolding) but are terminated by thermodynamically stable G-C base pairs.

The weights of the scoring terms have not been optimized; the weight of each scoring term is 1.0 with the exception of the smallComplement term. This term has a weight of 0.1 because it addresses a design goal (stability with respect to nuclease degradation) of lower priority.

Sequence Optimization Algorithm

The task of the sequence optimization algorithm is to identify a set of RNA sequences that correspond to a low design penalty score. The algorithm consists of 3 stages:

In the first stage, the RNA sequences are randomized, i.e. the nucleotides of the RNA sequences are randomly chosen. The randomization is performed such that nucleotides that are designed to form base pairs are Watson-Crick complementary. The probabilities of choosing the bases A,C,G,U are 0.2, 0.3, 0.3, 0.2 respectively, corresponding to a G+C content of 60%. It is possible to define constant sequence regions that are not modified by the sequence optimization algorithm. This computational stage is finished once the initial identity of all residues has been specified.

In the second stage, the sequences are iteratively modified using a Monte Carlo algorithm combined with a Metropolis criterion (this approach is also called stochastic tunneling).³⁷ Nucleotides that correspond to lower-case characters in the input sequence data are not modified during the optimization. The objective function of this optimization stage is the rule-based score component (the sum of the terms listed in the section Sequence design rule component). This computational stage is finished after a user-defined number of iterations (default: 10000 iterations).

In the third stage, the set of RNA sequences are further optimized (using the same Monte Carlo algorithm) using as an objective function that is the sum of the rule-based score component and the secondary structure similarity component. This computational stage is finished after a used-defined number of iterations (default: 1000 iterations).

The user can set the number of iterations of the second and third stage. This 3-stage approach of generating optimized sequences is re-run five times, and the set of RNA sequences that corresponds to the lowest objective function score is returned as a result.

Secondary structure prediction programs used for comparison

NUPACK

The NUPACK program pairs (part of NUPACK software version 3.0) was used with the option –multi for multi-strand secondary structure prediction.¹⁶

RNAcofold

The RNAcofold program (part of the Vienna package 1.7.2) was used with default parameters.²⁵

pairfold

The pairfold program of the MultiRNAFold package (version 2.0) was used with default parameters.²⁶

Matthews Correlation Coefficient as a measure of prediction quality

The Matthews Correlation Coefficient (MCC) is widely used to compare the performance of binary classifiers.³⁸ For a set of RNA strands (with a total number of n residues), a multi-strand RNA secondary structure can be represented by a n×n matrix (“base pair matrix”) that has matrix elements which are one for residues that are base-paired and zero otherwise. To compute the MCC for a predicted secondary structure, we compute the base pair matrix corresponding to the predicted secondary structure and the reference secondary structure. Each element of the predicted base pair matrix corresponds to one of 4 cases; depending on whether it is a true positive, false positive, false negative or true negative prediction. From the four numbers (true positives (TP), false positives (FP, the total number), true negative (TN), false negatives (FN)), the Matthews Correlation Coefficient (MCC) is computed using the equation: $\mathit{MCC}=\frac{TP\ast TN-FP\ast FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}$

Experimental procedures

As described in the results section, a triangular RNA structure consisting of 4 strands was experimentally tested for complex formation in order to test the viability of the sequence design approach. The experimental steps are described in detail in this section.

RNA preparation

Synthetic DNA molecules coding for the antisense sequence of the designed RNA were purchased from IDT DNA and amplified by PCR using primers containing the T7 RNA polymerase promoter. PCR products were purified using the QiaQuick PCR purification kit and RNA molecules were prepared enzymatically by in vitro transcription using T7 RNA polymerase. Samples were incubated at 37 °C for four hours in a buffer containing 15 mM MgCl₂, 2 mM spermidine, 50 mM Tris buffer (pH 7.5), 2.5 mM NTPs, 10 mM DTT, 0.1 μg/μl IPP, and 0.8 u/μl RNasin; the reaction was quenched by adding 5 μl of RQ1 RNase-free DNase (10u/μg) for a reaction volume of 200 μl, followed by 30 additional minutes of incubation. Samples were purified on a denaturing urea gel (PAGE) (8% or 10% acrylamide, 8M urea). The RNA was eluted from gel slices overnight at 4 °C into buffer containing 300 mM NaCl, 10 mM Tris pH 7.5, 0.5 mM EDTA. After precipitating the RNA in two volumes of 100% ethanol, samples were rinsed twice with 75% ethanol, vacuum dried, and dissolved in TE buffer.^{39, 40}

Co-transcriptional α[P³²]-ATP body-labeling of RNA molecules

DNA templates (containing the T7 RNA polymerase promoter) were added to the transcription mixture (diH₂O, 50 mM Tris pH 7.5, 10 mM MgCl₂, 2 mM spermidine, 2.5 mM NTPs, 10 mM DTT) containing α[³²P]-ATP (10 mCi/ml) for body-labeling. Transcription was initiated with the addition of T7 RNA polymerase and stopped after 4 hours with RQ1 RNase-free DNase. Labeled material was purified as described above.

Non-denaturing PAGE experiments

All assembly experiments reported in this study were analyzed on 8% (19:1) non-denaturing polyacrylamide native gels containing 2 mM Mg(OAc)₂ and 50 mM KCl and run at 4ºC with running buffer (89 mM Tris-borate, pH 8.3/15 or 2 mM Mg(OAc)₂). Prior to the addition of the buffer and Mg(OAc)₂, the RNA samples containing cognate RNA molecules at concentrations 3 μM were heated to 90ºC for 3 minutes and immediately snap cooled at 25 ºC followed by assembly buffer addition (tris-borate buffer (89 mM, pH 8.3), 2 mM Mg(OAc)₂) and incubation for 20 minutes. An equal volume of loading buffer (same buffer with 0.01% bromphenol blue, 0.01% xylene cyanol, 50% glycerol) was added to each sample before loading on the native gel. Gels were run for 4 hours, at 25 W with the temperature set to be below 10ºC, dried under vacuum, exposed to a phosphoimager screen for 16 hours, and scanned using a Storm 860 phosphoimager. Band quantification was performed using commercially available ImageQuant software. Equally sized boxes were drawn around the bands corresponding to the assembled RNA complexes. The yields of RNA complexes were calculated by dividing their corresponding quantified values by the total sum of the values for all other complexes present in the corresponding lane.

RNA sequences used in this example

The RNA sequences used are listed below. Nucleotides that underwent sequence optimization are shown in upper case; the remaining nucleotides (shown in lower case) correspond to either the chosen 3-way junction motif or the starting sequence motifs.

A:gggaaAUGACUCUcgucagGACACUCUCcgucagCUCUGUGUGcgucagAGUCG

B:ggaaGUCACGGUCUCgacgacgAGAGCGACUcgcaaccACACUGGUGAC

C:ggaaCAGUGUgacgacgCACACAGAGcgcaaccCACUGC

D:ggaaGCAGUGgacgacgGAGAGUGUCcgcaaccGAGACC

3-way junction motif

The 3-way junction that is used for the triangular RNA structure (described in the Results section) was identified using the RNAjunction database, by searching for a 3-way junction that contains an inter-helix angle that is similar to 60° and two inter-helix angles similar to 150°.³³ This structural element (RNAJunction accession ID 11836) was extracted from the Thermus thermophilus 16S ribosomal RNA structure (PDB: 2J00). The triangular structure was identified using a combinatorial search performed with the NanoTiler software.³⁴