State-dependent doubly weighted stochastic simulation algorithm for automatic characterization of stochastic biochemical rare events

Abstract

In recent years there has been substantial growth in the development of algorithms for characterizing rare events in stochastic biochemical systems. Two such algorithms, the state-dependent weighted stochastic simulation algorithm (swSSA) and the doubly weighted SSA (dwSSA) are extensions of the weighted SSA (wSSA) by H. Kuwahara and I. Mura [J. Chem. Phys. 129, 165101 (2008)]10.1063/1.2987701. The swSSA substantially reduces estimator variance by implementing system state-dependent importance sampling (IS) parameters, but lacks an automatic parameter identification strategy. In contrast, the dwSSA provides for the automatic determination of state-independent IS parameters, thus it is inefficient for systems whose states vary widely in time. We present a novel modification of the dwSSA—the state-dependent doubly weighted SSA (sdwSSA)—that combines the strengths of the swSSA and the dwSSA without inheriting their weaknesses. The sdwSSA automatically computes state-dependent IS parameters via the multilevel cross-entropy method. We apply the method to three examples: a reversible isomerization process, a yeast polarization model, and a lac operon model. Our results demonstrate that the sdwSSA offers substantial improvements over previous methods in terms of both accuracy and efficiency.

INTRODUCTION

Stochasticity plays an important role in many biological processes. The significance of this role is particularly evident when stochastic behavior gives rise to biochemical rare events. These events are often accompanied by profound consequences to the underlying system. For example, a recent study indicates that rare mutations in stem cells can cause blood disorders such as chronic myeloid leukemia and paroxysmal nocturnal hemoglobinuria.¹ Because rare events can require a very long time period to be observed in a natural setting, conducting in vivo or in vitro experiments may not be feasible. As an alternative, properly formulated in silico simulations can provide essential information.

One popular mathematical approach for characterizing biochemical rare events utilizes Monte Carlo methods such as the stochastic simulation algorithm (SSA).² Although the SSA is straightforward to implement, it is not efficient for simulating a rare event, as a huge number of realizations will be required to witness a single occurrence. This inefficiency can be overcome with importance sampling (IS),³ a general technique that uses an alternate distribution to estimate a distribution of interest. In 2008, Kuwahara and Mura developed the weighted stochastic simulation algorithm (wSSA),⁴ which incorporated IS into the SSA for efficient characterization of rare events. The wSSA is designed to determine the probability that, given an initial state, the system reaches a state in a prescribed rare event set before the final simulation time. The wSSA alters the underlying probability distribution of reaction firings at each time step such that the system is artificially shifted toward the desired rare event. The bias introduced in this process is then corrected using a likelihood ratio between the original probability mass function (PMF) and the altered PMF, yielding an unbiased estimator. Although the wSSA can be efficient, its efficiency as well as accuracy largely depend on the choice of IS parameters. In particular, a poorly chosen set of IS parameters can generate a wSSA estimate that is far less accurate than the SSA estimate. For systems where favorable values of IS parameters are unknown, users must adopt the costly trial and test method. The large computational burden imposed by this method limits the size of systems that can be interrogated with the wSSA.

This issue was resolved with the recent development of the doubly weighted SSA (dwSSA).⁵ When combined with the multilevel cross-entropy (CE) method,⁶ the dwSSA automatically discovers IS parameter values that yield low-variance rare event probability estimates for any given system. Use of the dwSSA leads to a dramatic reduction in computation time compared to both the original SSA and the wSSA.⁵ Despite this favorable performance, there is still room for improvement, as the dwSSA employs constant (i.e., system state-independent) IS parameters. In contrast, systems whose species populations vary widely in time require state-dependent IS parameters to yield the lowest possible estimator variance. The state-dependent wSSA (swSSA) (Ref. ⁷) handles variation in the system state by computing IS parameters that depend on the relative propensity of each reaction at the current time step. However, like the wSSA, the swSSA does not offer an efficient strategy for choosing optimal IS parameters.

In this paper we present a novel modification of the dwSSA: the state-dependent doubly weighted stochastic simulation algorithm (sdwSSA), which automatically and efficiently computes state-dependent IS parameters with minimal input from the user. Our presentation is structured as follows: Section 2 provides background on rare event probability estimation using Monte Carlo simulation. Section 3 describes the detailed algorithm of the sdwSSA. In Sec. 4, we apply the sdwSSA to three examples of increasing complexity. Finally in Sec. 5, we summarize our contributions and discuss future areas of research.

BACKGROUND

Rare event probabilities and the SSA

Here, we give a brief review of the SSA and define the class of rare events examined in this paper. We begin by assuming a well-stirred chemical system whose N species populations at time t are represented as $\mathbf{X}\left(t\right)$. The system evolves in time by firing M reactions {R₁, …, R_M}, whose propensities at time t are in the set $\{a_j\left(\mathbf{X}\left(t\right)\right):j=1,...,M\}$, with sum $a_0\left(\mathbf{X}\left(t\right)\right)$. Starting at the initial state ${\mathbf{x}}_0$, the “direct method” implementation of the SSA chooses the time to the next reaction τ and the index of the next reaction j^′ as exponential (with mean $1/a_0\left(\mathbf{x}\right)$) and categorical (with probabilities $a_j\left(\mathbf{x}\right)/a_0\left(\mathbf{x}\right)$) random variables, respectively. These random draws repeat until some stopping time T, which we define as the smaller of the first time to reach the rare event and the final simulation time (which will later be denoted by t). Given ${\mathbf{x}}_0$, the probability of a single SSA trajectory $\mathbf{J}\equiv ({\tau }_1,j_1^{\prime },...,{\tau }_{N_{\mathcal{T}}},j_{N_{\mathcal{T}}}^{\prime })$, with the notation τ_i denoting that the dwell time preceding the ith reaction firing lies within dτ of τ_i, can be expressed as follows:

$$\begin{array}{ccc}\hfill {\mathrm{P}}_{\text{SSA}}\left(\mathbf{J}\right)& =& \prod _{i=1}^{N_{\mathcal{T}}}\left[a_0\left(\mathbf{X}\left(t_i\right)\right)e^{-a_0\left(\mathbf{X}\left(t_i\right)\right){\tau }_i}d\tau \times \frac{a_{j_i^{\prime }}\left(\mathbf{X}\left(t_i\right)\right)}{a_0\left(\mathbf{X}\left(t_i\right)\right)}\right]\hfill \\ & =& \prod _{i=1}^{N_{\mathcal{T}}}\left[a_{j_i^{\prime }}\left(\mathbf{X}\left(t_i\right)\right)e^{-a_0\left(\mathbf{X}\left(t_i\right)\right){\tau }_i}d\tau \right],\hfill \end{array}$$ (1)

with $t_i\equiv {\sum }_{j=1}^i{\tau }_j$ and $N_{\mathcal{T}}$ is the total number of reactions that fire in the interval $[0,\mathcal{T}]$.

In this paper we are interested in estimating rare event probabilities of the form $p({\mathbf{x}}_0,\mathcal{E};t)$, defined as the probability that given the initial state ${\mathbf{x}}_0$, the system reaches any state in the rare event set E at least once before time t. The Monte Carlo estimator for this probability using the SSA is given by

$${\widehat{p}}_{\text{SSA}}({\mathbf{x}}_0,\mathcal{E};t)=\frac{1}{K}\sum _{k=1}^K\left[I_{\{S\left({\mathbf{J}}_k\right)\cap \mathcal{E}\}}\right],$$ (2)

where K is the total number of trajectories, ${\mathbf{J}}_k$ is the kth SSA trajectory simulated over time interval $[0,\mathcal{T}]$, and $I_{\{S\left({\mathbf{J}}_k\right)\cap \mathcal{E}\}}$ is an indicator function that takes a value of 1 if any state in E is visited by ${\mathbf{J}}_k$, and 0 otherwise. We note that the quantity in Eq. 2 is equivalent to the total number of trajectories that reached a state in E by time t, divided by K.

Doubly weighted SSA

The doubly weighted SSA (dwSSA) as presented in Ref. 5 uses IS to bias both reaction selection and time to the next reaction. The system state under the dwSSA evolves in time according to predilection functions given by

$$b_j\left(\mathbf{X}\left(t\right)\right)\equiv {\gamma }_j{a}_j\left(\mathbf{X}\left(t\right)\right),b_0\left(\mathbf{X}\left(t\right)\right)=\sum _{j=1}^M{b}_j\left(\mathbf{X}\left(t\right)\right),$$ (3)

where each γ_j is a positive constant. The next reaction index j^′ is chosen using the set of predilection functions, and τ becomes an exponential random variable with mean $1/b_0\left(\mathbf{X}\left(t\right)\right)$. Thus, the probability of a system trajectory Junder the dwSSA is given by

$$\begin{array}{ccc}\hfill {\mathrm{P}}_{\text{dwSSA}}\left(\mathbf{J}\right)& =& \prod _{i=1}^{N_{\mathcal{T}}}\left[b_0\left(\mathbf{X}\left(t_i\right)\right)e^{-b_0\left(\mathbf{X}\left(t_i\right)\right){\tau }_i}d\tau \times \frac{b_{j_i^{\prime }}\left(\mathbf{X}\left(t_i\right)\right)}{b_0\left(\mathbf{X}\left(t_i\right)\right)}\right]\hfill \\ & =& \prod _{i=1}^{N_{\mathcal{T}}}\left[b_{j_i^{\prime }}\left(\mathbf{X}\left(t_i\right)\right)e^{-b_0\left(\mathbf{X}\left(t_i\right)\right){\tau }_i}d\tau \right].\hfill \end{array}$$ (4)

The bias that was introduced by the predilection functions can be corrected by multiplying 4 by the following weight:

$$\begin{array}{ccc}\hfill W_{\text{dwSSA}}\left(\mathbf{J}\right)& =& \prod _{i=1}^{N_{\mathcal{T}}}\left[\frac{a_{j_i^{\prime }}\left(\mathbf{X}\left(t_i\right)\right)e^{-a_0\left(\mathbf{X}\left(t_i\right)\right){\tau }_i}}{b_{j_i^{\prime }}\left(\mathbf{X}\left(t_i\right)\right)e^{-b_0\left(\mathbf{X}\left(t_i\right)\right){\tau }_i}}\right]\hfill \\ & =& \prod _{i=1}^{N_{\mathcal{T}}}[\exp \left\{\left(b_0\left(\mathbf{X}\left(t_i\right)\right)-a_0\left(\mathbf{X}\left(t_i\right)\right)\right){\tau }_i\right\}\times {\left({\gamma }_{j_i^{\prime }}\right)}^{-1}].\hfill \end{array}$$ (5)

It was shown in Ref. 5 that the multilevel CE method of Rubinstein and Kroese⁶ provides a closed-form solution in the dwSSA for each reaction's optimal parameter estimate:

$${\widehat{\gamma }}_j^{*\left(n\right)}=\frac{{{\displaystyle \sum }}_k^{\prime }\left(W_{\text{dwSSA}}({\mathbf{J}}_k^{(n-1)};{\widehat{\gamma }}^{(n-1)})\times n_{kj}\right)}{{{\displaystyle \sum }}_k^{\prime }\left(W_{\text{dwSSA}}\left({\mathbf{J}}_k^{(n-1)};{\widehat{\gamma }}^{(n-1)}\right)\times {\sum }_{i=1}^{N_{{\mathcal{T}}_k}}\left[a_j\left({\mathbf{X}}_k^{(n-1)}\left(t_{ki}\right)\right){\tau }_{ki}\right]\right)}.$$ (6)

Here, ${\widehat{\gamma }}^{(n-1)}$ is the estimate of the optimal dwSSA biasing parameters in the (n)th level of the multilevel CE method, ${\mathbf{J}}_k^{(n-1)}$ is the kth dwSSA trajectory parameterized with ${\widehat{\gamma }}^{(n-1)}$, and n_kj is the total number of times reaction R_j fires in the kth trajectory. The index k in ${\sum }_k^{\prime }$ includes only the trajectories reaching the rare event. The multilevel CE method defines a series of intermediate “less rare” events and sequentially biases the system towards these events until the target rare event is reached. The process starts by simulating $K_{\text{CE}}$ trajectories of the system in the interval $[0,\mathcal{T}]$ using the dwSSA with all parameters set to 1 (≡ SSA). We record the top $\lceil \rho K_{\text{CE}}\rceil$ trajectories (where ρ is typically ∼10⁻²) that evolve farthest in the direction of the set E, and we label those states reached by the $\lceil \rho K_{\text{CE}}\rceil$ recorded trajectories that are closest to E as ${\mathcal{E}}_0$. The set ${\mathcal{E}}_0$ represents a “less rare” event, and we solve for the corresponding optimal dwSSA parameters ${\widehat{\gamma }}^{\left(0\right)}$. This process repeats n times, until the intermediate set of states ${\mathcal{E}}_n$ is contained in the target rare event set E. We note that Eq. 6 represents one of M uncoupled equations from the final step of the multilevel algorithm in Ref. 5, where ${\widehat{\gamma }}^{*\left(n\right)}\equiv {\widehat{\gamma }}^{*}$. In practice, each of these equations is solved at every level of the CE method until the final parameter estimates are obtained. For an intuitive explanation of why Eq. 6 works, we note that the numerator represents a weighted sum of the total number of times reaction R_j fires across the successful trajectories, whereas the denominator is a weighted sum of the expected total number of times reaction R_j will fire across those same trajectories. Reactions that are needed to fire more often than their average behavior to reach the rare event will thus acquire a ${\widehat{\gamma }}_j^{*}$ greater than 1, whereas reactions needed to fire less often than average will acquire a ${\widehat{\gamma }}_j^{*}$ less than 1.

SDWSSA FORMULATION AND THE MULTILEVEL CROSS-ENTROPY METHOD

If our goal is to simply transform γ_j in Eq. 3 into a state-dependent IS parameter, the number of possible transformations is infinite. However, it is important that any state-dependent biasing scheme be computationally inexpensive and, more importantly, allow for a closed-form solution for the IS parameters when combined with the cross-entropy method. In Ref. 5, the authors showed that although the wSSA predilection function was simple to compute, its formulation did not give rise to a closed-form solution for the wSSA parameters. In Secs. 3A–III B, we present a novel state-dependent importance sampling scheme whose IS parameters are easily computable in closed form. Section 3A introduces the sdwSSA and describes its state-dependent IS strategy. Section 3B integrates the sdwSSA into the cross-entropy framework and derive s a closed form solution for the optimal state-dependent IS parameters.

State-dependent doubly weighted SSA

It is well known that the optimal importance biasing scheme for any IS problem is state-dependent. In typical biochemical systems, molecular populations of species change constantly during a simulation as reactions fire. If only one IS parameter is used for each reaction regardless of the system state, then γ_j is a positive constant that is multiplied by $a_j\left(\mathbf{X}\left(t\right)\right)$ at every time step. In this case, the best choice for γ_j would be a value that perturbs the jth reaction by the “right amount” for “most of the visited states,” which is the precise strategy used by the dwSSA. For a reaction R_j whose propensity changes substantially as the system evolves, this strategy will under- and over-perturb R_j when its propensity takes on values that are much larger or smaller than average. We can improve such sub-optimal biasing with a properly formulated state-dependent biasing scheme.

The most obvious approach for making γ_j state-dependent is to set it to a time-varying function of the system state, i.e., ${\gamma }_j\left(\mathbf{X}\left(t\right)\right)$. However, this is not a good formulation for two reasons. First, closed-form expressions for ${\gamma }_j^{*}$ are not available when γ_j is a continuous function. Second, the system state alone is not sufficient to determine the amount of perturbation each reaction requires. Many different configurations of the state vector can yield the same propensity value for a reaction involving more than one species, and the possible number of states may be infinite. A better form for γ_j would be a discrete function that depends on the relative propensity, $a_j\left(\mathbf{X}\left(t\right)\right)/a_0\left(\mathbf{X}\left(t\right)\right)$, which corresponds to the likelihood of choosing R_j as the next reaction to fire. For simplicity, we assign a new variable ${\pi }_j\left(\mathbf{X}\left(t\right)\right)$ to denote the jth relative propensity, i.e., ${\pi }_j\left(\mathbf{X}\left(t\right)\right)\equiv a_j\left(\mathbf{X}\left(t\right)\right)/a_0\left(\mathbf{X}\left(t\right)\right)$.

In short, our proposed state-dependent biasing scheme discretizes ${\pi }_j\left(\mathbf{X}\left(t\right)\right)$ into non-overlapping bins, and we estimate a constant biasing parameter for each bin. Thus, compared to the dwSSA, the sdwSSA requires additional biasing parameters for each reaction as well as bin discretization end points for each reaction. Specifically, the sdwSSA predilection function is given by

$$\begin{array}{ccc}& & b_j\left(\mathbf{X}\left(t\right)\right)\equiv {\gamma }_j\left({\pi }_j\left(\mathbf{X}\left(t\right)\right)\right)\times a_j\left(\mathbf{X}\left(t\right)\right),\hfill \\ & & b_0\left(\mathbf{X}\left(t\right)\right)=\sum _{j=1}^M{b}_j\left(\mathbf{X}\left(t\right)\right),\hfill \end{array}$$ (7)

where γ_j(π_j) is a step function defined by

$${\gamma }_j\left({\pi }_j\right)=\left\{\begin{array}{cc}\hfill {\gamma }_{j1},& \hfill \text{if}{\pi }_j\le c_j^1\\ \hfill {\gamma }_{j2},& \hfill \text{if}{c}_j^1<{\pi }_j\le c_j^2\\ \hfill ⋮& \hfill ⋮\\ \hfill {\gamma }_{j{\beta }_j},& \hfill \text{if}{c}_j^{{\beta }_j-1}<{\pi }_j\end{array}\right.,0<c_j^1<\cdots <c_j^{{\beta }_j-1}<1.$$ (8)

Here, β_j is the total number of bins used to discretize π_j. The number of end points required for β_j bins is β_j + 1, and the minimum and maximum possible values of any relative propensity are 0 and 1, respectively. Therefore, we need (β_j + 1 − 2) total end points, which are denoted by $\{c_j^1,\cdots ,c_j^{{\beta }_j-1}\}$ in Eq. 8. These end points are defined by the following process. During the nth round of CE simulations, we determine the relative propensity range of each reaction parameterized with ${\widehat{\gamma }}_j^{(n-1)}$. After completing these simulations, we divide each relative propensity π_j into β_max bins, where β_max is a global variable denoting the maximum number of bins for any reaction. In the next round of CE simulations, we record the number of reaction firings in each bin. We identify bins with fewer than κ_min firings, where κ_min is the minimum number required for each bin. We then repeatedly merge each of these bins with the adjacent bin having the fewest number of firings until the aggregate bin has at least κ_min firings. Upon completion, we update the coordinates and numbers of reaction firings in all merged bins. Once we have completed merging, the end points of β_j bins are given by $\{0,c_j^1,\cdots ,c_j^{{\beta }_j-1},1\}$. For convenience, we let cdenote a list of vectors $\{[c_1^1,\cdots ,c_1^{{\beta }_1-1}],\cdots ,[c_M^1,\cdots ,c_M^{{\beta }_M-1}]\}$.

As with the dwSSA, the sdwSSA biases both the index of the next reaction and the time to that reaction. Using the biasing scheme in Eqs. 7, 8, the probability of the reaction trajectory in Eq. 1 under the sdwSSA is given by

$$\begin{array}{cc}\hfill {\mathrm{P}}_{\text{sdwSSA}}\left(\mathbf{J}\right)& {\displaystyle =\prod _{i=1}^{N_{\mathcal{T}}}\left[b_{j_i^{\prime }}\left(\mathbf{X}\left(t_i\right)\right)e^{-b_0\left(\mathbf{X}\left(t_i\right)\right){\tau }_i}d\tau \right]}\end{array}$$ (9a)

$$\begin{array}{ccc}& & =\prod _{i=1}^{N_{\mathcal{T}}}[({\gamma }_{j_i^{\prime }}\left({\pi }_{j_i^{\prime }}\left(\mathbf{X}\left(t_i\right)\right)\right)\times a_{j_i^{\prime }}\left(\mathbf{X}\left(t_i\right)\right))\hfill \\ & & \times e^{-({\sum }_{j=1}^M{\gamma }_j\left({\pi }_j\left(\mathbf{X}\left(t_i\right)\right)\right)\times a_j\left(\mathbf{X}\left(t_i\right)\right)){\tau }_i}d\tau ].\hfill \end{array}$$ (9b)

The sdwSSA predilection function in Eq. 9a has been written in detail in Eq. 9b, to emphasize that it depends on the relative propensity of reactions at each time step. Similarly, the trajectory weight to correct the bias has the same dependence:

$$\begin{array}{ccc}\hfill W_{\text{sdwSSA}}\left(\mathbf{J}\right)& =& \prod _{i=1}^{N_{\mathcal{T}}}\left[\frac{a_{j_i^{\prime }}\left(\mathbf{X}\left(t_i\right)\right)e^{-a_0\left(\mathbf{X}\left(t_i\right)\right){\tau }_i}}{({\gamma }_{j_i^{\prime }}\left({\pi }_{j_i^{\prime }}\left(\mathbf{X}\left(t_i\right)\right)\right)\times a_{j_i^{\prime }}\left(\mathbf{X}\left(t_i\right)\right))e^{-({\sum }_{j=1}^M{\gamma }_j\left({\pi }_j\left(\mathbf{X}\left(t_i\right)\right)\right)\times a_j\left(\mathbf{X}\left(t_i\right)\right)){\tau }_i}}\right].\hfill \end{array}$$ (10)

The product of Eqs. 9a, 10 equals the probability 1, which is the probability of an unbiased SSA trajectory. Thus, the sdwSSA weight is the ratio between the SSA and the sdwSSA of trajectory probabilities. As illustrated in Sec. 3B, the value of the biasing scheme of Eqs. 7, 8 is that it gives rise to closed form solutions for all ${\sum }_{j=1}^M{\beta }_j$ IS parameters. In addition, the biasing scheme imposes very little computational overhead: only the original reaction propensity is required to determine the degree of perturbation in Eq. 8.

The sdwSSA and the cross-entropy method

The derivation of a closed-form solution for the sdwSSA parameter values can be obtained in a similar manner to that used for the dwSSA. Following the same logic as in Ref. 5, we derive the following system of ${\sum }_{j=1}^M{\beta }_j$ equations:

$$\begin{array}{ccc}& & \sum _{k=1}^K\left[I_{\{S\left({\mathbf{J}}_k^{\left(0\right)}\right)\cap \mathcal{E}\}}\times W_{\text{sdwSSA}}\left({\mathbf{J}}_k^{\left(0\right)};{\gamma }^{\left(0\right)}\right)\times \underset{\gamma }{\nabla }\ln {\mathrm{P}}_{sdwSSA}({\mathbf{J}}_k^{\left(0\right)};\widehat{{\gamma }^{*}})\right]\hfill \\ & & =\mathbf{0},\hfill \end{array}$$ (11)

where $\widehat{{\gamma }^{*}}=\{[{\widehat{\gamma }}_{11}^{*},...,{\widehat{\gamma }}_{1{\beta }_1}^{*}],...,[{\widehat{\gamma }}_{M1}^{*},...,{\widehat{\gamma }}_{M{\beta }_M}^{*}]\}$ and ${\mathbf{J}}_k^{\left(0\right)}$ is the kth sdwSSA trajectory parameterized with ${\gamma }^{\left(0\right)}$. Here we note that γγ cannot necessarily be expressed as a matrix, because each reaction can have a different value for β_j.

Next, we substitute Eq. 9a into Eq. 11 to obtain

$$\begin{array}{ccc}\hfill \mathbf{0}& =& \sum _{k=1}^K\left[I\times W\times \underset{\gamma }{\nabla }\ln \left(\prod _{i=1}^{N_{{\mathcal{T}}_k}}\left[b_{j_{ki}^{\prime }}\left({\mathbf{X}}_k\left(t_{ki}\right)\right)e^{-b_0\left({\mathbf{X}}_k\left(t_{ki}\right)\right){\tau }_{ki}}d\tau \right]\right)\right]\hfill \\ & =& \sum _{k=1}^K\left[I\times W\times \underset{\gamma }{\nabla }\ln \left(\prod _{i=1}^{N_{{\mathcal{T}}_k}}\left[{\widehat{\gamma }}_{j_{ki}^{\prime }}^{*}\left({\mathbf{X}}_k\left(t_{ki}\right)\right)a_{j_{ki}^{\prime }}\left({\mathbf{X}}_k\left(t_{ki}\right)\right)\right.\right.\right.\hfill \\ & & \left.\left.\left.\times \exp \left\{-{\tau }_{ki}\sum _{j=1}^M\left[{\widehat{\gamma }}_j^{*}\left({\mathbf{X}}_k\left(t_{ki}\right)\right)a_j\left({\mathbf{X}}_k\left(t_{ki}\right)\right)\right]\right\}d\tau \right]\right)\right],\hfill \end{array}$$ (12)

where the subscripts in the first two factors inside the summation have been removed. Upon taking the logarithm, collecting terms not depending on $\widehat{{\gamma }^{*}}$ in C_ki, and simplifying, we obtain

$$\begin{array}{ccc}\hfill \mathbf{0}& =& \sum _{k=1}^K\left[I\times W\times \underset{\gamma }{\nabla }\left(\sum _{i=1}^{N_{{\mathcal{T}}_k}}\left[\ln \left({\widehat{\gamma }}_{j_{ki}^{\prime }}^{*}\left({\mathbf{X}}_k\left(t_{ki}\right)\right)\right)\right.\right.\right.\hfill \\ & & \left.\left.\left.-{\tau }_{ki}\sum _{j=1}^M\left[{\widehat{\gamma }}_j^{*}\left({\mathbf{X}}_k\left(t_{ki}\right)\right)a_j\left({\mathbf{X}}_k\left(t_{ki}\right)\right)\right]+C_{ki}\right]\right)\right].\hfill \end{array}$$ (13)

After differentiation, we obtain a scalar version of Eq. 13 for all β_j bins of all M reactions, which leads to the following detailed closed-form expression for each optimal parameter estimate:

$$\begin{array}{ccc}& & {\widehat{\gamma }}_{jr}^{\left(n\right)}=\frac{{{\displaystyle \sum }}_k^{\prime }\left(W_{sdwSSA}({\mathbf{J}}_k^{(n-1)};{\widehat{\gamma }}^{(n-1)})\times n_{kjr}\right)}{{{\displaystyle \sum }}_k^{\prime }\left(W_{sdwSSA}({\mathbf{J}}_k^{(n-1)};{\widehat{\gamma }}^{(n-1)})\times {{\displaystyle \sum }}_i^{\prime }{a}_j\left({\mathbf{X}}_k^{(n-1)}\left(t_{ki}\right)\right){\tau }_{ki}\right)},\hfill \\ & & j=1,\cdots ,M,r=1,\cdots ,{\beta }_j,\hfill \end{array}$$ (14)

where n_kjr is the total number of times reaction j fires with ${\widehat{\gamma }}_{jr}^{(n-1)}$ as its IS parameter in the kth trajectory. We emphasize the similarity between Eqs. 6, 14. In both expressions, the summation operator ${\sum }_k^{\prime }$ includes only those trajectories that have reached the rare event; in the latter expression, ${\sum }_i^{\prime }$ also includes only those time steps where reaction R_j fired at time t_ki, with ${\widehat{\gamma }}_{jr}^{(n-1)}$ as its IS parameter. Equation 14 represents one of ${\sum }_{j=1}^M{\beta }_j$ uncoupled equations from the final step of the multilevel CE algorithm, where ${\widehat{\gamma }}^{\left(n\right)}\equiv {\widehat{\gamma }}^{*}$. We note that the numerator in Eq. 14 represents a weighted sum of the total number of times R_j fires with ${\widehat{\gamma }}_{jr}^{(n-1)}$ as its IS parameter over the trajectories that reached the rare event. Similarly, the denominator is a weighted sum of the expected total number of times R_j will fire with ${\widehat{\gamma }}_{jr}^{(n-1)}$ as its IS parameter across those same trajectories. Therefore, ${\widehat{\gamma }}_{jr}^{*}$ will be greater than 1 if the rth IS parameter for R_j is chosen more often than on average to reach the rare event and less than 1 otherwise.

An important consideration when using the multilevel CE method is that the system reaches a rare event after passing through multiple rounds of “less rare” events. The relative propensity range spanned by a reaction upon reaching the first less rare event may differ greatly from the one spanned by the same reaction after reaching the final (i.e., target) rare event. We have resolved this difficulty by dynamically measuring the relative propensity range and adjusting bin sizes at every step of the multilevel CE method.

The entire process for rare event characterization with the sdwSSA and the multilevel cross-entropy method can be compactly described using the following two algorithms: core sdwSSA and CE-DB (cross entropy-dynamic binning). Lines 5, 14, 16 (core sdwSSA) and 1, 7, 10, 12, 16, 17, 19, 21 (CE-DB) contain instructions that are specific to the sdwSSA (i.e., that differ from dwSSA). First, we learn the optimal state-dependent biasing parameters γ and bin end points c using CE-DB, which calls the core sdwSSA in each level of the multilevel cross-entropy method with $K_{\text{CE}}$ number of trajectories. Once the CE-DB returns γ andc , they are substituted into the core sdwSSA along with K (the total number of realizations) to estimate the rare event probability $p({\mathbf{x}}_0,\mathcal{E};t)$. In our experience, the number of realizations K required to accurately compute ${\widehat{p}}_{\text{sdwSSA}}({\mathbf{x}}_0,\mathcal{E};t)$ is much greater than $K_{\text{CE}}$ required to accurately compute ${\widehat{\gamma }}_{\text{sdwSSA}}^{*}$. In core sdwSSA, ${\nu }_j$ and t_f represent the state change vector for R_j and the simulation end time, respectively.

Algorithm: Core sdwSSA

Input:$K,\gamma$ and c

1: mK ← 0

2: fork = 1 to Kdo

3:  t ← 0, $\mathbf{x}\leftarrow {\mathbf{x}}_0$, w ← 1

4:  evaluate all $a_j\left(\mathbf{x}\right)$ and calculate $a_0\left(\mathbf{x}\right)$

5:  evaluate all ${\gamma }_j\left({\pi }_j\left(\mathbf{x}\right)\right)$ and $b_j\left(\mathbf{x}\right)$; calculate $b_0\left(\mathbf{x}\right)$

6:  whilet ⩽ tfdo

7:  if$\mathbf{x}\in \mathcal{E}$then

8:   mK ← mK + w

9:   break out of the while loop

10:  endif

11:   generate two unit-interval uniform random numbers r1 and r2

12:   $\tau \leftarrow {b_0}^{-1}\left(\mathbf{x}\right)\ln (1/r_1)$

13:   j ← smallest integer satisfying ${\sum }_{i=1}^j{b}_i\left(\mathbf{x}\right)\ge r_2{b}_0\left(\mathbf{x}\right)$

14:   $w\leftarrow w\times {\left({\gamma }_j\left({\pi }_j\left(\mathbf{x}\right)\right)\right)}^{-1}\times \exp \left\{(b_0\left(\mathbf{x}\right)-a_0\left(\mathbf{x}\right))\tau \right\}$

15:   t ← t + τ, $\mathbf{x}\leftarrow \mathbf{x}+{\nu }_j$

16:   update all $a_j\left(\mathbf{x}\right)$ and $a_0\left(\mathbf{x}\right)$; recalculate ${\gamma }_j\left({\pi }_j\left(\mathbf{x}\right)\right)$, $b_j\left(\mathbf{x}\right)$ and $b_0\left(\mathbf{x}\right)$

17:  endwhile

18: endfor

19: return${\widehat{p}}_{sdwSSA}({\mathbf{x}}_0,\mathcal{E};t)=m_K/K$

Algorithm: CE-DB (cross entropy-dynamic binning)

Input:$K_{\text{CE}},\rho ,{\beta }_{max,}$ and κmin

1: $\gamma \leftarrow \{v_1,\cdots ,v_M\}$, where vj is a vector of 1s with length βmax

2: i ← −1

3: repeat

4:  i ← i + 1

5:  while running core sdwSSA with $K=K_{\text{CE}}$do

6:   mark the $\lceil \rho K_{\text{CE}}\rceil$ trajectories evolving farthest in the direction of E

7:   record min(πj) and max(πj)

8:  endwhile

9:  ${\mathcal{E}}_i\leftarrow$ at most $\lceil \rho K_{\text{CE}}\rceil$ states closest to E reached by the marked trajectories (one per trajectory)

10:  $c_j^r\leftarrow \text{min}\left({\pi }_j\right)+\frac{\text{max}\left({\pi }_j\right)-\text{min}\left({\pi }_j\right)}{{\beta }_{max}}\times r,r\in \{1,\cdots ,({\beta }_{max}-1)\}$

11:  while running core sdwSSA with $K=K_{\text{CE}}$do

12:   record the number of firings among βmax bins for each reaction

13:   store information of trajectories that reach ${\mathcal{E}}_i$

14:  endwhile

15:  forj = 1 → Mdo

16:   merge bins until every bin contains greater than κmin reaction firings

17:   update $\{c_j^1,\cdots ,c_j^{{\beta }_j-1}\}$ according to the result from step 16

18:  endfor

19:  $\gamma \leftarrow$ result of Eq. 14 evaluated using ${\mathcal{E}}_i$ and trajectories from step 13

20: until${\mathcal{E}}_i\subseteq \mathcal{E}$

21: return$\widehat{{\gamma }^{*}}=\gamma$ and c

The two input parameters in the CE-DB, β_max and κ_min, are specific to the sdwSSA and control the dynamic binning strategy. Based on our experience, we recommend setting β_max = 10 and κ_min = 20. In Sec. 4, we test the sensitivity of the rare event estimate with respect to these parameters to illustrate the robustness of the sdwSSA.

Once CE-DB completes and returns ${\widehat{\gamma }}^{*}$ and c, we substitute these values into the core sdwSSA to obtain the estimate ${\widehat{p}}_{\text{sdwSSA}}({\mathbf{x}}_0,\mathcal{E};t)$. Thus the total complexity of the rare event characterization process is (2n × the complexity of the sdwSSA), where n is the number of steps taken by the CE-DB. All examples we tested used n ⩽ 4. For these examples, the time needed for the CE-DB was much less than the time required for the core sdwSSA.

Finally, we note that the above two algorithms are easily parallelized. Specifically, the K trajectories simulated in the core sdwSSA can be generated independently. In all examples below, we execute the core sdwSSA and the CE-DB using a parallel computing cluster. Source code for CE-DB and the core sdwSSA is available upon request.

EXAMPLES

We illustrate sdwSSA performance on the following three examples: a reversible isomerization process, a yeast polarization model, and a lac operon model. For each example, we compare sdwSSA results and central processing unit (CPU) time with that of dwSSA. Unless otherwise mentioned, we use the default parameter values listed in Table 1.

Table 1.

List of input parameters for the core sdwSSA and the CE-DB

Parameter default value		Description
K	106	Number of realizations used to compute $\widehat{p}$
$K_{\text{CE}}$	105	Number of realizations used to compute ${\widehat{\gamma }}^{*}$
ρ	0.01	Fraction of trajectories in CE-DB
βmax	10	Maximum number of reaction bins
κmin	20	Minimum number of data points per bin

To ensure fair comparison, we computed the dwSSA estimate with the same value of $K_{\text{CE}}$ as with the sdwSSA. As the dwSSA required a larger value of K to exhibit comparable accuracy to the sdwSSA, we continued simulating dwSSA trajectories until the dwSSA estimate uncertainty was approximately equal to that of the sdwSSA. When possible, we also estimated rare event probabilities using the swSSA parameterized with the optimal parameter values given in Ref. 7. Finally, we computed a 68% confidence interval for every estimate using the method described in Ref. 8.

To study the relationship between β_max and the accuracy of an sdwSSA estimate, we compared the uncertainties computed with different values of β_max ∈ {1, 2, …, 15}, where the sdwSSA estimate with β_max = 1 is equivalent to a dwSSA estimate. We performed a similar comparison with κ_min when applicable. All results were obtained by running in parallel on a 54 processor cluster (Intel Xeon 2.27 GHz).

Finally, we simplified our definition of a rare event in the following three examples by limiting the states of interest E to those governed by only a single species S. Specifically, we define a threshold species count θ^S above/below which the event occurs, rewriting $p({\mathbf{x}}_0;\mathcal{E};t)$ as $p({\mathbf{x}}_0;{\theta }^S;t)$.

Reversible isomerization

Our first example is taken from Ref. 7 and concerns isomers A and B that are interconverted according to the following two reactions:

$$\begin{array}{ccc}\hfill A& \stackrel{k_1}{\to }& B,k_1=0.12\hfill \\ \hfill B& \stackrel{k_2}{\to }& A,k_2=1\hfill \end{array}$$

with ${\mathbf{x}}_0=\left[1000\right]$.

We examine the rare event probability $p({\mathbf{x}}_0,{\theta }^B;t)\equiv p({\mathbf{x}}_0,30;10)$, the probability that the population of species B reaches 30 before time 10, given that the initial population is [100 0]. For this simple system the state space is finite, and it is possible to calculate the exact probability ($p({\mathbf{x}}_0,30;10)=1.191\times {10}^{-5}$) by constructing a generator matrix⁹.

The optimal parameters for the dwSSA and the sdwSSA were learned from running the dwSSA multilevel CE method and the CE-DB, respectively. The optimal parameters for the swSSA were taken from Ref. 7. Table 2 summarizes the results. For each method, the rare event probability estimate, estimate uncertainty, CE-DB run time, and total simulation time are displayed. The optimal set of biasing parameters employed in each method is listed in Table 3.

Table 2.

Results for the reversible isomerization model.

Method	$\widehat{p}({\mathbf{x}}_0,{\theta }^B;t)$	68% uncertainty	CE-DB time (s)	Total time (s)
swSSA	1.190 × 10−5	0.002 × 10−5	NA	27
dwSSA	1.190 × 10−5	0.002 × 10−5	36	1.29 × 105
sdwSSA	1.193 × 10−5	0.002 × 10−5	22	30

Table 3.

Importance sampling parameters for the reversible isomerization process.

Method	Algorithmic parameters
swSSA	${\gamma }_1^{max}=20,{\rho }_1^0=0.5$
dwSSA	${\widehat{\gamma }}^{*}=\left[1.3010.719\right]$
sdwSSA	${\widehat{\gamma }}^{*}=\{[2.69,1.74,1.26,1.11,1.06,1.03,1.02,1.02,1.06,1.00],$
	[1.01, 0.99, 0.97, 0.97, 0.95, 0.92, 0.83, 0.62, 0.40]},
	$\mathbf{c}=\left\{\right[0.30,0.38,0.46,0.54,0.61,0.69,0.77,0.85,0.92],$
	[0.15, 0.23, 0.31, 0.39, 0.46, 0.54, 0.62, 0.70]}

The total sdwSSA runtime is approximately equal to the runtime of the swSSA. Although the sdwSSA did not require any prior information to obtain the estimate in Table 2, the swSSA was given a window of parameter values that contained the optimal biasing parameter. Without this prior information, the number of trials to find the optimal swSSA biasing parameters (and thus the total simulation time) would be significantly greater. The dwSSA runtime to reach the accuracy of the sdwSSA estimate in Table 2 is about 4300 times greater than the sdwSSA runtime. Moreover, the sdwSSA required less time to estimate its optimal biasing parameters than the dwSSA: CE-DB utilized one fewer intermediate rare event than the dwSSA multilevel CE method. For this example, it is clear that a state-dependent biasing strategy significantly improved efficiency in estimating $p({\mathbf{x}}_0,30;10)$.

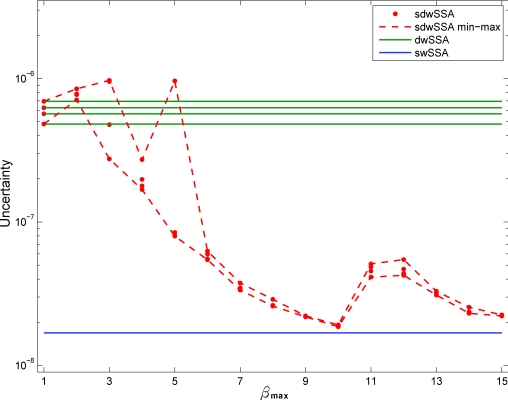
The sdwSSA estimate in Table 2 was obtained with β_max = 10 and κ_min = 20. If we decrease β_max to 1, the sdwSSA becomes equivalent to the dwSSA regardless of the value used for κ_min. We therefore expected the accuracy of the sdwSSA estimate to increase with increasing β_max, with this trend ending only when the value of β_max leads to the creation and merging of superfluous bins. For this example, we recomputed sdwSSA estimate uncertainties (by re-running the CE-DB and the core sdwSSA) using values of β_max in {1, 2, …, 15}, keeping all other parameters the same as before. Figure 1 compares the results of four independent sdwSSA estimates at each value of β_max to the dwSSA and swSSA.

Figure 1.

Uncertainty vs β_max for the reversible isomerization process. For each β_max, four independent sdwSSA estimates are obtained. The two dotted red lines connect the minimum and maximum uncertainties at each β_max value. The blue line corresponds to the uncertainty obtained from K = 10⁶ swSSA simulations, parameterized with the optimal IS parameters listed in Table 3. The four green lines represent uncertainties of dwSSA estimates.

As expected, the sdwSSA uncertainty decreases with increasing β_max, although the four estimates for β_max ⩽ 6 exhibit high variability. This variability diminishes for larger β_max, indicating a more consistent discretization of relative propensities. As β_max reaches a value of 11, we see a reproducible increase in uncertainty. This increase is specific only to the reversible isomerization model (see examples below). We suspect that it is due to an artifact of our binning strategy. We note that the uncertainty at β_max = 11 is still an order of magnitude less than the lowest uncertainty achieved by dwSSA estimates. As we further increase β_max, the uncertainty again decreases toward that achieved by the swSSA.

Figure 1 does not show the effects of varying κ_min. Each isomerization reaction fires at least 80 000 times in a single simulation, so unless we increase κ_min to 200, the algorithm yields the same estimate as in Table 2 with κ_min = 20. We thus conclude that this rare event probability estimate is not sensitive to κ_min.

Yeast polarization

Next we consider the pheromone-induced G-protein cycle in Saccharomyces cerevisiae. This system is taken from Ref. 5 and consists of seven species x = [R  L  RL  G  G_a  G_bg  G_d], whose dynamics are represented by the following eight reactions:

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill R1:& \hfill \varnothing \stackrel{k_1}{\to }R& \hfill k_1=0.0038\\ \hfill R2:& \hfill R\stackrel{k_2}{\to }\varnothing & \hfill k_2=4.00\times {10}^{-4}\\ \hfill R3:& \hfill L+R\stackrel{k_3}{\to }RL+L& \hfill k_3=0.042\\ \hfill R4:& \hfill RL\stackrel{k_4}{\to }R& \hfill k_4=0.010\\ \hfill R5:& \hfill RL+G\stackrel{k_5}{\to }{G}_a+G_{bg}& \hfill k_5=0.011\\ \hfill R6:& \hfill G_a\stackrel{k_6}{\to }{G}_d& \hfill k_6=0.100\\ \hfill R7:& \hfill G_d+G_{bg}\stackrel{k_7}{\to }G& \hfill k_7=1.05\times {10}^3\\ \hfill R8:& \hfill \varnothing \stackrel{k_8}{\to }RL& \hfill k_8=3.21,\end{array}\end{array}$$

with ${\mathbf{x}}_0=\left[502050000\right]$. For this system, we estimated the rare event probability $p({\mathbf{x}}_0,{\theta }^{G_{bg}};t)\equiv p({\mathbf{x}}_0,40;5)$; i.e., the probability that the population of G_bg reaches 40 before time 5. To accurately estimate this probability using any method, it is necessary to bias more than one reaction of the system. However, the tortuous trial and error procedure associated with optimizing two or more parameters of the swSSA prohibits us from estimating $p({\mathbf{x}}_0,{\theta }^{G_{bg}};t)$ with this method. The dwSSA and the sdwSSA estimates were obtained by first computing respective optimal biasing parameters using the multilevel CE method with $K_{\text{CE}}={10}^6$, followed by simulating K = 10⁷ sdwSSA and 6 × 10⁸ dwSSA trajectories to estimate the rare event probability. We note that due to the high intrinsic stochasticity, we increased the values for $K_{\text{CE}}$ and sdwSSA K by ten times their default values. The simulation results and optimal biasing parameters are summarized in Tables 4, 5, respectively.

Table 4.

Results for the yeast polarization model.

Method	$\widehat{p}({\mathbf{x}}_0,{\theta }^{G_{bg}};t)$	68% uncertainty	CE-DB time (s)	Total time (s)
dwSSA	1.058 × 10−11	0.010 × 10−11	51	3116
sdwSSA	1.082 × 10−11	0.010 × 10−11	51	132

Table 5.

Optimal IS parameters for the yeast polarization model.

j	${\widehat{\gamma }}_{dwSSA}^{*}$	${\widehat{\gamma }}_{sdwSSA}^{*}$
1	0.786	[0.729 1.216 0.971 0.889 2.137]
2	0.670	[0.939 0.766 0.790 0.988 0.418 0.778 0.151 0.945]
3	1.800	[1.477 1.631 1.785 1.899 1.929 1.903 1.839 1.826 1.863]
4	0.692	[0.366 0.455 0.465 0.547 0.620 0.612 1.194]
5	1.687	[1.042 3.455 4.743 3.136 2.237 1.659 1.380 1.277 1.222 1.186]
6	0.250	[0.356 0.368 0.343 0.325 0.284 0.246 0.237 0.184 0.148 0.121]
7	0.987	[1.001]
8	2.048	[2.064 2.072 2.029 1.796 2.413 2.446 2.443]
j		c
1		[0.000259 0.00031 0.000362 0.000414]
2		[0.000822 0.0011 0.00137 0.00164 0.00192 0.00219 0.00246]
3		[0.115 0.172 0.23 0.287 0.344 0.402 0.459 0.517]
4		[0.00571 0.00857 0.0114 0.0143 0.0171 0.0200]
5		[0.069 0.138 0.207 0.276 0.345 0.414 0.483 0.552 0.621]
6		[0.0398 0.0796 0.119 0.159 0.199 0.239 0.279 0.318 0.358]
7		NA
8		[0.175 0.219 0.262 0.306 0.35 0.394 ]

In Table 4, the simulation time of the dwSSA to yield an estimate of similar accuracy as the sdwSSA is 24 times greater than the sdwSSA simulation time. When we compare ${\widehat{\gamma }}_{\text{dwSSA}}^{*}$ to ${\widehat{\gamma }}_{\text{sdwSSA}}^{*}$ in Table 5, the largest differences are observed in the parameters of R₄, R₅, and R₆ (ignoring the parameters of R₁ and R₂, which were previously shown to have a negligible influence on the accuracy of the probability estimate). The sdwSSA parameters of the other reactions (excluding R₁ and R₂) do not show appreciable variation between bins and are in general agreement with the optimal dwSSA parameters. We conclude that the use of state-dependent IS parameters for R₄, R₅, and R₆ is largely responsible for the almost 25-fold computational gain of the sdwSSA over the dwSSA.

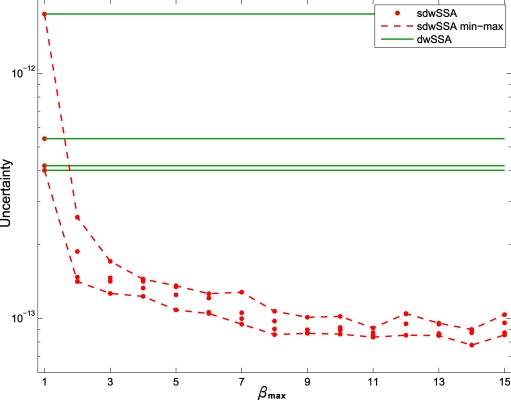
We next measured the sensitivity of ${\widehat{p}}_{\text{sdwSSA}}$ to β_max. As before, we computed four independent sdwSSA probability estimates for β_max = {1, …, 15}. Figure 2 displays their uncertainties. As expected, the uncertainties gradually decrease with increasing β_max. Unlike with the reversible isomerization model, we do not display the swSSA uncertainty for the yeast model since it is not feasible to optimize multiple swSSA IS parameters.

Figure 2.

Uncertainty vs β_max for the yeast polarization model. For each β_max, four independent instances of the CE-DB with $K_{\text{CE}}={10}^6$ were executed, followed by four instances of the core sdwSSA with K = 10⁷. Each red dot corresponds to the uncertainty of sdwSSA estimates, and two red lines connect the minimum and the maximum uncertainties in each β_max value. The four green lines represent dwSSA uncertainties.

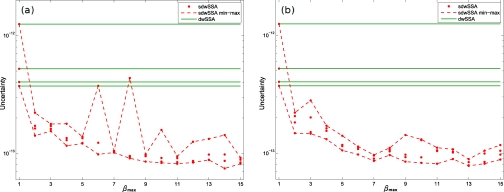
Finally, we evaluated the sensitivity of ${\widehat{p}}_{\text{sdwSSA}}$ to the κ_min parameter. We executed the CE-DB and the core sdwSSA as before, using either κ_min = 10 or κ_min = 30. The results are shown in Fig. 3. We see no apparent uncertainty differences among estimates generated with κ_min = 20 (Fig. 2) and κ_min = 30 (Fig. 3b). However, estimate uncertainty varies more strongly between the four ensembles using κ_min = 10 (Fig. 3a). We hypothesize that this higher variability is due to an insufficient number of reaction firings in each bin used to estimate the optimal sdwSSA parameters. Since the yeast system exhibits high intrinsic stochasticity, consistent estimates of IS parameters likely require >10 reaction firings in each bin. This helps to illustrate a general point: whereas setting κ_min too high can decrease β_j, leading to suboptimal exploration of the relative propensity range, setting it too low can increase estimate variance. For the problems we have tested, κ_min = 20 seems to confer proper discretization of the relative propensity range as well as reliable estimation of sdwSSA parameters.

Figure 3.

Uncertainty vs β_max for the yeast polarization model. All data were generated using the same simulation settings as in Fig. 2, except for the value of κ_min. Panel (a) was generated with κ_min = 10, and panel (b) was generated with κ_min = 30. Estimated uncertainties obtained with κ_min = 10 display significantly higher variability among the four ensembles than the estimates obtained with κ_min = 20 or κ_min = 30. As the magnitude of the rare event probability is very small, we suspect that greater numbers of firings are required in each bin to obtain reliable estimates of the state-dependent IS parameters.

Lac operon

Our last example is a lac operon model¹⁰ consisting of 12 species (x = [M_R  R  R₂  O  R₂O  I  I_ex  I₂R₂  M_Y  Y  YI_ex  Y_tot]) and the following 25 reactions:

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill R1:& \hfill \varnothing \stackrel{k_1}{\to }{M}_R& \hfill k_1=0.111\\ \hfill R2:& \hfill M_R\stackrel{k_2}{\to }{M}_R+R& \hfill k_2=15.0\\ \hfill R3:& \hfill 2R\stackrel{k_3}{\to }{R}_2& \hfill k_3=103.8\\ \hfill R4:& \hfill R_2\stackrel{k_4}{\to }2R& \hfill k_4=0.001\\ \hfill R5:& \hfill R_2+O\stackrel{k_5}{\to }{R}_{2}O& \hfill k_5=1992.7\\ \hfill R6:& \hfill R_{2}O\stackrel{k_6}{\to }{R}_2+O& \hfill k_6=2.40\\ \hfill R7:& \hfill 2I+R_2\stackrel{k_7}{\to }{I}_2{R}_2& \hfill k_7=1.293\times {10}^{-6}\\ \hfill R8:& \hfill I_2{R}_2\stackrel{k_8}{\to }2I+R_2& \hfill k_8=12.0\\ \hfill R9:& \hfill 2I+R_{2}O\stackrel{k_9}{\to }{I}_2{R}_2+O& \hfill k_9=1.293\times {10}^{-6}\end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill R10:& \hfill I_2{R}_2+O\stackrel{k_{10}}{\to }2I+R_{2}O& \hfill k_{10}=9963.2\\ \hfill R11:& \hfill O\stackrel{k_{11}}{\to }O+M_Y& \hfill k_{11}=0.50\\ \hfill R12:& \hfill R_{2}O\stackrel{k_{12}}{\to }{R}_{2}O+M_Y& \hfill k_{12}=0.010\\ \hfill R13:& \hfill M_Y\stackrel{k_{13}}{\to }{M}_Y+Y& \hfill k_{13}=30.0\\ \hfill R14:& \hfill Y+I_{ex}\stackrel{k_{14}}{\to }Y{I}_{ex}& \hfill k_{14}=0.249\\ \hfill R15:& \hfill Y{I}_{ex}\stackrel{k_{15}}{\to }Y+I_{ex}& \hfill k_{15}=0.10\\ \hfill R16:& \hfill Y{I}_{ex}\stackrel{k_{16}}{\to }Y+I& \hfill k_{16}=60000\\ \hfill R17:& \hfill I_{ex}\stackrel{k_{17}}{\to }I& \hfill k_{17}=0.920\\ \hfill R18:& \hfill I\stackrel{k_{18}}{\to }{I}_{ex}& \hfill k_{18}=0.920\\ \hfill R19:& \hfill M_R\stackrel{k_{19}}{\to }\varnothing & \hfill k_{19}=0.462\\ \hfill R20:& \hfill M_Y\stackrel{k_{20}}{\to }\varnothing & \hfill k_{20}=0.462\\ \hfill R21:& \hfill R\stackrel{k_{21}}{\to }\varnothing & \hfill k_{21}=0.20\\ \hfill R22:& \hfill R_2\stackrel{k_{22}}{\to }\varnothing & \hfill k_{22}=0.20\\ \hfill R23:& \hfill Y\stackrel{k_{23}}{\to }\varnothing & \hfill k_{23}=0.20\\ \hfill R24:& \hfill Y{I}_{ex}\stackrel{k_{24}}{\to }I& \hfill k_{24}=0.20\\ \hfill R25:& \hfill I_2{R}_2\stackrel{k_{25}}{\to }2I& \hfill k_{25}=0.20\end{array}\end{array}$$

The lac operon genetic switch has been widely studied since it was first discovered in 1960. Specifically, the positive feedback loop underlying the switch has garnered wide interest among researchers because it is accountable for the all-or-none bistable response of the lac operon. The key player in the positive feedback loop is lacY, which facilitates lactose import.

In this example, we consider the rare event probability $p({\mathbf{x}}_0,{\theta }^{Y_{tot}};t)\equiv p({\mathbf{x}}_0,120;0.5)$, i.e., the probability that the total number of Y molecules reaches 120 before time 0.5 given the initial condition ${\mathbf{x}}_0=\left[0001004817700000\right]$. We computed dwSSA and sdwSSA probability estimates for this system using the same simulation settings as in the yeast polarization model (except that K = 4.5 × 10⁷ for the dwSSA). The simulation statistics and the optimal biasing parameters are listed in Table 6 and the Appendix, respectively.

Table 6.

Results for the lac operon model.

Method	$\widehat{p}({\mathbf{x}}_0,{\theta }^{Y_{tot}};t)$	68% uncertainty	CE-DB time (h)	Total time (h)
dwSSA	3.75 × 10−15	0.07 × 10−15	9.33	97.36
sdwSSA	3.72 × 10−15	0.07 × 10−15	11.47	59.52

The total simulation time in Table 6 shows that the dwSSA takes ∼4 days to obtain an estimate of similar accuracy as the sdwSSA estimate, which required less than 2.5 days. We also note that the dwSSA multilevel CE method used three intermediate rare events (${\mathcal{E}}_1=18,{\mathcal{E}}_2=65$, and ${\mathcal{E}}_3=117$) to estimate its optimal biasing parameters, while the multilevel CE method for the sdwSSA required only two (${\mathcal{E}}_1=18$ and ${\mathcal{E}}_2=60$).

A close look at the optimal IS parameter values in Table 7 (with associated bin end points in Table 8) reveals that many of the 25 state-dependent biasing parameters are in agreement with the corresponding state-independent dwSSA parameters. However, several sdwSSA parameters show differences that are worthy of discussion. One group of parameters (e.g., ${\widehat{\gamma }}_1^{*}$ and ${\widehat{\gamma }}_{11}^{*}$) show the same biasing directions in both the dwSSA and the sdwSSA but differ in their magnitudes. The sdwSSA parameter values indicate that R₁ and R₁₁ require significantly more perturbation as they become more likely to fire. In particular, the relative propensity range of R₁₁ is made up of several bins whose optimal IS parameter values are >100. The optimal dwSSA parameter for this reaction is 32.42, which is roughly equivalent to the average sdwSSA parameter value taken over all R₁₁ bins. In the dwSSA regime, setting γ₁₁ ⩾ 32.42 will over-perturb R₁₁ when it is not likely to fire; conversely, decreasing γ₁₁ will under-perturb R₁₁ when it is likely to fire. Reactions R₁ and R₁₁ in the lac operon network are similar to reactions R₄, R₅, and R₆ in the yeast polarization model in that they show the greatest benefit from using state-dependent biasing parameters.

Table 7.

Complete list of optimal IS parameters employed by the dwSSA and the sdwSSA in the lac operon model.

Reaction index	${\widehat{{\gamma }^{*}}}_{\text{dwSSA}}$	${\widehat{{\gamma }^{*}}}_{\text{sdwSSA}}$
1	0.48	[0.41, 0.54, 0.23, 0.14]
2	0.82	[1.15, 0.79, 1.00, 0.78]
3	0.83	[0.81, 5.57]
4	1.66e-83	[1.80e-82]
5	0.88	[1.28, 1.35]
6	1.33	[0.21]
7	1.09	[0.094, 0.54, 1.33, 0.29, 0.58]
8	0.89	[0.63, 0.32]
9	0.95	[1.05, 0.98, 1.13, 1.10, 0.89, 1.09, 0.66, 0.91, 0.79, 1.21]
10	1.00	[1.09, 1.11, 1.07, 0.74, 0.88, 0.88]
11	32.42	[13.14, 22.35, 18.82, 36.02, 17.06, 93.93, 98.64, 127.5, 116.2, 122.3]
12	1.82e-86	[0.0019]
13	1.35	[1.36, 1.40, 1.40, 1.23, 1.30, 1.52, 0.72, 0.29]
14	1.00	[0.96, 1.00, 1.00, 1.00, 1.00, 1.00, 1.00, 1.00, 1.00, 0.99]
15	0.95	[0.11, 0.46, 0.89, 0.91, 0.52, 0.38]
16	1.00	[1.00, 1.00, 1.00, 1.00, 1.00, 1.00, 1.00, 0.97, 0.99]
17	1.00	[1.00, 1.00, 1.01, 1.00, 1.00, 1.01, 1.00, 1.02, 1.02, 1.00]
18	1.00	[0.99, 1.00, 1.00, 0.99, 0.99, 1.00, 1.00, 1.00, 0.99, 0.99]
19	0.19	[3.97]
20	0.20	[0.028, 0.13, 0.17, 1.51, 0.66]
21	0.87	[0.057]
22	8.35e-86	[9.01e-85]
23	0.72	[0.80, 0.69, 0.88, 0.72, 0.61, 0.59, 0.34, 1.30, 0.38, 0.48]
24	0.44	[0.47, 1.13, 1.36, 0.42, 0.25, 0.41]
25	1.44e-87	[1.73e-86]

Table 8.

End points of bins associated with the optimal sdwSSA IS parameters in Table 7.

Reaction index	c
1	[3.29, 5.70, 8.11] × 10−7
2	[4.65, 9.31, 13.8] × 10−5
3	[0.0012]
4	NA
5	[0.011]
6	NA
7	[0.0031, 0.0063, 0.0093, 0.012]
8	[0.00013]
9	[1.63, 3.26, 4.90, 6.53, 8.17, 9.80, 11.4, 13.0, 14.7]× 10−3
10	[0.057, 0.11, 0.17, 0.23, 0.29]
11	[1.13, 2.26, 3.38, 4.51, 5.64, 6.77, 7.89, 9.02, 10.2] × 10−6
12	NA
13	[0.00067, 0.0013, 0.0020, 0.0027, 0.0034, 0.0040, 0.0047]
14	[0.088, 0.18, 0.27, 0.35, 0.44, 0.53, 0.62, 0.71, 0.80]
15	[4.68, 6.24, 7.80, 9.36, 10.9] × 10−7
16	[0.19, 0.28, 0.37, 0.47, 0.56, 0.66, 0.75, 0.84]
17	[0.10, 0.20, 0.30, 0.40, 0.50, 0.60, 0.70, 0.80, 0.90]
18	[0.05, 0.10, 0.15, 0.21, 0.26, 0.31, 0.36, 0.41, 0.46]
19	NA
20	[1.03, 2.07, 3.10, 4.14] × 10−5
21	NA
22	NA
23	[2.82, 5.64  8.46, 11.2, 14.1, 16.9, 19.7, 22.5, 25.4]× 10−5
24	[0.94, 1.24, 1.56, 1.87, 2.18] × 10−6
25	NA

A second group of parameters exhibit an opposite biasing scheme in the dwSSA versus the sdwSSA. Reactions R₅ and R₁₉ are discouraged using optimal dwSSA parameters, yet they are encouraged in the sdwSSA. We note that both reactions utilize fewer than three bins after undergoing merging. If R₅ and R₁₉ were important for accurately estimating the rare event probability, we would expect them to require a greater number of relative propensity bins containing monotonically varying parameter values. Thus, we hypothesize that the probability estimate is relatively insensitive to the parameters of these two reactions. To confirm this hypothesis, we recomputed parameter values for the dwSSA and sdwSSA with different random number generator seeds. In the second set of dwSSA parameters, γ₅ changed from 0.88 to 1.81 and γ₁₉ from 0.19 to 0.95. The corresponding second set of sdwSSA parameters also showed high variability in their values. Thus, we conclude that $\widehat{p}({\mathbf{x}}_0,{\theta }^{Y_{tot}};t)$ is not sensitive to γ₅ and γ₁₉ in both the dwSSA and sdwSSA.

CONCLUSION

We have developed a novel modification of the doubly weighted SSA (dwSSA)—the state-dependent doubly weighted SSA (sdwSSA)—which yields an accurate estimate of a rare event probability, even for systems where the relative propensities vary widely over time. The sdwSSA is a natural extension of the dwSSA which reduces to the latter when β_max, the maximum number of bins used to discretize relative propensity, is set to 1. Consequently, the sdwSSA retains all benefits of the dwSSA while providing greater computational efficiency. It achieves this by automatically computing the optimal set of state-dependent biasing parameters and subsequently using these parameters to accurately estimate a rare event probability. Numerical results reported in Sec. 4 demonstrate the improved accuracy and efficiency of the method. For practical purposes, it is important that the sdwSSA not only improves estimate accuracy but also adds minimal computation to the existing dwSSA framework. We have achieved this requirement by (1) proposing a specific form for the state-dependent biasing parameter that yields a closed-form solution when coupled with the multilevel cross-entropy method, and (2) incorporating a dynamic binning strategy into the cross-entropy framework that requires no additional realizations over the dwSSA.

The sdwSSA discretizes the relative propensity range of each reaction to arrive at a closed-form expression of its biasing parameters. For each reaction, we interpret the β_j state-dependent biasing parameters as a step function, i.e., any relative propensity value between $c_j^{i-1}$ and $c_j^i$ is assigned γ_ji. While leaving the discretization scheme unchanged, a higher order interpolation could be subsequently used as an alternative approach for determining the amount of perturbation for each reaction. Future work will focus on customizing the binning strategy for individual reactions such that key reactions for a given rare event are identified and their parameters computed using an optimal interpolation method.

APPENDIX: SUPPLEMENTAL INFORMATION ON LAC OPERON MODEL

This section presents the optimal importance sampling parameter values and associated bin end points for the lac operon model.