Thermodynamics of Biological Processes

Abstract

There is a long and rich tradition of using ideas from both equilibrium thermodynamics and its microscopic partner theory of equilibrium statistical mechanics. In this chapter, we provide some background on the origins of the seemingly unreasonable effectiveness of ideas from both thermodynamics and statistical mechanics in biology. After making a description of these foundational issues, we turn to a series of case studies primarily focused on binding that are intended to illustrate the broad biological reach of equilibrium thinking in biology. These case studies include ligand-gated ion channels, thermodynamic models of transcription, and recent applications to the problem of bacterial chemotaxis. As part of the description of these case studies, we explore a number of different uses of the famed Monod–Wyman–Changeux (MWC) model as a generic tool for providing a mathematical characterization of two-state systems. These case studies should provide a template for tailoring equilibrium ideas to other problems of biological interest.

1. Introduction: Thermodynamics is Not Just for Dead Stuff

Thermodynamics has long been a key theory in biology, used in problems ranging from the interpretation of binding both in vitro and in vivo to the study of the conformations of DNA whether under the action of optical traps in well-characterized solutions or in the highly compacted state of the cellular interior. Despite this long tradition, there is often the sneaking suspicion that because thermodynamics (perhaps more properly referred to as thermostatics) is a theory of equilibrium that tells us how to reckon the “terminal privileged states” of systems (Callen, 1985), it is somehow irrelevant for thinking about the behavior of living cells which are demonstrably not in equilibrium. While the terminal state of a living system is death, there are many problems for which an equilibrium treatment is not only a good starting point, but may be the most appropriate tool for the problem of interest.

In a now classic article, Eugene Wigner spoke of the “unreasonable effectiveness of mathematics in the natural sciences,” (Wigner, 1960), expressing surprise at the truth of Galileo’s earlier assertion that “Mathematics is the language with which God has written the universe.” In the time since Wigner’s article, many others have taken liberties with his theme by noting the seemingly unreasonable effectiveness of other specific ideas in a much more general context than they were originally intended, and now it is our turn to add our names to the list. Indeed, the unreasonable effectiveness of equilibrium ideas for inherently out-of-equilibrium problems has already been developed by Astumian for specific cases such as a colloidal particle falling through water and a single molecule being stretched by an atomic force microscope (Astumian, 2007). This chapter complements that of Astumian by exploring the perhaps surprising effectiveness of equilibrium thermodynamics in thinking about a wide range of biological problems.

Our chapter has several goals. First, we describe the key theoretical foundations required for the application of equilibrium statistical mechanics models to problems spanning from ligand-gated ion channels to the action of enhancers in transcriptional regulation. In addition, we address conceptual issues related to the applicability of equilibrium concepts by using arguments about separation of time scales to determine when equilibrium ideas can be appropriately used in a living biological context, even though the cell as a whole is not in equilibrium. With these theoretical preliminaries in hand, we carry out a series of illustrative case studies from the last decade or so that show the broad reach of equilibrium ideas to a number of topics that are both timely and exciting. One of our main goals is to argue that equilibrium ideas are a good jumping-off point for thinking quantitatively about a range of problems in cell biology. In particular, they often lead to mathematical formulae that can be explicitly tested in biological experiments to arrive at a deeper understanding of a proposed mechanism. These ideas will be made explicit in the examples to follow.

2. States and Weights from the Boltzmann Rule

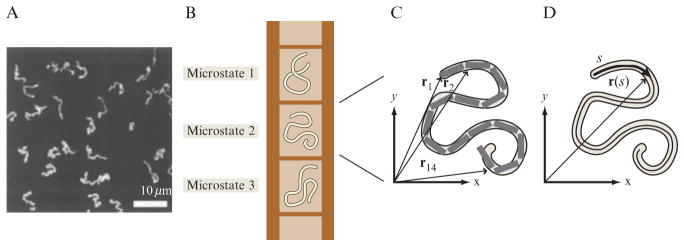
For all of the biological examples we wish to examine, the problem formulation plays out the same way. Our starting point is the notion of a “microstate,” one of the many distinct ways that the microscopic objects making up our macroscopic system can be arranged. For example, if we are interested in the disposition of a fluorescently labeled DNA molecule on a surface, there are many different ways in which the molecule can lie down on the surface, as shown in Fig. 2.1. Each one of these conformations is a distinct microstate but they all share the common feature that the molecule is adsorbed on the surface (Maier and Radler, 1999). Similarly, if we have a collection of ligands in solution, both the positions and the momenta of the different ligands can be shuffled around without changing the overall concentration and temperature, for example. Again, each such arrangement corresponds to a different microstate. The job of statistical mechanics is to compute the relative probabilities of all the microstates consistent with the constraints imposed on the system. The constraints are defined by macroscopic variables like temperature, mean distance between the ends of the DNA, or the concentration of ligands in solution. For problems of biological interest, the challenge is to determine what set of microstates are biologically equivalent, and then to enumerate these micro-states and calculate their probabilities. For example, a receptor in the presence of many molecules of ligand in solution may be considered “activated” if any one of the individual ligand molecules is bound, although these would all be considered distinct microstates. In practice, it would be tedious or impossible to actually enumerate the microstates for any real system, but the toolkit of statistical mechanics provides elegant methods to accurately estimate their numbers and probabilities, even for complex living systems.

Figure 2.1.

Microstates for DNA on a surface. (A) Fluorescence microscopy image of dye-labeled λ-phage DNA on a surface (Maier and Radler, 1999). Each configuration observed corresponds to a different microstate. (B) Schematic showing a series of different allowed microstates for a given DNA molecule on a surface. (C) Discrete representation of the microstate of the DNA molecule. The molecule is divided into a series of segments and there is a vector r_i which points to the ith segment. Each microstate is characterized by a different set of positions. (D) Continuous representation of the microstate of the DNA molecule. Each point on the molecule has its position defined by the vector r(s), where s is the arclength along the molecule.

For thinking about processes in the living world, one relevant constraint is the assumption of fixed temperature, which is equivalent to imposing the constraint of constant mean energy. For some biological systems, such as endothermic animals, this approximation is almost true, and in nearly all biological systems, the temperature changes very slowly compared to the rapid molecular transformations that we consider here. This is one example of the importance of the separation of time scales in the application of thermodynamics concepts to biological systems; as long as we can treat temperature as being nearly constant, we can vastly simplify the task of determining the probabilities of the microstates in the system. In this case, statistical mechanics provides us with an elegant and compact formula for the probabilities of all the microstates in the form of the celebrated Boltzmann formula, namely,

$$p_i=\frac{e^{-\beta E_i}}{Z},$$ (2.1)

where E_i is the energy of the microstate i, β = 1/k_BT, k_B is the Boltzmann constant, and T is the temperature. The denominator in this expression is obtained by summing over the Boltzmann factors (exp(−βE_i)) for each of the distinct microstates and is known as the partition function. The key intuition provided by this formula is that the probability of every microstate of the system is solely determined by its energy. For many biological experiments, it is easier to determine the probability of a state (e.g., the concentration of ligand-bound receptors) than to directly measure its energy. Within this framework, the two properties can be conveniently interconverted.

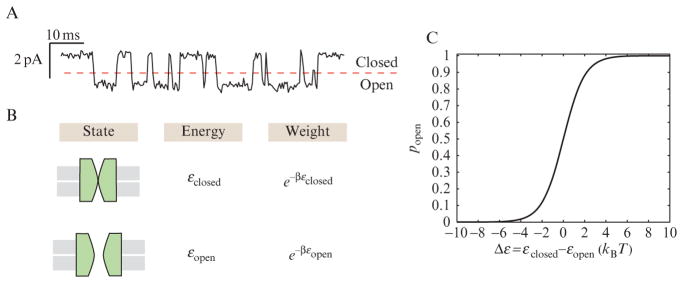
Perhaps the simplest problem of biological interest to which these ideas can be applied is that of a “two-state” ion channel like that shown in Fig. 2.2. In such models, it is assumed that the channel has only two states, closed and open, and the probabilities of these two states can be read off from the fraction of the time spent in each state, as is shown in Fig. 2.2A. There are several underlying assumptions explicit in this treatment, including the idea that the channel has no “memory” of how long it has been open or closed, and the idea that all the channels in a population are functionally equivalent. In other words, the system is assumed to be ergodic, such that the average open probability for a single channel examined over time should be the same as the average fraction of channels in a population that happens to be open at any given instant. For cases where these assumptions are reasonable (or nearly reasonable), statistical mechanics tells us how to compute the probabilities of each of the states from their energies, or equivalently to compute their energies from their probabilities. In this chapter, we will repeatedly resort to the same cartoon depiction of the Boltzmann rule by showing a cartoon of the states and their corresponding Boltzmann weights which are obtained by exponentiating the energy of the relevant state, as shown in Eq. (2.1), and multiplying the Boltzmann factor by its associated multiplicity. For a channel like the one being considered here, the corresponding states and weights are shown in Fig. 2.2B. Using these ideas, we see that the probability of the open state is obtained as the ratio

Figure 2.2.

States and weights for ion channel dynamics. (A) Current trace showing how the channel transitions back and forth between the open and closed states (Keller et al., 1986). By evaluating the fraction of time spent in either of these two states, we can compute the open (and closed) probability. (B) States of the two-state ion channel, the corresponding energies and the Boltzmann weights. (C) Plot of the probability of the channel being open as a function of the difference in energy between the open and closed states. This difference in energy can be tuned by the driving force such as ligands, voltages and tension on the membrane. The expression plotted corresponds to Eq. (2.3).

$$p_{\text{open}}=\frac{e^{-\beta {\epsilon }_{\text{open}}}}{e^{-\beta {\epsilon }_{\text{open}}}+e^{-\beta {\epsilon }_{\text{closed}}}},$$ (2.2)

where ε_open and ε_closed are the energies of the open and closed states, respectively. This expression can be rewritten in the alternative fashion

$$p_{\text{open}}=\frac{1}{1+e^{-\beta \mathrm{\Delta }\epsilon }},$$ (2.3)

where Δε = ε_closed − ε_open. The functional form introduced above is used widely in the fitting of opening-probability curves (Keller et al., 1986; Perozo et al., 2002; Zhong et al., 1998) and is shown in Fig. 2.2C. Our interest here was simply to note the way in which this functional form arises completely naturally from the ideas of statistical mechanics.

Of course this is a deliberate oversimplification, as an ion channel that is opening and closing must go through a continuum of multiple structural states in between. However, inspection of the time trace in Fig. 2.2A reveals that the amount of time spent during these transitions is relatively brief compared to the time that the channel typically dwells in either the open or closed states, so for purposes of estimating probabilities, we may make the useful simplification that the system exists primarily in just these two states. Furthermore, we acknowledge that any one state, for example, “open,” may in reality represent several or many structurally distinct substates that are equivalent as far as their biological function is concerned, that is, the amount of current that passes through them. One of the most useful properties of the thermodynamic framework for the analysis of biological systems is its flexibility with respect to the precision with which the states are defined; depending on the exact question being asked, the investigator can choose how finely to delineate the various states of the system. Overall, we argue that extremely simple models such as the two-state ion channel seem to fit experimental data unreasonably well, and furthermore provide extremely useful intuition as a starting point for thinking about highly complex systems.

There are many different kinds of ion channels, characterized not only by their selectivities for different ions, but also by the classes of driving forces that gate them (Hille, 2001). Regardless, from the two-state statistical mechanics perspective adopted here, the difference in gating mechanisms from one channel to the next is embodied in the dependence of Δε on the driving force, whether it is the voltage applied across the membrane, the concentration of some ligands, or the tension in the membrane. This is where the power and utility of the statistical mechanics approach becomes clear. All of the different environmental influences that may affect the opening and closing of the ion channel may be characterized with respect to their effect on the energy (or equivalently, on the probability) of the closed versus open state. So, the expectations for the behavior of a channel with multiple different ligands, or a channel affected by both ligand binding and voltage, can be described quantitatively within this framework, using energy as a universal currency. Formally, it is straightforward to predict quantitatively how a channel with multiple environmental influences is expected to respond when the several different factors operate independently of one another. If the factors such as ligand binding and voltage are not in fact independent, that will be revealed by the failure of the data (measurement of open probability as a function of these two variables) to fit the simple model, and the actual energy of the coupling between the factors can then be calculated.

3. Binding Reactions and Biological Thermodynamics

3.1. Thermodynamic models of binding

One of the poster children for the usefulness of equilibrium thermodynamics and its statistical mechanics partner ideas in biology is the study of binding reactions (Dill and Bromberg, 2003; Hill, 1985; Klotz, 1997). To illustrate our points, we focus on several key case studies. First, we use simple ideas about binding reactions to highlight a few key points about transcriptional regulation. With these ideas in hand, we turn to a class of models that have served as a centerpiece in the analysis of biological cooperativity, namely, the Monod–Wyman–Changeux models (MWC; Monod et al., 1965) which, we will argue, serve in the same capacity in biology that the Ising model introduced to describe the magnetic properties of materials does in physics (Brush, 1967; Plischke and Bergersen, 2006). Both the MWC model and the Ising model make the extremely useful simplifications that, first, the individual elements within a complex system can exist only in a countable number of discrete states (rather than in a continuum), and that an individual element can sometimes change its state. For the simplest cases, such as the spins making up a magnet or ion channel opening, the number of discrete states is just two, but as we will see below, this same framework can be readily expanded to include more than two states.

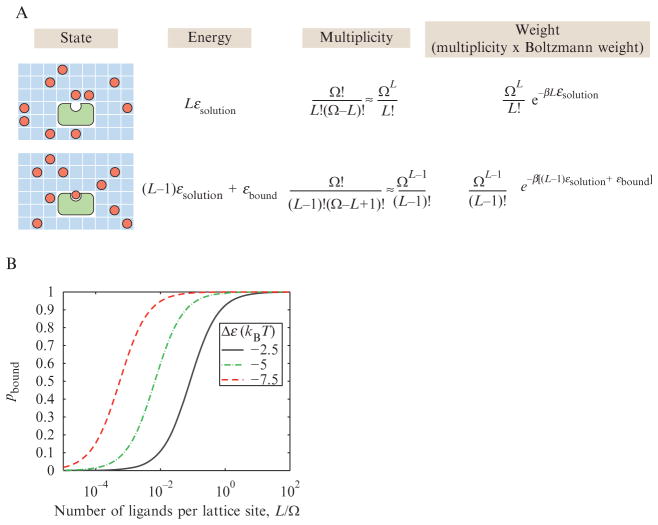
As a biological case with very broad applicability, we start by considering binding problems in which several different molecular species can exist either separately or in complexes. As shown in Fig. 2.3A, the simplest receptor–ligand binding system can exist in one of two classes of states, or one of two macrostates. Either the receptor is unoccupied or occupied by a ligand molecule. However, for each of these macrostates, there are many different microscopic realizations of the system since the ligands can be distributed in many different ways throughout the solution. For simplicity, we introduce a model of the solution known as a “lattice model” in which the solution is divided into a huge number Ω of boxes and the configurations of the solute molecules are captured by their placement on these lattice sites. This idea is captured in the “multiplicity” column in Fig. 2.3A which tells us the number of distinct ways of arranging our L ligands in the lattice model of the solution adopted here. In reality, of course, the unbound ligands are not confined to boxes in the solution volume; they may exist at any location. However, the lattice model provides an unreasonably effective approximation to a continuous solution in the limit where the number of possible lattice positions is taken to be very large, and it greatly simplifies the statistical mechanics task of enumerating the microstates (Dill and Bromberg, 2003). To find the total statistical weight, we simply multiply the multiplicity of the two macrostates times their associated Boltzmann factors which depend upon their corresponding energies (i.e., upon the energy of binding ε_bound and the energy of being in solution ε_solution).

Figure 2.3.

Statistical mechanics of receptor–ligand binding. (A) We consider a lattice model of L ligands in solution, represented as a lattice of Ω boxes, and one receptor. There are two broad classes of allowed states (i.e., two macrostates), those in which the receptor is empty and those in which the receptor is occupied by one of the ligands. To enumerate the microstates that make up each of the two macrostates, we count the number of ways that the ligands in solution can be distributed among the Ω boxes; this leads to the multiplicity factor. Furthermore, we assume that in the solution, the ligand has an energy ε_solution and while bound to the receptor its energy drops to ε_bound, and these two energies define the Boltzmann factors associated with each of the two macrostates. (B) Plot of the probability of receptor occupancy as a function of the concentration of ligands as shown in Eq. (2.4) for three different choices of the difference in binding free energy between the solution and the receptor.

With the statistical weights in hand, we can now compute the probability of either of the two macrostates as its statistical weight divided by the sum of the statistical weights of all of the possible microstates. In particular, this leads to a formula for the probability of the receptor to be occupied by a ligand of the form

$$p_{\text{bound}}(L)=\frac{\frac{L}{\mathrm{\Omega }}{e}^{-\beta \mathrm{\Delta }\epsilon }}{1+\frac{L}{\mathrm{\Omega }}{e}^{-\beta \mathrm{\Delta }\epsilon }},$$ (2.4)

where Δε = ε_bound − ε_solution is the energy loss of the ligand upon binding to the receptor and we have assumed that the number of ligands L is much less than the size of the solution represented by the number of boxes in the lattice model, Ω. The factor L/Ω accounts for the loss in translational entropy of the ligand upon binding. As written, this equation describes the probability of receptor occupancy as a function of the number of ligands in our lattice model of solution. This probability is plotted in Fig. 2.3B as a function of several choices of Δε. However, to make contact with concentrations, it is convenient to rewrite this expression by using the volume per elementary box in our lattice model (v) and occupied by ligand as a function of ligand concentration [L]. In particular, we can write the number of ligands L as L = [L]Ωv, in which case the equation takes on a familiar form

$$p_{\text{bound}}([L])=\frac{\frac{[L]}{K_{\text{d}}}}{1+\frac{[L]}{K_{\text{d}}}},$$ (2.5)

where $K_{\text{d}}=\frac{e^{\beta \mathrm{\Delta }\epsilon }}{v}$ is the equilibrium dissociation constant which provides the concentration at which the receptor has a probability of being occupied of 1/2.

In most interesting biological systems, the concentration of ligand will change over time (e.g., because of changes in cellular signaling), so the system is not truly in equilibrium. However, this is another instance where the separation of time scales is important. As long as the rate at which the ligand concentration changes is relatively slow compared to the individual rates of ligand binding and unbinding, the system can be considered to be nearly in equilibrium at each moment in time, with the probability of ligand binding simply adjusting as its concentration changes slowly.

Often in binding problems that are biologically interesting, the simple functional form defined above is not consistent with the data. This is usually the case when, for example, more than one ligand may bind to the same receptor simultaneously, or when ligand binding causes receptor dimerization. The general biochemical problems of understanding cooperativity and allostery have historically received a great deal of attention (Cui and Karplus, 2008). Below, we will argue that these more complex situations may also be analyzed usefully within this same formal framework. Indeed, the classic MWC model for allostery and cooperativity is a statistical mechanical model that considers molecules that intrinsically exist in a distribution of possible conformational states and assigns these different states different binding affinities (Cui and Karplus, 2008; Gunasekaran et al., 2004). But first, with the basics of the statistical mechanics of single-ligand binding under our belt, we are now equipped to attack a specific problem of biological interest, the regulation of gene expression.

3.2. Thermodynamic models of transcription

Regulation is one of the great themes of biology. Few are left unimpressed after watching the ordered cell divisions and differentiation that attend embryonic development, which serves as a great reminder of what has been dubbed “the regulatory genome” (Davidson, 2006). The roots of regulatory biology are largely to be found in the study of prokaryotes (Ackers et al., 1982; Jacob et al., 2005; Ptashne and Gann, 2002), and these simple single-celled organisms continue to provide valuable insights into transcription and other processes of the central dogma of molecular biology (Buchler et al., 2003; Michel, 2010; Wall et al., 2004). One of our arguments is that the systems that were the early proving ground for our understanding of regulation, namely, questions centering on bacterial metabolism and the bacteriophage life cycle, can now be used as a test bed for a more stringent, systematic, and quantitative attack on questions in regulation. One of the earliest systematic uses of thermodynamic models for computing the properties of a regulatory network was carried out by Ackers and Shea on the decision-making apparatus in bacteriophage lambda (Ackers et al., 1982). More recently, those efforts were generalized to consider the question of how various transcription factors by virtue of being present or absent from regulatory regions of the DNA can conspire to yield combinatorial control of the expression of a particular gene (Bintu et al., 2005a,b; Buchler et al., 2003). In the time since, these ideas have been used even more aggressively for an ever-increasing set of regulatory architectures (Dodd et al., 2005; Fakhouri et al., 2010; Giorgetti et al., 2010; Kuhlman et al., 2007).

To see the way in which these ideas play out most simply within the statistical mechanics framework, consider the case of repression of transcription by a transcription factor (repressor), as shown in Fig. 2.4. The idea is one of simple competition. The promoter can either be unoccupied, occupied by RNA polymerase, or occupied by repressor, but not by both simultaneously. The transcriptionally active state corresponds to that state in which RNA polymerase is bound to the promoter. In the thermodynamic models, all attention is focused on promoter occupancy, and it is assumed that the level of gene expression is proportional to the probability of promoter occupancy by RNA polymerase (Straney and Crothers, 1987). As with the examples worked out above for the two-state ion channel and the simple binding problem, we can compute the probability of interest by resorting to the states and weights diagram shown in Fig. 2.4 which tells us that the probability of promoter occupancy is given by

Figure 2.4.

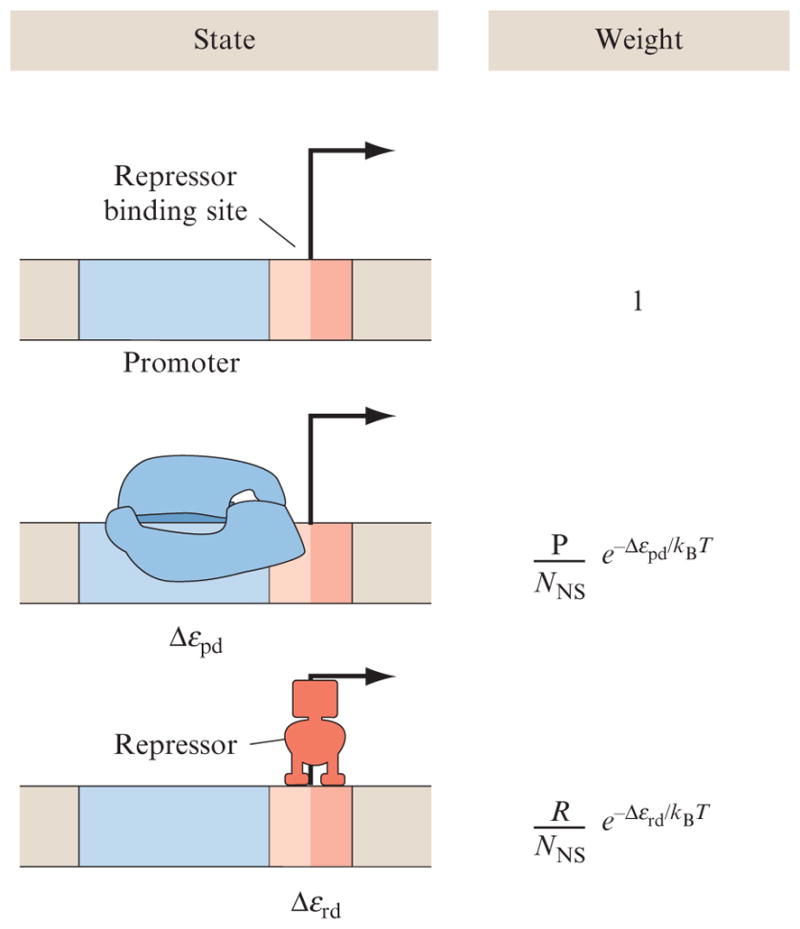
States and weights for simple repression. A promoter has a binding site for a repressor molecule which excludes the binding of RNA polymerase. The statistical weights of the different states depend upon the number of polymerases (P), the number of repressors (R), and their respective energies of binding to DNA, Δε_pd, and Δε_rd. To derive these weights, we use the same approach as that described for ligand–receptor binding, except now we assume that both polymerases and repressors when not bound to the promoter are distributed among N_NS sites on the bacterial genome (this is essentially the size of the genome). The energies in the Boltzmann factors are computed as the difference between the energy when repressor or polymerase is bound specifically to the promoter region of the DNA and when they are bound nonspecifically somewhere else on the genome (Bintu et al., 2005b).

$$p_{\text{bound}}=\frac{\frac{P}{N_{\text{NS}}}{e}^{-\beta \mathrm{\Delta }{\epsilon }_{\text{pd}}}}{1+\frac{P}{N_{\text{NS}}}{e}^{-\beta \mathrm{\Delta }{\epsilon }_{\text{pd}}}+\frac{R}{N_{\text{NS}}}{e}^{-\beta \mathrm{\Delta }{\epsilon }_{\text{rd}}}}.$$ (2.6)

Here, the probability is expressed as a function of the number of poly-merases (P), the number of repressors (R), the size of the genome N_NS in base pairs, and the relevant energy differences that characterize the binding of polymerase and repressor to promoter and operator DNA, Δε_pd and Δε_rd, respectively. Details about how this formula is obtained in analogy to the probability of the ligand binding to a receptor from Eq. (2.4) are shown in the caption of Fig. 2.4.

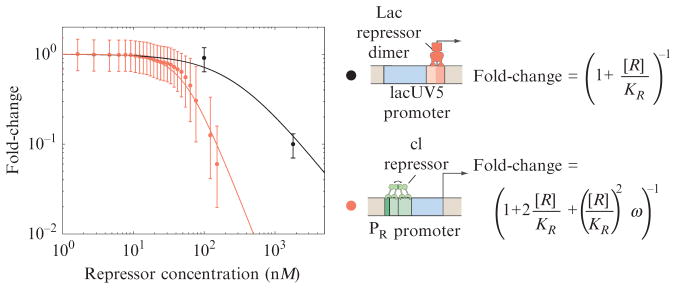
From an experimental point of view, often the most convenient measurable quantity for carrying out the kind of quantitative dissection that is possible using thermodynamic models of gene expression is the fold-change, defined as the ratio of the level of expression in strains that harbor the repressor molecule to the level of expression in strains that do not. This definition can be generalized to an array of different regulatory architectures by always computing the ratio of the level of expression in the regulated strain to that in an unregulated strain. The prediction for the fold-change that follows from the thermodynamic model of simple repression described above is fold-change = p_bound(R)/p_bound(R = 0). For repression, the fold-change is always less than one, while for activation, the fold-change is greater than one. As shown in Fig. 2.5, several different bacterial promoters have had their fold-change systematically characterized, and we compare the measured value with the thermodynamic models that are appropriate for the particular promoter. Such experiments lead to knowledge of the parameters of the promoter architecture such as the relevant binding energies. Using these parameters, falsifiable predictions about the gene regulatory input–output relations can be generated (Bintu et al., 2005a).

Figure 2.5.

Fold-change in gene expression. Two different promoters have been characterized as a function of the number of repressors (Oehler et al., 1994; Rosenfeld et al., 2005). The thermodynamic models predict a precise dependence of the fold-change in gene expression on the concentration of repressors. The theoretical predictions are given by the curves, and the experimental results for two different promoters are given by the data points. These predictions were obtained using the reasoning outlined in Fig. 2.4, equation 2.5, and the weak promoter approximation described in Bintu et al. (2005a,b).

The idea to use models based on equilibrium ideas to describe the transcriptional output of a promoter might seem ill-conceived, given that transcription is an inherently out-of-equilibrium process with key steps like the elongation stage of transcription leading to mRNA production being essentially irreversible. Still, the key thing to keep in mind is what makes equilibrium ideas useful in these settings is always the separation of time scales. For example, even in the setting in which statistical mechanics and thermodynamics are typically taught, that of an ideal gas, the gas is thought of as being held in a container that is impermeable (i.e., molecules cannot escape). In reality, no such container exists! Still, if the diffusion of the gas out of the container occurs on times scales that are much slower than the rate at which the gas explores the volume of the container (i.e., the time for a molecule to diffuse from one end of the container to the other), then we can consider the gas to be in equilibrium. Similarly, if transcription factor and RNA polymerase binding and falling off the DNA occur on time scales that are distinct from the time scales associated with initiation of transcription, we can treat the different states representing combinations of transcription factors bound to promoter DNA as being in equilibrium with each other. This is illustrated in Fig. 2.6. A more intuitive way of restating this conclusion is that the rate of transcription should depend on the concentration and activity of the transcription factors, a proposition that is likely to be widely accepted. Here, we have simply developed the formal underpinnings of this assertion.

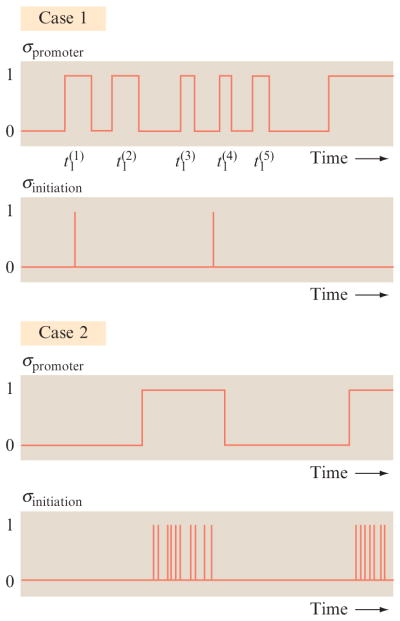
Figure 2.6.

Transcriptional time series for several different classes of rate constants. The schematic emphasizes two scenarios in which thermodynamic models of gene regulation are valid. In case 1, the promoter switches fast on the time scale defined by transcription initiation, while in case 2, the opposite limit is illustrated. In both limits, the steady-state number of transcripts (mRNA degrades due to the action of RNases and by dilution after cell division) is proportional to the fraction of time the promoter is in the active state (state 1), which can be computed using equilibrium techniques. We are grateful to Alvaro Sanchez for his articulation of the ideas embodied in this figure.

3.3. The unreasonable effectiveness of MWC models

In the world of statistical mechanics, the Ising model has celebrity status and can be argued to be one of the most useful conceptual frameworks in all of physics. One of the arguments we want to make here is for a similar status for the MWC model in the context of biology (Monod et al., 1965). The biological essence of the MWC philosophy is that many of the molecules of life, or complexes consisting of many molecules, can exist in several different functional states (e.g., inactive and active), and their propensity to bind ligands is different in those states. For a protein that is activated by ligand binding, the simplest picture is that the free energy of the inactive state is intrinsically lower, making it more likely in the absence of ligands. However, if the binding energy for ligands is greater when the molecule is in the active state, then the presence of ligands can shift the equilibrium toward this state. What this means in turn is that as ligands are titrated in, the active state will ultimately be the thermodynamic winner. More generally, the same kind of enumeration of discrete states can be applied to any other reversible biological transformation such as protein phosphorylation and dephosphorylation, and transport into or out of a subcellular compartment. There are many important and nuanced features of this idea, some of which will be made mathematically explicit in the case studies to be given in the remainder of the chapter.

3.3.1. MWC and hemoglobin: Where it all began

The MWC model in its various forms has been applied in many different contexts. The most famous example and a story told many times before concerns the application of these ideas to the binding of oxygen to hemoglobin. Because hemoglobin can bind four separate oxygen molecules, there are at least five distinct states of occupancy: empty, single-, double-, triple-, and quadruple occupancy (we are glossing over the possible distinctions among the substates within these states; e.g., a single hemoglobin tetramer with two bound oxygens may carry those oxygens either on the two alpha chains, the two beta chains, or one of each). One of the most important experimental findings about these binding probabilities is the existence of cooperativity: one way of couching it is the idea that the K_d for adding the next ligand depends upon how many ligands are already present. In this situation, the simple binding curves such as those shown in Fig. 2.3B fit the experimental data very poorly. In this case, people often resort to a richer binding curve known as a Hill function, which is a generalization of the functional form shown in Eq. (2.5) to the case where the ratio [L]/K_d in the numerator and the denominator is raised to the power n,

$$p_{\text{bound}}([L])=\frac{{\left(\frac{[L]}{K_{\text{d}}}\right)}^n}{1+{\left(\frac{[L]}{K_{\text{d}}}\right)}^n}.$$ (2.7)

The parameter n is the so-called Hill coefficient and is usually associated with the degree of cooperativity. For the hemoglobin case, the cooperativity concept was developed by Linus Pauling in 1935 specifically as a way to explain the nontrivial shape of the observed binding curve (Pauling, 1935). In this framework, the binding of one oxygen molecule to hemoglobin alters its affinity for the subsequent binding of another oxygen molecule to another site. While conceptually attractive and very useful for fitting experimental data, the Pauling model for cooperativity and subsequent elaborations of it (Koshland et al., 1966) require an explicit accounting for how each ligand affects the energetics of subsequent binding events. This formulation becomes increasingly unwieldy if other kinds of interactions are also considered. For example, the metabolic byproduct 2,3-bisphosphoglycerate (2,3-BPG) is found at high concentrations in red blood cells and binds to a site on the hemoglobin tetramer far from the heme groups, substantially decreasing the affinity of hemoglobin for oxygen as part of the blood-based oxygen delivery system in mammals (Benesch and Benesch, 1967). Incorporation of 2,3-BPG into a Pauling-style model for hemoglobin (or, similarly, incorporation of the Bohr effect, etc.) requires a proliferation of coupling terms describing how the binding of each ligand affects the affinity for every other possible ligand (Phillips et al., 2009a).

The MWC view of the cooperativity problem is fundamentally different. The original MWC model took the approach of assuming that hemoglobin itself could exist in only two distinct structural states: in one, the binding of oxygen to all the sites is weak, while in the other, it is strong; there is also an energy penalty to be paid when switching from the state in which oxygen is bound weakly to the one in which it is bound more strongly. The cooperativity in this case arises from the fact that the penalty for binding one, two, three, or four oxygen molecules tightly is the same regardless of the number of molecules. In other words, the presence of one or more bound ligands simply alters the probability of the protein being in each of the two structural states (or in the language of statistical mechanics, alters the energy difference Δε between the two; Monod et al., 1965). Inclusion of 2,3-BPG in this framework is straightforward; binding of 2,3-BPG also alters the population distribution between the states, lowering the relative energy of the weak oxygen-binding state, and therefore driving the population of hemoglobin molecules in that direction. For this first-order model, the ligands can all be assumed to stabilize or destabilize each possible protein structural state independently, and the effect of combining the various different ligands can be predicted by calculating the linear combination of all of the binding energies with respect to the state probabilities. Though the hemoglobin example was historically foundational, we believe that the MWC framework for biological statistical mechanics can be even more usefully applied to an unreasonably broad range of biological problems by virtue of its intrinsic ability to describe systems that exist primarily in a countable number of discrete functional states.

3.3.2. MWC and ligand-gated ion channels: Cooperative gating

The general applicability of the MWC philosophy is perhaps best illustrated with the example of ion channels. This time our discussion is based on an ion channel that is gated by the binding of ligands. Even though it is an oversimplification, we continue with the picture of ion channels that have only two allowed conformational states, an open state which permits the flow of ions and a closed stated which forbids any ionic current. Further, imagine an ion channel like the nicotinic acetylcholine receptor that has two binding sites for ligands, meaning that there are four possible states of occupancy when the channel is in a given state: unoccupied by ligand, occupied by ligand on site 1, occupied by ligand on site 2, and occupied by ligands on both sites 1 and 2. This is a reasonable first description of the acetylcholine receptor involved in the neuromuscular junction, which is also one of the best-studied ligand-gated channels, though detailed studies show that a faithful interpretation of these channels requires more than this simplest of models provides (Colquhoun and Sivilotti, 2004). The interesting twist that results from exploiting the MWC framework is that the binding energy for the ligands is different in the open and the closed state. All of these eventualities are shown in Fig. 2.7A.

Figure 2.7.

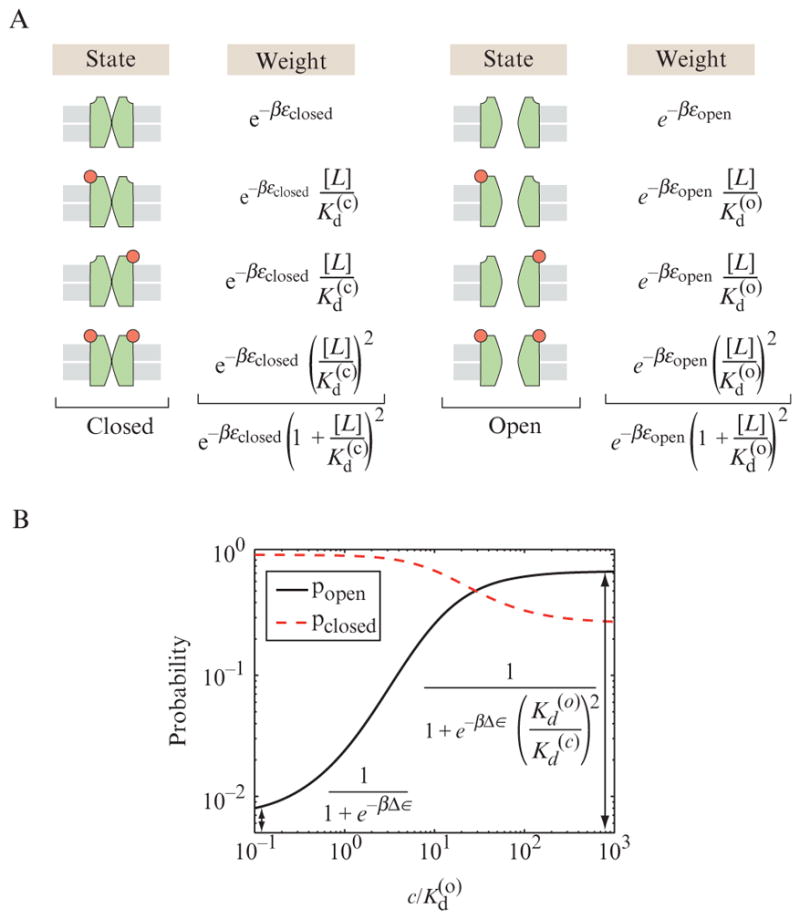
MWC model of ligand-gated ion channel. The channel is presumed to exist in one of two states, closed and open. The binding affinities of the ligands for the two binding sites on the channel are the same and they depend upon whether the channel is closed or open. This dependence leads to cooperative binding of the ligands. (A) States and weights for a toy model of a ligand-gated ion channel with two binding sites for the gating ligand. (B) Probability of the two states of the channel (open and closed) as a function of the gating ligand. Notice how in the absence of ligand the probability of the channel being open is the same as that calculated in Eq. (2.3), while the presence of ligand biases the channel toward the open state. The parameters used are Δε =ε_open − ε_closed = 5k_BT and K_d^(c)/K_d^(o) = 20.

If we make the simplifying assumption that the binding energy for the two different sites is identical, then the statistical weights of the different states can be written in the simple form shown in Fig. 2.7A. The outcome of this model is that the open probability as a function of ligand concentration has the simple but subtle form

$$p_{\text{open}}=\frac{e^{-\beta {\epsilon }_{\text{open}}}{\left(1+\frac{[L]}{K_{\text{d}}^{(\text{o})}}\right)}^2}{e^{-\beta {\epsilon }_{\text{open}}}{\left(1+\frac{[L]}{K_{\text{d}}^{(\text{o})}}\right)}^2+e^{-\beta {\epsilon }_{\text{closed}}}{\left(1+\frac{[L]}{K_{\text{d}}^{(\text{c})}}\right)}^2}.$$ (2.8)

The parameters that come into play here include the energies of the open and closed states, namely, ε_open and ε_closed, and the dissociation constants for the ligand when in the open and closed states, namely, K_d^(o) and K_d^(c), while the concentration of the ligands themselves is given by [L]. Note that this functional form bears some resemblance to that worked out earlier for the simple two-state ion channel, but as a result of the fact that the concentration-dependent terms come in a quadratic fashion, the dependence of the open probability on the ligand concentration is sharper than revealed in our earlier model. This sharpness can be explored by looking at the way that the open probability changes with concentration. Not surprisingly and just as in the case of hemoglobin, more careful studies of the dynamics of ligand-gated channels reveal behavior that is more nuanced than that captured in the simplest MWC model (Colquhoun and Sivilotti, 2004). Nevertheless, the simple treatment represents a very good first approximation to describing the system that can be used to build intuition and refine the precision of the quantitative questions that can be brought to bear. Within the same statistical mechanics framework, more sophisticated models can be constructed by including more precisely defined structural states and including the possibility for energetic coupling between the two ligand-binding sites (Colquhoun and Sivilotti, 2004).

3.3.3. MWC and chemotaxis: Cooperativity in signal detection

One of the most beloved microscopy videos in the history of modern biology was taken by David Rogers and shows the purposeful motion of a neutrophil as it chases down a bacterium, Staphylococcus aureus. This compelling directed motion, a few frames of which are shown in Fig. 2.8, captures people’s imaginations because at first blush one cannot avoid a sense of amazement that so many different processes can be so exquisitely synchronized on such short time scales. Indeed, similar rich and complex behavior of the single-celled Paramecium led some to wonder whether they were capable of some form of primitive thought (Greenspan, 2006). One of the captivating features of the Rogers video is that the neutrophil “knows” which way to go in order to track down its prey, revealing a specific example of the widespread phenomenon of chemotaxis. Though eukaryotic chemotaxis is a field unto itself, the study of chemotaxis in bacteria is, in many ways, the fundamental paradigm of signal transduction and has also been fruitfully viewed through the prism of equilibrium statistical mechanics (Berg, 2004).

Figure 2.8.

Snapshots from the Rogers video showing the directed motion of a neutrophil. Three different frames from the video separated by one-second time intervals reveal that the cell has made a sharp right turn in its pursuit of the bacterium (video by David Rogers, Venderbilt University and digital capture by Tom Stossel, Brigham and Women’s Hospital, Harvard Medical School).

The motion of a bacterium such as E. coli is characterized by “runs” and “tumbles” in which the bacterium moves forward in a nearly straight path, reorients in the tumbling process, and then heads off in a new direction (Berg, 2000). Bacterial chemotaxis refers to the way in which bacteria will bias the frequency of their tumbles in the presence of a gradient of che-moattractants (Cluzel et al., 2000). At the molecular level, this behavior is mediated by surface-bound chemoreceptors and cytoplasmic response regulators that communicate with the flagellar rotary apparatus (Falke et al., 1997). To illustrate how equilibrium statistical mechanics has been used to study chemotaxis, we consider the simplified scenario shown in Fig. 2.9. This watered-down version of the chemotaxis process centers on membrane-bound receptors that can bind soluble chemoattractants in the surrounding medium. The receptor communicates the presence of che-moattractants in the external milieu by modifying response regulators within the cell through phosphorylation. More precisely, from the standpoint of the statistical mechanics approach advocated here, the receptor can be either in an inactive or an active state, with only the active state able to perform the posttranslational modification of the response regulator. The balance of the active and inactive states of the receptor is determined, in turn, by whether or not the receptor is occupied by a ligand. Just as the balance between the open and closed states of the ligand-gated channel is altered by the presence of a ligand, here, the kinase activity of the receptor is tuned by ligand binding.

Figure 2.9.

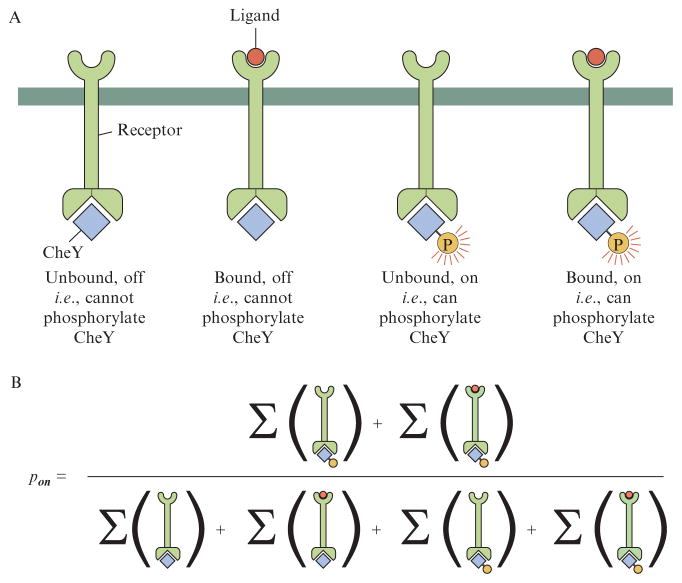
States of a single chemoreceptor. (A) The chemoreceptor can exist in four distinct states, characterized by whether or not it is occupied by a ligand and by whether it is in the active state or not. (B) The probability of being in the active (on) state is obtained by summing over the statistical weights of the states where the receptor is active and normalizing by summing over the statistical weights of all states.

To compute the probability that a given receptor is activated and hence that the frequency of tumbles is altered, we resort to precisely the same states and weights philosophy already favored throughout the chapter. We begin with the simplest model of an isolated chemoreceptor, as shown in Fig. 2.9. In this case, the states and weights are shown in the figure and reflect the four eventualities that can be realized: the receptor is either inactive or active and ligand-bound or not. When the ligand is bound, the entropy of the ligands in solution is changed and there is an additional binding energy. This results in probability of being active of the form

$$p_{\text{active}}=\frac{e^{-\beta {\epsilon }_{\text{active}}}\left(1+\frac{[L]}{K_{\text{d}}^{(\text{active})}}\right)}{e^{-\beta {\epsilon }_{\text{active}}}\left(1+\frac{[L]}{K_{\text{d}}^{(\text{active})}}\right)+e^{-\beta {\epsilon }_{\text{inactive}}}\left(1+\frac{[L]}{K_{\text{d}}^{(\text{inactive})}}\right)},$$ (2.9)

where we have introduced the energies ε_active and ε_inactive to capture the energy of the receptor in the active and inactive states, respectively, and K_d^(active) and K_d^(inactive) to capture the equilibrium dissociation constant for the ligand to bind the receptor when in the active and inactive states, respectively. The states and weights corresponding to this model are shown in Fig. 2.10.

Figure 2.10.

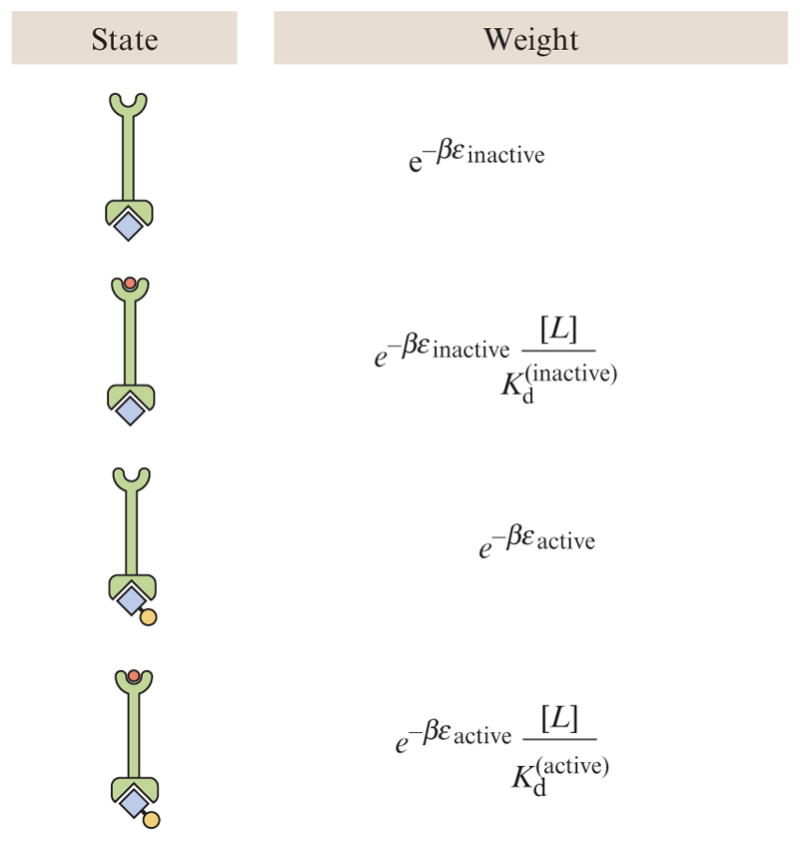
States and weights for chemoreceptors in the chemotaxis process. This figure shows the states and weights for a single receptor.

One of the most important outcomes of systematic quantitative experimentation on bacterial chemotaxis is the recognition that the behavior is much more cooperative than indicated by the simple formula derived above (Sourjik and Berg, 2002). The first level of sophistication beyond the naïve model written above is to incorporate the idea that chemoreceptors exist in clusters (Mello and Tu, 2005). In this case, as shown in Fig. 2.11A, the various weights conspire to yield an expression for the probability of the active state as a function of the concentration of chemoattractant, namely,

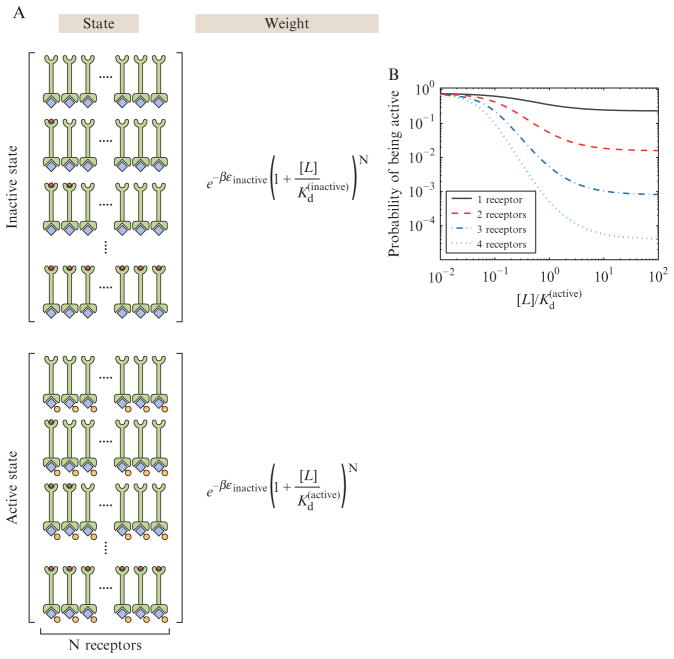
Figure 2.11.

MWC model for bacterial chemotaxis. The chemotactic receptors are modeled to exist in clusters with N distinct receptors. Collectively, these receptors can either be in the off or on state, where when on they are able to phosphorylate their downstream response regulator. (A) States and weights diagram for the receptors. (B) Plot of the probability of the active state as a function of the concentration of chemoattractant for different numbers of receptors within a cluster. The parameters used for the plots are Δε = ε_active − ε_inactive = −2k_BT and K_d^(inactive)/K_d^(active) = 1/20.

$$p_{\text{active}}=\frac{e^{-\beta {\epsilon }_{\text{active}}}{\left(1+\frac{[L]}{K_{\text{d}}^{(\text{active})}}\right)}^N}{e^{-\beta {\epsilon }_{\text{active}}}{\left(1+\frac{[L]}{K_{\text{d}}^{(\text{active})}}\right)}^N+e^{-\beta {\epsilon }_{\text{inactive}}}{\left(1+\frac{[L]}{K_{\text{d}}^{(\text{inactive})}}\right)}^N}.$$ (2.10)

In this scenario, N individual receptor molecules within a cluster are envisioned as acting as a unit, where the entire cluster can interconvert between the active and inactive states. This translates into the sharpness of the transition from inactive to active shown in the plot in Fig. 2.11B. Conceptually, the cooperativity for ligand-based activation of the clusters of receptor molecules can be treated in much the same way as the cooperativity for oxygen binding in the MWC model for hemoglobin.

Structurally, the chemotaxis receptors can, in fact, be seen in trimeric clusters on the bacterial surface (Briegel et al., 2009; Shimizu et al., 2000), in support of the validity of this treatment. In fact, this picture is itself only the starting point of a much more sophisticated set of models which acknowledge the collective action of many such receptors as the trimers are arranged in structurally connected networks. Such models even account for the possibility that different receptor types can interact, thus explaining the intriguing experimental observation that the presence of a ligand for one type of chemotaxis receptor can alter the apparent sensitivity of the bacteria to ligands for other receptor types. These models accomplish this without the need to postulate the existence of any unidentified signaling pathways that would enable this kind of crosspathway communication (Keymer et al., 2006; Mello and Tu, 2005). Yet, a further complication in the chemotaxis signaling system is the fact that receptors can be reversibly methylated at several sites in response to continuous stimulation, allowing adaptation over a wide range of ligand concentrations. Within the MWC framework, these posttranslational modifications can also be incorporated as effectively independent “ligands” that alter the probability that the receptors will be either active or inactive, by altering the relative stability of the two states. A statistical mechanics model based on these ideas for modifying the population distribution of simple two-state receptors is unreasonably well-able to reproduce experimental data over a broad range of conditions, including the prediction of system behavior for mutants where methylation is either constitutively on or off at any of several of the possible modification sites (Keymer et al., 2006).

3.3.4. MWC and eukaryotic transcriptional regulation: From nucleosomes to enhancers

A less familiar example of the use of MWC-like models is to binding problems involving DNA and its binding partners. In particular, in a recent set of papers, it was suggested that by analogy to the inactive and active states of a protein, DNA could be either inaccessible or accessible to binding by transcription factors (Mirny, 2010; Raveh-Sadka et al., 2009). One concrete mechanism for how that idea might be realized in a biological system is that the DNA could either be wrapped up in nucleosomes (inaccessible) or open for interaction with other factors. In Fig. 2.12A, we show a schematic of the states and weights for this case, with the “ligands” in this case now being DNA-binding proteins such as transcription factors which bind to some enhancer. For the concrete case shown in the figure, inspired by an enhancer in Drosophila, we consider an enhancer region containing seven binding sites, all of which have the same affinity for the transcription factor of interest (though this simplification is not at all crucial).

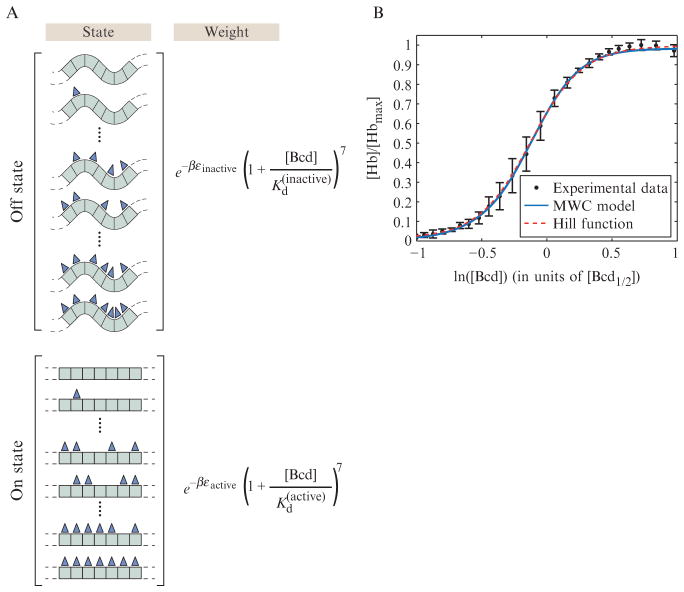
Figure 2.12.

MWC model for eukaryotic action at a distance. The regulatory region of the DNA is pictured here to have seven distinct binding sites. The organization of the DNA itself is further posited to exist in two different states. Following the MWC philosophy, the binding energy of the transcription factors (pictured here as triangles) depends upon whether the DNA is in the “closed” or “open” state. (A) States and weights corresponding to the model. (B) Data for the normalized level of Hunchback protein as a function of the level of Bicoid protein (Gregor et al., 2007) measured in units of [Bcd_1/2], the concentration of Bicoid protein for which [Hb]/[Hb_max] = 1/2, overlaid with a fit to a Hill function [Hb]/[Hb_max] = b(1 + f([Bcd]/K_d)⁵)/(1 + ([Bcd]/K_d)⁵) and the MWC model shown in Eq. (2.11). The parameters of the Hill function are b = 0.01, f = 99, and K_d = 0.88. For the MWC model, we took the limit K_d^(inactive) → + ∞ and used the parameters K_d^(active) = 0.3, and Δε = ε_active − ε_inactive = 9.5 k_BT.

The idea embodied in the figure is once again that embodied in an MWC model. This means that the system can exist in two overall states (accessible and inaccessible) and that the affinity of the relevant ligands for their target sites depends upon which of the two overall conformational states the system is in. An equivalent way of stating this is that the relative population distribution and therefore relative stability for each of the two DNA conformational states is influenced by the binding of the ligands. For the particular example shown here, we were loosely inspired by the binding of the transcription factor Bicoid in its role as an activator of a second gene known as Hunchback, two genes that play a specific role in the much larger process of development in the Drosophila embryo (Gilbert, 2010). For simplicity, we assume that each of the seven distinct bicoid target sites has the same binding energy and that there is no cooperativity in the sense that the binding of one protein does not alter the binding energy of a second molecule of the bicoid protein to one of the other sites. As a result, the partition function can be evaluated simply in the closed form shown here and results in the level of Hunchback activation given by

$$[\text{Hb}]=[{\text{Hb}}_{max}]\frac{e^{-\beta {\epsilon }_{\text{active}}}{\left(1+\frac{[\text{Bcd}]}{K_{\text{d}}^{(\text{active})}}\right)}^7}{e^{-\beta {\epsilon }_{\text{active}}}{\left(1+\frac{[\text{Bcd}]}{K_{\text{d}}^{(\text{active})}}\right)}^7+e^{-\beta {\epsilon }_{\text{inactive}}}{\left(1+\frac{[\text{Bcd}]}{K_{\text{d}}^{(\text{inactive})}}\right)}^7},$$ (2.11)

where [Bcd] and [Hb] are the Bicoid and Hunchback concentrations, respectively. The data for the relationship between bicoid binding and hunchback expression has been explored in a recent paper (Gregor et al., 2007). Empirically, the authors of that study found that the expression of Hunchback can be fit to a Hill function that depends upon the concentration of Bicoid. An example of both the Hill function approach favored in that study and the MWC functional form described here are shown in Fig. 2.12B. At this point, the quantitative dissection of developmentally important enhancers in eukaryotes is still in the very early stages, and there is a huge amount still to be done both in carrying out experiments that are at once quantitative and revealing and in finding the right set of “knobs” that can be tuned in both these experiments and the models that are developed in response. Our discussion is meant simply to illustrate the types of questions that are currently being considered and the way that simple thermodynamics are beginning to be used to answer those questions (Fakhouri et al., 2010).

3.3.5. The biological reach of MWC models

Of the nearly 5700 citations at the time of this writing of the original paper by Monod, Wyman, and Changeux (Monod et al., 1965), many are concerned with the limits and validity of this class of models and how they can be used to reflect on a broad class of biological problems with special interest in the fitting of some class of data. Our intent here has mainly focused instead on what such models assume about the molecules they describe and how to use simple ideas from equilibrium statistical mechanics to compute the MWC expressions for binding probability.

It is important to realize that in all of the case studies set forth here, the key point is to illustrate the style of analysis and not the claim that the particular models are the final word on the subject in question. For example, our treatment of the ligand-gated ion channel, while a useful starting point, has been found to miss certain detailed features of the gating properties of these channels. Similarly, our introduction to the MWC approach for bacterial chemotaxis has swept many of the key nuances for this problem under the rug. For example, to really capture the detailed behavior of these systems requires positing a heterogeneous clustering of the different types of chemoreceptors. As concerns transcriptional activation in eukaryotic enhancers, the use of models like that presented here is in its infancy and may end up not being the right picture at all. The key reason for promoting these models is that they provide quantitative hypotheses about the processes of interest which can be used a starting point for developing experiments that test them. As is often the case for the application of simplified analytical models to biological systems, their most useful role can be to help the investigator determine what information is missing. To a first approximation, experimental data that are extremely well-fit by MWC models may be reasonably assumed to operate more-or-less as discrete state systems, where the relevant separation of time scales has rendered the equilibrium assumption of statistical mechanics to be close to correct. In such cases, no further complexifications of the mechanism need be postulated to explain the phenomenon at hand, at least within the limits of the available data which is well fit by the simple model. In the more interesting and perhaps more common case where the simplest statistical mechanics models reveal systematic differences from the data, new kinds of experiments may suggest themselves that will account for the discrepancies and reveal more insight into the workings of the system. Thus, a careful comparison of theory and experiment can serve to uncover quantitative details of the mechanism, whether it be gene regulation, ion-channel gating, or detection of chemoattractant.

4. The Unreasonable Effectiveness of Random-Walk Models

So far, our emphasis has been almost exclusively on binding problems. However, our argument that equilibrium ideas have a broad reach in the biological setting transcends these applications. To demonstrate that point, we close with a brief discussion of the power of such thinking in the context of random-walk models in general and their uses for thinking about polymer problems in particular. The random-walk model touches on topics ranging from evolution to economics, from materials science to biology (Rudnick and Gaspari, 2004). For our purposes, we reflect on the random-walk model in its capacity as the first approach one is likely to try when thinking about the equilibrium disposition of polymers, including those referred to by Crick as the two great polymer languages, namely, nucleic acids and proteins. Though the particular case study we address here concerns proteins that harbor tethered receptor–ligand pairs, the same underlying ideas can be applied just as well to nucleic acids for thinking about the ubiquitous process of DNA looping in transcriptional regulation, for example, (Garcia et al., 2007; Rippe, 2001).

There is a vast literature on the use of models from equilibrium statistical mechanics to explore the properties of biological polymers (de Gennes, 1979; Grosberg and Khokhlov, 1997). As usual, the idea is to figure out what the collection of allowed microstates is for the biological polymer of interest (an example for the conformations of DNA was given in Fig. 2.1). Perhaps the simplest example imagines the polymer of interest in much the same way we would think of a chain of interlinked paper clips. In particular, we treat the polymer as a chain of N segments, each of which has length a. We then posit that each and every configuration has the same energy (and hence the same Boltzmann factor) and thus, the problem of finding the probability of different configurations becomes one of counting their degeneracies. For example, those macrostates, characterized by a particular end–end distance which can be realized in the most different ways are the most likely. These ideas and their generalizations have been used to consider many interesting problems (Phillips et al., 2009b). One of the most celebrated examples that we will not elaborate on here concerns the use of these ideas in the setting of single-molecule biophysics where it has now become routine to manipulate individual proteins and nucleic acids. Indeed, the force-extension properties of these biological polymers are so well described by ideas of equilibrium polymer physics that stretching individual DNA molecules has become a way to calibrate various single-molecule apparatus such as optical and magnetic traps.

To get a sense of how these ideas from polymer physics insinuate themselves into biological binding problems hence building upon the earlier parts of the chapter, we consider the simple competition between a tethered ligand–receptor pair and soluble competitor ligands. This kind of motif exists in a number of signaling proteins and has also been the basis of fascinating recent experiments in synthetic biology (Dueber et al., 2003). In particular, the toy model introduced here mimics a synthetic receptor–ligand pair in which the actin cytoskeletal regulatory protein, N-WASP, has been modified to include a single PDZ domain, thus allowing N-WASP activity to be artificially brought under the influence of the PDZ ligand. Furthermore, a copy of the ligand is also attached to the modified N-WASP, with both ligand and receptor domains attached by flexible unstructured protein domains that serve as tethers. As shown in Fig. 2.13A, there are three distinct classes of states available to the system. In the first state, the tethered ligand and receptor are bound to each other. In the second state, the receptor is unoccupied. In the third state, one of the soluble ligands is bound to the receptor. The question we are interested in addressing is the relative probability of the two different bound states and how they depend upon the concentration of soluble ligands.

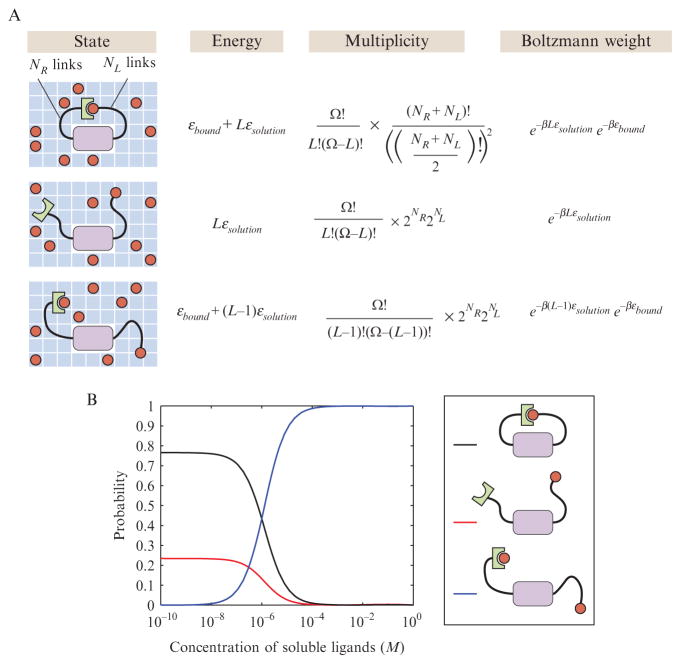
Figure 2.13.

Random-walk models of tethered ligand–receptor pairs. (A) Schematic of the tethered ligand–receptor pair and the associated statistical weights. The multiplicities for the polymer are computed using a one-dimensional toy model of the tether. N_R and N_L represent the number of right- and left-pointing segments out of the total N = N_R + N_L. The rest of the parameters are defined as in Fig. 2.3. For more realistic calculations, see Van Valen et al. (2009). (B) Concentration dependence of the probabilities of the different states that can be realized by the tethered ligand–receptor pair. The parameters used in the plot are Δε = ε_bound − ε_solution = − 15 K_BT and a probability of looping given by the one-dimensional random walk of 10⁻⁶. The volume of the elementary box v has been chosen to be approximately 1.67 nm³.

The intuitive argument is that the probability that the receptor will be occupied by a ligand is a result of the competition between the tethered ligand and its soluble partners. As the concentration of the soluble ligands is increased, it becomes increasingly likely that they will form a partnership with the tethered receptor. To explore the nature of this competition, we compute the ratio of the probabilities for the free and tethered ligands. For the purposes of the model shown in Fig. 2.13A, we treat the tether using the simplest one-dimensional model of a random walk since all we are trying to demonstrate is the concept, as opposed to the quantitative details. What this means really is that we evaluate the entropic cost of loop formation using a one-dimensional model which makes it a simple counting exercise to determine the fraction of conformations which close on themselves. Stated simply, if we think of each monomer in the polymer as pointing left or right, then loop formation in this context requires that the number of right and left-pointing monomers be the same. The key point is that in the closed conformation, the two tethers have many fewer conformations available to them in comparison with the case when they are no longer linked, and each side is free to flop around on its own. The result of this competition as a function of the soluble ligand concentration is shown in Fig. 2.13B, and is consistent with our intuition in the sense that in the high concentration limit, the receptor is saturated by soluble ligands. The specific concentration at which the tethered ligand and the soluble ligands have the same probability of being bound to the receptor depends upon the looping probability. As the relative flexibility and length of the tethers are varied experimentally, the quantitative predictions of this simple model can be rigorously tested (Dueber et al., 2003).

5. Conclusions

Thermodynamics is unreasonably effective in the biological setting, but effective it is. As noted by Einstein in his autobiography, “A theory is the more impressive the greater the simplicity of its premises is, the more different kinds of things it relates, and the more extended its area of applicability. Therefore the deep impression which classical thermodynamics made upon me. It is the only physical theory of universal content concerning which I am convinced that, within the framework of the applicability of its basic concepts, it will never be overthrown.” (Schilpp, 1970).

Equilibrium thermodynamic ideas and their statistical mechanics partner concepts pervade not only the in vitro domain of traditional biochemical binding reactions, but also permeate our thinking for more biologically relevant in vivo examples ranging from gene regulation to signaling networks to the physical limits on biological detection (Bialek and Setayeshgar, 2005, 2008). In this chapter, we have tried to articulate some of the fundamentals of equilibrium models for a variety of different problems. Our analysis has focused more on the conceptual underpinnings that on the specific and detailed ways that biological data is greeted by these kinds of models. Here, we have described a few of our favorite examples of the confrontation of the models and corresponding experiments, and many more can be found elsewhere (Bintu et al., 2005a,b; Hill, 1985; Keymer et al., 2006; Klotz, 1997; Mello and Tu, 2005; Phillips et al., 2009c). We have argued that conceptually part of the reason for the effectiveness of equilibrium ideas in the biological setting is likely a matter of separation of time scales, and the most unreasonably effective simplification underlying the MWC and statistical mechanical treatment of these problems, that they exist primarily in a countable number of interconvertible functional states rather than as a squishy continuum.

In his book “How the Mind Works,” Steven Pinker notes “The linguist Noam Chomsky once suggested that our ignorance can be divided into problems and mysteries. When we face a problem, we may not know its solution, but we have insight, increasing knowledge, and an inkling of what we are looking for. When we face a mystery, however, we can only stare in wonder and bewilderment, not knowing what an explanation would even look like. I wrote this book because dozens of mysteries of the mind have recently been upgraded to problems. Every idea in the book may turn out to be wrong, but that would be progress, because our old ideas were too vapid to be wrong.” (Pinker, 2009). In our view, one of the most important reasons for the potency of the quantitative slant which equilibrium models are but one example of is that they are a tool for generating specific and detailed hypotheses which are a step along the way to turning mysteries into problems and which give us an opportunity to design experiments that can tell us whether we are wrong. The rigorous framework of statistical mechanics provides no space for being vapid.