Repeatability of Measured Brain Volume by Atlas-Based Method Using T1-Weighted Image

Abstract

The aims of this study were to (1) investigate the repeatability of measured volumes using the atlas-based method in each area of the brain, and (2) validate our hypothesis that the repeatability of the measured volumes with the atlas-based method was improved by using smoothed images. T1-weighted magnetic resonance images were obtained in five healthy subjects using the 1.5-T scanner. We used Statistical Parametric Mapping 5 and WFU PickAtlas software (theory of the Talairach brain atlas). Volumes inside region-of-interest (ROI) were measured in ten sets (five subjects × right and left) on six ROIs, respectively. One set comprises five images (one subject × five 3D-T1WIs). The percentage change was defined as [100 × (measured volume–mean volume in each set)/mean volume in each set)]. As a result, the average percentage changes using non-smoothed image on each ROI were as follows: gray matter, 0.482%; white matter, 0.375%; cerebrospinal fluid images, 0.731%; hippocampus, 0.864%; orbital gyrus, 1.692%; cerebellum posterior lobe, 0.854%. Using smoothed images with large FWHM resulted in improved repeatability on orbital gyrus. This is the first report of repeatability in each brain structure and improved repeatability with smoothed images using the atlas-based method.

Background

There are many evaluation methods for brain morphometry [1–3], and there are two major methods of brain volumetry using T1-weighted magnetic resonance images (T1WI): the voxel-based morphometry method [4] and the region-of-interest (ROI) method. In the first technique, brain volume is evaluated using smoothed images. However, in the other, brain volume is evaluated using non-smoothed images. The ROI method includes techniques such as the manually traced ROI method [5–7] and atlas-based method [8, 9]. The manual measurement method is difficult, time consuming, and susceptible to rater bias. The atlas-based method employs semi-automated algorithms and is operator-independent. This study requires that all measurements are analyzed with consistent precision. Therefore, we use the atlas-based method in the present study. It is important to study and understand how the repeatability of measured volumes varies under different conditions (i.e., static magnetic field strength, transmission and/or receiver coil, imaging sequence). Therefore, studies on the repeatability of brain volume measurements have been recently reported [10–15].

The first aim of this study was to investigate the repeatability of measured volumes using the atlas-based method in each area of the brain. The spatial distortion of brain images is different in each area, thus affecting repeatability. Therefore, we expected that repeatability would be different in each area of the brain. The second objective was to validate our hypothesis that the repeatability of the measured volumes with the atlas-based method was improved by using smoothed images. To the best of our knowledge, no study has reported repeatability by the atlas-based method using smoothed images.

Methods

Subjects

A total of five healthy subjects participated in this study. Three-dimensional T1WI (3D-T1WI) were obtained from each subject five times in 1 day. MR images were inspected by a board-certified radiologist, and subjects with the following findings are excluded from the study: brain tumors, infarctions, hemorrhage, and white matter lesions. Subject data are: Age average ± standard deviation is 27.4 ± 2.4 years; all subjects were males; no mental disorders or blackouts. Scanning protocol was approved by the ethical committee of our institution. After the study had been explained to the subjects, written informed consent was obtained from all of them.

MRI Scanning Protocol

MRI data were obtained using the 1.5-T scanner (MAGNETOM VISION, Siemens Medical Solutions, Erlangen, Germany). The circularly polarized head coil was used as the transmission-receiver coil. 3D magnetization-prepared rapid gradient echo (3D-MP-RAGE) was used to obtain 128 contiguous sagittal T1WI with a slice thickness of 1.25 mm for volumetric analysis (repetition time/echo time = 9.7/4 ms; inversion time = 300 ms; flip angle = 12°; field of view = 22 cm; number of excitations = 1; 256 × 200 pixel matrix). The voxel dimensions were 0.8594 × 1.1 × 1.25 mm.

Image Preprocessing for Repeatability by the Atlas-Based Method

We used Statistical Parametric Mapping 5 (SPM5) software [16] for the following processing. The 3D-MP-RAGE images in native space were bias-corrected (default condition in SPM5), spatially normalized (default condition in SPM5), and segmented into gray matter (GM), white matter (WM), and cerebrospinal fluid images (CSF) [4] (default condition in SPM5); the voxel sizes of the normalized output images were set in 2 × 2 × 2 mm. During the modulation step in SPM5, the voxel values of the normalized GM, WM, and CSF images were multiplied by a measure of relative volumes of warped and unwarped structures derived from the nonlinear step of spatial normalization (Jacobian determinant). Resulting GM images were smoothed with a Gaussian kernel of 6, 8, and 12 mm full-width at half maximum (FWHM) by SPM5. WM images and the CSF images were performed by the same procedures.

Statistical Analysis for Measurement of Volume Using ROIs

ROIs were obtained by WFU PickAtlas (theory of the Talairach brain atlas) [8]. We used the following ROIs (Fig. 1): GM, WM, CSF, hippocampus (HC), orbital gyrus (OG), and cerebellum posterior lobe (CPL). Measurements of volume on GM, HC, OG, and CPL were performed using normalized GM images. Measurements of volume on WM or CSF were performed using normalized WM or CSF images. Volumes inside ROI were measured in each subject on the left and right side using the normalized images. Volumes inside ROI were measured ten sets (five subjects × right and left) on GM, WM, CSF, HC, OG, and CPL, respectively. One set is composed of five images (one subject × five 3D-T1WIs). The percentage change was defined as [100 × (measured volume−mean volume in each set)/mean volume in each set)]. The average percentage change was calculated through 50 percentage changes (five subjects × five 3D-T1WIs × right or left) on GM, WM, CSF, HC, OG, and CPL, respectively. That is, the low average percentage change denotes high repeatability. We obtained 24 average percentage changes (six ROIs × non-smoothed, 6 mm FWHM, 8 mm FWHM, or 12 mm FWHM). We compared six average percentage changes (i.e., measured volume on GM, WM, CSF, HC, OG, or CPL) using non-smoothed images when volumetric plasticity was examined. Moreover, to evaluate the repeatability of the volume measurements with the atlas-based method in smoothed images, we determined the average percentage changes on GM, WM, CSF, HC, OG, and CPL in the non-smoothed, 6 mm FWHM, 8 mm FWHM, and 12 mm FWHM, respectively. Statistical significance of differences between the groups of different ROI or FWHM was examined using analysis of variance (ANOVA) and the Tukey–Kramer method as a post hoc test. Statistical significance of both tests was set at P < 0.05.

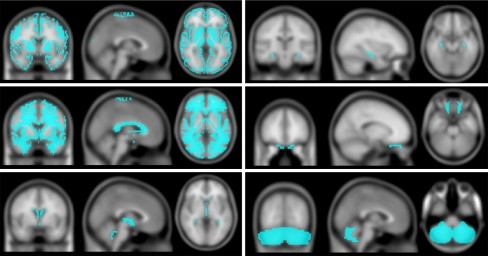
Fig. 1.

ROIs are superimposed on the T1 template image. We used ROIs as follows: gray matter (top left), white matter (middle left), cerebrospinal fluid (bottom left), hippocampus (top right), orbital gyrus (middle right), and cerebellum posterior lobe (bottom right). ROI volumes were measured for each subject on the left and right side

Results

Repeatability by Atlas-Based Method Using Non-smoothed Images

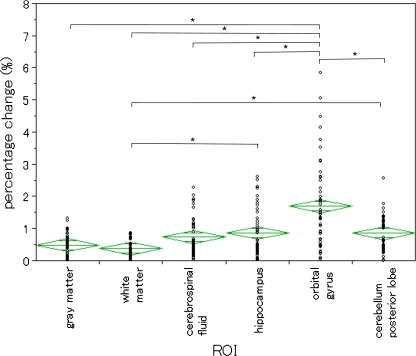
Six average percentage changes using non-smoothed images were shown in Fig. 2. The average percentage changes on each ROI were as follows: GM (0.482 ± 0.340 (mean value ± standard deviation)) %; WM (0.375 ± 0.233) %; CSF (0.731 ± 0.570) %; HC (0.864 ± 0.733) %; OG (1.692 ± 1.321) %; and CPL (0.854 ± 0.591) %. There was a significant difference between six average percentage changes in ANOVA (P < 0.05). The average percentage change on OG was higher than the average percentage changes on other ROIs. Therefore, these results revealed that repeatability on OG was relatively low.

Fig. 2.

Repeatability by the atlas-based method in non-smoothed images. We showed percentage changes in each ROI. The breadth of each green rhomboid shows the number of cases in the group, the height shows the 95% confidence interval, the middle line shows the average of the group, and the horizontal lines in the upper and lower parts show the overlap marks. There was a significant difference in ANOVA (P < 0.05). In addition, where there was a significant difference in the Tukey–Kramer method, (*) is displayed. Percentage change value for OG was larger than the percentage change values for all ROIs

Repeatability by Atlas-Based Method Using Smoothed Images

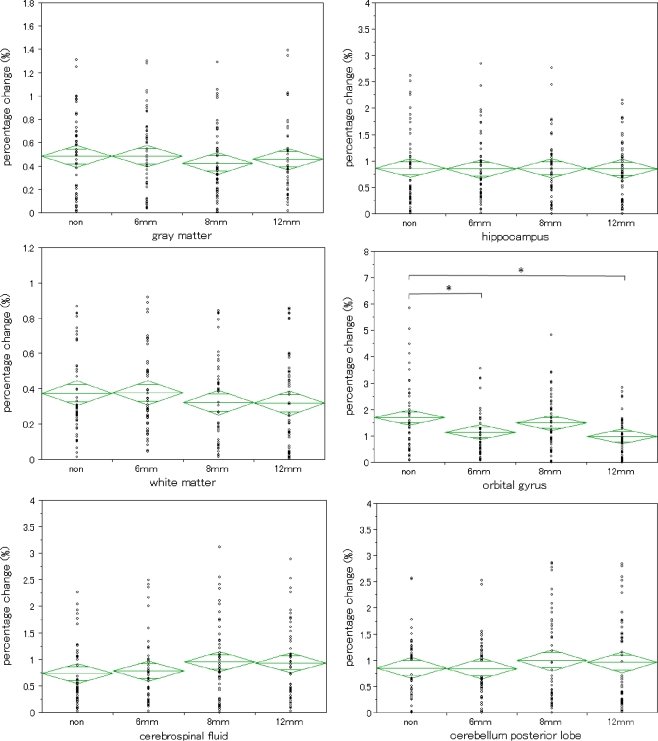
Four average percentage changes were shown in Fig. 3 and Table 1 when using smoothed images with different FWHM on six ROIs, respectively. For OG, there was a significant difference in ANOVA (P = 0.0020). Therefore, we tested the significant difference between different FWHMs in the Tukey–Kramer method. As a result, non–6 mm FWHM comparison and non–12 mm FWHM comparison revealed a significant difference. There was no significant difference in ANOVA for GM, WM, CSF, HC, or CPL. Using smoothed images with large FWHM resulted to the improved repeatability of the atlas-based method on OG.

Fig. 3.

Repeatability by atlas-based method in smoothed images. The breadth of each green rhomboid shows the number of cases in the group, the height shows the 95% confidence interval, the middle line shows the average of the group, and the horizontal lines in the upper and lower parts show the overlap marks. For white matter (left middle), cerebrospinal fluid (left bottom), hippocampus (right top), and cerebellum posterior lobe (right bottom), there were no significant differences in ANOVA. For orbital gyrus there was a significant difference in ANOVA (P = 0.0020). For only orbital gyrus, repeatability by the atlas-based method was improved by using smoothed images

Table 1.

Repeatability by atlas-based method in smoothed images

ROI name	Full width at half-maximum
	Non	6 mm	8 mm	12 mm
Gray matter	0.48 ± 0.34	0.48 ± 0.34	0.42 ± 0.32	0.46 ± 0.33
White matter	0.38 ± 0.23	0.38 ± 0.24	0.32 ± 0.25	0.32 ± 0.27
Cerebrospinal fluid	0.73 ± 0.57	0.78 ± 0.63	0.95 ± 0.75	0.93 ± 0.71
Hippocampus	0.86 ± 0.73	0.84 ± 0.64	0.86 ± 0.61	0.85 ± 0.55
Orbital gyrus	1.69 ± 1.32	1.13 ± 0.89	1.49 ± 1.06	0.98 ± 0.69
Cerebellum posterior lobe	0.85 ± 0.59	0.84 ± 0.56	1.00 ± 0.86	0.96 ± 0.83

The average percentage changes and the standard deviations on each ROI are shown

Discussion

In the present study, the average percentage changes using non-smoothed images on GM and WM were smaller than 0.5%. These results did not contradict the report by Shuter et al. [10]. The results presented above demonstrated that the atlas-based method was superior for the repeatability, when we needed to detect a slight change for brain volumetry. However, there were slight differences in the same subject with the atlas-based method under the consecutive imaging (i.e., acquisition day, geometry of head and coil, sequence, and other factors were same). This difference may mask real changes during the course of longitudinal studies. When we want to observe a slight percentage change, we should note the repeatability of the volumetry method. Signal-to-noise ratio (SNR), motion artifacts, and flow artifacts were slightly different at each data acquisition. Therefore, measured volume slightly changes even if images of a subject were acquired under consecutive imaging.

The average percentage change on OG showed low repeatability (=high percentage change) compared to other ROIs. There are two main reasons that the repeatability on OG has declined: first, spatial normalization error; and second, ROI volume. The relationship between repeatability and spatial normalization error may be described as follows. Magnetic susceptibility change in OG is large compared to other ROIs because orbit and nasal sinuses occupy the area near the OG. Image distortion is caused by magnetic susceptibility change. Spatial normalization involves applying a spatial transformation that moves and warps images into the same standard anatomical space defined by a template. That is, spatial normalization error may be greater when image distortion is large. Therefore, repeatability on OG has declined.

The relationship between repeatability and ROI volume is described as follows. When spatial normalization error of the same distance is caused, the effluence rate of small ROI is large compared with that of a large ROI. For example, when a spatial normalization error of 1 mm³ is caused in ROI of 1 mm³, the effluence rate is 100%. However, when a spatial normalization error of 1 mm³ is caused in ROI of 1,000 mm³, the effluence rate is relatively small. Repeatability on OG has declined because the volume inside the ROI of OG is relatively small. Therefore, we thought that repeatability on OG has declined for the above-mentioned two reasons.

We expected that repeatability by the atlas-based method using smoothed images was improved, because the influence of spatial normalization error and signal non-uniformity are decreased by using a smoothed image. Results of this study included a significant improvement in only OG and no significant differences in other ROIs. It is plausible that the influence from image distortion is relatively small, because WM has a large ROI volume. In addition, it is plausible that the influence from signal non-uniformity is relatively great. Therefore, when the influence from signal non-uniformity was decreased by using smoothed images, we were able to find a significant difference in WM. However, we considered that using a smoothed image did not serve to decrease the influence from signal non-uniformity, because we did not find any significant difference in WM. On the other hand, there was a significant improvement in OG. It is plausible that the influence from image distortion is relatively large, because OG has a small ROI volume. In addition, it is plausible that the influence from signal non-uniformity is relatively small. We estimated that using a smoothed image has decreased the influence from image distortion because a significant difference was found in OG.

A major limitation of the current study was that the results cannot apply to other processes. A change of the analysis image quality (i.e., contrast, SNR) and analysis algorithm (i.e., segmentation algorithm, normalization algorithm) resulted in precision changes. However, the present study provided information about the repeatability to researchers because results on GM and WM in the present study did not contradict the report by Shuter et al. [10].

The second limitation of our study was that it should be noted that the influence from using the smoothed image is changed by the distance of the spatial normalization error. Thus, a smoothed image can be used for measurement of the volume by the atlas-based method when one subject is observed longitudinally under the same environment. However, the atlas-based method with a smoothed image is not useful when volume measurements are observed cross-sectionally with multiple subject data. The spatial normalization error (=amount of image distortion) changes between multiple subjects. It is unusual to use a smoothed image but we want to find an applied field.

The third limitation of our study was that we had only five subjects, scanned five times each. Exact result is obtained in a study with many samples. However, the addition of the number of the samples leads to the extension of the study period. We employed ‘five subjects × five times’ rather than ‘one subject × 25 times’, because we expected that the repeatability was influenced by brain-shape variation.

Conclusions

To the best of our knowledge, this is the first atlas-based method study to show that the use of smoothed images can improve repeatability in brain volumetry. In addition, the present study showed that the repeatability of measured volumes using the atlas-based method changed in each area of the brain. It is important to understand the repeatability of the brain volumetry method.