Utility-Aware Screening with Clique-Oriented Prioritization

Abstract

Most methods of deciding which hits from a screen to send for confirmatory testing assume that all confirmed actives are equally valuable and aim only to maximize the the number of confirmed hits. In contrast, “utility-aware” methods are informed by models of screeners’ preferences and can increase the rate at which the useful information is discovered. Clique-oriented prioritization (COP) extends a recently proposed economic framework and aims—by changing which hits are sent for confirmatory testing—to maximize the number of scaffolds with at least two confirmed active examples. In both retrospective and prospective experiments, COP enables accurate predictions of the number of clique discoveries in a batch of confirmatory experiments and improves the rate of clique discovery by more than three-fold. In contrast, other similarity-based methods like ontology-based pattern identification (OPI) and local hit-rate analysis (LHR) reduce the rate of scaffold discovery by about half. The utility-aware algorithm used to implement COP is general enough to implement several other important models of screener preferences.

2 Introduction

Deciding which initial positives (“hits”) from a high-throughput screen (HTS) to submit for confirmatory experiments is a basic task faced by all screeners.^1,2,3 Most methods of selecting hits aim only to maximize the number of confirmed hits, assuming that all confirmed actives are equally valuable regardless of their novelty.^4,5,6,3,7,8 We hypothesize, in contrast, that the molecules that establish the activity of new molecular scaffolds are more valuable, and this notion can be formalized in “utility-aware” methods so as to alter which hits are sent for confirmatory testing. Ultimately, these methods can increase the rate at which the useful information is discovered in a screen.

To a limited extent, this hypothesis has been supported by three distinct narratives in the literature. First, the selection of hits for follow up is an important step that affects the sensitivity of the screening campaign. Several studies have shown that there can be a substantial number of false negatives buried in screening data, indicating that HTS data can be noisy enough that true actives are missed,^5,9,10 and careful statistics can recover some of these false negatives.^3,7,8,9

Second, the first utility-aware method—diversity-oriented prioritization (DOP)—was successfully applied to HTS data so as to increase the rate of active scaffold discovery by as much as 17%.¹⁰ DOP works by formalizing a preference often stated by screeners: they are not looking for active molecules as much as looking for novel active scaffolds.^11,12 DOP defines a scaffold—or a particular cluster—as active if at least one example of the scaffold is successfully confirmed active and uses this definition to derive a utility-aware prioritization algorithm. Together, these two narratives suggest that some actives remain undiscovered and that formalizing screeners’ preferences could improve the rate of discovery by focusing attention on the most informative examples.

Some methods use molecular clustering to improve the design of HTS experiments. For example, several pick molecules for follow-up using statistical tests on the data from a single-dose screen to find clusters of active molecules.^13,14,8 These methods favor clusters that contain several active molecules, and attempt to simultaneously send many very similar molecules for confirmatory testing. As intended, these methods successfully increase the number of active molecules identified in confirmatory testing. Rather than picking large groups of similar molecules for follow up, our method aims to maximize the number of clusters with at least two successfully confirmed active examples.

Our effort to consider the diversity of hits in addition to activity is closely related to similar work in the internet and database search field.^15,16,17,18 Likewise, recent work in chemical informatics has suggested considering activity when picking diverse sets of molecules can be desirable.¹⁹ In line with these efforts, this study extends the DOP method¹⁰ by (1) introducing a more complex utility function which more accurately models many screeners’ preferences and (2) deriving a more general utility-aware prioritization algorithm which can accommodate several important screener preferences.

In this study, we define a scaffold as active if at clique of at least two of its examples have been confirmed as actives. This reflects the preferences of medicinal chemists stated in several personal communications; they prefer that the activity of a scaffold is established by more than one active example before they choose to pursue it further. This definition motivates the development of a more general and more complex utility-aware prioritization algorithm, which can optimize many different choices of a utility function. Although we focus on just one definition of a clique, a flexible prioritization algorithm is important because screeners have different preferences.²⁰ The clique definition of an active scaffold and prioritization algorithm together yield a new method: clique-oriented prioritization (COP), which we validate in both retrospective and prospective experiments.

3 Data

3.1 Single-Dose HTS

For most of our experiments, we use a screen based on a fluorescence polarization assay for molecules that inhibit MEX-5. The technical details of the assay and subsequent analysis can be found in PubChem (PubChem AIDs 1832 and 1833). For 301, 856 small molecules screened in duplicate, activity is defined as the mean of the final, corrected percent inhibition. We use 301, 617 of these for which all necessary data are available. After filtering out molecules with autofluorescence and those without additional material readily available, there remain 1322 with at least one screen-activity greater than 25%. These are labeled “hits” and tested for dose-response behavior in the first batch of confirmatory experiments. Of these tested molecules, 839 yield data consistent with inhibitory activity. Each hit is considered a confirmed “active” if the effective concentration at half maximal activity (EC50) is less than or equal to 20μM. Using this criterion, 410 molecules are designated active.

3.2 Quantitative HTS

We apply our methods to two additional screens: a screen for inhibitors of BAZ2B protein (AID 504333)²¹ and a screen for inhibitors of JMJD2A-tudor domain (AID 504339).²² The BAZ2B screen identifies 3, 205 actives with inhibitory EC50 less than or equal to 10μM out of 359, 824 molecules; the JMJD2A screen identifies 5, 974 actives out of 388, 413 molecules.

Both of these screens are Quantitative High-Throughput Screens (qHTS)—in which every compound in the library of small molecules is tested for dose-response behavior. This allows us to simulate a two-stage HTS: a single dose primary screen followed by a confirmatory dose-response experiment. We choose the single-dose datapoint measured at 11μM to simulate the primary-screen activity, while blinding the EC50s for these compounds from our analysis until they are prioritized for follow-up experiments in the simulation.

4 Methods

4.1 Scaffold Clusters

Often, HTS campaigns aim to identify as many new scaffolds as possible. Sometimes intellectual property concerns dictate both avoiding particular scaffolds and defining discoveries using the scaffold concept. Furthermore, it is scaffolds, not specific hits from the screen, which are often the most important starting points from which lead-refinement proceeds.^11,12,23,24 Therefore, we focus on scaffold-based clustering. Nonetheless, our methods can be easily adapted to similarity-based clustering if desired. To do so, molecules would be grouped by similarity rather than by common scaffold.

The molecules from this screen are clustered into groups with common scaffolds. These scaffold groups are disjoint sets of molecules. Scaffolds are computed from the structure of each molecule using the definition of molecular frameworks described in:²⁵ contiguous ring systems and the chains that link two or more rings together. In order to ensure our findings are not overly dependent on the choice of scaffold definition, we replicate our experiments using a modification of this definition which replaces every atom in the scaffold with a carbon. The results of the carbon-scaffold experiments are not presented because their results are not notably different.

Although molecular frameworks are only an approximation of a medicinal chemists’ subjective concept of a scaffold,^24,23 frameworks are commonly used in chemical informatics because they are clearly defined and easy to compute. Although we define scaffolds as the molecular frameworks, COP is compatible with more sophisticated scaffold detection algorithms; all it requires is that molecules are placed in structurally sensible groups.

4.2 Economic Framework

COP, just like DOP, extends a recently described economic framework for interpreting HTS data, initially introduced to decide how many hits to send for confirmatory testing.⁹ This framework is used to iteratively choose each batch of hits to be sent for confirmatory testing so as to maximize the expected surplus of the batch: the expected utility minus the expected cost. The expected surplus is computed using three mathematical models: utility, cost, and predictive. The utility model specifies the preferences of the screener, the cost model tracks the cost of running a confirmatory experiment, and the predictive model guesses the outcome of future confirmatory experiments.

4.3 Cost Model

The cost model is relevant in two ways. First, in some scenarios, the cost of acquiring different molecules varies. In the context of HTS, however, all molecules under consideration are usually equally accessible. Therefore, we assume that it costs the same amount to send each molecule for confirmatory testing. Second, there is both a large fixed and smaller variable cost associated with sending molecules for confirmatory tests. Consequently, the confirmatory tests are most efficiently performed in large batches, just as is done in practice.

4.4 Predictive Model

We consider two predictive models: a logistic regressor (LR)²⁶ and a neural network with a single hidden node (NN1),²⁷ structured to use the screen activity as the single independent variable and the result of the associated confirmatory experiment as the single dependent variable. Both models are trained using gradient descent on the cross-entropy error using the monotonic prior defined in.¹⁰ This protocol yields models whose outputs are interpretable as probabilities, allowing us to define

$$P(x)\{\begin{array}{ll}1\hfill & \text{if}\text{molecule}x\text{is}\text{active}\hfill \\ 0\hfill & \text{if}\text{molecule}x\text{is}\text{inactive}\hfill \\ z_x\hfill & \text{if}\text{molecule}x\text{untested},\hfill \end{array}$$ (1)

where z_x is the output of the predictive model on molecule x, and P (x) is used to parameterize a family of independent binomial distributions, each one modeling the distribution of confirmatory test outcomes for a particular molecule as a single biased coin-flip.

4.5 Utility Model

The utility model, U(D), assumes the screener has rational preferences characterized as a monotonically increasing function of the total discovery so far, D. In this study, we define the total discovery as the sum of the discovery across all scaffolds

$$D=\sum _{i}d(a_i),$$ (2)

where i ranges over all the scaffolds, a_i is the number of confirmed active molecules with the ith scaffold, and d(·) is the “discovery function” that returns the total discovery yielded by the scaffold group as a function of the total actives discovered so far. In this study, a scaffold is considered to be ‘active’ if at least two examples of the scaffold have been confirmed active. This is equivalent to defining the discovery function as

$$d(a)\{\begin{array}{ll}1\hfill & \text{if}a\ge 2\hfill \\ 0\hfill & \text{if}a<2\hfill \end{array}.$$ (3)

Several other definitions of the discovery function are explored in the Discussion.

4.6 Prioritization Algorithm

Consistent with the economic framework, we propose selecting the next batch of molecules to send for confirmatory testing so as to maximize the expected marginal discovery (EMD) of the next batch. The proof in¹⁰ demonstrates that maximizing the EMD is a very good approximation for maximizing profit, as long as the very reasonable assumption holds that the utility function is an increasing function of discovery and a fixed cost model is used, as is the case in our framework.

In the case of COP, as we will see, prioritizing molecules by EMD does not work. Instead, molecules should be ordered and picked based on their amortized expected marginal discovery (AEMD, pronounced “aimed”) score, which is computed from the EMD of each molecule and described in the following sections. Prioritizing molecules by AEMD maximizes the EMD of the of the next batch.

A separate strategy is required to choose molecules to include in the first batch, before the predictive models have been trained and the probability vector can be computed. In many situations, prioritizing molecules by HTS activity for the first batch may be appropriate. We propose choosing the first batch using the non-parametric prioritization algorithm described in Section 4.9.

4.7 Expected Marginal Discovery

If the goal is to maximize discovery, molecules within a scaffold group should be screened in order of decreasing likelihood of activity. Given this ordering constraint, it becomes sensible to ask what the EMD of each molecule in the group. This question, of course, depends on the reasonable presumptions that the marginal discovery function is always greater than or equal to zero and the utility function is an increasing function of discovery.

For each molecule in a scaffold group, with the constraint that within a scaffold group they are screened in order of decreasing likelihood of activity, we can compute the EMD of each molecule as

$$\text{EMD}=\sum _{r=1}^{n_x}P(x\text{is}r\text{th}\text{active})d^{\prime }(r),$$ (4)

where P (x is rth active) is the probability molecule x is the rth active molecule in its scaffold group, n_x is the number of molecules with the same scaffold as x, and d′(·) is the “marginal discovery function,” defined as

$$d^{\prime }(r)=d(r)-d(r-1).$$ (5)

P (x is rth active) is computed as

$$P(x\text{is}r\text{th}\text{active})=P(x)P([r-1]\text{actives}\text{before}x),$$ (6)

where P (x)—the probability that x is active—is computed using Equation 1, and P ([r − 1] actives before x) is the probability that the number of molecules with the same scaffold confirmed active before molecule x is tested is exactly equal to r − 1. This last probability can be computed by convolving the binomial distributions associated with each molecule in the scaffold group tested prior to x. With this machinery, we compute the expected discovery of a batch of molecules by summing up the EMD associated with each molecule in the batch.

The EMD of a batch of molecules is the sum of each molecule’s EMD, so prioritizing molecules by EMD maximizes the expected utility of the next batch. This result holds while the marginal discovery function is monotonically decreasing and the utility is an increasing function of discovery. Using EMD as a priority in this way is exactly the strategy successfully used by¹⁰ to prioritize hits with a decreasing marginal discovery function. Unfortunately, COP does not satisfy this condition; its marginal discovery function is not monotonically decreasing. In this case AEMD scores can be used to prioritize molecules.

4.8 Amortized Expected Marginal Discovery

The EMD is computed using an ordering constraint that enforces, within a scaffold group, molecules to be tested in order of decreasing likelihood of activity. When the marginal discovery function is monotonically decreasing, ordering molecules by EMD does not violate this constraint. However, non-monotonic marginal discovery functions, like COP, shuffle the order within scaffold groups. Therefore, we seek to define a new score which will be on average equal to the EMD of a batch, while when used for prioritization will not violate the ordering constraint.

Letting D̄ be a vector of EMD values such that each component corresponds with an untested molecule within a single scaffold group ordered in the same way their EMD was calculated, we propose “amortizing” vector D̄ in a particular way to generate a vector of AEMD scores Ā guaranteed to be monotonically decreasing, and therefore guaranteed to prioritize molecules within a scaffold group in the same order used to compute their EMD. The amortization algorithm requires D̄ from which it computes the AEMD vector Ā:

1. Given a vector of EMDs associated with a set of untested molecules with the same scaffold, D̄, initialize the AEMD vector Ā to be an empty vector of the same length.

2. Start with first component of D̄ by letting the iteration variable i be 1.

3. Let another iteration variable j equal arg max_j [mean of components i to j of D̄], the index which maximizes the amortized value of component i.

4. Assign the mean of components i to j of vector of D̄ to components i to j of Ā.

5. While unassigned components in Ā remain, increment i to j + 1 and return to step 3.

This algorithm redistributes the values of D̄ to generate a monotonically decreasing vector.

For example, consider a scaffold group containing three untested molecules with the probabilities {0.8, 0.5, 0.3}. Using a clique-oriented discovery model (Equation 3), the computed EMD vector is {0, 0.4, 0.15} from which the amortization algorithm computes the AEMD vector as {0.2, 0.2, 0.15}. Consider another scaffold group with two untested molecules and one confirmed active molecule. Suppose the probabilities for this group are {1, 0.4, 0.2}. The expected marginal discovery is {0, 0.4, 0.12} which yields the AEMD scores {0.4, 0.12} corresponding to the first and second untested molecules in the group. A reference implementation, coded in Python, of the algorithm required to compute AEMD scores from an ordered probability vector and an arbitrary marginal discovery function is included in the Supporting Information.

When the batch boundary falls at the edge of a scaffold’s amortization group (computed in step 3 and stored in j), the sum of the AEMDs in the next batch is exactly the EMD of the batch; otherwise the sum of AEMDs is a very close approximation that only barely slightly overshoots the true EMD. Therefore, as we would hope, sorting all the molecules from all the groups by their AEMD scores and choosing the top molecules for confirmatory testing maximizes the EMD of the batch while maintaining the within-scaffold ordering used to compute the EMD scores.

4.9 Non-Parametric Prioritization

The AEMD algorithm presented in prior sections is relatively complicated and requires several parameters to be learned from the data. In contrast, we also developed a simpler non-parametric solution to COP that does not require parameters to be learned from the data. The non-parametric COP (COP-NP) algorithm for cliques of size c prioritizes molecules as follows:

1. For each scaffold group, let a be the number of molecules within the group that have already been confirmed active.

2. Within each group, sort the untested molecules in the scaffold group by their activity in the primary screen and consider two cases: (a) a ≥ c and (b) a < c.

   1. If a ≥ c then assign priority 0 to all the untested molecules.

   2. Otherwise, assign the priority of the top (c – a) molecules to be the activity of the untested molecule with the (c – a)th highest activity. Assign priority 0 to the rest of the untested molecules.

3. Across the entire screen and all scaffold groups, select those molecules with highest priority for further testing.

This implementation assumes that higher activities in the primary screen are desirable and that the worst possible activity is zero.

As we will see, COP-NP often works as well as the more complicated AEMD algorithm, even though it does not 3t any parameters to the data. However, COP-NP cannot predict how many scaffolds will be discovered in the next batch, nor can it accommodate more the complicated discovery functions described in the Discussion.

5 Results

5.1 Scaffold Distributions in Screen

A skewed distribution of scaffolds in HTS data would motivate our algorithm by revealing redundant experiments where molecules are prioritized by HTS activity alone. We considered three sets of molecules: the full set of molecules from the screen (the Library), the first batch sent for dose-response confirmation (the Dosed), and the molecules subsequently confirmed as active (the Active). There were 301, 617, 1, 322 and 410 molecules, and 84, 440, 1, 043, and 331 scaffolds (respectively) in each of these sets. Each scaffold was represented by, on average, 3.57, 1.27, and 1.24 examples (respectively). The molecules were not distributed evenly amongst scaffolds; a few scaffolds were disproportionately frequent and a large number were represented by a single example (Table 1). These results were expected and reflect the robust observation that molecules follow a power-law distribution when clustered.²⁸ Similar distributions would be expected if the data had been clustered by almost any clustering algorithm.

Table 1.

Scaffold distributions. The “Library” is the approximately 300, 000 molecules screened in the initial HTS assay, “Dosed” are the molecules sent for dose-response confirmation in the first batch, and “Active” are those molecules subsequently confirmed as active. For each set of molecules, the top panel displays the frequency of the top five most common scaffolds and the proportion of the total dataset that each scaffold group represents. The bottom panel displays the number of scaffolds with exactly 1, 2, 3, 4 or 5 examples in the data (frequency) and the proportion of data that these scaffold groups represent.

Rank	Number of Examples			Proportion of Data
	Library	Dosed	Active	Library	Dosed	Active
1	7215	19	6	0.023	0.014	0.015
2	1104	10	5	0.004	0.008	0.012
3	886	8	5	0.003	0.006	0.012
4	797	8	5	0.003	0.006	0.012
5	704	7	4	0.002	0.005	0.010

Frequency	Number of Scaffolds			Proportion of Data
	Library	Dosed	Active	Library	Dosed	Active
1	42889	887	285	0.142	0.671	0.695
2	14599	101	26	0.097	0.153	0.127
3	8065	30	12	0.080	0.068	0.088
4	5132	10	4	0.068	0.030	0.039
5	3382	9	3	0.056	0.034	0.037

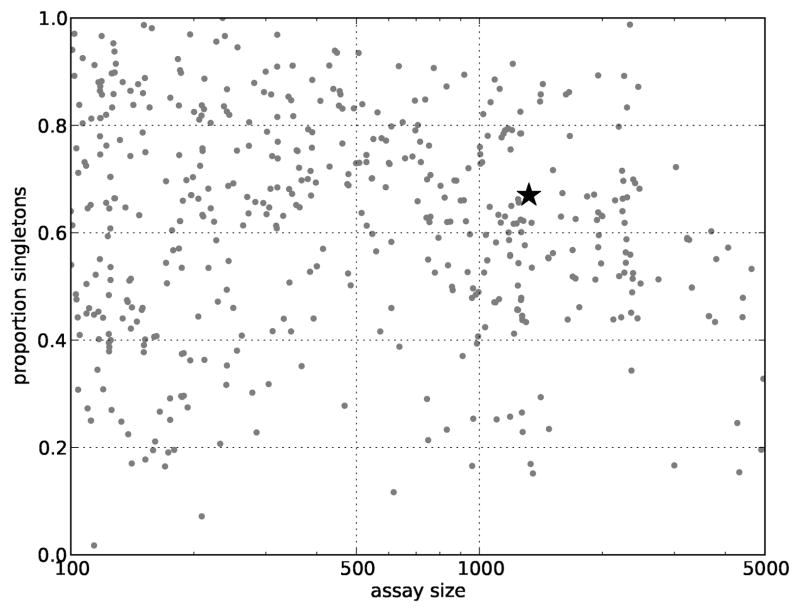
Strikingly, 67% of the dosed molecules were singletons: the only example of their scaffold sent for confirmatory tests. If the aim of the screen is to find active scaffolds supported by at least two confirmed active examples, this means that more than two thirds of the confirmatory tests were wasted on confirming molecules that will not yield useful information. Similarly, though less dramatic, more than 14% of the screened molecules were singletons. These distributions were not unique to this screen but observed across hundreds of screens from PubChem (Figure 1).

Figure 1.

Singleton proportion. Each point in this figure corresponds to a PubChem screen executed on 100 to 5000 molecules, the typical size of confirmatory screens. The star corresponds with the dose-response experiment of the MEX screen used in this study. Across these screens, about 55% of molecules are singletons, the only example of their scaffold.

The consistent observation of such a high number of singletons means a substantial number of molecules sent for confirmatory experiments cannot be used to confidently establish the activity of a scaffold. To a limited extent, this point should be tempered by the fact that there is no definitive definition of scaffold. Some of these singletons may be de-orphaned and grouped with others when a different scaffold definition is used. Likewise, careful library design with this concern in mind is more likely to substantially shift this distribution.²⁹ Nonetheless, the striking prevalence of singletons is a consequence of the robustly observed power-law distribution of molecules and is not likely to be improved much by shifting the definition of a scaffold.

These distributions give us some clues as to COP’s behavior. First, we predict that COP would substantially alter how molecules are prioritized. Second, we predict, in a best case scenario, that COP could as much as triple the number of active cliques discovered from a fixed number of confirmatory experiments. Of course, there are more precise ways of predicting the performance improvements possible with COP, but empirical benchmarks are more important at this stage.

5.2 Predicting Yield

One test of our mathematical machinery is to assess whether it can accurately predict yield—the number of clique discoveries in a batch of experiments—using Equation 4 in conjunction with either of the two predictive models, LR and NN1.

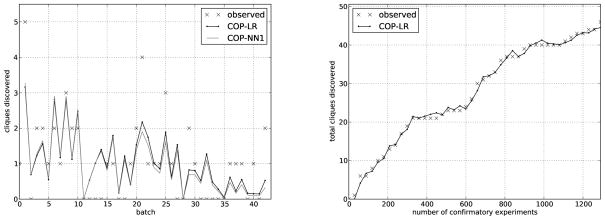
In this experiment, the 1322 molecules with known dose-response outcomes were ordered by their HTS activity in decreasing order. They were then divided into plates of 30 molecules each. The yield of each plate was predicted by training a predictive model (LR or NN1) on the outcomes of all prior confirmatory tests, as described in the Methods section. The predicted probabilities of activity were then used in conjunction with Equation 4 to predict the number of clique discoveries in each plate. The predictions of LR and NN1 were quite close to the observed yield, demonstrating that the COP mathematical machinery can predict the number of clique discoveries in a plate (Figure 2).

Figure 2.

Prediction confirmation of clique discoveries. The predicted discoveries of active cliques (LR and NN1) along with actual, observed discoveries (labeled “data”). Compounds were ordered by HTS activity and grouped into batches of 30. (left) Predictions and observations of clique discoveries in each batch. (right) Predictions and observations of total cliques after each batch.

5.3 Reordering Hits

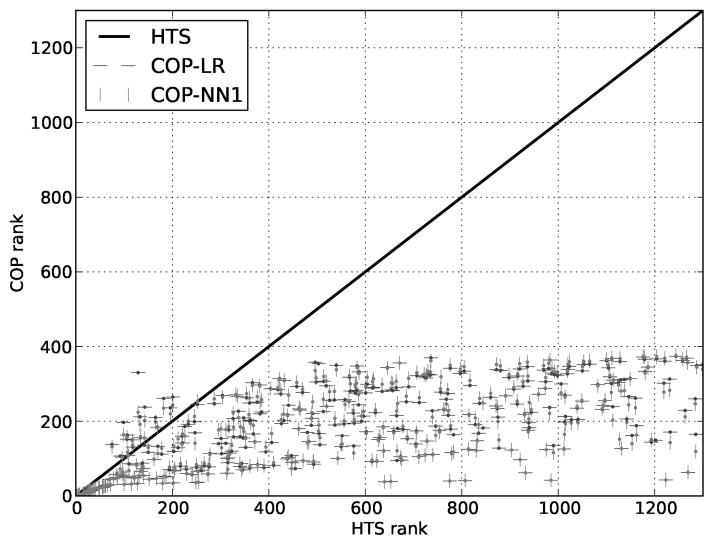
Another test of COP is to verify that it modiffes the order in which molecules are sent for confirmatory testing. In the first experiment, we compared the order of the dosed molecules as ranked by HTS activity to the order generated by the COP algorithm as described in the Methods section. The dosed molecules were batched in plates of 30 and COP was iteratively used pick the molecules in the next batch. In most of these experiments, COP-NP also performed comparably but is omitted for clarity.

Two important observations were made in this experiment. First, COP reduced the number of confirmatory experiments required to discover the same scaffolds discovered using HTS ordering (Figure 3). LR and NN1 found all the cliques in the data in 376 and 378 confirmatory experiments (respectively). Therefore, the remaining batches of molecules are not tested, implying that resources could be saved.

Figure 3.

Reordering hits. For the Dosed molecules, a comparison of COP (using LR or NN1) ranks to HTS ranks indicates that COP substantially reorders the hits for followup.

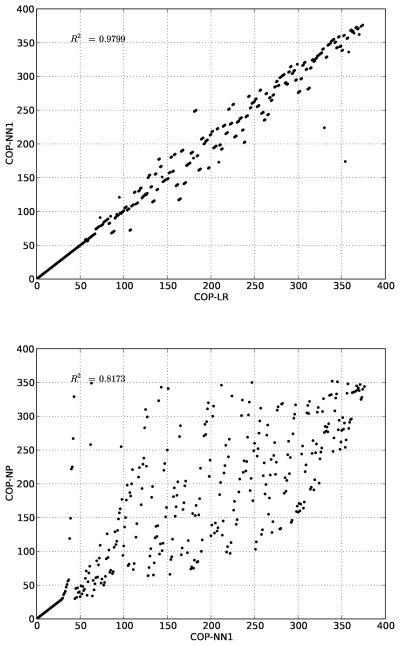
Second, the ranks generated by LR, NN1, and NP are well-correlated (Figure 4). This suggests that subtle differences in the predictive model may not substantially affect how molecules are ordered. Furthermore, of the three methods, NP is the most different, suggesting that—on other datasets—the most substantial differences in performance maybe between COP-NP and parameterized versions of COP.

Figure 4.

Comparing COP orderings. (top) COP-LR and COP-NN1 rank molecules in nearly the same order. (bottom) COP-NP rank molecules somewhat differently than COP-LR.

The results of this first experiment should be interpreted with caution; only the Dosed molecules were available to the COP algorithm in this test. In practice, all the library’s molecules would be available and it is possible that different results could be realized.

5.4 Increasing Clique Discovery Rate

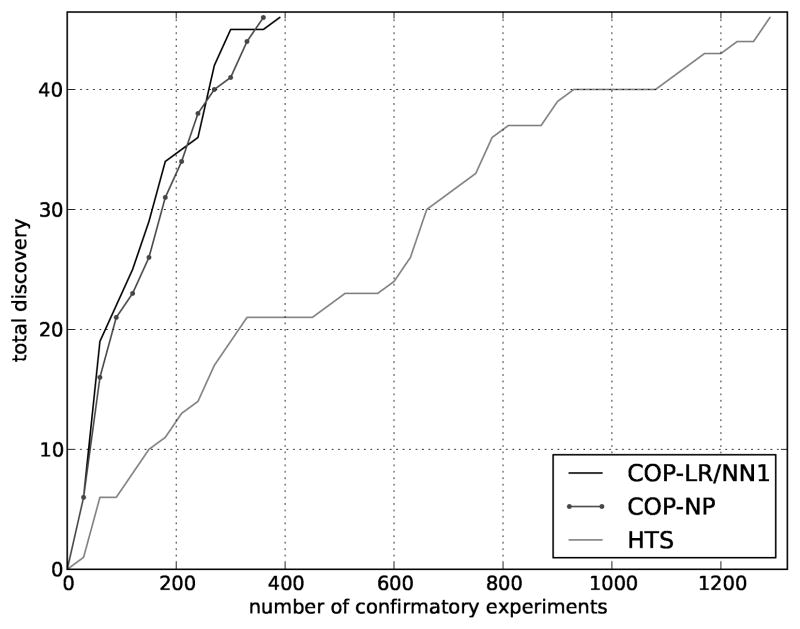
The most important in silico test of COP is to verify that it increases the rate of clique discovery. In this experiment, the 1322 dosed molecules are prioritized by COP in batches of 30. For a fixed number of confirmatory experiments, more cliques are discovered using COP (Figure 5). For batches of 30, COP discovers an average of 3.54 cliques per batch, compared to 1.07 when molecules are ordered by HTS activity, almost exactly the three-fold improvement we expected as a best case scenario. This result was consistent for both the LR and NN1.

Figure 5.

Improvement in scaffold discovery rate. The number of cliques discovered by COP versus HTS ordering as a function of the number of 30 molecule plates sent for confirmatory tests. In this figure, COP used the NN1 predictive model. The results using LR yield an identical curve.

5.5 Prospective Validation

Although these retrospective experiments are promising, the most important overall test of COP is a prospective experiment. In this experiment, we presumed a realistic batch size of 500 molecules and used COP, in conjunction with both predictive models, to pick the next batch. The COP batch was compared with the next batch selected by HTS activity alone.

Even without the results of the confirmatory tests, this experiment reinforces several results from the retrospective experiments. First, the batches generated by LR and NN1 are almost identical, with only 9 molecules different, corresponding with the observation that LR and NN1 yield almost identical performance in the retrospective experiments. Second, the predicted increase in discovery rate agrees well with the retrospective estimates. LR predicts a three-fold increase in the rate of clique discovery (54.2 compared with 17.4). Likewise, NN1 predicts a similarly high 2.5-fold increase in the rate of clique discovery (41.9 compared with 16.2).

Finally, as many molecules as possible were obtained and sent for confirmatory testing (460 for LR and NN batches and 477 for the HTS batch). These experiments confirm that more cliques were discovered in the COP batches; 30 cliques were discovered in both LR and NN1 batches, compared with 9 cliques in the HTS batch. Furthermore, these yields were fairly close to the predictions made by the COP machinery. Although LR and NN1 slightly overestimated COP’s yield, they slightly underestimated the improvement relative to HTS ordering. Respectively, LR and NN1 predicted 3.1-fold and 2.6-fold increases, while clique discovery increased by 3.3-fold in the experiment.

5.6 Comparison to OPI and LHR

Finally, to further examine the behavior of COP, we use the qHTS data to simulate a two-stage HTS experiment as described in the Data section. In these benchmark experiments, we sent molecules for confirmation in batches of 500 using the COP algorithm and two methods from the literature—local hit-rate analysis (LHR)⁸ and ontology-based pattern identification (OPI)¹⁴—using the default settings recommended by their designers. As the designers of LHR suggest, we also benchmark a third method a variation of LHR—which we abbreviate as LHR3—that prioritizes molecules using LHR but sends at most 3 molecules per scaffold for follow up. LHR, LHR3, and OPI work by ranking molecules higher when their structural neighbors have a statistically higher activity in the primary screen than expected by chance. Like all commonly used methods of prioritizing hits, OPI and LHR neither use information from confirmatory experiments run on prior batches nor attempt to maximize the structural diversity of the confirmed hits.

Implicit in this experimental structure is the view that if and only if an acceptable dose-response curve is obtained then the molecule is a true active. This, of course, is not always the case. For example, impurities in the library can often cause molecules tested in dose-response to be either false positives or false negatives. With more complete data, like data from dry-power retests, it would be possible to use the exact same framework prioritize molecules in a more accurate manner. Therefore, this limitation not so much a limitation of COP but more of a limitation of our testing strategy.

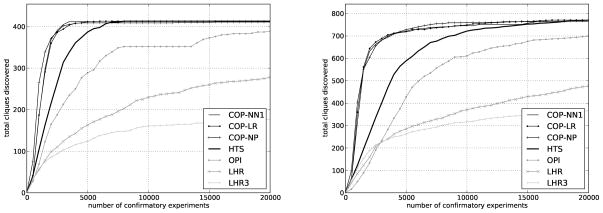
COP consistently discovered more scaffolds than LHR and OPI on both qHTS datasets (Figure 6). All three variants of COP (LR, NN1, and NP) performed comparably with each other, about two times better than ranking by HTS activity alone, while LHR, LHR3, and OPI performed worse than HTS ranking. These data confirmed results from both the retrospective and prospective experiments on the MEX data. COP substantially increased the rate of scaffold discovery.

Figure 6.

Comparison on qHTS data. On both the (left) BAZ2B and (right) JMJD2A-tudor datasets, COP substantially outperforms both HTS ranking and existing methods like LHR and OPI.

6 Discussion

Both retrospective and prospective experiments demonstrate that COP increases the rate of clique discovery from an HTS experiment by as much as three-fold. The key result of this work is that screener’s preferences, when more accurately modeled, can be applied to change the order in which molecules are tested so as to increase the rate of discovery.

This study focuses on a particular discovery model by defining a unit of discovery as a clique of two active molecules with the same scaffold. This choice of a discovery model is certainly not a settled decision, and we expect this to begin a conversation, rather than end one, about what exactly screeners hope to find in a HTS experiment. For example, some screeners might find singleton hits useful if they are the only example of their scaffold in the whole library.

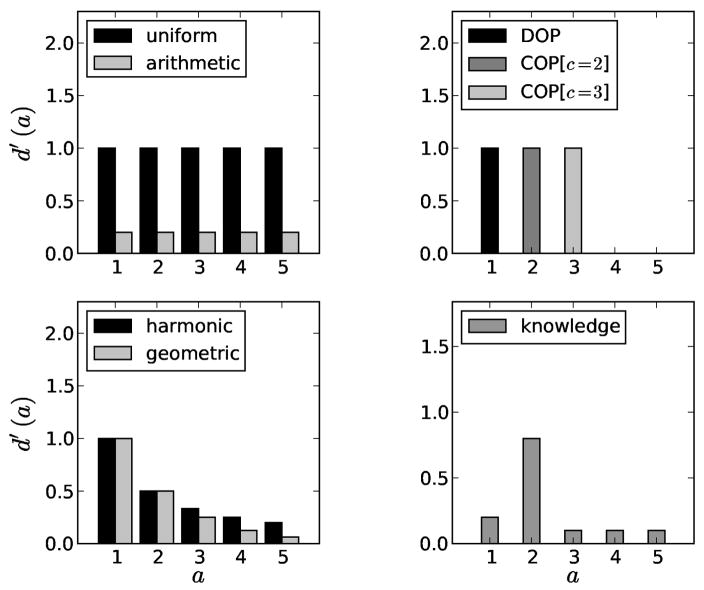
While the best choice of a discovery model is still open for discussion, our mathematical machinery is general enough to handle several important cases (Figure 7). For example, standard HTS prioritization which ignores scaffold groups can be emulated by choosing the uniform marginal discovery

Figure 7.

Possible marginal discovery functions. Uniform and arithmetic discovery functions suppose that each example of a scaffold is worth the same amount. The diversity-oriented function only values the first example of every scaffold. The clique-oriented functions only value either the second or third active example of the group. The harmonic and geometric (shown with r = 0.5) functions value each active less and less as more of the same scaffold are discovered. The knowledge-based function intends to model a more complex preference, similar to COP, but also valuing singletons and larger cliques.

$$d^{\prime }(a)=1.$$ (7)

More interestingly,¹² describes both harmonic and arithmetic weighting schemes which are used to modulate how a molecule classifier’s performance is scored. These weighting schemes are statements about the screener’s preferences and can be formulated as marginal discovery functions,

$$d^{\prime }(a)=1/a$$ (8)

for the harmonic weighting scheme and

$$d^{\prime }(a)=1/n$$ (9)

for the arithmetic weighting scheme, where, within each scaffold group, a is the number of active examples and n is the total number of examples in the group. Likewise, COP can be generalized to expresses several definitions of a clique

$$d(a)\{\begin{array}{ll}1\hfill & \text{if}a\ge c\hfill \\ 0\hfill & \text{if}a<c,\hfill \end{array}$$ (10)

where c is the minimum number of confirmed actives required to define a clique. This generalization exposes that DOP is a special case of COP with c = 1.

Entirely new discovery functions are imaginable. For example, a geometric discovery function

$$d^{\prime }(a)=r^{a-1}$$ (11)

would exhibit diminishing returns like the harmonic model while allowing the rate at which discovery decays to be tuned with the parameter 0 < r < 1. A more “knowledge-based” function, based on informal surveys of screeners, suggests a function like

$$d^{\prime }(a)\{\begin{array}{ll}0.2\hfill & \text{if}a=1\hfill \\ 0.8\hfill & \text{if}a=2\hfill \\ 0.1\hfill & \text{if}a>2,\hfill \end{array}$$ (12)

which formalizes the notions that occasionally singleton actives are interesting, a scaffold is confirmed by a second active is much more likely to be interesting, and subsequent confirmed actives provide some information but not as much as finding new scaffolds. Of course, the actual values here are entirely subjective and chosen merely to illustrate a point. It may be possible to learn the discovery function from empirical data by observing which scaffolds screeners decide to pursue in real HTS experiments,

$$d(a)=P(\text{scaffold}\text{pursued}\text{by}\text{screener}\mid a),$$ (13)

in a strategy related to those used in some economic studies.^30,31,32 This possibility raises questions about how the chemical details of the scaffold might influence its value to the screener. Perhaps the discovery function would be usefully defined as

$$d(a)=P(\text{scaffold}\text{pursued}\text{by}\text{screener}\mid a,i,\mathcal{S}),$$ (14)

where 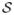is the chemical structure of the scaffold and i is the number of confirmed inactive examples in this scaffold group. These possibilities, of course, are beyond the scope of this study and will be left to future work.

Furthermore, all these utility-aware methods of prioritization can and should be used simultaneously with other HTS analysis methods. For example, other prioritization methods designed to reduce false positives—by using better controls, chemical information, or other strategies —are all entirely compatible with COP; the priorities generated by these methods can either be substituted for the HTS activity or be presented as an additional independent variable to the predictive model.

Moreover, COP is a seamless extension of a previously defined economic framework and can, therefore, be used to compute the marginal cost of discovery (MCD).⁹ The MCD is the predicted number of confirmatory experiments required to discover one more clique of actives, and yields an optimal strategy for deciding how many molecules should be sent for confirmatory testing. The key point here is that the mathematical machinery developed for COP is a unifying framework which expresses all prior work, inspires new possibilities, and yields functional prioritization algorithms in all cases.

7 Conclusion

When screeners’ preferences are rigorously formulated, they can be applied to increase the rate of information discovery from HTS experiments in utility-aware protocols. COP follows from the observation that screeners look for a clique of a few active examples of a scaffold to establish the scaffold’s activity; in both retrospective and prospective experiments, COP shuffles the order in which hits are confirmed and, thereby, increases the rate of clique discovery by up to three-fold.