Ion-Selective Electrodes with Unusual Response Functions: Simultaneous Formation of Ionophore–Primary Ion Complexes with Different Stoichiometries

Abstract

It is well known that the selectivity of an ion-selective electrode (ISE) depends on the stoichiometry of the complexes between its ionophore and the target and interfering ions. It is all the more surprising that the possibility for the simultaneous occurrence of multiple target ion complexes with different complex stoichiometries was mostly ignored in the past. Here we report on the simultaneous formation of 1:1 and 1:2 complexes of a fluorophilic crown ether in fluorous ISE membranes, and how this results in what look like super-Nernstian responses. These increased response slopes are not caused by mass transfer limitations and can be readily explained with a phase boundary model, a finding that is supported by experimentally determined complex formation constants and excellent fits of response curves. Not only Cs⁺ but also the smaller ions Li⁺, Na⁺, K⁺, and NH₄⁺ form 1:1 and 1:2 complexes with the fluorophilic crown ether, with cumulative formation constants of up to 10^15.0 and 10^21.0 for of the 1:1 and 1:2 complexes, respectively. Super-Nernstian responses of the type observed with these electrodes are probably not particularly rare, but lacking in the past an adequate discussion in the literature remained ignored or misinterpreted. Preliminary calculations also predict sub-Nernstian responses and potential dips of a similar origin. The proper understanding of such phenomena will facilitate the development of new ISEs based on ionophores that form complexes of higher stoichiometries.

Introduction

The majority of measurements with ionophore-based ion selective electrodes (ISEs) are performed in their Nernstian range.^1–9 Deviations from the linear response in this range typically indicate trouble. Examples include Donnan failure at the upper detection limit,^10,11 and responses to interfering ions^5,12 or sample contamination (or depletion) by currentless transmembrane ion fluxes at the lower detection limit.^13–17 Considerable effort has been spent to explain these effects with quantitative models, taking into account thermodynamics and, where necessary, mass transport.

While the underlying concepts of phase boundary potentials and complexation equilibria are simple, the quantitative discussion of the response of ionophore-doped ISEs becomes complicated when more than one ionophore complex needs to be considered. A typical example is the selectivity optimization by selection of an optimum molecular ratio of ionophore and ionic sites, which depends on the charges of the target (i.e., primary) and interfering ions and the stoichiometries of their complexes with the ionophore.^18–21 Another example illustrating an increased level of complexity is given by the apparently non-Nernstian response observed when a primary and an interfering ion form complexes of different stoichiometries and co-exist in the ISE membrane over a wide activity range.^22–26 This can result, for instance, in apparently half-, two thirds-, and twice-Nernstian responses. Note that in neither of these examples the experimentally observed ionophore forms more than one type of complex with any type of sample ion. This simplifies the theoretical treatment considerably. However, we believe that the current literature does not properly reflect on the number of cases in which individual ions form simultaneously more than one type of complexes in the ISE membrane. Such cases may be much more common than was anticipated in the past.

Surprisingly, the simultaneous formation of multiple complexes of the ionophore with the primary ion in ISE membranes was largely ignored in the past. The discussion of the Mg²⁺ response of an ionophore-based ISE in a constant background of Ca²⁺ included a brief qualitative remark about the possibility of the co-existence of 1:1 and 1:2 ionophore complexes with Mg²⁺, and it was pointed out that the same might also be true for Ca²⁺.²⁷ However, attempts to fit experimental data quantitatively were based on a model in which Mg²⁺ formed only 1:1 and Ca²⁺ only 1:2 complexes. A more in-depth investigation was hindered at the time by the lack of routine methods to determine the stabilities of ionophore complexes in ISE membranes, as they have recently become available. ^28–31 The simultaneous formation of 1:1 and 1:2 complexes was also explicitly reported for ISE membranes doped with the iodide ionophore [9]mercuracarborand-3.³² Indeed, the coexistence of the two types of complexes was intentionally favored by choice of an appropriate ratio of ionic sites and ionophore. However, super-Nernstian responses were not observed, possibly because the work focused on lower detection limits in the absence of interfering ions.

In this paper, we report on a fluorophilic crown ether ionophore that forms simultaneously 1:1 and 1:2 complexes with both the primary and several interfering ions. This affects not only potentiometric selectivities but also results in super-Nernstian responses in the lower activity range of the calibration curve. In the past, there were only two well-documented reasons for super-Nernstian slopes, i.e., ion fluxes^13–17 and the presence of more than one type of ions in the ISE membrane, with one distinct stoichiometry for each ion (as mentioned above).^22–26 This contribution shows that developers of ISEs should be aware of another cause for non-Nernstian responses, i.e., the simultaneous formation of multiple ionophore complexes of one type of ions, as discussed in this contribution.

Experimental Section

Materials

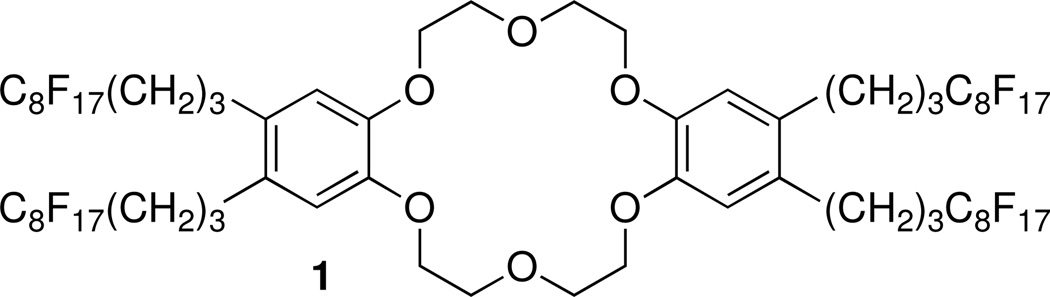
All reagents were of the highest commercially available purity. Sample solutions were prepared using deionized and charcoal-treated water (0.18 MΩ m specific resistance) obtained from a Milli-Q PLUS reagent grade water system (Millipore, Bedford, MA). Perfluoroperhydrophenanthrene was used as received from Alfa Aesar (Ward Hill, MA). Sodium tetrakis[3,5-bis(perfluorohexyl)-phenyl]borate^33–35 was prepared according to a reported procedure. The synthesis of the fluorophilic ionophore 4,4’,5,5’-tetrakis(1H,1H,2H,2H,3H,3H-heptadecafluoroundecyl)dibenzo-18-crown-6 (1, see Figure 1) was described previously.³⁶

Figure 1.

Structure formula of ionophore 1.

Ion-selective membranes

Fluoropore filters (pure polytetrafluoroethylene, PTFE; 47 mm diameter, 0.45 µm pore size, 50 µm thick, 85% porosity) from Millipore were sandwiched between note cards, and a hole punch was used to cut out 13 mm diameter disks. Liquid-phase membranes were prepared using one disk as an inert mechanical support for the fluorous sensing membrane; only for measurements involving the tetraphenylphosphonium ion (PPh₄⁺) stacks of six disks were used instead in order to increase the membrane thickness. To impregnate the filter disks with liquid sensing phase, 10 to 15 µL of a perfluoroperhydrophenanthrene solution of ionophore (2 mmol L⁻¹) and ionic sites (tetrakis[3,5-bis(perfluorohexyl)phenyl]borate ; 33 or 71 mol % with respect to the ionophore) was applied to the surface of the porous filter disk(s), into which the fluorous solutions permeated spontaneously, changing the filters’ appearance from opaque white to translucent with a glossy surface.

Electrodes

The fluorous membranes were then mounted into custom-machined electrode bodies made from poly(chlorotrifluoroethylene).³⁵ A screw cap with an 8.3 mm diameter hole in the middle was screwed onto bodies holding the membranes, mechanically sealing the membrane perimeter while leaving its center exposed. An inner filling solution was added into the electrode body (1 mmol L⁻¹ of KCl) along with an AgCl-coated Ag wire. An electrochemical cell was obtained by immersion of the thus fabricated measuring electrode and a double-junction type external reference electrode (DX200, Mettler Toledo, Switzerland; saturated KCl as inner solution, and 1 mol L⁻¹ LiOAc as bridge electrolyte) into the sample solution. Prior to measurements, the fluorous membrane electrodes were conditioned for 2 to 3 h in 100 mmol L⁻¹ KCl solution.

Potentiometric Measurements

EMF Suite 1.03 software (Fluorous Innovations, Arden Hills, MN) was used to control an EMF 16 potentiometer (Lawson Labs, Malvern, PA). Selectivity coefficients were determined with the fixed interference method (FIM)³⁷ and separate solution method (SSM).³⁷ Nernstian responses to the cations were confirmed for all single salt solutions in the concentration range where selectivities were tested. All response times in the Nernstian region were shorter than 20 s, and there was no indication that these response times were not limited solely by the speed with which samples were exchanged. In the range of the super-Nernstian responses, response times of up to several minutes were observed, as it is often seen in activity ranges in which minor changes in sample activities cause major changes in the composition of the ISE membrane bulk.³⁸ Ion activities were calculated according to a two-parameter Debye-Hückel approximation.³⁹ Confidence intervals for all binding constants were estimated using rules of error propagation and the error of ±0.15 for the logarithms of all selectivity coefficients.

Calculations

Mathematica 8 (Wolfram Research, Champaign, IL) was used to calculate response curves, fit experimental data, and predict membrane compositions on the basis of measured equilibrium constants.

Results and Discussion

Because of their unique low polarity and polarizability,^40,41 fluorous ISE membranes provide exceptionally high selectivities and very low detection limits.^35,42–48 Therefore, we were intrigued by the possibility of a K⁺-selective fluorous membrane ISE doped with the fluorophilic 18-crown-6 ether ionophore 1, which was recently reported in the organic chemistry literature as a phase transfer catalyst.³⁶ The focus of the first report describing ionophore 1 was on its use for the biphasic catalysis of the Finkelstein reaction.³⁶ However, efficient extraction of potassium picrate from aqueous solutions into perfluoro-1,3-dimethylcyclohexane was also demonstrated, and under otherwise identical conditions no sodium picrate extraction into the fluorous phase was observed. This result was not too surprising since it is well known that the host cavity of 18-crown-6 fits the size of the K⁺ ion fairly well. Since the use of fluorophilic Ag⁺, H⁺, and CO₃^2–-selective ionophores resulted in exceptionally selective ISEs when fluorous phases were used as the membrane matrix,^43,46,48 the performance of ionophore 1 in a fluorous ISE membrane appeared worthwhile exploring.

Response slopes and selectivities of membranes with 71 mol % ionic sites

Initial experiments were performed with membranes containing ionic sites and ionophore in a molar ratio 71:100 (i.e., 71 mol %). The selection of this ratio was based on the expectation that K⁺ forms 1:1 complexes with the ionophore, and it was guided by the theory that predicts^18,21 ratios of ionic sites and ionophore that optimize potentiometric selectivities. For an ionophore that forms only 1:1 complexes with K⁺, the 71 mol % ratio ensures that there is an excess of uncomplexed free ionophore in the ISE membrane and that the potentiometric selectivity remains high when the membrane is exposed to K⁺ solutions, loading the membrane bulk with K⁺ (whose concentration, for reasons of bulk electroneutrality,^7,9,11 is equivalent with the concentration of the ion exchanger sites provided by tetrakis [3,5-bis(perfluorohexyl) phenyl]borate).⁷ To the contrary, for interfering ions large enough to form 1:2 complexes, the 71 mol % ratio of ionic sites and ionophore results in an amount of ionophore insufficient to bind all interfering ions in 1:2 complexes, which reduces the interference from such ions.^18–21

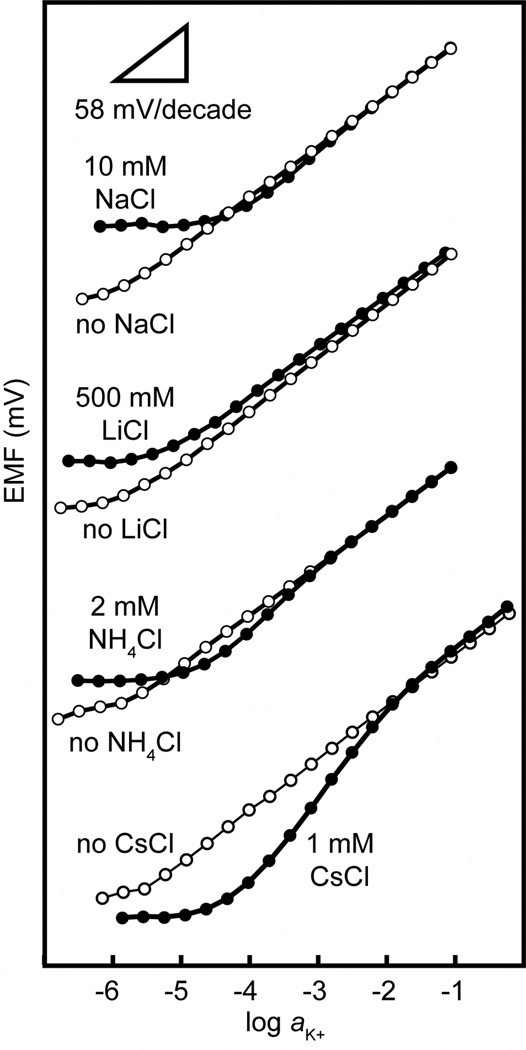
Calibration curves for the 71 mol % ISEs were measured in the absence of other cations for Na⁺, Li⁺, K⁺, Cs⁺, and NH₄⁺, confirming Nernstian responses to all five cations. Figure 2 shows as an example the K⁺ response (open circles). Nernstian responses to K⁺ all the way down to the detection limit were also observed when the fixed interference method was used to determine the selectivity for K⁺ over Na⁺ and Li⁺ (Figure 2, upper half; filled circles). For this purpose, a KCl solution containing 10 mM Na⁺ or 500 mM Li⁺ was diluted stepwise with aliquots of a solution containing only 10 mM Na⁺ or 500 mM Li⁺, respectively. Table 1 lists the selectivity coefficients determined from these measurements.

Figure 2.

Potentiometric response of an ISE based on a perfluoroperhydrophenanthrene membrane doped with ionophore (1) and anionic sites (71 mol % relative to 1): Response to K⁺ in the absence of interference ions (open circles) and in the presence of interfering ions (filled circles; 10 mmol L⁻¹ NaCl, 500 mmol L⁻¹ LiCl, 2.0 mmol L⁻¹ NH₄Cl, or 1.0 mmol L⁻¹ CsCl).

Table 1.

FIM selectivity coefficients, $K_{\mathrm{K},J}^{\text{pot}}$, for PPh₄⁺, Na⁺, Li⁺, NH₄⁺, and Cs⁺ relative to K⁺ for ionophore-doped membranes with a 71 or 33 mol % site ratio as well as for ionophore-free ion exchanger membranes.

	$\text{log }{K}_{\mathrm{K},J}^{\text{pot}}$ (71% site ratio)	$\text{log }{K}_{\mathrm{K},J}^{\text{pot}}$ (33% site ratio)	$\text{log }{K}_{\mathrm{K},J}^{\text{pot}}$ (no ionophore)a
PPh4+	+8.0	+2.4	+17.1
Li+	−4.8	−4.6	−1.4
Na+	−2.4	−2.1	−1.0
NH4+	−2.5	−0.7	+0.6
Cs+	−2.9	+1.3	+2.5

^aCalculated from ref. 35

Quite different and very unusual response curves were observed in FIM measurements performed to determine the K⁺ selectivity relative to the interfering ions Cs⁺ and NH₄⁺, i.e., when a KCl solution containing a fixed concentration of Cs⁺ or NH₄⁺ was diluted stepwise with aliquots of a solution that only contained one of these interfering ions (see Figure 2, lower half; filled circles). In these two cases, the response to K⁺ was Nernstian only in the upper activity range, and then went through a super-Nernstian region as the K⁺ activity was lowered, eventually reaching an EMF value determined by the activity of the interfering ion alone. The super-Nernstian response was observed below a 1 mM K⁺ activity when a 2 mM NH₄⁺ background was present, and below a 10 mM K⁺ activity when a 1 mM Cs⁺ background was used. Selectivity coefficients for Cs⁺ and NH₄⁺ were calculated in the conventional way by extrapolation of the Nernstian range of the K⁺ response to the EMF value observed when the EMF was determined by the activity of the interfering ion alone.³⁷ Reassuringly, the thus obtained selectivity coefficients for Cs⁺ and NH₄⁺ were close to those determined with the separate solution method $(\text{FIM}:\text{log}{K}_{\mathrm{K},\text{Cs}}^{\text{pot}}=-2.86,\text{log}{K}_{\mathrm{K},\text{NH}4}^{\text{pot}}=-2.50;\text{SSM}:\text{log}{K}_{\mathrm{K},\text{Cs}}^{\text{pot}}=-3.15,\text{log}{K}_{\mathrm{K},\text{NH}4}^{\text{pot}}=-2.70)$.

The super-Nernstian response of these ISEs to K⁺ in the presence Cs⁺ or NH₄⁺ calls for an explanation. Transmembrane ion fluxes were reported to cause similar response curves,⁴⁹ but their super-Nernstian responses occur at lower sample concentrations since transmembrane ion fluxes typically are not large enough to bias sample concentrations in the millimolar range. Because in this work the super-Nernstian responses were observed in the presence of the larger interfering ions Cs⁺ and NH₄⁺ but neither in the presence of Li⁺ and Na⁺ nor in the absence of interfering ions, we initially considered the formation of both 1:1 and 1:2 complexes between the ionophore and Cs⁺ or NH₄⁺, and the exclusive formation of 1:1 complexes between the ionophore and Li⁺, Na⁺, and K⁺. Indeed, it is well known from the literature that Cs⁺ forms 1:2 complexes with 18-crown-6 ether derivatives.⁴

Response curves and selectivities with 33% site ratio membrane

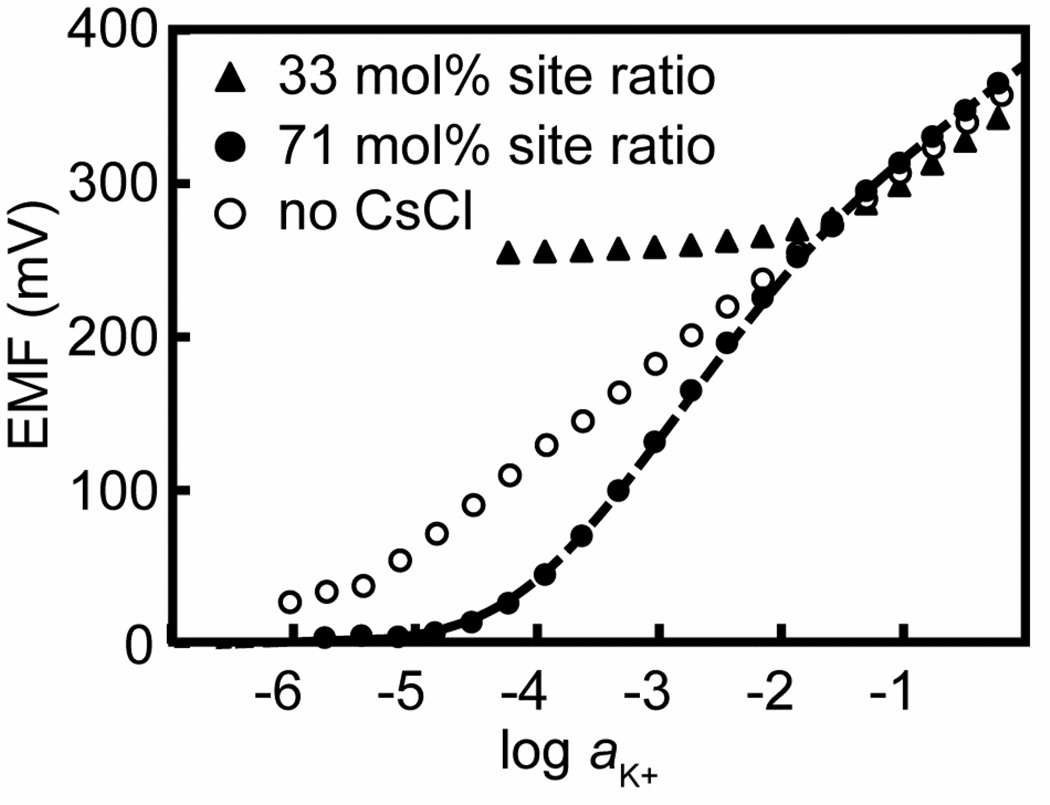
To test the hypothesis that Cs⁺ and NH₄⁺ form 1:2 complexes with ionophore 1, we measured the response curves and selectivities of ISE membranes that contained ionic sites and ionophore in a 33 mol % ratio. The threefold excess of ionophore over cations in these membranes favors the formation of 1:2 complexes. As a result, we expected significantly worse selectivities for K⁺ over Cs⁺ and NH₄⁺ than in the case of the 71 mol % membranes, in which there is an insufficient amount of ionophore to permit all cations to form 1:2 complexes with 1.

Indeed, the experimental results are consistent with major differences between the host–guest chemistry in 33 and 71 mol % membranes. On one hand, no super-Nernstian responses were observed for the 33 mol % membranes under any circumstances (see Figure 3 for the K⁺ response in the presence of a background of 1.0 mM Cs⁺; see Figures S1, S2, and S3 for the K⁺ responses in the presence of a background of Li⁺, Na⁺, and NH₄⁺, respectively). On the other hand, the interference from Cs⁺ and NH₄⁺ increased with the lower concentration of ionic sites, as it was expected (see Table 1). The change in $\text{log}{K}_{\mathrm{K},\text{NH}4}^{\text{pot}}$ from −2.50 at the 71% site ratio to −0.67 at the 33% site ratio corresponds to a roughly seventy-fold increase in NH₄⁺ interference, and the change in $\text{log}{K}_{\mathrm{K},\text{Cs}}^{\text{pot}}$ from −2.86 to +1.29 corresponds to an increase in Cs⁺ interference by more than 4 orders of magnitude. Meanwhile, the selectivity over Li⁺ and Na⁺ hardly changed, which appeared to be consistent with the exclusive formation of 1:1 complexes with Li⁺, Na⁺, and K⁺.

Figure 3.

Potentiometric K⁺ responses of an ISE based on a perfluoroperhydrophenanthrene membrane doped with ionophore (1, 2.0 mmol L⁻¹) and anionic sites at a site-to-ionophore ratio of 71 mol % (filled circles) or 33 mol % (diamonds) in the presence of 1 mmol L⁻¹ Cs⁺. For comparison, the K⁺ response curve for a 71 mol % membrane in the absence of interfering ions is shown (open circles). The response of the 71 mol % membrane was fitted (broken line) with the model described in the text and the following parameters: K_ex= 10^−2.51, K_KL= 10^15.1, K_KL2 = 10^6.0, K_CsL = 10^11.5, and K_CsL2 = 10^8.3.

However, a model based on 1:1 and 1:2 complexes for Cs⁺ and NH₄⁺ and exclusive 1:1 complexes for Li⁺, Na⁺, and K⁺ failed to explain all experimentally observed selectivities and the peculiar shape of the responses to K⁺ in the presence of Cs⁺ and NH₄⁺. In particular, 1:1 complex formation with K⁺ seemed inconsistent with the substantial increase of the PPh₄⁺ interference on the K⁺ response when the concentration of ionic sites was increased from 33 to 71 mol % (see Table 1). A quantitative model consistent with all experimental data could only be obtained when this model was expanded to permit 1:1 and 1:2 complexes for all five cations.

Phase Boundary Model Based on 1:1 and 1:2 Complexes for all Ions

A phase boundary model to describe the potentiometric response of ISE membranes doped with 1 was developed as similarly described for other ionophore-doped ISE membranes.^9,11,50,51 The EMF response can be described by the Nernst equation:

$$\mathit{\text{EMF}}=E_i^{\mathrm{o}}+\mathrm{R}T{z}_i^{-1}{\mathrm{F}}^{-1}\text{ ln}(a_{\mathrm{i},\text{aq}}/[i])$$ (1)

where a_i,aq is the activity of the ion i in the aqueous phase, [i] is the concentration of the uncomplexed ion i in the membrane phase, and $E_i^{\mathrm{o}}$ is a term that is characteristic of the ion i and the ISE membrane composition and includes all sample-independent contributions from the ISE and reference electrode. The assumptions underlying such a phase boundary model were discussed elsewhere,^9,11,50,51 and are described here only briefly. They are that (i) local equilibrium is achieved at the sample–membrane interface, (ii) any membrane internal potential difference (diffusion potential) and the phase boundary potential at the membrane/internal filling solution interface are sample independent, (iii) ion pairs in the ISE membrane have a negligible effect on the EMF, and (iv) activity coefficients in the membrane phase do not depend on the composition of the aqueous sample and are constant for all species in the membrane. The key task necessary to apply the phase boundary model to the system under consideration is to calculate [i] as a function of the multiple chemical equilibria involved. Here, this involves the set of equations that includes the definition of all four complexation constants

$$K_{\mathit{\text{iL}}}=[i\mathrm{L}]/({[i]}_{\text{mem }}[\mathrm{L}])$$ (2)

$$K_{\mathit{\text{iL }}2}=[i{\mathrm{L}}_2]/({[i]}_{\text{mem }}[i\mathrm{L}])$$ (3)

(i being either the primary ion, I, or an interfering ion, J), the mass balance for the ionophore

$${[\mathrm{L}]}_{\text{tot}}=[\mathrm{L}]+[\text{IL}]+[{\text{IL}}_2]+[\text{JL}]+[{\text{JL}}_2]$$ (4)

electroneutrality in the bulk of the ISE membrane

$$[\mathrm{R}]=[\mathrm{I}]+[\text{IL}]+[{\text{IL}}_2]+[\mathrm{J}]+[\text{JL}]+[{\text{JL}}_2]$$ (5)

(with [R] as the concentration of ionic sites), and the ion exchange equilibrium at the interface of the aqueous sample and an ionophore-free ion exchanger membrane

$$K_{\mathit{\text{ex}}}=a_{\mathrm{I},\text{aq}}[\mathrm{J}]/(a_{\mathrm{J},\text{aq}}[\mathrm{I}])$$ (6)

The set of equations 1 to 6 cannot be solved numerically to give the EMF as a function of a _{I, aq}, but FIM response curves can be obtained as parametric plots by calculation of pairs of a _{I, aq} and EMF values, where both the a _{I, aq} and EMF values are a function of [L]. For such calculations, [L] was varied in a range that permits EMF predictions in the desired range of log a _{I, aq}. Figure 3 shows the experimentally measured EMF response to K⁺ in the presence of a constant activity of Cs⁺ for a membrane with 71 mol % ionic sites (filled circles) along with a response curve computed following this method (broken line). Further examples are given in the Supplementary Information for this paper, which shows the K⁺ responses in a background of Li⁺, Na⁺, or NH₄⁺ (see Figures S1 to S3). In all four cases, the response curves calculated with a suitable set of the parameters a _{J, aq}, [L]_tot, [R], K_ex, $E_i^{\mathrm{o}}$, K_IL, K_IL2, K_JL, and K_JL2 fit the experimentally determined EMF very well. In the following, it will be shown that the values of the parameters used to compute the response curves in Figures 3, S1, S2, and S3 not only result in good fits, but are indeed physically meaningful and are either known experimental variables or are consistent with other experimental data.

The values of [L]_tot, [R], and a _{J, aq} are determined by weighing during the preparation of the ISE membranes and sample solutions, and the value of K_ex corresponds to the experimentally determined selectivity coefficient of an ionophore-free ion exchanger membrane with the same membrane matrix.^42,52 The other parameters necessary to predict a FIM response curve are $E_i^{\mathrm{o}}$, K_IL, K_IL2, K_JL, and K_JL2. A unique set of numerical values for these five parameters cannot be determined from fitting of FIM response curves alone. For example, while keeping all other parameters constant, a tenfold increase in K_IL shifts the onset of the response to the ion I to lower activities of I, but this effect is cancelled by a concomitant tenfold increase in K_JL (see Supporting Information, Figure S4). Also, on a logarithmic scale, the width of the K⁺ activity range in which a super-Nernstian response is observed for the 71 mol % membranes is given by the expression log (K_JL2/K_IL2) (see Supporting Information, Figure S5). The only effect of a simultaneous increase of K_IL2 and K_JL2 by the same numerical factor is a shift of the response curve to higher EMF values, but this shift cannot be used to determine K_IL2 or K_JL2 since $E_i^{\mathrm{o}}$ is also a fitting parameter and has the same effect on the response curve. Therefore, to assess the suitability of the response model proposed here, values for K_IL, K_IL2, K_JL, and K_JL2 were determined independently from potentiometric selectivities.

Potentiometric Determination of Stabilities of 1:1 and 1:2 Complexes

The formation constants of the 1:1 and 1:2 complexes of K⁺ and four other cations were determined by analysis of the selectivities of ionophore-doped and ionophore-free membranes for a complexing over a noncomplexing ion. This method^29,53,54 was already used in the past to determine complex stabilities in fluorous membranes.^43,45,48 For the purpose of this work, tetraphenylphosphonium (PPh₄⁺) was chosen as the ion that does not form complexes with the ionophore.

As Table 1 shows, the selectivity of an ionophore-free ion exchanger ISE for PPh₄⁺ over all tested metal cations and NH₄⁺ is much larger than in the case of ionophore-doped ISE membranes with 33 and 71 mol % ionic sites. This confirms the formation of complexes between the ionophore and Na⁺, Li⁺, K⁺, Cs⁺, and NH₄⁺. Stability constants were determined from the potentiometric selectivities in an analogous way as described in the literature for systems with only one type of primary ion complex, ^{29,43,45,48,53,54} but taking into account the formation of multiple complexes, as described by equations 2 and 3. For this purpose, an iterative approach was taken. It was at first assumed that only iL₂ complexes form in membranes with 33 mol % ionic sites, an assumption justified by the large excess of free ionophore in those membranes. This permitted an estimate of the cumulative complex formation constant of the 1:2 complexes (i.e., the product K_iL K_iL2). The potentiometric selectivities of the 71 mol % membranes were then used to calculate K_iL using the value of the product K_iL K_iL2, as determined from the selectivities of the membranes with 33 mol % ionic sites. Once K_iL is known, K_iL2 can be readily calculated from K_iL K_iL2. Subsequent calculation of the concentrations of the complexes iL and iL₂ in the 33 mol % membranes using the thus obtained K_iL and K_iL2 values confirmed the validity of the initial assumption that iL complexes are of low concentration in membranes with 33 mol % ionic sites. For example, the concentration of the K⁺L complex in these membranes in the range of the Nernstian response to K⁺ was found to be 9.5 × 10⁻⁷ mol L⁻¹, which is far lower than the corresponding concentrations of the K⁺L₂ complex and the free ionophore of 6.5 × 10⁻⁴ and 7.0 × 10⁻⁴ mol L⁻¹, respectively.

The thereby determined complexation constants are shown in Table 2. The stabilities of the 1:1 complexes fall in the order of Li⁺ < Na⁺ < K⁺ > NH₄⁺ > Cs⁺. The maximum for K⁺ agrees with the reported optimum size of the ionophore cavity for K⁺. The constants for the formation of 1:2 complexes from 1:1 complexes and an additional ionophore molecule fall into the order of Li⁺ ≈ Na⁺ ≈ K⁺ < NH₄⁺ < Cs⁺. It is not surprising that the larger ions form the more stable 1:2 complexes, but it is quite remarkable—and in view of the existing ISE literature quite surprising—that the small ions Li⁺, Na⁺, and K⁺ also form 1:2 complexes with quite substantial stabilities.

Table 2.

Formation constants of 1:1 and 1:2 complexes (as log K_JL and log K_JL2, respectively) as determined from potentiometric selectivities.

	Log KJL	Log KJL2
Li+	11.7 ± 0.3	6.1 ± 0.2
Na+	13.8 ± 0.3	6.2 ± 0.2
K+	15.0 ± 0.3	6.0 ± 0.2
NH4+	12.9 ± 0.3	6.9 ± 0.2
Cs+	11.7 ± 0.3	8.1 ± 0.2

The ten complex stabilities determined from the potentiometric selectivities (see Table 2) can now be compared to the corresponding values used to calculate the response curves shown in Figures 3, S1, S2, and S3 (see respective figure captions). In all ten cases, the values used to calculate the response curves shown in these figures are within the confidence intervals of the complex formation constants, as estimated from the errors of the potentiometric selectivities. Moreover, using the complex stabilities shown in Table 2 and the expression log (K_JL2/K_IL2) for membranes with [L]≪[IL], [IL₂], [JL], [JL₂], the interfering ion that causes the largest super-Nernstian response range is predicted to be Cs⁺. These findings are consistent with experimental observations (see Figure 2) and further supports the suitability of the response model.

Comparison of Complex Stabilities of 1 with Literature Data

To date, the stabilities of perfluoro-15-crown-5 complexes are the only reported data that quantitatively describe crown ether complexation in a fluorous phase.⁴⁵ Because of the strongly electron withdrawing nature of 20 fluorine atoms, the stabilities of perfluoro-15-crown-5 complexes are extremely small and offer only a poor comparison to put the stabilities of the complexes of the fluorophilic crown ether 1 into a context. There is also a shortage of data on the stabilities of 1:2 complexes of crown ethers in media of low polarity. Lacking more similar systems, the stabilities of the complexes of 1 are compared here with the stabilities of complexes formed by dibenzo-18-crown-6 (DB18C6), dibenzo-24-crown-8 (DB24C8) and dibenzo-30-crown-10 (DB30C10) in 1,2-dichloroethane (see Table 3).⁵⁵ These data show some interesting trends. With the exception of the complex of K⁺ and DB24C8, there is an overall trend Li⁺ < Na⁺ < K⁺ > Cs⁺, which is consistent with observations for the fluorophilic ionophore 1. The stabilities of the complexes of Li⁺, Na⁺, K⁺, and Cs⁺ increase on average approximately hundredfold from DB18C6 to DB24C8, and approximately tenfold from DB24C8 to DB30C10. This suggests that in media of low polarity all four cations can benefit from interactions with more than six oxygens, which is consistent with the observation that 1:2 complexes of the 18-crown-6 derivative 1 are observed for all four metal cations.

Table 3.

Stability of 1:1 complexes (log K_JL) between various cations and crown ethers in perfluoroperhydrophenanthrene (this work) and in 1,2-dichloroethane.

	perfluoroperhydrophenanthrene	1,2-dichloroethane
	1	DB18C6	DB24C8	DB30C10
Li+	11.7	6.7a	8.6a	9.6a
Na+	13.8	8.47b, 9.8a	11.9a	11.4a
K+	15.0	9.36b, 9.9c	10.4c	12.4c
NH4+	12.9	-	-	-
Cs+	11.7	6.55b	8.5c	9.4c

^aFrom ref. 61;

^bfrom ref. 57;

^cfrom ref. 55.

Interesting is the increase of 5.0 ± 0.5 orders of magnitude in the binding constants from DB18C6 in 1,2-dichloroethane to 1 in a fluorous phase for all four metal cations. This increase is of a similar extent as the difference of 3.6 orders of magnitude between the formation constants of the protonated tridodecylammonium cation in a poly(vinyl chloride) membrane plasticized with bis(2-ethylhexyl) sebacate (logK 11.8)⁵⁶ and the formation constant of the protonated tris{(perfluorooctyl)pentyl}amine in the fluorous perfluoroperhydrophenanthrene (logK 15.4).⁴³ Both examples are consistent with the general observation that the stabilities of complexes between ions and electrically neutral ionophores increase as the polarity of the medium decreases (see, e.g., refs. 11 and 57), and the fact that among condensed phases fluorous liquids have the lowest polarity and polarizability.⁴¹

Returning to the issue of 1:2 complexation, it is important to note that it is well known that crown ethers with a host cavity too small to accommodate a specific cation readily form 1:2 complexes, often referred to as sandwich complexes.^6,58 In this regard, it is interesting to note that dibenzo-18-crown-6 forms more stable 1:2 complexes with the large ion Cs⁺ than 18-crown-6, benzo-18-crown-6, and dicyclohexano-18-crown-6.⁵⁹ It was hypothesized that this is the result of the rigid structure of dibenzo-18-crown-6, which among these four crown ethers has the largest similarity to the fluorophilic ionophore 1. It is possible that similar rigidity enhances the stability of the 1:2 complexes of 1. Notably, the crystal structure of a dibenzo-18-crown-6 complex of Cs⁺ shows a total of 12 Cs–O distances in a relatively narrow range of 308 to 351 pm, confirming coordination of all 12 oxygens to the Cs⁺ ion.⁶⁰

Effect of the Multiple Complex Stoichiometries on Response Slopes

Knowing the stabilities of the Cs⁺ and NH₄⁺ complexes of the fluorophilic ionophore 1, it is possible to revisit the super-Nernstian K⁺ responses of the ISE membranes doped with 1 and 71 mol % ionic sites. Importantly, it is now possible to quantitatively explain these super-Nernstian responses on the basis of the ISE membrane compositions calculated from the experimentally determined complex formation constants (see Figs. 4 and 5).

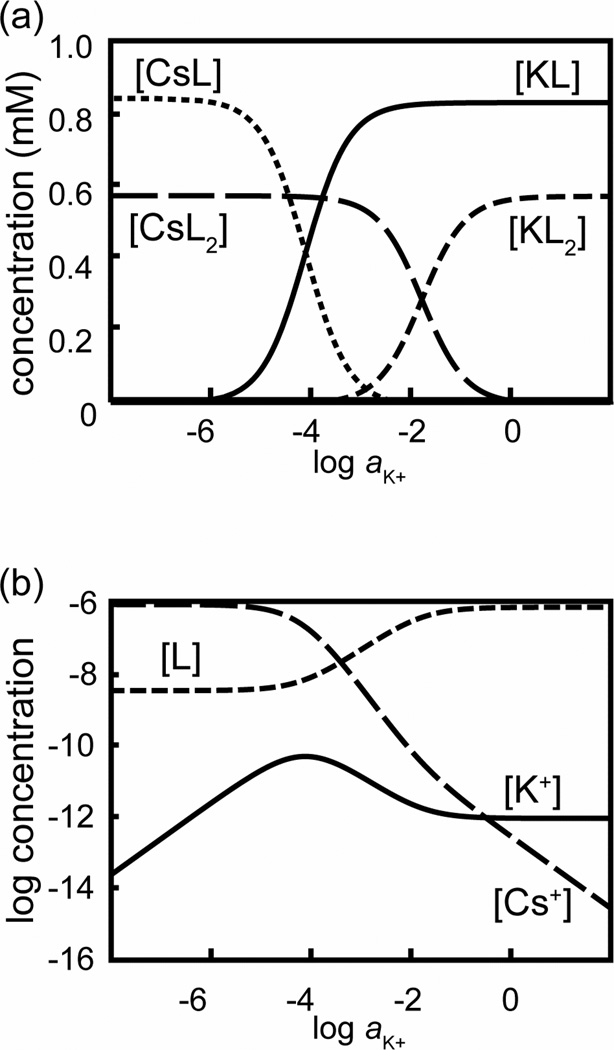
Figure 4.

Calculated composition of an ISE membrane based on ionophore 1 and 71 mol % ionic sites when exposed to 1 mM Cs⁺ and a varying activity of K⁺, corresponding to the K⁺ response in a Cs⁺ background shown in Figure 2: Membrane concentrations of (a) complexes between ionophore and K⁺ and Cs⁺, and (b) free ionophore and free K⁺ and Cs⁺ ions (note the logarithmic scale). All parameters used to calculate these concentrations are the same as for fit of the EMF in a Cs⁺ background, as shown in Figure 3 (broken line).

Figure 5.

Calculated composition of an ISE membrane based on ionophore 1 and 71 mol % ionic sites when exposed to 2 mM NH₄⁺ and a varying activity of K⁺, corresponding to the K⁺ response in a NH₄⁺ background shown in Figure 2: Membrane concentrations of (a) complexes between ionophore and K⁺ and NH₄⁺, and (b) free ionophore and free K⁺ and NH₄⁺ ions (note the logarithmic scale). All parameters used to calculate these concentrations are the same as for the fit of the EMF in a Cs⁺ background, as shown in Figure 3 (broken line) except for K_ex= 10^−0.55, K_NH4L =10^12.9 and K_NH4L2 = 10^7.0, which are specific to NH₄⁺.

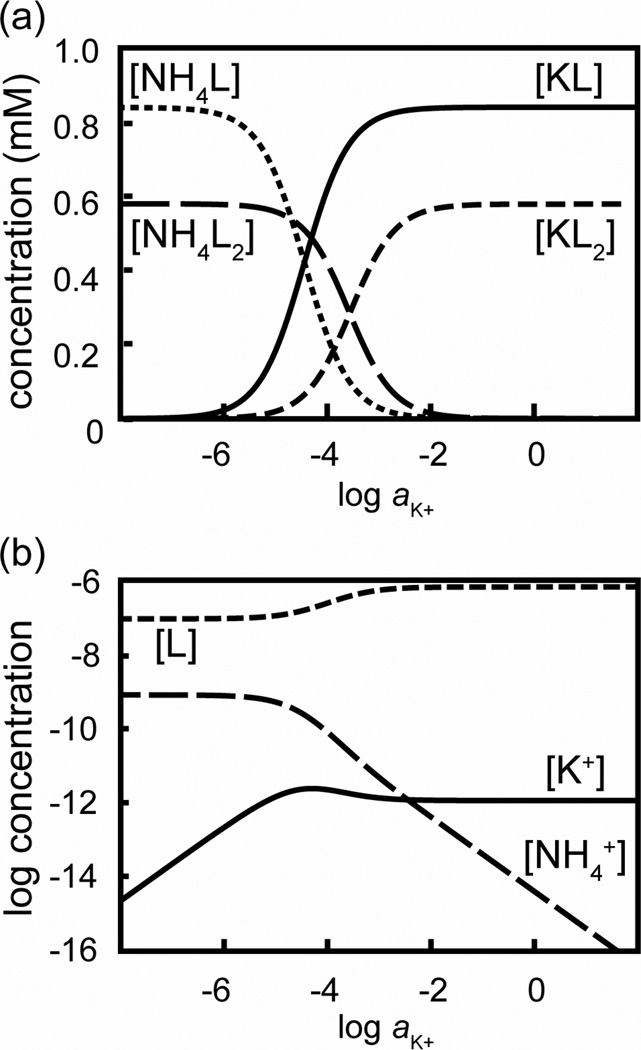
Figure 4 shows the concentrations of the free ionophore 1 (represented as L) and the 1:1 and 1:2 complexes of K⁺ and Cs⁺ in the ISE membrane as the activity of K⁺ increases in the aqueous phase; it corresponds directly to the K⁺ response in a Cs⁺ background as shown in Figure 2. As expected, the concentration of free ionophore at low sample activities of K⁺ is very small, and the membrane is loaded mostly with 1:1 and 1:2 complexes of Cs⁺. At high K⁺ activities, the membrane is loaded with 1:1 and 1:2 complexes of K⁺, but because of the weaker stability of the 1:2 complexes of K⁺, the free ionophore concentration is higher. Most important for the response curve is the K⁺ activity at which the concentration of Cs⁺L complexes in the ISE membrane has fallen to 50% of its value at very low K⁺ activities; it is roughly hundred times lower than the K⁺ activity at which the membrane concentration of Cs⁺L₂ complexes has fallen to 50% of its value at very low K⁺ activities. In the intermediate range between 0.1 and 10 mM K⁺, the two most abundant ionophore species in the ISE membrane are K⁺L and Cs⁺L₂, and the membrane composition is continuously changing as a function of the K⁺ activity in the sample. The super-Nernstian response to K⁺ in this range is the result of the increase in concentration of free ionophore, and the concomitant decrease in the concentration of free K⁺ in the ISE membrane.

Figure 5 shows the analogous case for NH₄⁺. The overall trends are very similar, but the range of K⁺ activities in the sample for which K⁺L and NH₄⁺L₂ are the most abundant species is only about one order of magnitude wide. This explains the smaller maximum slope in the K⁺ response curve in the presence of a constant background of NH₄⁺, and makes clear why in the case of NH₄⁺ the range of the super-Nernstian response is narrower. Note also that the decrease in the concentration of the free K⁺ in the ISE membrane from the lower to the upper end of the super-Nernstian response is smaller here than in the case of Cs⁺ (see Figs. 4 and 5).

The width of the activity range in which the super-Nernstian response slope is observed does not depend on the concentration of the NH₄⁺ or Cs⁺, as follows from the width of this range given by log (K_JL2/K_IL2). Note that this expression and the relevant complex formation constants from Table 2 predict ranges of the super-Nernstian K⁺ response of 0.1, 0.2, 2.1, and 0.9 on a logarithmic scale for solutions with a constant activity of Li⁺, Na⁺, Cs⁺, and NH₄⁺, respectively. These values are in very good agreement with the widths of the experimentally observed super-Nernstian K⁺ response ranges in a background of Cs⁺ or NH₄⁺, and the fact that no such responses are observed in the presence of Li⁺ or Na⁺. Note that higher activities of NH₄⁺ or Cs⁺ in the sample shift the super-Nernstian response range to higher activities of K⁺ but do not affect the width of the super-Nernstian response range. This can be seen from the K⁺ activities that mark the lower and upper ends of the super-Nernstian response, which are a_J,aq K_JL (K_ex K_IL)⁻¹ and a_J,aq K_JL K_JL2 (K_ex K_IL K_IL2)⁻¹, respectively (see Supporting Information).

Conclusions

The belief that 18-crown-6 ether ionophores do not form 1:2 complexes with K⁺ and smaller cations goes back several decades. It may be partly explained by the fact that such complexes are less stable in polar solvents, with which a lot of the conventional host–guest chemistry has been performed. In the field of ionophore-based ISEs, erroneous conclusions may have also been taken because quantitative and testable models to predict potentiometric selectivities were not available in the past.

This work not only showed that the small ions Li⁺, Na⁺, K⁺ and NH₄⁺ form both 1:1 and 1:2 complexes with the fluorophilic crown ether 1, but it also demonstrated that the simultaneous formation of more than one type of complex of the primary ion can result in super-Nernstian responses with an origin not previously reported in the literature. The first well documented explanation for super-Nernstian responses used to be ion fluxes, a phenomenon often referred to as “Hulanicki effect”. While our understanding of ion fluxes has increased drastically,^13–17 it is clear that they do not explain all super-Nernstian responses. Apparently twice-Nernstian responses caused by the co-existence of primary and interfering ion complexes in ISE membranes over a wide range of sample activities were the first examples of super-Nernstian responses that could be explained by phase boundary equilibria alone.^22–26 In those cases, each ion formed only one type of complex in the ISE membrane. This contribution introduces super-Nernstian responses caused by the simultaneous formation of more than one primary ion complex in the ISE membrane. Preliminary calculations also predict sub-Nernstian responses and potential dips of a similar origin (see Figure S7 of the Supporting Information); they can be explained with the same model but result from different combinations of complex stabilities. Since any type of complex with a stoichiometry higher than 1:1 is formed stepwise from at least one complex of smaller stoichiometry, it appears likely that super-Nernstian and sub-Nernstian responses of this type are much more common than the literature suggests.

Importantly, we do not intend to convince readers to intentionally make ISEs that exhibit the unusual response slopes described in this paper. ISEs respond more slowly in activity ranges in which a minor change in sample activity causes a substantial change in the ionic composition of the ISE membrane bulk.³⁸ This is also true for most of the super-Nernstian response range of the fluorophilic crown ether ISEs discussed here, and is clearly a disadvantage. However, we anticipate that a better theoretical understanding of unusual response slopes will help ISE developers to avoid time-consuming misguided efforts to improve the selectivities and reproducibility of new ISEs that exhibit such responses. Hopefully, a better understanding of non-Nernstian responses will also prevent others from giving up prematurely on promising ionophores whose use initially results in puzzling response characteristics.