Skip to main content
PMC home page
Springer logoLink to Springer
. 2011 Oct 28;74(1):185–193. doi: 10.3758/s13414-011-0222-7

Observers can voluntarily shift their psychometric functions without losing sensitivity

Michael Morgan 1,2,✉, Barbara Dillenburger 1, Sabine Raphael 1, Joshua A Solomon 2
PMCID: PMC3264850  PMID: 22033949

Abstract

Psychometric sensory discrimination functions are usually modeled by cumulative Gaussian functions with just two parameters, their central tendency (μ) and their slope (1/σ). These correspond to Fechner’s “constant” and “variable” errors, respectively. Fechner pointed out that even the constant error could vary over space and time and could masquerade as variable error. We wondered whether observers could deliberately introduce a constant error into their performance without loss of precision. In three-dot vernier and bisection tasks with the method of single stimuli, observers were instructed to favour one of the two responses when unsure of their answer. The slope of the resulting psychometric function was not significantly changed, despite a significant change in central tendency. Similar results were obtained when altered feedback was used to induce bias. We inferred that observers can adopt artificial response criteria without any significant increase in criterion fluctuation. These findings have implications for some studies that have measured perceptual “illusions” by shifts in the psychometric functions of sophisticated observers.

Keywords: 2-D shape and form, Adaptation, Aftereffects, Decision making

To measure the effect of attention, adaptation, or context on the appearance of a stimulus, rather than just the effect on sensitivity, a common method is to use the method of single stimuli (MSS) and look for shifts in the central tendency of the psychometric function (Ayhan, Bruno, Nishida, & Johnston, 2011; Burr, Cicchini, Arrighi, & Morrone, 2011; Leopold, O’Toole, Vetter, & Blanz, 2001; Taya, Adams, Graf, & Lavie, 2009; Winawer, Huk, & Boroditsky, 2010). For example, in a study by Winawer et al., 2010, observers classified a random-dot stimulus as moving left versus right, and a psychometric function was determined as the coherence of the motion varied between predominantly leftwards and predominantly rightwards (Fig. 1, top left panel). Normally, the observer would classify a stimulus with zero coherence as moving left and right with equal probabilities, but after adaptation the psychometric function shifted away from the adapting direction, with the result that a stationary stimulus was classified as moving in the direction opposite from the adaptor.

Fig. 1.

Fig. 1

Open in a new tab

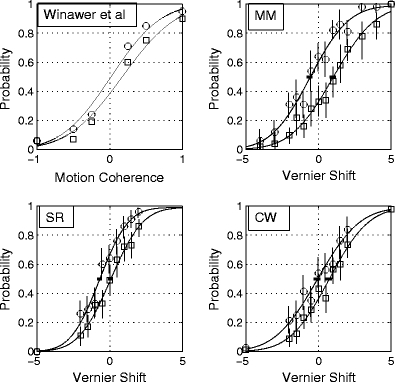
The first panel (top left) shows data from Winawer et al. (2010). The vertical axis shows the probability of classifying the motion direction left versus right. The remaining panels show psychometric functions from a three-dot vernier alignment task, in which the magnitude of the physical shift of the centre dot (horizontal axis) was sampled from a set of fixed values without replacement. The units of displacement are Weber fractions as percentages (100 * target shift/interpatch distance). Negative shifts are shifts “down.” The vertical axis is the probability with which the observer classifies a shift as “up” versus “down.” Vertical bars are 95% confidence limits based on the binomial distribution. The circles show data taken with the observers’ natural biases; the rectangles with a deliberately feigned bias in the opposite direction. All curves are best-fitting two-parameter (μ, σ) cumulative Gaussian functions. The small horizontal bars at .5 on the ordinate show the 95% confidence intervals for the mean of the psychometric function μ, obtained from 160 simulated runs of the experiment using the maximum-likelihood fits of μ and σ

The unusual aspect of the Winawer et al. (2010) study was that this shift was produced merely by imagining the adapting stimulus. Our Fig. 1 (top left panel) shows the data from their Fig. 2 (top left panel), replotted with the best-fitting two-parameter (μ, σ) cumulative Gaussian psychometric functions. The μ parameter is the position on the x-axis of the .5 probability point. A change in μ by itself produces a lateral (left- or rightwards) shift of the whole function, without changing its shape. The σ parameter is a measure of internal noise and determines the slope (spread) of the function. Large values of σ indicate a shallow slope, and thus lower sensitivity of the observer to changes in the physical signal. In the figure we are examining, it is noteworthy that the shift in central tendency (μ) due to imagery (from .017 to .172) is less than 30% of σ for these functions, and that these values for σ are similar between the two conditions (.537 and .587).

Fig. 2.

Fig. 2

Open in a new tab

The figure shows data from the bisection task, presented with the same conventions as in Fig. 1

The question we raise here is whether the MSS can distinguish between perceptual shifts and response bias. To discuss this possibility, we introduce the concept of a “natural criterion.” There is an obvious sense in which MSS tasks such as vernier acuity, bisection acuity, red versus green colour discrimination, and motion direction discrimination all have natural null points. Natural criteria are those that the observer can be verbally instructed to adopt without the need to show them the null point, and without the need for response feedback. We can now define a perceptual shift as a translation of the psychometric function, which occurs without a change in the observer’s natural criterion. A previous study of an undoubtedly perceptual effect, the Müller-Lyer “illusion,” showed that the shift takes place without any change in the slope of the psychometric function, and thus without any measurable increase in sensory noise (Morgan & Glennerster, 1991; Morgan, Hole, & Glennerster, 1990). From visual inspection, the same appears to be the case in the data of Leopold et al. (2001) on face adaptation and in those of Winawer et al. (2010) on adaptation to imaginary motion.

Response bias, however, can also change the mean of the psychometric function in MSS. One type of response bias is the tendency to favour one of the two response categories when observers are unsure of their answer. This bias could be deliberate, or it could be due to an unconscious tendency to comply with the experimenter’s hypothesis (Rosenthal & Rubin, 1978). Forcing the observer to adopt an unnatural criterion would have a similar effect. For example, in three-dot vernier acuity, stimuli could be compared with an imaginary curved line, rather than an imaginary straight line.

The experimental question is whether observers can adopt an unnatural criterion in a classification task so as to deliberately shift the mean point of their psychometric function, and if so, whether this would be betrayed by a change in the slope of the function. There is no a priori answer to this question. One possibility is that response biases will change the slope of the psychometric function as well as its mean (μ). The reasoning is that an artificial criterion may be harder to maintain than a natural one, and its value will therefore fluctuate. Such criterial fluctuations are indistinguishable from sensory noise (Fechner, 1860; quoted in Solomon, 2011, p. 2). If artificial criteria were harder to maintain, we could detect when observers were using an artificial criterion from a flattening of the psychometric function. The other possibility is that artificial criteria can be maintained just as constantly as natural ones. If this is the case, there would be no flattening of the psychometric function, and one would then have to be sceptical about whether the MSS could ever distinguish perceptual effects from response biases, in the absence of strong supporting evidence such as a convincing demonstration (which the Müller-Lyer illusion, for example, provides).

We therefore think it is important to determine experimentally whether observers can deliberately introduce biases into their psychometric functions without changing their slopes, and this is what our experiments here set out to determine. Previous studies of criterion effects in classification tasks (Healy & Kubovy, 1981; Lee & Janke, 1964, 1965) have not used natural criteria but arbitrary points along a continuum such as brightness, and thus are not relevant to the question we pose here. They have also used externally imposed noise so that the observers could not avoid making errors. In the tests we describe here, there was always a natural criterion, and the only source of noise was internal. To the best of our knowledge, our study is the first attempt to see whether observers can voluntarily move their psychometric function away from its natural physical null point without changing its slope.

In the experiments described below, we used two methods of encouraging observers to adopt artificial criteria in three-dot vernier and bisection tasks. In Experiment 1, we simply asked observers to produce a voluntary bias in favour of one of the two responses. In Experiment 2, we tried to alter their response strategies with feedback. Unlike Herzog and Fahle (1999) and Herzog, Ewald, Hermens, and Fahle (2006), who also manipulated feedback, we specifically told our observers to maximize the number of “correct” responses.

A word about terminology is needed before describing the experimental method. The MSS can be used to measure both bias and sensitivity. Traditional two-alternative forced choice (2AFC) is different, because it does not involve categorization with respect to an internal standard. However, it is becoming increasingly common to measure biases with the MSS and to refer to the method as 2AFC (Kane, Bex, & Dakin, 2009; Taya et al., 2009), presumably on the grounds that both methods involve two possible responses. We should make it clear that our remarks about MSS apply to these cases as well, even when they are called 2AFC. The melding of 2AFC and MSS into a single category cannot be called incorrect, since there are clear borderline cases, for example when the observer has to decide whether a stimulus is more blurred in the horizontal or the vertical direction (Sawides et al., 2010). The real distinction is not in the method but in the signal detection model, since 2AFC has two external noise sources, versus the one in MSS (Morgan, Watamaniuk, & McKee, 2000). However, it would be useful if abstracts would give precise information about method, which the term “2AFC” no longer provides. We remark in passing that a useful distinction has also been lost between 2AFC, where the signal interval is randomized, and what used to be called the “method of constant stimuli,” where the standard always appears first (Morgan et al., 2000), and which is really a variety of MSS even though it has two intervals.

General method

Subjects

Two of the subjects were authors (M.M. and S.R.), and the third was an experienced psychophysical observer (C.W.) who was not involved in the design of the experiment.

Stimuli

The stimuli were presented on the LCD display of a MacBook Pro laptop computer with screen dimensions 33 × 20.7 cm (1,440 × 900 pixels) viewed at 0.57 m, so that 1 pixel subtended 1.25 arcmin of visual angle. The background screen luminance was 21 cd/m2. Stimulus presentation was controlled by MATLAB and the PTB3 version of Psychtoolbox (Brainard, 1997). On each trial, the display consisted of a horizontal array of three fuzzy patches, each with an identical two-dimensional Gaussian profile (space constant σ = 12.5 arcmin) and maximum luminance 40 cd/m2. The distance between the leftmost and rightmost patches was 200 pixels (250 arcmin), and in each session the displacement of the centre patch from the exact centre point between the outer patches was chosen randomly on each trial, without replacement, from a set of 110 values, containing 10 repetitions each of a set of 11 values, which were either {−5, –2, –1.5, –1, –0.5, 0, 0.5, 1, 1.5, 2, 5} pixels or twice those values. The extreme values were included to look for finger errors, which were extremely rare. In the vernier task, the displacements were upwards and downwards; in the bisection task, they were leftwards and rightwards. Observers signalled their decision on each trial using the arrow keys on the keyboard.

Procedure

Each trial began with a 0.5-s fixation cross in the centre of the screen, which appeared as soon as the observer had pressed the key from the previous trial. The cross was followed by a 0.5-s blank, and then by the stimulus for 0.2 s, which was immediately followed by a 0.2-s pattern mask consisting of randomly placed patches like the targets. To prevent the subjects using landmarks to locate the centre dot of the array, the stimulus was randomly perturbed from the fixation point position on each trial independently in x- and y-position from a uniform probability density function with limits ±25 pixels (±25% of the interpatch separation).

Statistical analysis

To determine whether two or more psychometric functions differed in μ and/or σ, we used two kinds of test: likelihood ratio and bootstrapping. These tests are described in the Appendix.

Experiment 1

In conditions without intentional bias, the observer attempted to make an unbiased decision using a natural criterion. In conditions with intentional bias, the observer was instructed to respond correctly when the direction of offset appeared clear, but when uncertain, was instructed to choose one of the two response buttons.

S.R. had five sessions of vernier discrimination without intentional bias, followed by ten with intentional bias, followed by five without intentional bias. M.M. performed ten sessions without bias, followed by ten with a bias. Subject C.W. had eight sessions of unbiased training followed by nine sessions biased.

In the bisection task, S.R. had five sessions without intentional bias, followed by five with a bias in the direction opposite to her natural bias. M.M. had five biased sessions, which were compared to those previously collected without bias using the APE (adaptive probit estimation) procedure (Watt & Andrews, 1981).

There was no feedback at any time.

Results

The results of the vernier experiment are shown in Fig. 1 and Table 1. In the “unbiased” condition, S.R. in fact had a bias of ~1%, which is not unusual in these kinds of experiments. In the following block of sessions, S.R. was asked to introduce a bias in the opposite direction to her earlier, natural bias. This in fact moved her bias close to zero. The small horizontal error bars on the means of the two functions that represent the 95% confidence intervals show that the shift in bias was highly significant. Subject M.M. started out with a small spontaneous negative bias, which he was then able to convert into a larger positive bias. Observer C.W. was unbiased to start with and then voluntarily produced a rightwards shift of his psychometric function.

Table 1.

Results of Experiments 1 and 2

Subject, Condition Task μ σ Log L χ 2
M.M. Biased V 1.00 (0.75/1.19) 2.29 (2.03/2.5) −459.18
M.M. Control V −0.57 (−0.87/–0.42) 2.11 (1.83/2.27) −455.60
M.M. B + C (same μ) V 0.20 2.33 −968.67 −107.78***
M.M. B + C (diff. μ) V −0.59/0.98 2.20 −915.25 0.94 (NS)
S.R. Biased V −0.06 (−0.13/0.21) 1.74 (1.50/1.92) −503.60
S.R. Control V −0.69 (−0.89/–0.57) 1.55 (1.33/1.67) −461.34
S.R. B + C (same μ) V 0.32 1.69 −990.01 −50.14***
S.R. B + C (diff. μ) V 0.06/–0.71 1.65 −965.69 1.50 (NS)
C.W. Biased V 0.72 (0.40/0.88) 2.13 (1.88/2.34) −477.22
C.W. Control V 0.07 (−0.13/0.21) 2.29 (2.01/2.50) −450.20
C.W. B + C (same μ) V 0.36 2.24 −942.58 −30.32***
C.W. B + C (diff. μ) V 0.75/0 2.21 −928.13 1.42 (NS)
M.M. Biased B 0.98 (0.57/1.32) 2.94 (2.48/3.29) −230.40
M.M. Control B −1.7 (−2.13/–1.4) 2.74 (2.25/3.02) −304.70
M.M. B + C (same μ) B 0.59 3.26 −587.47 −104.74***
Μ.Μ. Β + C (diff. μ) B 0.96/–1.72 2.83 −535.28 0.36 (NS)
S.R. Biased B 0.99 (0.54/1.28) 2.92 (2.49/3.3) −224.95
S.R. Control B −1.22 (−1.62/–0.9) 2.54 (2.04/2.92) −207.73
S.R. B + C (same μ) B −0.14 2.96 −465.79 −66.22***
S.R. Β + C (diff. μ) B 0.96/–1.26 2.73 −433.33 1.3 (NS)
S.R. +1.75 VBF −0.49/–1.64 1.811 789.6 2.16 (NS)
S.R. –1.75 VBF −0.506/1.47 1.935 869.4 6.74**
C.W. –1.75 VBF 0.076/1.547 2.232 1,017.58 0.26 (NS)
M.M. +1.75 VBF 0.367/–1.87 2.32 1,170.00 0.38 (NS)
M.M. –1.75 VBF −0.369/1.628 2.37 1,179.50 0.04 (NS)
Open in a new tab

Numbers in parentheses represent 95% confidence intervals. See the text for further details about the data. B, biased; C, control; V, vernier; B, bisection; VBF, vernier with biased feedback; Log L, log likelihood. ** p < .01; *** p < .001; NS, p > .05

Table 1 gives the fitted values of μ and σ (cols. 3 and 4) for the various data sets indicated in the first and second columns. For example, the first line refers to observer M.M. in the biased vernier (V) condition. The code M.M. B + C indicates that the data from the biased (B) and control (C) sessions were combined. The code “same μ” means that the combined data were fitted with the same value of μ for both B and C conditions; the code “diff. μ” means that different values of μ were used for B and C. In the latter case, there are two values of μ in column 3, the first for B and the second for C. Column 5 gives the log-likelihood value associated with each fit. The last column (6) gives chi-square values for the difference in fitted parameters between the B and C conditions above. The calculation of chi-square is explained in the Appendix.

It is noteworthy that the bias affected all points on the psychometric function, with the exception of those at asymptote. This is what would be expected from signal detection theory with linear transduction and additive noise, but not from a threshold model. The implication is that subjects can consistently rate their certainty and bias their responses accordingly.

Figure 2 and Table 1 show the results of the bisection task. For both observers, there was clear and significant change in the function means without any obvious change in slope.

Experiment 2

The task was three-dot vernier alignment as in Experiment 1, except that feedback was used. A small black or white square appeared after every response to indicate whether the response was “right” or “wrong” relative to an arbitrary physical criterion. In the baseline condition, the criterion was zero offset. In the positive offset condition, it was 1.75 (Weber fractions as percentages), which was somewhere between 0.5σ and 1.0σ of the psychometric functions determined in Experiment 1. In the negative offset, it was −1.75 (Weber fractions as percentages). Cues with the actual criterion were never presented, to avoid ambiguity. Subjects were instructed to maximize the number of “correct” responses, and they knew that the criterion defining a correct response was arbitrary and had to be learned. Various amounts of practice were given until performance appeared stable, and then ten sessions were run in each criterion condition. The analysis below is based on these ten sessions. Subject C.W. was run in the negative offset condition only; his data are compared to those with the unbiased criterion from Experiment 1.

Experiment 2 results

Figure 3 shows the psychometric functions from Experiment 2. It will be seen that, in four of five cases, subjects had no difficulty in shifting accurately to the new criterion without any obvious loss of precision. For subjects M.M. and C.W., there was no significant difference in the slopes of the function between the natural criterion condition (zero offset) and the shifted criteria (see the Appendix). For S.R., the difference in slopes did reach significance (χ 2 = 6.76, df = 2, .01 < p < .05). This arose because of a significant difference between the zero and rightwards offsets; no other comparisons were significant (see the Appendix for details).

Fig. 3.

Fig. 3

Open in a new tab

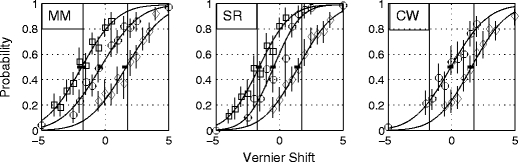
Results of Experiment 2, in which subjects were given feedback when classifying vernier offsets as “up” versus “down” relative to a criterion of zero (red curves), –1.75 (green), or +1.75 (blue). The units of displacement are Weber fractions as percentages (100 * target shift/interpatch distance). The nonzero criteria are marked by vertical lines. For further explanations, see the text and the legend of Fig. 1

General discussion

The results show that observers can deliberately manipulate the bias in a psychometric function without any obvious change in slope. This conclusion is supported by two types of statistical test (generalized likelihood ratio and bootstrapping; see the Appendix), both of which confirmed significant effects of intentional bias (i.e., criterion shift) on psychometric mean and no significant effects of intentional bias on psychometric slope (except for 1 observer in one condition of Exp. 2). Whatever additional noise was introduced by manipulating their response criteria, it must have been small in comparison to the existing noise. Therefore, contrary to one hypothesis, sizable response biases (i.e., criterion shifts) do not necessarily diminish discriminability. Of course, we cannot prove the null hypothesis that there is absolutely no effect of bias on the slope of the function. Instead, the point we intend to make is simply that the psychometric shifts due to deliberate response biases strongly resemble the psychometric shifts in studies of putatively perceptual bias (Ayhan et al., 2011; Burr et al., 2011; Leopold et al., 2001; Taya et al., 2009; Winawer et al., 2010).

If we had found a decrease in sensitivity with bias, there would have been several possible explanations. One is criterial fluctuation, as discussed in the introduction. Other possibilities include a sensory nonlinearity and offset-dependent sensory noise, which would have made discrimination more difficult at higher stimulus levels. The fact that we did not find a decrease of psychometric slope with bias indicates that the range of cue values we used was such that any nonlinearity was trivial in comparison to a roughly constant amount of sensory noise.

Previous work (Lages & Treisman, 1998, 2011) supported the conclusion that the mean of a psychometric function can be manipulated without significant changes in its slope. Lages and Treisman (1998) presented subjects with a 2.5-cpd reference grating that they had to remember, followed after a retention interval by a block of sessions, on each of which they had to decide whether a test grating was higher or lower in frequency than the reference (note that the method was MSS, not 2AFC). In different blocks, the range of tests was centred at 2.25, 2.5 (the standard), or 2.75 deg. The psychometric functions showed clear and statistically significant shifts in mean towards the mean of the range. Lages and Treisman (2011) reported similar results for orientation discrimination. Unfortunately for our purposes, the slopes of the psychometric functions were not compared across conditions, but from inspection and from their Tables 1, 2 and 3 (Lages & Treisman, 1998), they do not seem to have changed much. A complication in interpreting any change in slope is that it may vary with the stimulus range in any case, independently of criterion noise. However, these studies do not speak strongly to the questions we have raised, since at no stage was a natural criterion used.

Herzog et al. (2006) and Herzog and Fahle (1999) manipulated vernier acuity by introducing false feedback on certain trials at small shifts in one direction. Psychometric functions were not presented, but the manipulation seems to have had the expected effect of shifting the response distribution. Overall, the incorrect feedback caused an increase in the number of incorrect responses relative to the baseline condition. This would be expected if the observers were confused about whether to use their natural criterion or the one suggested by the feedback. In our Experiment 2, subjects tried to maximize the number of “correct” responses and were able to shift their psychometric functions without significantly changing their slope, except for 1 subject in one condition.

The question arises of how observers in Experiment 1 used the instruction to respond on one button when unsure of their answer. A simple model shows how. We suppose that an observer sets a threshold criterion for the absolute internal value of the signal. If the signal falls below that threshold, the observer always responds on the same button. If the absolute value of the signal is greater than the criterion, he or she responds according to its sign. If R is random Gaussian noise with unit variance and zero mean, s is the signal, and c is the criterion, then the probability of the positively biased response is given by the probability that

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \left( {{\mathbf{R}} + s} \right) > - c, $$\end{document}

which is simply the integral of the Gaussian probability density function between –c and infinity. It will be seen that this model is entirely equivalent to an observer with a nonzero mean (μ) and that σ is not affected. Figure 4 shows the results of a simulation, with unit noise variance, in which the threshold could be as large as 2σ without affecting the slope of the function. The criterion is in units of σ varied between 0 and 2. The best-fitting values for σ (going from right to left) were 0.9986, 0.9997, 1.002, 1.0017, 0.9999, 1.0011.

Fig. 4.

Fig. 4

Open in a new tab

Results of simulating an observer who sets a threshold criterion for the absolute level of the internal signal. If the signal falls below that threshold, the observer always responds on the same button. If the absolute value of the signal is greater than the threshold, the observer responds according to its sign. For further explanations, see the text

The finding that observers can easily shift their criterion in a classification task has implications for the use of the MSS to measure perceptual biases. It is an established practice to measure these biases by the shift in the central tendency of psychometric functions (Bruno, Ayhan, & Johnston, 2010; Burr, Tozzi, & Morrone, 2007; Morgan & Glennerster, 1991; Morgan et al., 1990; Taya et al., 2009). In some cases, different laboratories have not agreed on the results (cf. Bruno et al. vs. Burr et al). Often these shifts are a small fraction of the spread (σ) of the psychometric function, and in these circumstances it is legitimate to ask whether every possible precaution has been taken to ensure that observers have not consciously or unconsciously introduced a response bias or criterion shift into their responding in response to the perceived goal of the experiment. As the present experiment has shown, this bias would not necessarily be detected by any change in the slope of the function.

In their study using an imaginary adaptor, Winawer et al. (2010) carefully considered the possibility that their result was due to a response bias rather than a perceptual bias. They tried to rule this out by introducing a delay between the imaginary adaptor and the test, arguing that a genuine perceptual effect, as opposed to a response bias, would be expected to decay with time. Trying to defeat the cognitive expectations of subjects in this clever way is definitely the way forward, but interpretation of the results depends on how much the subjects knew. In this case, the subjects were described as “naïve volunteers from the MIT (n = 64) and Stanford (n = 68) communities [who] received course credit or were paid for participation.” If they were psychologists, or if they were allowed to communicate, it is feasible that they might expect adaptation to decay with time. A stronger test would be to use the “storage” of motion adaptation in the dark (Honig, 1967; Morgan, Ward, & Brussell, 1976; Thompson & Movshon, 1978) in subjects who were genuinely unaware of the phenomenon. If the effect of an imaginary adaptor showed storage in the dark but not in the light, this would be good evidence for a perceptual effect rather than a response bias. But it would be essential that the subjects, and if possible the experimenter, did not know of the “storage” effect. We note in passing that the use of subjects carrying out a study for course credit is quite possibly ideal for finding the Rosenthal compliance effect.

Another case that might deserve critical reexamination in the light of our results is the claim that attentional load affects the extent of adaptation to a moving stimulus (Chaudhuri, 1990; Rees, Frith, & Lavie, 1997, 2001). The claim is that if the subject’s attention is distracted from the adaptor by a “high-load” foveal task, the extent of adaptation is reduced. One reason for doubting this claim is that a classic study by Wohlgemuth (1911) looked for this effect and failed to find it. Most studies of this phenomenon have measured the strength of the motion aftereffect by its subjective duration, a measure that is known to be subject to the Rosenthal compliance effect (Sinha, 1952). In a series of studies using genuinely naïve subjects (optometry students who knew nothing about attentional load theory), no effect of attentional load was found, although instructions designed to reduce the duration had a significant effect (Morgan, submitted). The only study of which we are aware using a 2AFC measure of the effects of adaptation on contrast sensitivity failed to find any effect of attentional load (Morgan, 2011) on any point of the threshold-versus-contrast function, including detection. The only study we know of using MSS was by Taya et al. (2009), who presented a single stimulus that the observer had to classify as moving left versus right. Psychometric functions were not presented, but it can be calculated that the mean shifts of ~1 pixel/second were very close to the absolute velocity threshold for motion, and would thus have been close to the levels of sensory noise, as in the experiments we have reported here.

We cannot assert that the responses of any subject in any MSS experiment were unconsciously or otherwise biased, either by their expectations or by desire to conform to a group standard. However, what is well established is that observers can be very easily influenced by social factors (Rosenthal & Rubin, 1978; Sinha, 1952). The precautions that would have to be taken to avoid these effects would have to be similar to those in a rigorous clinical trial. Not only would the observers have to be completely unaware of the purpose of the experiment, but the experimenter too would have to be “blind,” to avoid influencing the subjects. Psychophysical studies seldom if ever meet these standards. Observers are often said to be “naïve” without any details about the extent of their knowledge or their social contacts with other subjects. Sometimes they are students meeting a course requirement.

We conclude that observers can easily change the central tendencies of their psychometric functions by introducing a response bias or change in criterion, and that such shifts cannot be taken as evidence for genuinely perceptual biases without supporting evidence. In particular, the vague specification of subjects as “naïve” needs to be made more precise, and precautions are needed against experimenter influence on potentially compliant subjects. In controversial cases, a clear demonstration can be helpful.

Acknowledgments

Open Access

This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.

Appendix

Experiment 1

To assess whether the functions in Experiment 1 were different in slope, a likelihood analysis was carried out. First, the functions were fit individually to Gaussian cumulative density functions and the likelihoods of the independent fits recorded. These are the fits shown by the continuous curves in Figure 1. The two sets of data were then combined into a single fit with two parameters (μ, σ) and the likelihood of this fit compared to a four-parameter model with separate means and sigma for the two sets of data (μ 1, σ 1, μ 2, σ 2). Let L c and L u be the likelihoods of the best-fitting constrained and unconstrained models. Established theory (Hoel, Port, & Stone, 1971) states that under the null hypothesis that the constrained model captures the true state of the world,

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ X = - 2ln\left( {{L_{\text{c}}}/{L_{\text{u}}}} \right) $$\end{document}

is asymptotically distributed as chi-square with 2 degrees of freedom (for the difference in the number of parameters). Table 1 shows values for the mean (μ) and standard deviation (σ) derived from maximum-likelihood fits of a cumulative Gaussian function to data, and the log-likelihood values associated with the fit (col. 5). The figures in parentheses are the lower and upper 95% confidence limits determined by bootstrapping. The origins of the data for each fit are shown in column 1. The first two letters of the code specify the subject (M.M., S.R., or C.W.). The biased and control conditions are B and C, respectively. The rows with the code “B + C (same μ)” show the results of the two-parameter fit in which μ and σ were the same for the B and C trials. The rows with the code “B + C (diff. μ)” show the results of the three-parameter fit in which μ but not σ was permitted to vary between the B and C trials. In this row, the two fitted μ values are shown in the order μB/μC. The second column indicates whether the task was vernier (V) or bisection (B) or the vernier biased feedback task (VBF). The final column shows the χ 2 values for the comparison between the four-parameter fits to the data and the more constrained fits—that is, 2 * (L B + C – L B – L C). Three asterisks indicate p < .001, two asterisks indicate p < .01, and “NS” indicates p > .05.

Table 1 shows that the difference between the two-parameter (same μ, σ) and four-parameter fits to the data was highly significant. This could have been the result of different values of μ, σ, or both of these. However, the difference between the three-parameter fit (diff. μ) and the four-parameter fit was not significant, except in one case. We can conclude that the functions were significantly different in μ but not in σ.

To supplement the likelihood-ratio test of significance, we carried out a bootstrap analysis. Two blocks of data equal in size to the experimental data were simulated 160 times using the same values for μ and σ obtained as maximum-likelihood values fitted to the original experimental data for the control block. The 160 pairs of values of fitted σ values from the two simulated blocks were then compared to the observed difference between the control and the biased blocks to find the percentage of simulated differences having a larger absolute value than the observed difference. The same analysis was then carried out using μ and σ from the biased data to generate the simulations. The results for the control and biased blocks, respectively, were 25% and 35% (subject M.M.), 19% and 16.5% (S.R.), and 35% and 32% (C.W.). The same analysis carried for differences in μ gave percentages of zero in all cases. This analysis supports the conclusion that the difference in μ between control and biased blocks was highly significant, while the difference in σ was not.

In the bisection task for both observers, the biased and unbiased psychometric functions differed significantly (Table 1), but not in the fit with different means and the same σ in the two blocks.

Experiment 2

For subjects M.M. and C.W., there was no significant difference in the slopes of the functions between the natural-criterion condition (zero offset) and the shifted criteria, using the likelihood-ratio method of analysis summarized in Table 1. For S.R., there was a significant difference between the zero and negative-offset conditions, but no other comparisons were significant.

Contributor Information

Michael Morgan, Email: Michael.Morgan@nf.mpg.de.

Barbara Dillenburger, Email: Barbara.Dillenburger@nf.mpg.de.

Sabine Raphael, Email: Sabine.Raphael@nf.mpg.de.

Joshua A. Solomon, Email: J.A.Solomon@city.ac.uk

References

  1. Ayhan I, Bruno A, Nishida S, Johnston A. Effect of the luminance signal on adaptation-based time compression. Journal of Vision. 2011;11(7):22. doi: 10.1167/11.7.22. [DOI] [PubMed] [Google Scholar]
  2. Brainard DH. The Psychophysics Toolbox. Spatial Vision. 1997;10:433–436. doi: 10.1163/156856897X00357. [DOI] [PubMed] [Google Scholar]
  3. Bruno A, Ayhan I, Johnston A. Retinotopic adaptation-based visual duration compression. Journal of Vision. 2010;10(10):30. doi: 10.1167/10.10.30. [DOI] [PubMed] [Google Scholar]
  4. Burr DC, Cicchini GM, Arrighi R, Morrone MC. Spatiotopic selectivity of adaptation-based compression of event duration [Comment letter] Journal of Vision. 2011;11(2):21. doi: 10.1167/11.2.21. [DOI] [PubMed] [Google Scholar]
  5. Burr D, Tozzi A, Morrone MC. Neural mechanisms for timing visual events are spatially selective in real-world coordinates. Nature Neuroscience. 2007;10:423–425. doi: 10.1038/nn1874. [DOI] [PubMed] [Google Scholar]
  6. Chaudhuri A. Modulation of the motion aftereffect by selective attention. Nature. 1990;344:60–62. doi: 10.1038/344060a0. [DOI] [PubMed] [Google Scholar]
  7. Fechner, G. (1860). Elemente der Psychophysik. Leipzig: Breitkopf & Hartel.
  8. Healy AF, Kubovy M. Probability matching and the formation of conservative decision rules in a numerical analog of signal detection. Journal of Experimental Psychology: Human Learning and Memory. 1981;7:344–354. doi: 10.1037/0278-7393.7.5.344. [DOI] [Google Scholar]
  9. Herzog MH, Ewald KRF, Hermens F, Fahle M. Reverse feedback induces position and orientation specific changes. Vision Research. 2006;46:3761–3770. doi: 10.1016/j.visres.2006.04.024. [DOI] [PubMed] [Google Scholar]
  10. Herzog MH, Fahle M. Effects of biased feedback on learning and deciding in a vernier discrimination task. Vision Research. 1999;39:4232–4243. doi: 10.1016/S0042-6989(99)00138-8. [DOI] [PubMed] [Google Scholar]
  11. Hoel PG, Port SC, Stone CJ. Introduction to statistical theory. Boston: Houghton Mifflin; 1971. [Google Scholar]
  12. Honig WK. Studies of the storage of the aftereffect of seen movement. Chicago: Paper presented at the annual meeting of the Psychonomic Society; 1967. [Google Scholar]
  13. Kane D, Bex PJ, Dakin SC. The aperture problem in contoured stimuli. Journal of Vision. 2009;9(10):1–17. doi: 10.1167/9.10.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Lages M, Treisman M. Spatial frequency discrimination: Visual long-term memory or criterion setting? Vision Research. 1998;38:557–572. doi: 10.1016/S0042-6989(97)88333-2. [DOI] [PubMed] [Google Scholar]
  15. Lages M, Treisman M. A criterion setting theory of discrimination learning that acounts for anisotropy and other effects. In: Solomon JA, editor. Fechner’s legacy in psychology: 150 years of elementary psychophysics. Brill: Leiden; 2011. [Google Scholar]
  16. Lee W, Janke M. Categorizing externally distributed stimulus samples for three continua. Journal of Experimental Psychology. 1964;68:376–382. doi: 10.1037/h0042770. [DOI] [PubMed] [Google Scholar]
  17. Lee W, Janke M. Categorizing externally distributed stimulus samples for unequal molar probabilities. Psychological Reports. 1965;17:79–90. doi: 10.2466/pr0.1965.17.1.79. [DOI] [PubMed] [Google Scholar]
  18. Leopold DA, O’Toole AJ, Vetter T, Blanz V. Prototype-referenced shape encoding revealed by high-level aftereffects. Nature Neuroscience. 2001;4:89–94. doi: 10.1038/82947. [DOI] [PubMed] [Google Scholar]
  19. Morgan, M. J. (2011). Wohlgemuth was right: Distracting attention from the adapting stimulus does not decrease the motion after-effect. Vision Research. doi:10.1016/j.visres.2011.07.018 [DOI] [PMC free article] [PubMed]
  20. Morgan MJ, Glennerster A. Efficiency of locating centres of dot-clusters by human observers. Vision Research. 1991;31:2075–2083. doi: 10.1016/0042-6989(91)90165-2. [DOI] [PubMed] [Google Scholar]
  21. Morgan MJ, Hole GJ, Glennerster A. Biases and sensitivities in geometrical illusions. Vision Research. 1990;30:1793–1810. doi: 10.1016/0042-6989(90)90160-M. [DOI] [PubMed] [Google Scholar]
  22. Morgan MJ, Ward RM, Brussell EM. The aftereffect of tracking eye movements. Perception. 1976;5:309–317. doi: 10.1068/p050309. [DOI] [PubMed] [Google Scholar]
  23. Morgan MJ, Watamaniuk SNJ, McKee SP. The use of an implicit standard for measuring discrimination thresholds. Vision Research. 2000;40:109–117. doi: 10.1016/s0042-6989(00)00093-6. [DOI] [PubMed] [Google Scholar]
  24. Rees G, Frith CD, Lavie N. Modulating irrelevant motion perception by varying attentional load in an unrelated task. Science. 1997;278:1616–1619. doi: 10.1126/science.278.5343.1616. [DOI] [PubMed] [Google Scholar]
  25. Rees G, Frith C, Lavie N. Processing of irrelevant visual motion during performance of an auditory attention task. Neuropsychologia. 2001;39:937–949. doi: 10.1016/S0028-3932(01)00016-1. [DOI] [PubMed] [Google Scholar]
  26. Rosenthal R, Rubin DB. Interpersonal expectancy effects: The first 345 studies. The Behavioral and Brain Sciences. 1978;1:377–386. doi: 10.1017/S0140525X00075506. [DOI] [Google Scholar]
  27. Sawides L, Marcos S, Ravikumar S, Thibos L, Bradley A, Webster M. Adaptation to astigmatic blur. Journal of Vision. 2010;10(12):22. doi: 10.1167/10.12.22. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Sinha D. A experimental study of a social factor in perception: The influence of an arbitrary group standard. Patna: University Journal; 1952. pp. 7–16. [Google Scholar]
  29. Solomon JA, editor. Fechner’s legacy in psychology: 150 years of elementary psychophysics. Leiden: Brill; 2011. [Google Scholar]
  30. Taya S, Adams WJ, Graf EW, Lavie N. The fate of task-irrelevant visual motion: Perceptual load versus feature-based attention. Journal of Vision. 2009;9(12):1–10. doi: 10.1167/9.12.12. [DOI] [PubMed] [Google Scholar]
  31. Thompson PG, Movshon JA. Storage of spatially specific threshold elevation. Perception. 1978;7:65–73. doi: 10.1068/p070065. [DOI] [PubMed] [Google Scholar]
  32. Watt RJ, Andrews DP. APE: Adaptive probit estimation of psychometric functions. Current Psychological Reviews. 1981;1:205–213. doi: 10.1007/BF02979265. [DOI] [Google Scholar]
  33. Winawer J, Huk AC, Boroditsky L. A motion aftereffect from visual imagery of motion. Cognition. 2010;114:276–284. doi: 10.1016/j.cognition.2009.09.010. [DOI] [PubMed] [Google Scholar]
  34. Wohlgemuth, A. (1911). On the After-Effect of seen movement. British Journal of Psychology, Monograph Supplemet No.1, 1–117.

Articles from Attention, Perception & Psychophysics are provided here courtesy of Springer

RESOURCES