Abstract
Using dynamic nuclear polarization (DNP)/nuclear magnetic resonance instrumentation that utilizes a microwave cavity and a balanced rf circuit, we observe a solid effect DNP enhancement of 94 at 5 T and 80 K using trityl radical as the polarizing agent. Because the buildup rate of the solid effect increases with microwave field strength, we obtain a sensitivity gain of 128. The data suggest that higher microwave field strengths would lead to further improvements in sensitivity. In addition, the observation of microwave field dependent enhancements permits us to draw conclusions about the path that polarization takes during the DNP process. By measuring the time constant for the polarization buildup and enhancement as a function of the microwave field strength, we are able to compare models of polarization transfer, and show that the major contribution to the bulk polarization arises via direct transfer from electrons, rather than transferring first to nearby nuclei and then transferring to bulk nuclei in a slow diffusion step. In addition, the model predicts that nuclei near the electron receive polarization that can relax, decrease the electron polarization, and attenuate the DNP enhancement. The magnitude of this effect depends on the number of near nuclei participating in the polarization transfer, hence the size of the diffusion barrier, their T1, and the transfer rate. Approaches to optimizing the DNP enhancement are discussed.
INTRODUCTION
Dynamic nuclear polarization (DNP) is a method of enhancing nuclear magnetic resonance (NMR) signals by transferring the large Boltzmann polarization of unpaired electrons to the nuclear spin reservoir, thereby enhancing the NMR signal intensities by several orders of magnitude.1, 2 Since DNP greatly enhances the signal-to-noise ratio, it permits otherwise prohibitively long experiments to be performed and/or acquisition of enhanced information, both in shorter periods of time. There are many situations that can benefit greatly from the enhanced sensitivity of DNP. For instance, protein samples exhibit spectra that are intractable without multidimensional experiments. Concurrently, the multiple dimensions and the magnetization transfer steps involved in acquisition of these spectra often lead to results with low sensitivity. Thus, there are now many examples where the quality of spectra of biological samples improves dramatically with polarization enhancement.3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 Another compelling illustration of the utility of DNP involved NMR studies of surfaces where spectral acquisition required many days or weeks of signal averaging without DNP, whereas with DNP excellent results were obtained in less than an hour.14
Continuous wave (CW) DNP in insulating solids generally proceeds via one of three mechanisms, depending on the relative magnitude of the nuclear Larmor frequency (ω0I), and the homogeneous (δ) and inhomogeneous linewidths (Δ) of the electron paramagnetic resonance (EPR) spectrum. In the case ω0I ≫ δ, Δ (the EPR spectrum is narrow compared to the nuclear Larmor frequency), the solid effect (SE) (Refs. 15, 16, 17) governs the DNP process. Since the SE utilizes forbidden electron-nuclear transitions, the transition moments exhibit a dependence. Therefore, the experimentally observed SE enhancements at high field (≥5 T) and liquid-N2 temperatures (80–90 K) in contemporary DNP experiments have until recently been limited to ∼5–15,18, 19, 20, 21 although higher enhancements have been obtained at lower fields and liquid-helium temperatures.22, 23 In contrast, in the regime Δ > ω0I > δ, the three-spin cross effect (CE) becomes dominant.24, 25, 26, 27, 28, 29, 30 The CE utilizes biradicals, where two electrons are tethered together in the correct relative orientation,28, 29, 30 as polarizing agents, and to date it has proven to be the most efficient DNP mechanism for high field experiments, yielding 1H enhancements of up to 250.31, 32 The third mechanism, thermal mixing (TM), is important when the EPR spectrum is homogeneously broadened – when Δ, δ ⩾ ω0I.33, 34, 35 However, at high fields (≥5 T) the g-anisotropies of many polarizing agents are typically larger than the homogeneous contributions to the linewidth, and therefore, TM has not been an important mechanism in most contemporary magic angle spinning DNP experiments. However, at the lower temperatures (∼1.5 K) used in dissolution DNP where the EPR line behaves homogeneously, it could be dominant.36
Considerable effort has been focused on understanding the steps involved in the transfer of the large electronic polarization to nuclei. Quantum mechanical treatments were used to describe the two-spin interaction in the SE,37, 38, 39 and the three-spin interaction in the CE,30 and rate equations have been used to describe the buildup of polarization in the bulk.27, 40 More recently, simulations were used to understand interactions in small systems of spins,41, 42 and finally experiments monitoring the attenuation of electron polarization were performed to better understand the behavior of the electron spin reservoir during DNP.39, 43, 44 However, as we continue to optimize DNP experiments via modifications to samples, development of polarizing agents, instrumentation, and implementation, including pulsed-DNP techniques, it is important to understand all the steps and limiting factors active in the DNP polarization transfer.
The goal of this paper is to provide a description of the transfer of polarization from the electrons to the nuclei guided by experimental data, and to determine the role of the “diffusion barrier” in this process. Interestingly, the “diffusion barrier” has been defined in a variety of ways, and its size has been measured with both indirect and direct experiments, resulting in conflicting estimates of the barrier radius. The initial discussion of a spin-diffusion barrier was included in the pioneering work of Bloembergen45 on the effects of paramagnetic relaxation in crystals. Subsequently, Khutsishvili defined the barrier size in terms of the shift in the resonance frequency due to electron-nuclear coupling relative to the NMR linewidth.46 Blumberg proposed a similar definition, stipulating the radius as the position where the electron nuclear coupling became larger than the local dipolar field (giving a slightly larger radius than Khutsishvili).47 Goldman,48 and Schmugge and Jeffries,22 used the Blumberg definition together with relaxation data to indirectly predict barriers with radii of 16 to 17 Å. In the 1970s, Wolfe, in a series of elegant experiments using single crystals, directly measured the radius of the diffusion barrier in Yb3+/Nd3+-doped yttrium ethyl sulfate (YES) and Eu2+ doped crystals of CaF2.49, 50, 51 In particular at ∼1.7 K, the electron T1 (hereafter T1s) becomes long and it is possible to observe resonances from nuclei adjacent to the paramagnetic center as well as the large line due to the bulk resonance whose position is unshifted by the paramagnet. Saturation of the bulk resonance with a weak field subsequently saturates all of the lines in the spectrum except those from nuclei immediately adjacent to the metal center, indicating that essentially all nuclei directly communicate with the bulk. The radius of the diffusion barrier derived from these measurements is ∼5 Å which is significantly smaller than predicted by the Khutsishvili and Blumberg definitions and estimated by Goldman and Schmugge and Jefferies. Interestingly, this distance is comparable to the C· → –CH2– distance on trityl (OX063)- suggesting it may be unnecessary to consider the spin-diffusion barrier at all. Finally, we should mention that other efforts directed at measuring the size of the diffusion barrier are discussed in greater detail in the recent review article by Ramanathan.52
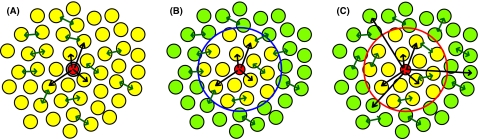
In this paper, we consider the role of partial or total quenching of spin-diffusion on the DNP process. With this goal in mind, we have focused on SE experiments, as this mechanism is the simplest of the three CW DNP mechanisms, involving only two spins in the initial polarization transfer. We have performed a series of experiments where we measured (1) the time constant for the polarization buildup, (2) the polarization enhancement, ɛ, and (3) the ω1S dependence of ɛ. In order to explain our experimental observations, we consider three models based on differential equations describing the polarization transfer from electrons to the bulk nuclei, each representing a different pathway of polarization transfer, and we attempt to fit our data to each model. The models, which are shown schematically in Figure 1, consider (A) transfer of electron polarization to all the nuclei, (B) transfer first to the nuclei neighboring the electron (inside the “diffusion barrier”) and then to the bulk and (C) finally to nuclei outside the “diffusion barrier” and subsequently to the bulk via 1H spin-diffusion. Model (A) is the null hypothesis, for which the spins inside the diffusion barrier do not consume much electron polarization, either because they are few in number, or their T1s are long enough that they do not use much polarization. In view of the experimental results from Wolfe showing a very thin barrier, it is important to consider this case. Model (B) follows the mechanism discussed by Blumberg and Khutsishvili where the barrier is passable due to coupling of the spin-diffusion process to other interactions, albeit slowly, so that spins near the electron are polarized first, and then polarization diffuses outward to the bulk nuclei. This model has been used recently by Hovav et al., where calculations are done in Liouville space with a single “core” nucleus and bulk nuclei to which polarization diffuses.42 Model (C) does not allow spin-diffusion across the barrier – in the spirit of Wolfe's experimental results where protons within 3–4 Å do not show any diffusion. However, there will be polarization transfer from the electron to nuclei within the spin-diffusion barrier, and due to T1 relaxation, these nuclei can act as a polarization sink.
Figure 1.
Three possible models for the transfer of polarization from an electron (red) to nearby nuclei (yellow) and the bulk nuclei (green). In (A), we show a model where spin-diffusion is fast among all nuclei that receive polarization. Due to the rate of this diffusion process, all nuclei maintain nearly the same polarization, and thus, one can consider only the total nuclear polarization. In (B), spin-diffusion is fast among both the nearby and bulk nuclei. However, there is a slow spin-diffusion step to transfer polarization between these two groups. In this case, we allow electron-nuclear polarization transfer only to nearby nuclei and then to the bulk via spin-diffusion. In (C), spin-diffusion is fast among the bulk nuclei. However, we do not allow any transfer of polarization between the nearby and bulk nuclei, but rather allow for a fast DNP step to the nearby nuclei, and a slow DNP step to the bulk nuclei. We note these illustrations are not representative of the shape of the spin-diffusion barrier, nor the number of nuclei inside it.
The model that best fits the experimental data – the magnitude of the enhancement, the polarization build-up time, and the ω1S dependence – is case (C). However, the protons of trityl are on the border of the 5 Å radius measured by Wolfe, suggesting that our diffusion barrier may have a larger radius.53 We also note that when the microwave field strength is not limiting, the solid effect has the potential to provide very large enhancements at high fields and can further increase the sensitivity gain per unit time by an acceleration factor, κ = T1I/TB, since the solid effect generates polarization on a time scale shorter than the nuclear T1.
The paper is organized as follows. In Sec. 2, we outline three mathematical models for solid effect polarization transfer and the rate equations that describe each. Section 3 provides the experiments details, and Sec. 4 describes the experimental results including the pulse sequence used to acquire the data, and the experimental polarization buildup times acquired as a function of the microwave field, ω1S. This is followed by a discussion of the experimental results and includes a description of the approximate size of the diffusion barrier based on data from the experiments of Wolfe49, 50, 51 and a structure of Finland trityl determined via EPR measurements and quantum chemical calculations.53
THEORY
Rate equations
To understand the transfer of electron polarization to bulk nuclear polarization, we employ a slow (seconds) time-scale, and use linear differential equations to describe this transfer. To obtain these expressions, we first consider a Liouville space calculation that leads to the differential equations given in Eq. 7 below.
We start by examining the Hamiltonian describing a single electron and many nuclei. This Hamiltonian governs interactions leading to electron-nuclear polarization transfer in the microwave rotating frame, where we will assume the microwave frequency is near the condition for positive, double quantum (ΔmS = ±1, ΔmI = ±1) DNP enhancement (ωMW = ω0S − ω0I). The terms of the Hamiltonian in Eq. 1 are the electron Zeeman, nuclear Zeeman, electron-nuclear coupling, nuclear-nuclear coupling, and microwave Hamiltonians, respectively. Δω0S is the microwave offset from the electron Larmor frequency, the are the nuclear Larmor frequencies, the Aj are the secular electron-nuclear dipole couplings, Bj and Cj are the non-secular electron-nuclear dipole couplings, is the nuclear-nuclear coupling tensor, and ω1S is the microwave field strength. Note that, because we are in the rotating frame, rapidly oscillating electron-nuclear dipole terms have been dropped,
| (1) |
Note that our Hamiltonian, H, only describes interactions between spins, and does not include interaction of the spins with the lattice. In principle, it is possible to describe the full system with
| (2) |
where Hf(t) and ρ(t) describe the full spin system and lattice. However, such an approach is prohibitively difficult, and we are only interested in the state of the spin system, so we will use a superoperator approach to include the relaxation brought about by the lattice interaction with the spin system.54 The superoperator equation is given in Eq. 3, where σ is a column vector describing the state of the spin system,
| (3) |
In Eq. 3, the superoperator H is given by , where H is the Hamiltonian from Eq. 1, E is the identity operator, and is the transpose of H. Γ is the relaxation superoperator, which describes population transfer between states of the spin system brought about by the matrix. If we consider the basis set defined by (Sz, I1z, I2z, …, S+, S−, …), then Γ will contain the relaxation rates for individual states along its diagonal, and any cross-relaxation between spins on the off-diagonal. σeq is the equilibrium population, where (such that H0σeq = 0, where ). We want to model observations made over the time scale of the nuclear relaxation, which allows us to assume that many of the quantum-mechanical states in the system have reached quasi-equilibrium. A state in quasi-equilibrium evolves rapidly compared to the time scale of observation (up to ∼100 ms in our case). This causes the state to react relatively quickly to changes in other states that are not in quasi-equilibrium. Although the state in quasi-equilibrium may change on the time scale of the observation, it is still reasonable to use the following approximation for that state, which we denote by σj, allowing for a quasi-steady-state solution of the value of the state σj in terms of the other states,
| (4) |
We will assume quasi-equilibrium for all states except the polarization states (Sz, I1z, I2z, …). A similar assumption was made by Hovav et al. when computing the evolution of polarization.41 In particular, they assume a quasi-equilibrium of the coherences connecting eigenstates of the static Hamiltonian to accelerate their computations. For our arguments, we do not go into the eigenframe, since this was only necessary for the method of computation. We also go one step further, assuming quasi-equilibrium for states without a transverse component, which we will refer to as spin-order states (I1zI2z, for example). One may note that the results in Hovav et al. do not show any oscillations that would result from a coherence not in quasi-equilibrium, suggesting this approach is reasonable.41
For states involving a coherence (Sx, I1x, …), the assumption of quasi-equilibrium is clearly reasonable since the lifetime is on the order of 1 μs for the electron, and is on the order of 1 ms for a nucleus. Also, we may do this for states including a factor of Sz (SzI1z, SzI2x, …), since the electron T1 is on the order of 1 ms (although we will not initially make this assumption for the electron polarization itself). This leaves the states describing nuclear spin-order (I1zI2z, for example). These spin-orders represent the buildup of polarization on one nucleus that is dependent on the state of another. We do expect some of this behavior, because the state of one nucleus will change the offset of the DNP condition on another. However, this effect is small, and therefore, the spin-orders should also remain small. Nuclear spins that are distant from the electron should have relatively uniform polarization due to rapid spin-diffusion, which will suppress spin-order. Spins near to the electron will have less uniform polarization, although their T1s will be shorter so that the lifetime of spin-order adjacent to the electron will be reduced. Thus, it should be a reasonable approximation to include spin-order in the quasi-equilibrium assumption.
Under the quasi-equilibrium assumption, we set derivatives of all states to zero, except the polarization states (Sz, I1z, I2z, …). We group the states in quasi-equilibrium into two column vectors: σQ contains the states in quasi-equilibrium whose derivatives are zero, and σP contains the polarization states. As such, we can rewrite Eq. 3 with the quasi-equilibrium assumption(), and divide the superoperator matrices H and Γ into sub-matrices HPP, HQP, HQQ, ΓPP, ΓQP, and ΓQQ,
| (5) |
We will assume that we can omit all cross-relaxation; thus, we can eliminate the two matrices (ΓQP) that couple the polarization states to the states in quasi-equilibrium. It is also possible to eliminate HPP from Eq. 5, which describes coherent transitions between polarization states, because there are no terms in the Hamiltonian driving transitions directly between these states. This results in Eq. 6, for which we discuss the remaining terms,
| (6) |
Omission of cross-relaxation implies that ΓPP and ΓQQ are diagonal matrices that contain T1 relaxation rates of all the spins and relaxation rates of all the states in quasi-equilibrium, respectively. The products −ΓPPσP and ΓPPσP, eq lead to T1 loss and recovery towards thermal equilibrium, respectively. Although their magnitudes are much smaller, −ΓQQσQ and ΓQQσQ, eq lead to loss and recovery towards thermal equilibrium of non-polarization states, respectively.
The matrix HQP contains terms that connect the polarization states to the states in quasi-equilibrium, namely, the non-secular electron-nuclear dipole couplings (HIS excluding zz terms), the non-secular parts of the nuclear-nuclear dipolar coupling (HII excluding zz terms), and the microwave Hamiltonian (HM).
All terms in the Hamiltonian appear in the matrix HQQ. In the particular basis set we are using, the Zeeman terms (HS and HI) will appear on the diagonal of HQQ. The diagonal element of HQQ corresponding to a particular state will give the frequency at which a particular state oscillates from real to imaginary, which we will refer to as the phase oscillation of that state. An important point: states with a slow phase oscillation are likely to play a major role in the DNP and spin-diffusion processes. When there is transfer to a state with slow phase-oscillation, that state does not rapidly invert its sign and invert the transfer, and hence becomes populated (note that population transfer can occur between two or more rapidly oscillating states if there is a match of the frequencies, but in our case we match to the polarization states which are not oscillating). Of course, high-order states that are less likely to be accessed will not play a major role, even if their phase-oscillation is slow.
This is a simplification of the resonance condition, since many additional states may be involved in the resonance, complicating the situation. The electron-nuclear and nuclear-nuclear dipole couplings (HIS and HII) will connect the states in HQQ, and as a result, resonance conditions will be a complex function of many of the couplings. HM will also connect the states in HQQ, although because the microwave is far off-resonant, its effects will be less important.
We now rearrange Eq. 6 to produce Eq. 7 which shows that the polarization states are linearly coupled under the quasi-equilibrium assumption, and discuss several processes that will occur during DNP as described by Eq. 7. For each process, we will give a differential equation that shows how the process will manifest itself in our model,
| (7) |
Relaxation
The matrix ΓPP is diagonal and contains the longitudinal relaxation rates of all spins in the system. With some rearranging of Eq. 7, we see the term ΓPP(σP, eq − σP) that is responsible for all electron and nuclear T1 loss and recovery. Relaxation loss of coherences occurs via the matrix ΓQQ. Additionally, although small, there is some population of the states in quasi-equilibrium, which contributes to polarizations of the spins via the term . Without this term, the loss due to some conversion of polarization to coherence would cause calculated polarizations to fall short of the thermal equilibrium. Although important for exact Liouville space calculations, this term only makes small contributions here and will not be explicitly included in our treatment. Therefore, the effects of T1 relaxation will appear in our model as
| (8) |
Spin-diffusion
The non-secular terms in the nuclear-nuclear dipolar Hamiltonian will generate double- and zero-quantum coherences between nuclei. This generation of the coherences occurs via the matrix HQP, but once generated are governed by the matrix QQ + ΓQQ. The diagonal elements of HQQ, which result from HI, determine that double-quantum coherences of spins j and k () oscillate at a frequency , so they will not become populated, whereas the zero-quantum () are nearly static and, thus, can be populated. Once the zero-quantum coherence is generated, polarization loss on nucleus j and polarization gain on nucleus k will be proportional to the population of the coherence, as is given by the matrix HQP. This inverse proportionality results in conservation of polarization during spin-diffusion.
Transfer to many other states will affect the population of the coherence. This is how the spin-diffusion barrier manifests itself in this picture. The secular coupling (AjSzIjz + AkSzIkz), appearing in the matrix HQQ, will transfer the zero-quantum coherence, , to with a rate proportional to Aj − Ak, where the net oscillation frequency is either higher or lower depending on the state of the electron. As a result, it will be more difficult to transfer polarization into this coherence and, therefore, inhibit spin-diffusion leading to the spin-diffusion barrier. In fact, without relaxation of the states involved, spin-diffusion would be completely quenched, but non-zero relaxation rates of and in ΓQQ give a finite rate of spin-diffusion. Note that nuclear dipole couplings will also have the same offsetting effect, although to a much smaller extent.
It is interesting to note that if the Sz state of the electron either has a short lifetime or is rapidly modulated by the microwave field (near on-resonant radiation), then it will be difficult to populate . This will help accelerate spin-diffusion. The former case is described by Horvitz.55 The latter case is electron-nuclear decoupling.22, 54, 56 We note that our experiments are much too far off-resonant for electron-nuclear decoupling to be significant. Therefore, Eq. 9 gives the rate of spin-diffusion in our model, in a form that conserves polarization, and note that does not change significantly with microwaves on or off,
| (9) |
Off-resonant electron saturation
The microwave Hamiltonian (HM) generates electron coherence (i(S+ − S−)) via the matrix HQP. Once there, terms in HQQ resulting from the electron-Zeeman (HS) and electron-nuclear couplings (HIS) will govern the electron coherence's further evolution. The Zeeman (Δω0SSz) and secular couplings (AjSzIjz) will combine to give an ensemble of oscillation frequencies of the electron. For the solid effect, this oscillation is fast, so the electron coherence will be rapidly returned to electron polarization via HM in HQP. However, there will be a small average population of the coherence, and this will be subjected to electron T2 relaxation, resulting in partial saturation of the electron. We note that aside from transferring from i(S+ − S−) to various i(S+ − S−)Ijz states (leading to offsets on the oscillation frequency), transfer out of the electron coherence is slow compared to equilibration of the electron coherence with the electron polarization. The result is that off-resonant saturation of the electron is largely decoupled from other processes. As such, we may then use a single loss term to describe the off-resonant saturation of the electron, as shown in Eq. 10. Note that k0 will vary with the oscillation frequency of the electron; however, for a relatively narrow EPR resonance, the variation in k0 will be small enough that it can be approximated with a single value,
| (10) |
Solid effect DNP
The initial step of the solid effect matches that of the off-resonant microwave irradiation, with a transfer of electron polarization to electron coherence via the HQP matrix. However, in this case the non-secular electron-nuclear dipole coupling () in the HQQ matrix drives the electron coherence to electron-nuclear zero- and double-quantum coherences. Assuming the double-quantum DNP condition is satisfied (ωMW ≈ ω0S − ω0I), the double quantum coherence () has a phase oscillation near zero, and therefore, this state becomes populated. The microwave field ((ω1S/2)(S+ + S−)) then converts this to , and finally the non-secular electron-nuclear dipole coupling () in the HQP matrix generates nuclear polarization. Of course, as with the other processes, this will be offset by secular couplings to other spins.
We should note that the solid effect does not generally conserve polarization as spin-diffusion does. First, we already noted there is off-resonant saturation of the electron. Second, loss of nuclear polarization can occur when transferred to . This effect will occur without an applied microwave field, and as a result, this will manifest itself in the observed T1I so we do not need to further account for it. Therefore, if we account for off-resonant saturation of the electron, we can then also consider the solid effect to be polarization conserving, and can represent the solid effect process in our model as
| (11) |
Higher order processes
One should note that under DNP conditions, the matrix HQQ is not block-diagonal, meaning that every spin polarization is connected to every other spin polarization, although in many cases very weakly. This results from transfers with more steps inside the HQQ matrix, which can lead to interesting results. Hovav et al. have recently shown an example of this with a chain of coupled spins.42 We will describe polarization transfer between spins via coupled differential equations. However, one should note that although our formulas suggest polarization transfers between spin pairs, this does not mean additional spins are not involved in those transfers, and the rate constants driving polarization between spin-pairs may be larger or smaller due to these effects.
Rate equations
We can now write rate equations describing the polarization transfer, as shown in Eq. 12, and discuss why this formula is reasonable,
| (12) |
In Eq. 12, PS represents the electron polarization, and the represent the nuclear polarizations. T1S and give the longitudinal relaxation. describes nuclear spin-diffusion, which in this form is polarization conserving (). Off-resonant saturation of the electron is given by −k0PS. Finally, the solid effect is given by , which is also treated as polarization conserving, since we have already accounted for off-resonant electron saturation.
We now examine Eq. 12 in limiting situations to calculate enhancements and time constants for the polarization transfer.
Implications of the rate equations
There are several unknown parameters in Eq. 12, including the rate constants of polarization transfer and spin-lattice relaxation. The polarization transfer rate constants are for DNP driven polarization transfer from the electron to the jth nucleus () and spin-diffusion mediated transfer from the jth to the kth nucleus (). The spin-lattice relaxation rate constants are for the ith nucleus and 1/T1S for the electron. Finally, the rate constant for partial saturation of the electron due to the off-resonant microwave field is k0. In the absence of simplifying assumptions, these equations are not particularly useful. We, therefore, consider the nuclear polarization adjacent to the electron, and the average nuclear polarization of bulk nuclei. The nuclei in the immediate vicinity of the electron are few in number; in fact, for Finland trityl, 1H ENDOR performed by Bowman et al. showed the closest approach of a solvent proton to be 4.8 Å from the electron,53 and on the border of the ∼5 Å diffusion barrier observed by Wolfe. One may consider where the electron-nuclear dipolar coupling and nuclear-nuclear dipole coupling become similar in magnitude; however, if one considers protons ∼3 Å apart, this occurs at ∼25 Å away from the electron. As a result, almost all nuclei in a sample with 40 mM radical concentration would fall inside this boundary. Clearly, the diffusion barrier must fall between these limits, but for the moment we will not make assumptions about the distance. We will, however, assume some nuclei are within the barrier. For simplicity, we also assume these near neighbor protons (using the parlance of Wolfe et al.) within the barrier are equal in polarization, and describe them with a single polarization term, , where (n) refers to the nearby nuclei; their DNP and spin-lattice relaxation rates are and , respectively. Note we have dropped the superscript j because we are considering the near neighbor nuclei as equivalent.
As one moves away from the electron to the more distant bulk nuclei, we encounter a polarization gradient, resulting from a finite rate of spin-diffusion. This gradient will attenuate the DNP rate because transfer from electrons will be inhibited by the higher nuclear polarization near the electron. However, in many cases it is not difficult to account for this polarization gradient. We will argue in a forthcoming paper that it is not usually necessary to explicitly include spin-diffusion. This is a result of the fact that when spin-diffusion is sufficiently rapid, the polarization gradient (but not the average polarization) equilibrates quickly relative to the total DNP buildup time, and the ratio of nuclear polarization near the electron to the average nuclear polarization remains approximately constant throughout most of the DNP buildup processes. One may then use an effective rate constant, , which is some fraction of the average DNP rate constant, and accounts for the attenuated rate of DNP. This constant gives the rate of polarization transfer when multiplied by the difference of the electron polarization and the spatially averaged bulk nuclear polarization, allowing us to forgo explicit inclusion of the polarization gradient in our models. It is safe to use these assumptions if the initial DNP polarization transfer is rate limiting and, therefore, has a strong influence on the DNP enhancement, as one would see from a dependence of enhancement on microwave power. Similar arguments can be used to describe the transfer of polarization from nearby nuclei to bulk nuclei, the effective rate given here as kSD, where SD refers to the spin-diffusion process between the nearby and bulk nuclei (this is different from because this rate constant refers to a single nuclear pair, whereas kSD refers to the net diffusion between nearby and bulk nuclei).
We will use the effective rate constants, kSD and (and will see in our experimental results that this is justified by a strong power dependence). We also introduce , , and NS which are the number of bulk and nearby nuclei in the sample that are being treated equivalently, and the number of electrons in the sample, respectively. Using these assumptions, Eq. 12 can be rewritten as
| (13) |
It is the case that off-resonant saturation in our experiments is not negligible, with k0 being as large as 0.31 ms−1, which competes with 1/T1S of 0.71 ms−1. k0 can be calculated via the Bloch equations57 for off-resonant irradiation as shown in Eq. 14, if the field strength and T1S and T2S are known,
| (14) |
It is then possible to eliminate k0 from the equations, and maintain the form of Eq. 13 via the definitions in Eq. 15,
| (15) |
One should note that this causes the amount of polarization available for DNP to decrease, if k0 is on the order of , since in all cases.
Here, we have separated the rate equations for the bulk and near neighbor nuclear polarizations. Knowing the mechanism via which polarization transfers from electrons to bulk nuclei is crucial in order to understand the primary processes of DNP. Therefore, three cases of polarization transfer are tested here and illustrated in Figure 1.
Case (A): As noted above, the experimental evidence from Wolfe's experiments suggests that the spin-diffusion barrier is much thinner than is commonly assumed, and therefore, it is important to consider the limiting case where it vanishes. Thus, in case (A), we examine the possibility of ignoring nearby nuclei, or equivalently treating them as part of the bulk, and transferring polarization directly to the bulk. If nuclei adjacent to the electron are omitted from consideration, then Eq. 13 simplifies to Eq. 16, which is commonly found in the literature.27, 58, 59, 60 Here, we have dropped the superscript (b) from kDNP and T1I, since we are no longer differentiating between bulk and near neighbor nuclei,
| (16) |
Assuming that the electron rapidly reaches quasi-equilibrium (dPS/dt = 0) leads to Eq. 17,
| (17) |
Here, we introduce TB, which is the time constant for the appearance of polarization due to microwave irradiation, and , which is the polarization obtained on the nuclei in an infinitely long DNP experiment. Experimentally measuring T1I and TB then allows one to calculate the expected enhancement in this model, as given in Eq. 18,
| (18) |
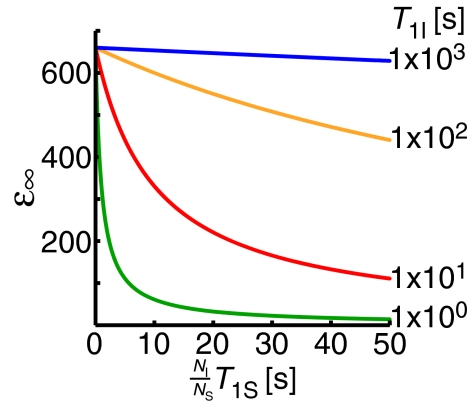
Under a specific set of experimental conditions determined by the temperature and sample characteristics, there is an upper bound on the enhancement that is less than |γS/γI|. It is a function of the number of nuclei per electron (NI/NS), and the electron and nuclear spin-lattice relaxation times (T1S, T1I). In Figure 2, we plot ɛ∞ calculated when (NI/NS)kDNPT1S ≫ 1 and k0 ≈ 0. We see that increasing T1I increases the maximum possible enhancement as does increasing the electron concentration, whereas increasing T1S decreases enhancement. Although these parameters can be difficult to vary independently, they may be optimized in a sample by changing the electron and proton concentrations, or by varying the temperature or the paramagnetic center to alter T1S.
Figure 2.
Maximum solid effect DNP enhancement, ɛ∞ as a function of the product (NI/NS)T1S at different values of the nuclear spin lattice relaxation time T1I. Note that as the nuclear T1I increases, the maximum DNP enhancement also increases.
Case (B): In case (B), we examine a two-step model in which the major path of polarization to the bulk is through the nearby nuclei adjacent to the electron spin via a slow spin-diffusion step. By requiring polarization to proceed initially from the electron to the nearby nuclei, and then to the bulk, we obtain Eq. 19, where we have dropped the superscripts on kDNP since we only transfer to nearby nuclei,
| (19) |
One may again assume a fast quasi-equilibrium of the electron with the nearby nuclei, but it is not clear that quasi-equilibrium between the nearby and bulk nuclei is reasonable. Instead, we assume that the derivatives of the nearby and bulk nuclear polarization have a proportionality, α, and utilize this to solve for the buildup time (see Appendix for derivation),
| (20) |
Also, we may calculate the enhancement given in Eq. 21,
| (21) |
The constants C and D are calculated, along with intermediate constants A and B, and are given in Eq. 22,
| (22) |
In this case, we must also calculate the observed nuclear longitudinal relaxation rate, , because it will be different from . This is because represents the bulk spin-lattice relaxation, but does not include relaxation enhancement that results from spin-diffusion to paramagnetically relaxed nuclei adjacent to the electron,
| (23) |
Case (C): In case (C), we consider the buildup of nuclear polarization if some electron polarization transfers to nearby nuclei (which act as a polarization sink), and some transfers directly to more distant bulk nuclei without being transferred to the nearby nuclei first. In this case, we assume that polarization transfer from the nearby nuclei to the bulk via spin-diffusion is ineffective, a situation that may be created both by fast spin-lattice relaxation of nearby nuclei and by the spin-diffusion barrier,45, 47, 48, 49, 50, 51, 61, 62, 63, 64
| (24) |
The nearby nuclei and electrons should both reach quasi-equilibrium, and therefore, we may set both of their derivatives to zero. However, for a clearer understanding of this process, we start by simply setting . Writing as a function of PS then allows us to rearrange dPS/dt as shown in Eq. 25,
| (25) |
Defining a new and allows us to simplify the equations
| (26) |
In this form, we see that the transfer to the nearby nuclei simply depletes the overall amount of polarization that is available from the electron, and also increases the effective electron relaxation rate. One may then evaluate the differential equations in Eq. 26 in the same manner as was done for Eq. 16, and obtain the buildup time and enhancement in Eq. 27,
| (27) |
EXPERIMENTAL
The power-dependence experiment seen in Figure 6 was performed with a 30 mW microwave source operating at 139.5 GHz. All other experiments were recorded using a 120 mW source operating at 140.0 GHz. A coiled TE011 resonator (Q ∼ 1000) was used to enhance the microwave field strengths to obtain electron nutation frequencies of up to 3.5 MHz, and to also act as a solenoid NMR coil.65 Electron nutation frequencies were determined using a two-pulse echo where the second pulse was set to approximately the length of a π-pulse, and the first pulse was incremented. A value of T1S = 1.43 ms was measured for trityl radical using a saturation recovery experiment, with a 3 ms saturation pulse and detected with a Hahn echo. T2S = 890 ns was measured by incrementing the delay in a Hahn echo. This was performed at several pulse lengths and powers, and the reported T2S was extrapolated to infinite pulse length, thus removing dephasing effects from electron-electron couplings. A double-balanced 1H, 13C RF circuit was used for RF irradiation and detection. Balancing of the circuit has greatly decreased arcing between the iris of the microwave resonator and the waveguide. 40 mM OX063 trityl (a gift from K. Golman and J.-H. Ardenkjær-Larsen of Nycomed Innovation AB, now GE Healthcare, Malmö, Sweden) was used as a polarizing agent, being dissolved in a 60:25:15 (by volume) 13C3-glycerol:D2O:H2O solution for the experiments in Figure 6, and dissolved in a 60:40 (by volume) 13C3-glycerol:D2O solution for all other experiments. All experiments were performed at 80 K. The magnetic field was set to a position corresponding to the positive solid effect matching condition, ωMW = ω0S − ω0I, for 1H polarization. Experiments were performed by first applying a saturating train of pulses on both the 1H and 13C channels, followed by microwave irradiation for some period, and finally 1H polarization was transferred to 13C via cross-polarization (CP) (Refs. 66 and 67) and observed via echo-detection.68 For nuclear T1 measurements, a delay was placed between the microwave irradiation period and the CP period, and the polarization decay was measured rather than the buildup. Because our spectrometer can perform both the required NMR and EPR measurements, all nutation frequencies, T1S and T2S, and DNP buildups and enhancements were measured on the same sample, and the sample was not removed between these measurements. The exception to this statement is the power dependence illustrated in Figure 6, which was recorded earlier.
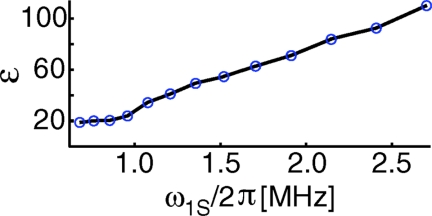
Figure 6.
Microwave field strength dependence of the solid effect DNP enhancement, ɛ, after 10 s (relative to off-signal acquired with 10 s recycle delay).
RESULTS AND DISCUSSION
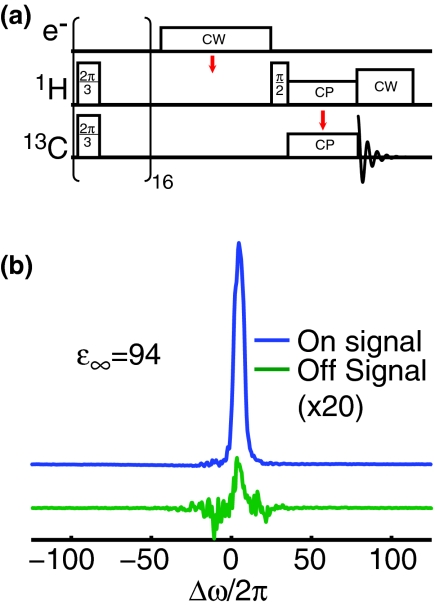
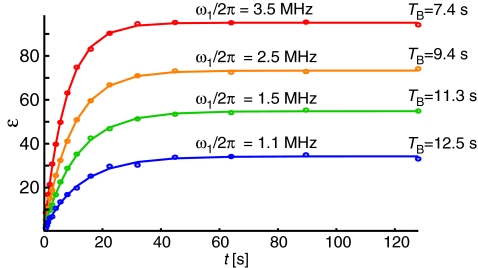
Figure 3 shows an enhancement of 94 obtained using the full microwave strength (ω1S/2π = 3.5 MHz). We recorded the on-signal with a 10 s recycle delay (RD) and the off-signal with an 18 s recycle delay, and scaled the peak amplitudes to give the relative intensity that would be obtained for an infinite recycle delay on both on- and off-signal, where the scaling factor is given by (1 − exp (tRD/TB))−1 where tRD is the recycle delay, and TB the characteristic buildup time. When the buildup time and T1 are different, as seen in Figures 45, a better measure of the improvement in signal-to-noise ratio is sensitivity (S/N*t−1/2) rather than enhancement, which in this case is a factor of 128. (One may take more factors into account when calculating improvements from DNP, such as dilution of the sample and bleaching due to the electron spin, as done recently by Jannin et al.69) To our knowledge, this is the best gain in sensitivity reported for contemporary DNP experiments using the solid effect with 1H enhancement at high fields (5 T). Additionally, we see in Figure 6 that as we increase the microwave field strength, we do not yet observe evidence of saturation of the solid effect.
Figure 3.
(a) Pulse sequence used for acquisition of DNP enhanced signals. Following saturation of the 1H and 13C magnetization is a long CW microwave pulse that transfers electron polarization to 1H that is subsequently transferred to 13C for observation. (b) Comparison of enhanced 13C signal and the off-signal, recorded with recycle delays of 10 s and 18 s, respectively. We scale both spectra to the amplitude that would be obtained with an infinitely long recycle delay, based on buildup and T1 data.
Figure 4.
Microwave field dependence of the DNP enhancement and buildup times. The length of polarization time is varied to observe the magnitude of the NMR signal, allowing one to determine the DNP buildup time, TB. Measurement is taken at four power levels.
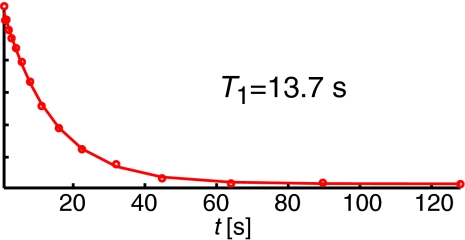
Figure 5.
Nuclear T1 () measured by first polarizing 1H via DNP for 10 s, then turning off the microwaves for some period of time and observing the magnetization decay with a rate constant of .
We attribute our high enhancement to the use of a TE011 microwave cavity, which is a high-Q (∼1000), fundamental mode structure and, thus, gives a large gain in the microwave field strength. This suggests that if microwave field strength is not a limiting factor, then DNP with a narrow line radical via the solid effect could perform very well at high fields, since it can give both large enhancements and decrease the recycle delay. In contrast, in most cases high microwave fields have not been shown to decrease the buildup times when the cross effect is the dominant DNP mechanism (a recent exception can be found in Feintuch et al.21).
To gain more information about the DNP processes from these experiments, we test each of the models discussed in Sec. 2 and determine whether they fit the observed buildup curves and enhancements. We first note that the strong power dependence seen in Figure 6 shows that spin-diffusion is sufficiently fast to use effective rate constants to account for polarization gradients due to finite rates of spin-diffusion. Thus, the three models that we proposed that use this assumption are valid. Crucial to testing these models are the buildup curves shown in Figure 4, where we have incremented polarization times at increasing microwave field strengths to observe the DNP buildup time, TB, and enhancements. In Figure 5, we show the data where we have polarized the sample for 10 s, and then incremented a delay in order to observe T1 relaxation ().
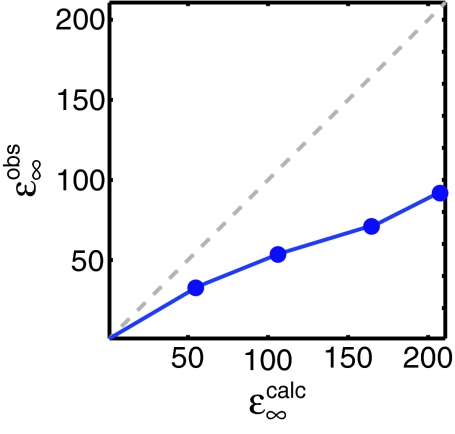
Case (A): In this case, we have neglected any important role of nearby nuclei. If this model is correct, then we may calculate the value of ɛ∞ from TB and using Eq. 18. Taking the values for TB in Figure 4, from Figure 5, and from Table 1, we calculate the value of ɛ∞ for each field strength and show this in Figure 7 according to model (A), using Eq. 18.
Table 1.
Using the Bloch equations and T1S = 1.43 ms, T2S = 890 ns, (see Sec. 3 for details) and , we calculate the electron polarization available for DNP, as defined in Eq. 4. Note that Δω0S = ω0I.
| 3.5 | 459 |
| 2.5 | 539 |
| 1.5 | 611 |
| 1.1 | 632 |
Figure 7.
Calculated and experimentally observed solid effect DNP enhancements for the observed buildup times shown in Figure 4 and using Eq. 7. Note that the experimentally observed enhancements are significantly lower than expected theoretically indicating that the model discussed as Case (A) is not supported by the experimental data.
One can see that for each microwave field strength, the observed enhancement is lower than the enhancement predicted by case (A). This indicates that case (A) is not sufficient to describe the polarization transfer, and some additional process must be attenuating the total enhancement. Fits to cases (B) and (C) explore whether this attenuation is due to an inefficient transfer of polarization to the bulk via a spin-diffusion step, or due to depletion of the electron polarization by a transfer to isolated nearby nuclei, respectively.
Case (B): We next consider the two-step model, for which we have an initial DNP step to nearby nuclei, and then a slow spin-diffusion step to bulk nuclei. In this case, we are confronted with many parameters, and more complicated formulas, so we refer to computer simulations to find a solution. We utilize the equations found in Sec. 2 and Appendixes A, B to quickly calculate accurate and TB rather than solving the differential equations numerically. One may note that there are several unknown parameters, including kDNP, kSD, , , T1S, , and , whereas we have three known parameters, TB, , and ɛ∞. Therefore, we must sample the space to obtain the range of acceptable solutions. We fix T1S at 1.4 ms because and T1S always appear together in our equations; thus, it is redundant to vary both parameters. We take TB, , and ɛ∞ for full microwave field strength (3.5 MHz) and use a simplex routine to fit calculated values to these experimental measurements, using the fit function given in Eq. 28. We weight the enhancements, observed T1I and TB equally, and also apply a penalty if the simulation uses a ratio of bulk nuclei to electrons that is less than 1500 (for our sample, there are ∼1640 protons per electron),
| (28) |
We performed 1000 simplex fits using the MATLAB (Ref. 70) fminsearch function, with random starting positions between the upper and lower starting bounds specified in Table 2 (the simplex fit does not prevent solutions from being outside the bounds). The error, σ, is evaluated for the three parameters and minimized. Of the 1000 simplex fits, 191 fits have an rms <0.5. We tabulate the range of each of the six parameters used for these 191 fits in Table 2, and also show one example fit. We see that it is possible to fit the experimental data to this model; however, we find for all solutions that which is physically unreasonable (Table 2 two right columns), as proximity to the electron causes paramagnetic relaxation and results in a short T1I.45 Thus, the experimental data are not explained satisfactorily with reasonable parameters by this model, and therefore, we discard it.
Table 2.
Parameters used to simulate the experimental data to Case (B) model, and some of the results. The simulation was performed only for the full microwave field strength (3.5 MHz) with the measured parameters TB = 7.4 s, ɛ∞ = 94, and .
| Lower starting bound | 1 | 1 | 0 | 0 | 0 | 0 |
| Upper starting bound | 1000 | 1000 | 1 | 2 | 30 | 300 |
| Max. value for fit | 4537 | 4.4 | 3.9 | 0.16 | 668.1 | 10.1 |
| Min. value for fit | 340 | 0.6 | 0.1 | 0.03 | 15.1 | 4.6 |
| Example fit | 519 | 3.0 | 1.0 | 0.03 | 45.6 | 9.3 |
Case (C): We finally consider the case for which some polarization is transferred to nearby nuclei that act as a polarization sink, and some polarization is transferred directly to the bulk nuclei. Again, not all of the parameters are experimentally determined; however, we can group the parameters from Eq. 27 as and , and calculate these directly from , TB, and ɛ∞, as shown in Eq. 29,
| (29) |
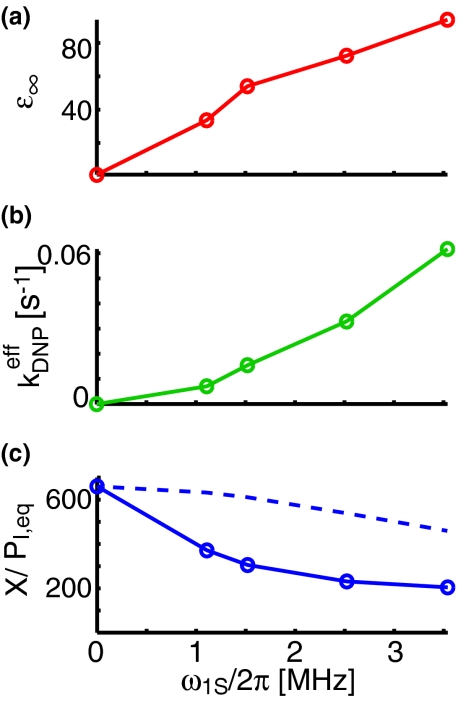
Calculated values for and are plotted in Figure 8 for each of the four microwave powers for which buildup curves were recorded, and also for the value of the parameters at zero microwave power.
Figure 8.
Fit parameters for spin-diffusion barrier model. (a) Enhancement at infinite time from the four buildup curves shown in Figure 4, and also for buildup with no microwave power. (b) Values calculated for from experiment. (c) Values calculated for (solid line) from experiment and (dashed line) from Bloch equations.
As seen in Figure 4, the enhancement increases and the buildup time decreases with an increase in the microwave field strength, ω1S. This is consistent with an increasing value of , as one would expect. Furthermore, we see that the calculation of yields a rate constant that does not increase linearly, but in fact is accelerating upwards as the microwave strength is increased. This additional gain in the magnitude of the rate constant will lead to shorter buildup times; however, we note that it is accompanied by a decreasing value of , thus the actual enhancement may be attenuated. We also calculate from the experiments, which we show in Figure 8, and see that it is decreasing as we increase the microwave field strength towards a minimum value. Again, this is what we would expect to see, as increases with the microwave field strength, where eventually the polarization transfer to nearby nuclei becomes saturated. Because all parameters calculated from the experimental data behave as expected when the microwave field strength is changed, we believe this model is presently the optimal description of the polarization transfer in the solid effect.
By comparing three different models to experimental data, we have shown evidence that the primary mechanism for enhancement of bulk nuclear polarization transfer is direct transfer of electron polarization to bulk nuclei, rather than transfer through the nearby nuclei via a slow spin-diffusion step. However, we note that this does not exclude slow diffusion from the nearby nuclei to the bulk, but does suggest that there is no major contribution from this process.
Our results have implications both on the consequence of the spin-diffusion barrier, and the distance for which it is possible to perform direct solid effect DNP transfers. We first point out that we do not expect there to be a sharp drop off in the rate of spin-diffusion; rather, the rate of diffusion varies continuously. This means that to define a spin-diffusion barrier, we must assign some cutoff for the rate. The natural choice for this would be that the diffusion rate from a particular spin to the bulk is equal to that of the spin's rate of polarization transfer to the lattice; therefore, spins in the barrier would contribute more towards polarization loss than towards polarization of the bulk. This is essentially the definition which Wolfe proposed.49 With this definition, Wolfe showed that only about 12 protons or 19F nuclei near a paramagnetic impurity were actually out of contact with the bulk via spin-diffusion in a paramagnetically doped crystal (Y(C2H5SO4)3·9H2O:Yb3+) or in CaF2, respectively.49, 50, 51 However, in the latter case, one proton at a distance of 5.2 Å was on the border of the barrier, where the transfer rates to the bulk and lattice were about the same. This is an important result, as it shows definitively that a spin-diffusion barrier exists, albeit much smaller than in many previous treatments.
The experiments of Bowman et al. show that the nearest proton to the trityl center is at least 4.8 Å away.53 It seems unlikely that between radii of 4.8 Å and 5.2 Å, there are sufficiently many protons to account for the depletion of electron polarization seen in our experiments. There are some important differences, however, that could allow the barrier to be larger in our experiments. The first difference is temperature. Wolfe actually shows that the proton found at 5.2 Å goes from being in strong contact with the bulk at 1.4 K to being in strong contact with the lattice at 4 K, suggesting the diffusion barrier is getting larger with higher temperature. This increase ceases at 4 K; however, the reason for this is that both 1/T1I and the diffusion rate constant to the bulk are linearly dependent on the relaxation rate constant of the electron, 1/T1S.49 At higher temperature, where there is significantly more motion in the system, fluctuations in the dipolar field due to that motion will contribute to nuclear spin-lattice relaxation. Near the electron, these fluctuations in the field will be stronger, but will not depend on the electron T1. As a result, the nuclear relaxation rate becomes faster. If the spin-diffusion rate does not have as large of an increase, which is possible since the rates no longer only depend on the electron T1, then the spin-diffusion barrier will expand.
The second difference is that the number of bulk spins in Wolfe's experiment was large enough, and the T1 of these spins was long enough that the polarization of the bulk could be treated as fixed. In our experiments, the bulk spins become polarized, and as a result the rate of transfer from nearby to bulk decreases. Additionally, the polarization of a nucleus under DNP conditions will be far from equilibrium, accelerating its T1 relaxation. Using the definition that the barrier occurs where the rate of diffusion to the bulk equals the spin-lattice relaxation rate implies that with a decrease in the diffusion rate and increase in T1 relaxation, the diffusion barrier will also get larger. Because of the large depletion of available polarization we observe and the differences between experiments, we expect that our barrier is larger than the barrier observed by Wolfe.
To gain insight into how many “near neighbor” nuclei there are, we consider the value of in the case that , which is shown in Eq. 30,
| (30) |
To obtain = 211, which is the case for ω1S/2π = 3.5 MHz in Figure 8c, one needs . This implies that if there are ∼10 nuclei within the barrier, then must be ∼12 ms, whereas if there are ∼100 nuclei within the barrier, then is ∼120 ms; in other words, if the is longer, more spins must be inside the diffusion barrier to account for our observations. Since it is not clear what the rate of paramagnetic relaxation is, though, it is difficult to determine the “diffusion barrier” radius and the number of nuclei within this radius with these experiments.
Our results also highlight the ability of the solid effect to transfer polarization over large distances. Afeworki and co-workers had shown that it is possible to transfer polarization over 30–60 Å distances in 15.1 MHz 13C-DNP experiments.71 Our results support this finding since our model requires direct transfer of polarization to bulk nuclei, and further demonstrate that distant transfers are also possible at much higher nuclear Larmor frequencies.
CONCLUSIONS
We demonstrate through fitting several models to experimental data that polarization is primarily transported from the electron directly to bulk nuclei. This is opposed to the polarization being transferred to nearby nuclei and then to the bulk via a slow spin-diffusion step. Also shown is that the polarization available from the electron is decreased because of the polarization transferred to nearby nuclei that is then rapidly relaxed away, which is described by . Finally, we see that it is necessary to take into account experimental conditions when considering the spin-diffusion barrier, as its effective size depends on relative rates that vary under different conditions.
Additionally, DNP via the solid-effect, using the narrow line trityl radical, has shown a gain in sensitivity of 128. Enhancements are still increasing with microwave field strength at our peak available power, suggesting that where higher field strengths available, the solid effect can be a very useful DNP mechanism because it both leads to large enhancements and further boosts sensitivity by decreasing the buildup time.
ACKNOWLEDGMENTS
This research was supported by the National Institutes of Health through Grants Nos. EB002804 and EB002026. A.B.B. was partially supported by graduate research fellowships from the National Science Foundation. B.C. was supported in part by the Deutsche Forschungsgemeinschaft (DFG research fellowship CO802/1-1). We thank Loren Andreas for valuable discussions.
APPENDIX A: SOLVING ONE-STEP TRANSFER EQUATIONS WITHOUT FAST EQUILIBRIUM
Here, we present a solution of a general pair of differential equations at long times without assuming a fast equilibrium. We will solve the following two equations:
| (A1) |
We begin by assuming that the first and second derivatives are proportional for Pa and Pb, and have proportionality, α, that is constant in time. We can solve for the necessary value of α for time independence by requiring the second derivatives have the same proportionality as the first derivatives – a consequence of time independence of α,
| (A2) |
One can then take the second derivatives and, using the proportionality constant of the first derivatives, solve for the value of α by satisfying the second part of Eq. A2,
| (A3) |
Setting these two results equal, we obtain the following:
| (A4) |
Given α, we may now solve for the buildup time, TB. Since we know the proportionality of the first derivatives, we can say the following:
| (A5) |
We do not offer analytic solutions to and , but note that these are not necessary to solve to determine the buildup time, TB. Plugging this equation into Eq. A1, we can obtain the buildup rate,
| (A6) |
Thus, the buildup rate is given by the coefficient of Pa,
| (A7) |
We point out that once the time derivative of α goes to zero, it forces all derivatives to have the same proportionality. Once this condition is met for one time, it will continue to be met for all times.
Now that we know how to solve a case where fast equilibrium (dPa/dt = 0) is not a valid assumption, we apply this technique to a system of three equations.
APPENDIX B: TWO-STEP DNP TRANSFER
For the two step transfer, it should be possible to approach both steps by assuming proportionality of the derivatives; however, the solutions to the proportionality constants will involve quartic equations, which do not have general solutions as do quadratic equations. As an alternative, we take the fast equilibrium solution of the electrons, and apply the assumption of proportionality of derivatives for the second (nearby to bulk nuclei) transfer step. We note that assumption of fast equilibrium of the electrons in the one-step transfer is in fact a very good solution, and we present the alternative here only as example before presenting it in the more difficult case of a two-step transfer.
To begin, we present the rate equations governing the two-step transfer,
| (B1) |
In this case, we assume the electron reaches a fast equilibrium, so that dPS/dt = 0; thus, PS(t) can be written as shown in Eq. B2,
| (B2) |
We may now substitute this into ,
| (B3) |
We now assume that where α is constant in time. If we take the second derivatives of and , and substitute , we obtain the following equations:
| (B4) |
Setting these equal, we obtain Eq. (B5),
| (B5) |
Now that we have obtained α, we can calculate the buildup rate, TB, by substituting into ,
| (B6) |
Again we can obtain the buildup time from the coefficient to ,
| (B7) |
Another important point here is that due to the spin-diffusion, the observed T1I will not be equal to . Rather, it is a function of the spin-diffusion, , and . We can obtain this easily by setting kDNP = 0 in the above formulas, causing A = 0 as well,
| (B8) |
Finally, we calculate the equilibrium nuclear polarization, which is a trivial calculation, as it only requires setting all derivatives to zero. We already have set dPS/dt = 0 in Eq. B2. Here, we show the result of setting ,
| (B9) |
Finally, we set to obtain the nuclear enhancement,
| (B10) |
Thus, we have obtained formulas for the observed buildup time, TB, the enhancement, ɛ, and the observed nuclear relaxation time, .
References
- Overhauser A. W., Phys. Rev. 92(2), 411 (1953). 10.1103/PhysRev.92.411 [DOI] [Google Scholar]
- Carver T. R. and Slichter C. P., Phys. Rev. 92(1), 212 (1953). 10.1103/PhysRev.92.212.2 [DOI] [Google Scholar]
- Hall D., Maus D., Gerfen G., Inati S., Becerra L., Dahlquist F., and Griffin R., Science 276(5314), 930 (1997). 10.1126/science.276.5314.930 [DOI] [PubMed] [Google Scholar]
- Rosay M., Weis V., Kreischer K. E., Temkin R. J., and Griffin R. G., J. Am. Chem. Soc. 124(13), 3214 (2002). 10.1021/ja0176752 [DOI] [PubMed] [Google Scholar]
- Rosay M., Zeri A., Astrof N., Opella S., Herzfeld J., and Griffin R., J. Am. Chem. Soc. 123(5), 1010 (2001). 10.1021/ja005659j [DOI] [PubMed] [Google Scholar]
- Rosay M., Lansing J., Haddad K., Bachovchin W., Herzfeld J., Temkin R., and Griffin R., J. Am. Chem. Soc. 125(45), 13626 (2003). 10.1021/ja036898k [DOI] [PubMed] [Google Scholar]
- Mak-Jurkauskas M. L., Bajaj V. S., Hornstein M. K., Belenky M., Griffin R. G., and Herzfeld J., Proc. Natl. Acad. Sci. U.S.A. 105, 883 (2008). 10.1073/pnas.0706156105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maly T., Debelouchina G. T., Bajaj V. S., Hu K.-N., Joo C.-G., Mak-Jurkauskas M. L., Sirigiri J. R., van der Wel P. C. A., Herzfeld J., Temkin R. J., and Griffin R. G., J. Chem. Phys. 128(5), 052211 (2008). 10.1063/1.2833582 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barnes A. B., De Paëpe G., van der Wel P. C. A., Hu K.-N., Joo C.-G., Bajaj V. S., Mak-Jurkauskas M. L., Sirigiri J. R., Herzfeld J., Temkin R. J., and Griffin R. G., Appl. Magn. Reson. 34(3), 237 (2008). 10.1007/s00723-008-0129-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bajaj V. S., Mak-Jurkauskas M. L., Belenky M., Herzfeld J., and Griffin R. G., Proc. Natl. Acad. Sci. U.S.A. 106(23), 9244 (2009). 10.1073/pnas.0900908106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bajaj V. S., Mak-Jurkauskas M. L., Belenky M., Herzfeld J., and Griffin R. G., J. Magn. Reson. 202, 9 (2010). 10.1016/j.jmr.2009.09.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Debelouchina G. T., Bayro M. J., van der Wel P. C. A., Caporini M. A., Barnes A. B., Rosay M., Maas W. E., and Griffin R. G., Phys. Chem. Chem. Phys. 12(22), 5911 (2010). 10.1039/c003661g [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akbey Ü., Franks W. T., Linden A., Lange S., Griffin R. G., Rossum B. J. von, and Oschkinat H., Angew. Chem., Int. Ed. 49(42), 7803 (2010). 10.1002/anie.201002044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lesage A., Lelli M., Gajan D., Caporini M. A., Vitzthum V., Mieville P., Alauzun J., Roussey A., Thieuleux C., Mehdi A., Bodenhausen G., Coperet C., and Emsley L., J. Am. Chem. Soc. 132, 15459 (2010). 10.1021/ja104771z [DOI] [PubMed] [Google Scholar]
- Jeffries C. D., Phys. Rev. 106(1), 164 (1957). 10.1103/PhysRev.106.164 [DOI] [Google Scholar]
- Jeffries C. D., Phys. Rev. 117(4), 1056 (1960). 10.1103/PhysRev.117.1056 [DOI] [Google Scholar]
- Abragam A. and Proctor W. G., C. R. Acad. Sci. 246 (1958). [Google Scholar]
- Becerra L., Gerfen G., Temkin R., Singel D., and Griffin R., Phys. Rev. Lett. 71(21), 3561 (1993). 10.1103/PhysRevLett.71.3561 [DOI] [PubMed] [Google Scholar]
- Hu K., Bajaj V., Rosay M., and Griffin R., J. Chem. Phys. 126(4), 044512 (2007). 10.1063/1.2429658 [DOI] [PubMed] [Google Scholar]
- Corzilius B., Smith A. A., Barnes A. B., Luchinat C., Bertini I., and Griffin R. G., J. Am. Chem. Soc. 133, 5648 (2011). 10.1021/ja1109002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feintuch A., Shimon D., Hovav Y., Banerjee D., Kaminker I., Lipkin Y., Zibzener K., Epel B., Vega S., and Goldfarb D., J. Magn. Reson. 209, 136 (2011). 10.1016/j.jmr.2010.12.010 [DOI] [PubMed] [Google Scholar]
- Schmugge T. J. and Jeffries C. D., Phys. Rev. 138, A1785 (1965). 10.1103/PhysRev.138.A1785 [DOI] [Google Scholar]
- de Boer W., J. Low Temp. Phys. 22(1–2), 185 (1976). 10.1007/BF00655221 [DOI] [Google Scholar]
- Kessenikh A. V., Lushchikov V. I., Manenkov A. A., and Taran Y. V., Sov. Phys. Solid State 5(2), 321 (1963). [Google Scholar]
- Kessenikh A. V., Manenkov A. A., and Pyatnitskii G. I., Sov. Phys. Solid State 6(3), 641 (1964). [Google Scholar]
- Hwang C. F., and Hill D. A., Phys. Rev. Lett. 19(18), 1011 (1967). 10.1103/PhysRevLett.19.1011 [DOI] [Google Scholar]
- Wollan D. S., Phys. Rev. B 13, 3671 (1976). 10.1103/PhysRevB.13.3671 [DOI] [Google Scholar]
- Hu K., Yu H., Swager T., and Griffin R., J. Am. Chem. Soc. 126(35), 10844 (2004). 10.1021/ja039749a [DOI] [PubMed] [Google Scholar]
- Hu K.-N., Song C., Yu H.-h., Swager T. M., and Griffin R. G., J. Chem. Phys. 128(5), 052302 (2008). 10.1063/1.2816783 [DOI] [PubMed] [Google Scholar]
- Hu K.-N., Debelouchina G. T., Smith A. A., and Griffin R. G., J. Chem. Phys. 134, 125105 (2011). 10.1063/1.3564920 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song C., Hu K.-N., Joo C.-G., Swager T. M., and Griffin R. G., J. Am. Chem. Soc. 128, 11385 (2006). 10.1021/ja061284b [DOI] [PubMed] [Google Scholar]
- Matsuki Y., Maly T., Ouari O., Karoui H., Le Moigne F., Rizzato E., Lyubenova S., Herzfeld J., Prisner T. F., Tordo P., and Griffin R. G., Angew. Chem. 48, 4996 (2009). 10.1002/anie.200805940 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duijvestijn M. J., Manenschijn A., Smidt J., and Wind R. A., J. Magn. Reson. 64, 461 (1985). [Google Scholar]
- Goldman M., Spin Temperature and Nuclear Magnetic Resonance in Solids (Clarendon, Oxford, 1970). [Google Scholar]
- Duijvestijn M. J., Wind R. A., and Smidt J., Physica B & C 138(1–2), 147 (1986). 10.1016/0378-4363(86)90503-6 [DOI] [Google Scholar]
- Jannin S., Comment A., Kurdzesau F., Konter J. A., Hautle P., Brandt B. v. d., and Klink J. J. v. d., J. Chem. Phys. 128(24), 241102 (2008). 10.1063/1.2951994 [DOI] [PubMed] [Google Scholar]
- Jeschke G. and Schweiger A., Mol. Phys. 88(2), 355 (1996). [Google Scholar]
- Wenckebach W. T., Appl. Magn. Reson. 34(3), 227 (2008). 10.1007/s00723-008-0121-9 [DOI] [Google Scholar]
- Weis V., Bennati M., Rosay M., and Griffin R. G., J. Chem. Phys. 113(16), 6795 (2000). 10.1063/1.1310599 [DOI] [Google Scholar]
- Abragam A. and Goldman M., Rep. Prog. Phys. 41(3), 395 (1978). 10.1088/0034-4885/41/3/002 [DOI] [Google Scholar]
- Hovav Y., Feintuch A., and Vega S., J. Magn. Reson. 207(2), 176 (2010). 10.1016/j.jmr.2010.10.016 [DOI] [PubMed] [Google Scholar]
- Hovav Y., Feintuch A., and Vega S., J. Chem. Phys. 134, 0745091 (2011). 10.1063/1.3526486 [DOI] [PubMed] [Google Scholar]
- Nagarajan V., Hovav Y., Feintuch A., Vega S., and Goldfarb D., J. Chem. Phys. 132, 214504 (2010). 10.1063/1.3428665 [DOI] [PubMed] [Google Scholar]
- Granwehr J. and Köckenberger W., Appl. Magn. Reson. 34(3), 355 (2008). 10.1007/s00723-008-0133-5 [DOI] [Google Scholar]
- Bloembergen N., Physica (Amsterdam) 15, 386 (1949). 10.1016/0031-8914(49)90114-7 [DOI] [Google Scholar]
- Khutsishvili G. R., Sov. Phys. JETP 15, 909 (1962). [Google Scholar]
- Blumberg W. E., Phys. Rev. 119(1), 79 (1960). 10.1103/PhysRev.119.79 [DOI] [Google Scholar]
- Goldman M., Phys. Rev. 138, A1675 (1965). 10.1103/PhysRev.138.A1675 [DOI] [Google Scholar]
- Wolfe J. P., Phys. Rev. Lett. 31(15), 907 (1973). 10.1103/PhysRevLett.31.907 [DOI] [Google Scholar]
- Wolfe J. P. and Markiewicz R. S., Phys. Rev. Lett. 30(22), 1105 (1973). 10.1103/PhysRevLett.30.1105 [DOI] [Google Scholar]
- Hansen A. D. A. and Wolfe J. P., Phys. Lett. 66A(4), 320 (1978). [Google Scholar]
- Ramanathan C., Appl. Magn. Reson. 34(3), 409 (2008). 10.1007/s00723-008-0123-7 [DOI] [Google Scholar]
- Bowman M., Mailer C., and Halpern H., J. Magn. Reson. 172(2), 254 (2005). 10.1016/j.jmr.2004.10.010 [DOI] [PubMed] [Google Scholar]
- Ernst R. R., Bodenhausen G., and Wokaun A., Principles of Nuclear Magnetic Resonance in One and Two Dimensions (Clarendon, Oxford, 1987). [Google Scholar]
- Horvitz E. P., Phys. Rev. B 3(9), 2868 (1971). 10.1103/PhysRevB.3.2868 [DOI] [Google Scholar]
- Schweiger A. and Jeschke G., Principles of Pulse Electron Paramagnetic Resonance (Oxford University Press, Oxford, UK, 2001). [Google Scholar]
- Bloch F., Phys. Rev. 70(7–8), 460 (1946). 10.1103/PhysRev.70.460 [DOI] [Google Scholar]
- Leifson O. S. and Jeffries C. D., Phys. Rev. 122(6), 1781 (1961). 10.1103/PhysRev.122.1781 [DOI] [Google Scholar]
- Jeffries C. D., Dynamic Nuclear Orientation (Interscience, New York, 1963). [Google Scholar]
- Abragam A. and Goldman M., Nuclear Magnetism: Order and Disorder (Oxford University Press, New York, 1982). [Google Scholar]
- Bloembergen N., Purcell E. M., and Pound R. V., Phys. Rev. 73(7), 679 (1948). 10.1103/PhysRev.73.679 [DOI] [Google Scholar]
- Kaplan J. I., Phys. Rev. B 3, 604 (1971). 10.1103/PhysRevB.3.604 [DOI] [Google Scholar]
- H. E.RorschachJr., Physica (Amsterdam) 30, 38 (1964). 10.1016/0031-8914(64)90200-9 [DOI] [Google Scholar]
- Gennes P. G. de, J. Phys. Chem. Solids 7(4), 345 (1958). 10.1016/0022-3697(58)90284-1 [DOI] [Google Scholar]
- Weis V., Bennati M., Rosay M., Bryant J. A., and Griffin R. G., J. Magn. Reson. 140, 293 (1999). 10.1006/jmre.1999.1841 [DOI] [PubMed] [Google Scholar]
- Hartmann S. R. and Hahn E. L., Phys. Rev. 128(5), 2042 (1962). 10.1103/PhysRev.128.2042 [DOI] [Google Scholar]
- Pines A., Gibby M. G., and Waugh J. S., J. Chem. Phys. 56(4), 1776 (1972). 10.1063/1.1677439 [DOI] [Google Scholar]
- Hahn E. L., Phys. Rev. 80, 580 (1950). 10.1103/PhysRev.80.580 [DOI] [Google Scholar]
- Vitzthum V., Borcard F., Jannin S., Morin M., Miéville P., Caporini M. A., Sienkiewicz A., Gerber-Lemaire S., and Bodenhausen G., ChemPhysChem 12, 2929 (2011). 10.1002/cphc.201100630 [DOI] [PubMed] [Google Scholar]
- MathWorks, MATLAB, MathWorks, Natick, MA, 2009.
- Afeworki M., Vega S., and Schaefer J., Macromolecules 25(16), 4100 (1992). 10.1021/ma00042a009 [DOI] [Google Scholar]