Linear Regression with an Independent Variable Subject to a Detection Limit

Abstract

Background

Linear regression with a left-censored independent variable X due to limit of detection (LOD) was recently considered by 2 groups of researchers: Richardson and Ciampi, and Schisterman and colleagues.

Methods

Both groups obtained consistent estimators for the regression slopes by replacing left-censored X with a constant, that is, the expectation of X given X below LOD E(X|X<LOD) in the former group and the sample mean of X given X above LOD in the latter.

Results

Schisterman and colleagues argued that their approach would be a better choice because the sample mean of X given X above LOD is available, whereas E(X|X<LOD) is unknown. Other substitution methods, such as replacing the left-censored values with LOD, or LOD/2, have been extensively utilized in the literature. Simulations were conducted to compare the performance under 2 scenarios in which the independent variable is normally and not normally distributed.

Conclusion

Recommendations are given based on theoretical and simulation results. These recommendations are illustrated with 1 case study.

Introduction

Statistical tools have been developed to deal with a variety of problems due to limit of detection (LOD). However, there remain few methodologic options for cases in which the independent variable is subject to an LOD. In most relevant published work the response variable, rather than the independent variables, was subject to an LOD, such as, Hughes et al.,¹ Lyles et al.,² Berk and Lachenbrunch,³ Helsel,⁴ Lubin et al.,⁵ Chu et al.,⁶ and the Tobit model.⁷

When an independent variable is subject to an LOD, substitution methods are frequently used to bypass the problem for a variety of reasons. For example, in a recent study by Moulton et al.,⁸ a regression relation between plasma viral load and CD4+ T-lymphocyte’s percentage was sought, in which the independent variable, plasma viral load, is subject to an LOD. Because the plasma viral load was not the major focus of the study, samples below 400, the LOD, were substituted by $400/\sqrt{2}$. In a separate study by Liang and colleagues,⁹ a value of half of the LOD was imputed for the unobserved viral load measurements. Some nonstandard substitution methods were examined recently. In 2003, Richardson and Ciampi¹⁰ proposed replacing an unobserved predictive variable x with E(X | X ≤ LOD), assuming x was an independent variable. If E(X | X ≤ LOD) can be correctly specified, this method leads to consistent estimates. A drawback of this method is that the estimation of E(X | X ≤ LOD) relies strongly on a parametric model (see the section entitled “The Exposure Variable X is Known to be Normally Distributed” for details). To avoid this shortcoming, Schisterman et al.¹¹ proposed replacing an unobserved predictive variable x with the sample mean of X given X above LOD, an approach that does not require a parametric model for the distribution of X.

The purpose of this work is to compare the performance of substitution methods to that of a maximum likelihood method. This paper is organized as follows. In Statistical Methods, we introduce all methods under consideration. In Simulation Studies, we compare the small-sample performance of these competing methods with a simulation study. In A Case Study, we perform an analysis of the BioCycle study, a longitudinal study linking hormones levels and oxidative stress. Some mathematical derivations are provided in Appendix A, and an SAS program implementing the maximum likelihood estimator (MLE) is given in Appendix B.

This paper is related to that published by Little,¹² in which complete case, available case analysis, conditional mean imputation (OLS), MLE, and Bayesian approaches were reviewed and compared. Many of our results concur with the underlying theory discussed in the works of Little and Rubin,¹³ and Schafer¹⁴ among others.

Statistical Methods: Linear Regression When an Independent Variable is Left Censored

Assume the relationship between the continuous outcome variable Y and the continuous independent exposure variable X takes the following linear regression form:

$$Y=\alpha +\beta X+\epsilon$$ (1)

where ε is random noise assumed to be independent of X and follows a normal distribution with mean 0 and variance σ²; α and β are the intercept and slope, respectively.

We assume X may be subject to multiple LODs. Because the LOD may vary from subject to subject, we denote LOD_i the LOD for the ith exposure X_i. When X_i is below LOD_i, the value is not observed. Let x_i be the exposure outcome from the ith individual (i =1,2,…, n). We assume x₁, …, x_m are observed, whereas x_m+1, …, x_n are below LOD_m+1, …, LOD_n respectively. The following methods have been used in the literature.

1. Unbiased estimates of α and β can be obtained by simply discarding observations with X_i ≤ LOD_i, which will be referred to as the deletion method. It provides valid inference because the missingness only depends on X variable, see Little¹² and Little and Rubin.¹³

2. Observations with X_i ≤ LOD_i are replaced by LOD_i, or LOD_i/2, or ${\mathit{LOD}}_i/\sqrt{2}$ when X_i ≤ LOD_i. These are the commonly used substitution methods.

3. Assume the LOD is a constant, LOD_i = LOD for all i. Observations with X_i ≤ LOD are replaced by $\frac{1}{m}{\sum }_{i=1}^n{x}_i(1-M_i)1_{\{x_i>\mathit{LOD}\}}$, where M₁, ···, M_n is the missing indicator, that is, M_i = 0, if x_i is observed; M_i = 1, if x_i is below the LOD. This is the Schisterman, Vexler, Whitcomb, and Liu (SVWL) method.¹¹

4. Assume the LOD is a constant, LOD_i =LOD for all i. Observations with X_i ≤ LOD are replaced by E(X|X<LOD). This is the Richardson and Ciampi (RC) method.¹⁰ However, E(X|X<LOD) needs to be estimated before this method can be used in practice.

5. Parameter inference is estimated by the maximum likelihood method based on parametric distributional assumptions.

When $X\sim N\left({\mu }_x,{\sigma }_x^2\right)$, that is, the exposure variable X is normally distributed, the log-likelihood function is the summation of the contributions from each individual and can be written as

$$logL=\sum _{i=1}^{m}log(l_{i1})+\sum _{i=m+1}^{n}log(l_{i2})$$ (2)

Where

$$l_{i1}=\frac{1}{2\pi \sigma {\sigma }_x}exp\left\{-\frac{{\epsilon }_i^2}{2{\sigma }^2}-\frac{{(x_i-{\mu }_x)}^2}{2{\sigma }_x^2}\right\},$$ (3)

$$l_{i2}=\frac{\mathrm{\Phi }\left\{Q\left[{\mathit{LOD}}_i-\mu -{\sigma }^{-2}{Q}^{-2}\beta {\epsilon }_{i\mu }\right]\right\}}{\sqrt{{\sigma }^2+{\beta }^2{\sigma }_x^2}}exp\left\{-\frac{{{\epsilon }_{i\mu }}^2}{2{\sigma }^2}\left(1-\frac{{\beta }^2}{{\sigma }^2{Q}^2}\right)\right\},$$ (4)

where ε_i = y_i − α − βx_i, ε = y_i − α − βμ_x, Φ(x) is the cumulative Gaussian distribution function and $Q=\sqrt{{\sigma }_x^{-2}+{\beta }^2{\sigma }^{-2}}$.

Appendix A shows the derivation of the likelihood function (4). Appendix B provides an SAS code implementing the MLE.

Simulation Studies

The Exposure Variable X is Known to be Normally Distributed

A set of Monte Carlo simulations was conducted to evaluate the performance of the following methods: deletion; substitution methods by replacing the censored x_i by LOD, $LD/\sqrt{2}$, or LOD/2; SWVL; RC; and MLE. We also include inferences from the data before deletion, termed full inference in the tables. The proportion of the left censoring, P, for the exposure variable, X, and the sample size, N, in each simulation trial were chosen as P = (0.4, 0.2) and N = (100, 200). In each case, y = α + βx + ε and ε ~ N (0, 1), where α =1, β =1. For each simulation condition, 1000 independent trials were generated. For each simulation trial, x was generated randomly from a normal distribution N(2, 1). The LOD was set to be 2 + Φ⁻¹ (P), such that on average P percentage of observations are below LOD= 2 + Φ ⁻¹ (P). When the random sample is less than 2 + Φ ⁻¹ (P), x is defined as left censored. For the deletion method, the linear regression model was fit based on the data with the exposure level greater than 2 + Φ ⁻¹ (P) to estimate the intercept α and the slope β. For all substitution methods and SWVL, censored values were imputed according to the definitions in the previous section. For the RC method, we first compute the marginal MLEs μ̂_x and σ̂_x based on a left-censored normal model with the log-likelihood function:

$$\text{logL}=(n-m)\times ln\mathrm{\Phi }\left(\frac{\mathit{LOD}-{\mu }_x}{{\sigma }_x}\right)-mln\left(\sqrt{2\pi }{\sigma }_x\right)-\sum _{i=1}^m\frac{{(x_i-{\mu }_x)}^2}{2{\sigma }_x^2}.$$

Then were placed the left-censored values by ${\widehat{\mu }}_x-{\widehat{\sigma }}_{x}exp\left[-\frac{{(\mathit{LOD}-{\widehat{\mu }}_x)}^2}{2{\widehat{\sigma }}_x^2}\right]/\mathrm{\Phi }\left(\frac{\mathit{LOD}-{\widehat{\mu }}_x}{{\widehat{\sigma }}_x}\right)$, the expected value of X, E(X|X ≤ LOD), given X ≤ LOD. Linear regression models were fit for the imputed data to estimate both the intercept α and the slope β. For the MLE approach, no imputation is needed. The MLE of intercept α and the slope β was obtained through maximizing the log-likelihood function in equation (2). Standard errors were computed through the inverse of the observed Fisher information matrix. Their numerical values were obtained from output of the SAS procedure NLMIXED, see Appendix 2.

Table 1 summarizes the means of estimators and standard errors, and a 95% coverage probability from the 1000 simulations. A normal reference distribution is used as the asymptotic distribution of the estimators. The results suggest that the substitution methods replacing the censored x_i with LOD, $\mathit{LOD}/\sqrt{2}$, or LOD/2 provide biased estimates; however, the performance of substitution by $\mathit{LOD}/\sqrt{2}$ or LOD/2 appears better than LOD. The deletion method provides unbiased estimation, but is inefficient because it discards information contained in the left-censored observations. As expected, the SWVL is the same as the deletion method for the slope estimation, but with a slightly overestimated standard error such that the empiric coverage probabilities are higher than the 95% confidence level. Furthermore, SWVL provides a biased estimation for the intercept. As expected, the MLE and RC provide consistent and relatively efficient estimations. We recommend that if the exposure variable X is known to be normally distributed, one use the MLE or RC methods. Note that although the RC estimator is consistent, its standard errors are typically underestimated.

Table 1.

The Finite Sample Performance of the Deletion, Substitution, and Maximum Likelihood Methods: Mean ± Standard Error (95% Coverage Probability)

	N, Pa	Full	Deletion	Sub = LODb	Sub = LOD/√2c	Sub = LOD/2d	SVWLe	MLEf	RC(g)
Intercept	30, 0.4	1.00±0.42 (.94)	1.02±1.06 (.93)	−0.11±0.74 (.67)	0.73±0.52 (.90)	1.20±0.43 (.90)	0.38±1.41 (.97)	0.98±0.52 (.93)	0.98±0.47 (.90)
	30, 0.6	1.00±0.42 (.94)	1.00±1.81 (.92)	−1.30±1.21 (.52)	0.57±0.63 (.89)	1.35±0.45 (.86)	0.04±2.51 (.98)	0.93±0.69 (.94)	0.93±0.55 (.85)
	50, 0.4	1.00±0.32 (.94)	1.00±0.79 (.94)	−0.10±0.56 (.50)	0.72±0.40 (.88)	1.20±0.33 (.89)	0.36±1.05 (.96)	0.99±0.40 (.94)	0.99±0.36 (.90)
	50, 0.6	1.00±0.32 (.94)	1.00±1.30 (.93)	−1.22±0.90 (.29)	0.56±0.48 (.84)	1.34±0.35 (.81)	0.04±1.79 (.97)	0.96±0.52 (.94)	0.96±0.41 (.85)
Slope	30, 0.4	1.00±0.19 (.94)	1.00±0.15 (.93)	1.15±0.13 (.79)	1.06±0.11 (.92)	0.99±0.10 (.92)	1.00±0.18 (.99)	1.00±0.11 (.94)	1.00±0.11 (.92)
	30, 0.6	1.00±0.19 (.94)	1.00±0.20 (.92)	1.35±0.17 (.70)	1.09±0.13 (.93)	0.93±0.11 (.91)	1.00±0.27 (.99)	1.00±0.12 (.94)	1.00±0.12 (.91)
	50, 0.4	1.00±0.14 (.94)	1.00±0.10 (.94)	1.16±0.09 (.68)	1.07±0.08 (.91)	0.99±0.07 (.92)	1.00±0.13 (.99)	1.00±0.08 (.94)	1.00±0.07 (.93)
	50, 0.6	1.00±0.14 (.94)	1.00±0.14.(94)	1.35±0.12 (.52)	1.09±0.09 (.91)	0.93±0.08 (.90)	1.00±0.19 (.99)	1.00±0.08 (.94)	1.00±0.08 (.91)
Intercept	100, 0.2	1.00 ± 0.23 (.95)	1.00 ± 0.37 (.95)	0.56 ± 0.28 (.66)	0.83 ± 0.25 (.88)	1.02 ± 0.23 (.94)	0.65 ± 0.45 (.92)	1.00 ± 0.25 (.95)	1.00 ± 0.23 (.93)
	100, 0.4	1.00 ± 0.23 (.95)	1.00 ± 0.55 (.95)	−0.08 ± 0.39 (.21)	0.72 ± 0.28 (.72)	1.20 ± 0.23 (.84)	0.36 ± 0.72 (.92)	1.00 ± 0.28 (.94)	0.99 ± 0.25 (.90)
	200, 0.2	1.00 ± 0.0.16 (0.95)	1.00 ± 0.26 (.95)	0.56 ± 0.20 (.42)	0.83 ± 0.18 (.82)	1.02 ± 0.16 (.94)	0.65 ± 0.32 (.85)	1.00 ± 0.17 (.95)	1.00 ± 0.17 (.93)
	200, 0.4	1.00 ± 0.16 (0.95)	1.00 ± 0.39 (.95)	−0.08 ± 0.28 (.03)	0.72 ± 0.20 (.71)	1.20 ± 0.16 (.76)	0.35 ± 0.51 (.81)	1.00 ± 0.20 (.95)	1.00 ± 0.18 (.91)
Slope	100, 0.2	1.00 ± 0.10 (.95)	1.00 ± 0.15 (.95)	1.15 ± 0.13 (.76)	1.06 ± 0.11 (.91)	0.99 ± 0.10 (.94)	1.00 ± 0.18 (.98)	1.00 ± 0.11 (.95)	1.00 ± 0.11 (.94)
	100, 0.4	1.00 ± 0.10 (.95)	1.00 ± 0.20 (.95)	1.35 ± 0.17 (.44)	1.09 ± 0.13 (.88)	0.93 ± 0.11 (.89)	1.00 ± 0.27 (.99)	1.00 ± 0.12 (.95)	1.00 ± 0.12 (.93)
	200, 0.2	1.00 ± 0.07 (0.95)	1.00 ± 0.10 (.95)	1.16 ± 0.09 (.58)	1.07 ± 0.08 (.87)	0.99 ± 0.07 (.94)	1.00 ± 0.13 (.98)	1.00 ± 0.08 (.95)	1.00 ± 0.07 (.94)
	200, 0.4	1.00 ± 0.07 (0.95)	1.00 ± 0.14.(95)	1.35 ± 0.12 (.15)	1.09 ± 0.09 (.81)	0.93 ± 0.08 (.85)	1.00 ± 0.19 (.99)	1.00 ± 0.08 (.95)	1.00 ± 0.08 (.93)

^aN = the sample size and P = the proportion of left censoring.

^bThe left-censored values replaced with LOD.

^cThe left-censored values replaced with LOD/√2.

^dThe left-censored values replaced with LOD/2.

^eSVWL method.¹¹

^fMLE = maximum likelihood method

^(g)RC method.¹⁰ Note: The data are generated from X ~ N (2,1),ε~ N (0,1) and Y = 1 + X + ε with left censoring at 2 + Φ⁻¹ (P). In each scenario 1000 simulations were used to summarize the means, standard errors, and 95% coverage probabilities. Full refers to inferences from the data before deletion

The Exposure Variable X is not Normally Distributed

The simulation setups are the same as described in the previous section, except X is now generated from a Gamma distribution, Gamma(4,3), and a t-distribution with 10 degrees of freedom.

Table 2 summarizes the means of estimators and standard errors, and a 95% coverage probability from the 1000 simulations. The results suggest that moderate misspecification does not greatly distort inferences from the MLE and RC approaches. Meanwhile, the substitution methods do not work well under model misspecification. The deletion and SVWL methods are not appreciably biased. It is also worth noting that if the distribution is severely misspecified, neither the MLE nor RC method is recommended. One may presume that severe misspecification could be eliminated by careful inspection of a P-P or Q-Q plot, as long as the number of observations below the LOD is relatively small. However, in cases in which the distribution cannot be evaluated, methods that rely on distributional assumptions may yield highly biased estimates.

Table 2.

The Finite Sample Performance of the Deletion, Substitution, and Maximum Likelihood Methods with Misspecifications: Mean ± Standard Error (95% Coverage Probability)

	N, Pa	Full	Deletion	Sub =LODb	Sub = LOD/√2c	Sub=LOD/2d	SVWLe	MLEf	RCg
Intercept	30, 0.4	1.00±0.18 (.93)	1.01±0.33 (.93)	0.58±0.22 (.53)	0.53±0.23 (.46)	0.49±0.24 (.42)	0.30±0.42 (.64)	1.00±0.20 (.93)	1.00±0.20 (.92)
	30, 0.6	1.00±0.18 (.93)	1.02±0.60 (.92)	0.07±0.32 (.18)	0.17±0.30 (.21)	0.24±0.28 (.24)	−0.03±0.82 (.79)	1.02±0.26 (.93)	1.02±0.22 (.85)
	50, 0.4	1.00±0.14 (.94)	1.00±0.26 (.94)	0.58±0.17 (.32)	0.53±0.18 (.26)	0.49±0.18 (.22)	0.31±0.32 (.38)	1.00±0.16 (.94)	1.00±0.15 (.92)
	50, 0.6	1.00±0.14 (.94)	1.01±0.44 (.93)	0.08±0.25 (.04)	0.18±0.23 (.06)	0.25±0.22 (.07)	−0.04±0.60 (.59)	1.03±0.20 (.93)	1.03±0.17 (.86)
Slope	30, 0.4	1.00±0.17 (.94)	0.99±0.35 (.93)	1.36±0.30 (.78)	1.39±0.31 (.77)	1.41±0.32 (.77)	0.99±0.49 (.99)	1.01±0.21 (.94)	1.01±0.20 (.92)
	30, 0.6	1.00±0.17 (.94)	0.98±0.52 (.92)	1.64±0.43 (.70)	1.59±0.41 (.71)	1.54±0.39 (.73)	0.98±0.77 (.99)	1.01±0.25 (.93)	1.01±0.24 (.89)
	50, 0.4	1.00±0.13 (.94)	0.99±0.26 (.94)	1.35±0.22 (.67)	1.37±0.23 (.65)	1.39±0.24 (.65)	0.99±0.37 (.99)	1.01±0.16 (.93)	1.00±0.15 (.92)
	50, 0.6	1.00±0.13 (.94)	0.99±0.38.(94)	1.61±0.32 (.54)	1.56±0.30 (.56)	1.52±0.29 (.58)	0.99±0.55 (.99)	0.99±0.19 (.93)	0.99±0.18 (.90)
Intercept	100, 0.2	1.00 ± 0.10 (.95)	1.00 ± 0.12 (.95)	0.85 ± 0.11 (.70)	0.78 ± 0.11 (.49)	0.73 ± 0.12 (.36)	0.61 ± 0.15 (.23)	0.99 ± 0.10 (.94)	0.99 ± 0.10 (.94)
	100, 0.4	1.00 ± 0.10 (.95)	1.00 ± 0.18 (.95)	0.58 ± 0.12 (.08)	0.53 ± 0.13 (.46)	0.50 ± 0.13 (.03)	0.30 ± 0.22 (.07)	1.00 ± 0.11 (.94)	1.00 ± 0.11 (.92)
	200, 0.2	1.00 ± 0.07 (.94)	1.00 ± 0.09 (.95)	0.85 ± 0.08 (.47)	0.78 ± 0.08 (.20)	0.73 ± 0.08 (.10)	0.61 ± 0.10 (.03)	0.99 ± 0.07 (.95)	0.99 ± 0.07 (.95)
	200, 0.4	1.00 ± 0.07 (.94)	1.00 ± 0.13 (.94)	0.58 ± 0.09 (.004)	0.53 ± 0.09 (.001)	0.50 ± 0.09 (.0005)	0.30 ± 0.16 (.001)	1.00 ± 0.08 (.95)	1.00 ± 0.08 (.93)
Slope	100, 0.2	1.00 ± 0.09 (.95)	1.00 ± 0.13 (.95)	1.17 ± 0.12 (.71)	1.21 ± 0.13 (.64)	1.22 ± 0.14 (.65)	1.00 ± 0.17 (.99)	1.01 ± 0.10 (.94)	1.01 ± 0.10 (.93)
	100, 0.4	1.00 ± 0.09 (.95)	1.00 ± 0.18 (.94)	1.34 ± 0.15 (.42)	1.36 ± 0.16 (.38)	1.38 ± 0.17 (.37)	1.00 ± 0.25 (.99)	1.01 ± 0.11 (.94)	1.01 ± 0.11 (.92)
	200, 0.2	1.00 ± 0.06 (.95)	1.00 ± 0.09 (.95)	1.16 ± 0.08 (.49)	1.20 ± 0.09 (.38)	1.22 ± 0.10 (.38)	1.00 ± 0.12 (.99)	1.01 ± 0.07 (.94)	1.01 ± 0.07 (.93)
	200, 0.4	1.00 ± 0.06.(95)	1.00 ± 0.12.(95)	1.33 ± 0.11 (.12)	1.36 ± 0.11 (.10)	1.37 ± 0.12 (.09)	1.00 ± 0.17 (.99)	1.00 ± 0.08 (.94)	1.01 ± 0.08 (.92)

Note: The data are generated from X ~ t(10), a symmetric distribution with heavier tail. ε~ N (0,1) and Y = 1 + X + ε. All other setups are the same as in Table 1.

Based on these simulation results, we make the following recommendations. If the distribution of the exposure variable X is unknown, we distinguish between 2 situations. First, if X approximately follows a normal distribution with unknown parameters, we recommend the MLE or RC method. This recommendation extends to cases when X follows a known parametric distributional assumption other than a normal distribution with the likelihood changed to reflect this alternative distributional assumption. Second, if the distribution of X cannot be appropriately approximated by a normal distribution, we suggest using the deletion method, which appears to be conservative. If we are really ignorant about the data below the LOD, then we should avoid strong distributional assumptions.

A Case Study: Association between Sex Hormone–Binding Globulin and Oxidative Stress

The BioCycle study was created in response to limited knowledge surrounding the effects of oxidative stress on female fecundity and fertility. The study takes the necessary first step to addressing this question by investigating the effects of oxidative stress on the female menstrual cycle. To do this, the longitudinal study was created with the primary goal of assessing the relationship between endogenous hormones and biomarkers of oxidative stress as well as antioxidant status during the menstrual cycle. The prospective cohort study followed 259 regularly menstruating, premenopausal women for 2 menstrual cycles. The detailed study design is described elsewhere.¹⁵

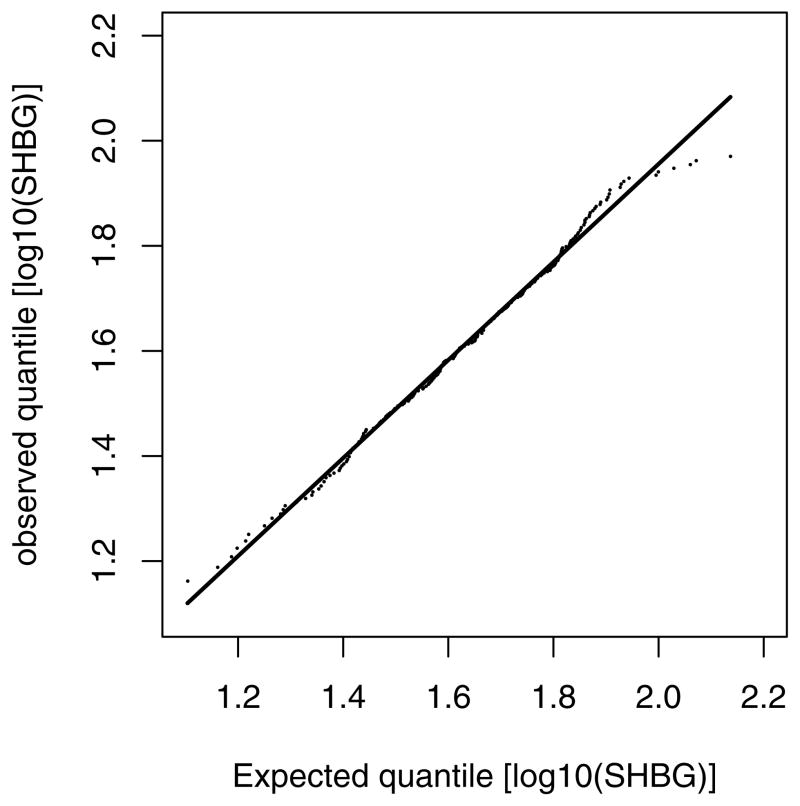
Although the study examined a number of hormones and biomarkers of oxidative stress, this example will focus on sex hormone–binding globulin (SHBG), a glycoprotein regulated by levels of free androgens, estrogens, and insulin as well as thiobarbituric acid–reactive substances, a measure of oxidative stress. There are a total of 249 women with nonmissing SHBG values and oxidative stress on their second visit on the 7th day of study. We wish to investigate the association between SHBG levels and oxidative stress by using the mode log₁₀(oxidative stress) = α + β log₁₀(SHBG) + ε. The MLE of intercept α and slope β are obtained through maximizing the log-likelihood function in (2). Among the 249 women, only 2 have SHBG below the LOD. Figure 1 shows the Q-Q plot for the log₁₀-transformed SHBG data. In the Q-Q plot, the expected quantiles are computed by ${\widehat{\mu }}_x+{\widehat{\sigma }}_x{\mathrm{\Phi }}^{-1}\left(\frac{\mathit{Rank}(x_i)-0.5}{\text{N}}\right)$ with μ̂_x = 1.63 and σ̂_x = 0.2 estimated by the maximum likelihood method for the marginal distribution of SHBG. The plot suggests the normal assumption for log(SHBG) is appropriate.

Figure 1.

The Q-Q plot of SHBG.

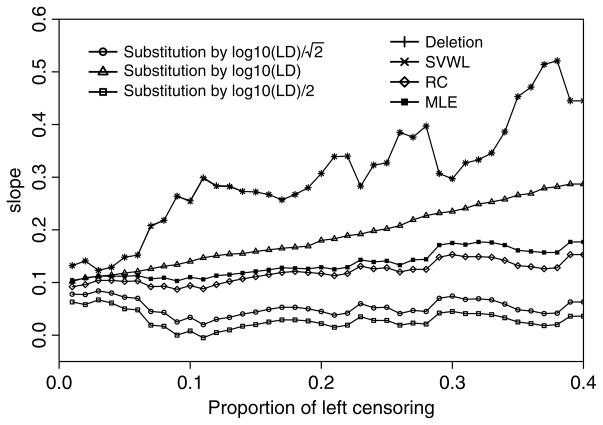
Because of the small percentage of data below the LOD (ie, 2 of 249), all estimates behave similarly. To compare these estimators further, we experimentally increased the LOD of SHBG such that up to 40% of observations were left censored. For each of p% left-censored data, we repeated the regression analysis by using the previously described 7 methods. Figure 2 presents β, the slope estimate. Similar to the first example, it suggests that the MLE, RC, and substitution method with left-censored values replaced by ${log}_{10}(\mathit{LOD})/\sqrt{2}$ provide estimates that are robust to the proportion left censored. In this example, because only 2 of 240 women had values below the LOD, the RC method can be implemented based on the actual mean below the LOD. Note, this implementation of the RC method is different from the implementation described in the section entitled “The Exposure Variable X is Known to be Normally Distributed.” Therefore, in theory, the RC method provides a consistent estimate. We observed that the MLE performed almost as well as the RC method, providing additional evidence in support of the MLE approach.

Figure 2.

The slope estimations for all 7 methods for the model log₁₀(oxidative stress) = α + β log₁₀(SHBG) + ε. Note that SVWL and deletion method result to the same estimators.

Discussion

This paper compares a number of methods for regression with an independent variable subject to LOD. Through simulations and 2 case studies, we demonstrated that the commonly used substitution methods of replacing left-censored values with LOD, $\mathit{LOD}/\sqrt{2}$ or LOD/2 provide biased estimates for the intercept and the slope. Furthermore, the 95% confidence intervals do not provide the nominal coverage for the intercept and the slope. The simple deletion method provides an unbiased estimate, but is inefficient because it does not utilize the information contained in the observations below the LOD. The SWVL method gives the same estimates of the slope as the deletion method, but with overestimated standard errors, and it is biased for the intercept.

Model (1) can be easily extended to a multiple linear regression model Y = α + βX + γ′Z + ε where a vector of covariates Z is included in the model. When Z is not subject to an LOD and the left-censored covariate X follows a normal distribution, the likelihood function remains the same if we redefine ε_i = y_i − α − βx_i − γ′Z and ε_iμ = y_i − α − βμ_x − γ′Z. We have attached an SAS program to obtain the MLE of these parameters. In general, assume, x_i, i = 1…, n are independent identically distributed random variables with a distribution function F_x and a density f_x.

Other than the MLE and the RC methods, the multiple imputation method is a promising alternative. Readers are referred to Little and Rubin¹³ and Schafer¹⁴ for this powerful tool. IVEware, the freeware program based on sequential multiple imputation, can handle covariates and can create imputations subject to the constraint that the missing value is below an LOD. Please visit http://www.isr.umich.edu/src/smp/ive/ for details.

When the parametric distribution assumption for the left-censored variable X is correct, the MLE and the RC methods provide consistent estimates. However, the RC method gives slightly underestimated standard errors; thus, the empiric coverage probabilities are slightly less than the 95% confidence level. The drawback of the MLE and RC approaches is that they rely on distributional assumptions, which may limit their use in practice. Fortunately, the MLE and the RC approaches do not appear very sensitive to violations of the distributional assumptions. To check the robustness of the results to the distributional assumption for the censored data, one would need to perform sensitivity analyses. Because the distribution of the censored data is unknown and cannot be inferred from the observed data, further exploration along these lines would provide more insight.

As 1 reviewer pointed out, it would be interesting to compare the performance of these methods when LOD is treated as a random variable and when there is an upper LOD. Further research is needed in this aspect.

Table 3.

The Finite Sample Performance of the Deletion, Substitution, and Maximum Likelihood Methods with Misspecifications: Mean ± Standard Error (95% Coverage Probability)

	N, Pa	Full	Deletion	Sub = LODb	Sub = LOD/√2c	Sub = LOD/2d	SVWLe	MLEf	RCg
Intercept	30, 0.4	1.00±0.19 (.94)	1.00±0.49 (.93)	0.67±0.28 (.77)	0.69±0.27 (.78)	0.70±0.27 (.78)	0.66±0.53 (.91)	0.94±0.21 (.93)	0.94±0.21 (.92)
	30, 0.6	1.00±0.19 (.94)	1.00±0.95 (.92)	0.29±0.48 (.67)	0.49±0.37 (.71)	0.61±0.32 (.76)	0.51±1.06 (.94)	0.90±0.26 (.94)	0.90±0.23 (.89)
	50, 0.4	1.00±0.15 (.94)	1.00±0.37 (.94)	0.68±0.22 (.67)	0.69±0.21 (.69)	0.71±0.21 (.70)	0.66±0.40 (.88)	0.94±0.17 (.93)	0.94±0.16 (.92)
	50, 0.6	1.00±0.15 (.94)	1.00±0.70 (.93)	0.30±0.36 (.51)	0.49±0.28 (.57)	0.61±0.24 (.65)	0.51±0.77 (.92)	0.90±0.20 (.93)	0.90±0.18 (.89)
Slope	30, 0.4	1.00±0.36 (.95)	1.00±0.87 (.93)	1.49±0.64 (.88)	1.47±0.62 (.88)	1.45±0.61 (.88)	1.00±0.97 (.96)	1.11±0.43 (.93)	1.11±0.44 (.93)
	30, 0.6	0.99±0.36 (.95)	0.99±1.40 (.92)	1.91±0.97 (.85)	1.68±0.80 (.86)	1.53±0.72 (.88)	0.99±1.61 (.96)	1.17±0.53 (.94)	1.16±0.53 (.93)
	50, 0.4	1.00±0.27 (.95)	1.00±0.65 (.94)	1.48±0.48 (.84)	1.45±0.47 (.83)	1.44±0.47 (.85)	1.00±0.73 (.97)	1.10±0.34 (.94)	1.10±0.34 (.93)
	50, 0.6	1.00±0.27.(95)	1.00±1.02.(93)	1.87±0.72 (.79)	1.66±0.61 (.82)	1.51±0.54 (.85)	1.00±1.15 (.97)	1.15±0.40 (.94)	1.15±0.40 (.93)
Intercept	100, 0.2	1.00 ± 0.10 (.95)	1.00 ± 0.16 (.95)	0.88 ± 0.12 (.81)	0.85 ± 0.12 (.76)	0.83 ± 0.12 (.72)	0.80 ± 0.16 (.78)	0.97 ± 0.11 (.94)	0.97 ± 0.11 (.94)
	100, 0.4	1.00 ± 0.10 (.95)	1.00 ± 0.26 (.95)	0.68 ± 0.15 (.44)	0.70 ± 0.15 (.47)	0.71 ± 0.15 (.49)	0.66 ± 0.28 (.78)	0.94 ± 0.12 (.92)	0.94 ± 0.11 (.91)
	200, 0.2	1.00 ± 0.07 (.95)	1.00 ± 0.11 (.95)	0.88 ± 0.08 (.68)	0.85 ± 0.09 (.57)	0.83 ± 0.09 (.51)	0.80 ± 0.11 (.60)	0.94 ± 0.08 (.93)	0.94 ± 0.08 (.93)
	200, 0.4	1.00 ± 0.07 (.95)	1.00 ± 0.18 (.95)	0.68 ± 0.11 (.15)	0.69 ± 0.10 (.17)	0.71 ± 0.10 (.19)	0.66 ± 0.19 (.58)	0.94 ± 0.08 (.90)	0.94 ± 0.08 (.88)
Slope	100, 0.2	1.00 ± 0.19 (.95)	1.00 ± 0.31 (.95)	1.21 ± 0.25 (.86)	1.25 ± 0.26 (.84)	1.27 ± 0.27 (.83)	1.00 ± 0.34 (.97)	1.06 ± 0.21 (.94)	1.06 ± 0.21 (.94)
	100, 0.4	1.00 ± 0.19 (.95)	0.99 ± 0.45 (.94)	1.47 ± 0.34 (.72)	1.45 ± 0.33 (.73)	1.43 ± 0.53 (.74)	0.99 ± 0.50 (.99)	1.10 ± 0.24 (.93)	1.10 ± 0.24 (.93)
	200, 0.2	1.00 ± 0.13 (.95)	1.00 ± 0.22 (.95)	1.22 ± 0.18 (.77)	1.25 ± 0.19 (.72)	1.27 ± 0.19 (.71)	1.00 ± 0.24 (.97)	1.06 ± 0.15 (.93)	1.06 ± 0.15 (.93)
	200, 0.4	1.00 ± 0.13 (.95)	1.00 ± 0.31.(95)	1.46 ± 0.24 (.50)	1.44 ± 0.23 (.52)	1.43 ± 0.23 (.54)	1.00 ± 0.35 (.97)	1.10 ± 0.17 (.92)	1.10 ± 0.17 (.91)

Note: The data are generated from X ~ Gamma(4,3), a right-skewed distribution, ε~ N (0,1) and Y = 1 + l n(X) + ε. All other setups are the same as in Table 1.

APPENDIX A

Let $Q=\sqrt{{\sigma }_x^{-2}+{\sigma }^{-2}{\beta }^2}$, ε_i = y_i − α − βx_i, and ε_iμ = y_i − α − βμ_x, Φ(x) be the cumulative Gaussian distribution function, we shall derive the likelihood function in equation (4).

$$\begin{array}{l}\prod _{i=m+1}^n{\int }_{-\infty }^{{\mathit{LOD}}_i}exp\left\{-\frac{{({\epsilon }_i)}^2}{2{\sigma }^2}-\frac{1}{2}ln\left({\sigma }^2\right)\right\}exp\left\{-\frac{{(x_i-\mu )}^2}{2{\sigma }_x^2}-\frac{1}{2}ln\left({\sigma }_x^2\right)\right\}{dx}_i\\ =\prod _{i=m+1}^n{\int }_{-\infty }^{{\mathit{LOD}}_i-\mu }exp\left\{-\frac{{\left\{y_i-\alpha -\beta (t_i+\mu )\right\}}^2}{2{\sigma }^2}-\frac{1}{2}ln\left({\sigma }^2\right)\right\}exp\left\{-\frac{t_i^2}{2{\sigma }_x^2}-\frac{1}{2}ln\left({\sigma }_x^2\right)\right\}{dt}_i\\ =\prod _{i=m+1}^n{\int }_{-\infty }^{{\mathit{LOD}}_i-\mu }exp\left\{-\frac{{\left\{y_i-\alpha -\beta \mu \right\}}^2}{2{\sigma }^2}+\frac{\beta t_i(y_i-\alpha -\beta \mu )}{{\sigma }^2}-\frac{{\beta }^2{t}_i^2}{2{\sigma }^2}-\frac{t_i^2}{2{\sigma }_x^2}-\frac{1}{2}ln\left({\sigma }^2{\sigma }_x^2\right)\right\}{dt}_i\\ =\prod _{i=m+1}^n{\int }_{-\infty }^{{\mathit{LOD}}_i-\mu }exp\left\{-\frac{{{\epsilon }_{i\mu }}^2}{2{\sigma }^2}-\left(\frac{1}{2{\sigma }_x^2}+\frac{{\beta }^2}{2{\sigma }^2}\right){\left(t_i-\frac{\beta {\epsilon }_{i\mu }}{{\sigma }^{2}Q}\right)}^2+\frac{{\beta }^2{{\epsilon }_{i\mu }}^2}{2{\sigma }^{4}Q}-\frac{1}{2}ln\left({\sigma }^2{\sigma }_x^2\right)\right\}{dt}_i\\ =\prod _{i=m+1}^{n}exp\left\{-\frac{{\{y_i-\alpha -\beta \mu \}}^2}{2{\sigma }^2}+\frac{{\beta }^2{{\epsilon }_{i\mu }}^2}{2{\sigma }^{4}Q}-\frac{1}{2}ln\left({\sigma }^2{\sigma }_x^2\right)\right\}{\int }_{-\infty }^{{\mathit{LOD}}_i-\mu }exp\left\{-\left(\frac{1}{2{\sigma }_x^2}+\frac{{\beta }^2}{2{\sigma }^2}\right){\left(t_i-\frac{\beta {\epsilon }_{i\mu }}{{\sigma }^{2}Q}\right)}^2\right\}{dt}_i\\ =\prod _{i=m+1}^{n}exp\left\{-\frac{{{\epsilon }_{i\mu }}^2}{2{\sigma }^2}+\frac{{\beta }^2{{\epsilon }_{i\mu }}^2}{2{\sigma }^{4}Q}-\frac{1}{2}ln\left({\sigma }^2{\sigma }_x^2\right)\right\}\frac{1}{\sqrt{Q}}\mathrm{\Phi }\left\{\sqrt{Q}\left[{\mathit{LOD}}_i-\mu -\frac{\beta {\epsilon }_{i\mu }}{{\sigma }^{2}Q}\right]\right\}\\ =\prod _{i=m+1}^n\frac{1}{Q}\mathrm{\Phi }\left\{Q\left[{\mathit{LOD}}_i-\mu -{\sigma }^{-2}{Q}^{-2}\beta {\epsilon }_{i\mu }\right]\right\}exp\left\{-\frac{{{\epsilon }_{i\mu }}^2}{2{\sigma }^2}+\frac{{\beta }^2{{\epsilon }_{i\mu }}^2}{2{\sigma }^2{Q}^2}-\frac{1}{2}ln\left({\sigma }^{2}Q\right)\right\}\\ =\prod _{i=m+1}^n\frac{\mathrm{\Phi }\left\{Q\left[{\mathit{LOD}}_i-\mu -{\sigma }^{-2}{Q}^{-2}\beta {\epsilon }_{i\mu }\right]\right\}}{\sqrt{{\sigma }^2+{\beta }^2{\sigma }_x^2}}exp\left\{-\frac{{{\epsilon }_{i\mu }}^2}{2{\sigma }^2}\left(1-\frac{{\beta }^2}{{\sigma }^2{Q}^2}\right)\right\}\end{array}$$

APPENDIX B

/*****************************************************************
**Data structure: Y = response variable, X = exposure, D = censoring indicator*
** LOD = limit of detection, Z = other covariates. *
*** mux: the mean of the covariate variable *
*** sigmax: the standard deviation of the covariate variable *
*** alpha: the intercept in the regression model *
*** beta: the slope in the regression model *
*** betaz: the slope of z variable *
*** In the statement parms mu= sigmax= sigma= alpha= beta=, *
*** specify the starting value of parameters *
******************************************************************/
Proc NLMIXED data=yourdata;
  parms mux= sigmax= sigma= alpha= beta= betaZ=;
     Q=sqrt(1/sigmax**2+beta**2/sigma**2);
     e=y-alpha-beta*x-z*betaz; emu=y-alpha-beta*mux-z*betaz;
     LL1=(−e**2/sigma**2/2-log(sigma**2*sigmax**2)/2
         −(x-mux)**2/sigmax**2/2;
     LL2=(1-beta**2/sigma**2/Q**2)*(−emu**2/sigma**2/2)
         −log(sigma**2+beta**2*sigmax**2)/2
         +log(probnorm(Q*(LOD-mux-beta*emu--z*betaz/sigma**2/Q**2)));
     logL=(1-D)*LL1+D*LL2;
     model Y~general(logL);
run;