QSAR studies on a number of pyrrolidin-2-one antiarrhythmic arylpiperazinyls

Abstract

The activity of a number of 1-[3-(4-arylpiperazin-1-yl)propyl]pyrrolidin-2-one antiarrhythmic (AA) agents was described using the quantitative structure–activity relationship model by applying it to 33 compounds. The molecular descriptors of the AA activity were obtained by quantum chemical calculations combined with molecular modeling calculations. The resulting model explains up to 91% of the variance and it was successfully validated by four tests (LOO, LMO, external test, and Y-scrambling test). Statistical analysis shows that the AA activity of the studied compounds depends mainly on the PCR and JGI4 descriptors.

Electronic supplementary material

The online version of this article (doi:10.1007/s00044-010-9540-x) contains supplementary material, which is available to authorized users.

Introduction

α₁-Adrenergic receptors (α₁-AR) are members of the G-protein coupled superfamily of receptors, which modulate intercellular biochemical processes in response to changes in the extracellular concentration of the neurotransmitter norepinephrine and the circulating hormone epinephrine, leading to widespread physiological actions that make them attractive targets for drug discovery (Becker et al., 2004; Golan 2008; He et al., 2008; Zhong and Minneman 1999). They are responsible for a number of physiological functions (Abbas et al., 2006; Graham et al., 1996; Piascik et al., 1999) in:

1. cardiovascular tissues regarding vascular smooth contraction and blood pressure regulation,

2. noncardiovascular tissues regarding the human prostate smooth muscle contraction or the regulation of cerebral microcirculation.

Thus, α₁-AR antagonists can be useful in the treatment of hypertension, benign prostatic hyperplasia (BPH), lower urinary track symptoms (LUTS), or cardiac arrhythmia (Carmeliet and Mubagwa, 1998; Chiu et al., 2008; Jain et al., 2008; Koshimizu et al., 2007; Nargund and Grey, 2008; Thiyagarajan, 2002).

Now, in the globalization era, determined by speed, uncertainty and instability people live in increasing stress leading to a rise in the incidence of cardiovascular diseases. Cardiac arrhythmia may be caused by abnormal impulse formation, abnormal impulse propagation, or both (Matyus et al., 1997) it remains a major source of morbidity and mortality in developed countries. For example, between 0.5 and 1 million North Americans and Europeans die each year because of sudden cardiac death, which corresponds to 10–20% of all deaths among adults in the Western world (Goldberger et al., 2008; Huikuri et al., 2001; Kromhout, 2007). In the past decade, the treatment of arrhythmia has been dramatically altered by the development of nonpharmacological therapies, such as targeted ablation of arrhythmogenic tissues and implantable cardioverter defibrillators (ICDs), as well as the limited efficacy and proarrhythmic potential of conventional antiarrhythmic (AA) drugs (Estrada and Darbar, 2008). AA drugs have been classified by Vaughan Williams mainly based on their effects on cardiac action potentials into classes I–IV and later correlated to their effects on Na⁺ channel, β-receptors, and K⁺ and Ca²⁺ channels (Hashimoto, 2007; Vaughan Williams, 1992).

In the course of our studies directed to search for new α₁-AR antagonists, among which a series of (4-arylpiperazin-1-yl)propylpyrrolidin-2-one or 3-alkyl-3-phenylpyrrolidin-2-one derivatives, it was shown that the compounds obtained also showed marked AA and hypertensive activities. The ED₅₀ values determined for a number of them was lower than or comparable with the reference compounds (Kulig et al., 2003, 2004, 2007, 2009; Malawska et al., 2002, 2005). For a large number of chemometric analyses reported in medical research, there are relatively few studies on the application of QSAR analysis to AA species (Debnath et al., 2003; Fumagalli et al., 2005; Pallavicini et al., 2006; Turabekova et al., 2008). In this context, the aim of this study, being a part of our drug design project, is to find a model explaining the AA activity of a series of 1-[3-(4-arylpiperazin-1-yl)propyl]pyrrolidin-2-one derivatives applying the quantitative relationship between structural parameters and AA activity. The quantitative structure–activity relationship (QSAR) equation for our compounds is presented and discussed.

Computational methods

1-[3-(4-Arylpiperazin-1-yl)propyl]pyrrolidin-2-one derivatives

Thirty-three analogs of 1-[3-(4-(aryl)piperazin-1-yl)propyl]pyrrolidin-2-one were chosen from the reports published by us between 2002 and 2009 (Kulig et al., 2003, 2004, 2007, 2009; Malawska et al., 2002, 2005). The source publications concern the synthesis of over 70 arylpiperazine derivatives and their pharmacological test results. About 20 of these compounds display a lack of α₁-ARs activity and 40 compounds display a lack of AA activity. These compounds are considered to be irrelevant for the model formulation and they were excluded from the current study. Thus, the set of the remaining 33 compounds displaying both α₁-ARs and AA activity are appropriate for a QSAR analysis and are listed in Table 1. The external set should include about 10–30% of the entire set and should represent activities and structures that cover the whole range of the training set (Gramatica, 2007). Consequently the initial data set was split into two subsets: a training subset (N _TS = 25) and a external cross-validation subset included randomly selected compounds number: 1, 3, 8, 17, 21, 23, 25, 30 (N _EXT = 8).

Table 1.

Structures and affinities for AA action of 1-[3-(4-arylpiperazin-1-yl)propyl]pyrrolidin-2-one derivatives used in the current work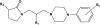

Compounds	AA activity		R1	R2	R3
	Observed	Predicted
1 a	2.01	2.09	H	H	H
2	1.79	1.86	H	2-OMe	H
3 a	1.80	1.79	H	2-Cl	H
4	1.54	1.71	H	2-F	H
5	2.52	2.24	H	2-OEt	H
6	1.45	1.46	H	3-CF3	H
7	1.43	1.43	OH	2-OMe	H
8 a	1.40	1.44	OH	4-Cl	H
9	1.79	1.58	OH	2-F	H
10	1.64	1.60	OH	3-OMe	H
11	1.97	2.15	OH	2-OEt	H
12	1.55	1.56	OH	2-Me	H
13	2.23	2.21	OH	2-OH	H
14	1.77	1.79	OH	2-OiPr	H
15	1.31	1.31	OH	2-CF3	H
16	1.54	1.53	OH	2,4-diF	H
17 a	1.48	1.32	OH	2-OMe, 5-Cl	H
18	2.37	2.54	OH	2-OMe	3,3-diPh
19	2.13	2.17	OH	2-CF3	3,3-diPh
20	2.53	2.37	OH	2-Me	3,3-diPh
21 a	2.66	2.55	OH	2-OEt	3,3-diPh
22	2.38	2.33	OH	H	3,3-diPh
23 a	1.60	1.88	OH	H	H
24	1.92	1.86	O(CO)NHEt	2-OMe	H
25 a	2.19	1.99	O(CO)NHiPr	2-OMe	H
26	1.52	1.56	O(CO)NHnPr	2-OMe	H
27	1.77	1.81	O(CO)nPr	2-OiPr	H
28	2.00	2.00	O(CO)NHiPr	2-Cl	H
29	1.66	1.75	O(CO)NHEt	H	H
30 a	1.88	1.95	O(CO)iPr	H	H
31	1.47	1.51	O(CO)NHnB	H	H
32	1.52	1.42	O(CO)NHnPr	H	H
33	1.36	1.37	H	2-OH	H

The ΑΑ expressed as −log ED₅₀ values, in mM/kg

^aCompounds excluded in the model generation procedures; external data set, AA observed activity by pharmacological tests, AA predicted activity by Eq. 1

Molecular descriptors and methods

In order to identify the effect of the molecular structure on the AA activity a QSAR analysis of the selected compounds was performed.

1. The AA activity data expressed as ED₅₀ (mg/kg) are taken from the source publications and recalculated to ED₅₀ (mM/kg). Logarithmic values (−log ED₅₀) are listed in Table 1 as AA observed activity. Each ED₅₀ (mg/kg) value was obtained from independent experiments in adrenaline included arrhythmia in anaesthetized rats (Szekeres and Papp, 1975).

2. For the molecular 3D structure calculations the Gaussian® 03 (version 6.1) package was used (Frisch et al., 2004). The three-dimensional structures of the pyrrolidin-2-one derivatives in their neutral state were obtained through full optimization based on the AM1 quantum chemical procedure. Harmonic vibrational analysis was used to ascertain whether the resulting geometries were the true energy minima structures. All the molecules were minimized until the root mean square (RMS) gradient value was smaller than 10⁻⁶ a.u. Next, resulting molecular 3D structure was used for the calculation of the descriptors set and to visualize the distribution of charge in a molecule (the map of the electrostatic potential in the form of a 3D plot). In order to obtain reliable energetic and accurate data on electronic properties of molecules the single-point energy calculations were performed at the DFT/B3LYP level of theory using the 6-31G** basis set. Suitable maps of the electrostatic potential were plotted based on the electronic and nuclear charge distribution obtained from the energy calculations results. The Gaussian suite of programs calculates the electrostatic potential maps and surfaces as the distribution of the potential energy of unit positive charge in a given molecular space, with a resolution controlled by the grid density. In Fig. A in the Supplementary file representative plots for extreme difference in the charge distribution pattern are shown (Frisch et al., 1998; Leach, 2001).

3. For the calculation of the descriptors the Talete srl, DRAGON for Windows Version 5.5-2007 package was used. Dragon descriptors include 22 different logical blocks. The total number of calculated descriptors was 3224. Several criteria were used to reduce this number while optimizing the information content of the descriptors set. First, descriptors for which no value was available for all the compounds were disregarded. Second, descriptors of which the value is constant (or near-constant) inside each group of descriptors were excluded. For the remaining descriptors, if two descriptors showed a correlation coefficient greater than 0.9, the one showing of the highest pair correlation with the others descriptors was removed. After these automatic screening procedures, a set of 385 descriptors was obtained for further analysis. To reduce the vast number of descriptors to the 50 that correlated best with the experimental data, the “Feature Selection and Variable Screening” methods available in Statistica® (version 8.0) (2008) software were applied. Then, the chosen descriptors were used as regressors of the model: they are collected in Table A in the Supplementary file and a detailed description of these descriptors can be found in the literature (Todeschini and Consonni, 2002).

Statistical analysis

The Multiple Linear Regression (MLR) (Allison, 1999) and correlation analyses were carried out using the Statistica® (version 8.0) (2008) software. The forward stepwise regression analysis yielded a three-parametric model describing the biological activity as a function of molecular descriptors. The statistical quality of the regression equations was evaluated by parameters such as the correlation coefficient R, the squared correlation coefficient R ², the adjusted squared correlation coefficient R ²_adj, the Root Mean Squared Errors (RMSE) and the variance ratio F. The statistical significance (P level) of a result was determined as P ≤ 0.01 (Bland, 2000).

The model obtained in this study was validated by calculations of the validated squared correlation coefficient (Q ²) values and prediction error sum of squares (called SPRES) values. The Q ² values were calculated from the general internal cross-validation procedures “leave-one-out” test (LOO) and “leave-many-out” test (LMO) and external tests (EXT) (Baumann, 2005; Golbraikh and Tropsha, 2002; Hawkins, et al., 2003; Kubinyi 1997a, b). Abbreviations Q ²_LOO, Q ²_LMO, Q ²_EXT (and QS_LOO, QS_LMO, QS_EXT) have been used in their’s usual meaning for the tests listed above. In addition, the robustness of the proposed model was checked by permutation testing: parallel models were developed based on a fit to randomly reordered Y-data (Y-scrambling, Y-randomization) (Gramatica, 2007; Tropsha, 2010; Tropsha et al., 2003). According to the basic approach of Wold and Eriksson (1995) all randomization methods consisted of ten randomization runs for any data set size.

All computations were performed on a HP 6200 wx workstation.

Results and discussion

Table 1 reports the observed AA activity, expressed as −log ED₅₀ (mM/kg) values in adrenaline included arrhythmia in anaesthetized rats. All the tested compounds showed AA stimulation as the –log ED₅₀ values are between 1.31 and 2.66.

In this study we have limited the number of presented equations to this of the best regression model of the whole set. The model is given as follows together with the statistical and validation parameters:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{gathered} {\text{AA}} = \, -{ 6}0. 1 6 7\left( { \pm 1 3.00 5} \right){\text{ JGI4 }} + { 12}. 3 3 4\left( { \pm 3. 8 4 1} \right){\text{ PCR}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \, 0. 9 8 6\left( { \pm 0. 2 1 3} \right){\text{ Hy}} - 20. 1 10\left( { \pm 6.0 7 2} \right) \hfill \\ \end{gathered} $$\end{document} 1

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{gathered} R \, = \, 0. 9 5 3,\,R^{ 2} = \, 0. 90 9,\,R_{\text{adj}}^{2} = \, 0. 8 4 4 ,\,F \, = { 14}.0 40, \hfill \\ {\text{RMSE }} = \, 0. 1 4 1,\,N_{\text{TS}} = { 25},\,N_{\text{EXT}} = { 8},\,P < 0.0 1, \hfill \\ Q_{\text{LOO}}^{2} = \, 0. 7 4 4,\,{\text{QS}}_{\text{LOO}} = \, 0. 1 7 8,\,Q_{\text{LMO}}^{2} = \, 0. 7 3 6,\,{\text{QS}}_{\text{LMO}} = \, 0. 1 7 5,\,Q_{\text{EXT}}^{2} = \, 0. 8 5 8,{\text{ QS}}_{\text{EXT}} = \, 0. 1 6 8\hfill \\ R_{Y}^{2} = \, 0.0 7 4,\,Q_{Y}^{2} = \, 0.0 2 2 ,\hfill \\ \end{gathered} $$\end{document} where N is the number of compounds included in the [training (TS)/external (EXT)] data set, R the correlation coefficient, R ² the squared correlation coefficient, R ²_adj the adjusted squared correlation coefficient, RMSE the root mean squared errors, F the variance ratio, P the significance of the variables in the model, Q ²_LOO, Q ²_LMO, Q ²_EXT, R ²_Y, and Q ²_Y the correlation coefficient of the adequate validation methodologies.

The presented QSAR analysis yields a model incorporating three descriptors. Since the Topliss and Costello rule (1972) allows the use of up to five descriptors for a training set consisting of 25 compounds and the relation R ²_adj < R ² is true, the model in not overparametrized. However, for AA action we did not fit any better correlation using more descriptors in multi-parameter correlations. The correlation coefficient R of this relationship is 0.95 and explains up to 91% of all variance data for AA activity. Moreover, the F test value together with RMSE at the P level of 1 × 10⁻⁵ suggests that the equation has a good correlation with the data and is statistically significant. Every descriptor in the regression equation must be independent. The correlation between each descriptor was calculated and is presented in form of a Pearson correlation matrix in Table 2. As can be seen from these numbers all predictors have a pair correlation minimal covariance <0.5 which assures that any collinearity of predictors is not present. Table 1 reports the AA activity predicted by Eq. 1. A plot of the predicted activity versus the residual values was prepared to determine the existence of systematic errors in the model development (see Fig. B in the Supplementary file). The uniform distribution of residues indicates no systematic error (Belsley et al., 2005). The plots of observed AA activities versus those predicted by Eq. 1 together with the corresponding predicted intervals are shown in Fig. C in the Supplementary file. Compound number 5 is out of 91% prediction threshold and exhibits high AA activity in contrast to other compounds of similar structure having low hydrophobic factor i.e., compounds 2, 4–6. This incidence may be explained by unique structural features. This plot proves that the model as a good descriptive power. Summing up the linear model seems to be adequately fit to the data, all predictors have P < 0.01 and one can conclude that all are independently associated with AA activity.

Table 2.

Pearson correlation matrix of the parameters used in this study

	JGI4	PCR	Hy
JGI4	1.00
PCR	0.47	1.00
Hy	0.39	−0.22	1.00

JGI4 Mean topological charge index of order 4, PCR ratio of multiple path count over path count, Hy hydrophilic factor

In an attempt to determine the utility of Eq. 1 as model of AA activity four validation analyses were carried out i.e., LOO, LMO, Y-scrambling, and external predictivity (Kiralj and Ferreira, 2009). In the field of statistical techniques the LOO and LMO are used for internal validation. From a theoretically acceptable model the R ² cannot have smaller values than Q ²_LOO and Q ²_LMO or Q ²_EXT. Overall, the best model is achieved when Q ²_LOO ≤ R ² ≥ Q ²_LMO and Q ²_LOO ≈ Q ²_LMO. Commonly, Q ²_LOO > 0.5 is considered as proof of the reasonably predictive capability of the equation. Q ²_LOO > 0.7 indicates the stable and predictive potential of the equation. Nevertheless a high Q ²_LOO value does not indicate a high predictive power of the model. On the other hand if R ² < Q ²_LOO the model is overfitted. As can be seen from the statistics presented next to Eq. 1 in our case R ² > Q ²_LOO, which means that our model is not overfitted. The LMO test is usually used to verify results obtained from the LOO test. In the Q ²_LMO procedure ten iterations were performed with five molecules left out in each iteration (e.g., tenfold, 80/20 cross validation) (Kiralj and Ferreira, 2009; Tropsha, 2010). The results of the LMO test are collected in Table 3. On average, the overall test steps R ² > Q ²_LMO and Q ²_LOO ≈ Q ²_LMO which is another proof that the model is not underdetermined. In order to ascertain whether the good results of the model described by Eq. 1 are not due to chance correlation or structural dependency of the training set, the Y-scrambling tests were performed. The results of ten runs of Y-randomization tests are shown in the Table 4. The average values are smaller than 0.2, which, according to Wold and Eriksson (1995), points to the absence of chance correlation (Kiralj and Ferreira, 2009; Tropsha, 2010). The low R ²_Y and Q ²_Y values prove that our model is valid. To validate the predictive power of the mathematical model more explicitly one needs to conduct validation on the external set of data (Gramatica, 2007; Kiralj and Ferreira, 2009). Therefore, the EXT test was carried out on the groups of compounds including 30% of the data set. As mentioned above, a subset of eight randomly selected compounds was removed from the entire set to be used in the validation procedure. For external compounds (1, 3, 8, 17, 21, 23, 25, and 30) Q ²_EXT = 0.86 combined with the fact that there are no outliers which exhibit a systematic error, conclusively prove the good predictive potency of the quantitative relationship constructed on the basis of the AA activity. Thus, in our opinion, the derived models can be used for the prediction of the AA commotion for new compounds in a series of analogs. The 3-parametric equation defines the best model for this subset of data. Molecular descriptors incorporated in the equation are: JG4I, PCR, and Hy. All the obtained descriptors belong to different logical blocks of descriptors such as the Topological charge indices (TCI) (JGI4), (Gálvez et al., 1996, 1995, 1994; Rios-Santamarina et al., 1998). The Walk and path counts (PCR) (Diudea et al., 1994; Randic, 1980; Razinger, 1986; Rücker and Rücker, 1993, 2000), and the Molecular properties (Hy) (Todeschini et al., 1997). Brief detailed descriptions of these descriptors can be found in the literature (Todeschini and Consonni, 2002). The obtained model incorporates descriptors of rather structural nature due to the regression coefficient value (see Eq. 1). As can be easily noticed, the descriptors influencing the investigated properties the most are JG4I and PCR. All descriptors related to physico-chemical properties of the molecule (except two) were excluded during the statistical analysis (Table A in the Supplementary file). This means that the structure and geometry of the molecule affect the AA activity, rather than its physico-chemical properties. Looking more closely at the chosen descriptors and their statistics in Table 5 JGI4 and PCR have |BETA| > 1 (Achen, 1982).

Table 3.

The results of the LMO test

Number of runs	Number of excluded compounds in the LMO test	Q 2LMO	QSLMO
1	26, 22, 33, 11, 20	0.76	0.18
2	13, 9, 33, 29, 22	0.82	0.12
3	20, 7, 32, 14, 24	0.71	0.21
4	24, 20, 9, 19, 16	0.74	0.17
5	29, 28, 32, 20, 33	0.66	0.21
6	24, 6, 18, 14, 19	0.73	0.16
7	24, 9, 13, 20, 16	0.67	0.20
8	16, 27, 20, 22, 13	0.69	0.21
9	22, 19, 14, 27, 9	0.87	0.09
10	14, 5, 32, 2, 13	0.71	0.19
Average values		0.74	0.17

Table 4.

R ²_Y and Q ²_Y values after ten Y-scrambling tests

Number of runs	Order of compounds in observed y vector in the Y-scrambling test	R 2Y	Q 2Y
1	9, 4, 32, 24, 19, 27, 12, 33, 29, 11, 22, 26, 15, 6, 20, 14, 28, 5, 31, 16, 13, 10, 2, 18, 7	0.07	0.01
2	12, 19, 14, 9, 26, 20, 33, 16, 32, 28, 24, 22, 27, 29, 5, 10, 4, 6, 18, 7, 2, 31, 11, 15, 13	0.12	0.05
3	16, 19, 22, 33, 11, 6, 2, 7, 26, 4, 5, 24, 31, 15, 10, 20, 29, 14, 27, 13, 28, 12, 32, 18, 9	0.06	0.02
4	28, 12, 4, 20, 15, 11, 24, 2, 9, 7, 31, 6, 29, 18, 16, 26, 19, 22, 14, 33, 5, 27, 10, 32, 13	0.06	0.01
5	32, 2, 16, 20, 6, 22, 19, 15, 14, 5, 26, 29, 7, 4, 18, 12, 28, 11, 10, 33, 31, 27, 9, 24, 13	0.09	0.01
6	32, 19, 13, 12, 6, 20, 28, 10, 27, 31, 33, 16, 7, 14, 11, 29, 24, 15, 26, 4, 5, 9, 2, 22, 18	0.08	0.05
7	15, 31, 2, 20, 27, 9, 28, 13, 19, 12, 33, 24, 7, 14, 11, 29, 5, 16, 22, 32, 18, 26, 10, 6, 4	0.04	0.00
8	7, 28, 10, 31, 11, 22, 19, 29, 33, 12, 27, 18, 32, 20, 6, 13, 2, 9, 5, 15, 26, 4, 24, 14, 16	0.03	0.00
9	27, 29, 24, 33, 28, 4, 19, 31, 32, 12, 9, 14, 13, 7, 18, 22, 26, 5, 20, 11, 16, 10, 15, 6, 2	0.05	0.00
10	27, 6, 10, 2, 14, 31, 19, 29, 32, 4, 26, 11, 18, 12, 9, 13, 15, 24, 28, 33, 16, 5, 22, 7, 20	0.13	0.07
Average values		0.07	0.02

Table 5.

Multiple regression results

	BETA	Standard error	B	Standard error	t(14)	P level
Intercept			−20.1101	6.07174	−3.31209	0.005137
JGI4	−0.870898	0.188244	−60.1674	13.00513	−4.62644	0.000392
PCR	1.026828	0.319750	12.3345	3.84092	3.21134	0.006277
Hy	0.604621	0.130843	0.9856	0.21329	4.62095	0.000396

The molecular charge distribution plays an important role in many biological and pharmacological activities. Kier and Hall (1999) developed the concept of E-states, an electrotopological-state index for atoms in a molecule. For calculating TCI descriptors, H-depleted molecular structure is represented as a graph G. TCI are calculated using the “inverse square topological distance matrix” where the charge influence decreases with the square of the distance. Gálvez et al. (1996, 1995) introduced the ‘‘inverse square topological distance matrix’’ denoted by D* in which matrix elements are the inverse square of the corresponding element in the topological distance matrix D. The diagonal entries of the topological distance matrix remain the same, so diagonal entries of D* are 0. Finally,

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{JGIk}} = {\frac{\text{GGIk}}{{\left( {N - 1} \right)}}}{\text{ and }}\,{\text{GGIk}} = \sum\limits_{{i = 1,{\kern 1pt} j = i + 1}}^{{i = N - 1,{\kern 1pt} j = N}} {\left| {{\text{CT}}_{i,j} } \right|\delta (k,\,D_{i,j} )} , $$\end{document} 2

where, δ is where d is Kronecker’s delta and CT_ij = m _ij−m _ji [m stands for the elements of the M matrix M = A × D*; A is the adjacency (N × N) matrix of the molecular graph G, where N is the number of vertices (atoms different to hydrogen)]. Thus, GGIk represents the sum of all the CT_ij terms, with D _ij = k, being D _ij the entries of the topological distance matrix (D) and k ranging from 1 up to 10. These indexes represent a strictly topological quantity plausibly correlating with the charge distribution inside the molecule.

In other words, the TCI estimates the charge transfer between pair of atoms, and hence the global charge transfer in the molecule. The JGI4 parameter varies within the investigated set from 0.040 (compound 1, unsubstituent) to 0.016 (compound 17, for which R₁-OH, R₂-2-OMe, 5-Cl, and R₃-H). In Fig. A in the Supplementary file, the differences in the distribution of the electrostatic charge in compounds 1 and 17 are visualized. Because the sign of the regression coefficient is negative, an increase of this predictor values will result in a decrease in AA activity. This suggests that some unique charge distribution is needed for increase AA activity.

The PCR descriptor is related to the molecular complexity of the graph (Trinajstic, 1992) i.e., to molecular branching and size as derived from the ratio of multiple path count over path count and it is sensitive to the substituent position within the investigated set as it varies from 1.182 (compound 31, for which O(CO)NHnB substituent R₁ and H substituted R₂ and R₃) to 1.309 (complex derivative 21, for which of R₁-OH, R₂-2-OEt and R₃-3,3-diPh). Because the sign of the regression coefficient is positive, a decrease of this predictor will result in a decrease in AA stimulation. Our earlier qualitative investigations (SAR) led us to similar conclusions (Kulig et al., 2007; Nowaczyk et al., 2009, 2010). The remaining parameter of the model (Hy) is the hydrophilic factor. It is a simple empirical index related to the hydrophilicity of compounds. In our data set the Hy index varies between −0.8 and 0.4. According to the sign of the BETA coefficient (Table 5), an increase in the hydrophilicity of the compounds will result in an increase in the predicted feature, although the relatively low absolute BETA values indicate that their significance in the model is not crucial.

Conclusions

In this study we have developed a mathematical model for the prediction of the AA activity of a series of 1-[3-(4-arylpiperazin-1-yl)propyl]pyrrolidin-2-ones containing various substituents on the aryl, propyl, and pyrrolidin-2-one moieties. The resulting model displays a good fit with the experimental data, with a correlation coefficient of 0.95 and explains up to 91% of the variance. In addition, the cross-validation coefficients reflecting the predictive power of the regression, Q ²_LOO is 0.74, and Q ²_LMO is 0.74. The Y-scrambling test proved that the good statistics obtained for Eq. 1 are not due to chance correlation or structural dependency of the training set. In addition, the external test showed a Q ²_EXT of 0.86 which proves a good predictability of the AA by the model (Eq. 1). The main purpose of this investigation was to determine the parameters which best describe the biological activity of a number of arylpiperazines derivatives. The results obtained here show that the activity of these compounds is mainly determined by the JGI4-, PCR- , and Hy-values. The model provides important information on the structure–activity relationships of these types of compounds at the molecular level relevant for the design of new AA derivatives. The JGI4 of a potent agent should be as low as possible while PCR- and Hy-values should be high. On the basis of these results in combination with previous evidences we can conclude that the interaction of the 1-[3-(4-arylpiperazin-1-yl)propyl]pyrrolidin-2-one moiety with the arrhythmic species is greatly increased by the structure and the geometry of the molecule rather than its physico-chemical properties. More extensive in silico studies are in progress and will be reported in due course.

Electronic Supplementary Material

Below is the link to the electronic supplementary material.