Evaluation of an asymmetry parameter for curve-fitting in single-chemical and mixture toxicity assessment

Abstract

In mixture toxicity, concentration-effect data are often used to generate conclusions on combined effect. While models of combined effect are available for such assessments, proper fitting of the data is critical to obtaining accurate conclusions. In this study an asymmetry parameter (s) was evaluated for data-fitting and compared with our previous approach. Inhibition of bioluminescence was assessed with Vibrio fischeri at 15, 30 and 45-minutes of exposure with seven or eight concentrations and a control (each duplicated) for each single-chemical (A or B) and mixture (A:B). Concentration-effect data were fitted to sigmoid curves using the four-parameter logistic function (4PL) and the five-parameter logistic minus one-parameter (5PL-1P) function. For the 4PL, parameters included minimum effect, maximum effect, EC₅₀ and slope, while for the 5PL-1P the minimum effect parameter was removed and an asymmetry parameter was added. A total of 72 mixture toxicity data sets were evaluated, representing 432 single-chemical and 216 mixture curves. Mean coefficients of determination (r²) for all 648 curves showed that the 5PL-1P gave better fitting (0.9982 ± 0.0018) than the 4PL (0.9973 ± 0.0030). For both functions, the sum-of-squares of the residuals (SS-Res) was determined for each curve. The 5-parameter rational regression best described the relationship between the decrease in sum-of-squares of the residuals (i.e., 4PL: SS-Res – 5PL-1P: SS-Res) and log s, with fitting improved the most at low values of s (s < 0.8). This held even when curves with r² values ≤ 0.9970 were removed from the analyses. Subsequent review of the combined effects obtained via the 4PL and the 5PL-1P functions resulted in a change in the interpretation of combined effect in 39/216 (18%) cases.

1. Introduction

The fundamental requirement for demonstration of a toxic effect is an increase in effect with an increase in concentration (or dose). In a toxicity test, when a sufficient number of concentrations of a toxicant are tested and the sample size is large enough, a concentration-effect curve can be generated from the data. Such curves are often shown as sigmoid curves. Sigmoid curves generally have a region that is relatively linear between about 16 and 84% effect (Eaton and Klaassen, 1996), but tend to bend, sometimes substantially, at lower and higher effect levels. Frequently, toxicity data are fitted to sigmoid curves and such curves may be used to compare the response of an organism to different toxicants.

In developing curves that relate effect to concentration, a three-parameter logistic model has commonly been used to obtain accurate estimates of midpoint, slope and upper asymptote. However, a basic assumption therein that is not always verified is whether the resulting curve is symmetrical (Van der Graff and Schoemaker, 1999). In some instances the curves are asymmetrical and this can affect conclusions derived from the analysis. To address this concern, Van der Graff and Schoemaker (1999) developed an approach for determining the asymmetry of concentration-effect curves, based on work by Richards (1959). Recent research has shown that concentration-effect curves are often asymmetrical and that inclusion of an asymmetry parameter can improve fitting of concentration-effect data (Gottschalk and Dunn, 2005; Giraldo et al., 2002; Van der Graff and Schoemaker, 1999).

In toxicity testing, the number of concentrations tested is often restrained by time and costs. Sigmoid curves may be developed from such concentration-effect data and used in hazard or risk assessments for single-chemicals or mixtures. To obtain accurate curves, the data need to be fitted using the best available approach. In mixture toxicity, for example, it has been shown that the same set of concentration-effect data, when analyzed by different models, can generate different conclusions on the combined effect observed (Pounds et al., 2004).

For a recent series of studies examining mixture toxicity of soft electrophile-containing mixtures, a four-parameter logistic (4PL) function was used to develop sigmoid curves for the agents individually and for their mixtures (Dawson et al., 2010; 2008; 2006; Gagan et al. 2007). This 4PL function gave minimum effect, EC₅₀, slope, and maximum effect values for each curve. In some instances, however, it was noted that sigmoid curves were not symmetrical and that the asymmetry often tended to be most prominent at lower concentrations. As a result of these observations, more recent work has used what is referred to as a five-parameter logistic minus one-parameter (5PL-1P) function in order to fit concentration-effect data to sigmoid curves (Dawson et al., 2011). For the 5PL-1P function an asymmetry parameter was added, accompanied by removal of the minimum effect parameter. While the 5PL-1P includes asymmetry it remains a four-parameter function for data-fitting, so it allows for a direct comparison of 5PL-1P fitting with that of the 4PL.

In this study, concentration-effect data, both single-chemical and mixture, for 72 binary combinations were analyzed using both the 4PL and 5PL-1P functions to assess the value of incorporating an asymmetry parameter into curve-fitting. The combined effect obtained for each of the mixture curves was compared between the two approaches to determine the frequency with which the two approaches gave a different combined effect.

2. Materials and methods

2.1 Chemicals and Reagents

All chemicals tested were purchased from Sigma-Aldrich (Milwaukee, WI) in high purity (≥95%) and used without further purification. Chemicals tested included reactive or potentially reactive electrophiles, including mono-, di- and tri-halogenated acetonitriles, halogenated ethyl acetates, various Michael acceptor and S_N2 or S_N2-H-polar agents, and a model non-polar narcotic.

Microtox^® diluent, reconstitution solution and freeze-dried bacterial reagent were obtained from SDIX (Newark, DE). Vials of bacterial reagent were kept frozen at −20°C prior to reconstitution. Bacterial vials were reconstituted about 15–20 minutes prior to test initiation. In testing a given A:B combination, separate vials of bacterial reagent were used for agent A-alone, agent B-alone and the A:B mixture.

2.2 Toxicity testing

Inhibition of bioluminescence using the marine bacterium Vibrio fischeri was determined with a Microtox^® analyzer and the basic acute toxicity testing procedures noted previously (Dawson et al., 2010). For each chemical combination, each agent was tested alone (agent A or agent B) and combined (A:B), with toxicity assessment after 15, 30 and 45-minutes of exposure. Therefore, for each combination, there were six single-agent toxicity curves and three mixture toxicity curves. Typically, seven or eight concentrations were tested (in duplicate) along with a duplicated control. Initial readings for each control or treatment vial were made prior to chemical exposure. Test concentrations were prepared as serial dilutions, with the dilution factor used (1.6, 1.75, 1.867) having been selected for the agents based on prior testing. Within testing, for any given combination the same dilution factor was used for agents A and B singly and when combined.

2.3 Procedures for developing concentration-effect curves

Toxicity data were collected and input into SigmaPlot (v. 11.0; Systat Software, Chicago, IL) worksheets as previously described for data-fitting with the 4-parameter logistic (4PL) (Dawson et al., 2010) and 5-parameter logistic minus one-parameter (5PL-1P) (Dawson et al., 2011) functions. The essential difference between the two functions is that the 4PL fits the data points to a sigmoid curve while calculating the minimum effect, EC₅₀, slope and maximum effect values, whereas the 5PL-1P adds an asymmetry parameter (s) but removes the minimum effect parameter (Dawson et al., 2011).

The 4PL function used equation (1):

$$\text{y}=min+(\text{max}-\text{min})/(1+(\text{x}/\text{EC}50)\wedge (-\text{Hillslope}))$$ (1)

in which y = % effect, min = minimum effect, max = maximum effect, x = concentration, and ^ indicates exponential form (i.e., to the power of). Two constraints were used for fitting the 4PL function: a) 0.1 < min < 1; b) max < 100.

For the 5PL-1P function, an asymmetry parameter was added to replace the minimum effect parameter of the 4PL, so curve-fitting remained a four-parameter function. It has been termed a 5PL-1P (five-parameter logistic minus one parameter) function to indicate that it is not the standard four-parameter logistic (4PL) function found within SigmaPlot (Dawson et al., 2011). Parameters for the 5PL-1P function were maximum effect, EC₅₀, Hillslope and s – an asymmetry parameter. Curve fitting was performed using equation (2):

$$\text{y}=\text{max}/{(1+{(\text{xb}/\text{x})}^{\wedge }\text{Hillslope})}^{\wedge }\text{s}$$ (2)

in which y = % effect, max = maximum effect, x = concentration, s – asymmetry and ^ indicates exponential form. The variable xb was determined from equation (3)

$$\text{xb}={\text{EC}50}^{\ast }{10}^{\wedge }({(1/\text{Hillslope})}^{\ast }log(2^{\wedge }(1/\text{s})-1)).$$ (3)

Within SigmaPlot the regressions were run with automatic estimation of the initial parameters. The following three constraints were used for fitting the data to sigmoid curves: a) EC₅₀ > 0; b) 0.1 < s < 10; and c) max < 100.

In addition to evaluating actual experimental data with these functions, theoretical studies were conducted. In these analyses, curves developed from idealized values were prepared and plotted to permit visualization of the effect of adding an asymmetry parameter (i.e., 5PL-1P).

2.4 Evaluation of 4PL vs. 5PL-1P curve-fitting using r² and sum-of-squares of residuals

Initial comparison of the two curve-fitting functions was undertaken by examining the coefficient of determination (r²) for all single-chemical and mixture curves obtained from the 72 data sets. In regression analyses, the coefficient of determination is a statistical method typically used when the primary purpose is to predict future outcomes. It accounts for the proportion of variability in a data set (Steel and Torrie, 1980). Mean r² values were determined for all curves (648), all single-chemical curves (432), and all mixture curves (216). Additionally, mean values were calculated for each exposure duration (15, 30, 45-min.) to assess how fitting changed over testing time. Subsequently, the sum-of-squares of the residuals (SS-Res) for each curve was recorded and these were tabulated for both the 4PL and 5PL-1P functions. The difference between the SS-Res for the two functions (i.e., 4PL SS-Res – 5PL-1P SS-Res) was then calculated on a curve-by-curve basis and those values were plotted versus the log of the asymmetry parameter (log s) obtained for each curve from 5PL-1P curve-fitting. Plots were made using log s rather than s, to better show the effect of the asymmetry parameter, especially in the region of s < 1.0. The relationship between 4PL SS-Res – 5PL-1P SS-res and log s was analyzed using the 5-parameter rational regression procedure (SigmaPlot). This relationship was assessed for all single-chemical and mixture curves, for all 30 and 45-min curves, and when all curves with r² ≤ 0.9970 were removed from the analysis; with the latter analysis having been conducted to determine how much influence curves with lower r² values had on the overall relationship between SS-Res and s.

2.5 Comparison of combined effects between functions using dose-addition model

For each combination and exposure duration, predicted concentration-effect curves for dose-addition were developed from the appropriate single-chemical data (Dawson et al., 2011). Then experimental EC₅₀ values for each mixture were divided by the predicted EC₅₀ value for dose-addition, giving an EC₅₀-additivity quotient (EC₅₀-AQ) value for the mixture (Dawson et al., 2011). Each of the 72 data sets was evaluated by both the 4PL and 5-PL-1P functions, so EC₅₀-AQs from the two curve-fitting functions were available for all mixture curves. This allowed for direct comparison of the combined effect for the mixtures between the two functions. In assessing combined effect, EC₅₀-AQ values <0.90 were considered to be greater-than dose-additive, EC₅₀-AQs from 0.90 – 1.10 dose-additive, and EC₅₀-AQs >1.10 less-than dose-additive (Dawson et al., 2010).

3. Results

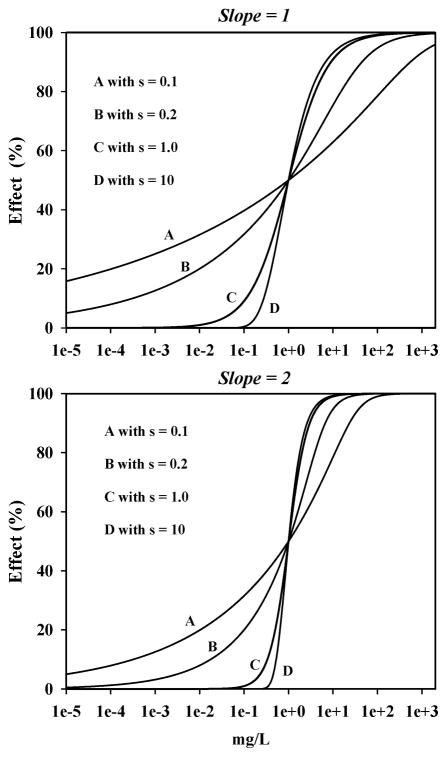
To visualize the effect of adding an asymmetry parameter (s) on concentration-effect data curve-fitting, several theoretical analyses were conducted. In the first example, when s = 1.0 5PL-1P-derived curves were, as expected, virtually identical to those fitted by the 4PL. When s varied from 1.0, however, 5PL-1P-derived curves of the same data were changed; with the changes being most prominent when s values were below 1.0 (Fig. 1). The magnitude of the change can be seen to also depend on the slope of the concentration-response curves; such as when the slope of the curves was changed from 1.0 to 2.0 (Fig. 1). Slope values of 1.0 and 2.0 were selected for these analyses since most of the chemicals tested in this study had slope values between 0.6 and 2.2 at each time-point (not shown).

Figure 1.

Theoretical 5PL-1P-derived concentration-effect curves at varying values of asymmetry (s) for two slope values. At s = 1.0, in both plots, the curves are symmetrical. The curves become asymmetrical when s is <1.0 or >1.0, but the asymmetry is more prominent at low values of s as seen by examining curves at s = 0.1 and s = 10; each having an s value one order of magnitude different than the symmetrical curve. An increase in slope from 1.0 to 2.0 shows a narrowing of separation between curves having the s values used in the analyses.

With effects of adding an asymmetry parameter having been visualized to be more prominent at low values of s (above), a second set of theoretical data was developed to directly compare fitting between the 4PL and 5PL-1P functions for two s values: s = 0.2 and s = 1.0 (Fig. 2). Fitting of the 5PL-1P (data points) and 4PL (curve) functions showed a relatively poor match at s = 0.2 when compared with the virtually identical matching of data points (5PL-1P) and curve (4PL) at s = 1.0. For the former curve (s = 0.2), the EC₅₀ for the 4PL was 0.83, while for the latter it was 1.00. The fitting of the data with the 4PL (r² = 0.9800) was poorer than that for the 5PL-1P (r² = 1.000), with a corresponding reduction in the SS-Res values for the 5PL-1P (1.0 × 10⁻⁴) versus the 4PL (120). At s = 1.0 the two functions both had EC₅₀ values = 1.00 and r² values of 1.000.

Figure 2.

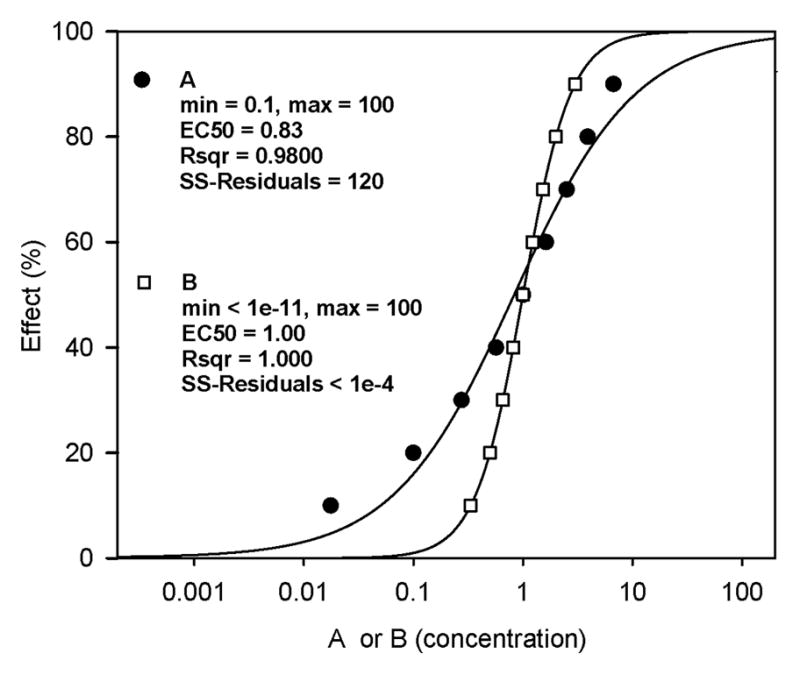
Theoretical concentration-effect data evaluated by the 4PL (curves) and 5PL-1P (symbols) functions at two asymmetry values (s = 0.2 represented by plot A; s = 1.0 represented by plot B). For s = 1.0, the 4PL curve clearly fits the 5PL-1P data (represented by open squares) well with identical EC₅₀, r² and sum-of-squares of the residuals (SS-Residuals) values. For s = 0.2, the 4PL-derived curve fits the 5PL-1P data (represented by closed circles) rather poorly (i.e., r² = 0.9800), with a corresponding increase in SS-Residuals to 120 and a decrease in the EC₅₀ (0.83) from the 5PL-1P-derived value (1.00).

Based on these theoretical analyses, experimental data were examined for similar findings to exemplify the importance of including an asymmetry parameter. Experimental concentration-effect data for 3-chloro-2,4-pentanedione were analyzed by both the 4PL and 5PL-1P functions (Fig. 3). For the 4PL the EC₅₀ was 1.25 mg/L, with a concentration-effect curve slope of 1.57 and r² of 0.9899. With the 5PL-1P the EC₅₀ was 1.34 mg/L, but the slope was much higher at 3.07 and the r² was 0.9993. The difference between the two curve-fitting functions was a result of the experimental data being asymmetrical (i.e., s = 0.26).

Figure 3.

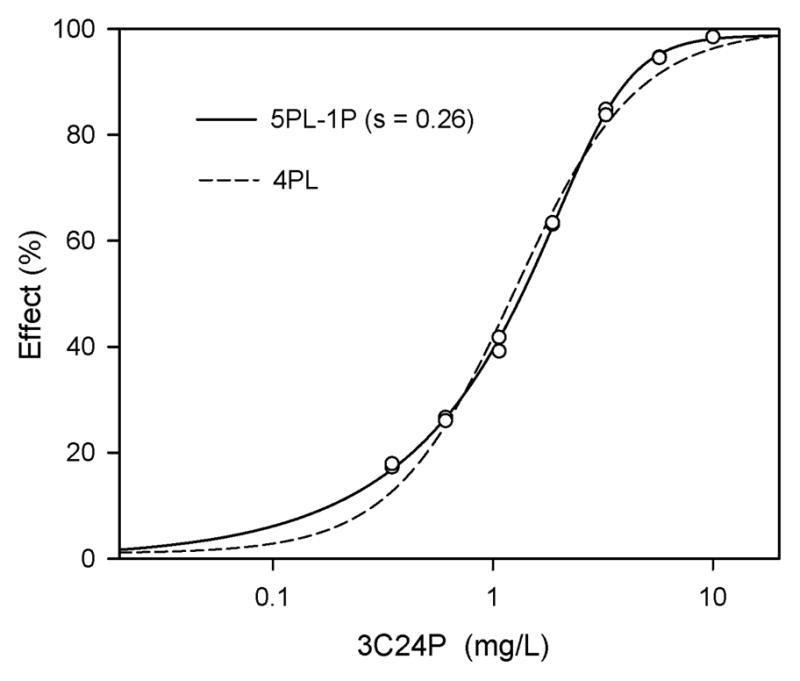
Experimental concentration-effect data for the Microtox^®-determined toxicity of 3-chloro-2,4-pentanedione (3C24P) after 45-min of exposure. Plotting of the actual data points (open circles) shows asymmetry (s = 0.26) when compared to the symmetrical 4PL curve. Incorporation of an asymmetry parameter to data fitting by using the 5PL-1P function resulted in improved fitting visually (i.e., all data points touch the 5PL-1P line) and statistically (i.e., 5PL-1P - r² = 0.9993; 4PL - r² = 0.9899).

Results for 25 of the data sets included in this report have been published (Dawson et al., 2010; 2011). To keep the size of this report manageable, specific details of the results for the 47 unpublished data sets will be provided in future papers. This study included 13 sham (i.e., A:A) and 57 true (i.e., A:B) combinations. However, one sham and one true combination were tested twice (for quality control purposes), giving a total of 72 data sets for evaluation.

For each single-chemical and mixture concentration-effect curve, the r² value was calculated for both the 4PL and 5PL-1P functions. From those values, 489/648 curves (75.4%) had higher r² values with the 5PL-1P function, 112 curves (17.3%) had the same r² for the two functions (upon rounding), and 47 curves (7.3%) had higher r² values with the 4PL. For the latter, the higher r² values were about evenly distributed across the three exposure times (15-min. = 2.2%, 30-min. = 2.2%, 45-min. = 2.9%).

Mean r² values for the 4PL and 5PL-1P functions (Table 1), for all curves and across several sub-groupings showed in all cases that the 5PL-1P curves generated higher r² values. These data, however, were not normally distributed, so a t-test could not be conducted on the mean values. Instead, the Mann-Whitney rank sum test indicated that median r² values obtained from the 5PL-1P function were significantly different (p < 0.001) from those obtained with the 4PL (not shown).

Table 1.

Mean^a r² (± s.d.) for 5PL-1P vs. 4PL curve-fitting

Concentration-effect curves	n	5PL-1P	4PL
All	648	0.9982 (0.0018)	0.9973 (0.0030)
Single-chemical	432	0.9981 (0.0019)	0.9972 (0.0029)
Mixture	216	0.9983 (0.0014)	0.9975 (0.0031)
15-min	216	0.9980 (0.0015)	0.9972 (0.0025)
30-min	216	0.9982 (0.0019)	0.9974 (0.0028)
45-min	216	0.9983 (0.0018)	0.9973 (0.0036)

^aData were not normally distributed, not be evaluated by the t-test

Since the value of a statistical test for differences across median r² values is questionable in this situation, for each of the two curve-fitting functions the sum-of-squares of the residuals (SS-Res) for each curve was determined. As expected, mean SS-Res values were typically lower for the 5PL-1P when compared with the 4PL; when all curves were considered and across various sub-groupings (Table 2).

Table 2.

Differences in mean SS-residuals for 4PL vs. 5PL-1P curve-fitting

Concentration-effect curves	n	4PL	5PL-1P	mean SS-Res 4PL – mean SS-Res 5PL-1P
		mean SS-Res	mean SS-Res
All	648	32.67	19.52	13.15
Single-chemical	432	35.28	20.31	14.97
Mixture	216	27.44	17.96	9.48
15-min	216	31.01	19.81	11.20
30-min	216	33.83	20.18	13.65
45-min	216	33.16	18.58	14.58

Based on these results, on a curve-by-curve basis, individual 5PL-1P SS-Res values were subtracted from the corresponding 4PL SS-Res and the difference was plotted versus the log of the asymmetry value obtained from the appropriate 5PL-1P curve-fitting (Table 3, Fig. 4). The analysis showed, generally, that larger differences in SS-Res values between the two functions were more common at low values of s, especially when s < 0.8; which represents greater asymmetry along the lower segment of concentration-effect curves (Dawson et al., 2011). The 5-parameter rational regression test was used to evaluate this relationship statistically for: all single-chemical and mixture curves, all 30 and 45-min curves, and for all curves having an r² value > 0.9970 (Table 3). In each case fitting of the data to the best fit line was statistically significant at p < 0.0001.

Table 3.

Summary of 5-parameter rational regression analyses

Concentration-effect curves	r2	n	p
All single-chemical and mixture curves	0.6892	648	< 0.0001
All 30 and 45-min curves	0.6992	432	< 0.0001
All curves with r2 > 0.9970	0.6644	586	< 0.0001

Figure 4.

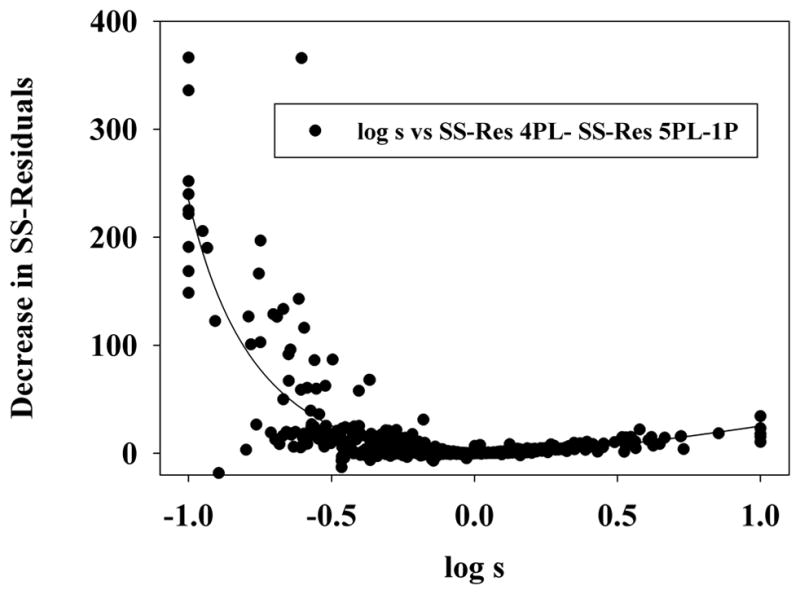
Analysis and plot of log s vs. the decrease in sum-of-squares of the residuals (SS-Res) between the 4PL and 5PL-1P curve-fitting functions, using the 5-parameter rational regression, for 648 Microtox^®-derived single-chemical and mixture concentration-effect curves.

For each of the 72 data sets, there were three mixture curves, one each for the 15, 30 and 45-min exposure durations. Mean EC₅₀-AQ values were compared between the two functions by exposure duration (Table 4). While the 5PL-1P had slightly higher mean EC₅₀-AQ values at each time-point, it was not a general trend. When the mean EC₅₀-AQ for the 4PL was subtracted from the mean EC₅₀-AQ for the 5PL-1P, the difference was ≤ 0.015 AQ for each time-point (Table 4, column 4), thereby indicating that sometimes the 5PL-1P gave a higher EC₅₀-AQ and other times the 4PL did so. The average actual AQ difference (i.e., the higher EC₅₀-AQ minus the lower EC₅₀-AQ) between the two functions at each time-point ranged from 0.058 – 0.085 AQ when examined by exposure duration (Table 4, column 5).

Table 4.

Mean EC₅₀-AQ values for the 5PL-1P and 4PL functions by exposure time

Exposure time	Mean EC50-AQ	Mean EC50-AQ	EC50-AQ	EC50-AQ
	5PL-1P (low, high)	4PL (low, high)	Mean Difference (5PL-1P – 4PL)	Actual Mean Differencea
15-min	1.079 (0.53, 1.71)	1.076 (0.75, 1.68)	0.006	0.085
30-min	1.075 (0.61, 1.58)	1.064 (0.61, 1.73)	0.011	0.064
45-min	1.085 (0.68, 1.65)	1.070 (0.67, 1.75)	0.015	0.058

^aCalculated as the higher EC₅₀-AQ minus the lower EC₅₀-AQ of the two functions

For the mixtures, 39/216 (18.1%) curves had EC₅₀-AQ values that were judged to be different between the 5PL-1P and 4PL analyses (EC₅₀-AQ values not shown) based on the classifications noted earlier. These instances of differing combined effect were spread fairly evenly across exposure times, with 15 being at 15-min, and 12 each at 30 and 45-min. For three combinations, each of the three mixture curves was judged to have given a different combined effect between the two functions. Furthermore, 8 combinations had two of the three mixtures give different combined effects, while 14 combinations had one mixture give a different combined effect. For the remaining 47 combinations, all three mixtures showed the same combined effect across both curve-fitting functions. Included in those 47, were 11/13 sham combinations and both of the combinations that were tested twice.

Overall, 25/72 combinations (34.7%) had at least one mixture give a different combined effect between the 5PL-1P and 4PL curve-fitting functions. These differences in EC₅₀-AQ values between functions were not just small ones, as just three had AQ differences that were < 0.05, while 19 had AQ differences that were ≥ 0.10. The mean AQ difference for these 39 curves was 0.121 ± 0.075 (low 0.03, high 0.29), which was greater than that for the mean AQ difference for all mixture curves (0.069 ± 0.065; low 0.00, high 0.29). Median values (0.08 5PL-1P vs. 0.05 4PL) for the groups were significantly different at p < 0.001 with the Mann-Whitney rank sum test.

Asymmetry was further evaluated by examining the range of s values when each function gave higher (or equivalent) r² values. As noted above the 5PL-1P gave higher r² values for 489 curves, the 4PL gave higher r² values for 47 curves and the two functions gave the same r² for 112 curves. Examination of s value ranges (< 0.50; 0.50 – 1.00; 1.01 – 1.50; > 1.50) showed that the 5PL-1P always had the most instances of better fitting within each range and it always gave the best fit when s > 1.50 (Table 5). The 4PL sometimes gave the higher r² when the s value was between 0.50 – 1.00, but this occurred only 11.8% (32/271) of the time, whereas the 5PL-1P gave the best fit in that range 63.4% (172/271) of the time. When the 5PL-1P and 4PL functions gave equal fitting, s values were nearly always between 0.5 and 1.5. An s value of 1.0 represents a symmetrical concentration effect curve.

Table 5.

Number of s values per function giving the higher r² for each range of s values.

s	higher r2	higher r2	r2 equal for 5PL-1P and 4PL
	w/5PL-1P	w/4PL
< 0.50	155	10	3
0.50 – 1.00	172	32	67
1.01 – 1.50	65	5	42
> 1.50	97	0	0

Further examination of s values was undertaken to determine whether s values could be related to the reactive/non-reactive nature of the chemical toxicity singly or when combined. Some agents exert toxicity through non-reactive means. These agents typically show little, if any, increase in toxicity as exposure time increases. This is signified by time-dependent toxicity (TDT) values that are low (e.g., < 10%) or negative (see Dawson et al., 2008; 2010; 2011; Gagan et al. 2007). Agents that are strongly reactive tend to show profound increases in toxicity over testing time (i.e., TDT > 100%). Other agents give TDT values between about 10 and 90%. The latter of these are thought to represent agents that exert toxicity that is partly reactive and partly non-reactive (Dawson et al., 2010; 2011). When mean s values were examined by the function giving the higher r² while also considering TDT values of each agent singly, the results suggested that at the lower end of s values, toxicity was more likely to be due to exposure to a strongly reactive toxicant (Table 6).

Table 6.

Mean asymmetry (s) values for various concentration-effect curve groupings^a

Concentration-effect curves	n	mean s ± s.d.	min. s	max. s
all single-chemical and mixture curves	648	1.01 ± 1.12	0.10	10.00
Single agent curves
full TDT agent	159	0.50 ± 0.16	0.16	0.93
no or partial TDT agent	273	1.35 ± 1.43	0.10	10.00
Mixture curves
full TDT for both agents	45	0.47 ± 0.12	0.26	0.73
full TDT agent w/a no or partial TDT agent	66	0.80 ± 0.72	0.17	3.67
partial TDT agent w/a no or partial TDT agent	105	1.25 ± 1.15	0.17	10.00

^afull TDT – agent typically has time-dependent toxicity (TDT) > 100%

partial TDT – agent typically has TDT between about 10 and 90%

no TDT – agent typically has TDT <10% (see Dawson et al., 2008; 2010; 2011)

4. Discussion

The complexity of chemical mixture toxicity assessment can be discerned simply by examining the myriad experimental designs, testing protocols, data analysis methodologies, combined effects models, risk assessment approaches and perspectives on issues in the field (e.g., Backhaus et al., 2010; Haddad and Krishnan, 1998; Greco et al., 1995; Yang, 1994; Pöch, 1993; Calabrese, 1991). With the variety of both toxic effects and living organisms, perfect methods for assessing mixture toxicity do not exist (Yang et al., 1989). While these efforts are often designed for public health or ecosystem protection (Backhaus et al., 2010; Borgert et al., 2004; Groten et al., 2004; Mumtaz et al., 2004) they also often have differing goals with respect to mixture toxicity.

Among the approaches taken in such research, comparing actual experimental effects to theoretical models of combined effect is common. Frequently, mixture toxicity is evaluated against concentration (or dose) addition, independence or other models of combined effect (LeBlanc and Omstead, 2004; Altenburger et al., 2000; Backhaus et al., 2000; Broderius et al., 1995; Pöch, 1993; Broderius and Kahl, 1985). When this is the case it becomes critical to not only have an appropriate experimental design but a data analysis methodology that allows for accurately evaluating experimental mixture toxicity against the combined effect model(s) selected.

Results of this study suggest that with the mixture toxicity testing and data analysis protocols used, removal of the minimum effect parameter (as used with the 4PL) and addition of an asymmetry parameter (as used with the 5PL-1P) improves fitting of concentration-response data to a sigmoid curve. Analysis of the coefficient of determination (r²) values between the two functions showed that the 5PL-1P gave as good or better curve-fitting as the 4PL for about 92% of single-chemical and mixture curves. By examining the 4PL - SS-Res minus the 5PL-1P SS-Res vs. log s, it was shown that the improvement in fitting with the 5PL-1P was statistically significant. So it appears that addition of the asymmetry parameter allows for a better characterization of agents based on curve parameters.

While improved curve-fitting is important, the key feature to ascertain was whether improved fitting affected combined effect interpretation for mixtures. Dose-addition is a model of mixture toxicity based on the addition of equieffective doses, in which it is assumed that agents A and B act like a sham combination of A + A or B + B, respectively (Pöch, 1993). When A and B are equieffective, then half of A and B together should show this same level of effect, e.g., 50 %. Substances with similar action and properties are expected to show a dose-additive combined effect. This model was first described and used for isobologram analyses by Loewe and Muischnek (1926). Bliss (1939) described this type of model, which he termed “simple similar action” for combinations of toxic chemicals. Herein, when considering whether mixtures were dose-additive or not, about 18% of curves were placed in a different combined effect category when using the 5PL-1P versus when results from the 4PL were used to determine the combined effect. Moreover, 34% of combinations had at least one mixture curve that gave a different combined effect between the two curve-fitting functions. It could be argued that the range of additivity quotient (AQ) values used herein for dose-addition (0.90 – 1.10) was too narrow (i.e., 1.00 ± 0.20 is often considered “additive”; Hodges et al., 2006; Broderius et al., 1995). However, our previous results, which were derived from tests that have included using at least seven duplicated concentrations/curve and testing of “sham” combinations (the latter being rather rare among mixture toxicity assays), support the narrower designation (Dawson et al., 2011; 2010; 2008; Gagan et al., 2007). With that having been stated, using the broader range of AQ values (0.80 – 1.20) to represent a dose-additive combined effect had little effect on the total number of “different” combined effect designations between the 4PL and 5PL-1P functions (39 for the narrower dose-addition range, 38 for the broader range).

The results support inclusion of an asymmetry parameter for concentration-effect curve-fitting, but it was also found noteworthy that for the majority of curves in which the 4PL gave a higher r² value than the 5PL-1P (39/47 – 83%), that at least one of the agents: 1) showed non-reactive toxicity (e.g., non-polar narcosis) or 2) had time-dependent toxicity values that suggested some of its toxicity was of a non-reactive nature (see Dawson et al., 2011; 2010 for more information). Further examination of mean s values between the two curve-fitting functions and TDT of the agents, whether given singly or in a mixture, strongly suggested a relationship between asymmetry of concentration-effect curves and reactive toxicity.

5. Conclusions

Inclusion of an asymmetry parameter in concentration-effect curve fitting was evaluated for 72 binary combinations of toxicants. Two four-parameter curve-fitting functions, the 5PL-1P, which included asymmetry, and the 4PL, which did not, were used to evaluate 648 single-chemical and mixture curves derived from Microtox^® testing. Analysis of coefficient of determination (r²) values, differences in the sum-of-squares of the residuals between functions, and changes in combined effects interpretation (as judged by additivity quotient values) suggested that including an asymmetry parameter (s) improved fitting of concentration-effect data to sigmoid curves. Improvement was seen most prominently at low s values, which corresponds to effects along the lower portion of the curves (Dawson et al., 2011) and appeared to be the result of toxicity caused by reactive agents.

Abbreviations

5PL-1P

five-parameter logistic minus one parameter

4PL

four-parameter logistic

SS-Res

sum of squares of the residuals

s

asymmetry parameterl

TDT

time-dependent toxicityl

AQ

additivity quotient