Abstract
Cancer genomes are complex, carrying thousands of somatic mutations including base substitutions, insertions and deletions, rearrangements, and copy number changes that have been acquired over decades. Recently, technologies have been introduced that allow generation of high-resolution, comprehensive catalogs of somatic alterations in cancer genomes. However, analyses of these data sets generally do not indicate the order in which mutations have occurred, or the resulting karyotype. Here, we introduce a mathematical framework that begins to address this problem. By using samples with accurate data sets, we can reconstruct relatively complex temporal sequences of rearrangements and provide an assembly of genomic segments into digital karyotypes. For cancer genes mutated in rearranged regions, this information can provide a chronological examination of the selective events that have taken place.
The genome of a cancer cell is a portrait of the mutational forces and selection pressures experienced by the emergent malignant clone, displaying enormous somatic variation ranging from small-scale point mutations, often numbering in thousands per cancer, to large-scale chromosomal rearrangements resulting in complex patterns of genomic architecture and copy number changes (Bignell et al. 2007, 2010; Pleasance et al. 2010a,b). Unlocking the temporal dynamics of these complex genomic structures may provide important insights into the mechanisms of cancer development. Although recent methods have emerged that use information across many samples to make inferences on the order of events (Stephan-Otto Attolini et al. 2010), extracting this information from a single sample has great potential applicability. For example, identifying the earliest events in the genesis of massive DNA amplification may give clues as to which genes or fusion genes are the target of the amplicon (Campbell et al. 2008); inferring rearrangement or point mutation signatures through the cancer's evolution in time may indicate changes in mutational forces experienced by the clone (Pleasance et al. 2010a); and comparing genomic profiles of metastases and primary tumors can help time the onset of metastasis (Shah et al. 2009; Ding et al. 2010; Campbell et al. 2011).
The acquisition of structural rearrangements in the developing cancer clone transforms the genome from its diploid, germline configuration to the eventual chaotic karyotype we observe in many tumors. Historically, from experiments such as array hybridization, the cancer genome is presented in wild-type genomic order as a series of discrete chromosomal segments of fixed copy number (Olshen et al. 2004). Techniques can now determine the integer allelic copy numbers within each segment (Greenman et al. 2010; Van Loo et al. 2010; Yau et al. 2010). Of course, such approaches do not capture the potentially dispersed nature of these segments that can be seen by, for example, fluorescent in situ hybridization (FISH). Now, paired-end read data from massively parallel sequencers can be used to identify how these segments connect together. Specifically, reads bridging a somatic breakpoint will have ends mapping to disparate regions of the reference genome, revealing both the orientation and connectivity between pairs of genomically linked segments (Campbell et al. 2008). These technologies thus enable the generation of comprehensive catalogs of somatic mutations of all categories from cancer samples (Ding et al. 2010; Pleasance et al. 2010a,b). In particular, the annotation of all genomic rearrangements in a given sample together with highly detailed data on allelic copy number of disrupted chromosomal segments opens the possibility of reverse-engineering the history of rearrangements that have taken place and constructing contigs of digital karyotypes of cancer genomes to base-pair resolution.
Graph theory has seen particular utility in this area of research. For example, frameworks such as De Bruijn graphs have aided the assembly of genomes (Pevzner 2000; Zerbino and Birney 2008), and breakpoint graphs have had success in constructing rearrangement phylogeny across species, pioneered with several contributions from Sankoff and Pevzner (Sankoff and Blanchette 1999; Pevzner 2000; Bader and Ohlebusch 2007; Bader et al. 2008; Alekseyev and Pevzner 2009; Warren and Sankoff 2009a,b). These methods have also been adapted to genomes containing duplications (Alekseyev and Pevzner 2007) and cancer (Raphael et al. 2003; Raphael and Pevzner 2004; Ozery-Flato and Shamir 2009). These methods generally start from known contigs of segments. Although massively parallel sequencing is producing information about cancer genomes in unprecedented detail, we will see that they do not directly produce chromosomal sequences and specific methods are required to investigate rearrangement in cancer for the type of data we are considering.
Here we report the formal exposition and practical implementation of graph theory methods for reconstructing contigs derived from the eventual architecture of a cancer genome and the temporal sequence of rearrangements that generated them. We also develop a statistical model for intercalating the parallel processes of small-scale point mutation and large-scale genomic rearrangement in molecular time. We demonstrate that this mathematical framework works well with complete data sets, albeit with limitations imposed by the quality of the data and the complexities of the genomes. These techniques are illustrated with the pedagogic example shown in Figure 1 and the real examples described in Figure 3 below. These include new data from a primary breast cancer, PD3904, along with the cell lines HCC1187 and NCI-H209 that we have previously investigated (Howarth et al. 2008; Stephens et al. 2009; Pleasance et al. 2010b).
Figure 1.
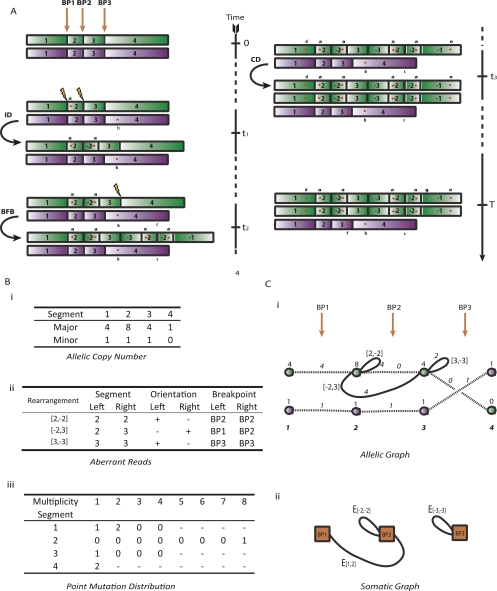
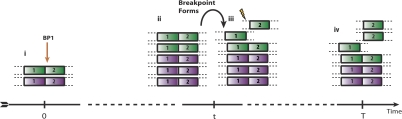
Genome evolution. Here we describe an example portion of the genome undergoing somatic rearrangement. (A) The evolution of the region through time, subject to three rearrangements—an inverted duplication, a breakage-fusion-bridge cycle, and a chromosomal duplication. (Green and purple) The parental alleles. The numbers indicate the segmental regions, a negative sign meaning a segment is in reversed orientation. (Red stars) Single-nucleotide mutations, a, b, …, g. (B) The observables. (i) Contains allelic integer copy numbers, counting each parental segment. (ii) Contains rearrangement data; the two segments forming the left and right connection are indicated, the negative sign indicating reversed orientation, along with the breakpoints involved by each segment. (iii) The distribution of single nucleotide mutations; the number in row s and column m counts the number of mutations in segments numbered s with multiplicity m. (C) Graphical representations of these data. (i) The allelic graph, representing the segments and their connectivity. Each node represents an allele of a segmented region; the numbers on nodes are major and minor copy numbers. Each black solid (curved) edge represents a rearrangement between two segments; the numbers on the edge represent the number of genomic copies of the connection. Each dotted black edge indicates a germline connection between two consecutive segments. The horizontal direction of each end of each edge indicates the side of the segment that is attached. (ii) The somatic graph. Each node represents a somatic breakpoint. Each edge connects two nodes, representing a rearrangement implicating the two associated breakpoints. Each end is attached to the side of the breakpoint the rearrangement involves.
Figure 3.
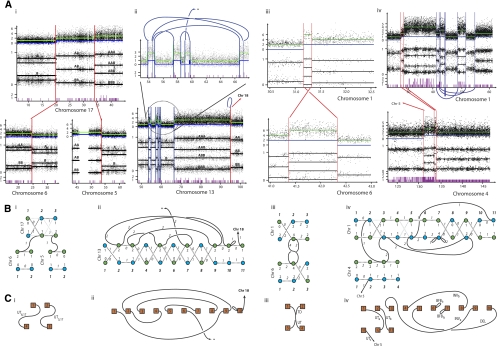
Copy number segment connectivity. Here we display copy number segmentation, rearrangement data, and single-nucleotide mutation data for four sets of rearrangements. The first two (i and ii) involve primary breast cancer sample PD3904, iii and iv involve cell lines HCC1187 and NCI-H209, respectively. Each chart in A presents the output from the PICNIC segmentation algorithm, the upper plot being total copy number and the central plot representing genotype intensity. (The lower plot) Single-nucleotide mutations. (Green) Total copy number; (blue) minor copy number. (Blue) The intra-chromosomal rearrangements; (red) inter-chromosomal rearrangements. (B) Allelic graphs for each rearrangement cluster. (Gray lines) Alternative graph topologies. The blue and green node colors highlight individual parental chromosomes. (C) Somatic graphs for the clusters. Each component represents a transformation, the type indicated with a label. The acronyms are defined in Figure 2.
Results
A pedagogic example
To provide motivation and describe both the type of information produced and the questions these data generate, consider the hypothetical example given in Figure 1. Here we observe a region of the genome throughout transformation from wild-type formation to rearranged cancer genome.
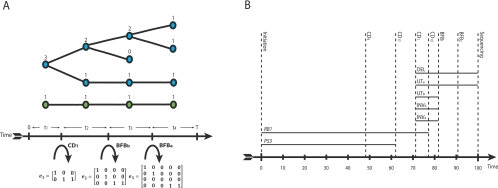
We start with two parental copies of a genomic region at a nominal time zero. We assume that there is a single-nucleotide (point) mutation process mutating the genome at a fixed rate per megabase per time unit. Over the time interval (0, t1), the region accumulates two mutations, labeled a and b. At time t1 we have our first genomic transformation, an inverted duplication (ID) in which the region from positions BP1 to BP2 is copied and inserted in inverted orientation adjacent to the original region. Note that we now have two copies of the point mutation a. Over the time period (t1, t2), one of the contigs accumulates another point mutation c, at which point we have our second transformation—a breakage-fusion-bridge (BFB) cycle. This process occurs when a double-stranded DNA (dsDNA) break acquired during the G0/1 phase of the cell cycle is duplicated during DNA replication, and the two identical chromosomal ends are directly joined, leading to an inverted orientation of the two copies of the segment at the breakpoint (Lo et al. 2002; Bignell et al. 2007). In our hypothetical example, the breakpoint BP3 represents the position where the duplicated chromosomal arms or segments were joined. These three breakpoints split the original genomic configuration into four segments (labeled 1, 2, 3, and 4 in Fig. 1), noting that each segment has a constant copy number and is demarcated at each end by either rearrangements or telomeres. This series of duplications now results in four copies of mutation a. The period (t2, t3) witnesses the arrival of two more mutations d and e, at which point we see our third transformation—a chromosomal duplication (CD). The final time period (t3, T) results in two more mutations f and g, at which point the genome is sequenced. We now have the three chromosomes displayed, which we represent algebraically as three sequences of segment numbers: 2×[1 2 −2 3 −3 2 −2 −1] and [1 2 3 4], the negative signs implying reversed orientation.
The evolution as we have just described cannot, of course, be observed. Given such a sample, we instead would perform a variety of experiments to investigate the genome. Firstly, we can use a microarray to investigate the integer allelic copy number. For our example, this would reveal both the genomic coordinates of the four segments and three breakpoints and give the number of copies for each parental allele. These data are displayed in Figure 1Bi. This tells us how many copies and the genomic coordinates of the segments, but not how they are connected. Our second step is to use massively parallel paired-end sequencing to determine this. Specifically, any paired-end reads that bridge a somatic connection can be identified because they have end sequences that map to disparate regions of the reference genome, or an end in reversed orientation. This will tell us both which segments are pairwise connected and which ends of those segments are attached. This will identify three possible aberrant connections, given in Figure 1Bii. Paired reads of type [2, −2] arise when they bridge the connection of the right end of a copy of the second segmented region to the same end of an identical segment. This can occur at any of the four intersections denoted algebraically as [… 2 −2 …] in Figure 1A. Paired reads of type [−2, 3] arise when they bridge one of the four connections of the left end of a copy of the second segment to the left end of a copy of the third segment (type [−3, 2] are equivalent, reading an inverted genome). Finally, paired reads of type [3, −3] occur when they bridge any of the two somatic connections of the right side of two copies of third segments. Our third experimental approach uses the sequences in the ends of paired reads to identify the point mutations. Comparing the frequency of reads that contain the mutated base to those containing the wild-type reference base allows us to infer the number of genomic copies of each point mutation. The resulting data for this example are given in Figure 1Biii.
Given these observables, several natural questions arise. Firstly, how can we use these data to construct the digital karyotypes 2×[1 2 −2 3 −3 2 −2 −1] and [1 2 3 4]? Secondly, from the example we saw that of the three genomic transformations, the ID produced the two rearrangements [2, −2] and [2, −3], the BFB event resulted in a single rearrangement [3, −3], and the CD produced no rearrangement data. Can we find a general method to cluster the rearrangements into transformations, and can we use these clusters to identify the types of transformation that have taken place? Thirdly, we know from the evolution described in Figure 1A that the three events occurred in the order ID < BFB < CD. If we know what transformations have taken place, is there a method to formally deduce this order? Finally, we have seen that in the first segmental region, there were two mutations, d and e, that have two genomic copies. These occurred prior to the BFB event. There is also one mutation with a single genomic copy, g. This occurred after the BFB event. The ratio of these two classes of counts will be a function of the timing of the BFB event. The final question we consider is the following: Can we use the point mutation data to estimate when the transformations occurred?
Our approach uses the observables to investigate these questions with the following six steps: The first step extracts the mutation portfolio of the cancer genome with a range of modern sequencing techniques. The second step constructs the allelic graph. This is a way of representing both the allelic integer copy number segments and the connectivity between them. The third step considers path-walking techniques to extract chromosomal contigs. The fourth step constructs the somatic graph. This is a dual graph to the allelic graph and describes how different rearrangements and breakpoints cluster together into single genomic transformations. This also allows us to classify the transformations that have taken place into standard classes of genomic rearrangement. The fifth step implements in silico transformations on the reference genome to infer the likely order of events that took place. This technique also assembles the segments into digital karyotypes. The sixth step takes any putative order of events and uses the point mutation data to obtain maximum likelihood estimates of when the events took place.
In the following two sections, we provide a heuristic overview of these techniques, discussing a pedagogic example and then clinical data. Validation of the algorithm predictions with fluorescent in silico hybridization (FISH) is then detailed. An assessment of the accuracy and robustness of the methods and results are given with the aid of in silico simulations. A discussion then follows. A detailed description of the approach in Methods completes the study.
Method overview
The overall aim of our approach is to reverse-engineer the genomic evolution portrayed in Figure 1. Our techniques rely on six steps: Finding the genome mutation portfolio, constructing the allelic graph, finding paths in this graph to form digital karyotypes, constructing the somatic graph, and classifying the genomic transformations, determining their order, and finally timing rearrangements. We now describe each of these stages in detail.
The first step, determining the genomic data, is summarized in Figure 1B for this example.
The second stage is to represent the copy numbers and rearrangements with the allelic graph (Fig. 1Ci). The nodes represent both parental copies of each of four regions, giving 2 × 4 nodes. The numbers assigned to nodes are the allelic copy numbers (totaling 20, the number of segments). Each edge (connecting two nodes) represents a genomic connection between two adjacent segments (represented by the nodes). The straight dashed edges represent wild-type (germline) connections between segments. The curved solid edges represent somatically acquired connections between segments formed through rearrangement. Each end of an edge connects to either the left or right side of each node, corresponding to whether the left or right side of the segment is attached, respectively. The number assigned to each edge indicates the total number of such connections (for details of the calculations involved, see Methods and the Supplemental Material).
The third step constructs contigs. As we walk through the graph reading consecutive nodes, we are traversing contiguous segments represented by the nodes and so constructing digital karyotpes. For the example in Figure 1Ci, the leftmost and rightmost nodes represent the first and fourth regions that have telomeres at the ends, thus we start from such a node and walk through the graph until another telomere is reached (we assume no internal somatic telomeres for simplicity). Notice that the allelic graph has two components. If we walk across the simpler component with one copy of each edge and node, reading off the regions, we have [1 2 3 4]. This represents the (purple) wild-type chromosome in Figure 1A. The remaining component has copy numbers 4, 8, 4, and 0 associated with the nodes. We thus have four telomeric ends and so two paths to construct. Walking through the graph, we have two possibilities: two copies of [1 2 −2 3 −3 2 −2 1] or, alternatively, [1 2 −2 1] and [1 2 −2 3 −3 2 −2 3 −3 2 −2 1]. Note that the former pair of paths represents the final genomic conformation in Figure 1A. We explore further methods to deduce the correct configuration.
The fourth step is to construct the somatic graph given in Figure 1Cii. This graph enables the grouping of rearrangements into “events.” Each node now represents the genomic position of a somatic DNA break (rather than chromosomal segment), sequentially numbered BP1 to BP3 in Figure 1. Each edge represents an observed rearrangement. So, for BP1 (the break between segments 1 and 2) in Figure 1A, the segment to the right of BP1 (segment 2) is joined to the segment to the right of BP2 (segment 3). We represent this in the somatic graph as an arc (labeled E[1,2]) from the right side of BP1 to the right side of BP2. From the paired-end sequencing, we have also observed a rearrangement that joins the segment to the left of BP2 to itself, labeled E[−2,−2], and E[−3,−3], joining the left side of BP3 to itself. The utility of this construction is that each component of the resulting graph represents a set of rearrangements involved in the same genomic transformation (see Methods). The topology of these components can then be used to identify the type of genomic transformation. Figure 2 contains this information for a set of nine standard transformations observed in cancer genomes. We thus have two components in Figure 1Cii to compare with this dictionary of possibilities. We recognize the larger component as an ID and the smaller as a BFB. Finally, we note that because the total number of copies of telomeric nodes is six, there are three chromosomes, the reference genome is diploid, and so we must also have had a single CD. We have thus identified all three transformations that have taken place.
Figure 2.
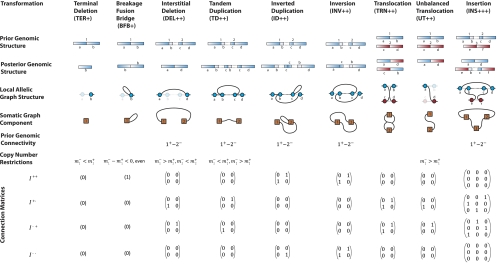
Transformation dictionary. A description of the effects for nine transformation classes named in the header row. The first and second rows describe the change in the genome. The third row highlights the allelic graph structure. The fourth row gives the corresponding somatic graph component. The fifth row describes genomic connectivity prior to the transformation. The sixth row describes the copy number profiles following the transformation. The remaining rows give the connection matrices. The signs associated with transformations indicate the orientation of the genome at breakpoints. All information is displayed for breakpoints arising in wild-type (non-inverted) regions of the genome. 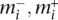 represent copy numbers for segments to the left and right side of breakpoint i.
represent copy numbers for segments to the left and right side of breakpoint i.  indicates that the right side of breakpoint i must be genomically connected to the left side of breakpoint j prior to the transformation.
indicates that the right side of breakpoint i must be genomically connected to the left side of breakpoint j prior to the transformation. 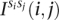 indexes rearrangement between breakpoints i and j, where Si and Sj are the genomic orientations at the breakpoints.
indexes rearrangement between breakpoints i and j, where Si and Sj are the genomic orientations at the breakpoints.
The fifth step tests different orders of these transformations in silico upon the germline genome to determine which reproduce the observed copy number profile and are thus consistent with the observed data. We have three events and so 3! orders to test. For each transformation we know which breakpoints are involved so we can implement the transformations upon the algebraic representations of chromosomes in an in silico manner. Consider the incorrect order ID < CD < BFB. From the allelic graph we have two components to consider. One is simply a wild-type chromosome and thus has no transformations to implement. This can be represented algebraically as [1 2 3 4]. It remains to apply the ID from breakpoint BP1 to BP2, a CD, and a BFB at BP3, to the other component, in that order. Initially, we have a single chromosome of the four segments [1 2 3 4]. We then have an ID from BP1 to BP2, giving us [1 2 −2 3 4]. The CD then gives us 2×[1 2 −2 3 4]. Finally, we apply the BFB at BP3. There are two copies of this position, but either gives us the final set of contigs—[1 2 3 4] from one allele and [1 2 −2 3 −3 −2 2 −1], [1 2 −2 3 4] from the other. Now when we examine the allelic copy numbers, we find the minor and major copy numbers for each segmental region are, in turn, (1, 3), (1, 6), (1, 3), and (1, 1). This does not match the observed values (Fig. 1Bi), and the order is rejected. The only order of transformations that correctly reproduces the observed allelic copy numbers is ID < BFB < CD, the evolution portrayed in Figure 1A.
We have now successfully identified and ordered the genomic transformations. The final step is to use the point mutations to time the transformations. The time points of Figure 1A are nominal, so we turn to real examples to effectively demonstrate these techniques.
Clinical data
In Figure 3Ai, we see the copy number profiles of chromosomes 5, 6, and 17 of primary breast cancer sample PD3904. There are two rearrangements between these chromosomes (highlighted in red). One is a genomic connection linking the right side of the first segment of chromosome 6 to the left side of the second segment of chromosome 17, denoted [16, 217]. The allelic graph (Fig. 3Bi) tells us that there is one genomic copy of this connection. This connection is between separate chromosomes, and so the simplest explanation is an unbalanced translocation, UT6,17. Note that segment 16 has a copy number of two and is homozygous. This region must have experienced a loss of one parental copy, CL6, followed by a duplication of the remaining allele, CD6. UT6,17 must have occurred after CD6 to ensure a single genomic connection (CL6 < CD6 < UT6,17). We also have the single genomic connection [15, 317], another unbalanced translocation, UT5,17. Region 317 has copy number three, indicating duplication (CD17), a duplication that again must have occurred before the translocation (CD17 < UT5,17). An in silico implementation of these events on the chromosomes (see the Supplemental Material) correctly recapitulates the observed data providing a parsimonious ordering of events, resulting in the following five digital karyotypes: [117 217 317], [16 217 317], [16 26], [15 25], and [15 317]. Note that we can also see this by constructing walks across the allelic graph. (There is also an alternative allelic graph that gives a slightly distinct solution.) (See the Supplemental Material.)
We now analyze these events chronologically by relating the multiplicities of point mutations in each segment to their copy number changes following the genomic transformations. Region 16 has 64 heterozygous single-nucleotide mutations, which must have occurred after duplication CD6, and only three homozygous mutations, which must have occurred before, indicating an early duplication. By assuming that these point mutations occur at a fixed Poisson rate, we can combine these counts with the evolution of copy number segments to estimate the duplication time. Specifically, because the three homozygous mutations occur on the one undeleted copy in the first time period prior to duplication and the 64 heterozygous mutations fall on either of two copies in the second time period following duplication, the ratio of these two time periods should be 3:32. We cannot determine the absolute times because any mutation count can result from a fast mutation rate in a short period of time or from a slow mutation rate over a long time period. We can, however, determine the relative time periods, which are normalized to percentages (see Methods). Indeed, the first time period has estimated time (see Methods) 8.57% (=3/35) (c.i. 1.80%–19.96%). Similarly, region 317 has 128 heterozygous and 14 homozygous mutations, implying that CD17 has an estimated time of 26.60% (c.i. 16.48%–37.79%). These are relatively distinct values suggesting that events occurred during distinct cell divisions.
Now having constructed a quantitative rearrangement history, the timing of these events can be examined in locations containing cancer genes to investigate the chronological implications on selection. When examining cancer genes for this example, we found a homozygous nonsense USP6 variant on chromosome 6. This gene, if causative, was likely to have been inactivated before the duplication event; otherwise, it would be heterozygous.
The resulting combination of orderings and timings can now be combined into a summary timeline of events (Fig. 4A).
Figure 4.
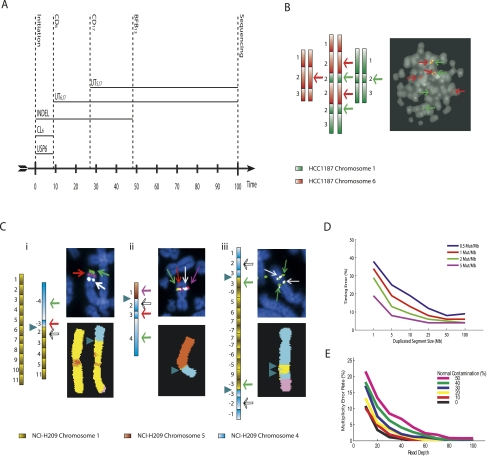
Validation. (A) The estimated timeline of rearrangement and selection events through oncogenesis relative to a molecular clock (along the horizontal axis) for the two clusters of PD3904. Events that can be timed are represented by vertical lines. Events that can only be ordered relative to these times are indicated by horizontal lines. (B,C) The predicted sequences of segments and FISH images for the two clusters of Figure 3iii,iv, respectively. Each segment is represented as a rectangle, with light to dark shading indicating the left and right ends of each segment. The number labels for each segment are as described in Figure 3 and the Supplemental Material. Green and red segments correspond to chromosomes 1 and 6 of HCC1187. Yellow, blue, and brown segments represent chromosomes 1, 4, and 5 of NCI-H209. Arrows indicate positions and luminescence of probes designed to test predicted adjacency of segments. For HCC1187, the green and red probes hybridize to segment 2 of chromosomes 1 (denoted 21) and 26, respectively. For Ci, white, red, and green probes hybridized to 21, 34, and 44, respectively. Magenta, white, red, and green probes in Cii hybridized to 15, 24, 34, and 44, respectively. Green and white probes in Ciii hybridized to 31 and 24, respectively. Breakpoints between chromosomes are represented by triangles. (D) The mean error of predicted rearrangement times. Mutations were generated at background prevalence of 0.5, 1, 2, and 5 mutations per megabase. Tandem duplications were constructed of lengths 1, 5, 10, 25, 50, and 100 Mb at random times. The mean errors of the prediction time of rearrangements from 1000 simulations are indicated. (E) The predicted error of multiplicity for normal contamination ranging from 0% to 50%, and read depth up to 100.
Validation
We now have a methodology to construct the rearrangement histories of some clusters of rearrangements, and we would like to examine the veracity of the predictions. The only feature that we can examine experimentally with reasonable ease is the predicted chromosomal contigs. This can be achieved with FISH techniques on cell lines. We implemented this approach for the two clusters of rearrangements in cell lines HCC1187 and NCI-H209 (rather than primary sample PD3904, where the source of DNA is limited), those of Figure 3iii,iv.
Using the techniques we have outlined above, the cluster of rearrangements between chromosomes 1 and 6 in HCC1187 is most parsimoniously explained as an unbalanced translocation, then a tandem duplication, followed by chromosomal duplication (UT < TD < CD) (for details of the evolution, see the Supplemental Material). This prediction results in the six contigs 2×[16 26 36], 2×[16 26 21 26 21 31], and 2×[11 21 31] given in Figure 4B. Using green and red FISH probes binding to segments 21 and 26, respectively, we would predict from the solution that there would be two copies of wild-type chromosome 1 (each with an isolated green probe), two copies of wild-type chromosome 6 (each with an isolated red probe), and two identical derivative chromosomes, each containing a red–green–red–green pattern. This is indeed what was observed (see Fig. 4B; Supplemental Material).
Applying our methodology to the complex cluster of rearrangements in NCI-H209 resolves the evolution into a combination of two chromosomal duplications, three unbalanced translocations, two inversions, a deletion, and two breakage-fusion-bridge cycles (see Methods; Supplemental Material). This results in four predicted contigs—[11 21 31 41 51 61 71 81 91 101 111], [−44 −34 21 31 41 51 111], [15 24 34 44], and [14 24 34 31 −91 51 61 71 −71 71 −71 −61 −51 91 −31 −34 −24 −14] (see Fig. 4C). We used FISH to examine the four predicted contigs (see the Supplemental Material). This confirmed not only the sequence of segments [−44 −34 21] bridging the translocations between chromosomes 1 and 4 (Fig. 4Ci), and the sequence [15 24 34 44] bridging the translocation between chromosomes 1 and 5 (Fig. 4Cii), but the genomic fold back caused by two breakage-fusion-bridge events is clearly reflected in the duplicated FISH probes shown in Figure 4Ciii.
Collectively, these data do not provide direct proof of the transformations we claim. However, they do confirm the predicted karyotype structure, implying that our rearrangement histories are correct.
Accuracy
Having constructed timelines of transformations, it is natural to enquire into the accuracy of results and their robustness under perturbation of the cancer genomes mutation portfolio.
We have assumed a unique breakpoint in regions of copy number change. Any paired read bridging the associated rearrangement has two ends that can act as primers for PCR confirmation, which resolves the breakpoint to base-pair level. In Supplemental Table 2 of Campbell et al. (2008), for example, we find that 43/94 rearrangements are direct joins of clean dsDNA breaks, without either overlap or inserted (non-templated) sequence. The remaining rearrangements all had a few bases (<9) of micro-homology (sequence identical and overlapping from either side of the breakpoint) that non-homologous end-joining DNA repair mechanisms used, but, importantly, we found no larger-scale sequence homology indicative of homologous recombination. Twenty-three out of 94 also had small shards of unmappable sequenced (<32 bases). These data suggest that each copy number change is associated with a specific and unique breakpoint and our assumptions are reasonable.
The accuracy of the predicted transformation orders is sensitive to the copy number estimates. Any error here will result in very different paths in the allelic graph and will adversely affect predictions of karyotype and transformation orders. This is also compounded by normal contamination, which has the effect of reducing the separation of copy number intensity between distinct copy numbers, making integer copy number estimation somewhat more difficult. For example, 50% contamination in a diploid sample will have similar differences between copy number intensities to a quadraploid cell line.
Furthermore, any incorrectly called or missed rearrangements will change the allelic and somatic graph topologies, making the identification of transformations difficult. This is compounded by the incompleteness of the Figure 2 dictionary. For example, NCI-H209 has 64 breakpoints identified by copy number segmentation, of which 55 (86%) had associated rearrangements found from sequencing data (×39 coverage, 112 Gb of sequence). HCC1187 (a sample with much lower coverage, 7 Gb of sequence) had 50 breakpoints identified by copy number segmentation of which only 21 (42%) rearrangements were found, along with one balanced breakpoint. All 51 of these breakpoints, along with two other balanced breakpoints, were found by FISH (Howarth et al. 2008; Supplemental Material). Comparison with Figure 2 enabled classification of 26 of these breakpoints; 14 were from unbalanced translocation, four from tandem duplications, two from terminal deletions, and six from deletions. However, 13 involved three clusters of rearrangements that could not be classified. Together this suggests that Figure 2 is a relatively comprehensive list, although further extensions are clearly required. The remaining 14 breakpoints could not be resolved into rearrangements and were of unknown type.
The accuracy of timing predictions will depend on both the point-mutation prevalence and the length of the genome under consideration. This was examined by simulating tandem duplications of various lengths, at random times, under different mutation prevalence to determine the accuracy of prediction. The lengths varied from 1 to 100 Mb, and the mutation prevalence varied from 0.5 to 5 mutations per megabase. Reasonable precision was obtained for duplication sizes and mutation prevalence that are typically observed in samples (see Fig. 4D; a prevalence × length ∼25 has a timing error ∼10%).
There will also be additional error arising from the estimation of multiplicity. This noise will increase with the degree of normal contamination and decrease with the depth of coverage. To consider these effects, we simulated mutations of multiplicities one and two in a diploid region and determined the error in multiplicity estimates for normal contamination between 0% and 50% and read depth between 10 and 100. The error was remarkably small, as seen in Figure 4E. Sample NCI-H209 is a cell line with no normal contamination and coverage of ×30, implying an error of ∼1%. For the primary sample PD3904, this was slightly higher with contamination of 26% and similar coverage giving an error of ∼3%. These levels of error will have a relatively small effect on the accuracy of timing estimation.
Discussion
We have developed a technique to help reconstruct the history of rearrangements responsible for cancer genome karyotypes. This uses allelic copy number segmentation, rearrangements, and somatic single-nucleotide mutation distributions, and so is based entirely on the final observed portfolio of mutations.
The simplest application of this method is to construct digital karyotypes with path-walking techniques that have classically required chromosomal painting. The number of solutions for the method used can become prohibitive for regions with higher copy numbers, and more efficient methods such as Pevzner et al. (2001) and Idury and Waterman (1995) may prove applicable to these types of multi-chromosomal problems. Furthermore, the solutions that these methods present may also contain circular loop solutions in general. Although this is biologically plausible as circular double-minutes, more specific approaches such as Fleischner (1990) and Raphael and Pevzner (2004) may be appropriate to differentiate circular and linear solutions.
This method also has the capacity to identify both the class and order of genomic transformations. However, transformations of greater complexity than those seen in Figure 2 are possible (as described in Methods [Fig. 3ii] and chromosomes 3 and 5 of NCI-H209 [Supplemental Material]; but see also Berger et al. 2011 and Stephens et al. 2011). Although classifying the transformations is not possible in these cases, the graph-walking techniques are generally applicable and can be used to reconstruct digital karyotypes. A fuller exploration of the biology behind these intricate cases is clearly warranted, and we believe the tools developed above will help unravel their genesis.
We also make chronological inferences on both genomic transformations and selection, which may have other applications—identifying periods of genomic instability, for example, or understanding the order of key oncogenic events; distinguishing early drivers, important to the induction of pre-cancerous clones, from more recent driving events that may be fueling metastasis. We note that the estimated times indicate when rearrangements occur relative to a background generation of point mutations, a rate that may vary with differing exposures to mutagenic environments. Consequently, these times should be viewed as a molecular rather than chronological clock, indicating the transformations’ likely occurrence within the accumulating mutational burden.
There are limitations to these methods. Firstly, temporal information is gleaned when rearrangements collude to produce complex genomes, telling us little about genomes less prone to rearrangement. Having smaller rearranged segments or lower point mutation rates will also reduce the accuracy of timing estimates. Secondly, missing data result in incomplete histories. For example, some rearrangements observed with chromosomal painting and associated copy number changes should lead to specific paired reads that are absent in the final data set. For the data presented, we found 65% of them. The missing data can be due to insufficient read depth, a problem easily rectified by deeper sequencing, but could also be breakpoints occurring in regions that are difficult to map uniquely, such as centromeric breaks or those formed by mechanisms relying on homology. The data presented are based on ends of ∼30 bases. Ends much longer than this are now possible, which will reduce missing data. Applying de novo assembly techniques to regions around putative breakpoints may help complete data sets and shed light on these difficulties. However, this will not help when deletion events remove all copies of a somatically acquired breakpoint. The construction of a full portrait of the rearrangement history then presents a complex hidden variable problem.
These methods also rely on precise data. High normal contamination (>50%) will make precise copy number estimation difficult, which is further complicated by higher ploidy. For complex products of rearrangements, such as those implicating mechanisms leading to amplicons, accurate data sets cannot be easily constructed, making rearrangement inference difficult. Furthermore, these techniques apply to a single clone. Until single-cell sequencing is realized, predictions for samples with greater cell-to-cell heterogeneity will be difficult.
The techniques we have introduced will thus be limited to well-curated clusters of rearrangements until more complete mutation portfolios for cancer genomes are obtained.
These techniques are publicly available with the implementation GRAFT (Genome Rearrangement Assembly For Tumors; www.sanger.ac.uk/genetics/CGP/Software/GRAFT).
Methods
We now describe each step of our approach in more detail.
Extracting mutation portfolios
To construct the mutation portfolio, we require integer allelic copy number segmentation, rearrangements of those segments, and the distribution of single-nucleotide mutations within each copy number segment.
Integer allelic copy segmentation for tissue contaminated with normal cells is possible on various platforms (e.g., see Van Loo et al. 2010; Yau et al. 2010). We used PICNIC on Affymetrix Genome Wide SNP 6.0 arrays, an algorithm initially designed for cell lines (Greenman et al. 2010) that has been updated to provide segmentation and normal contamination estimates for primary tissue samples (http://www.sanger.ac.uk/genetics/CGP/Software/PICNIC). Segmentation includes start and end coordinates, along with major and minor copy number estimates for each region, M and m. The resulting segmentation for the genomes analyzed can be found in the Supplemental Material. PD3904 had an estimated 26% normal contamination.
To identify rearrangements, paired-end read data were produced via Illumina GAX2 machines. Rearrangements were identified by extracting reads with ends that were either proximal to a copy number change, or where two read ends occur either side of a copy number neutral breakpoint (such as a translocation). We filtered for somatic events by selecting cases in which no corresponding reads were found in the reference sample. Confirmation of putative rearrangements was by polymerase chain reaction (PCR), which also resolves breakpoints down to the base-pair level.
The single-nucleotide somatic mutation loci were identified by filtering paired reads with ends containing single nucleotides that differ from the reference normal sample. The “multiplicity” of each mutation was estimated by taking all reads with an end that contains the position of the mutant base and comparing the number of reads containing the mutant base to the number of reads with a wild-type base. Specifically, each mutation exists in a segmented region with major and minor copy numbers M and m (obtained from PICNIC). Each somatic mutation initially occurs on one of the parental chromosomes (it is not known which one) and so has at most M copies when sequenced and has a multiplicity r ∈ {1, 2, …, M} to be estimated. If the position of the somatic mutation had ns and nw overlapping reads containing somatic and wild-type bases, and there was normal contamination π, we used a binomial model to provide maximum likelihood estimates of the number of chromosomal copies r containing that mutation
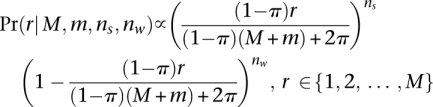 |
An explanation of this form, the resulting lists of point mutations, and the distributions of multiplicities within each copy number segment are given in the Supplemental Material.
Allelic graph
We now assume that we have a complete mutation portfolio for the genome under consideration. To find the genomic architecture that explains this configuration of copy number changes and rearrangements, we introduce the allelic graph, a graph construct in which nodes represent the allelic copy number segments and edges represent their pairwise connectivity (Fig. 3B).
To construct the allelic graph, we represent each copy number segmental region with two nodes, one for each parental allele, arranged in wild-type genomic order. The numbers associated with each pair of nodes are the major and minor allelic copy numbers (the allocation to top and bottom nodes is arbitrary). Each edge linking two nodes represents the existence of genomic connections between two corresponding segments. These edges fall into two classes depending on whether the two segments have this connection in the matched wild-type (normal) sample. We term these “wild-type” and “somatic” edges. To construct these, we need the following important principle.
Principle of allelic copy number conservation
Breakpoints are the genomic locations implicated in rearrangements, mainly coordinates of the ends of copy number segments but also positions of copy neutral rearrangements such as translocation. Consider then the local neighborhood of any breakpoint, as depicted in Figure 5. Initially, there are two parental copies of the genome either side of the breakpoint (Fig. 5i), which are connected together in wild-type formation. There will be a moment during clonal development when this breakpoint is implicated in a rearrangement. Prior to this event, there may have been other rearrangements affecting the number of copies of this region, but all connections across this position will be wild type (Fig. 5ii). The rearrangement then implicates the breakpoint. This will likely involve a single chromosome, and so the somatic change involves one particular parental allele; the other allele is unaffected at this breakpoint and remains in wild-type configuration (Fig. 5iii). Although there will be other rearrangements that alter the number of copies of these segments, it is highly improbable that the same breakpoint will be implicated, resulting in the final portrait of Figure 5iv. We then find that when we consider the allelic copy numbers of the two copy number segments bridging a breakpoint, two of them must be equal, which are also connected together in wild-type formation. The other two alleles, quite possibly unequal, must be involved in the somatic rearrangement. Note that some copies of these alleles may also be connected together in wild-type formation.
Figure 5.
Allelic copy number conservation. A notional sketch of the implication of a breakpoint. (i) The two parental alleles either side of the breakpoint. (ii) After some time, we may have more than one copy of each. (iii) The breakpoint is implicated on one chromosome of one allele. (iv) Further copy number changes occur leaving one parental allele conserved across the breakpoint.
We can now use this observation to construct the edges of the allelic graph. Wild-type edges represent the normal genomic configuration, joining segments adjacent in the germline. We take all pairs of copy number segments consecutive in the germline and identify the alleles with identical parental copy numbers. These are genomically connected, and so the corresponding nodes are joined with a wild-type edge. These are the dashed straight edges in Figure 3B. The other two nodes represent alleles involved in the somatic formation of the breakpoint. Some copies of these may also be connected in the germline and are also joined by a wild-type edge. Formally, we represent this as follows.
Each segmental region is labeled as sc for segment s of chromosome c. The major and minor copy numbers 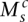 and
and 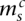 represent the larger and smaller allelic copy numbers (allocation is arbitrary if equal) and are each associated to a node. We know from the principle of allelic copy number conservation that at least one of (
represent the larger and smaller allelic copy numbers (allocation is arbitrary if equal) and are each associated to a node. We know from the principle of allelic copy number conservation that at least one of (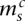 ,
, 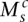 ) matches at least one of (
) matches at least one of (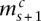 ,
, 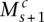 ), and the corresponding segments are connected. We let
), and the corresponding segments are connected. We let 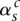 index how the copies of major and minor alleles of segment sc connect to neighboring segment (s + 1)c. The value
index how the copies of major and minor alleles of segment sc connect to neighboring segment (s + 1)c. The value 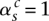 indicates that the major alleles (copy numbers
indicates that the major alleles (copy numbers 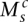 and
and 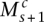 ) are joined together, as are the minor alleles (copy numbers
) are joined together, as are the minor alleles (copy numbers 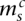 and
and 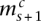 ) (the corresponding nodes are attached with the horizontal dashed edges). The value
) (the corresponding nodes are attached with the horizontal dashed edges). The value 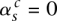 indicates that major and minor alleles are joined together (
indicates that major and minor alleles are joined together (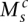 with
with 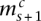 and
and 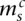 with
with 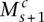 , the angled straight dashed edges). In general, we have, for 1 ≤ s < Sc
, the angled straight dashed edges). In general, we have, for 1 ≤ s < Sc
When a segment has equal major and minor copy numbers, we cannot unambiguously determine how the wild-type edges join, doubling the number of valid allelic graphs. This occurred at 17% of breakpoints we examined.
Somatic edges represent connections acquired somatically by the cancer clone (the curved continuous lines). Each somatic edge corresponds to a single genomic rearrangement, representing a somatic connection between two segments. For each segment involved, either the left or right side is connected. The corresponding end of the somatic edge then extends from the corresponding node in the left or right direction, respectively. Subsequently, each end of an edge either points in a leftward or a rightward direction, resulting in a bidirectional graph, a type of graph that has seen utility in assembly problems (Myers 2005; Medvedev et al. 2007). To draw the somatic connection, we need to identify the node involved, that is, specify whether the major or minor allele is implicated. Generally, the allele involved in a somatic edge can be identified unambiguously by applying the principle of allelic copy number conservation and finding the wild-type edges linking nodes of unequal copy number.
Consider the breakpoint separating the copy number segments with allelic copy numbers 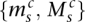 and
and 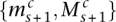 . We indicate the parental alleles involved in the formation of this somatic breakpoint with binary parameter
. We indicate the parental alleles involved in the formation of this somatic breakpoint with binary parameter 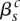 . The value
. The value 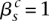 indicates that major allele
indicates that major allele 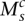 and its wild-type partner (the allele it is connected to with a straight wild-type edge) were involved. The value
and its wild-type partner (the allele it is connected to with a straight wild-type edge) were involved. The value 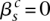 indicates that the minor allele
indicates that the minor allele 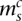 and its wild-type partner were involved. This is represented formally as follows:
and its wild-type partner were involved. This is represented formally as follows:
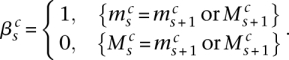 |
When both the major and minor alleles are equal in value to their wild-type partner, we have to consider both possibilities, doubling the number of allelic graphs.
Each valid array pair 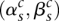 describes a unique “topology” for the allelic graph. We now assume that a single topology is under consideration.
describes a unique “topology” for the allelic graph. We now assume that a single topology is under consideration.
To complete the graph, we need to quantify the edges, or equivalently, count the number of times pairs of segments connect in the specified orientation. To deduce this, we invoke the following observation.
Edge conservation principle
Each end of every segment must do one of three things. Firstly, it could be attached to its wild-type partner. Secondly, it could be somatically attached to another segment. Finally, it could be capped with a telomere. These possibilities must account for all genomic copies of the segment. Thus, we find that the sum of the number of copies of all edges (and telomeres) touching the left (respectively, right) side of the allelic node must equal the allelic copy number of that node.
For all the examples we considered there were no somatic telomeres, and for simplicity of presentation we now assume that all telomeres are at wild-type positions.
These calculations constitute an integer programming problem (see the Supplemental Material). We solved this with brute force, which provided sufficient efficiency for the problems we encountered. This completes the description of the allelic graph, and we now have a complete representation of both allelic copy number segmentation and corresponding rearrangements. We make five remarks concerning this construction.
Firstly, note that each edge arising from a breakage-fusion-bridge cycle accounts for two copies of a node because the single rearrangement is involving two copies of the region represented by the node. For example, the BFB edge attached to the right of segment 71 in NCI-H209 only has two copies but accounts for all four copies of 71 (Fig. 3Biv).
Secondly, such systems of equations neither have to have a solution (the topology being tested may be incorrect and be rejected), nor a unique solution (different combinations of rearrangements may produce the same data). It is possible that the frequencies of reads corresponding to the edges can be used to determine the most likely solution (see the Supplemental Material). The examples we considered only had one solution, however.
Thirdly, the examples we have considered have not included any somatic telomeres. The construction we described includes the possibility of somatic telomeres that will form in processes such as chromosomal arm loss. These may be identified by finding paired reads such that one end contains the telomeric repeat pattern of TTAGGG or CCCTAA.
Fourthly, fundamental to our construction is the assumption that each breakpoint is implicated once in a single chromosome, which the principle of allelic copy number conservation requires. However, repair mechanisms mediated by homologous recombination may violate this assumption. For example, gene transfer can copy one segment and substitute it in the same position on another chromosome, using the same two breakpoints twice, which results in copy neutral LOH. If we consider moving across one of the breakpoints into LOH, both parental copy numbers change (1,1 to 0,2). This violates allelic copy number conservation. There will also be no discordant reads bridging the breakpoint. These two facts can help identify these positions. The methods we introduced need extending to cater for such effects. However, an examination of consecutive allelic copy numbers in the segmentation used in Bignell et al. (2010) revealed very few candidate regions, and none were present in the examples presented. Furthermore, the resultant DNA only differs at single-nucleotide polymorphisms, and so there are no structural differences.
Finally, we note that the allelic graph as defined is analogous to the breakpoint graph that is commonly used in the literature to investigate rearrangements (Pevzner 2000). Specifically, a contig of segments is often represented as a breakpoint graph in which pairs of consecutive nodes of the graph are arranged in the linear sequence as they appear in the contig. The edges that connect the nodes of this graph come in two categories. Firstly, there are the straight edges (denoted black edges in the literature) that connect segments consecutive in the observed contig and so are analogous to the somatic connections in our constructions. Secondly, there are curved arc edges (denoted gray edges) that connect numerically consecutive segments and so represent pairs of segments that would have been originally connected. These are analogous to the wild-type connections in the allelic graph. For the data we have, we typically do not have contigs. Instead, we have simply reversed the breakpoint graph in the following sense. Writing the segments of a contig out in order essentially represents the genome at its final stage. By writing out the copy number segments in wild-type order, we are instead representing the genome at its initial state. The curved gray edges of the breakpoint graph then become our wild-type straight edges, and the straight black edges of the breakpoint graph become the curved somatic edges in our allelic curve. This reversal of representation allows us to describe the copy number and rearrangement information without having to know the structure of the contigs, which, after all, is one of the aims of this study, which we now address.
Graph walking
We wish to use the allelic graph to assemble the segments into contigs. Many assembly methods have been developed that use overlapping sequences and use frameworks such as De Bruin graphs to construct sequences of contigs for genomes with unknown sequence (Pevzner 2000; Zerbino and Birney 2008). The problem we consider here is distinct; we know the sequence for each segment and how they are pairwise connected. We are simply trying to put these pairwise connections of two consecutive segments into contigs of multiple segments.
To do this, we now assume that we have a complete allelic graph. This means that we know how parental copies of each genomic segment connect to each other, the orientation of the connected segments, and how many copies of these connections exist. This information enables us to glue together these segments into digital karyotypes. To construct a solution, we simply start from a node representing a segment with a telomere and walk along the edges of the graph (away from the telomere) until another telomeric node is reached, respecting the bidirectionality dictated by the graph. This walk is equivalent to joining consecutive segments and so reconstructs individual chromosomes. The number of telomeric nodes counts the number of such paths, and so the number of chromosomes, twice. The edge and node counts tell us how many times each connection and segment must be used by all such paths.
Consider the example given in Figure 3Bii, which consists of a complex cluster of 11 copy number segments of chromosome 13 involving six intra-chromosomal rearrangements and two translocations, one to chromosome 18 and another that could not be identified (represented as *) either because it involved a repetitive region that could not be mapped or because it is capped by a telomere. There are six ends and so three contigs to construct. The topology of the allelic graph reveals a component that is a wild-type chromosome (the blue nodes). The other two contigs derive from the remaining component, which is comprised entirely from the remaining parental allele. One is simply a translocation to chromosome 18. For the remaining contig, we walk through the allelic graph starting from * following the only possible solution; the palindromic contig [* 7 −5 3 9 2 10 −10 −2 −9 −3 5 −7 *]. We have thus assembled the genome without any assumptions on the rearrangements that have taken place.
Other examples with greater complexity may well contain more than one solution, and more sophisticated methods are required. We took the following exhaustive approach. Each vertex has the same number of edges approaching the segment from one side, m, that exit from the other. Any path using an approaching edge can continue onto any of the exiting edges on the other side. Thus, we assign a permutation matrix to each node from the symmetric group Sm, describing how all edges either side of the node are pairwise connected. This encapsulates all possible paths through the allelic graph. One then starts from a telomeric node and follows the path dictated by the permutations to obtain a viable chromosome structure. Repeating this process for all possible combinations of permutation matrices will produce all possible paths.
Clearly only one of these solutions can have plausibly arisen during the cancer's development. We now explore methods to help reveal which set of contigs is likely to be correct, and what rearrangements led to this structure.
Somatic graph
We would like to investigate the extent to which we can firstly cluster rearrangements into single transformations and secondly identify their nature. To achieve these two aims, we introduce the somatic graph.
The allelic graph essentially described how the segments are connected. The somatic graph is a dual graph, describing instead how rearrangements and breakpoints relate. A breakpoint is the genomic position implicated in a rearrangement. One of the two segments either side of this position is attached in rearrangement to the end of another, possibly remote, segment, marking the location of a second breakpoint. Rearrangements thus connect pairs of breakpoints. We then first form a single node for each breakpoint. For any chromosome there must be one less breakpoint than the number of segmented regions. These are arranged horizontally in genomic order as shown in Figure 3C. They are numbered sequentially so that breakpoint b corresponds to the position between segments b and b + 1. Each rearrangement links two breakpoints (possibly the same breakpoint twice). This connection is represented by an edge connecting the associated nodes. The segment to the left or the right of the breakpoint is implicated by each rearrangement. We represent this by attaching the end of the edge to the left or right side of the node, respectively. As with the allelic graph, each end of each edge has two possible directions, resulting in a bidirectional graph. The relationship between components and genomic transformations is a general phenomenon that relies on the following principle.
Somatic graph component principle
Any edge connecting a pair of nodes in the somatic graph represents an individual rearrangement between the two corresponding breakpoints. These events must have arisen simultaneously. Conversely, as a breakpoint is implicated once in a single moment, all rearrangements involving that breakpoint must have occurred at the same time. We thus conclude that all edges touching the node corresponding to that breakpoint represent rearrangements that occurred concurrently. We can extend this argument inductively across all nodes and edges within a single component of the somatic graph to conclude that each component represents events that occurred simultaneously.
We would like to be able to use each component to help identify the underlying transformation that took place at that moment. There is a variety of standard transformations that modify genomic segments in a cancer genome. In this study, we consider the dictionary of nine transformations described in Figure 2. Each transformation generates a distinct set of breakpoints that are pairwise connected in the somatic graph by edges representing somatic rearrangements between them.
To encapsulate the structure of each component and help characterize the nature of the underlying transformation, we introduce binary connection matrices. These matrices index the connections between breakpoints represented by edges in the somatic graph. Each edge represents a rearrangement involving two breakpoints. This also involves two segments. Each segment is either to the left or the right side of the breakpoint involved. Each end of the edge then has left or right directionality (−/+), corresponding to the side of the breakpoint implicated in the rearrangement. Each edge has two ends and so four possible orientations associated with it, resulting in four matrices. The resulting matrices for standard transformations are indicated in Figure 2.
In general, the components of the somatic graph are readily identifiable via standard stepwise search algorithms (Gross and Yellen 2004). Each component of the graph belongs to a transformation. The somatic graph is bidirectional, so we represent each component within b breakpoints by four b × b binary connection matrices: 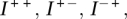 and
and  . Specifically
. Specifically
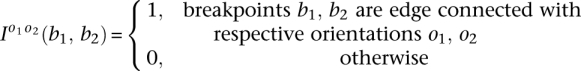 |
Note that these matrices have the following symmetries under transposition:
 |
For any rearranged cancer genome, the culpable genomic transformations result in the observed components of the somatic graph. We can now compare the connection matrices from each somatic graph component to Figure 2 to identify the possible transformations that have taken place. Note that we must consider various permutations of the data. Firstly, the order of the breakpoints needs to be permuted (permute the rows and columns of the connection matrix); the formulation listed represents a specific use of breakpoints. Secondly, the genome at a breakpoint could have been inverted from a preceding transformation. Any transformation operating on a segment on one side of a breakpoint will thus appear to operate on the opposite side of the breakpoint when viewed in the reference genome. This changes the side of the node that the corresponding edge attaches to, and so the sign of one of the matrix superscripts. We thus need to consider all possible genomic orientations at the breakpoints.
Many transformations require two breakpoints to be genomically connected prior to the transformation event. For example, a tandem duplication from breakpoint b1 to b2 requires the segment to the right of b1 (as viewed in the reference genome) to be connected to the segment on the left of b2, which is represented as 1+ ∼ 2−. If the genome at b1 was inverted by an earlier transformation, it will be the segment to the left of b1 (as viewed in the reference genome) that is genomically connected, and the condition becomes 1− ∼ 2−. Any permutations of breakpoints or reversed orientations also need to be applied to these conditions of connectivity (for an explicit example of these transformations, see the Supplemental Material).
The specific comparisons are implemented as follows.
We have the four observed connection matrices  for B breakpoints i, j = 1, 2, …, B and orientations o1, o2 ∈ {±}. We have a candidate test transformation with connection matrices
for B breakpoints i, j = 1, 2, …, B and orientations o1, o2 ∈ {±}. We have a candidate test transformation with connection matrices 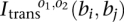 from Figure 2. We test a set of orientations τi ∈ {±}, i = 1, 2, …, B and a breakpoint permutation σ ∈ SB to see if all elements of the permutated observed connection matrices match the test transformation connection matrices:
from Figure 2. We test a set of orientations τi ∈ {±}, i = 1, 2, …, B and a breakpoint permutation σ ∈ SB to see if all elements of the permutated observed connection matrices match the test transformation connection matrices:
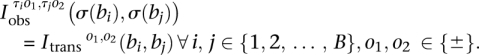 |
If we find a match, then this tells us three things. Firstly, the tested transformation is a valid class. Secondly the genome at breakpoint bi has orientation τi immediately prior to its formation. Thirdly, any requirements of genomic connectivity 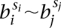 from the transformation dictionary in Figure 2 become
from the transformation dictionary in Figure 2 become 
A few remarks are in order. Firstly, there may be more than one match, and we must check all possibilities. Secondly, the number of breakpoints and number of edges represented in the test and observed matrices have to be equal to obtain a match; otherwise, the test transformation can be rejected without further comparison. Thirdly, the symmetries of the connection matrices outlined above mean that we only need to check a subset of these elements (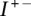 and the upper triangular portions of
and the upper triangular portions of 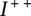 and
and  would suffice, e.g.). Fourthly, the symmetries in some of the transformations mean that not all permutations need be considered. Specifically, both the inversion and the translocation are symmetric (see Fig. 2), and no permutations are necessary. The insertion connection matrices are invariant under three-cycle permutations of breakpoints, and so only the three transpositions need be considered (i.e., swap pairs of breakpoints). Fifthly, if this fails to identify the transformation, we consider the possibility that subsequent rearrangements may have deleted all copies of some breakpoints. This means that some of the unit entries in
would suffice, e.g.). Fourthly, the symmetries in some of the transformations mean that not all permutations need be considered. Specifically, both the inversion and the translocation are symmetric (see Fig. 2), and no permutations are necessary. The insertion connection matrices are invariant under three-cycle permutations of breakpoints, and so only the three transpositions need be considered (i.e., swap pairs of breakpoints). Fifthly, if this fails to identify the transformation, we consider the possibility that subsequent rearrangements may have deleted all copies of some breakpoints. This means that some of the unit entries in 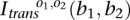 may be zero in
may be zero in 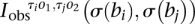 . The two INVs of Figure 3Civ are examples of this, each having a somatic connection removed by BFBs.
. The two INVs of Figure 3Civ are examples of this, each having a somatic connection removed by BFBs.
By comparing the information from each component of the breakpoint graph to the dictionary of Figure 2, we can identify the set of possible transformations that caused the breakpoints. This just leaves the large-scale events such as chromosomal gain and loss that do not implicate breakpoints. To determine this, we calculate the difference in the observed number of telomeric nodes to the original number at wild type. This counts the number of chromosomal losses (CL) or duplications (CD) twice. We need to make an adjustment if there are any unbalanced translocations (UTs) taking place, as each such event will lose a chromosome.
We now have a general method to identify standard classes of transformations that have taken place. However, we note that the dictionary of transformations given in Figure 2 is unlikely to be complete. Take the example in Figure 3ii, where we have three localized copy number gains with a copy number of 3 surrounded by a copy number of 1. This simple-looking copy number profile actually involves a complex of six internal rearrangements, one rearrangement to an unknown location and a translocation. The four components of the resulting breakpoint graph point toward some interesting complexities. The components {1, 2, 4, 9}, {3, 8}, and {5, 7} are three transformations likely to have produced these segments along with component {6}, linking to some other unknown region. The final component {10} involves a BFB and the translocation. Given the copy numbers, this suggests the final transformation caused breakpoint 10, a BFB doubling the complex arrangement of segments. This is further reinforced by the palindromic contig, the path-walking method produced in the previous section. However, instead of losing the genome to the right of the breakpoint (as is normal with a BFB cycle), the remaining segment was stitched to a region in chromosome 18. Note that although we cannot classify these rearrangements into any of the standard classes of Figure 2, the machinery has still allowed us to point to an interesting probable sequence of events.
We now assume that we have constructed a complete list of candidate transformations involved in the cancer genome's formation. This provides no indication of which order they are likely to have occurred in. We now consider this problem in more detail.
Ordering transformations
We now assume that we have a list of candidate transformations, and we know the mutually exclusive sets of breakpoints each transformation implicates. We wish to determine which possible orders of these events are consistent with the observed data. Note that the solution will not necessarily be unique (two transformations on separate chromosomes can occur in either order with the same result).
We take a two-pronged attack to determine the possibilities. We first demonstrate that the number of copies of somatic connections limits the number of possible sequences of transformations. The second approach involves in silico implementation of transformations to see which possible orders recapitulate the observed copy number profile.
The principle of allelic copy number conservation assumes that breakpoints occur at unique positions on single chromosomes. The rearrangements forming these breakpoints are assumed to do so once with a somatic edge count of 1. Any subsequent transformation from the dictionary of Figure 2 will do no more than double either node or edge counts. Consider the allelic graph of Figure 1Ci. The rearrangement associated with the BFB has an edge count of 2. This was originally 1 at formation and requires at least one subsequent event so was either the first or second transformation. The two edges associated with the ID have an edge count of 4. When this first forms, the edge counts are 1, and so we require two subsequent events. This must have been the first event. The edge counts then tell us the only possible order, ID < BFB < CD.
In general, an allelic graph edge has count e. Higher values imply earlier events and allow us to place restrictions on the possible orders of transformations. Specifically, an edge with value e must have received at least 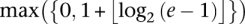 ensuing duplications after its formation. We can maximize this over all somatic edges associated with the transformation to obtain the minimum number of subsequent transformations that took place.
ensuing duplications after its formation. We can maximize this over all somatic edges associated with the transformation to obtain the minimum number of subsequent transformations that took place.
At this stage, we still do not know whether any putative order of transformations is consistent with the observed data. To test any candidate order, we start from a germline configuration of the genome and sequentially apply each transformation in silico to identify which cases recapitulate the observed copy number data. Specifically, for any putative order of transformations T1 < T2 < T3 < … < TR, we have (for more details, see the Supplemental Material):
Step 1: Construct algebraic chromosomes in a germline configuration of segments
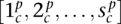 for each parental allele p of chromosome c.
for each parental allele p of chromosome c.Step 2: For transformation Tr, find the positions of all rmax breakpoints
 implicated by the transformation in the algebraic chromosomes (there may be more than one location for each breakpoint).
implicated by the transformation in the algebraic chromosomes (there may be more than one location for each breakpoint).Step 3: Sequentially apply transformation Tr to algebraic chromosomes (as defined in Fig. 2; see also the Supplemental Material) trying all positions found in Step 2. If not possible with any combination of breakpoint positions, reject the transformation order.
Step 4: Count the allelic copy numbers from algebraic chromosomes. If these values agree with the experimentally observed values, output both the order of events and the resulting algebraic contigs; otherwise, reject the order.
These methods are capable of dealing with considerably greater complexity; the cluster of NCI-H209 (Fig. 3Aiv) results from two inversions (INVa, INVb), two breakage-fusion-bridge cycles (BFBa, BFBb), a deletion (DEL), three unbalanced translocations (UTa, UTb, UTc), and two chromosomal duplications (CD1, CD4). The only possible temporal orders that recapitulate the observations satisfy the following partial ordering:
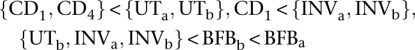 |
In silico implementation of transformations suggests that there are two possible configurations (depending on which chromosome the DEL occurs) (for details, see the Supplemental Material). Only one solution has a wild-type copy of chromosome 1. We cannot without additional information distinguish the two possibilities. However, chromosomal painting on the cell line suggested that there is a wild-type copy of chromosome 1, and the final genomic structure for this complex of rearrangement is composed of the four chromosomes shown in Figure 4C, three of which are rearranged.
We note that the allelic graph has two choices at the second and fourth breakpoints of chromosome 1 (Fig. 3Biv, gray dashed lines). Altering the connections at the fourth breakpoint separates the two ends of inversion INVa and is rejected as an allelic graph. Altering the connections at the second breakpoint switches the copy of chromosome 1 involved in the UTa event but has no effect on the order of rearrangements. It does, however, affect the resulting chromosomes, again resulting in no wild-type copy of chromosome 1 and so is rejected.
Timing evolution
From the previous section, we have one or more possible temporal orderings of rearrangements. Our aim is to estimate the time periods in which rearrangements occurred from the multiplicities of somatically acquired point mutations occurring in the rearranged segments. We now take each genomic segment, along with a proposed order of rearrangements, and track its evolution over the cancer's lifetime. This can be structured in terms of rooted binary “segmental evolution trees” (see Fig. 6A). Each node represents a copy of that segment during a time interval between rearrangements. Two nodes corresponding to consecutive time intervals are connected via an edge when either the rearrangement between the two time intervals does not affect that segment, or when it is duplicated. If a segment is deleted by a transformation, the node representing the segment prior to the transformation has no daughter nodes. The number of leaves emanating from the node present at the final time period is then equal to the multiplicity of any point mutations that occur in that segment during that time period. These are the numbers associated with each node.
Figure 6.
Timing. (A) The evolution tree for the rearranged allele of segment 51 from NCI-H209 (see Fig. 3Biv), which undergoes three transformations—a chromosomal duplication and two breakage-fusion-bridge cycles, resulting in four time periods. Each node represents a single genomic segment during a single time period. Three adjacency matrices e1, e2, and e3 are binary representations of the duplication events. The numbers at each node count the number of emanating leaves. These are obtained by matrix multiplication of the adjacency matrices (in reverse order) to the index vector [1,1,1,1,1]. (B) The predicted time line for the NCI-H209 rearrangement cluster.
Consider the example given in Figure 6A. This describes the evolution of segment 51 from the rearrangement cluster of NCI-H209 in Figure 3iv. We have seen that this cluster undergoes two CDs, two INVs, three UTs, two BFB cycles, and a DEL. The events that affect the number of copies of the segment are CD1, BFBa, and BFBb. To represent this, we start with two nodes, one for each allele. The first event is CD1, which duplicates one of the alleles. BFBb then duplicates one of the resulting copies. One of the daughter nodes has a value zero because the next event, BFBa, duplicates one of the copies but deletes the other (for evolution, see the Supplemental Material). There are thus three leaves present at the end of the evolution from the blue parental node, which is the number associated with the node. The other allele is unaffected throughout and has a value of 1.
If we assume that mutations are generated as a Poisson process, we can then use the distribution of mutation counts within segments to estimate the time periods. Formally, we proceed as follows: We denote the estimated number of mutations that have k genomic copies in copy number segment s at the end of the tumor's evolution by 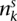 (we drop the chromosome index c for simplicity of exposition). We assume that there are R transformations bridged by time intervals t1, t2, …, tR+1 that we are trying to estimate. These have a fixed total time T. Each node of the evolution tree represents a single copy of a segment during a single time period. These are connected by an edge if they are either unaffected by the transformation between the two time periods, or the latter results from duplication of the first segment. The numbers associated with each node, lr,i (i and r index the nodes, representing the i-th copy of the segment prior to transformation r), are the multiplicities that any mutation occurring in that time interval will have at the end of the tumor development. These values equal the number of leaves emanating from the node at time T. This information is readily encoded by constructing adjacency matrices for each transformation. Specifically, if the segment s in question has I copies prior to transformation r, after which it has J copies, then the I × J binary matrix
(we drop the chromosome index c for simplicity of exposition). We assume that there are R transformations bridged by time intervals t1, t2, …, tR+1 that we are trying to estimate. These have a fixed total time T. Each node of the evolution tree represents a single copy of a segment during a single time period. These are connected by an edge if they are either unaffected by the transformation between the two time periods, or the latter results from duplication of the first segment. The numbers associated with each node, lr,i (i and r index the nodes, representing the i-th copy of the segment prior to transformation r), are the multiplicities that any mutation occurring in that time interval will have at the end of the tumor development. These values equal the number of leaves emanating from the node at time T. This information is readily encoded by constructing adjacency matrices for each transformation. Specifically, if the segment s in question has I copies prior to transformation r, after which it has J copies, then the I × J binary matrix 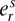 flags how the segments evolve. That is,
flags how the segments evolve. That is, 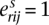 indicates that segment copy j derives from copy i following transformation r. We then multiply these matrices together to give the leaf counts at each node. Specifically
indicates that segment copy j derives from copy i following transformation r. We then multiply these matrices together to give the leaf counts at each node. Specifically
Next, assume that somatic point mutations occur at a rate of one per time unit per megabase of DNA. Now, if segment s has a length ρs megabases, then the copy associated with node (r, i) is assumed to accrue mutations with a Poisson distribution with mean ρstr during time interval tr. These mutations will all have 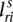 genomic copies in the final genome. Now, for any multiplicity k, there will be
genomic copies in the final genome. Now, for any multiplicity k, there will be 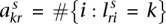 such segments (and so nodes) producing mutations with k copies at rate
such segments (and so nodes) producing mutations with k copies at rate 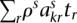 .
.
However, the observed count of mutations 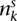 is likely to include errors. If matrix
is likely to include errors. If matrix 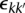 represents the probability that a mutation with k copies is estimated to have k′ copies, then the number
represents the probability that a mutation with k copies is estimated to have k′ copies, then the number 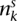 of mutations classified (rightly or wrongly) as having k copies will be Poisson-distributed with mean rate
of mutations classified (rightly or wrongly) as having k copies will be Poisson-distributed with mean rate 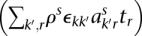 . Note that
. Note that 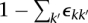 is the probability that the mutation is not classified and can be used to represent the likelihood that the mutation is not detected. (This will be more likely for low-multiplicity mutations as more paired-end read depth coverage is required to differentiate them from artifact. In all applications we used the identity matrix as the error matrix, assuming perfect multiplicity estimation.) In summary, we find that:
is the probability that the mutation is not classified and can be used to represent the likelihood that the mutation is not detected. (This will be more likely for low-multiplicity mutations as more paired-end read depth coverage is required to differentiate them from artifact. In all applications we used the identity matrix as the error matrix, assuming perfect multiplicity estimation.) In summary, we find that:
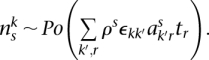 |
Combining this likelihood across all counts and segments provides a Poisson regression problem to estimate the rearrangement interval times t1, t2, …, tR. Most transformation events will affect more than one segment (such as CD). Clearly, the time that this occurs must be the same for all segments. Note that all time parameters scale with mutation prevalence in this expression. Subsequently, the absolute times or rates cannot be determined from these equations. We remove this redundancy by fixing the total time T at unity. All estimated times can then be thought of as a proportion of the accumulated mutational burden.
These restrictions can be formulated into linear constraints on the interval times and the timing estimation achieved by constrained maximum likelihood. When more than one topology or in silico simulation provides a viable transformation sequence, we use maximum likelihood to identify the most probable case. These solutions seed Markov chain Monte Carlo (MCMC) techniques to produce posterior distributions for the timing events, from which confidence intervals are assigned. These estimates are conditional on the mutation multiplicity estimates. For lower read depth data and higher contamination, there will be additional variation from the error in these estimates. To model this significantly complicates the MCMC and was not implemented in this study. Confidences arising from low contamination and deep sequencing data such as NCI-H209 will be relatively accurate; other confidence estimates should be viewed with more caution.
We note that these methods are only applicable to transformations that increase copy number and mutation multiplicity, so we can estimate the exact timing of the CD events but not UTs, for example. However, the ordering of all transformations can be combined with these times to construct timelines of evolution.
For example, when examining the timings for rearrangement cluster NCI-H209 in Figure 3iv, only the events CD1, CD4, BFBa, and BFBb increase copy number and can be timed. The CD4 event occurred at 47.8% (ci 42.6%–78.5%) through tumor development, the CD1 event occurred at 71.4% (ci 58.8%–78.6%) with BFBb and BFBa following at 82.4% (ci 80.5%–97.0%) and 91.6% (ci 86.5%–97.0%). The proximity in both time and position of the two BFB events are indicative of a single erroneous duplication event occurring during a single cycle of cell division.
Chromosomes 13 and 17 of NCI-H209 consist entirely of copy-neutral LOH (see the Supplemental Material). The most parsimonious explanation suggests chromosomal loss with duplication of the remaining chromosome (CL < CD). Only CD increases copy number and can have its timing estimated, resulting in estimates 77.6% (ci 74.3%–80.6%) and 62.4% (ci 57.3%–67.8%), for chromosomes 13 and 17, respectively, implying that duplications probably occurred during separate cell divisions.
We examined these regions for mutations in cancer genes and found that chromosome 13 of NCI-H209 contains a homozygous mutation in RB1 and chromosome 17 contains a homozygous mutation in TP53. Both mutations must have occurred prior to CD. Selection of RB1 and TP53 thus occurred before 77.6% and 62.4% of the acquisition of mutational burden, respectively. All this quantitative temporal information can be combined with the ordering determined previously to construct a timeline of the cancer's evolution (Fig. 6B).
Acknowledgments
This work was funded by the Wellcome Trust. S.N. was supported by an MRC studentship.
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.118414.110.
References
- Alekseyev MA, Pevzner PA 2007. Whole genome duplications and contracted breakpoint graphs. SIAM J Comput 36: 1748–1763 [Google Scholar]
- Alekseyev MA, Pevzner PA 2009. Breakpoint graphs and ancestral genome reconstructions. Genome Res 19: 943–957 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bader M, Ohlebusch E 2007. Sorting by weighted reversals, transpositions, and inverted transpositions. J Comput Biol 14: 615–636 [DOI] [PubMed] [Google Scholar]
- Bader M, Abouelhoda MI, Ohlebusch E 2008. A fast algorithm for the multiple genome rearrangement problem with weighted reversals and transpositions. BMC Bioinformatics 9: 516 doi: 10.1186/1471-2105-9-516 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger MF, Lawrence MS, Demichelis F, Drier Y, Cibulskis K, Sivachenko AY, Sboner A, Esgueva R, Pflueger D, Sougnez C, et al. 2011. The genomic complexity of primary human prostate cancer. Nature 470: 214–220 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bignell GR, Santarius T, Pole JC, Butler AP, Perry J, Pleasance E, Greenman C, Menzies A, Taylor S, Edkins S, et al. 2007. Architectures of somatic genomic rearrangement in human cancer amplicons at sequence-level resolution. Genome Res 17: 1296–1303 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bignell GR, Greenman CD, Davies H, Butler AP, Edkins S, Andrews JM, Buck G, Chen L, Beare D, Latimer C, et al. 2010. Signatures of mutation and selection in the cancer genome. Nature 463: 893–898 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell PJ, Stephens PJ, Pleasance ED, O'meara S, Li H, Santarius T, Stebbings LA, Leroy C, Edkins S, Hardy C, et al. 2008. Identification of somatically acquired rearrangements in cancer using genome-wide massively parallel paired-end sequencing. Nat Genet 40: 722–729 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell PJ, Yachida S, Mudie LJ, Stephens PJ, Pleasance ED, Stebbings LA, Morsberger LA, Latimer C, McLaren S, Lin M, et al. 2011. The patterns and dynamics of genomic instability in metastatic pancreatic cancer. Nature 467: 1109–1113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding L, Ellis MJ, Li S, Larson DE, Chen K, Wallis JW, Harris CC, McLellan MD, Fulton RS, Fulton LL, et al. 2010. Genome remodelling in a basal-like breast cancer metastasis and xenograft. Nature 464: 989–990 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleischner H 1990. Eulerian graphs and related topics I and II. Annals of Discrete Mathematics 45. Elsevier, New York [Google Scholar]
- Greenman CD, Bignell G, Butler A, Edkins S, Hinton J, Beare D, Swamy S, Santarius T, Chen L, Widaa S, et al. 2010. PICNIC: An algorithm to predict absolute allelic copy number variation with microarray cancer data. Biostatistics 11: 164–175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross L, Yellen J 2004, Handbook of Graph Theory, CRC Press, Boca Raton, FL [Google Scholar]
- Howarth KD, Blood KA, Ng BL, Beavis JC, Chua Y, Cooke SL, Raby S, Ichimura K, Collins VP, Carter NP, et al. 2008. Array painting reveals a high frequency of balanced translocations in breast cancer cell lines that break in cancer-relevant genes. Oncogene 27: 3345–3359 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Idury RM, Waterman MS 1995. A new algorithm for DNA sequence assembly. J Comput Biol 2: 291–306 [DOI] [PubMed] [Google Scholar]
- Lo AWI, Sabatier L, Fouladi B, Pottier G, Ricoul M, Murnane JP 2002. DNA amplification by breakage/fusion/bridge cycles initiated by spontaneous telomere loss in a human cancer cell line. Neoplasia 4: 531–538 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medvedev P, Georgiou K, Myers G, Brudno M 2007. Computability of models for sequence assembly, algorithms in bioinformatics. 7th International Workshop, WABI 2007, LNCS Vol. 4645, pp. 289–301 [Google Scholar]
- Myers EW 2005. The fragment assembly string graph. Bioinformatics 21: ii79–ii85 [DOI] [PubMed] [Google Scholar]
- Olshen AB, Venkatraman ES, Lucito R, Wigler M 2004. Circular binary segmentation for the analysis of array-based DNA copy number data. Biostatistics. 5: 557–572 [DOI] [PubMed] [Google Scholar]
- Ozery-Flato M, Shamir R 2009. Sorting cancer karyotypes by elementary operations. J Comput Biol 16: 1445–1460 [DOI] [PubMed] [Google Scholar]
- Pevzner PA 2000. Computational molecular biology: An algorithmic approach. MIT Press, Cambridge, MA [Google Scholar]
- Pevzner PA, Tang H, Waterman MS 2001. An Eulerian path approach to DNA fragment assembly. Proc Natl Acad Sci 98: 9748–9753 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pleasance ED, Cheetham K, Stephens PJ, McBride D, Egocheaga I, Greenman CD, Lin M, Ordonez G, Bignell GR, Ye K, et al. 2010a. A comprehensive catalogue of somatic mutations from a human cancer genome. Nature 463: 191–196 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pleasance ED, Stephens PJ, O'Meara S, McBride D, Meynert A, Jones D, Lin M, Beare D, Lau KW, Greenman CD, et al. 2010b. A small cell lung cancer genome. Nature 463: 184–190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raphael BJ, Pevzner PA 2004. Reconstructing tumor amplisomes. Bioinformatics 20: i265–i273 [DOI] [PubMed] [Google Scholar]
- Raphael BJ, Volik S, Collins C, Pevzner PA 2003. Reconstructing tumor genome architectures. Bioinformatics 19: ii162–ii171 [DOI] [PubMed] [Google Scholar]
- Sankoff D, Blanchette M 1999. Phylogenetic invariants for genome rearrangements. J Comput Biol 6: 431–445 [DOI] [PubMed] [Google Scholar]
- Shah SP, Morin RD, Khattra J, Prentice L, Pugh T, Burleigh A, Delaney A, Gelmon K, Guliany R, Senz J, et al. 2009. Mutational evolution in a lobular breast tumour profiled at single nucleotide resolution. Nature 461: 809–813 [DOI] [PubMed] [Google Scholar]
- Stephan-Otto Attolinia C, Chenga Y, Beroukhim R, Getz G, Abdel-Wahabg O, Levineg RL, Mellinghoff IK, Michora F 2010. A mathematical framework to determine the temporal sequence of somatic genetic events in cancer. Proc Natl Acad Sci 107: 17604–17609 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephens PJ, McBride DJ, Lin M, Varela I, Pleasance ED, Simpson JT, Stebbings LA, Leroy C, Edkins S, Mudie LJ, et al. 2009. Complex landscapes of somatic rearrangement in human breast cancer genomes. Nature 462: 1005–1010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephens PJ, Greenman CD, Fu B, Yang F, Bignell GR, Mudie LJ, Pleasance ED, Lau KW, Beare D, Stebbings LA, et al. 2011. Massive genomic rearrangement acquired in a single catastrophic event during cancer development. Cell 144: 27–40 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Loo P, Nordgard SH, Lingjærde OC, Russnes HG, Rye IH, Sun W, Weigman VJ, Marynen P, Zetterberg A, Naume B, et al. 2010. Allele-specific copy number analysis of tumors. Proc Natl Acad Sci 107: 16910–16915 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren R, Sankoff D 2009a. Genome halving with double cut and join. J Bioinform Comput Biol 7: 357–371 [DOI] [PubMed] [Google Scholar]
- Warren R, Sankoff D 2009b. Genome aliquoting with double cut and join. BMC Bioinformatics Suppl 110: S2 doi: 10.1186/1471-2105-10-S1-S2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yau C, Mouradov D, Jorissen R, Colella S, Mirza G, Steers G, Harris A, Ragoussis J, Sieber O, Holmes C 2010. A statistical approach for detecting genomic aberrations in heterogeneous tumor samples from single nucleotide polymorphism genotyping data. Genome Biol 10: R2 doi: 10.1186/gb-2010-11-9-r92 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zerbino DR, Birney E 2008. Velvet: Algorithms for de novo short read assembly using de Bruijn graphs. Genome Res 18: 821–829 [DOI] [PMC free article] [PubMed] [Google Scholar]