Calling amplified haplotypes in next generation tumor sequence data

Abstract

During tumor initiation and progression, cancer cells acquire a selective advantage, allowing them to outcompete their normal counterparts. Identification of the genetic changes that underlie these tumor acquired traits can provide deeper insights into the biology of tumorigenesis. Regions of copy number alterations and germline DNA variants are some of the elements subject to selection during tumor evolution. Integrated examination of inherited variation and somatic alterations holds the potential to reveal specific nucleotide alleles that a tumor “prefers” to have amplified. Next-generation sequencing of tumor and matched normal tissues provides a high-resolution platform to identify and analyze such somatic amplicons. Within an amplicon, examination of informative (e.g., heterozygous) sites deviating from a 1:1 ratio may suggest selection of that allele. A naive approach examines the reads for each heterozygous site in isolation; however, this ignores available valuable linkage information across sites. We, therefore, present a novel hidden Markov model-based method—Haplotype Amplification in Tumor Sequences (HATS)—that analyzes tumor and normal sequence data, along with training data for phasing purposes, to infer amplified alleles and haplotypes in regions of copy number gain. Our method is designed to handle rare variants and biases in read data. We assess the performance of HATS using simulated amplified regions generated from varying copy number and coverage levels, followed by amplicons in real data. We demonstrate that HATS infers the amplified alleles more accurately than does the naive approach, especially at low to intermediate coverage levels and in cases (including high coverage) possessing stromal contamination or allelic bias.

Tumor development and growth can be viewed as an evolutionary process (Nowell 1976). Genetic variation in the form of somatic alterations (e.g., mutations, translocations) and inherited polymorphisms provide the raw material for the acquisition of tumor-related traits. Copy number aberrations (CNAs)—regions of somatic amplification (amplicons) or deletion—are a hallmark of tumor genomics. Recurrent amplicons have been observed over two decades (Kallioniemi et al. 1992; Joos et al. 1995; Cher et al. 1996; Korn et al. 1999; Paris et al. 2004; Zhao et al. 2005; Sun et al. 2007a) and are believed to be advantageous to the tumor during tumor development.

Genome-wide scans of CNAs have progressed in resolution from technologies such as traditional comparative genomic hybridization (CGH) to array-based CGH (Solinas-Toldo et al. 1997; Bentz et al. 1998), including tiling array CGH (Ishkanian et al. 2004) and single nucleotide polymorphism (SNP) arrays (Wang et al. 1998; Lin et al. 2004); methods for copy number detection on such platforms oftentimes utilize hidden Markov models (HMMs; see Supplemental Methods). The recent advent of high-throughput, next generation sequencing (NGS) platforms now offers tremendous opportunities in characterizing genomes—healthy or disease-affected—at the nucleotide level of resolution.

Modern sequencing of genomes is massively parallel. The subject's DNA is first sheared, after which the laboratory-amplified fragments are sequenced, producing short reads that are several dozen bases long (Ronaghi et al. 1996; Gharizadeh et al. 2002; Bentley et al. 2008; McKernan et al. 2009). Reads are aligned to the human reference genome (Bentley et al. 2008; Li et al. 2008a, b; Alkan et al. 2009; Langmead et al. 2009; Li and Durbin 2009; McKernan et al. 2009). Since reads at a site are assumed to sample each of its two original copies (or more, in the case of amplicons), multiple independent reads can be observed to cover each haploid copy of a site in a manner following the Poisson distribution with genome-wide expectation Λ (as determined by the laboratory amplification step).

Multiple computational approaches for detecting structural variants and copy number changes within NGS data have been developed (Dalca and Brudno 2010). One such class of methods utilizes paired-end sequence information for detection of germline insertions, deletions, and inversions (Tuzun et al. 2005; Korbel et al. 2007; Bentley et al. 2008; Chen et al. 2009; Hormozdiari et al. 2009; Lee et al. 2009; McKernan et al. 2009). Another such class examines depth of reads to infer germline copy number variants (CNVs) (Xie and Tammi 2009; Yoon et al. 2009). This read depth paradigm was also applied to tumor and matched normal tissues to detect copy number and breakpoints of CNAs in tumors (Chiang et al. 2009). A third class combines read depth with mate pairs for CNV calling (Medvedev et al. 2010).

In addition to CNAs, inherited polymorphisms are clearly related to cancer biology and predisposition. Classic examples include the highly penetrant mutations in BRCA1 (Hall et al. 1990; Miki et al. 1994) and BRCA2 (Wooster et al. 1995) that lead to breast cancer. More recently, genome-wide association studies (GWAS) have led to the discovery of more modestly penetrant variants that are associated with human traits (McCarthy et al. 2008; Hindorff et al. 2009; Witte 2010), including cancer susceptibility (Amundadottir et al. 2006; Freedman et al. 2006; Zanke et al. 2007; Amos et al. 2008; Easton and Eeles 2008; Fletcher et al. 2008; Hung et al. 2008; Thorgeirsson et al. 2008; Ahmed et al. 2009; Le Marchand 2009; Song et al. 2009; Wu et al. 2009; Chung et al. 2010; Stadler et al. 2010a, b; Turnbull et al. 2010).

GWASs stem partially from modern population genetics, which offers ample data and models to understand sequence polymorphisms—mostly single nucleotide variants (SNVs)— along with their correlation to one another and to disease phenotypes (Hartl and Clark 2007). Specifically, the nonrandom allele combinations of proximal SNVs along a single genomic copy, called haplotypes, are a useful unit of local genomic variation. Although haplotypes are not observed directly from genotype data, computational phasing methods (Kimmel and Shamir 2005; Rastas et al. 2005; Eronen et al. 2006; Scheet and Stephens 2006; Browning and Browning 2007; Sun et al. 2007b) distinguish maternal from paternal alleles, thus reconstructing germline haplotypes. Amplicons in cancer typically lie along a haplotype.

Since the somatic genome is a descendent of the germline genome, recent studies have explored the relationships between these distinct but related genomes (Jones et al. 2009; Kilpivaara et al. 2009; Olcaydu et al. 2009). For example, a particular heterozygous locus in a tumor may “prefer” to have one germline allele somatically amplified over another. Such an event has been demonstrated in a targeted fashion in mouse skin tumors (Nagase et al. 2003; de Koning et al. 2007) and in human colorectal cancers (Ewart-Toland et al. 2003; Hienonen et al. 2006). The latter studies found the AURKA gene to be preferentially amplified when containing a low penetrance (T > A) germline variant. In order to robustly perform this type of analysis genome-wide, allelic copy number status must first be measured; several existing algorithms do this on SNP arrays (Nannya et al. 2005; Komura et al. 2006; Laframboise et al. 2007; Korn et al. 2008). We recently reported such an analysis and discovered new links between germline SNP variants within somatic amplicons in glioblastoma SNP array data (Dewal et al. 2010; LaFramboise et al. 2010). The higher resolution, coverage, and larger dynamic range of NGS platforms now compel us to address such questions on tumor sequence data. As a first step, we must determine allelic copy number status of the reference alleles and SNVs within amplicons.

We present a novel method for analyzing NGS data in order to distinguish the amplified from the nonamplified alleles within tumor CNA regions, which themselves can be identified beforehand from the same data. We assume that only one of the chromosomes in a homologous pair undergoes amplification along an amplicon, as the majority of amplifications were observed to be monoallelic versus biallelic in earlier work (LaFramboise et al. 2005). As we later show, the statistical signal for allelic imbalance of amplification that is coming from a single heterozygous site is often inconclusive due to limitations of coverage, sequencing bias, and stromal contamination. We, therefore, collate information from multiple heterozygous sites by leveraging the known structure of linkage disequilibrium (LD) between these variants within the population being interrogated. Specifically, we develop an HMM-based approach, called Haplotype Amplification in Tumor Sequences (HATS), that reports the amplified alleles, and thus haplotypes, in the tumor sample based on (1) coordinates and copy number of CNA regions in a tumor sample called by existing methods, (2) allele-specific counts of reads from tumor and matched normal sequences (when available) corresponding to those regions (Li et al. 2009), (3) genotype calls of sites within those regions, and (4) independent training data consisting of phased haplotype sequences from the same population as that of the sample. This training data provides LD information across sites, allowing for more accurate haplotype construction versus examining each site in isolation. In contrast to prior work based on SNP array data (Dewal et al. 2010), HATS is able to handle information unique to sequencing, such as rare or low frequency variants, including novel SNV sites or somatic mutations not represented in the training data. Evaluation of HATS using synthetic data sets as well as real tumor data, obtained from The Cancer Genome Atlas (TCGA) (Network 2008), emphasizes that HATS detects the amplified allele (within called amplicons) more accurately than an alternative, naive approach over 99% of the time. The gain is especially prominent at lower to intermediate levels of average coverage, as well as in cases (including high coverage) involving stromal contamination or allelic bias.

Results (Evaluation)

For each heterozygous site within a called amplicon a (of copy number C_a) in a tumor sample, the naive model compares the counts of reads that observe each allele and designates the allele with the greater read count as the amplified allele (see Methods). If the read counts are equal, no call is made. The naive model is thus vulnerable to allele-specific biases in addition to fluctuations in read counts that occur at low coverage levels. HATS is designed to address these issues. HATS examines the allele-specific read depth and calculates allelic biases for each site within a, along with leveraging known LD structure over multiple sites (see Methods), to call the amplified alleles.

The advantage that this provides to HATS must be gauged. We summarize the performance of both the naive model and HATS using the metric sensitivity, or the probability of a gold standard amplified allele at a heterozygous site being correctly called as amplified. We examine only those sites within regions known to be amplified, called a priori by a copy number-calling algorithm or a different platform such as array CGH. Thus, specificity, in this case—the fraction of nonamplified alleles (within an amplicon) called as nonamplified—is identical to sensitivity. We first derive the power of the naive model theoretically. Afterward, we determine the sensitivity of the naive model and HATS using simulated data, followed by real data.

Theoretical power of the naive model

The number of reads that cover each haploid copy of a site follows the Poisson distribution with genome-wide expectation Λ. At a heterozygous site, Λ and 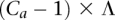represent the mean read counts for the nonamplified and amplified alleles, respectively. The combined mean for both alleles is , and the diploid coverage is 2Λ. The theoretical power of the naive model is the total probability of the amplified allele possessing a read count greater than that of the nonamplified allele, with the space of read count pairs generated from Poisson curves with respective means just mentioned. This is described more formally in Supplemental Methods. Results over a range of values for 2Λ and C_a are shown in Supplemental Figure S1.

Performance of HATS and the naive model in simulations

To measure the sensitivity of HATS across a variety of tumor data set scenarios, we generated numerous synthetic data sets containing amplicons and assessed HATS' ability to call the amplified alleles within the amplicons. We performed the same for the naive model as a baseline comparison. Simulations revealed that HATS' sensitivity eclipses that of the naive model over 99% of the time in practical data sets.

In further detail, simulation of a particular data set first requires training data consisting of phased germline genotypes for d unrelated individuals from the same population. We select n of the d individuals to comprise the test data (indexed by 1 ≤ j ≤ n). Stretches of somatic amplification are randomly generated and applied along the genome of each sample j such that these recurrent stretches overlap across the samples. Each CNA amplicon a in j thus consists of a gold-standard amplified and nonamplified haplotype pair. For a heterozygous genotype at a site in a, counts of reads that observe the amplified allele and nonamplified allele are sampled from Poisson distributions with respective mean haploid coverages 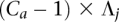and Λ_j. For a homozygous site in a, counts of reads that observe the allele are sampled from a Poisson distribution with mean haploid coverage . In the scenarios that incorporate allelic bias (described later), these read counts may be adjusted to reflect the simulated bias.

For each sample j, the allele-specific read count information along each amplicon in j is analyzed by the naive model. In addition, the training data of (d – n) samples, along with genotype information, copy number C_a, tumor allelic read counts, and normal allelic read counts (for calculating bias) along each amplicon in j are analyzed by HATS. We define accuracy as the fraction of gold-standard amplified alleles along heterozygous sites in each simulated CNA region a that is correctly called as amplified.

Setting n > 1 is only relevant for scenarios in which allelic bias is simulated, as multiple samples provide a better estimate of the bias. When not simulating bias, we set n = 1 and employ a d-fold cross-validation scheme in which each a in each j is processed by the naive method and HATS, the latter using a training data set of (d – 1) samples. Again, overlapping amplicon coordinates are applied to each j.

The variability across the synthetic data sets is implemented via a set of seven parameters, described in Table 1. We perform 100 trials for each parameter value combination when iterating over the parameter space, performing a d-fold cross-validation per trial if n = 1. To prevent an explosive growth of the parameter space, we iterate over only one parameter at a time, while maintaining the other parameters at their default values. The exception to this is when we simulate bias, in which we explore the space of the last two parameters, as described later.

Table 1.

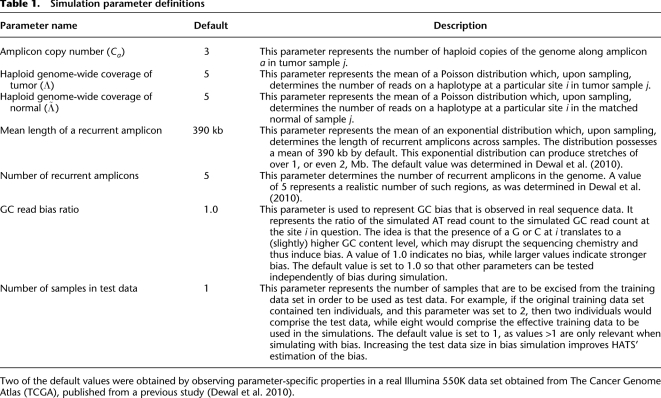
Simulation parameter definitions

Toward determining sensitivity for a parameter value combination, we focus only on those accuracies (from the combination's trials) whose corresponding amplicons cover at least a threshold of v heterozygous sites. An example plot of accuracies for each amplicon a versus the number of heterozygous sites in a is depicted in Figure 1A (using example parameter values 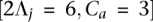). Note that as the number of heterozygous sites in a increases, the accuracies converge to a peak for either method. The peak thus represents an asymptotic measure for accuracy, which we assign as the sensitivity. A large value for v isolates those points contributing to the peak while avoiding the discreteness effects observed in small values. To determine the value of each peak, we perform k-means clustering on those points passing v, setting k = 1 for each method. The resulting centroid for each method represents the peak and thus the sensitivity for that method.

Figure 1.

Accuracy example and sensitivity of HATS and the naive method from simulations, European (CEU) training sata set. (A) Accuracies of each sample trial (2Λ_j = 6, C_a = 3). Each point in the embedded, raised-dot plot represents the accuracy for a particular amplicon a in sample j per trial. As the number of heterozygous sites in a increases, the accuracies converge to a peak for the naive method and a peak for HATS. We set the threshold v to 1000 and use k-means clustering to determine the centroids for each peak. The centroid for the naive model resides at ∼0.80, which is assigned as the sensitivity for the naive method for parameter values (2Λ_j = 6, C_a = 3). The centroid for HATS exists at ∼0.975. (B) Method sensitivities. This figure displays the simulation sensitivity results for HATS (with Genotype Error Correction [GEC] turned on or, by default, off) as well as for the naive method. The naive theoretical curve is included for comparison purposes, illustrating that the naive results can, indeed, be calculated theoretically. Note that it takes up to diploid coverage of 45 until the naive method can match the performance of HATS. The GEC mode noticeably improves performance at very low coverage levels for HATS. The training data set was obtained from the 1000 Genomes Project (http://www.1000genomes.org/).

Simulation results

We obtained three training data sets from the 1000 Genomes Project (The 1000 Genomes Project Consortium 2010), each of which contained phased haplotype sequences from individuals from a HapMap population (The International HapMap Consortium 2005). Any trio children were removed to preserve independence among individuals, resulting in the data sets respectively including d = 55 European (two trio children removed), d = 55 Yoruban (one trio child removed), and d = 59 Japanese and Chinese individuals. These data sets were used independently to avoid stratification effects. Data for additional individuals are expected to be available publicly over time. The HATS method, as well as the evaluation procedure above, can easily work with an expanded training set.

When simulating without bias, we observed that the first two parameters (regarding amplicon copy number and tumor haploid coverage) have the most impact on sensitivity. The fourth parameter, Mean Length of a Recurrent Amplicon, increases the number of heterozygous sites in a by virtue of increasing the span of a. We noted above that a longer a provides a better estimate of the asymptotic accuracy of each method. In Figure 1A, HATS performs better than the naive method in over 99.7% of points (representing amplicons) that each encompass at least v = 20 heterozygous sites. At the default parameter values, HATS does better in 99.3% of points that each encompass at least v = 20 heterozygous sites, with an average accuracy gap of 10.2%. When there is no restriction on v, HATS matches the naive method in 6.3% of points and outperforms it in 93.4% of points. Example plots depicting accuracy over varying numbers of heterozygous sites across varying diploid coverage levels are given in Supplemental Figure S2. Points encompassing at least v = 1,000 heterozygous sites converge to their associated peak, which indicates sensitivity.

The sensitivities of the two methods across varying levels of coverage (with a default copy number of 3) in the European individuals are depicted in Figure 1B. Both curves for HATS— with a Genotype Error Correction mechanism either enabled for low 2Λ_j (to recover an allele possibly missed due to no reads observing that allele at low coverage; see Supplemental Methods) or disabled—perform better than the naive model, especially at intermediate to lower coverage levels. We also show that the naive simulated sensitivity is congruent with its theoretical estimate. For both methods, the breakdown of sensitivities per read count observing a site over the coverage levels is given in Supplemental Figure S3. Sensitivities for Yoruban and Asian individuals are depicted in Supplemental Figure S4 and show similar performance.

Simulation results: Modeling biases

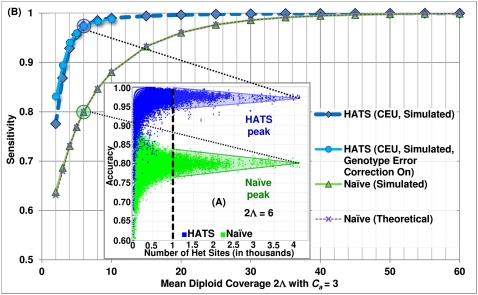
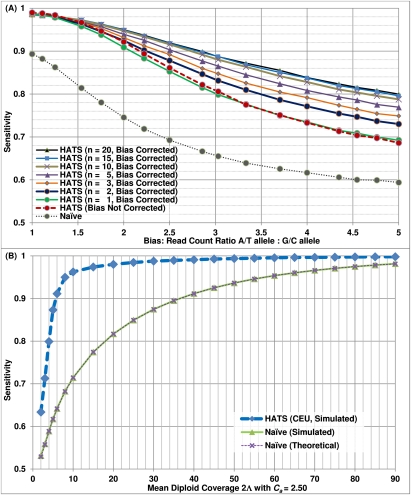
Real sequence data is known to contain bias, a common example of which is GC bias (Bentley et al. 2008; McKernan et al. 2009). While HATS' bias correction is designed to handle allele-specific biases in read counts in general, we test its ability to handle GC biases specifically. When simulating with bias, we vary the two parameters, GC Read Bias Ratio and Number of Samples in Test Data. The resulting sensitivities are depicted in Figure 2A. The former parameter models GC bias by representing the ratio of AT reads versus GC reads at a heterozygous site. The greater the ratio, the stronger the induced bias; a value of 1.0 signifies no induced bias. Note that this parameter only affects sites {G/A, G/T, C/A, C/T}. The latter parameter determines the test data size n, which, when increased, improves HATS' estimate of the bias and thus the performance.

Figure 2.

Results of simulated aspects of real tumor data. (A) Sensitivity of HATS with bias correction and the naive model from simulations, European (CEU) training data set. This figure displays the simulation sensitivity results for HATS with bias correction activated (using varying sample sizes to estimate bias), bias correction inactivated, and the naive model. The x-axis represents the simulated induced bias, ranging from 1.0 (representing no bias) to 5 (representing strong bias). HATS eclipses the naive method in all instances. When the simulated bias is weak and n > 1, bias correction performs only slightly less than does no bias correction by a 0.003 cost in sensitivity. However, bias correction quickly gains the upper hand as the simulated bias increases past 1.5 (or 2 in the case of n = 2). When n = 1, the estimate of bias is not as precise and results in a slightly weaker result (with a 0.008 sensitivity cost on average) unless the induced bias is very strong (3.33). Note that there is only a marginal improvement in performance when increasing the test data set size from 15 to 20. The reason is that this reduces the training data set size, which negatively impacts sensitivity; in addition, improvement in estimation of the bias plateaus. (B) Sensitivity of HATS and the naive model from simulations with stromal contamination, European (CEU) training data set, copy number 2.5. This figure displays the simulation sensitivity results for HATS as well as for the naive model, given a copy number of 2.5, which represents a tumor of copy number 3 with 50% stromal contamination of copy-neutral healthy cells. Note that the performance gap between the two methods remains wide, and the naive method does not catch up to HATS even at a very high diploid coverage of 90. The training data set was obtained from the 1000 Genomes Project (http://www.1000genomes.org/).

The figure depicts the performance of the naive model, HATS without bias correction (n = 1 is sufficient as n > 1 is relevant only when estimating bias), and HATS with bias correction. Our method consistently outperforms the naive model. Furthermore, bias correction becomes more effective as either the level of induced bias or n increases. When the simulated bias is weak and n > 1, bias correction performs only slightly less than does no bias correction by a 0.003 cost in sensitivity. However, bias correction quickly gains the upper hand as the simulated bias increases past 1.5 (or 2 in the case of n = 2). When n = 1, the estimate of bias is not as precise and results in a slightly weaker result (with a 0.008 sensitivity cost on average) unless the induced bias is very strong (3.33). Note that there is only a marginal performance improvement when increasing n from 15 to 20. The reasons are that the improvement in estimating the bias plateaus and that the training data set size is reduced, which negatively impacts sensitivity. The latter reason may be assuaged with a larger d. In general, the figure demonstrates that HATS can accommodate and correct for stronger biases with the tradeoff of performing slightly weaker—a loss of 0.003 in sensitivity for n > 1—for sites possessing smaller biases.

Simulation results: Modeling stromal contamination

In tumor data, the called copy number of an amplicon often deviates from an integer quantity. The reasons are that the tumor cells may not all carry the same aberration (i.e., intra-tumoral genetic heterogeneity) and that a tumor sample may be admixed with normal cell types (i.e., stromal contamination). We focus on the latter reason. A region that is amplified in the tumor (with C_a = 3) but copy-neutral in the healthy somatic cells may average to a noninteger copy number, e.g., 2.50 in the case of a 50-50 mixture. We extend HATS to handle noninteger copy numbers and test its performance on simulated regions with C_a = 2.50 and C_a = 2.80, with the respective results shown in Figure 2B and Supplemental Figure S5. Note that as coverage reduces, the sensitivity of HATS is smaller than that from equivalent coverage levels with C_a = 3. However, HATS maintains its gap over the naive method. More importantly, the naive simulated and theoretical curves do not converge with HATS' curve even when coverage is high or very high (in the case of C_a = 2.50), strongly suggesting that the naive method performs inadequately in the common scenario of imperfect tumor purity. The breakdown of (Fig. 2B) sensitivities per read count observing a site over 2Λ_j is depicted in Supplemental Figure S6.

Simulation results: Hemizygous deletions with stromal contamination

We have extended HATS to analyze heterozygous deletion mixtures, in which deleted alleles are difficult to identify as lost due to the reads coming from the stromal cells that observe those alleles. HATS thus utilizes these read counts (along with LD structure) to identify these alleles (and haplotypes) as the ones lost in the tumor. HATS can analyze data with a copy number between 1.5 and 2, exclusive. An example of simulation results (with C_a = 1.9) is depicted in Supplemental Figure S7. A potential future extension involves handling data with pure heterozygous deletions (C_a = 1) when matched normal information is available; this functionality is already partially implemented via HATS' Genotype Error Correction feature. We do not focus on pure homozygous deletions, as the lost alleles may be recovered by examining the matched normal genotypes or via existing germline imputation algorithms (Browning and Browning 2007). From this point onward, we return to focusing on amplifications only.

Performance of HATS and the naive model in real data

We also evaluate the performance of both methods on CNA regions in real data. We consider data that has been sequenced as well as typed on an independent platform such as SNP arrays. The sequenced tumor data would be of high enough coverage 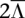to accurately obtain genotype, copy number, and allele-specific read count information beforehand. For any amplicon a with C_a ≥ 3, the amplified alleles that the naive method calls within a are treated as the gold standard for a, as simulation results in Figure 1B reveal the naive method's good performance at high coverage. Alternatively, the gold-standard amplified alleles may be called from the SNP array using, for example, B-allele frequency differences (see Methods in LaFramboise et al. [2010] for a detailed procedure and quality control filtering steps). In either case, we then down-sample a random fraction 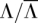of the reads to mimic a data set of lower coverage , for which we test the calling of the amplified allele by HATS versus the naive method. Call accuracy for is reported as the fraction of correct calls across 100 such subsampling trials.

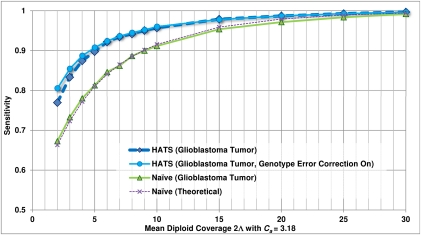
Performance is demonstrated in a glioblastoma tumor sample (TCGA-06-0877) of European descent, with whole genome sequence, array CGH, and SNP array data obtained from The Cancer Genome Atlas (Network 2008) (see Methods: Input data specifications). Chromosomes 2, 7, 12, 19, and 20 of this sample are called by array CGH as possessing a chromosome-wide average copy number of 2.6, suggesting a tumor copy number of 3, with up to 40% of sample cells being nontumor-related cells of copy number 2. We considered a specific CNA region at chr19:2.18-2.54Mb that is reported to possess a local average coverage of 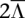= 33.7 and a local average copy number of C_a = 3.18, consistent with a local copy number of 4 in the 60% of sample cells that are tumor cells. Figure 3 presents call accuracy for this region across various levels of coverage , with the gold-standard amplified alleles called by the naive method on the tumor sequence data itself. As expected, both naive calling and HATS perform well when is high. As decreases, the performance gap between HATS and the naive method widens before shrinking slightly at low coverage. Utilizing the Genotype Error Correction, however, increases the performance. The breakdown of sensitivities per read count observing a site at is depicted in Supplemental Figure S8.

Figure 3.

Empirical sensitivity of HATS and the naive model, TCGA glioblastoma sample (TCGA-06-0877), Chr 19. This figure displays the sensitivity results for HATS and the naive method on an amplified region (chromosome 19: 2,181,615–2,541,253) in a glioblastoma patient (TCGA-06-0877) obtained from TCGA with a local copy number of 3.18. The naive theoretical curve is included for comparison purposes. The gold-standard amplified alleles were obtained by analyzing the region with the naive method using high coverage (33.7×) read counts, as simulations for a copy number of 3 indicated high sensitivity for the naive method at high coverage levels. The read counts were randomly down-sampled to result in varying coverage levels as displayed on the x-axis (with 100 trials of down-sampling performed per coverage level). The down-sampled read counts were passed to both HATS and the naive method. The reported amplified alleles were compared with the gold standard to indicate sensitivity. Note that for higher coverage levels, the performance of both HATS and the naive method is strong, which is expected as this was observed in the simulations. As coverage decreases, HATS maintains a marked performance improvement over the naive method. Tumor alignment files and copy number data for this patient were obtained from TCGA (see Methods: Input data specifications).

We ran this down-sampling analysis again, except with the gold-standard amplified alleles called from the SNP array data for the same sample. SNP arrays naturally possess a lower density of sites interrogated as compared to sequence data. Restricting HATS to only array sites forces it to ignore sites in the training data not typed on the array, resulting in weaker LD structure gleaned from the training data. Despite this, HATS retains its performance gain over the naive curve, as seen in Supplemental Figure S9. Moreover, only three heterozygous sites comprise the gold standard after quality control filtering in this case; HATS performed better than the naive method even with such few sites.

We consider another region at chr2:30-31Mb within the same sample possessing local 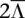= 38.7 and C_a = 2.50 (50% stromal contamination). We discuss findings in Supplemental Results, with HATS' markedly superior sensitivity illustrated in Supplemental Figures S10 and S12. These evaluation procedures reveal that HATS outperforms the naive model in real tumor data, even when sites are few and especially when coverage is reduced or stromal contamination is present.

Discussion

During recent years, algorithms have been developed for SNP array platforms to determine somatic allele-specific copy numbers of germline SNPs. Such data indicates CNAs and enables one to pinpoint potential disease-associated variants and, by virtue, haplotypes within the wide span of these regions. However, the drawbacks of these algorithms are the suboptimal resolution of the platform, and more importantly, issues with call fidelity: Amplified regions render these algorithms prone to incorrect genotype calls in tumor tissue. As NGS technologies offer nucleotide level resolution while avoiding SNP array issues that affect amplified call fidelity, we aimed to develop a novel method that could determine the amplified alleles, and thus, haplotypes in such data. To our knowledge, no other methods exist that call somatically amplified alleles and haplotypes in NGS data.

Determination of haplotypes is equivalent to locally phasing the tumor data using read counts from the tumor sample and haplotype frequencies from training data. Only one chromosome is assumed to be amplified along a homologous region. At its core, HATS builds an HMM, using allele-specific read counts as emissions and training haplotypes to model transitions. Usage of the training data is motivated by the notion that the haplotype constructed from the amplified alleles (called within an amplicon) should partially reflect a mosaic of existing haplotypes within the same population. The training haplotypes enable HATS to utilize linkage information from multiple sites, thus helping to improve power over that of the naive method. Within an amplicon a called a priori, HATS reports the amplified allele at each site that is polymorphic either in the sample or the training data, including those sites harboring rare variants or somatic mutations. We note that HATS is also able to handle hemizygous deletion mixtures. It can identify the deleted alleles or haplotypes that are otherwise difficult to identify as deleted (due to traces of those alleles coming from contaminating stromal cells).

The assumption of one chromosome being amplified is central to HATS. While evidence of the prevalence of monoallelic amplification has been found in previous studies (LaFramboise et al. 2005), along with recent studies recounting most amplification events to be low gain (Network 2011), we acknowledge that the extent to which one or both alleles is amplified still remains an open question. HATS in its current form may produce switch errors in phasing if applied on regions with both chromosomes amplified. However, the method can be extended by adding extra states representing candidate double amplifications. Such modifications would also help HATS toward phasing germline CNV regions. Currently, HATS is equipped to locally phase germline heterozygous CNVs of copy number 3 should those regions map uniquely to the reference genome. The caveat is that samples copy-neutral for those regions would be required to calculate any allele-specific biases. Another potential extension involves incorporating paired-end information, though the practical gain from this would need to be assessed, as the mate pair distance is typically smaller than the distance between polymorphic sites.

It should be noted that the constructed amplified haplotype may differ from the true tumor haplotype with respect to the order of sites. Genomic rearrangements in tumor DNA disrupt the local cellular copy of inherited germline sequence, potentially resulting in a somatic haplotype that differs from the corresponding germline haplotype. However, rearrangement information from tumor DNA may be lost during sequencing, as single reads are mapped to the reference sequence. As such, the amplified tumor haplotype as called by HATS would reflect the order of sites in the reference genome (and the inherited germline sequence) rather than that of the rearranged tumor haplotype. A similar limitation of our approach is the potential presence of mitotic recombination. This would imply different phasing for tumor versus normal data but would typically be limited to a small number of events (Cavenee et al. 1983; Paques and Haber 1999; Barbera and Petes 2006; LaFave and Sekelsky 2009).

The design philosophy of HATS envisions the algorithm as a tool in a workflow of algorithms for studying tumors, helping to open the door for allele-specific downstream analysis. At the same time, it is reliant on upstream data; namely, the a priori calling of the amplicon. This is done intentionally, as modularity is a fundamental design principle in building complex pipelines, and it guides us here as well. Furthermore, CNA and CNV calling has been studied extensively and has matured over the years to the point that it has become integral to existing pipelines (Network 2008, 2011). However, upstream errors can occur, some of which are safeguarded by HATS. For example, small errors in input amplicon copy number have little effect on HATS, which can naively validate copy number using tumor and matched normal read counts. The effect is further reduced due to the power HATS leverages from the training data. Other errors include amplicons that are a result of platform-specific biases (e.g., PCR bias). These can be caught by HATS' bias correction if they are allele-specific and appear in the matched normals as well. In addition, the power from the training data can help reduce the effect of spurious PCR biases that may occur within an amplicon span. The naive method, on the other hand, would be much more vulnerable to this. Other errors include inexact a priori amplicon breakpoint prediction, which could especially occur with the low resolution of arrays. Such errors may result in HATS calling an allele as amplified even if the site lies outside the amplicon in truth, or sites being ignored by HATS if, in truth, they lie within the amplicon boundary. However, some of these effects are mitigated when studying multiple tumors downstream. Amplicons due to artifact in one sample will likely not recur over multiple tumors and may thus be identified as unique or erroneous. Similarly, testing for recurrence will tease out amplicons under selection versus passenger amplicons that occur randomly and propagate due to duplication mechanisms or genomic instability during tumor evolution.

A possible alternative to HATS entails first computationally phasing the matched normal sequence (and, by virtue, the tumor sequence), ignoring valuable read count information during phasing. One might then assess tumor read counts at several sites within an amplicon to determine the particular phased haplotype targeted for amplification. We tested this approach on four regions from the glioblastoma patient (TCGA-06-0877), three of which lie on chromosome 2 and the last on chromosome 19 (see Supplemental Table S1). Only sites common to both the sequence data and SNP array were considered. The gold standard amplified alleles were determined using array calls. HATS performed with equal or greater accuracy on all four regions, while inaccuracies in phasing-first indicated switch error. These results support HATS' relevance to amplified allelic calling. Another advantage that HATS possesses over phasing-first is the ability to make calls on rare variants or somatic mutations using read depth information. Phasing algorithms, which also rely on germline training data, seem underpowered to do this. In addition, HATS may recover heterozygous calls at low coverage via its Genotype Error Correction; performing the same with a germline phasing algorithm for sequence data would require extra preprocessing overhead for the end user. Furthermore, several phasing algorithms assume Hardy-Weinberg equilibrium in the test data, which may not always be the case due to the presence of risk alleles (Marchini et al. 2006). Thus, phasing the tumor via the matched normal may not always lead to accurate results. On the contrary, as the constructed tumor haplotype would reflect the genome order of the reference sequence and matched normal as mentioned above, HATS could potentially be used to phase the germline alleles in the matched normal sample based on the tumor data.

One potential future avenue involves examining haplotypes within recurrent CNA regions across tumor samples to reveal such genes. This was performed previously on SNP arrays at the single SNP level (Dewal et al. 2010; LaFramboise et al. 2010) and can now be extended to next generation sequencing data. HATS' reporting of the amplified allele may serve as a first step in this downstream analysis possibility. One benefit is that sites that were not typed on SNP arrays may be revealed to be selectively amplified across tumors in sequence data. In addition, the improved call fidelity as compared to amplified allelic calls on SNP arrays may lead to more robust results.

More generally, the HATS algorithm is designed to call allelic imbalances (AIs) at genomic sites within a sample. AIs can provide important information in multiple scenarios. For example, AI in transcripts has been detected by RNA sequencing. Transcripts demonstrating this phenomenon have genetic or epigenetic influences driving this difference (Zhang et al. 2009; Heap et al. 2010; Tuch et al. 2010). Chromatin immunoprecipitation followed by high-throughput sequencing, ChIP-seq, can also reveal AI at heterozygous sites. In this context, allelic imbalance can reflect differential binding specificity of a particular DNA-protein interaction, thereby possibly highlighting functional variants.

In the pursuit of detecting causal or associated variants, it aids the cancer community to integrate somatic and germline DNA changes. We present a method that helps move toward this end in next generation tumor sequence data. The strong evaluation of HATS provides us confidence to offer the community this powerful local phasing method. We hope that cancer researchers will find it beneficial toward discovering variants and potential oncogenes.

Methods

Naive model parameters and input data specifications

We denote the read count for allele x ∈ {0, 1} at a genomic site i (a potential SNV site) in the tumor sample of individual j by r_x. Formally, r_x would be indexed as r_i,j,x, though indices for the site and individual are omitted for simplicity in the running text when clear from context. In the set of regions amplified in this sample, we consider each amplicon a in turn and denote its boundaries by 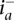and 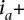. At an amplified heterozygous site 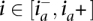, it is meaningful to ask which allele is amplified. A naive model for calling the amplified allele would simply choose the allele for which a greater number of reads is observed, denoted as arg-max_x{r_x}. A call is avoided in case of a tie.

With a probabilistic view in mind, r_x is a value of a random variable R_x ∼ Poisson(λ_x), where λ_x represents the site-, individual-, and allele-specific expectation for the number of tumor reads. This formulation interprets the naive call as choosing the allele for which the maximum likelihood estimate of λ_x is greater. This model makes use of no input data other than r_x and calls sites along the amplicon a independently of one another. It thus serves as a suitable performance baseline against HATS.

HATS model parameters

The contribution of this manuscript involves recovering the amplified allele based on a more careful modeling of λ_x. Specifically, λ₀ and λ₁ are assumed to be proportional to the number of copies of the respective alleles at site i in the tumor sample j at hand. We denote these numbers, or tumor genotype calls, by G₀ and G₁, respectively. The total copy number 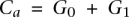at site i is >2 in an amplicon a, and our task of identifying the amplified allele is tantamount to distinguishing between the cases 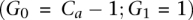and 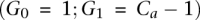. Furthermore, λ_x is assumed to be proportional to Λ, the average haploid coverage of the sequenced tumor j; Λ is a sample-specific quantity that depends on the sequencing resources invested in the data for that tumor. Lastly, NGS reads are known to be often biased toward particular nucleotides (Bentley et al. 2008; McKernan et al. 2009). Therefore, a realistic and general model for λ_x needs to account for such a site-specific (versus sample-specific) phenomenon. Our model then assumes this parameter is proportional to an allelic bias factor b_x local to this site. In summary, including site- and sample-specific subscripts (i, j) for completeness of the formal equation:

Note that by modifying the Poisson mean Λ via b_x, the model accommodates for genome-wide overdispersion in which the variance in read counts may exceed the expected variance (also Λ). Overdispersion in general may result from a positive correlation between events (Robinson and Smyth 2008) (e.g., overlapping reads covering a common interval) or from differing expected numbers of reads at different sites (Bentley et al. 2008; McKernan et al. 2009). Since each site may possess a unique bias b_x, the site- and allele-specific Poisson mean λ_x may also be unique at each site i in sample j. The combination of the varying λ_x across sites effectively implements the negative binomial (NB) distribution genome-wide. Existing methods estimate and use the NB distribution directly to model overdispersion in other types of sequencing data, such as in RNA-seq (Anders and Huber 2010; Robinson et al. 2010) and ChIP-seq (Anders and Huber 2010).

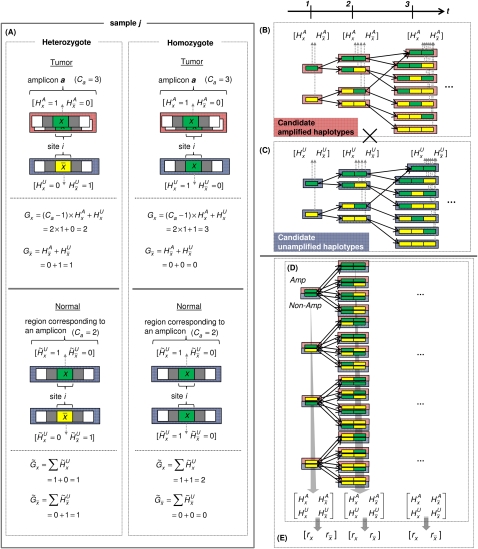
The definitions of λ_x, G_x, and C_a easily generalize to homozygous sites (where G_x = C_a for one of the alleles and G_x = 0 for the other) as well as copy neutral sites (C_a = 2). Furthermore, we consider the sequencing of not only the tumor but also of matched normal samples of the corresponding individuals (denoted by operator ^∼). Our model analyzes a tumor amplicon a only if the corresponding region in the matched normal is copy-neutral, thus preventing germline CNV regions from confounding the analysis. Read counts 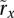for normal samples are analogously defined, as are the random variables: 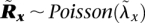, where 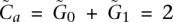, and

The genotype call at a site is, in fact, comprised of the haplotype calls at that site. We aim to distinguish the two haploid copies of the genome giving rise to the tumor genotype call. Within an amplicon a, we assume one of the haplotypes is (A)mplified while the other is (U)namplified (LaFramboise et al. 2005). We formally represent these ground truth haplotypes as binary strings 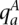and 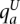, respectively, each listing the alleles along its sequence. We define the complement operator for allele x such that 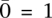and 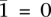. At a particular site 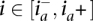, we denote by 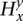the number of copy-neutral copies (0 or 1) of x along 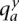, where 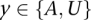; this is depicted in Figure 4A. Naturally, the tumor genotype call for an amplified allele x sums the copies on both haplotype calls, with amplification of a particular haplotype call represented by multiplication with a constant (C_a – 1):

The tumor genotype call for a nonamplified allele 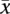is similar:

For the matched normal, the genotype call sums the copies of two nonamplified haplotype calls, as per the requirements of copy neutrality (see Fig. 4A):

Figure 4.

Parameter definition depictions, haplotype, genotype, and integrated HMM. The left half of the figure depicts the definitions of several model parameters, while the right half depicts examples of the four HMM models. (A) Model parameters are depicted for a heterozygous or homozygous site i in tumor and matched normal tissues for sample j. For a particular genotype call within a tissue, a diagram of the call is depicted, along with the corresponding H and G parameters. For example, for a heterozygous call within a tumor, the amplicon a (containing i) from the tumor is shown, depicting the amplified haplotype (with allele x amplified) within the red frame and nonamplified haplotype (allele 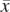) within the blue frame. The haplotypes emit their respective H values per site, followed by the definitions of the G values for each allele. Both H and G should be additionally subscripted by i and j formally, but these subscripts are excluded for simplicity's sake. For the amplified haplotype in red, 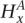= 1 since x is present (and amplified), while 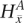= 0 since 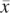is not present within that haplotype at i. For the nonamplified haplotype in blue, 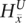= 1 since 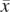is present (and not amplified), while 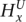= 0 since x is not present within that haplotype at i. (B) Example of the haplotype HMM for the amplified haplotype. Each state contained within a red frame represents a candidate amplified haplotype. Green boxes represent x while yellow boxes represent 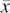. The H symbols emitted from a state correspond to the last allele in the haplotype represented by the state, as depicted by the dotted vertical arrows. The haplotype lengths generally grow from left to right due to addition of an allele at the current t. Note that at t = 3, most states represent haplotypes of length 3, with the exception of the topmost state, which represents a haplotype [green | green] of length 2. This haplotype merges two 3-SNP haplotypes [green | green | green] and [yellow | green | green] because they both are singletons in the training data. Both states [green | green] and [yellow | green] at t = 2 thus transition to state [green | green] at t = 3. (C) Haplotype HMM for the nonamplified haplotype. Note that it is identical to B except for the differing emitted symbols. (D) Genotype HMM that is the cross-product of the haplotype HMMs. For each pair of haplotypes, the amplified haplotype is depicted above the nonamplified haplotype within red and blue frames, respectively. Each pair of haplotypes inherits the H values from their respective haplotype HMMs. (E) Translated HMM upon incorporating the model data. Note that while the structure remains unchanged, the emitted symbols are translated from the H values to the read counts. The r_x variables should also include subscripts i and j for formal correctness, which were omitted here for simplicity's sake.

HATS hidden Markov model

We use an accepted model of human variation (Kimmel and Shamir 2005; Rastas et al. 2005; Eronen et al. 2006; Browning and Browning 2007; Sun et al. 2007b), presenting haplotypes 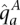and 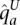as the output of two respective haplotype HMMs V^A and V^U, detailed below. We take a Cartesian product of the two haplotype HMMs to define a genotype HMM, for which the genotypes are the output. The read counts r_x are a probabilistic function of these genotypes, as explained above. HATS entails deciphering, for each site and sample, the likelihood of states within this genotype model, and then choosing the allele most likely to have been amplified. An overview of the model is provided in Figure 4B–E.

Haplotype HMM

In detail, the haplotype HMM 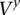is a state machine with probabilistic transitions and deterministic emissions. The states and transitions follow the haplotype models used by computational phasing algorithms for SNP array data (Kimmel and Shamir 2005; Rastas et al. 2005; Eronen et al. 2006; Browning and Browning 2007; Sun et al. 2007b). In a similar vein, we locally phase the tumor sequence data based on read counts in the sample data and haplotype counts in population-relevant training data.

The “time points” of 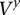consist of the set of sites i₁, i₂, …, i_M located within the amplicon a coordinates that are polymorphic (i.e., include a nonreference allele call) in the germline of the training data. Sites that are monomorphic in the training data do not provide information regarding the amplified allele and need not be analyzed here. Each time point t in 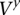maps to a genomic site i_t and is associated with a set of HMM states 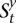. Each s ∈ 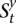is labeled by a binary string 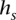, which represents a candidate local haplotype for polymorphic sites i_t-l(s)+1, …, i_t, where l(s) = |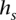|. State s emits 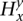values deterministically depending on 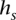[l(s)], the last symbol in 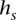: 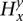= 1 for 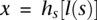and 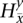= 0 for the complement allele. For every s ∈ 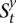in which t > 1, there exists at least one 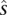∈ 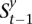that transitions to s such that they are consistent: The prefix of 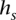of length (l(s) – 1), denoted as 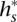, is a suffix of 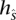. This relationship can be visualized in Figure 4B,C. Transitions are allowed only between consistent states.

Any of the multiple methods for learning a haplotype HMM from training data may be employed to choose lengths of state labels 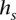and transition probabilities between a pair of consistent states. We implemented a simple such method, which relies on counts of 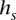in the training (D)ata ending at t—denoted by 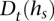. The concept behind this is that, at a given locus, a germline haplotype of a tumor sample is assumed to be identical to one of the training haplotypes, randomly switching the training sample that is locally identical to the tumor haplotype along the genome. This concept is a standard in germline genetics (Stephens et al. 2001; Scheet and Stephens 2006; Browning and Browning 2007). The candidate haplotype label of s is thus tested for such a local matching. We enforce 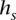labels to be as long as possible while maintaining 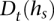≥ min(2, l(s)). This constraint prevents creating labels that are void in D or labels of length >1 that are singletons in D (to prevent overfitting), while, on the other hand, allowing labels of length 1 that represent rare or low frequency single nucleotide variants in D. The length of state labels thus trades off accuracy of training vs. overfitting.

The transition probability between consistent states 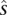and s is set as a Dirichlet prior based on :

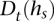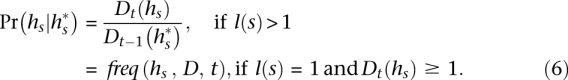The function freq() represents the haplotype frequency of 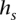in D ending at t. Recall that we never encounter the case in which |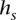| = 1 and 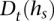= 0, as we ignore sites monomorphic in D. Such sites that are polymorphic only in the test sample data (rare variants or somatic mutations) are handled external to the HMM and are described in the section Enhancements and Optimizations below.

Genotype HMM

We construct a genotype HMM V by cross-multiplying V^A and V^U (see Fig. 4D). The M time points remain unchanged. At a given t, the set of states is the Cartesian product 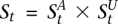. Thus, for each 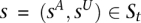, 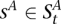and 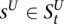. State s thus inherits its labels, denoted as 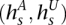, from its component states. Likewise, s inherits the 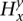values (over all y and x), which it emits deterministically. The transition probability from 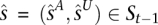to s is the product of the transition probabilities to the component states of s:

Integrated HMM

Our model for the read data is a new HMM V⁺ that is a replica of V, adding stochastic emissions on top of it (see Fig. 4E). For each state s ∈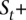, the emitted symbols are, instead, the read counts r_x for each allele x. Each s is still labeled with 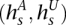and inherently represents the 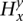values (over all y and x). Assuming C_a is known beforehand and that b_x is calculated, parameters G_x and λ_x can be calculated from 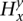(over all y and x). The emission probability for s is the probability of observing r_x, assuming an underlying Poisson distribution for the read counts at site i_t with mean λ_x. It is calculated on the Poisson distribution as

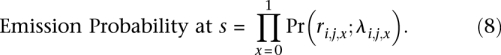HMM deciphering algorithm to call the amplified allele

The ultimate goal of the HMM is to decipher which allele x is amplified at t. Toward this end, we apply the forward-backward algorithm on V⁺, resulting in a probability P(s) for each state in V⁺. Let ⊆ represent those states whose amplified haplotype labels 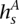end in x, or more formally, whose 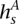labels possess x as the last symbol. HATS computes the total likelihood for each allele x by summing over the relevant P(s) values:

HATS finally reports the most likely such x to have been amplified at t via: arg-max_x{L_t(x)}. In the case of a tie, HATS designates Ø as the amplified allele at t to reflect this ambiguity.

Input data specifications

HATS jointly considers input regarding n tumor and matched normal samples (1 ≤ j ≤ n). Specifically, input data corresponding to a particular sample j includes the input data from the naive model, in addition to the following:

• (1) C_a (>2, obtained by preprocessing with a copy number-calling algorithm (Chiang et al. 2009) or typing the sample on another platform, e.g., array CGH);

• (2) Λ and 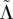(calculable beforehand);

• (3) 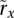and 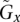for all i in each of the n samples that are copy-neutral at i, with the constraint that i resides in amplicon a in sample j; and

• (4) genotypes from the tumor of individual j that do not take copy number into account.

The latter two are obtainable via a genotype caller component from an alignment algorithm (Li et al. 2009). The third input specification—read counts from each i within copy-neutral regions in tumor and matched normal samples, such that i resides in an amplicon in at least one of the n input tumor samples—allows for calculation of the site-specific bias factor b_x. Estimation of b_x and the effects of the availability of matched normal data on this estimation are discussed in Supplemental Methods. This tumor and matched normal input data can be derived from aligned sequence data obtainable from any sequencing project or initiative. The tumor and matched normal data we used in Results was downloaded from TCGA. The respective URL and relevant dbGaP accession number are http://tcga-data.nci.nih.gov/tcga/, phs000178.v4.p4.

Lastly, HATS takes advantage of linkage information across multiple sites to call the amplified alleles, whereas the naive model ignores LD by examining each site individually. Toward this end, HATS uses training data (denoted above as D) for human germline variation, which entails phased haplotype sequence data on d unrelated individuals that are independently sampled from the same population as the n cancer patients whose tumors are to be analyzed. The training population can be determined as a preprocessing step using ancestry informative markers in the tumor samples. The training data itself can be obtained, for example, from the 1000 Genomes Project (The 1000 Genomes Project Consortium 2010).

Enhancements and optimizations

Tumor samples may include sites housing somatic mutations or variants that are unique to the samples and missing in the training data (e.g., singletons). HATS utilizes read depth, along with bias determination, to call the amplified allele at each such site. In addition, HATS possesses the ability to potentially recover an allele missed due to low coverage (Genotype Error Correction); this is integrated with a mechanism to utilize tumor genotypes to prune the explosive growth of states. Details on these enhancements are provided in Supplemental Methods.

Data access

The HATS source code, as well as instructions to build and run the software, is available at (http://tumorhats.sourceforge.net/).