Skip to main content
NCBI home page
Genome Research logoLink to Genome Research
. 2012 Feb;22(2):375–385. doi: 10.1101/gr.120477.111

De novo discovery of mutated driver pathways in cancer

Fabio Vandin 1, Eli Upfal 1, Benjamin J Raphael 1,1
PMCID: PMC3266044  PMID: 21653252

Abstract

Next-generation DNA sequencing technologies are enabling genome-wide measurements of somatic mutations in large numbers of cancer patients. A major challenge in the interpretation of these data is to distinguish functional “driver mutations” important for cancer development from random “passenger mutations.” A common approach for identifying driver mutations is to find genes that are mutated at significant frequency in a large cohort of cancer genomes. This approach is confounded by the observation that driver mutations target multiple cellular signaling and regulatory pathways. Thus, each cancer patient may exhibit a different combination of mutations that are sufficient to perturb these pathways. This mutational heterogeneity presents a problem for predicting driver mutations solely from their frequency of occurrence. We introduce two combinatorial properties, coverage and exclusivity, that distinguish driver pathways, or groups of genes containing driver mutations, from groups of genes with passenger mutations. We derive two algorithms, called Dendrix, to find driver pathways de novo from somatic mutation data. We apply Dendrix to analyze somatic mutation data from 623 genes in 188 lung adenocarcinoma patients, 601 genes in 84 glioblastoma patients, and 238 known mutations in 1000 patients with various cancers. In all data sets, we find groups of genes that are mutated in large subsets of patients and whose mutations are approximately exclusive. Our Dendrix algorithms scale to whole-genome analysis of thousands of patients and thus will prove useful for larger data sets to come from The Cancer Genome Atlas (TCGA) and other large-scale cancer genome sequencing projects.

Cancer is driven by somatic mutations in the genome that are acquired during the lifetime of an individual. These include single-nucleotide mutations and larger copy-number aberrations and structural aberrations. With the availability of next-generation DNA sequencing technologies, whole-genome or whole-exome measurements of the somatic mutations in large numbers of cancer genomes are now a reality (Mardis and Wilson 2009; International Cancer Genome Consortium 2010; Meyerson et al. 2010). A major challenge for these studies is to distinguish the functional “driver mutations” responsible for cancer from the random “passenger mutations” that have accumulated in somatic cells but that are not important for cancer development. A standard approach to predict driver mutations is to identify recurrent mutations (or recurrently mutated genes) in a large cohort of cancer patients. This approach has identified several important cancer mutations (e.g., in KRAS, BRAF, ERRB2, etc.), but has not revealed all of the driver mutations in individual cancers. Rather, the results from initial studies (The Cancer Genome Atlas Research Network 2008; Ding et al. 2008; Jones et al. 2008) have confirmed that cancer genomes exhibit extensive mutational heterogeneity with no two genomes—even those from the same tumor type—containing exactly the same complement of somatic mutations. This heterogeneity results not only from the presence of passenger mutations in each cancer genome, but also because driver mutations typically target genes in cellular signaling and regulatory pathways (Hahn and Weinberg 2002; Vogelstein and Kinzler 2004). Since each of these pathways contains multiple genes, there are numerous combinations of driver mutations that can perturb a pathway important for cancer. This mutational heterogeneity complicates efforts to identify functional mutations by their recurrence across many samples, as the number of patients required to demonstrate recurrence of rare mutations is very large.

An alternative approach to testing the recurrence of individual mutations or genes is to examine mutations in the context of cellular signaling and regulatory pathways. Most recent cancer genome sequencing papers analyze known pathways for enrichment of somatic mutations (The Cancer Genome Atlas Research Network 2008; Ding et al. 2008; Jones et al. 2008), and methods that identify known pathways that are significantly mutated across many patients have been developed (e.g., Boca et al. 2010; Efroni et al. 2011). In addition, algorithms that extend pathway analysis to genome-scale gene interaction networks have recently been introduced (Cerami et al. 2010; Vandin et al. 2011). Pathway or network analysis of cancer mutations relies on prior identification of the groups of genes in the pathways. While some pathways are well-characterized and cataloged in various databases (Kanehisa and Goto 2000; Jensen et al. 2009; Keshava Prasad et al. 2009), knowledge of pathways remains incomplete. In particular, many pathway databases contain a superposition of all components of a pathway, and information regarding which of these components are active in particular cell types is largely unavailable. These concerns, plus the availability of increasing numbers of sequenced cancer genomes, motivate the question of whether it is possible to discover groups of genes with driver mutations automatically, or mutated driver pathways, directly from somatic mutation data collected from large numbers of patients.

De novo discovery of mutated driver pathways seems implausible because of the enormous number of possible gene sets to test: e.g., there are more than 1026 sets of seven human genes. However, the current understanding of the somatic mutational process of cancer (McCormick 1999; Vogelstein and Kinzler 2004) places two additional constraints on the expected patterns of somatic mutations that significantly reduce the number of gene sets to consider. First, an important cancer pathway should be perturbed in a large number of patients. Thus, given genome-wide measurements of somatic mutations, we expect that most patients will have a mutation in some gene in the pathway. Second, a driver mutation in a single gene of the pathway is often assumed to be sufficient to perturb the pathway. Combined with the fact that driver mutations are relatively rare, most patients exhibit only a single driver mutation in a pathway. Thus, we expect that the genes in a pathway exhibit a pattern of mutually exclusive driver mutations, where driver mutations are observed in exactly one gene in the pathway in each patient (Vogelstein and Kinzler 2004; Yeang et al. 2008). There are numerous examples of pairs of mutually exclusive driver mutations including EGFR and KRAS mutations in lung cancer (Gazdar et al. 2004), TP53 and MDM2 mutations in glioblastoma (The Cancer Genome Atlas Research Network 2008) and other tumor types, and KRAS and PTEN mutations in endometrial (Ikeda et al. 2000) and skin cancers (Mao et al. 2004). Mutations in the four genes EGFR, KRAS, ERBB2 (also known as HER2), and BRAF from the EGFR–RAS–RAF signaling pathway were found to be mutually exclusive in lung cancer (Yamamoto et al. 2008). More recently, statistical analysis of sequenced genes in large sets of cancer samples (Ding et al. 2008; Yeang et al. 2008) identified several pairs of genes with mutually exclusive mutations.

We introduce two algorithms to find sets of genes with the following properties: (1) high coverage—most patients have at least one mutation in the set; (2) high exclusivity—nearly all patients have no more than one mutation in the set. We define a measure on sets of genes that quantifies the extent to which a set exhibits both criteria. We show that finding sets of genes that optimize this measure is in general a computationally challenging problem. We introduce a straightforward greedy algorithm and prove that this algorithm produces an optimal solution with high probability when given a sufficiently large number of patients, subject to some statistical assumptions on the distribution of the mutations (A Greedy Algorithm for Independent Genes section). Since these statistical assumptions are too restrictive for some data (e.g., they are not satisfied by copy-number aberrations) and since the number of patients in currently available data sets is lower than required by our theoretical analysis, we introduce another algorithm that does not depend on these assumptions. We use a Markov chain Monte Carlo (MCMC) approach to sample from sets of genes according to a distribution that gives significantly higher probability to sets of genes with high coverage and exclusivity. Markov chain Monte Carlo is a well-established technique to sample from combinatorial spaces with applications in various fields (Gilks 1998; Randall 2006). For example, MCMC has been used to sample from spaces of RNA secondary structures (Meyer and Miklos 2007), haplotypes (Bansal et al. 2008), and phylogenetic trees (Yang and Rannala 1997). In general, the computation time (number of iterations) required for an MCMC approach is unknown, but in our case, we prove that our MCMC algorithm converges rapidly to the stationary distribution.

We emphasize that the assumptions that driver pathways exhibit both high coverage and high exclusivity need not be strictly satisfied for our algorithms to find interesting sets of genes. Indeed, mutual exclusivity is a fairly strong assumption, and there are examples of co-occurring, and possibly cooperative, mutations such as VHL/SETD2/PBRM1 mutations in renal cancer (Varela et al. 2011), and CBF translocations and kinase mutations in acute myeloid leukemias (Deguchi and Gilliland 2002). Yeang et al. (2008) suggest a model in which mutations in genes from the same pathway were typically mutually exclusive, and mutations in genes from different pathways were sometimes co-occurring. It is also possible that mutations in some genes of an essential pathway are insufficient to perturb the pathway on their own and that other co-occurring mutations are necessary. In this case, there remains a large subset of genes in the pathway whose mutations are exclusive, e.g., a subset obtained by removing one gene from each co-occurring pair. The identification of these subsets of genes can be used as a starting point to later identify the other genes with co-occurring mutations.

We apply our algorithms, called De novo Driver Exclusivity (Dendrix), to analyze sequencing data from three cancer studies: 623 sequenced genes in 188 lung adenocarcinoma patients, 601 sequenced genes in 84 glioblastoma patients, and 238 sequenced mutations in 1000 patients with various cancers. In all three data sets, we find sets of genes that are mutated in large numbers of patients and are mostly exclusive. These sets include genes in the Rb, p53, mTOR, and MAPK signaling pathways, all pathways known to be important in cancer. In glioblastoma, the set of three genes that we identify is associated with shorter survival (Backlund et al. 2003). We also show that the MCMC algorithm efficiently samples multiple sets of six genes in simulated mutation data with thousands of genes and patients. Both the greedy and MCMC algorithms scale to whole-genome analysis of thousands of patients and thus will prove useful for analysis of larger data sets to come from The Cancer Genome Atlas (TCGA) and other large-scale cancer genome sequencing projects.

Results

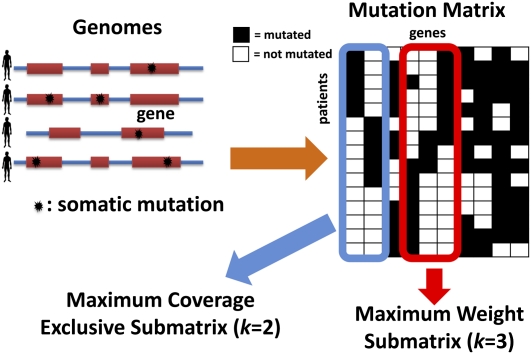
Consider mutation data for m cancer patients, where each of n genes is tested for a somatic mutation (e.g., single-nucleotide mutation or copy-number aberration) in each patient. We represent the mutation data by a mutation matrix A with m rows and n columns, where each row is a patient and each column is a gene. The entry Aij in row i and column j is equal to 1 if gene j is mutated in patient i, and it is 0 otherwise (Fig. 1). For a gene g, let Γ(g) = {i: Aig = 1} denote the set of patients in which g is mutated. Similarly, for a set M of genes, let Γ(M) denote the set of patients in which at least one of the genes in M is mutated: Γ(M) = ∪g∈MΓ(g). We say that a set M of genes is mutually exclusive if no patient contains more than one mutated gene in M, i.e., Γ(g) ∩ Γ(g′) = Ø for all g, g′ ∈ M. Analogously, we say that an m × k submatrix M consisting of k columns of a mutation matrix A is mutually exclusive if each row of M contains at most one 1. Note that the above definitions also apply when the columns of the mutation matrix A correspond to parts of genes (e.g., protein domains or individual residues). In the results below, we analyze data using both definitions of the mutation matrix.

Figure 1.

Figure 1.

Open in a new tab

Somatic mutations in multiple patients are represented in a mutation matrix. Gene sets are identified as exclusive submatrices or high weight submatrices.

Earlier studies (Ding et al. 2008; Yeang et al. 2008) employed straightforward statistical tests to test for exclusivity between pairs of genes. More sophisticated tests for pairwise exclusivity have also been proposed (Bradley and Farnsworth 2009). However, it is not clear how to extend such pairwise tests to larger groups of genes, particularly because the number of hypotheses grows rapidly as the number of genes in the set increases. Moreover, identification of pairs of mutually exclusive mutated genes is not sufficient for identification of larger sets (as suggested in Yeang et al. 2008), since mutual exclusion relations are not transitive. For example, consider two patients s1 and s2: In s1, only gene x is mutated; in s2, genes (y, z) are mutated. The pairs of genes (x, y) and (x, z) are mutually exclusive, but the pair (y, z) is not. In fact, finding the largest set of genes with mutually exclusive mutations is NP-hard by reduction from maximum independent set (Garey and Johnson 1990).

Instead, we propose to identify sets of genes (columns of the mutation matrix) that are mutated in a large number of patients and whose mutations are mutually exclusive. We define the following problem:

Maximum Coverage Exclusive Submatrix Problem: Given an m × n mutation matrix A and an integer k > 0, find a mutually exclusive m × k submatrix M of k columns (genes) of A with the largest number of nonzero rows (patients).

We show that this problem is computationally difficult to solve (for proof, see the Supplemental Material). Moreover, this problem is too restrictive for analysis of real somatic mutation data. We do not expect mutations in driver pathways to be mutually exclusive because of measurement errors and the presence of passenger mutations. Instead, we expect to find a set of genes that are mutated in a large number of patients and whose mutations exhibit “approximate exclusivity,” meaning that a small number of patients have a mutation in more than one gene in the set. Thus, we aim to find a set M of genes that satisfies the following two requirements:

  1. Coverage: Most patients have at least one mutation in M.

  2. Approximate exclusivity: Most patients have no more than one mutation in M.

There is an obvious trade-off between requiring mutual exclusivity in the set and obtaining low coverage versus allowing greater non-exclusivity in the set and obtaining larger coverage. We introduce a measure on a set of genes that quantifies the trade-off between coverage and exclusivity. For a set M of genes, we define the coverage overlap

graphic file with name 375equ1.jpg

Note that ω(M) ≥ 0 with equality holding when the mutations in M are mutually exclusive. To take into account both the coverage Γ(M) and the coverage overlap ω(M) of M, we define the weight

graphic file with name 375equ2.jpg

Note that the weight function W(M) is only one possible measure of the trade-off between coverage and exclusivity (see Methods).

The problem that we want to solve is the following:

Maximum Weight Submatrix Problem: Given an m × n mutation matrix A and an integer k > 0, find the m × k column submatrix 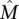Inline graphic of A that maximizes W(M).

Even for small values of k (e.g., k = 6), finding the maximum weight submatrix by examining all the possible sets of genes of size k is computationally infeasible: for example, there are ≈1023 subsets of size k = 6 of 20,000 genes. We show that the Maximum Weight Submatrix Problem is also computationally difficult to solve (for proof, see the Supplemental Material), and thus it is likely that there is no efficient algorithm to solve this problem exactly. The problem of extracting subsets of genes with particular properties has also been studied in the context of gene expression data. For example, biclustering techniques are commonly used to identify subsets of genes with similar expression in subsets of patients (Cheng and Church 2000; Getz et al. 2000; Tanay et al. 2002; Murali and Kasif 2003; Segal et al. 2003; Madeira and Oliveira 2004). Other variations, such as finding subsets of genes that preserve order of expression (Ben-Dor et al. 2003) or that cover many patients (Ulitsky et al. 2008; Kim et al. 2010), have been proposed. However, these approaches are not directly applicable to our problem as we seek a set of genes with few co-occurring mutations, while gene expression studies aim to find groups of genes with correlated expression.

We describe our approach considering mutation data at the level of individual genes. However, by adding columns to the mutation matrix, it is possible to apply our method at the subgene level by considering mutations in particular protein domains, structural motifs, or individual residues. (See the Known Mutations in Multiple Cancer Types section for an example.)

A greedy algorithm for independent genes

A straightforward greedy algorithm for the Maximum Weight Submatrix Problem is to start with the best pair M′ of genes and then to iteratively build the set M of genes by adding the best gene [i.e., the one that maximize W(M)] until M has k genes (see Methods for the pseudocode of the algorithm). This algorithm is very efficient, but in general, there is no guarantee that the set 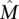Inline graphic that maximizes W(M) would be identified. However, we show that the greedy algorithm correctly identifies 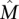Inline graphic with high probability when the mutation data come from a generative model, that we call the Gene Independence Model (for proof, see the Supplemental Material). In the Gene Independence Model: (1) each gene 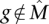Inline graphic is mutated in each patient with probability pg, independently of all other events, with pg ∈ [pL, pU] for all g. (2) 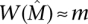Inline graphic. (3) Each of the genes in 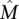Inline graphic is important, so there is no single subset of 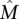Inline graphic that has a dominant contribution to the weight of 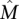Inline graphic. Condition 1 models the independence of mutations for genes that are not in the mutated pathway and is a standard assumption for somatic single-nucleotide mutations (Ding et al. 2008). Condition 2 ensures that the mutations in 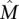Inline graphic cover a large number of patients and are mostly exclusive. For a formal definition of the Gene Independence Model, see the Supplemental Material.

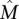Note that in the Gene Independence Model it is possible for the genes in Inline graphic to have observed mutation frequencies that are identical to those of genes not in Inline graphic, and thus it is impossible to distinguish the genes in 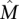Inline graphic from the genes not in {\hat M}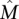Inline graphic using only the frequency of mutations, for any number of patients.

To assess the implications of this for the utility of the greedy algorithm on real data, consider the following setting: Observed gene mutation frequencies are in the range [3 × 10−5, 0.13] (derived from a background mutation rate of the order of 10−6 [The Cancer Genome Atlas Research Network 2008; Ding et al. 2008] and the distribution of human gene lengths). If somatic mutations are measured in n = 20,000 human genes and 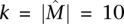Inline graphic, then approximately m = 2400 patients are required for the greedy algorithm to identify 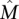Inline graphic with probability at least 1 − 10−4. Even if somatic mutations are measured in only a subset of genes (including all the genes in 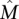Inline graphic), the bound above does not decrease much. For example, assuming that n = 600 genes are measured (as it is for recent studies) (The Cancer Genome Atlas Research Network 2008; Ding et al. 2008), including all the k = 10 genes in 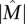Inline graphic, approximately m = 1800 patients are required to identify 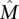Inline graphic with probability at least 1 − 10−4 using the greedy algorithm. This number of patients is not far from the range that will be soon be available from large-scale cancer sequencing projects (International Cancer Genome Consortium 2010) but is larger than what is available now. Moreover, we only have shown that the simple greedy algorithm gives a good solution when the mutation data come from the Gene Independence Model. This model is reasonable for some types of somatic mutations (e.g., single-nucleotide mutations) but not others (e.g., copy-number aberrations).

Markov chain Monte Carlo (MCMC) approach

To circumvent the limitations of the greedy algorithm described above, we developed a Markov chain Monte Carlo. (MCMC) approach that does not require any assumptions about the distribution of the mutation data or about the number of patients. The MCMC approach samples sets of genes, with the probability of sampling a set M proportional to the weight W(M) of the set. Thus, the frequencies that gene sets are sampled in the MCMC method provides a ranking of gene sets, in which the sets are ordered by decreasing sampling frequency. Thus, in addition to the highest weight set, one may also examine other sets of high weight (“suboptimal” sets) that are nevertheless biologically significant. Moreover, since the MCMC approach does not require any assumptions about independence of mutations in different genes, it is useful for analysis of copy-number aberrations (CNAs) that amplify or delete multiple adjacent genes and thus introduce correlated mutations. Both of these advantages will prove useful in analysis of real mutation data below.

The basic idea of the MCMC is to build a Markov chain whose states are the collections of k columns of the mutation matrix A and to define transitions between the states that differ by one gene. We use a Metropolis-Hastings algorithm (Metropolis et al. 1953; Hastings 1970) to sample sets Inline graphic of k genes with a stationary distribution that is proportional to ecW(M) for some constant c > 0. At time t, the Markov chain in state Mt chooses a gene w in Inline graphic and a gene v inside Mt, and moves to the new state Mt+1 = Mt\{v} ∪ {w} with a certain probability. In general, there are no guarantees on the rate of convergence of the Metropolis-Hasting algorithm to the stationary distribution. However, we prove that in our case the MCMC is rapidly mixing (Markov Chain Monte Carlo [MCMC] Algorithm section), and thus the stationary distribution is reached in a practical number of steps by our method. The MCMC algorithm is described in more detail in Methods.

Results on simulated mutation data

We first tested the ability of the MCMC algorithm to detect the set 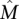Inline graphic of maximum weight W(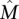Inline graphic) for different values of W(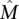Inline graphic). We simulated mutation data starting with a set M of six genes. For each patient, we mutate a gene (chosen uniformly at random) in M with probability p1, and if a gene in M is mutated, then with probability p2 we mutate another gene in M. Thus, p1 regulates the coverage of M, and p2 regulates the exclusivity of M. The genes not in M are mutated using a random model based on the observed characteristics of the glioblastoma data (described below). In particular, we simulated both single-nucleotide mutations and copy-number aberrations (CNAs). For the single-nucleotide mutations, genes were mutated in each patient according to the observed frequency of single-nucleotide mutations in the glioblastoma data, independently of other genes.2 We simulated CNAs by permuting the locations of the observed CNAs on the genome while maintaining their lengths. The procedure accounts for the fact that genes that are physically close on the genome might be mutated together in the same CNA, resulting in correlated mutations.

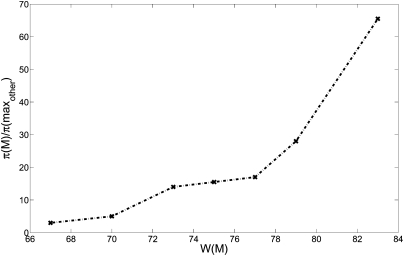
We ran the MCMC algorithm on sets of six genes for 107 iterations sampling every 104 iterations. Figure 2 reports the ratio between frequency π(M) at which M is sampled and the maximum frequency π(maxother) of any other sampled set. Note that the same value of W(M) is obtained with multiple different settings of the parameters p1 and p2. For example, with p1 = 0.81 and p2 = 0.04, the set M has W(W) = 67 (in expectation), and is sampled with frequency threefold greater than any other set.

Figure 2.

Figure 2.

Open in a new tab

Ratio between the sampled frequency π(M) of the maximum weight set, and the maximum frequency π(maxother) of any other set in the sample for different values of W(M).

The sampling ratio increases dramatically with the weight W(M) of the set.

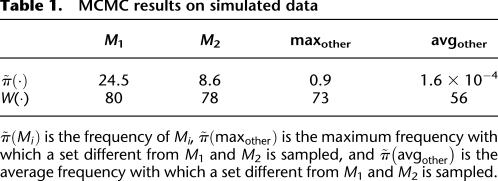
To test the ability to identify multiple high weight sets of genes, we simulated mutation data starting with two disjoint sets, M1 and M2, each containing six genes. For each patient, we mutate genes in M1 and M2 using the probabilities p1 and p2 as described above. The sets M1 and M2 correspond to two pathways with approximate exclusivity. The genes not in M1 or M2 were mutated using the random model described above. Table 1 shows the frequencies with which various sets are sampled in the MCMC. M1 and M2 are sampled with highest frequency. Moreover, the ratio of their frequencies is very close to the ratio of their probabilities in the stationary distribution of the MCMC. If the MCMC is sampling from the stationary distribution for the two sets M and M′, the ratio 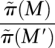Inline graphic should be close to e c[W(M) − W(M′)]. 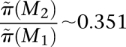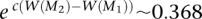In our simulations, Inline graphic, and Inline graphic.

Table 1.

MCMC results on simulated data

graphic file with name 375tbl1.jpg

Open in a new tab

Finally, we tested the scalability of our method to data sets containing a larger number of genes and varying numbers of patients. We simulated mutation data as described above on 20,000 genes and 1000 patients. The results in this case are very close to the ones presented above. In particular, M1 and M2 were the two sets sampled with highest frequency, and the frequency of each was >30%. Sets other than M1 and M2 were sampled with frequencies <1%. We were still able to identify the sets M1 and M2 when the number of patients was reduced to 150. M1 and M2 were sampled with frequency 13%, much higher than any other set. Based on these results, we anticipate that our algorithms would be useful on whole-exome sequencing studies with a modest number of patients.

Results on cancer mutation data

We applied our MCMC algorithm to somatic mutations from high-throughput genotyping of 238 oncogenes in 1000 patients of 17 cancer types (Thomas et al. 2007), and to somatic mutations identified in recent cancer sequencing studies from lung adenocarcinoma (Ding et al. 2008) and glioblastoma multiforme (The Cancer Genome Atlas Research Network 2008). In the glioblastoma multiforme analysis, we include both copy-number aberrations and single-nucleotide (or small indel) mutations, while in the lung adenocarcinoma analysis, we consider only single-nucleotide (or small indel) mutations. The MCMC algorithm samples sets with frequency proportional to their weights, and thus to restrict attention to sets with high weight, we report sets whose frequency is at least 1%. We also reduce the size of the mutation matrix by combining genes that are mutated in exactly the same patients into larger “metagenes.”

Known mutations in multiple cancer types

We applied the MCMC algorithm to mutation data from Thomas et al. (2007), who tested 238 known mutations in 17 oncogenes in 1000 patients of 17 different cancer types. Two hundred ninety-eight of the patients were found to have at least one of theses mutations, and a total of 324 individual mutations were identified. To perform our analysis, we built a mutation matrix with 298 patients and 18 mutation groups. These mutation groups were defined by Thomas et al. (2007) and grouped together mutations that occurred in the same gene, in the same functional domain of the encoded protein (e.g., kinase domain mutations or helical domain mutations of PIK3CA), or when a distinct phenotype was correlated with a specific mutation (e.g., the T790M mutation of EGFR known to be correlated with resistance to EGFR inhibitors). We ran the MCMC algorithm on sets of size k, for 2 ≤ k ≤ 10. In each case, we ran the MCMC for 107 iterations and sampled a set every 104 iterations. All sets sampled with frequency at least 1% in this and all later experiments are reported in Supplemental Material D.

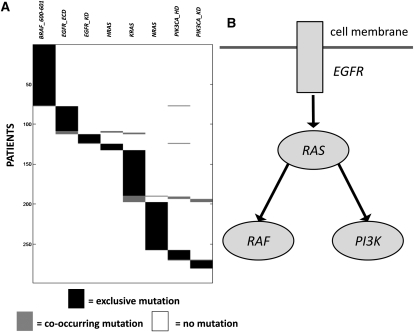
We perform a permutation test to assess the significance of the results: The statistic is the weight W(M) of the set, and the null distribution was obtained by independently permuting the mutations for each mutation group among the patients, thus preserving the mutation frequency for each mutation group. We use the observed frequency of mutation rather than a fixed background mutation rate because we want to assess the significance of coverage and exclusivity of a set of mutation groups given the frequency of mutation of the single mutation groups in the set.3 We identify a set of eight mutation groups (BRAF_600-601, EGFR_ECD, EGFR_KD, HRAS, KRAS, NRAS, PIK3CA_HD, PIK3CA_KD)4 that is altered in 280/298 of the patients (94%) with at least one mutation and has a total of 295 mutations (p < 0.01). The mutated genes are part of well-known cancer pathways (Fig. 3). There are many sets of size k = 10 that contain the set of size k = 8 above and also have high weight (see the Supplemental Material). In particular, there are two sets of size k = 10 that are altered in 287/297 (95%) of the patients and have a total of 302 mutations (p < 0.01). These two sets include the above eight mutation groups and (JAK2, KIT) and (FGFR1, KIT), respectively. We tested each pair of genes for mutual exclusivity with the (one-tailed) Fisher's exact test. No pair of genes showed significant mutual exclusivity, with minimum q-value 0.492. Thus, a standard test does not report any of the mutation groups identified by our method.

Figure 3.

Figure 3.

Open in a new tab

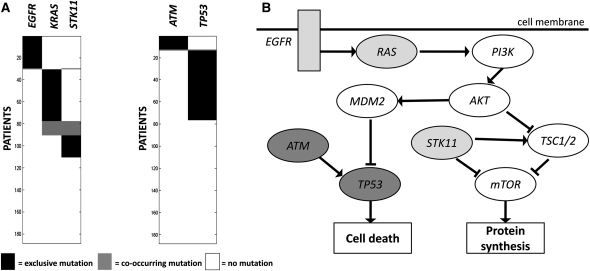
(A) High weight submatrix of eight genes in the somatic mutations data from multiple cancer types (Thomas et al. 2007). (Black bars) Exclusive mutations; (gray bars) co-occurring mutations. (B) Location of identified genes in known pathway. Interactions in the pathway are as reported in Ding et al. (2008).

Lung adenocarcinoma

We next analyzed a collection of 1013 somatic mutations identified in 623 sequenced genes from 188 lung adenocarcinoma patients from the Tumor Sequencing Project (Ding et al. 2008). In total, 356 genes were reported mutated in at least one patient. We ran the MCMC algorithm for sets of size 2 ≤ k ≤ 10. When k = 2, the pair (EGFR, KRAS) is sampled 99% of the time. This pair is mutated in 90 patients with a coverage overlap ω(M) = 0, indicating mutual exclusivity. When k = 3, the triplet (EGFR, KRAS, STK11) is sampled with frequency 8.4%. For k ≥ 4, no set is sampled with frequency >0.3%. The pairs (EGFR, KRAS) and (EGFR, STK11) are the most significant pairs in the mutual exclusivity test performed in Ding et al. (2008), and thus it is not surprising that we also identify them. However, the pair (KRAS, STK11) is not reported as significant using their statistical test. Thus, the coverage and mutual exclusivity of the triplet (EGFR, KRAS, STK11) is a novel discovery.

We performed a permutation test, as described in the Known Mutations in Multiple Cancer Types section, to compare the significance of (EGFR, KRAS) and (EGFR, KRAS, STK11). The P-values obtained are 0.018 and 0.005, respectively. Thus, the triplet (EGFR, KRAS, STK11) is at least as significant as the pair (EGFR, KRAS). The three genes EGFR, KRAS, and STK11 are all involved in the regulation of mTOR (Fig. 4), whose dysregulation has been reported as important in lung adenocarcinoma (Ding et al. 2008). In particular, STK11 down-regulates the mTOR pathway, and mTOR activation has been reported as significantly more frequent in tumors with gene alterations in either EGFR or KRAS (Conde et al. 2006). This supports the hypothesis that all three genes are upstream regulators of mTOR, explaining their observed exclusivity of mutations.

Figure 4.

Figure 4.

Open in a new tab

(A) High weight submatrices of two and three genes in the lung adenocarcinoma data. (Black bars) Exclusive mutations; (gray bars) co-occurring mutations. Rows (patients) are ordered differently for each submatrix, to illustrate exclusivity and co-occurrence. (B) The location of gene sets in known pathways reveals that the triplet of genes codes for proteins in the mTOR signaling pathway (light gray nodes), and the pair (ATM, TP53) corresponds to interacting proteins in the cell cycle pathway (dark gray nodes). Interactions in the pathway are as reported in Ding et al. (2008).

To identify additional gene sets, we removed the genes EGFR, KRAS, STK11 and ran the MCMC algorithm again on the remaining genes. We sample the pair (ATM, TP53) with frequency 56%, and compute that the weight of the pair is significant (p < 0.01). ATM and TP53 are known to directly interact (Khanna et al. 1998), and both genes are involved in the cell cycle checkpoint control (Chehab et al. 2000). Moreover, these genes have no known role in mTOR regulation (Fig. 4), consistent with the observation that their mutations are not exclusive with those in the triplet above. Note that the pair (ATM, TP53) was not sampled with high frequency before removing EGFR, KRAS, and STK11. The reason is that the coverage of (ATM, TP53) is not as high as other pairs in the triplet: for example, the pair (EGFR, KRAS) covers 90 patients (with a coverage overlap of 0), while the pair (ATM, TP53) covers 76 patients (with a coverage overlap of 1). Although the exclusivity of both sets is high, their coverage is low (<60%), suggesting that these gene sets are not complete driver pathways. We hypothesize that the coverage is low because (1) somatic mutations were measured in only a small subset of genes; (2) only single-nucleotide mutations and small indels in these genes were measured, and other types of mutations (or epigenetic changes) might occur in the “unmutated” patients. Either of these would reduce the coverage or imply that mutations in a superset of these genes were not measured.

We examined the overlap between the patients with mutations in (ATM, TP53) and those with mutations in (EGFR, KRAS, STK11). We found that the overlap was not significantly different from the expected number in a random data set, suggesting that mutations in these two sets are not exclusive. This is consistent with our model, in which the two sets are part of two different pathways. While neither of these sets is mutated in >60% of the patients, this does not imply that they are not part of important cancer pathways, for the same reasons regarding incomplete measurements outlined above.

Glioblastoma multiforme

We also applied the MCMC algorithm to 84 glioblastoma multiforme (GBM) patients from The Cancer Genome Atlas (The Cancer Genome Atlas Research Network 2008). Somatic mutations in these patients5 were measured in 601 genes. A total of 453 somatic single-nucleotide mutations were identified, and 223 genes were reported mutated in at least one patient. In addition, array copy number data were available for each of these 601 genes in every patient. We recorded a gene as somatically mutated in a patient if it was part of a focal copy-number aberration identified in The Cancer Genome Atlas Research Network (2008), discarding copy-number aberrations for which the sign of aberration (i.e., amplification or deletion) was not the same in at least 90% of the samples. Note that copy-number aberrations (even focal aberrations) typically encompass more than one gene, and the boundaries of such aberrations vary across patients. Since we only collapse genes into “metagenes” if they are mutated in exactly the same patients, we will not collapse all of the genes in focal copy-number aberrations into a “metagene” if the genes in the aberrations vary across patients. Thus, the genes in overlapping, but not identical, aberrations will remain separate in our analysis. If our algorithm selects any of these genes in a high weight set, it might select the gene (or genes) that is altered in the largest number of patients, a behavior that is similar to “standard” copy-number analysis methods that select the minimum common aberration. We ran the MCMC algorithm sets of sizes k (2 ≤ k ≤ 10) for 107 iterations, and sampling one set every 104 iterations.

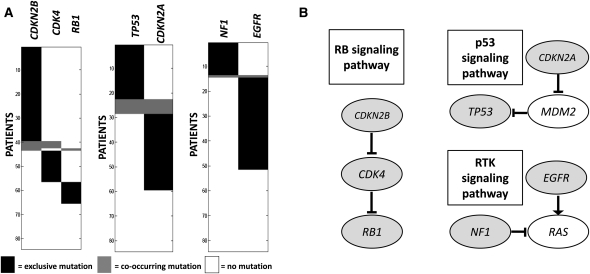
For k = 2, the pair of genes sampled with the highest frequency is (CDKN2B, CYP27B1), sampled with frequency 18%. For k = 3, the most frequently sampled set is (CDKN2B, RB1, CYP27B1), sampled with frequency 10%. The second most sampled pair (frequency 11%) was CDKN2B and a metagene containing six genes,6 and the second most sampled triplet (frequency 6%) was CDKN2B, RB1, and the same metagene. Moreover, the mutational profile of CYP27B1 was nearly identical to a metagene: CYP27B1 is mutated in all of the same patients as the metagene plus one additional patient with a single-nucleotide mutation in CYP27B1. Because of this one extra mutation, CYP27B1 was not merged into the metagene. Furthermore, the six genes in the metagene are adjacent on the genome and are mutated by a copy-number aberration (amplification) in all patients. This amplification also affects CYP27B1, which is adjacent to these genes. The amplification was previously reported, and the presumed target of the amplification is the gene CDK4 (Wikman et al. 2005). Thus, it is likely that the triplet (CDKN2B, RB1, CDK4) is the triplet of interest, and the somatic mutation in CYP27B1 identified in one patient does not have a biological impact. This example shows one of the advantages of the MCMC method: It allows one to identify additional “suboptimal” genes sets of high weight and those whose weight is close to the highest. We performed a permutation test, as described in the Known Mutations in Multiple Cancer Types section, to compare the significance of (CDKN2B, CDK4) and (CDKN2B, CDK4, RB1). The P-values obtained are 0.1 and <10−2, respectively. Therefore, the triplet (CDKN2B, CDK4, RB1) is at least as significant as the pair (CDKN2B, CDK4). CDKN2B, RB1, and CDK4 are part of the RB1 signaling pathway (Fig. 5), and abnormalities in these genes are associated with shorter survival in glioblastoma patients (Backlund et al. 2003). Thus, our method identifies a triplet of genes with a known association to survival rate directly from the somatic mutation data.

Figure 5.

Figure 5.

Open in a new tab

(A) High weight submatrices of two and three genes in the glioblastoma data. (Black bars) Exclusive mutations; (gray bars) co-occurring mutations. Rows (patients) are ordered differently for each submatrix, to illustrate exclusivity and co-occurrence. (B) Location of identified genes in known pathways. Interactions in pathways are as reported in The Cancer Genome Atlas Research Network (2008).

For k ≥ 4, no set is sampled with frequency ≥0.2%. We removed the set (CDKN2B, CDK4, RB1) from the analysis and ran the MCMC algorithm again. The pair (TP53, CDKN2A) is sampled with frequency 30% (p < 0.01). This pair is part of the p53 signaling pathway (Fig. 5). As discussed in the Lung Adenocarcinoma section, the fact that this pair is sampled with high frequency only after removing (CDKN2B, CDK4, RB1) is likely due to the fact that not all genes and mutations in the pathways have been measured, resulting in different coverage for the two pathways. Finally, removing both (CDKN2B, CDK4, RB1) and (TP53, CDKN2A), we identify the pair (NF1, EGFR) sampled with frequency 44% (p < 0.01). NF1 and EGFR are both part of the RTK pathway (Fig. 5), which is involved in the proliferation, survival, and translation processes.

Discussion

We introduce two algorithms for finding mutated driver pathways in cancer de novo using somatic mutation data from many cancer patients. Our algorithms, called De novo Driver Exclusivity (Dendrix), find sets of genes that are mutated in many samples (high coverage) and that are rarely mutated together in the same patient (high exclusivity). These properties model the expected behavior of driver mutations in a pathway, or a “subpathway.” We define a weight on sets of genes that measures how well a set exhibits these two properties. We show that finding the set M of genes with maximum weight is computationally difficult, derive conditions under which a greedy algorithm gives optimal solutions, and develop a Markov chain Monte Carlo (MCMC) algorithm to sample sets of genes in proportion to their weight. Furthermore, we prove that the Markov chain converges rapidly to the stationary distribution.

We applied our MCMC approach to three recent cancer sequencing studies: lung adenocarcinoma (Ding et al. 2008), glioblastoma (The Cancer Genome Atlas Research Network 2008), and multiple cancer types (Thomas et al. 2007). In the latter data set we identify a group of eight mutations in six genes that are present at least once in a large fraction of patients and are largely exclusive. In the first two data sets, we identified groups of two to three genes with those properties. These gene sets include members of well-known cancer pathways including the Rb pathway, the p53 pathway, and the mTOR pathway. In the glioblastoma data, the mutations in the three genes that we identify have been previously associated with shorter survival (Backlund et al. 2003). Notably, we discover these pathways de novo from the mutation data without any prior biological knowledge of pathways or interactions between genes. However, it is also important to note that some of the genes that were measured in these data sets were selected because they were known to have a cancer phenotype, and thus there is some ascertainment bias in the finding that individual genes (or groups of genes) are mutated in many samples.

The results on the Thomas et al. (2007) data and on simulated data illustrate that our algorithm is able to identify relatively large sets of genes with high coverage and high exclusivity. However, in the lung adenocarcinoma and glioblastoma data, the size of gene sets that we identify is relatively modest. It is not yet possible to conclude whether this is a real phenomenon or a consequence of limited data. For example, the number of patients and genes in these studies is relatively small, and the types of mutations that were measured was not comprehensive. For example, we examined only single-nucleotide (and small indel) mutations in lung adenocarcinoma, and these plus copy-number aberrations in the glioblastoma data. Other types of mutations, such as rearrangements, or even epigenetic changes could alter the function or expression of genes. In addition, considering mutation data at the level of individual genes might reduce the power to distinguish driver mutations from passenger mutations. Thus, it would be interesting to analyze the other data sets at “subgene” resolution to distinguish mutations at particular amino acid residues. We have shown that our algorithms are useful at a finer scale of resolution by introducing additional columns to the mutation matrix that correspond to protein domains, structural motifs, or other parts of a protein sequence.

The algorithms we presented assumed the availability of reasonably accurate mutation data. While the ability to measure somatic mutations from next-generation DNA sequencing data or microarrays is becoming more routine, there remain challenges in the identification of somatic mutations from these data with the incorrect prediction of somatic mutations (false positives) and the failure to identify genuine mutations (false negatives) (Meyerson et al. 2010). One particular source of false negatives is the heterogeneity of many tumor samples, which often include both normal cell admixture and subpopulations of tumor cells with potentially different sets of mutations. False negatives are a particular problem with samples with low tumor cellularity. Although the algorithms we propose are able to handle some false positives and false negatives, high rates of these errors would reduce the exclusivity and coverage, respectively, of a driver pathway. Moreover, this problem will be compounded if the genes in a driver pathway are mutated only in a subpopulation of tumor cells.

Our algorithms could be improved in several ways. First, we could include additional information in the scoring of mutations and gene sets. In the present analysis, we considered each mutation to have one of two states—mutated or normal. Extending our techniques to use additional information about the functional impact, or expression status, of each mutation is an interesting open problem. Second, alternative weight functions W(M) could be considered. For example, the inclusion of patient-specific mutation rates might provide a more refined way to analyze hypermutated patients. However, we note that some of our analytical results (e.g., the rapid mixing of the MCMC algorithm) relied on the particular form of the weight function W(M), and these results would also require modification to maintain similar performance. Finally, the performance of our algorithm in complex situations involving multiple, overlapping high weight sets of genes requires further analysis. It is not yet clear whether such complex situations arise in cancer mutation data.

Our algorithms will be useful for analysis of whole-genome or whole-exome sequencing data from large sets of patients, and we anticipate that with these comprehensive data sets it will be possible to identify larger sets of driver genes. Such data sets will soon be available from The Cancer Genome Atlas (TCGA) and other large-scale cancer sequencing projects. We expect that the de novo techniques introduced here will complement existing methods for assessing enrichment of mutations in known pathways. As larger cancer data sets become available, it will be interesting to compare the exclusive gene sets identified by our techniques to known cancer pathways. A key question in the analysis of these larger data sets is whether mutual exclusivity of driver mutations in genes in the same pathway is a widespread phenomenon, or whether it is a feature of particular genes, pathways, or cancer types. We anticipate that our algorithms will be helpful in addressing this question. In addition, it would be interesting to extend these ideas to other types of cancer genomics data, such as epigenetic alterations and structural aberrations. Finally, an intriguing future direction is to generalize these techniques to analyze combinations of (rare) germline variants in genetic association studies.

Methods

Complexity of the problem

The problems we are interested in are the Maximum Coverage Exclusive Submatrix Problem and the Maximum Weight Submatrix Problem (see Results for their definition). We show that these problems are computationally difficult (for proof, see the Supplemental Material).

Theorem 1. The Maximum Coverage Exclusive Submatrix Problem is NP-hard.

Theorem 2. The Maximum Weight Submatrix Problem is NP-hard.

Note that our weight W(M) is only one possible measure of the trade-off between coverage and exclusivity. For example, another approach is to minimize the maximum number of genes that co-occur in a patient. The associated problem remains computationally difficult as shown in Kuhn et al. (2005) (with additional generalizations in Dom et al. 2006).

A greedy algorithm and Gene Independence Model

We propose the following greedy algorithm for the Maximum Weight Submatrix problem.

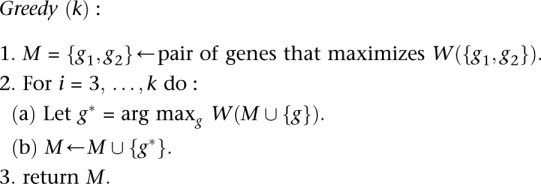graphic file with name 375equ3.jpg

The time complexity of the algorithm is O(n2 + kn) = O(n2). We analyze the performance of the algorithm on mutation matrices generated from the following Gene Independence Model.

Definition 1. Let A be an m × n mutation matrix such that 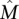Inline graphic is the maximum weight column submatrix of A and 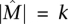Inline graphic. The matrix A satisfies the Gene Independence Model if and only if:

  • 1. Each gene 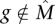Inline graphic is mutated in each patient with probability pg, independently of all other events, with pg ∈ [pL, PU] for all g.

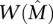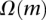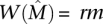  • 2. Inline graphic is Inline graphic, i.e., Inline graphic for a constant r, 0 < r ≤ 1.

  • 3. For all ℓ, any subset 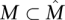Inline graphic of cardinality |M| = ℓ satisfies 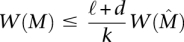Inline graphic, for a constant 0 ≤ d < 1.

We show that the greedy algorithm above will produce the optimal solution with high probability for any mutation matrix generated from the Gene Independence Model, when the number of rows (patients) is sufficiently large.

Theorem 3. Suppose ɛ > 0 and A is an m × n mutation matrix generated from the Gene Independence Model that satisfies

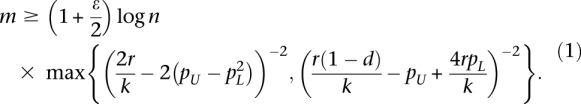graphic file with name 375equ4.jpg

Then the greedy algorithm identifies the m × k column submatrix 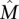Inline graphic with maximum weight 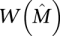Inline graphic with probability at least 1 − 2n−ɛ.

For proof of Theorem 3, see the Supplemental Material.

Markov chain Monte Carlo (MCMC) algorithm

The basic idea of MCMC is to build a Markov chain whose states are the possible configurations and to define transitions between states according to some criterion. If the number of states is finite and the transitions are defined such that the Markov chain is ergodic, then the Markov chain converges to a unique stationary distribution. The Metropolis-Hastings algorithm (Metropolis et al. 1953; Hastings 1970) gives a general method for designing transition probabilities that gives a desired stationary distribution on the state space. However, the Metropolis-Hastings method does not guarantee fast convergence of the chain, which is a necessary condition for practical use of this method. In fact, if the chain converges slowly, then it may take an impractically long time before the chain samples from the desired distribution. Defining transition probabilities so that the chain converges rapidly to the stationary distribution remains a challenging task. Despite significant progress in recent years in developing mathematical tools for analyzing the convergence time (Randall 2006), our ability to analyze useful chains is still limited, and in practice, most MCMC algorithms rely on simulations to provide evidence of convergence to stationarity (Gilks 1998).

We use a Metropolis-Hastings algorithm to sample sets Inline graphic of k genes with a stationary distribution that is proportional to e cW(M) for some c > 0, and we show that the resulting chain converges rapidly.

Initialization: Choose an arbitrary subset M0 of k genes in Inline graphic (the set of all genes).

Iteration: For t = 1, 2,…, obtain Mt+1 from Mt as follows:

  1. Choose a gene w uniformly at random from Inline graphic.

  2. Choose v uniformly at random from Mt.

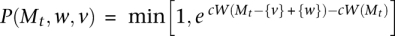  3. Let Inline graphic.7

  4. With probability P(Mt, w, v) set Mt+1 = M − {v} + {w}, else Mt+1 = Mt.

It is easy to verify that the chain is ergodic with a unique stationary distribution

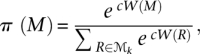graphic file with name 375equ5.jpg

where 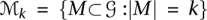Inline graphic. The efficiency of this algorithm depends on the speed of convergence of the Markov chain to its stationary distribution. We are able to analyze the mixing time of the chain because we do not restrict the set of states that the chain can visit, focusing instead on the desired stationary probabilities of the various states.

Let Inline graphic be the transition probability from initial state I to state M in t steps of the Markov chain. We measure the distance between the distribution of the chain at time t and the stationary distribution by the variation distance between the two distributions:

graphic file with name 375equ6.jpg

The ε-mixing time of the chain is

graphic file with name 375equ7.jpg

A chain is rapidly mixing if τ(ε) is bounded by a polynomial in the size of the problem (m and 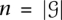Inline graphic in our case) and log ε−1.

We show that there is a nontrivial interval of values for c for which the chain is rapidly mixing (for proof, see the Supplemental Material). Our proof uses a path coupling argument (Bubley and Dyer 1997). In path coupling, we define coupling only on pairs of adjacent states in the Markov chain. Let Mt and 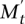Inline graphic be the states of two copies of the Markov chain at time t, and assume that 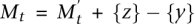Inline graphic (thus, the two states are adjacent in the Markov chain). We use the following coupling: Assume that the first chain chooses 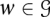Inline graphic and v ∈ Mt in computing the transition to Mt+1. The second chain uses the same w, and if v ∈ Mt ∩ Mt+1, it also uses the same v. Otherwise, if in the first chain v = y, then the second chain uses v = z. 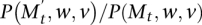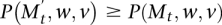If Inline graphic and the first chain performs a switch, then the second chain performs a switch with probability Inline graphic. If Inline graphic, then the second chain performs a switch whenever the first chain does, and when the first chain did not perform a switch the second chain switches with probability 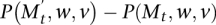Inline graphic. Our analysis applies the following simple version of path coupling adapted to our setting (see Bubley and Dyer 1997; Mitzenmacher and Upfal 2005):

Theorem 4. Let 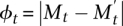Inline graphic, and assume that for some constant 0 < β < 1, E[φt+1|φt = 1] ≤ β, then the mixing time

graphic file with name 375equ8.jpg

Using the above, we prove the following convergence result for our chain.

Theorem 5. The MCMC is rapidly mixing for some c > 0.

Theorem 5 gives a range of values of c where the resulting chain will converge rapidly. We explored different values of c, and use the c = 0.5, which we found empirically to give the best trade-off between the exploration of different sets and the convergence to sets with high weight W(M) on simulated data. We use c = 0.5 for both the experiments on both simulated data and real cancer mutation data described below.

Extension to multiple sets of mutated genes

There are multiple capabilities that a cell has to acquire in order to become a cancer cell; for example, Hahn and Weinberg (2002) describe six capabilities. Thus, we expect that a small number of pathways will be mutated, and in each pathway the mutations in the corresponding genes will have both high exclusivity and high coverage. We aim to recover sets of genes in each of these pathways. If the sets of genes in each pathway are disjoint, then an iterative procedure will suffice: Once we identify a set M with high weight, we remove the genes in M from the analysis and look for high weight sets in the reduced mutation matrix. Thus, if two sets M1 and M2 of genes are disjoint and have high weight, then the iterative procedure finds both, because exclusivity is required only within and not between sets. If, instead, M1 and M2 have genes in common, then removing one of them could remove part of another. If the intersection is small, we will still be able to identify the remaining part of the other set. The problem of identifying two sets M1 and M2 of genes that both have high exclusivity and high coverage (but with no exclusivity between them) and have a number of genes in common is an interesting open problem.

Cancer data

In all tumor patients we consider, we use both single-nucleotide mutations and small indels reported in the original studies (Thomas et al. 2007; The Cancer Genome Atlas Research Network 2008; Ding et al. 2008). For glioblastoma patients, we also consider focal copy-number aberrations identified in the original study (The Cancer Genome Atlas Research Network 2008), discarding copy-number aberrations for which the sign of aberration (i.e., amplification or deletion) was not the same in at least 90% of the samples.

We reduce the size of the mutation matrix by combining genes that are mutated in exactly the same patients into larger “metagenes.” For example, suppose there exists a set S = {g1, g2} of two genes that are mutated in the same set of patients. Two sets X and Y with X\Y = {g1} and X\Y = {g2} satisfy W(X) = W(Y). Thus, both sets have the same probability. The same result holds when |S| > 2. To improve the efficiency of the MCMC sampling procedure, we replace a maximal set of genes T = {g1, g2,…} that are mutated in the same patients with a single “metagene” gT whose mutations are the same patients. Copy-number aberrations typically encompass more than one gene, and the boundaries of such aberrations vary across patients. Since we only collapse genes into metagenes if they are mutated in exactly the same patients, we will not collapse all of the genes in a copy-number aberration into a metagene if the genes in the metagene vary across patients.

Software

A Python implementation of Dendrix (De novo Driver Exclusivity) is available at http://cs.brown.edu/people/braphael/software.html.

Acknowledgments

We thank the anonymous reviewers for helpful suggestions that improved the manuscript. This work is supported by NSF grant IIS-1016648, the Department of Defense Breast Cancer Research Program, the Alfred P. Sloan Foundation, and the Susan G. Komen Foundation. B.J.R. is also supported by a Career Award at the Scientific Interface from the Burroughs Wellcome Fund.

[Supplemental material is available for this article.]

Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.120477.111.

2

For each gene, we used the observed frequency of mutation rather than a fixed background mutation rate to account for the differences in gene mutation frequencies observed in the real data.

3

Using the background mutation rate, some mutation groups would be reported as significantly mutated when considered in isolation (because of their significant coverage). Thus, larger sets of mutation groups containing these individually significant mutation groups would also be reported as significant, even if the pattern of mutations in the set is not surprising after conditioning on the observed frequency of mutations of single mutation groups.

4

The suffix of the mutation group identifies the positions of mutations in the gene, as in BRAF_600-601, or the mutated functional domain of the encoded protein, which is ECD for extracellular domain mutations, KD for kinase domain, and HD for helical domain, as described in Thomas et al. (2007).

5

Mutations were measured in 91 patients, but we removed seven patients who were identified as hypermutated in The Cancer Genome Atlas Research Network (2008). These patients have higher observed mutation rates, presumably due to defective DNA repair.

6

Genes in the metagene are TSFM, MARCH9, TSPAN31, METTL21B (also known as FAM119B), METTL1, CDK4, and AGAP2 (also known as CENTG1).

7

For ease of notation in this section, given sets A and B, we denote their difference by A − B = {x|x ∈ A and x ∉ B}, and their union by A + B = {x|x ∈ A or x ∈ B}.

References

  1. Backlund LM, Nilsson BR, Goike HM, Schmidt EE, Liu L, Ichimura K, Collins VP 2003. Short postoperative survival for glioblastoma patients with a dysfunctional Rb1 pathway in combination with no wild-type PTEN. Clin Cancer Res 9: 4151–4158 [PubMed] [Google Scholar]
  2. Bansal V, Halpern AL, Axelrod N, Bafna V 2008. An MCMC algorithm for haplotype assembly from whole-genome sequence data. Genome Res 18: 1336–1346 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Ben-Dor A, Chor B, Karp RM, Yakhini Z 2003. Discovering local structure in gene expression data: The order-preserving submatrix problem. J Comput Biol 10: 373–384 [DOI] [PubMed] [Google Scholar]
  4. Boca SM, Kinzler KW, Velculescu VE, Vogelstein B, Parmigiani G 2010. Patient-oriented gene set analysis for cancer mutation data. Genome Biol 11: R112 doi: 10.1186/gb-2010-11-11-r112 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bradley JR, Farnsworth DL 2009. Testing for mutual exclusivity. J Appl Stat 36: 1307–1314 [Google Scholar]
  6. Bubley R, Dyer M 1997. Path coupling: A technique for proving rapid mixing in markov chains. In FOCS '97: Proceedings of the 38th Annual Symposium on Foundations of Computer Science, p. 223 IEEE Computer Society, Washington, DC: doi: ieeecomputersociety.org/10.1109/SFCS.1997.646111 [Google Scholar]
  7. The Cancer Genome Atlas Research Network 2008. Comprehensive genomic characterization defines human glioblastoma genes and core pathways. Nature 455: 1061–1068 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Cerami E, Demir E, Schultz N, Taylor BS, Sander C 2010. Automated network analysis identifies core pathways in glioblastoma. PLoS ONE 5: e8918 doi: 10.1371/journal.pone.0008918 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Chehab NH, Malikzay A, Appel M, Halazonetis TD 2000. Chk2/hCds1 functions as a DNA damage checkpoint in G1 by stabilizing p53. Genes Dev 14: 278–288 [PMC free article] [PubMed] [Google Scholar]
  10. Cheng Y, Church GM 2000. Biclustering of expression data. Proc Int Conf Intell Syst Mol Biol 8: 93–103 [PubMed] [Google Scholar]
  11. Conde E, Angulo B, Tang M, Morente M, Torres-Lanzas J, Lopez-Encuentra A, Lopez-Rios F, Sanchez-Cespedes M 2006. Molecular context of the EGFR mutations: evidence for the activation of mTOR/S6K signaling. Clin Cancer Res 12: 710–717 [DOI] [PubMed] [Google Scholar]
  12. Deguchi K, Gilliland DG 2002. Cooperativity between mutations in tyrosine kinases and in hematopoietic transcription factors in AML. Leukemia 16: 740–744 [DOI] [PubMed] [Google Scholar]
  13. Ding L, Getz G, Wheeler DA, Mardis ER, McLellan MD, Cibulskis K, Sougnez C, Greulich H, Muzny DM, Morgan MB, et al. 2008. Somatic mutations affect key pathways in lung adenocarcinoma. Nature 455: 1069–1075 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Dom M, Guo J, Niedermeier R, Wernicke S 2006. Minimum membership set covering and the consecutive ones property. In Algorithm Theory—SWAT 2006: Proceedings of the 10th Scandinavian Workshop on Algorithm Theory, Riga, Latvia, July 6–8, 2006 (ed. Arge L, Freivalds R), pp. 339–350 Springer, New York [Google Scholar]
  15. Efroni S, Ben-Hamo R, Edmonson M, Greenblum S, Schaefer CF, Buetow KH 2011. Detecting cancer gene networks characterized by recurrent genomic alterations in a population. PLoS ONE 6: e14437 doi: 10.1371/journal.pone.0014437 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Garey MR, Johnson DS 1990. Computers and intractability; a guide to the theory of NP-completeness. Freeman, New York [Google Scholar]
  17. Gazdar AF, Shigematsu H, Herz J, Minna JD 2004. Mutations and addiction to EGFR: the Achilles ‘heal’ of lung cancers? Trends Mol Med 10: 481–486 [DOI] [PubMed] [Google Scholar]
  18. Getz G, Levine E, Domany E 2000. Coupled two-way clustering analysis of gene microarray data. Proc Natl Acad Sci 97: 12079–12084 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gilks W 1998. Markov chain Monte Carlo in practice. Chapman and Hall, London [Google Scholar]
  20. Hahn WC, Weinberg RA 2002. Modelling the molecular circuitry of cancer. Nat Rev Cancer 2: 331–341 [DOI] [PubMed] [Google Scholar]
  21. Hastings WK 1970. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 57: 97–109 [Google Scholar]
  22. Ikeda T, Yoshinaga K, Suzuki A, Sakurada A, Ohmori H, Horii A 2000. Anticorresponding mutations of the KRAS and PTEN genes in human endometrial cancer. Oncol Rep 7: 567–570 [DOI] [PubMed] [Google Scholar]
  23. International cancer genome consortium 2010. International network of cancer genome projects. Nature 464: 993–998 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Jensen LJ, Kuhn M, Stark M, Chaffron S, Creevey C, Muller J, Doerks T, Julien P, Roth A, Simonovic M, et al. 2009. STRING 8—a global view on proteins and their functional interactions in 630 organisms. Nucleic Acids Res 37: D412–D416 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Jones S, Zhang X, Parsons DW, Lin JC, Leary RJ, Angenendt P, Mankoo P, Carter H, Kamiyama H, Jimeno A, et al. 2008. Core signaling pathways in human pancreatic cancers revealed by global genomic analyses. Science 321: 1801–1806 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kanehisa M, Goto S 2000. KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res 28: 27–30 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Keshava Prasad TS, Goel R, Kandasamy K, Keerthikumar S, Kumar S, Mathivanan S, Telikicherla D, Raju R, Shafreen B, Venugopal A, et al. 2009. Human Protein Reference Database—2009 update. Nucleic Acids Res 37: D767–D772 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Khanna KK, Keating KE, Kozlov S, Scott S, Gatei M, Hobson K, Taya Y, Gabrielli B, Chan D, Lees-Miller SP, et al. 1998. ATM associates with and phosphorylates p53: mapping the region of interaction. Nat Genet 20: 398–400 [DOI] [PubMed] [Google Scholar]
  29. Kim Y, Wuchty S, Przytycka T 2010. Simultaneous identification of causal genes and dys-regulated pathways in complex diseases. In Research in Computational Molecular Biology: Proceedings of the 14th Annual International Conference, RECOMB 2010, Lisbon, Portugal, April 25–28, 2010 (ed. Berger B), pp. 263–280 Springer, New York [Google Scholar]
  30. Kuhn F, von Rickenbach P, Wattenhofer R, Welzl E, Zollinger A 2005. Interference in cellular networks: The minimum membership set cover problem. In Computing and Combinatorics: Proceedings of the 11th Annual International Conference, COCOON 2005, Kunming, China, August 16–19, 2005 (ed. Wang L), pp. 188–198 [Google Scholar]
  31. Madeira SC, Oliveira AL 2004. Biclustering algorithms for biological data analysis: A survey. IEEE/ACM Trans Comput Biol Bioinformatics 1: 24–45 [DOI] [PubMed] [Google Scholar]
  32. Mao J, To M, Perez-Losada J, Wu D, Del Rosario R, Balmain A 2004. Mutually exclusive mutations of the Pten and ras pathways in skin tumor progression. Genes Dev 18: 1800–1805 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Mardis ER, Wilson RK 2009. Cancer genome sequencing: a review. Hum Mol Genet 18: R163–R168 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. McCormick F 1999. Signalling networks that cause cancer. Trends Cell Biol 9: M53–M56 [PubMed] [Google Scholar]
  35. Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E 1953. Equation of state calculations by fast computing machines. J Chem Phys 21: 1087–1092 [Google Scholar]
  36. Meyer IM, Miklos I 2007. SimulFold: Simultaneously inferring RNA structures including pseudoknots, alignments, and trees using a Bayesian MCMC framework. PLoS Comput Biol 3: e149 doi: 10.1371/journal.pcbi.0030149 [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Meyerson M, Gabriel S, Getz G 2010. Advances in understanding cancer genomes through second-generation sequencing. Nat Rev Genet 11: 685–696 [DOI] [PubMed] [Google Scholar]
  38. Mitzenmacher M, Upfal E 2005. Probability and computing: Randomized algorithms and probabilistic analysis. Cambridge University Press, New York [Google Scholar]
  39. Murali TM, Kasif S 2003. Extracting conserved gene expression motifs from gene expression data. Pac Symp Biocomput 2003: 77–88 [PubMed] [Google Scholar]
  40. Randall D 2006. Rapidly mixing Markov chains with applications in computer science and physics. Comput Sci Eng 8: 30–41 [Google Scholar]
  41. Segal E, Battle A, Koller D 2003. Decomposing gene expression into cellular processes. Pac Symp Biocomput 2003: 89–100 [DOI] [PubMed] [Google Scholar]
  42. Tanay A, Sharan R, Shamir R 2002. Discovering statistically significant biclusters in gene expression data. Bioinformatics 18: S136–S144 [DOI] [PubMed] [Google Scholar]
  43. Thomas RK, Baker AC, Debiasi RM, Winckler W, Laframboise T, Lin WM, Wang M, Feng W, Zander T, MacConaill L, et al. 2007. High-throughput oncogene mutation profiling in human cancer. Nat Genet 39: 347–351 [DOI] [PubMed] [Google Scholar]
  44. Ulitsky I, Karp RM, Shamir R 2008. Detecting disease-specific dysregulated pathways via analysis of clinical expression profiles. In Research in Computational Molecular Biology: Proceedings of the 12th Annual International Conference, RECOMB 2008, Singapore, March 30–April 2, 2008 (ed. Vingron M, Wong L), pp. 347–359, Springer-Verlag, Berlin [Google Scholar]
  45. Vandin F, Upfal E, Raphael B 2011. Algorithms for detecting significantly mutated pathways in cancer. J Comput Biol 18: 507–522 [DOI] [PubMed] [Google Scholar]
  46. Varela I, Tarpey P, Raine K, Huang D, Ong CK, Stephens P, Davies H, Jones D, Lin ML, Teague J, et al. 2011. Exome sequencing identifies frequent mutation of the SWI/SNF complex gene PBRM1 in renal carcinoma. Nature 469: 539–542 [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Vogelstein B, Kinzler KW 2004. Cancer genes and the pathways they control. Nat Med 10: 789–799 [DOI] [PubMed] [Google Scholar]
  48. Wikman H, Nymark P, Vayrynen A, Jarmalaite S, Kallioniemi A, Salmenkivi K, Vainio-Siukola K, Husgafvel-Pursiainen K, Knuutila S, Wolf M, et al. 2005. CDK4 is a probable target gene in a novel amplicon at 12q13.3-q14.1 in lung cancer. Genes Chromosomes Cancer 42: 193–199 [DOI] [PubMed] [Google Scholar]
  49. Yamamoto H, Shigematsu H, Nomura M, Lockwood WW, Sato M, Okumura N, Soh J, Suzuki M, Wistuba II, Fong KM, et al. 2008. PIK3CA mutations and copy number gains in human lung cancers. Cancer Res 68: 6913–6921 [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Yang Z, Rannala B 1997. Bayesian phylogenetic inference using DNA sequences: A Markov chain Monte Carlo method. Mol Biol Evol 14: 717–724 [DOI] [PubMed] [Google Scholar]
  51. Yeang C, McCormick F, Levine A 2008. Combinatorial patterns of somatic gene mutations in cancer. FASEB J 22: 2605–2622 [DOI] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES