Global radiation damage at 300 and 260 K with dose rates approaching 1 MGy s⁻¹

Approximately half of global radiation damage to thaumatin crystals can be outrun at 260 K if data are collected in less than 1 s.

Abstract

Global radiation damage to 19 thaumatin crystals has been measured using dose rates from 3 to 680 kGy s⁻¹. At room temperature damage per unit dose appears to be roughly independent of dose rate, suggesting that the timescales for important damage processes are less than ∼1 s. However, at T = 260 K approximately half of the global damage manifested at dose rates of ∼10 kGy s⁻¹ can be outrun by collecting data at 680 kGy s⁻¹. Appreciable sample-to-sample variability in global radiation sensitivity at fixed dose rate is observed. This variability cannot be accounted for by errors in dose calculation, crystal slippage or the size of the data sets in the assay.

1. Introduction

In macromolecular X-ray crystallography, X-rays cause damage to the crystal under study (Blake & Phillips, 1962 ▶; Hendrickson, 1976 ▶; Garman & Schneider, 1997 ▶; Garman, 2003 ▶; Nave & Garman, 2005 ▶; Holton & Frankel, 2010 ▶). Two kinds of damage are distinguished in diffraction: ‘site-specific’ and ‘global’ damage. ‘Site-specific’ damage is manifested in electron-density maps as the motion of a small group of atoms in the unit cell (Helliwell, 1988 ▶; Burmeister, 2000 ▶; Weik et al., 2000 ▶; Leiros et al., 2001 ▶; Weik, Ravelli et al., 2001 ▶). To appear in the map, such motions must be repeated in each unit cell. ‘Global’ damage is manifested in the diffraction pattern as an overall or q-­dependent loss of diffraction-peak intensity (Gonzalez & Nave, 1994 ▶; Sliz et al., 2003 ▶; Kmetko et al., 2006 ▶, 2011 ▶; Owen et al., 2006 ▶; Shimizu et al., 2007 ▶; Warkentin & Thorne, 2010 ▶). The underlying damage is spread out within the cell and must be random from cell to cell.

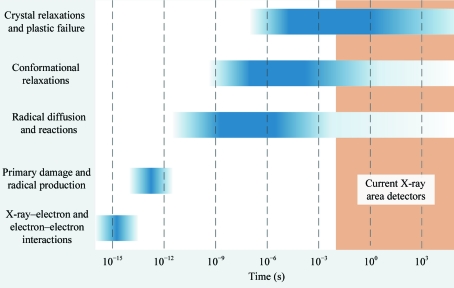
Radiation damage to macromolecular crystals involves a complex cascade of chemical and structural processes, which begins with the absorption/inelastic scattering of an X-ray photon and is followed by generation of secondary electrons, bond breaking and radical generation, radical diffusion and reactions, and rearrangements of atoms through bond breaking, conformational motions, molecular displacements, crystal deformations and plastic failure (Dertinger & Jung, 1970 ▶; Coggle, 1983 ▶). As shown in Fig. 1 ▶, these processes span timescales from femtoseconds to hours or days. While some kinds of site-specific damage [e.g. the reduction of metal ions (Schlichting et al., 2000 ▶; Berglund et al., 2002 ▶) or S—S bond breakage (Ravelli & McSweeney, 2000 ▶; Weik et al., 2000 ▶; Borek et al., 2007 ▶; Meents et al., 2010 ▶)] may be a consequence of a single process with a well defined rate-limiting step, global damage surely involves an array of processes spanning a range of timescales.

Figure 1.

Schematic illustration of the timescales of important radiation-damage processes in protein crystals. For a discussion of the timescales in radiochemistry, see Dertinger & Jung (1970 ▶) and Coggle (1983 ▶). Timescales for many of the slower radiation-damage-induced structural and lattice relaxations should be similar to those of non-radiation-induced relaxations (e.g. Henzler-Wildman & Kern, 2007 ▶; Bourgeois & Weik, 2009 ▶). Slow timescales for a component of global damage have been directly measured (Warkentin et al., 2011 ▶).

Radiation-damage processes are commonly categorized as either ‘primary’ or ‘secondary’ (Teng & Moffat, 2000 ▶; Murray & Garman, 2002 ▶; Warkentin & Thorne, 2010 ▶; Warkentin et al., 2011 ▶). Generally, primary processes occur first, happen on a shorter timescale and involve higher energy excitations than secondary damage, but experimentally distinguishing between primary and secondary damage is difficult. A more practical/experimentally relevant distinction for protein crystals is between those damage processes that become unimportant below the solvent glass-transition temperature T _g ≃ 200 K and those that persist (Weik, Kryger et al., 2001 ▶; Weik, Ravelli et al., 2001 ▶; Colletier et al., 2008 ▶; Warkentin & Thorne, 2009 ▶, 2010 ▶).

Cooling from room temperature to T ≃ 100 K decreases the global radiation sensitivities of protein crystals by one or more orders of magnitude (Blake & Phillips, 1962 ▶; Teng & Moffat, 2002 ▶; Kmetko et al., 2006 ▶, 2011 ▶; Owen et al., 2006 ▶; Southworth-Davies et al., 2007 ▶; Barker et al., 2009 ▶; Warkentin & Thorne, 2010 ▶). Most of this sensitivity decrease occurs between 300 and ∼200 K (Warkentin & Thorne, 2010 ▶). In this temperature range, the sensitivity can be described by an activation energy of 18 kJ mol⁻¹, which is consistent with activation energies for diffusion-limited reactions of radicals in aqueous solutions, solvent-coupled motions of protein side chains and other conformational relaxations. The characteristic timescales for diffusive liquid-like (or ‘solvent-dynamical’) motions should increase on cooling towards 200 K and this may account in part for the observed decrease in radiation sensitivity.

Fig. 1 ▶ schematically illustrates how the timescales of some important damage processes extend beyond ∼10 ms and into the range accessible with current X-ray area detectors (Kraft et al., 2009 ▶; Koerner & Gruner, 2011 ▶; Dinapoli et al., 2011 ▶).

Can these processes be outrun during structural data-set collection? Recent experiments and analysis (Warkentin et al., 2011 ▶) show that the answer, at least at some temperatures, is yes. Between 180 and 240 K global damage pro­gresses after the X-rays are turned off on a timescale of minutes to hours. The ‘dark progression’ rate is consistent with an activation energy of 14 kJ mol⁻¹, which is comparable to that for global radiation sensitivity in this temperature range, suggesting that both arise from a similar set of processes. At T = 240 K, approximately 27% of damage to thaumatin crystals was outrun by reducing the data-collection timescale from 20 to 10 min.

How much more damage can be outrun using larger dose rates and shorter data-collection times? In our previous experiments at CHESS, the maximum possible instantaneous dose rate was ∼8 kGy s⁻¹ and the data-run-averaged dose rate (equal to the dose per run divided by the sum of the irradiation time and time for ‘overhead’ including detector readout and goniometer motions) was smaller owing to large detector read-out times. Here, we report measurements at the Advanced Photon Source using a fast framing detector of the dose-rate dependence of radiation damage to thaumatin crystals at dose rates of up to 680 kGy s⁻¹.

2. Methods

2.1. Crystallization

Tetragonal thaumatin crystals were grown in 24-well plates using the hanging-drop method. Purified thaumatin powder (Sigma–Aldrich, St Louis, Missouri, USA) was dissolved to a concentration of 25 mg ml⁻¹ in 100 mM potassium phosphate buffer pH 6.8. A well solution was prepared by adding 1 M sodium potassium tartrate to the same buffer. 10 µl drops prepared by mixing 5 µl each of protein and well solution were suspended over 500 µl well solution.

2.2. Data collection

2.2.1. Data collection at the APS

X-ray diffraction data versus dose rate were collected on beamline 17-ID at the Advanced Photon Source (APS) using a PILATUS 6M detector (DECTRIS, Baden, Switzerland). The detector has a maximum frame rate of 12.5 Hz and a 3.6 ms readout time, so that frames with a counting time of 76.4 ms are possible.

A 50 µm circular beam of 1.00 Å X-rays with a top-hat profile was used in all experiments. The unattenuated flux was measured to be 3.3 × 10¹² photons s⁻¹ using a calibrated PIN diode (Hamamatsu Photonics S3584-06, Bridgewater, New Jersey, USA), which implies a flux density (averaged over the beam cross-section) of 1.7 × 10¹⁵ photons s⁻¹ mm⁻². The product of this flux density, the photon energy and the average mass-energy absorption coefficient of the atoms in the unit cell of thaumatin crystals gave a maximum dose rate of 680 kGy s⁻¹ (see §2.3 for details of the dose calculation). Lower dose rates (down to 3 kGy s⁻¹) were achieved using a set of aluminium attenuators built into the beamline and under computer control.

Crystals of size 200–300 µm were selected and mounted on MicroMounts (MiTeGen, Ithaca, New York, USA) in a ∼100 µm thick layer of NVH immersion oil (Cargille Labs, Cedar Grove, New Jersey, USA). For experiments at 300 K, a MicroRT capillary (MiTeGen; Kalinin et al., 2005 ▶) was filled with 50 µl mother liquor and placed over the crystal to prevent drying through the oil.

Owing to the bipyramidal habit of the crystals, the 200–300 µm cross-section corresponded to a length of up to 500 µm (from tip to tip). Care was taken to mount the crystals so that the 50 µm circular beam could be directed through just the tip, the center or at an intermediate location in between. Crystals of this size were used to ensure that our findings did not depend upon these geometrical factors (see §4).

Diffraction data were collected from 19 thaumatin crystals in three different modes as follows.

In ‘standard wedge mode’, used for average dose rates of 3.1 and 6.5 kGy s⁻¹, repeated sets of five 1° frames were collected. The detector’s exposure time (1/frame rate) was set to 0.8 and 0.4 s, respectively, to obtain a properly exposed image at each dose rate. After each five-frame set, the shutter was closed, the goniometer returned to its initial position and the next set was collected. Because goniometer resets took 2 s, in ‘standard wedge mode’ the instantaneous dose rate was larger than the average dose rate by factors of 1.5 and 2, respectively. Note that this mode is most analogous to that used in our previous experiments (Kmetko et al., 2006 ▶, 2011 ▶; Warkentin & Thorne, 2010 ▶; Warkentin et al., 2011 ▶); however, it does not contain detector readouts, only goniometer resets.

In ‘continuous wedge mode’, used for average dose rates between 13 and 103 kGy s⁻¹, the same five-frame data sets were repeatedly collected, but now collection occurred both as the goniometer advanced and as it returned, using custom control software. This eliminated the goniometer reset time, but approximately 0.64 s was still required for the goniometer to decelerate, reverse direction and accelerate. With a fixed exposure time of 80 ms, the instantaneous dose rate was 2.6 times the average dose rate for all dose rates.

In ‘quasi-still mode’, used for the highest dose rate of 680 kGy s⁻¹, the attenuators were removed, the sample was rotated only 0.001° per frame and frames were collected with an exposure time of 125 ms. This eliminated the goniometer deceleration and acceleration time so that the average and instantaneous dose rates were the same. Since the crystals were thoroughly damaged within ∼5 frames, the total rotation was less than 0.01°, so that the frames can be regarded as stills. True stills were not possible using the beamline’s control software.

2.2.2. Data collection at CHESS

To explore the validity of the metrics used in analyzing the data collected at the APS, a series of complete data sets were collected from a single large thaumatin crystal using the F1 station at CHESS. The incident X-ray wavelength was 0.979 Å. The flux was adjusted to ∼10¹⁰ photons s⁻¹ using attenuators and was approximately uniformly distributed over the 100 µm circular beam. The ∼500 µm crystal was mounted in a MicroRT capillary, an initial orientation was obtained with a 3° wedge, and the Strategy module of the HKL-2000 suite (Otwinowski & Minor, 1997 ▶) was used to determine the ideal ϕ range and frame width to minimize the dose per set. This allowed 11 consecutive complete data sets comprised of 45 1.78° frames to be collected from the same 80° angular range. Diffraction data were recorded with a Quantum Q270 detector (Area Detector Systems Corporation, Poway, California, USA), with an exposure time per frame of 1 s and a detector-readout time at the end of each frame of 3.4 s including any mechanical overhead. The resulting average dose per data set was ∼40 kGy. The average dose rate experienced by different parts of this crystal varied widely because the crystal was much larger than the beam and because of the large (80°) angular range of data collection. The maximum average dose rate (delivered to the crystal region illuminated at the center of rotation) was ∼400 Gy s⁻¹.

2.3. Data processing

Dose rates and doses delivered to each crystal were determined using the incident X-ray flux density, X-ray energy and circular top-hat beam profile by summing the mass-energy absorption coefficients for the atomic constituents of the unit cell. The cell composition was determined from the amino-acid sequence, the atomic composition of the amino acids, the solvent volume from the Matthews coefficient and the atomic composition of the solvent. The mass-energy absorption co­efficients for the X-ray energies used were obtained from NIST tables (http://www.nist.gov/pml/data/xraycoef/index.cfm). The mass-energy absorption coefficient includes energy deposition owing to photoelectric absorption, Compton scattering and pair and triplet production, as well as energy loss via emission of cascade fluorescence X-rays associated with complete atomic relaxation processes initiated by the primary vacancy as well as radiative energy loss by secondary charged particles as they slow to rest. The effects of X-ray attenuation in the finite thickness of our crystals were less than 2% and so were not taken into account. Non-uniform crystal irradiation during 5° oscillations was estimated (up to 20%) and corrected for. The doses calculated without this last correction agree to within 5% with those calculated using the program RADDOSE (Paithankar et al., 2009 ▶), which uses average atomic compositions and atomic absorption coefficients generated by the program Mucal. Corrections owing to fluorescence (<1%; Murray et al., 2004 ▶; Paithankar et al., 2009 ▶) and photoelectron escape (∼5% based on our beam and sample size; Sanishvili et al., 2011 ▶) from our samples were not taken into account. All quoted dose rates are average dose rates over the time required to collect each data set.

Data were processed according to the mode in which they were collected.

Data from both APS wedge modes were processed as in our previous studies (Kmetko et al., 2006 ▶, 2011 ▶; Warkentin & Thorne, 2010 ▶; Warkentin et al., 2011 ▶), except that XDS/XSCALE (Kabsch, 2010 ▶) were used instead of DENZO/SCALEPACK (Otwinowski & Minor, 1997 ▶). Each 5° wedge was independently indexed, integrated and internally scaled, including all full and partial reflections. A series of consecutive 5° wedges was then scaled together to obtain scaling B factors relative to the first set. We call these ‘relative scaling B factors’ throughout to differentiate them from relative Wilson B factors. The integrated intensities (from XDS) were summed to determine the dose at which the intensity fell to half its initial value, defined as the ‘half-dose’.

Data from the APS ‘quasi-still mode’ were indexed and integrated using a custom version of the XDS software (Kabsch, 2010 ▶) supplied by Wolfgang Kabsch. XDS was modified to allow the integration of highly partial reflections. Summed integrated intensities were used to determine the half-dose as above. B factors were determined by a custom scaling script as follows. Intensities were binned into 20 resolution bins covering equal k-space volumes. For successive runs, the average intensity of reflections in each bin was divided by the average intensity of reflections in that bin in the first run. The resulting ‘relative Wilson plots’ were fitted to the standard form for a B factor and the sensitivity was determined from these B factors as above. This procedure was also carried out on several data sets collected in ‘continuous wedge mode’, and the B-factor sensitivities determined by this method and by scaling consecutive wedges as described above differed by no more than 5%.

Data collected at CHESS were also used to investigate the validity of these quasi-still metrics and their correspondence with values determined from wedge data sets; see §4 and Fig. 5.

Full data sets collected at CHESS were processed using the HKL-2000 suite (Otwinowski & Minor, 1997 ▶). Each set consisted of 45 1.78° frames, which were divided and pro­cessed as follows. Neighboring non-overlapping sets of five frames were processed as though they were wedge sets using DENZO and SCALEPACK. That is, frames 1–5 from each of the 11 consecutive full data sets were scaled against each other to determine relative scaling B factors and this was repeated for frames 6–10, 11–15 etc. Comparison of these sets then revealed any variation of the B-factor increase with the ϕ range examined in each wedge. The summed intensity of each individual frame (from the output of DENZO) and of five-frame sets were determined and the half-dose values were compared.

3. Results

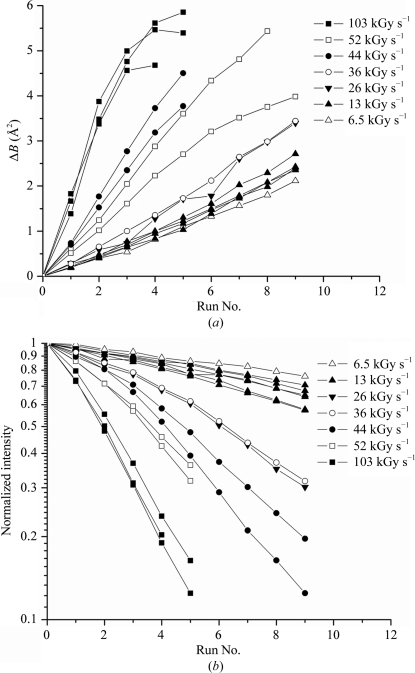
Fig. 2 ▶(a) shows the scaling B factor as a function of wedge number (proportional to dose) for all of the T = 260 K data collected at the APS in ‘continuous wedge mode’ (see §2). The different slopes are not largely a consequence of differences in sensitivity because different dose rates (6.5–100 kGy s⁻¹, corresponding to different levels of attenuation) were used for each curve and the exposure time was fixed. If they were plotted as a function of dose they would come closer to falling on top of each other, but would still deviate significantly (see Figs. 4 and 5). They are plotted ‘as is’ so that the curves may be inspected to verify a linear variation with dose at low doses in all cases. The sensitivities derived from such plots are discussed below. The nonlinearity in B at large doses has been observed before and is predicted by the radiation-damage model of Blake and Phillips (Blake & Phillips, 1962 ▶; Hen­drickson, 1976 ▶; Warkentin & Thorne, 2010 ▶).

Figure 2.

(a) Change in scaling B factor and (b) integrated intensity versus run number for thaumatin crystals at T = 260 K. Each run consisted of five 1° frames, which were (a) scaled against the first run to determine the relative scaling B factor and (b) summed and normalized to the intensity in the first run. The same exposure sequence was used for each curve and the dose rate was varied using attenuators. The B-factor sensitivity (Fig. 3 ▶ a) was determined from the initial slope in (a) and from the dose per run. The half-dose (Fig. 3 ▶ b) was determined from the run at which the intensity fell to half of its initial value and from the dose per run. Data at 13 kGy s⁻¹ were extended to I/I ₀ = 0.5 using an exponential fit. The data at 6.5 kGy s⁻¹ extend beyond the range of the plot to I/I ₀ = 0.51.

Fig. 2 ▶(b) shows the normalized intensity integrated versus wedge number for the same samples and dose rates as in Fig. 2 ▶(a). Again, the large variability in slope is a consequence of the different dose rates used for each curve. Each curve has a well defined half-dose, or else the half-dose is determined by extrapolation.

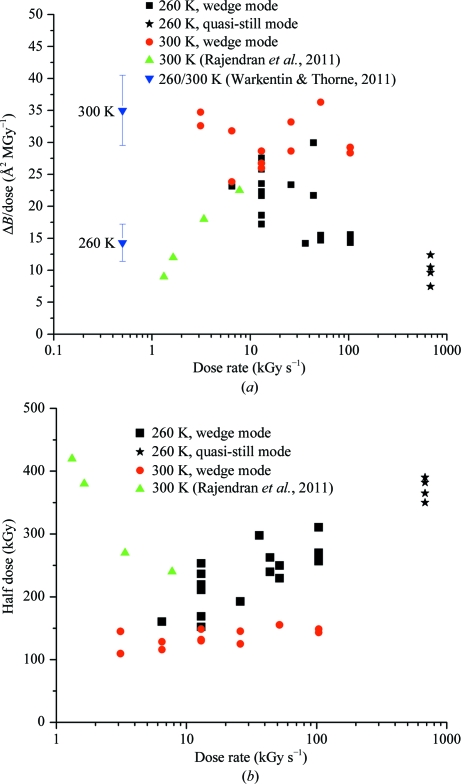
Figs. 3 ▶(a) and 3 ▶(b) show the sensitivity as determined by the scaling B-factor increase and the half-dose, respectively, versus dose rate for all of the APS wedge data at T = 300 and 260 K, the APS quasi-still data at T = 260 K and the results of some previous measurements on thaumatin at T = 300 K. Each point from the present work represents a complete set of wedge data versus dose from a single crystal; 30 data sets from 19 crystals are shown. At T = 300 K no dose-rate dependence can be reliably discerned in either damage metric, especially given the considerable scatter. At T = 260 K the data in Fig. 3 ▶ show a modest but clear dose-rate effect, which becomes clearer once the quasi-still points at 680 kGy s⁻¹ are taken into account. The initial crystal B factors, unit-cell volumes and mosaicities (as determined by XDS) were 21.2 ± 0.9 Ų, 520 000 ± 2000 ų and 0.049 ± 0.032°, respectively, at T = 300 K and 19.3 ± 2.2 Ų, 513 000 ± 4400 ų and 0.058 ± 0.030°, respectively, at T = 260 K; the actual T = 300 K mosaicities of thaumatin crystals determined from rocking curves acquired using a low-divergence beam are likely to be ∼0.01° or less. At the half-dose, the average changes in the unit-cell volume and mosaicity were 0.16 ± 0.16% and 0.011 ± 0.043°, respectively, at T = 300 K and 0.13 ± 0.28% and 0.026 ± 0.038°, respectively, at T = 260 K. Note that the sample-to-sample variability in these increases is larger than the increases themselves and that the order of magnitude of the variability is comparable to that in initial cell and mosaicity values. This suggests that the actual increases may be relatively small.

Figure 3.

(a) B-factor sensitivity and (b) half-dose versus average dose rate determined from 30 data sets collected using 17 thaumatin crystals. Data from two previous studies (Warkentin & Thorne, 2010 ▶; Rajendran et al., 2011 ▶) are also shown. The error bars on the data from Warkentin & Thorne (2010 ▶) indicate the standard deviation of the sensitivities of the >5 crystals examined at each temperature. The sensitivity at 260 K was determined by interpolation using the temperature dependence reported in that study.

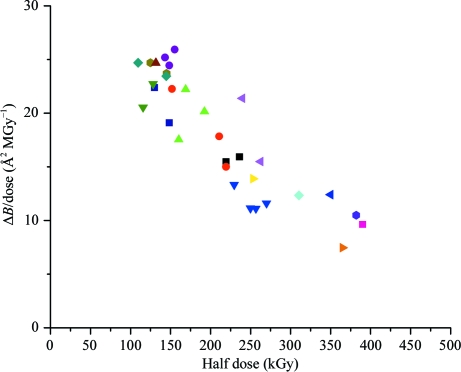
To explore the source of experimental crystal-to-crystal scatter, Fig. 4 ▶ shows the radiation-damage sensitivity (Fig. 3 ▶ a) determined from each crystal versus the half-dose (Fig. 3 ▶ b) for that crystal for all of the APS wedge data at T = 260 and 300 K. If all of the experimental scatter in Figs. 2 ▶ and 3 ▶ were owing to errors in dose calculations, Fig. 4 ▶ would show a simple inverse proportionality, since the sensitivity is determined by dividing ΔB by the calculated dose and the half-dose is proportional to the calculated dose. Although a significant inverse correlation is observed, Fig. 4 ▶ suggests that other sources of variability are also important.

Figure 4.

Comparison of damage metrics for all data sets in Fig. 3 ▶, excluding those collected at 680 kGy s⁻¹ and including sets collected from different regions of the same sample. Points with the same symbol shape and color were collected from different positions on the same crystal. If the dose-response of each crystal and region were identical, errors in dose calculation would cause these points to lie on a curve of inverse proportionality (see text). Deviations from inverse proportionality indicate either errors in determination of the metric from the data or deviations that are innate to the metric or to the response of each crystal region.

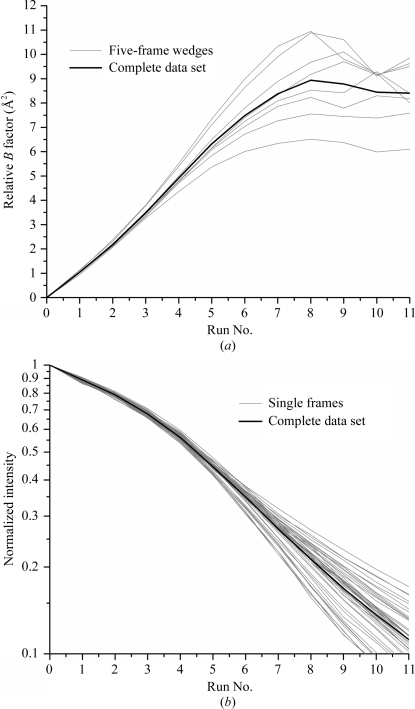
Deviations from inverse proportionality in Fig. 4 ▶ could result from errors in the determination of the metrics. Fig. 5 ▶ explores the robustness of both metrics using a series of complete room-temperature thaumatin data sets collected from a single crystal at CHESS that have been divided into a series of wedges (Fig. 5 ▶ a) or single frames (Fig. 5 ▶ b) with increasing dose.

Figure 5.

Variability in the determination of (a) the B-factor sensitivity and (b) the half-dose. Eight contiguous 5° wedge sets (a) or 45 contiguous single frames (b) were collected from the same crystal and processed independently (see §2). The resulting relative B factors and integrated intensities versus run number are compared with those obtained by processing the entire 45 frame data set. The B-factor sensitivities and half-doses determined from wedge and single-frame curves, respectively, vary from those determined from complete data sets by ∼10%. Both the B-factor and intensity curves vary smoothly through the angular range, i.e. curves for neighboring wedges or frames are correlated.

Fig. 5 ▶(a) shows the scaling B factor as a function of data-set number for wedge sets extracted and processed independently from the full CHESS data set. The individual B factors agree with their average to within 10% up to data set 5 (corresponding to a dose of ∼200 kGy), after which significant deviations are observed.

Fig. 5 ▶(b) shows the normalized summed intensity of each single frame (processed independently) as a function of data-set number for all of the individual frames in the crystal’s full data set. These agree with their average to within 5% up to the half-dose (∼200 kGy). Consequently, for a given crystal both the scaling B factor and normalized summed intensity do not depend on the particular wedge of data/range of ϕ angles analyzed. Furthermore, wedge (and for summed intensity, single-frame) data give estimates of these parameters that are of comparable accuracy to those obtained from complete data sets. In this way, the B-factor sensitivity and half-dose values obtained from quasi-still APS data can be quantitatively compared with values obtained from wedge sets. The validity of the comparison is discussed below.

4. Discussion

4.1. Dose-rate effect

What is clearest from our data for thaumatin is that any dose-rate dependence of either damage metric between 3 and 680 kGy s⁻¹ is small. At T = 300 K any dose-rate effect is too small to be reliably deduced from our data. At 260 K both the B-factor sensitivity and half-dose data (Fig. 3 ▶) indicate a modest reduction in damage rate with increasing dose rate, especially when the quasi-still data at 680 kGy s⁻¹ are included. An accurate estimate is difficult because of the large crystal-to-crystal scatter, but a crude estimate suggests that the sensitivity is decreased and the half-dose is increased by a factor of ∼1.5 at 100 kGy s⁻¹ and a factor of 2 at 680 kGy s⁻¹ relative to that at ∼10 kGy s⁻¹. These results suggest that the timescales for important radiation-damage processes are faster than our ∼1–10 s minimum data-collection time at T = 300 K, but that at 260 K at least some of these processes can be outrun.

4.2. Beam heating

In addition to driving radiochemistry, X-rays heat the sample (Kriminski et al., 2003 ▶; Mhaisekar et al., 2005 ▶; Snell et al., 2007 ▶). A temperature rise in excess of ∼10 K would complicate the interpretation of our results. Radiation sensitivity increases with increasing T (Warkentin & Thorne, 2010 ▶), so heating at large dose rates would make crystals appear to be more radiation-sensitive than they are at the nominal temperature of the experiment. The reduced high-dose-rate sensitivity that we observe at 260 K would then be an underestimate of the true constant-temperature effect and a small reduction at 300 K could be obscured. Heating could also produce transient changes in lattice constants and/or molecular structure during data collection, leading to diffraction-peak motion in reciprocal space and errors in measured peak intensities.

Heat transfer from protein crystals and X-ray beam heating have previously been analyzed (Kriminski et al., 2003 ▶). Assuming that the crystal is uniformly illuminated and that the heat-transfer rate is limited by the boundary layer at the crystal surface, the steady-state crystal temperature increase is

where L is the characteristic size of the illuminated volume (taken to be the beam diameter of 50 µm), v is the kinematic viscosity of the nitrogen-gas stream (1.9 × 10⁻⁶ m² s⁻¹; Kriminski et al., 2003 ▶), κ is the thermal conductivity of the nitrogen gas (9.8 × 10⁻³ W m⁻¹ K⁻¹; Kriminski et al., 2003 ▶), u is the velocity of the gas stream (1 m s⁻¹), I is the intensity of the incident X-ray beam (3.2 × 10⁶ W m⁻² at 680 kGy s⁻¹) and L _abs is the X-ray absorption length (∼4 mm).

Using this expression and these values, at average dose rates of 100 and 680 kGy s⁻¹ the calculated temperature increase is 1.3 and 8.5 K, respectively. The actual temperature rise is smaller than this if the crystal is larger than the beam (Kriminski et al., 2003 ▶). We can also calculate an upper bound on the amount of heating by assuming a simpler geometry in which the sample is a very long cylinder of radius r ₂. Energy is assumed to be deposited at a fixed power density (equivalent to the dose rate) within a radius r ₁ ≤ r ₂ (corresponding to the X-­ray beam radius) and along the sample’s length (i.e. there is no attenuation along the length). In this geometry, the maximum temperature rise, calculated in Appendix A , is 6.0 K at 1 MGy s⁻¹. This ‘upper bound’ is lower than the estimate from (1), which assumes that the beam has the same size as the crystal and thus neglects additional heat dissipation owing to the ‘fin’ effect provided by crystal regions outside the beam.

Consistent with these calculations, no evidence of heating is observed in the unit-cell parameters. Unit-cell expansions with dose were, as in previous studies, somewhat erratic. The largest measured expansion at doses up to the half-dose (Fig. 3 ▶ b) and at either temperature was ∼1% at a dose rate of 43 kGy s⁻¹; using the measured thermal expansion coefficient (Warkentin & Thorne, 2009 ▶) this would correspond to a temperature rise of 25 K. Much smaller expansions (typically 0.2% or less) were observed at other dose rates, corresponding to a maximum temperature rise of 5 K. At the highest dose rate (680 kGy s⁻¹), unit-cell parameters could not be accurately refined from the single frames. In some cases they decreased, and the largest increase was 0.5%. Given the variability, no correlation between cell-volume expansion and dose rate could be deduced. Since radiation damage itself typically causes cell expansion, we estimate that actual beam heating was less than 1 K in experiments at all but the highest (680 kGy s⁻¹) dose rate.

4.3. Sources of variability

A striking feature of Fig. 3 ▶ is the large (factor of two) discrepancy in the results obtained from supposedly identical experiments performed on different crystals or on different regions of the same crystal. Here, we will enumerate potential sources of error and attempt to estimate their magnitudes.

The most obvious source of error in radiation-damage experiments is in determining the dose. Potential sources of dose error have been discussed elsewhere (Kmetko et al., 2006 ▶, 2011 ▶). Fig. 4 ▶ shows that B-factor sensitivity and half-dose are not simply inversely proportional, including for data collected at different positions on the same crystal, so that dose errors owing to beam size and shape, illuminated crystal volume and absolute flux calibration cannot explain all of the variability we observe. Deviations from inverse proportionality in Fig. 4 ▶ can only be accounted for by crystal-to-crystal and region-to-region variability in dose response as quantified by the chosen metrics. These deviations must either be owing to errors in the determination of the quantities underlying the metrics (total integrated intensity and B factor), to some deficiency in the choice or definition of the metric or else to some inherent variability in the crystal response.

Fig. 5 ▶(a) demonstrates that a 5° wedge of data is as good as a complete data set for determination of the B factor to within 10% (up to the half-dose). Beyond the half-dose it should be no surprise that the B factor becomes poorly defined because its determination depends on high-resolution data, which disappear at large doses. Fig. 5 ▶(b) demonstrates that a single frame suffices to determine the half-dose to an accuracy of ∼5%. For a given crystal, B-factor sensitivities and half-dose are thus robust.

Based on this, we suggest that the dose response of a crystal region as quantified by B-factor sensitivity and half-dose contains large inherent variability that affects these two metrics at least somewhat independently. This partial independence is reasonable. The B factor is determined from resolution-dependent changes in intensities which are almost exclusively at high resolution (>4 Å). On the other hand, the half-dose is influenced by low-resolution data (<4 Å) since approximately half of the total intensity is in reflections at d < 4 Å. These metrics reflect order on correspondingly different length scales.

4.4. Comparison with previous studies

Several previous studies have examined the effect of dose rate on radiation damage to protein crystals. Sliz et al. (2003 ▶) used APS beamline 19-ID and maximum flux densities of ∼10¹⁵ photons s⁻¹ mm⁻² to study radiation damage to a total of three crystals: one each of two MHC class I complexes and a viral polymerase. At T = 100 K, reducing the maximum flux density by a factor of ten was found to have no significant effect on the decay of integrated intensities versus accumulated incident photon fluence (photons mm⁻²). This finding was interpreted as being consistent with the expected absence of secondary damage arising from diffusive processes at T = 100 K.

Leiros et al. (2001 ▶) studied damage to a total of four crystals of two proteins, drMTH and bovine trypsin, at T = 100 K using three dose rates ranging from 48 to 480 kGy s⁻¹ and from 8 to 190 kGy s⁻¹, respectively. For a fixed dose, the changes in unit-cell volume, mosaicity and Wilson B factor showed no clear correlation with dose rate.

Southworth-Davies et al. (2007 ▶) studied damage to lysozyme crystals at T = 300 K. As the dose rate was increased by a factor of 1.6 from 6 to 10 Gy s⁻¹, the half-dose increased by a factor of four. Such a large dose-rate dependence, corresponding to a factor of 25 reduction in sensitivity over a factor of ten in dose rate (compared with a factor of two reduction over roughly two orders of magnitude in dose rate found here at T = 260 K), and at such small dose rates (three to five orders of magnitude smaller than those used here) is unphysical and, as discussed elsewhere (Kmetko et al., 2011 ▶), is inconsistent with other measurements (Barker et al., 2009 ▶) in the same dose-rate range showing no dose-rate dependence. Additional work in this dose-rate regime is required in order to resolve these discrepancies.

Rajendran et al. (2011 ▶) reported T = 300 K B factors and half-doses deduced from complete data sets for four thaumatin crystals at dose rates from 1.3 to 7.7 kGy s⁻¹. Their data, which are reproduced in Figs. 3 ▶(a) and 3 ▶(b), show a factor-of-two increase in sensitivity with increasing dose rate in both metrics, opposite in sign to the effect that we observe at 260 K. Their half-doses are larger than the present T = 300 K values near ∼3 kGy s⁻¹ by a factor of 2–3 and their B-factor sensitivities are smaller than those reported here and by Warkentin & Thorne (2010 ▶) by a similar factor. Part of this discrepancy may arise from crystal-to-crystal scatter and the small number of crystals (one per dose rate) examined. Rajendran and coworkers used a continuous exposure while frames were collected using a PILATUS 6M detector, whereas we collected repeated 5° wedges of data with pauses in between the wedges for goniometer resets. Warkentin & Thorne (2010 ▶) used an ADSC Q210 with a 3.4 s readout time which added additional pauses. These pauses could allow time for relaxations within the crystal, which would affect the relative contributions of different damage products and could therefore influence the overall sensitivity. Our use of average rather than instantaneous dose rates should correct for this difference, and the lack of time evolution at T = 300 K on timescales longer than 100 ms seen here suggests than any relaxations are small. Rajendran and coworkers also collected and analyzed com­plete data sets rather than wedges, but as discussed above the full data sets and wedges examined here gave the same results.

Warkentin & Thorne (2010 ▶) examined the B-factor sensitivity (relative B factor versus dose) of 49 thaumatin crystals as a function of temperature from 100 to 300 K. Estimated instantaneous and average dose rates were ∼2 and 500 Gy s⁻¹, respectively. The average B-factor sensitivity at T = 300 K was 35 Ų MGy⁻¹ (Fig. 3 ▶ a), which is in good agreement with the present results. Interpolation of reported values at 270 and 240 K gives a value of ∼14 Ų MGy⁻¹ at T = 260 K, which at first sight appears to be inconsistent with the present results (Fig. 3 ▶ a). Based upon other measurements (e.g. Kmetko et al., 2011 ▶), the B-factor sensitivity is likely to be dose-rate independent below ∼10 kGy s⁻¹, so the discrepancy is likely to be a factor of two or less. Substantial sample-to-sample variability was observed there as here and this could account for part of the remaining discrepancy.

Based upon measurements of dark progression versus temperature in thaumatin crystals, Warkentin et al. (2011 ▶) discussed the feasibility of outrunning at least a fraction of radiation damage at temperatures above ∼200 K. The amount of damage that could be outrun would depend both on how rapidly data could be collected and on the distribution of timescales for the relevant damage processes. Extrapolating from dark-progression measurements and assuming a single damage timescale (i.e. a very narrow timescale distribution), the characteristic time for the ‘progressing’ component of damage was estimated to be 18 s at 270 K and 9 s at 300 K. In the present experiments, reducing the data-collection time by two orders of magnitude to ∼1 s produced no clear reduction in sensitivity at T = 300 K and only a factor of two reduction at 260 K. This suggests that the distribution of relevant damage timescales must be broad and/or that long-timescale damage processes make only a small (factor of two or less) contribution to total damage sensitivity in this temperature range.

5. Conclusions

We have determined the global radiation-sensitivity of thaumatin crystals at 260 and 300 K as a function of dose rate for dose rates ranging from 3 to 680 kGy s⁻¹. At T = 100 K, at which most crystallographic data are now collected, previous experiments and fundamental considerations suggest that the radiation-sensitivity is independent of dose rate. However, at temperatures somewhat below T = 300 K the present results indicate that significant sensitivity reductions are possible. The factor of two reduction for data collection in ∼1 s at 260 K should increase as collection times are pushed to 100 or 10 ms. Minimum collection times will be limited by the crystal size, molecular weight, beam heating and detector technology (Warkentin et al., 2011 ▶). Additionally, crystals will need to be kept stable in their mounts as the goniometer rotates at many revolutions per second. Data collection at 260 K is especially practical because ice crystals are unlikely to form provided external solvent is removed and because the vapour pressure of water is so low that dehydration will occur very slowly. Although radiation-sensitivities will still be much larger than those obtained at T = 100 K, reductions sufficient to enable a significant expansion of studies on unfrozen samples under more nearly native conditions seem feasible.

We have also shown that even nominally identical experiments probing global radiation damage can give results that differ by 50% or more. Results from a large number of samples must thus be averaged to draw statistically significant conclusions, as has been previously argued (Meents et al., 2007 ▶, 2010 ▶; Warkentin & Thorne, 2010 ▶). Consistent results are obtained when processing one frame or 100 frames, regardless of the metric, but only when data from a single crystal region are examined. The origin of the crystal-to-crystal and region-to-region variability and the identification of data-collection protocols and meaningful damage metrics that minimize it requires further study.

Appendix A.

We will consider an infinitely long cylinder whose axis is the beam axis. The cylinder has a radius r ₂ and the beam has a radius r ₁ which is smaller than r ₂. This geometry is appropriate to our experiments at the APS since the beam was always smaller than the cross-section of the crystal orthogonal to the beam. The assumption of infinite length neglects heat transfer in a direction parallel to the beam, so that all heat loss must be in the radial direction. For this reason, the infinite cylinder is more pessimistic than a finite cylinder. We are also ignoring the absorption of the beam by the sample, so that the intensity of the beam is always equal to its incident value.

We will compute the steady-state temperature rise. Transient effects (such as the rise time) are unimportant because the steady-state temperature rise is the maximum temperature rise; the temperature cannot ‘overshoot’ in the case of a constant-intensity beam (Incropera & DeWitt, 2002 ▶).

The steady-state temperature distribution in this geometry is described by

where A and B are constants set by the boundary conditions. The distribution is independent of the anglular and longitudinal coordinates.

The beam flux determines the heat flux q ₁ (per unit area) across a cylindrical surface bounding the beam. The constant A can be determined from

where k is the thermal conductivity of the cylinder. Since the same total heat flux passes through a cylindrical shell at any radius in steady state, the heat flux (per unit area) at r ₂ can be determined from

The temperature rise at the surface of the cylinder is related to this heat flux (per unit area) by the heat-transfer coefficient h,

The constant B can be determined from the temperature at r = r ₂,

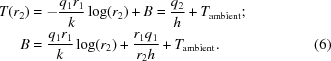Finally, q ₁ is related to the dose rate D by

provided that the dose rate is expressed per unit area (i.e. as W m⁻³, not W kg⁻³). This is a consequence of the fact that all of the heat deposited inside the cylindrical shell at r ₁ must exit that shell in steady state.

The resulting temperature distribution is

We assume D ≃ 1 MGy s⁻¹ ≃ 10⁹ W m⁻³, a sample density of 10³ kg m⁻³, k = 0.5 W m⁻¹ K⁻¹ and h = 300 W m⁻² K⁻¹ (Kriminski et al., 2003 ▶). This gives a temperature rise of 5.4 K at r = r ₁. The temperature at the center of the sample (assuming that the beam is uniform) is 0.6 K higher, or 6.0 K.