Abstract
When analysing gait, the identification of the period of stance is often needed. Forceplates are typically used, but in their absence kinematic data can be employed. Five kinematic methods have been previously described in the literature. However, these methods have not been compared to each other for overground or treadmill running. Therefore, the purpose of this study was to compare these five kinematic methods of identifying the stance phase with vertical ground reaction force data both during overground and treadmill running. We recruited forty recreational runners (20 males) for this study. Twenty runners underwent an instrumented gait analysis during overground running, and twenty were tested during instrumented treadmill running. All runners ran at 3.35 m·s−1. Each kinematic method was compared with stance identified from the vertical ground reaction force (gold standard) for overground running. This method was then repeated for treadmill running. Two methods were found to be valid and reliable for determining footstrike. These were the time when the distal heel marker reached a minimum vertical position, and when the vertical velocity of this same marker changed from negative to positive. These methods had absolute errors that ranged from 22.4 ms to 24.6 ms for both modes of running. Toe-off was best identified using peak knee extension, with absolute errors of 4.9 ms for overground running and 5.2 ms for treadmill running. Utilising automated kinematic methods of determining stance will aid researchers studying running when forceplates are unavailable.
Introduction
The study of gait often requires identification of footstrike and toe-off in order to properly divide the gait cycle into stance and swing. This identification is typically accomplished with forceplates, an instrumented walkway or footswitches. However, when these devices are unavailable, an alternative method is needed.
Several kinematic methods to determine footstrike and toe-off during walking have emerged in the literature. Dingwell et al. [1] used the timing of peak knee extension to separate walking strides. In a different approach, Alton et al. [2] chose the peak downward position of a lateral malleolus marker to identify footstrike and the time of increase in vertical position to identify toe-off. A study by Zeni et al. [3] employed the relative displacement between the sacral and foot markers to determine stance during treadmill and overground walking. They were the only authors that validated their method with forceplate data for treadmill walking. Their average absolute errors (henceforth, absolute error) were <20 ms for overground and treadmill walking.
Methods to determine stance during running may be different than for walking. Schache and colleagues [4] identified footstrike during running from the rapid decrease in vertical velocity of a toe marker. They used the increase in vertical velocity of the toe marker to identify toe-off. Using a different approach, Hreljac and Stergiou [5] noted that the sagittal plane angular velocity of the foot was at its minimum at footstrike. In addition, the sagittal plane angular velocity of the shank was at its minimum at toe-off. These authors were the only ones to validate their method with forceplate data for overground running. They found absolute and average RMS errors (henceforth, RMS error) less than 3 ms and 7 ms for footstrike and toe-off, respectively.
None of these methods have been compared to each other, nor have any methods been validated for treadmill use during running gait. Therefore, the purpose of this study was to compare the validity of these kinematic methods during overground and treadmill running. Only two studies employed methods based upon running gait, which has different mechanics than walking. Consequently, we hypothesised that the methods of Schache et al. [4] and Hreljac and Stergiou [5] would be the most accurate for determining both footstrike and toe-off during overground and treadmill running.
Methods
Twenty healthy recreational runners (25.1 ± 8.7 yrs, 10 males), were recruited for overground (OG) running. All runners identified themselves as rearfoot strikers and were running ≥16 km per wk. They provided informed consent prior to study inclusion according to the institution's Human Subjects Review Board. The Declaration of Helsinki ethical principals were followed. We placed 28 spherical retro-reflective markers on the segments of the right rearfoot, shank, thigh and pelvis with tape (BSN-JOBST, Rutherford College, NC, USA). Anatomical markers were applied: first and fifth metatarsal heads; medial and lateral femoral condyles, tibial plateaus and malleoli; iliac crests and greater trochanters bilaterally. Shells containing four tracking markers were placed on wraps on the posterior-lateral distal aspect of the thigh and shank segments. The rearfoot was tracked with three markers attached to the shoe around the rearfoot. Pelvis tracked with bilateral anterior superior iliac spine and sacrum markers. Runners wore Nike Air Pegasus footwear (Nike, Beaverton, OR, USA). They ran at 3.35 m/s along a 25 m runway striking a forceplate (Bertec, Columbus, OH, USA) at the runway center. Runners had several warm-up trials followed by five trials during which data were collected. Three-dimensional kinematic data were sampled at 120 Hz with an eight camera passive motion analysis system (VICON, Centennial, CO, USA) and filtered at 12 Hz with a fourth-order zero-lag Butterworth filter. No further filtering of the velocity or acceleration data were performed. Kinetic data were sampled at 1080 Hz and filtered similarly at 50 Hz.
For the instrumented treadmill (TM) validation, twenty additional recreational runners (24.5 ± 9.3 yrs, 10 males) were recruited. These runners fulfilled the same requirements previously described, yet they were separate group of runners as these data were collected as part of a different study. They all rated their TM running comfort ≥ seven out of ten, with zero being not comfortable and ten, very comfortable. Retro-reflective markers were placed as described previously. Following a three minute TM (AMTI, Watertown, MA, USA) warm-up at self-selected speed, they ran for two minutes at the 3.35 m/s following which five trials of 5 strides were recorded. Three-dimensional kinematic data were sampled at 200 Hz with an eight camera passive motion analysis system (VICON, Centennial, CO, USA) and filtered identically to OG data. Kinetic data were sampled at 1000 Hz and filtered similarly at 50 Hz. Sampling frequencies were different from OG data as TM data were collected in a different onsite laboratory as part of another study.
Data were trimmed, visually in VICON to 167 ms before and after stance for OG and 165 ms before and after stance for TM running. The strike index (SI) [6] was calculated as the position of the center of pressure at contact, relative to the length of the foot. A SI<0.34 indicates a rearfoot strike pattern, and this value ranged between 0.003 – 0.33 in these runners. Stance was first determined using the vertical ground reaction force (vGRF) from forceplate data for both OG and TM running. Footstrike (FS) was identified when vGRF exceeded 20 N. Toe-off (TO) was identified when vGRF dropped below 20 N. Stance was estimated using five kinematic methods reported in the literature for OG and TM running and compared to stance determined from vGRF.
1. Peak Knee Extension (PKEXT)
The time of peak knee extension was used to identify FS while the second peak knee extension was used to identify TO [1]. As the time between FS and TO is shorter than that between TO and the next FS, the appropriate event could be identified.
2. Foot Vertical Position (FPOSV)
The minimum vertical position of the distal heel (DIHE) marker (on heel counter base) was used to identify FS. The minimum vertical position of the 2nd metatarsal head (MTH2) marker was used to identify TO. This method was a slight modification from the method of Alton et al. [2] as they used a different marker set than the one in the current study.
3. Foot-Sacrum Displacement (FSDIS)
FS was defined at the time of maximum positive displacement in the direction of progression between the sacrum and DIHE. TO was defined as the maximum negative displacement, along the lab anterior-posterior axis, between the MTH2 and sacrum. This point in time is when the leg is maximally outstretched posteriorly relative to the pelvis. These methods are from Zeni et al. [3].
4. Foot Vertical Velocity (FVELV)
The change in vertical velocities from negative to positive of the DIHE and MTH2 markers was used to determine FS and TO, respectively. This method was modified from Schache et al. [4] as they used a different marker set than the one in the current study.
5. Angular Acceleration (ANGA)
The sagittal plane foot and shank 3D segment angles were determined in the lab coordinate system. FS was defined at the time of the local minimum of foot angular acceleration in the sagittal plane. TO was defined at the time of the local minimum of the shank angular acceleration in the sagittal plane [5]. The accelerations were determined using finite differences.
To analyse differences between stance determination methods during OG running, we computed absolute and root mean square (RMS) errors (in ms) between each method and the forceplate method for each trial. These errors were averaged across the five trials for each runner and across all runners. The same process was repeated for TM data. Along with calculating the separate absolute and RMS errors, we also computed a summed error, which represented a combination of the validity and consistency of the methods. Specifically, we computed the sum of the absolute value of the absolute error plus its standard deviation and the average RMS error plus its standard deviation.
Results
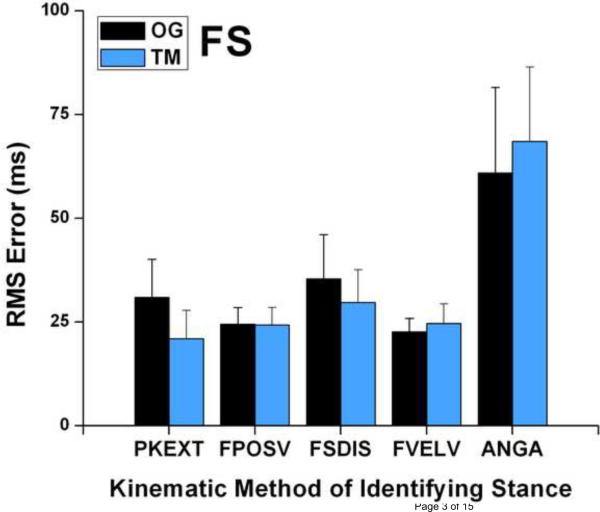
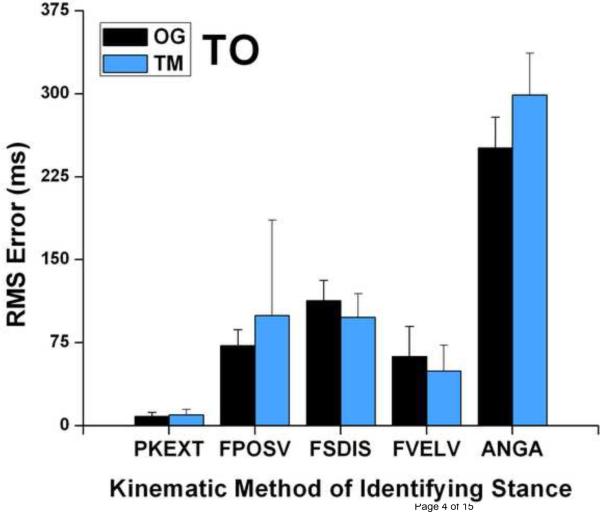
Overall, the absolute and RMS errors were similar for OG and TM running (Table 1 and Figure 1) although there were differences between methods. For OG running, ANGA, FVELV and FPOSV had absolute errors < 25.0 ms (stance length averaged 260 ms for OG). However, ANGA had the largest SD, 34.0 ms. Additionally, ANGA for TM was associated with RMS error twice the absolute error during OG running. For TM running, FPOSV, FVELV and PKEXT all had FS errors < 25 ms and SD < 10 ms. For TO, PKEXT was notably the most valid for OG and TM running, identifying TO < 6 ms later than the vGRF. All other methods were associated with ≥ 43.2 ms of error in identifying TO during both conditions.
Table 1.
Absolute (ABS) errors (mean (sd)) and summed (SUM) errors for the methods to determine footstrike (FS) and toe-off (TO) during overground (OG) and treadmill (TM) running. Units: ms.
| PKEXT | FPOSV | FSDIS | FVELV | ANGA | ||
|---|---|---|---|---|---|---|
| FS | ABS OG | −30.2 (9.7) | 24.3 (4.1) | −34.9 (10.8) | 22.4 (3.3) | −20.8 (34.0) |
| ABS TM | −20.0 (7.7) | 24.2 (4.2) | −29.2 (8.2) | 24.6 (4.7) | −56.6 (18.0) | |
| SUM OG | 80.0 | 56.9 | 91.8 | 51.6 | 136.3 | |
| SUM TM | 55.5 | 56.9 | 75.0 | 58.5 | 174.9 | |
|
| ||||||
| TO | ABS OG | 4.9 (6.3) | −72.2 (14.4) | 112.8 (18.5) | −43.2 (31.7) | −245.0 (27.2) |
| ABS TM | 5.5 (9.3) | −86.2 (66.0) | 98.0 (21.4) | −49.0 (4.7) | −297.7 (37.7) | |
| SUM OG | 23.2 | 173.4 | 262.9 | 164.6 | 556.3 | |
| SUM TM | 29.6 | 338.2 | 238.7 | 145.1 | 672.3 | |
Note: For ABS errors positive values indicate method identified event after vertical ground reaction force identification. For OG, 1 frame = 8.3 ms, for ITM, 1 frame = 5.0 ms. PKEXT: peak knee extension, FPOSV: foot vertical position, FSDIS: foot-sacrum displacement, FVELV: foot vertical velocity, ANGA: angular acceleration.
Figure 1.
Root mean square, RMS, errors for footstrike, FS, (a) and toe-off, TO, (b). Note similarity of foot vertical position, FPOSV, and foot vertical velocity, FVELV, during both modes of running at FS. Error bars represent one standard deviation. FSDIS: foot-sacrum displacement; ANGA: angular acceleration.
Based on the summed error results (Table 1), during OG running, FS was most accurately determined using FVELV (51.6 ms), closely followed by FPOSV (56.9 ms). The best method of determining FS for TM running was PKEXT (55.5 ms). However, both FPOSV (56.9 ms) and FVELV (58.3 ms) were nearly as accurate. For TO, PKEXT was the most accurate for both modes of running, with summed errors of 23.2 ms and 29.6 ms for OG and TM, respectively.
Our ANGA findings were in stark contrast with Hreljac and Stergiou [5], who also validated their findings with forceplate data. Thus, we felt it warranted further exploration. Close inspection of our data revealed multiple minima evident in foot and shank angular velocity curves that were not noted in Hreljac and Stergiou's data. These authors included fewer frames before stance, which we felt might account for different results. Therefore, we conducted a post-hoc analysis on a subset of five OG and five TM runners. We trimmed kinematic data to approximately 58 ms and 50 ms before stance for OG and TM trials, respectively, which approximated Hreljac and Stergiou [5]. Error in identifying FS OG increased from −20.8 (34.0 SD) ms to 78.3 (53.8 SD) ms. All other errors were similar to those calculated using untrimmed data.
Discussion
We aimed to identify the most accurate and reliable method of determining stance for both overground and treadmill running. Our results suggested that different kinematic methods should be used to identify FS and TO. Specifically, FVELV and FPOSV were most accurate for FS and PKEXT was most accurate for TO. For both FS and TO, the absolute and RMS errors were similar. These results only partially support our hypothesis of FVELV and ANGA being the most accurate. Overall, error SDs were not systematically reduced during TM running. This finding was surprising due to the controlled velocity and spatial constraints of the treadmill belt. Although other methods of detecting stance have been identified [6,7], we chose to focus on methods without pattern matching or optimisation of thresholds for marker positions and/or velocities.
Regarding FS, FPOSV and FVELV were the most accurate measures for both overground and treadmill running. Each of these methods was slightly modified from their original description due to differences in marker sets. Alton et al. [2] used a lateral malleolus marker and Schache et al. [4] used a toe marker. However, we used the distal heel marker on the heel of the shoe. The late identification of FS using these methods for treadmill and overground running was likely due to shoe compression that occurs slightly after FS. The compression delayed the peak downward position of the distal heel marker, which occurred slightly after FS was identified from the vGRF. Because these methods consistently (SDs less than 6 ms) identified stance late (22.4 to 24.6 ms late), it is conceivable a correction factor could be used to identify FS more accurately. Both methods were associated with the lowest standard deviations and low summed errors for treadmill and overground running. Therefore, both methods could be considered consistent and valid. Both PKEXT and FSDIS consistently detected FS early for overground and treadmill running. This difference was likely because the knee reaches peak extension near the end of swing but it begins to flex just prior to FS. This motion would result in both of these methods detecting FS early. However, these methods are likely to work better with walking gait where the leg is typically maximally extended and outstretched at FS [1,3]. Our increased error compared to Zeni and colleagues [3] reported errors likely relates to these differences between walking and running mechanics.
Results were different for identification of TO. PKEXT was associated with notably lower errors and lower standard deviations than the other methods tested for both overground and treadmill running. The method identified TO slightly late for both running modes, as a result of the knee beginning to flex just before TO during running. FSDIS identified TO later than PKEXT, likely due to continued posterior movement of the foot after it leaves the ground during running. FPOSV and FVELV both identified TO early, because the foot begins to move upwards prior to the end of stance. The subtle modification of Alton et al. [2], using minimum vertical position of the toe marker instead of the lateral malleolus, may have increased error for TO.
We expected that ANGA would be one of the most accurate of those tested, as it was one of two methods reported for running [5]. While it had the smallest absolute error for identification of FS during overground running, it was also the most variable. As consistency in the identification of events is important, this variability made it an undesirable choice. For FS and TO, it had the greatest summed error. We believe that the inaccuracy and variability of this method is due to the numerous oscillations in the angular acceleration curve. Trimming the data closer to stance did not substantially reduce the errors. It is possible the accuracy differences were due foot model differences. The current study tracked foot motion using a 3D model, while Hreljac and Stergiou used a 2D model with two foot markers. They identified optimal cut-off frequencies for each marker, which they did not describe. Differences in filtering could certainly alter the characteristics of the curves, which could influence the results.
The summed error calculation combined errors and variability into one value in order to help determine a best method. We felt that this error might provide a more comprehensive approach as one method might be accurate, but extremely variable and thus not useful. This error was helpful when assessing the results for ANGA, as it indicated that although ANGA had low absolute errors for FS, it was not the best method.
The threshold for stance detection and signal filtering could have influenced results [9]. To minimise filtering bias, filtering frequencies were determined by identifying where 95% of the signal content was retained. Furthermore, a 20 N threshold accurately identifies stance of ballistic movements, including running.
A limitation of this study was the 3.3 ms difference in timing resolution for the OG and TM data from differences in sampling frequencies (120 Hz, 8.3 ms/frame vs 200 Hz, 5 ms/frame). Theoretically, the lower timing resolution for the TM data could have produced lower errors due to fewer analog frames between video frames. However, there was no systematic decrease in errors calculated during TM running compared to OG running.
Conclusion
For identifying footstrike, foot vertical velocity (FPOSV) and foot vertical position (FVELV) were the most valid and consistent for overground and treadmill running.
For identifying toe-off, peak knee extension (PKEXT) was the most valid and consistent for overground and treadmill running.
Despite controlled velocity of the belt during treadmill running, standard deviations of results for stance identification were similar for both treadmill and overground running.
Acknowledgements
Authors thank Richard Willy for data collection assistance and Dr. Kurt Manal for manuscript discussions. Funding: Drayer Physical Therapy Institute, DOD W911NF-05-1-0097, and NIH 1S10RR022396-01.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Dingwell JB, Cusumano JP, Cavanagh PR, et al. Local dynamic stability versus kinematic variability of continuous overground and treadmill walking. J Biomech Eng. 2001;123(1):27–32. doi: 10.1115/1.1336798. [DOI] [PubMed] [Google Scholar]
- [2].Alton FL, Baldey L, Caplan S, et al. A kinematic comparison of overground and treadmill walking. Clin Biomech. 1998;13(6):434–40. doi: 10.1016/s0268-0033(98)00012-6. [DOI] [PubMed] [Google Scholar]
- [3].Zeni JA, Richards JG, Higginson JS. Two simple methods for determining gait events during treadmill walking using kinematic data. Gait Posture. 2008;27(4):710–14. doi: 10.1016/j.gaitpost.2007.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Schache AG, Blanch PD, Rath DA, et al. A comparison of overground and treadmill running for measuring three-dimensional kinematics of the lumbo-pelvic-hip complex. Clin Biomech. 2001;16(8):667–80. doi: 10.1016/s0268-0033(01)00061-4. [DOI] [PubMed] [Google Scholar]
- [5].Hreljac A, Stergiou N. Phase determination during normal running using kinematic data. Med Biol Eng Comput. 2002;38(5):503–6. doi: 10.1007/BF02345744. [DOI] [PubMed] [Google Scholar]
- [6].Cavanagh PR, Lafortune MA. Ground reaction forces in distance running. J Biomech. 1980;13(5):397–406. doi: 10.1016/0021-9290(80)90033-0. [DOI] [PubMed] [Google Scholar]
- [7].Winter DA, Quanbury AO, Hobson DA, et al. Kinematics of Normal Locomotion-A Statistical Study Based on T.V. Data. J Biomech. 1974;7(6):479–486. doi: 10.1016/0021-9290(74)90082-7. [DOI] [PubMed] [Google Scholar]
- [8].Stanhope SJ, Kepple TM, McGuire DA, et al. Kinematic-based technique for event time determination during gait. Med Biol Eng Comput. 1990;28(4):355–360. doi: 10.1007/BF02446154. [DOI] [PubMed] [Google Scholar]
- [9].Tirosh O, Sparrow WA. Identifying Heel Contact and Toe-Off Using Forceplate Thresholds With a Range of Digital-Filter Cutoff Frequencies. J Appl Biomech. 2003;19(2):178–184. [Google Scholar]