Risky movement increases the rate of range expansion

Abstract

The movement rules used by an individual determine both its survival and dispersal success. Here, we develop a simple model that links inter-patch movement behaviour with population dynamics in order to explore how individual dispersal behaviour influences not only its dispersal and survival, but also the population's rate of range expansion. Whereas dispersers are most likely to survive when they follow nearly straight lines and rapidly orient movement towards a non-natal patch, the most rapid rates of range expansion are obtained for trajectories in which individuals delay biasing their movement towards a non-natal patch. This result is robust to the spatial structure of the landscape. Importantly, in a set of evolutionary simulations, we also demonstrate that the movement strategy that evolves at an expanding front is much closer to that maximizing the rate of range expansion than that which maximizes the survival of dispersers. Our results suggest that if one of our conservation goals is the facilitation of range-shifting, then current indices of connectivity need to be complemented by the development and utilization of new indices providing a measure of the ease with which a species spreads across a landscape.

1. Introduction

The dynamics of range expansion is a key topic in ecology today. It is central to understanding how invasive species spread once established [1], and a greater understanding of an invasive's spatial dynamics can help improve strategies aimed at eradication or control [2–4]. Additionally, for most species, dispersal is likely to be one of the important factors determining their responses to climate change [5,6]. How well a species is able to track a shifting climate envelope will depend upon its dispersal characteristics on the one hand, and the amount and spatial distribution of suitable habitat across a landscape on the other [7]. Models of invasion dynamics are incorporating increasingly sophisticated descriptions of dispersal. For example, integro-difference models incorporating fat-tailed dispersal kernels have been shown to better predict the spatial spread of populations [8]. However, most of these models continue to use phenomenological descriptions of dispersal kernels, and do not account for the interdependence of movement rules and landscape that defines the shape of the kernel. Some recent work has begun to take a more mechanistic approach for plants; mechanistic models for wind-dispersed seeds have been used to generate dispersal kernels [9], which are used to calculate equilibrium spread rates. This approach can readily be extended to incorporate increased biological detail, such as stage-structure, in order to model the spread dynamics of long-lived species [10]. While there has been progress in incorporating mechanistic descriptors of dispersal into models for the spread of plants, there are few examples of behaviour-based dispersal models for the spread of animals (but see [11] for an example).

Animal ecologists have made considerable progress in identifying the characteristics of movement that make it more likely that a dispersing individual will successfully arrive at a destination patch [12,13]. Straight movement trajectories (i.e. high correlation in the direction of successive steps) almost always reduce the risk that an individual will suffer mortality before finding a habitat patch [14–16]. In addition, and quite obviously, organisms with greater perceptual range are expected to survive dispersal more frequently, all else being equal [13]. In other work, it has been demonstrated that the speed of movement that maximizes survival can depend upon both the risk of predation during dispersal and the need to forage while moving [12].

Establishing movement rules that minimize the risk of mortality during dispersal provides some initial insight into the types of strategies that organisms are likely to adopt given different types of landscape structure, risk of predation and food availability. However, it is important to recognize that the strategy that minimizes dispersal mortality will not necessarily be the strategy that optimizes key indices related to spatial population dynamics [17]. For example, we are frequently interested in managing populations existing in fragmented habitat, and here our conservation objective may be to maximize total population size or patch occupancy, or to minimize the risk of population extinction. Fragmented populations are generally less prone to extinction when there is a reasonable degree of long-distance dispersal between habitat patches [18], but a behavioural strategy that minimizes dispersal mortality is unlikely to lead to long-distance dispersal. Consider the case of individuals that have an extensive perceptual range and immediately bias their movement towards a patch when they detect it. Almost all of these individuals emigrating from a particular patch will disperse only to those few patches that are close to the first [16], and this will reduce the probability that more distant patches are recolonized should they become extinct.

In an evolutionary context, the strategy that evolves will not necessarily be the one that minimizes dispersal mortality, even if doing so maximizes individual fitness. The evolution of dispersal is shaped by a range of selective forces, including demographic and environmental stochasticity [19–21], inbreeding depression [22,23], kin competition [24–27] and spatial sorting [28,29]. In this setting, inclusive fitness and metapopulation selection become key concepts and they, along with individual fitness considerations, determine the evolutionary outcome (for a recent review on this topic, see [17]).

Here, we are primarily concerned with range expansion, and we consider the rate of expansion to be our key index. If we are trying to control an invasive species, then we typically try to minimize its rate of expansion, whereas in conserving native biodiversity we are often interested in improving the rate at which species can shift their biogeographic ranges to track a moving climate envelope. In the case of range expansion, the behavioural dispersal rules that maximize survival probability may be quite different from those that maximize the rate of range expansion. This is because the rate of range expansion is largely determined by the distance moved by the most dispersive individuals in a population. These highly dispersive individuals will typically employ riskier movement rules [16] that result in greater dispersal mortality relative to their less dispersive conspecifics.

In this contribution, we provide an initial comparison of how different movement rules perform in terms of (i) reducing dispersal mortality and (ii) maximizing the rate of range-shifting. For (i), we run simulations similar to many performed earlier [12,15,16], where individuals are forced to emigrate from a patch and follow specified dispersal rules. The proportion of individuals successfully reaching a patch is recorded. In (ii), our approach moves from simulations of single individuals to spatial population dynamics, and we determine how rate of range expansion responds to varying the movement rules. Finally, in (iii), we add evolutionary dynamics and consider how the movement rules that evolve at an expanding front differ from those obtained in a stationary population.

2. Methods

We use an individual-based model to simulate dispersal movements in continuous landscapes. We explore the effects of movement behaviour in relation to landscape structure, in terms of the spatial arrangement of habitat patches. Before introducing the movement model, we first describe the algorithm used for generating different landscape configurations. Finally, we describe the model that incorporates population and evolutionary dynamics.

(a). Generating landscapes

Our landscape generation method is in the spirit of Zollner & Lima [15]. We arrange patches across the landscape according to uniform, random and clumped distributions. For the first set of simulations, exploring the survival probability of single individuals, we use square landscapes of size 1000 × 1000 spatial units, each with 100 circular patches of a 1 unit radius. For the uniform distribution, the patches are evenly spaced as a 10 × 10 grid. For the random distribution, the midpoint of each patch is selected by drawing x and y coordinates from a uniform distribution. The clumped landscape was generated by randomly selecting five clump centres in the interior of the landscape. Next, 30 patches were selected around the centres, with their distance to the centre drawn from normal distribution with s.d. 75. The patches were chosen so that a distance between neighbouring patches was at least 1 unit. For the population-level simulations, we used the same method of generating the landscapes, but the landscape in these simulations was elongated (to allow for expanding population ranges) to 15 000 × 1500 units, with more patches (n = 2250) to maintain the same density. As the landscape was open (i.e. not toroidal), increasing the width to 1500 in these simulations served to reduce the influence of wide, uncrossable gaps, especially with clumped landscapes.

(b). Modelling individual movement

A wandering individual follows a biased correlated random walk [16]. In a correlated random walk (CRW), the direction of a step taken by the walker depends upon the direction of the immediately preceding step. The term ‘bias’ throughout this text refers to the tendency for moving towards a particular location in space, and should not be confused with a ‘bias’ meaning ‘shifting the walk orientation in one direction’ (e.g. as used by Heinz & Strand [30]). The bias parameter (b) represents the strength of bias towards a closest patch, and can range from 0 (unbiased, correlated walk) to 1 (biased, uncorrelated walk). The movement direction (ϕ) is drawn from a circular Cauchy distribution [31], with location (around which the distribution is clustered) being a weighted average of a direction of previous step (ϕ_{t − 1}) and a direction towards the centre of the closest habitat patch (Ψ_t), and with a concentration parameter (ρ). Therefore, the direction of each step is governed by the formula

2.1

where CCauchy is the circular Cauchy distribution, with the first term describing the preferred direction, and the second term (ρ) a directional persistence in the movement (ρ = 0 produces Brownian motion, and ρ = 1 means fully deterministic movement). Obviously, the calculation takes into account the circularity of ϕ and Ψ (see [31], ch. 1.3.1 for the details). We also assumed that b is a function of the time spent moving. Our reasoning is that dispersing individuals may move for a period prior to actively searching for the nearest destination patch. The switching may relate to energy reserves (as reserves are depleted they switch to an active patch search strategy) or to constraints imposed by time costs of dispersing. To incorporate the time-dependent bias, we used a generalized Michaelis–Menten-type equation,

2.2

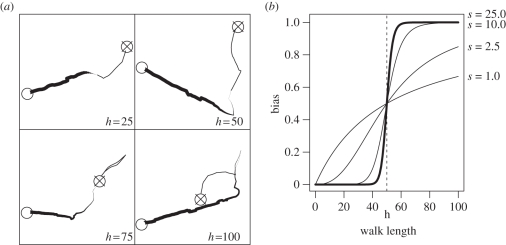
where t is time since departure from the natal patch, h is the switching time (i.e. the walk length at which bias is equal to 0.5) and s is a shape parameter. In the main set of simulations, we fixed s at 25, so that, in practice, the individual initially moved with unbiased CRW, and when reaching h steps it switched to a movement strongly biased towards the nearest patch (examples and function graph shown in figure 1).

Figure 1.

(a) Examples of biased correlated random walk movement paths with time-varying bias. Individuals depart from the patch marked with the crossed circle and arrive at the target patch (open circles). Paths differ in switching time (h); the step correlation was ρ = 0.95. Line thickness reflects the strength of the bias at a particular step. (b) The shape of the bias function with different values of the shape parameter (thick line, s = 25; thin lines, s = 1, 2.5 and 10) and switching time h = 50. When s is in (0, 1], the function is increasing towards an asymptote at 1; when s is in [−1, 0), the function decreases asymptotically towards 0; and when |s| > 1, it is sigmoidal, becoming steeper as the absolute value of s increases.

The step length is constant (equal to one spatial unit), and while moving individuals suffer a per-step risk of mortality, M. In all the results reported in this paper, M = 0.01. However, we have also conducted a sensitivity analysis where we varied M, using values of M = 0.005 and 0.02. Qualitatively, all results were remarkably similar. The landscapes we use have no explicit boundaries other than the extent of the patches, thus movement is limited only by mortality in the matrix.

(c). Incorporating population dynamics

Individuals emigrate from their natal patches with probability e. Emigrants move either until they die (owing to per-step mortality), or until they reach a non-natal patch, where they settle, produce offspring and die immediately after reproducing. Each adult individual produces a number of offspring drawn at random from the Poisson distribution with mean λ. Once all adults have reproduced, the juveniles are subject to competition. Each juvenile survives competition with probability K_p/N_p, where K_p is patch p's carrying capacity and N_p is the number of juveniles in that patch. If N_p < K_p, then all juveniles survive. Inside the patch, there are no other sources of mortality.

In each run, we release a population of 2000 identical individuals in an area including 7.5 per cent of all patches in the westernmost part of the landscape. We allowed the population dynamics to stabilize over 100 generations in this ‘enclosure’ (i.e. individuals are not allowed to settle outside this enclosure). Afterwards, the simulation continues for a further 2000 generations, during which the whole landscape becomes available for colonization. We recorded longitudinal abundance (i.e. position of settled individuals along the abscissa) of animals over simulation time, and calculated the expansion velocity towards the east (as the average shift of the range front during one timestep).

We repeated this scenario for the three different types of landscape described earlier, and for 100 values of h ranging from 1 to 2000 steps, ρ = 0.75, 0.90, 0.97 and 0.99, and s = 25. The carrying capacity (K) of each patch was 25 individuals, the emigration probability (e) was 10 per cent and mean offspring size (λ) was 2.

(d). Incorporating evolutionary dynamics

To include evolutionary dynamics, we initialized a population with a mixture of individuals with different alleles (range of h = 0–5000, range of ρ = 0–1) and introduced a 0.005 mutation probability for all alleles. When a mutation occurred, the value of a trait changed by a random amount within ±1 per cent of the allowed trait-specific limits (i.e. h up to ±50 and ρ up to ±0.01). The simulations were run for 10 000 generations. In most cases, this time extent allowed the expanding range to reach the opposite edge of the landscape. Such a long duration was necessary because of small subpopulation size, and thus relatively low number of dispersers. We excluded those rare simulations (with clumped landscape) when the population was trapped in the middle of landscape and did not expand further. Finally, to examine how our assumption of abrupt switching of movement mode influenced the results, we allowed the bias shape parameter s to evolve within a range from −25 to 25 (which also allowed for bias decreasing with time). In these evolutionary scenarios, we specifically looked at (i) expansion velocity, (ii) evolving phenotypes at the range front during the expansion and (iii) at the end of expansion, phenotype clines from the range margin towards the core.

3. Results

(a). Individual perspective

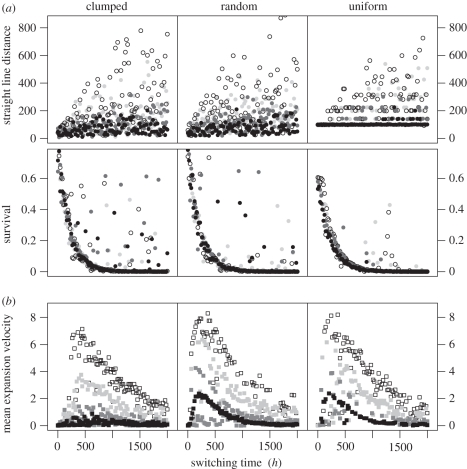
Unsurprisingly, individuals that begin biasing their movement towards a non-natal habitat patch earlier in their movement trajectory have a greater chance of survival than those postponing this until later (figure 2a). However, successful dispersers that switch behaviours after a longer period (i.e. those with a higher h) have typically arrived at more distant patches (figure 2a). Consistent with previous studies, we find that individuals that move in straighter lines (i.e. have a higher ρ) have a higher survival rate. We also find that surviving dispersers that travel in straighter lines typically disperse further. This is shown very clearly in figure 2a, where the colour of the points indicates the correlation of the movement path (darker points indicate less correlated movement). Across all three landscape types, when h > 1000, we observe a substantial number of dispersers travelling over 300 units; however, all of these individuals move with highly correlated walks. The great majority of individuals moving with lower correlation disperse less than 150 units (net distance), even when they have a high switching time. We observe no great qualitative differences in either survival probabilities or dispersal distances between landscape types. We note, however, that in uniform landscapes, individuals tend to have lowered survival—this is simply because the minimum straight-line distance is largest in this type of patch distribution (100 steps).

Figure 2.

Results of the simulations of (a) single individuals and (b) whole populations. Individuals were moving with biased correlated random walk with time-dependent bias in three types of landscapes. The varying parameters were the switching time (h) and path straightness (ρ, reflected in the shade of the symbols). (a) Straight-line distance made and survival probability of individuals moving until they reach a patch. A single point reflects one individual, for which the probability of survival after making n steps was calculated assuming 1% per-step mortality (M), thus survival = (1 − M)ⁿ. (b) Mean velocity of populations' expansion (longitudinal shift in spatial units per generation). Each point is a result of one simulation of a population with different parameters. The population was allowed to expand its range over 2000 generations. In calculation of the mean speed, we included only the timesteps until the range reached the border of the landscape. The values of parameter ρ ranged from 0.75 to 0.99 between individuals/populations. The shape of the bias function was a sharp sigmoid (s = 25). ρ = 0.99 (white symbols), ρ = 0.97 (light grey symbols), ρ = 0.90 (dark grey symbols) and ρ = 0.75 (black symbols).

(b). Population level

Compared with individual survival, the rate of range expansion (our population-level index) responded very differently to the movement rules (compare figure 2a with figure 2b). The relationship between expansion speed and switching time (h) is hump-shaped, right-skewed, with a maximum rate of range expansion obtained for a switching time between 250 and 500 steps. Path straightness (ρ) consistently increases the expansion speed. For example, on a clumped landscape, the maximum velocity of range expansion is 2.2 units per generation when ρ = 0.75, while it is 17.9 when ρ = 0.99 (see electronic supplementary material, table S1 for additional results for other values of ρ and for the other landscape structures). Changing the value of ρ has no substantial impact on the shape of the relationship between the switching time and the expansion velocity; for all ρ, we obtain the hump-shaped relationship between rate of expansion and h, and the fastest range expansion is always found for similar values of h (figure 2b).

(c). Evolutionary dynamics

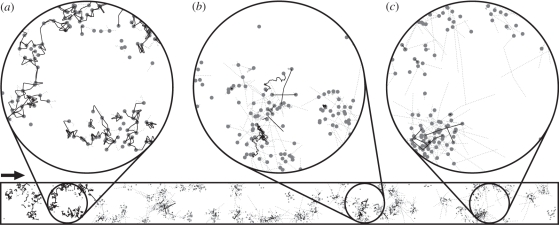
The evolved movement strategy at the range front can often be quite different from that selected in the core of a population. This is true for each of the three landscapes. Figure 3 shows an illustrative snapshot taken from our simulations. There are two useful ways to show the spatio-temporal trends in the evolution of a trait which both mirror how similar data may be collected in future field studies [32]. First, we can plot how movement behaviour traits change within a single patch from the point in time when that patch is first colonized during the range expansion (as in figure 4). Second, for a single point of time, we can plot how movement traits vary with distance from the expanding range margin (see electronic supplementary material, figure S1).

Figure 3.

Expanding and evolving population in the clumped landscape. Expansion is heading towards right. Points denote the patches and lines show the movement paths of dispersing individuals (grey lines depict unsuccessful dispersers). A transition between core subpopulations with neighbourhood dispersers and margin populations with long-distance dispersers is shown (at the end of 5000th generation). Three sections are magnified to show some characteristic processes taking place during the expansion. (a) Core population of short-range dispersers. (b) Less risky, local dispersers re-emerging in relatively recently established populations owing to mutation. (c) Freshly colonized patches consisting only of long-range dispersers. Number of grey dotted lines compared with solid lines illustrates the high mortality of the risky dispersers.

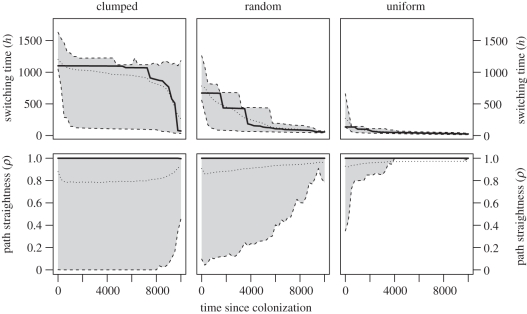
Figure 4.

The change in movement behaviour traits since patch colonization through time, in three types of landscape. The bias shape was fixed at s = 25. The shaded area and dashed line encloses 95% of values; thick lines are medians and dotted lines are means. Values are averaged over 25 simulations. Changes in these traits related to the distance of a patch to expanding wavefront are shown in electronic supplementary material, figure S1, and a comparison with results with evolving switching shape in electronic supplementary material, figure S3.

At an expanding front, patches tend to be colonized by individuals with a late switching time, h (i.e. individuals that move for a long period prior to biasing their movement to a habitat patch). Subsequent to patch colonization, we observe a reduction in h and, this decline in h occurs in a stepwise progression (figure 4). It is important to note that the switching time that evolves at the range-expanding front is much closer to that which maximizes the rate of range expansion (figure 2b) than to that which maximizes individual survival (figure 2a). Indeed, the actual survival of dispersers declines towards the range front, most markedly in the fragmented landscape (figure 5), which was accompanied by an increase in the net dispersal distance reached.

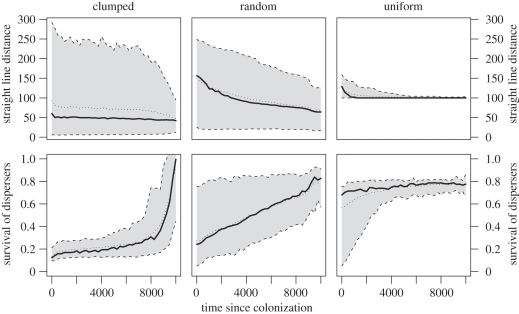
Figure 5.

Straight-line distance covered by dispersing individuals and their survival since patch colonization through time. Calculation of survival assumed that exactly 10% of population emigrated, therefore it slightly exceeds 100% in one case. The grey area encloses 95% of values, thick lines depict medians, dotted lines depict means. Values are averaged over 25 simulations. Changes in these traits related to the distance of a patch to expanding wavefront are shown in electronic supplementary material, figure S2, and comparison with results with evolving switching shape in electronic supplementary material, figure S4.

We observe a very similar pattern if we consider movement rules along a transect running from the front towards longer-established populations. At the front, there are high values of h, and h declines with distance from the front (see electronic supplementary material, figure S1). The decline in h away from the front is notably slower for a clumped landscape.

Most individuals employ a highly correlated walk regardless of where we look along the range, and this result is consistent for all landscapes. Interestingly, we do observe higher within-population variability for ρ towards the expanding range margin (figure 4), and this variation is much greater in random and clumped landscapes than it is for uniform landscapes. Particularly high variation in ρ occurred in clumped landscape, including individuals using a movement close to Brownian motion in the unbiased stage (ρ = 0). Using such a strategy, the individual benefits from low correlation in that it can intensively search the neighbourhood while still being able to disperse at long range, because it would switch to targeted movement extremely late (figure 4; electronic supplementary material, figure S1). Still, the expansion in clumped landscape progressed slowest when compared with other landscapes.

The most pronounced difference between the landscapes is in the transition from the populations of the risky, long-distance dispersers in the range margin to the short-range dispersers typical of the core (figure 5; electronic supplementary material, figure S2). For the core phenotypes, it is particularly difficult to progress across the aggregated landscape following the risky dispersers, hence they appear in newly colonized clumps of patches owing to mutation rather than through immigration (figure 3b). As a result, the zone delineated by the long-distance phenotype domination is much wider in the clumped landscapes. The opposite is observed in the uniform landscape, where the core phenotype follows shortly after the expansion front.

Finally, allowing the switching shape to evolve along with other movement parameters did not alter considerably the qualitative results. Yet allowing more flexible movement rules had a great impact on survival. Details of these simulations are shown in electronic supplementary material.

4. Discussion

Although substantial progress has been made both in the development of mechanistic models of animal movement and in the development and application of spatial models incorporating demographic processes, the two are rarely linked. In this paper, we have made such a link, and in doing so, progress towards developing theory on how a key population-level index of success—the rate of range expansion—is determined by the inter-patch movement rules employed by individuals. Importantly, our results demonstrate that behavioural rules that maximize individual survival are quite different from those that maximize the population's rate of range expansion. When we add evolutionary dynamics to the system, we demonstrate that selection at an expanding front favours behaviour that increases the rate of population expansion instead of behaviour that minimizes disperser mortality. Our results clearly reinforce the argument that models linking population dynamics and movement rules are urgently required [33], while also highlighting that an evolutionary perspective is informative, particularly considering the role of different levels of selection in driving observed dispersal behaviours [17].

Our results regarding the link between movement behaviour and individual survival are entirely consistent with those found by several previous authors [15,16,30,34]. This is not surprising as, for the most part, our model is similar to these previous models. In particular, our results agree with numerous previous demonstrations that individuals moving in straighter lines increase their probability of successfully arriving at a non-natal patch. This consistent result flows from the per-step risk of mortality; when inter-patch trajectories are more tortuous, total distance travelled is higher and there is a greater risk that individuals will die before arriving at a destination patch [5,15]. We also find that individuals that bias their movement towards a destination patch earlier are more likely to survive dispersal. Again, this is because of the reduction in the step length of inter-patch trajectories when individuals more swiftly orient towards a potential destination patch. One clear difference between this model and previous ones is that here we model the strength of bias to the nearest non-natal patch as time-dependent (a function of the number of steps already taken), whereas in our previous work [16] we treated it as location-dependent (a function of the distance to the nearest non-natal patch). Importantly, the key result—greater survival of individuals that rapidly orient towards a potential destination—is unaffected by the way the bias is modelled.

Whereas numerous previous studies have focused on how individual survival probabilities relate to inter-patch movement rules [12,15,34], few have considered the consequences of movement rules for spatial population dynamics [33]. This may be in part because high-quality empirical data on animal movements have only recently become available [35], so our ability to empirically address the question of movement rules is in its infancy [36]. Theoretically, however, we find that, at both individual and population level, correlated (straighter) movement trajectories perform better. Trajectories with higher correlation yield greater rates of range expansion, as well as improving an individual's probabilities of survival. Here, however, we observe that the greatest rate of range expansion is obtained for intermediate switching times: to maximize the rate of range expansion, individuals need to move for a period of time before biasing their trajectory towards a non-natal patch. Doing so, however, decreases individual survival, because as soon as switching time increases above 0, disperser survival declines. The reason for the hump-shaped relationship between switching time (h) and range expansion velocity is as follows. When switching time is short, individuals survive dispersal with high likelihood but do not tend to move far (they move to patches very close to the natal patch; figure 2a). Increasing switching time results in much greater range-dispersal distances, while simultaneously reducing survival (figure 2a). It is well known that long-distance dispersal events have a large influence on rates of range expansion [8,37]; thus, unsurprisingly, we find the faster rates of range expansion when switching time is longer and resultant dispersal distances increase. However, we do not find the maximum rate of range expansion for the very high values of switching time because when switching time reaches such high values, the survival rate of dispersers is extremely low. There is therefore a balance where the maximum rate of range expansion is obtained at intermediate switching times, when there is a combination of long-distance dispersal and survival high enough to maintain population growth at the expanding front.

The clear difference between those behavioural rules that are ‘best’ for an individual and those that are ‘best’ for a population is intriguing, and has potentially important implications, both for applied spatial ecology and for evolutionary biology. For example, much current conservation biology is focused on developing strategies that will be effective under rapid environmental change. Management strategies aimed at facilitating a species's range shift include the development of habitat networks and, more controversially, assisted colonization [38–40]. In this regard, our results highlight the need for these models to consider population-level outcomes, rather than examining only individual fitness effects. For example, the most effective habitat network in terms of facilitating the range expansion of a species may not be that which minimizes dispersal mortality. Similarly, when considering which types of species are most likely to perform well within habitat networks of a different design, we should not use individual fitness or survival as the only index of success. The same will be true as we begin to develop strategies for assisted colonization; we need to look beyond the short-term success of those individuals that are introduced and use population models that can project population-level measures of success over multiple generations. For assisted colonization, rather than only asking how many of the introduced individuals successfully survive introduction (or successfully reproduce) [41], we should consider how many more additional colonized habitat patches we obtain through the intervention than would have occurred without any action.

Our results are also of interest in evolutionary biology, because they highlight the tension between spatial assortment and selection acting at different levels [17,29]. It is already well established that at an expanding front, selection tends to favour more dispersive strategies [11,28,32,42], and this occurs despite both theoretical and empirical demonstrations that the lifetime reproductive success of an individual adopting a high-dispersal strategy can be substantially lower than of one adopting a low-risk strategy [43,44] (see also [11,45] for empirical demos). The benefit of dispersing more is that you increase the chances that some of your descendants remain at the expanding front through subsequent generations, but it can take several generations before the payoff of playing the high-risk strategy is realized in terms of number of descendants [44].

Most previous research exploring the evolution of dispersal at expanding range margins [28,32,46] has asked how emigration rates should evolve at expanding range margins (but see [47] for an example where seed dispersal distances were allowed to evolve). However, the movement rules adopted post-emigration may be at least as important as the emigration rate in determining the rate of range expansion. Our model provides some theoretical support to the idea that these movement rules may come under very strong selection at expanding range margins. There is considerable scope for future theoretical and empirical work exploring the joint evolution of movement rules with emigration and settlement rules. In particular, it would be interesting to consider how context-dependent emigration and settlement rules evolve during range expansions, and how these rules may themselves influence the evolution of inter-patch movement behaviour.

In developing more robust theory on the dynamics of range shift, it is important that we begin to consider the nature and role of environmental gradients. A substantial research effort has been devoted to understanding the processes that set species range limits [48–50], and theory has demonstrated that both the ecological [51,52] and evolutionary [53] structure of a species's range can differ substantially depending upon whether the gradient influences reproduction, survival or amount of habitat available. The few studies that have, to date, considered the dynamics of species shifting their ranges across environmental gradients have incorporated extremely simplified representations of the landscape and of dispersal [46,54,55]. Integrating features of these models with more complex movement behaviours, such as that described in our model, will offer the potential to predict how movement behaviours should evolve across both stationary and dynamic species' ranges and to understand the likely consequences of this evolution for spatial population dynamics.

We suggest that we will continue to find important demographic consequences of dispersal evolution, because dispersal responds to many complex forces, but has a central impact on individual- and population-level persistence. In particular, recently colonized regions may exhibit quite different spatial dynamics (owing to possessing individuals adopting range front dispersal strategies) than they would were they populated by individuals engaging in less risky dispersal behaviours. One obvious corollary of this is lower abundances in recently colonized regions owing to the increased mortality suffered by dispersers. Lower abundance, in turn, changes numerous important processes, including predator–prey dynamics and life-history evolution. Additionally, we know that as dispersal distance increases, populations can become synchronized at greater spatial scales [56]. So a further potential consequence of the increased dispersal distances that emerges from the evolution of movement rules could be greater synchronization of population dynamics in recently colonized regions. This could have important implications for regional risks of extinction. Clearly, then, further work on the consequences of dispersal evolution at range margins is urgently required.