Abstract
An important function of skeletal muscle is deceleration via active muscle fascicle lengthening, which dissipates movement energy. The mechanical interplay between muscle contraction and tendon elasticity is critical when muscles produce energy. However, the role of tendon elasticity during muscular energy dissipation remains unknown. We tested the hypothesis that tendon elasticity functions as a mechanical buffer, preventing high (and probably damaging) velocities and powers during active muscle fascicle lengthening. We directly measured lateral gastrocnemius muscle force and length in wild turkeys during controlled landings requiring rapid energy dissipation. Muscle-tendon unit (MTU) strain was measured via video kinematics, independent of muscle fascicle strain (measured via sonomicrometry). We found that rapid MTU lengthening immediately following impact involved little or no muscle fascicle lengthening. Therefore, joint flexion had to be accommodated by tendon stretch. After the early contact period, muscle fascicles lengthened and absorbed energy. This late lengthening occurred after most of the joint flexion, and was thus mainly driven by tendon recoil. Temporary tendon energy storage led to a significant reduction in muscle fascicle lengthening velocity and the rate of energy absorption. We conclude that tendons function as power attenuators that probably protect muscles against damage from rapid and forceful lengthening during energy dissipation.
Keywords: biomechanics, locomotion, tendon, muscle, strain
1. Introduction
Skeletal muscle produces mechanical energy to power movement, and also functions to dissipate energy when movement must be slowed or stopped. Energy dissipation involves active lengthening of muscle fascicles to convert mechanical energy into metabolic heat [1,2]. This function of muscle is important during a wide range of activities, such as negotiating obstacles [3] or downhill terrain [4] and when landing from a jump [5,6]. Active muscle lengthening is associated with high force output and a relatively high risk of contraction-associated damage [7,8]. A familiar example is the muscle soreness experienced in the days following a mountain hike. This soreness results not from the work during the climb, but from the damage to muscle fascicles as they lengthen to dissipate energy on the descent [7].
Muscles act in series with tendons that have elastic properties. Tendon elasticity provides a variety of important functions during movement [9], including the conservation of muscular work to improve the economy of movement [10,11] and amplification of muscle power for activities like jumping [9,12,13]. Studies of the role of tendon during active muscle lengthening have shown that a stretch applied to an active muscle-tendon unit (MTU) can be taken up solely by tendon stretch, with little or no muscle fascicle lengthening [14–16]. It has been proposed that this action of tendon could function as a mechanical buffer to protect muscle fascicles against damage associated with active lengthening [16]. However, tendon stretch is always followed by elastic recoil, releasing 80 to 90 per cent of the energy stored [17–20]. This energy can only be dissipated via active lengthening of muscle fascicles. Therefore, although tendon stretch potentially can delay and prolong the duration of active muscle lengthening, it cannot significantly reduce it in activities requiring energy dissipation.
Here, we test the idea that tendons reduce the rate of energy absorption by skeletal muscle during energy-dissipating activities. If tendons store energy rapidly and release it more slowly to do work on muscle fascicles, the effect could be a reduced peak power input to the muscle fascicles. Thus, power input to muscle would be attenuated by the temporary storage and release of energy in tendons, via a mechanism that in essence is the reverse of power amplification during activities like jumping [9]. It is important to note that the terms power amplification and attenuation do not suggest the addition or removal of energy from the system, but rather a change in the rate of energy transfer. To test the idea that tendons attenuate power during deceleration, we examined the lateral gastrocnemius MTU undergoing rapid and forceful lengthening as flexion of the leg joints absorbed the impact during landing from free fall. Such ‘drop-landings’ are probably among the highest-powered decelerations in locomotion [21,22]. We used wild turkeys for this study, as their distal leg muscles have calcified tendons that allow for accurate measurements of muscle force [4,11]. Independent calculations of whole MTU length (from video-based joint kinematics and tendon travel experiments) and direct measurements of muscle fascicle length (from sonomicrometry) allowed us to determine the length trajectory, and thus the function, of the series elastic tendon. We predicted that tendon elasticity would decouple lengthening of the muscle fascicles from the stretch imposed on the MTU during joint flexion. We also predicted that this decoupling would allow tendon to act as a power attenuator, which would be apparent from: (i) a prolonged duration of muscle fascicle energy absorption relative to the period of external energy absorption by the MTU; (ii) reduced lengthening velocities of the muscle fascicles relative to the whole MTU; and (iii) a reduced rate of power transfer to the muscle fascicle relative to power into the MTU.
2. Material and methods
Adult wild turkeys, Meleagris gallopavo, were obtained from a licensed breeder or from the wild and housed in the animal care facilities at Brown University. The six birds used in this study were maintained on an ad libitum commercial poultry diet and water. At experiment time, the mean body mass was 4.3 ± 1.5 kg (mean ± s.d.). Two individuals were significantly heavier than the other four (Kolmogorov–Smirnov two-tailed test; p < 0.001).
(a). Surgery and muscle-tendon unit instrumentation
Instrumentation procedures were identical to earlier studies [4,11], and therefore only briefly described here. Birds were induced and maintained on 2 to 4 per cent inhalable isoflurane anaesthesia throughout sterile surgical procedures. Body temperature was monitored via a thermocouple and adjusted using a heating pad and covers. In galliforms, the lateral gastrocnemius (LG) has a long distal soft tendon with a calcified ‘bony tendon’ region. This bony tendon region makes it possible to measure MTU force in vivo, by bonding foil strain gauges (FLK-1-11, Tokyo Sokki Kenkyujo Co., Ltd, Tokyo, Japan) onto the deep and superficial aspects of the bony tendon using cyanoacrylate glue [4,11].
Muscle fascicle length was recorded using a pair of sonomicrometry crystals (Sonometrics Inc., London, ON, Canada), which were implanted approximately 20 mm apart and 3 mm deep into the lateral and proximal region of the LG muscle belly, along the line of a muscle fascicle. We used electromyography to record electrical activity in the muscle, via bipolar twisted steel wire electrodes (Medwire, NJ, USA) [23] implanted midway between and 2 mm offset to either side from the muscle fascicle where length was measured. All instrument wires were routed subcutaneously and out through a small skin incision above the right acetabulum, where small electrical connectors (Microtech, Boothwyn, PA, USA) were soldered to the wires and sutured to the skin. Carprofen was administered as an analgesic and all birds were allowed to recover for 24 h prior to experiments.
(b). In vivo landing experiments
We used a ceiling-mounted pulley and rope system tied to a custom-made webbing harness that was strapped around the proximal (humeral) wing segment. This system permitted us to drop the birds from 1.5 m height, which is equal to a three-fold elevation of the centre of mass of the bird when standing. An added benefit of this system was that it almost entirely removed the effects of wing movements on landing velocity. From this height, the animals were able to land safely, repeatedly, in a controlled fashion, absorbing all of the impact by coordinated leg joint flexion.
We glued a vertical foam-board marker plate with two digitizable points onto the skin on the back of the bird, so that the points defined a line of known length pointing to the hip joint (acetabulum). Additional surface markers were placed over the leg (tibiotarsus) and foot (tarsometatarsus) bones to define the positions of the knee and ankle joints. These skin surfaces are tightly connected with the underlying bone, which minimizes error in subsequent estimates of leg bone and joint movement from marker coordinates. During landings, all marker points were recorded in lateral view at 250 fps using a high-speed camera (Fastcam 1280 PCI, Photron, San Diego, CA, USA) so that joint kinematics could be calculated. Sonomicrometry crystal measurements were recorded via a sonomicrometer (Sonometrics), and EMG signals were recorded at 1000× amplification with a 3 Hz to 10 kHz band-pass filter engaged (differential preamplifiers model DAM50, World Precision Instruments, Sarasota, FL, USA). Strain-gauge measurements were balanced and amplified 1000× (conditioner model 2120, Vishay Measurements Group, Raleigh, NC, USA). An LED/square-wave pulse was used to enable resynchronization of digitized video kinematics with muscle measurements, which were digitized at 4000 Hz (USB-6259 DAQ, National Instruments, TX, USA) and recorded onto a PC running IgorPro v. 6.0 (Wavemetrics, Lake Oswego, OR, USA).
(c). In situ experiments
When in vivo experiments were completed, each bird was induced (isoflurane via mask) and taken to a deep plane of anaesthesia. Force and length measurements were then obtained in situ from the isolated MTU, so that the strain gauges could be calibrated. We then generated a tetanic length–tension curve. The methodology closely followed previous studies [4,16] and is described briefly: We stimulated the LG through the tibial branch of the sciatic nerve via a bipolar nerve cuff, using a supra-maximal stimulus voltage (6–7 V) with a stimulus frequency of 100 pps and a train duration of 300 ms (generated using a Grass S48 stimulator).
The LG section of the gastrocnemius tendon was removed from its insertion and connected to a servomotor (310B-LR, Aurora Scientific, Ontario, Canada), a calibrated length-controlling and force-measurement tool, using a lightweight custom-made aluminium clamp and non-compliant steel aircraft cable. We recorded the nerve stimulus signal, MTU length and force from the muscle motor, tendon strain from the strain gauges and muscle fascicle length from the sonomicrometer at 4000 Hz onto a PC via IgorPro v. 6.0. At least three tetanic contractions were recorded from a passive tension set at 15–20 N. The average of the strain gauge signals was calibrated using the slope obtained from regressions against the motor force (N) from these three contractions [4]. This constant was then used to calculate force in vivo from tendon strain measurements. A tetanic length tension curve was measured to determine L0 and P0 for each muscle [24]. A length tension curve could not be obtained for one bird. Instead, L0 was estimated using the slope obtained from regression of fascicle length at toe-down against tetanic L0 for other birds (n = 6; r2 = 0.89). Similarly, a linear regression of muscle physiological cross-sectional area against tetanic P0 for the other birds (n = 6; r2 = 0.81) was used to estimate P0. All muscle fascicle and MTU strains were reported relative to L0 of the muscle.
(d). Measurement conditioning and data extraction
High-speed videos were inspected to ensure that the only trials analysed were where the bird landed with the instrumented leg first, and did not lose balance during energy absorption. External marker points in the high-speed videos were digitized in Matlab (The Mathworks, Inc.) using DLT Data Viewer [25]. Knee position was calculated as the intercept of two circles, with the centre and radius for each circle defined as hip position coordinates and femur length, and ankle position coordinates and tibiotarsus length, respectively. Using a script in Matlab, knee and ankle angle were calculated frame-by-frame from the marker point coordinates.
All subsequent data analyses were done in IgorPro v. 6.0. Muscle fascicle segment length measurements from the sonomicrometer were scaled to the full fascicle length. Fascicle lengths were measured in situ using callipers while the muscle was set at length close to L0. Signals from the superficial and deep strain gauges were averaged to cancel out bending, and the average in vivo signal was offset-corrected and calibrated using the constant derived from in situ tetanic contractions [4]. All measurements were inspected for high-frequency noise, which if present was smoothed using a quintic spline interpolation (s.d. = 0.01–0.1). Muscle strain for a given period was calculated as
| 2.1 |
where Li is the initial fascicle length, Lf is the final length and L0 is the muscle optimal length as determined in situ. By this calculation, lengthening strains are reported as negative. Muscle fascicle velocities were calculated by differentiating muscle fascicle length, and instantaneous muscle fascicle power was then calculated as the product of muscle fascicle velocity and MTU force. This value was divided by muscle mass to obtain the muscle mass-specific power value. We did not correct our power calculations for the effect of muscle fascicle pennation, because the very high forces would have the effective muscle fascicle gearing approach unity [26]. Muscle fascicle work was calculated as area under the power curve by integrating muscle fascicle power over each of the two landing periods.
During the impact-absorbing flexion of the leg joints, flexion at the ankle stretches the biarticular LG, while knee flexion shortens it (figure 1d). We used moment arm values derived from tendon travel experiments [27] combined with ankle and knee joint kinematics to calculate MTU work for comparison with muscle fascicle work. First, we calculated linear velocity of the whole MTU (VMTU) as
| 2.2 |
where ω is the angular velocity of joint rotation (radian s−1) and r is the muscle moment arm (cm). MTU power was then calculated as the product of MTU velocity and strain gauge force. Finally, MTU work was measured as the integrated area under the MTU power curve.
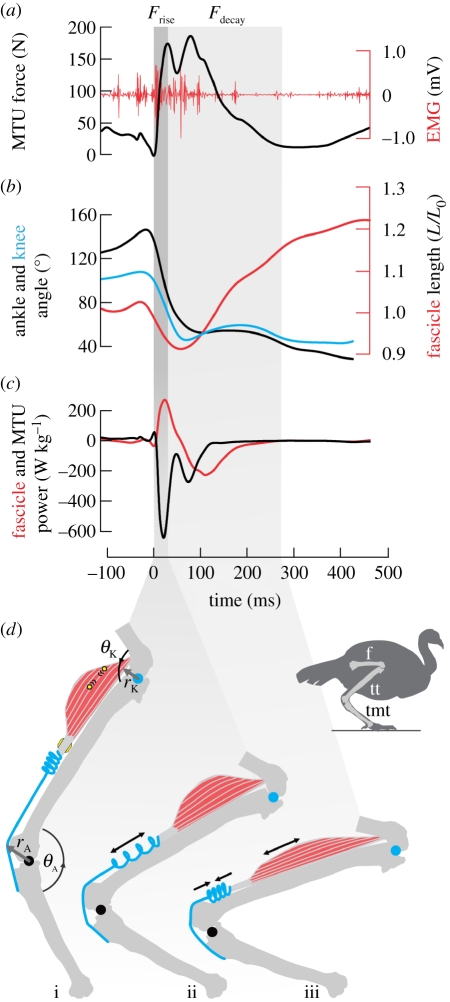
Figure 1.
Sample data and schematic of muscle-tendon unit (MTU) function during high-powered energy absorption. (a) Analysis was divided into a period of force rise (Frise, dark column), which was rapid, and force decay (Fdecay, light column), which occurred more slowly. (b) The majority of joint flexion occurred during Frise both at the ankle (black) and the knee (blue), while muscle fascicle lengthening (red, right axis, negative strain) typically occurred during Fdecay. (c) Power profiles of the MTU (black) and the fascicles (red) show that energy was initially absorbed by the MTU, while the rate of energy absorption by the muscle fascicles was lower and occurred later, during Fdecay. (d) A schematic of the pattern of tendon and muscle strain, as indicated by the sample data: joint flexion is accommodated by rapid tendon stretch during Frise (i–ii), followed by slower recoil of the tendon to lengthen muscle fascicles during Fdecay (ii–iii). We used direct measurements of muscle fascicle length via sonomicrometry (circles) and MTU force via strain gauges (quadrilaterals) on the calcified tendon (grey). MTU length was calculated from joint kinematics and muscle moment arms at the ankle (θA, rA) and knee (θK, rK). Bones: f, femur; tt, tibiotarsus; tmt, tarsometatarsus.
(e). Analyses and statistics
We aimed at identifying the role of series elastic tendon on the energy-absorbing function of the entire MTU as well as the muscle fascicles alone. Therefore, we divided all analysis into two periods: the period of force rise (Frise) and the period of force decay (Fdecay). This approach separated the period where energy was absorbed by tendon (Frise) from the period where tendon released energy (Fdecay). In some instances, the muscle produced a force impulse with two peaks (e.g. figure 1a). In these cases, the first peak in muscle force was used as period separation. Although this did not provide a perfect separation between periods of tendon energy absorption and release, it allowed for a consistent division between the initial event of impact energy absorption and subsequent events. To determine if tendon elasticity conferred a delay in, and a reduced rate of energy transfer to, the muscle fascicles, we compared average peak MTU velocity across all trials during Frise with average muscle fascicle velocity during Fdecay. To determine if tendon elasticity served a power-attenuating function during landing, we compared average MTU power across all trials during Frise with average muscle fascicle power during Fdecay.
Statistical comparisons used the mixed linear model ANOVA in Systat v. 12.0 (Systat Software, Chicago, IL, USA). Velocity or power was the dependent variable, trial nested within individual and tissue (MTU or muscle fascicles, also representative of the two force-periods) were fixed effects, while individual was factored as a random effect. Summary data for duration of MTU force-periods, joint flexion, muscle fascicle strain, and average MTU and muscle fascicle velocity and power are shown using box and whisker plots of median–quartiles data and data ranges. We report lengthening and lengthening velocities as negative and negative power and work values indicate energy absorption. Both power and work are reported as muscle mass-specific values.
3. Results
We divided our analysis into two periods: force rise (Frise), which lasted from toe-down until peak force was reached in the MTU, and force decay (Fdecay), which lasted until force returned to pre-landing level (figure 1). This division isolated the periods of tendon energy absorption (Frise) versus energy release (Fdecay; figure 1d). The duration of Frise was 58 ± 26 ms (mean ± s.d.), significantly shorter (ANOVA; F1,23 = 116.6, p < 0.0001) than the duration of Fdecay (164 ± 52 ms; figures 1a and 2a). MTU force reached a high level during Frise (236 ± 104 N; or 0.65 ± 0.29 peak active tension on the tetanic length–tension curve, P0 [24]; figure 1b). This corresponded to a peak muscle stress of 25.6 ± 11.6 N cm−2.
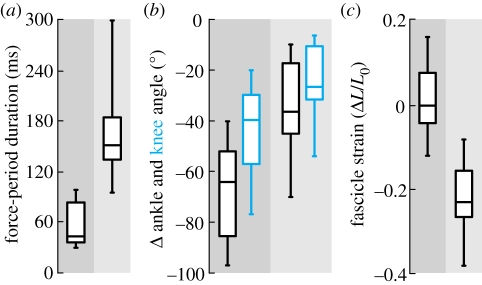
Figure 2.
Decoupling of MTU and muscle fascicle strain by tendon elasticity. (a) The duration of force rise (dark column) was significantly shorter than the duration of force decay (light column). (b) The majority of joint flexion at both the knee (blue) and the ankle (black) occurred during Frise. (c) The muscle fascicles remained near-isometric during Frise and even shortened (positive strain) in 50% of the landings, and lengthened substantially (negative strain) during Fdecay. Box midlines are data medians, perimeters are quartiles and whiskers indicate data ranges.
Decoupling of muscle fascicle strain from MTU strain was apparent during both of the landing periods (figure 1b). Two-thirds of the total impact-absorbing flexion at the ankle and the knee occurred during Frise (figure 2b), while during the same period the muscle fascicles remained near-isometric (average strain = 0.6 ± 1.9% L0; figure 2c). Conversely, only a third of the total joint flexion happened during Fdecay, but it was during this period that the muscle fascicles consistently lengthened by −25 ± 11% L0.
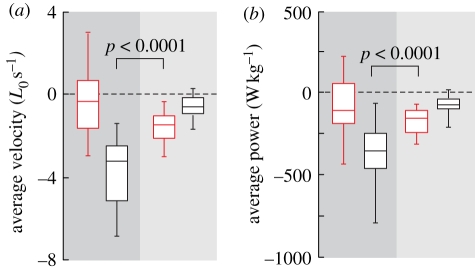
Velocity values calculated separately for the muscle fascicles and the MTU (figure 3a) showed that tendon elasticity significantly reduced the strain rates experienced by the muscle fascicles during deceleration. The average MTU lengthening rate during Frise was −3.8 ± 1.6 L0 s−1, while the average muscle fascicle lengthening rate during the same period was much lower and not significantly different from zero (−0.2 ± 1.7 L0 s−1). Muscle fascicle lengthening rates during Fdecay (−1.6 ± 0.8 L0 s−1), when energy was released from the tendon, were 2.4 times lower and statistically different (F1,24 = 66.3, p < 0.0001) from the lengthening rate of the MTU during Frise.
Figure 3.
Velocity dampening and power attenuation owing to tendon elasticity during energy absorption. (a) Average velocity of muscle fascicle (red) and MTU (black) relative to resting muscle fascicle lengths. Negative values indicate lengthening. The significant difference between lengthening velocity of the MTU during Frise and the muscle fascicles during Fdecay shows that tendon elasticity reduces the average rate of lengthening experienced by the muscle fascicles. (b) The significant difference between average MTU power during Frise and average muscle fascicle power during Fdecay shows that tendon elasticity attenuates power transfer to the muscle fascicles. Box midlines are data medians, perimeters are quartiles and whiskers indicate data ranges.
Power values calculated separately for the muscle fascicles and the MTU (figures 1c and 3b) showed that tendon elasticity significantly reduced the rate of energy absorption by the muscle fascicles. During Frise, the average power input to the MTU was −381 ± 183 W kg−1, while the power input to the muscle fascicles during the same period was only −80 ± 163 W kg−1. The energy absorbed in tendon stretch during Frise (figure 1d) was released during Fdecay at a slower rate, so that the average muscle fascicle power during Fdecay was only −189 ± 144 W kg−1. The twofold difference between average power input to the MTU during Frise and to the muscle fascicles during Fdecay was statistically significant (F1,24 = 55.2, p < 0.0001).
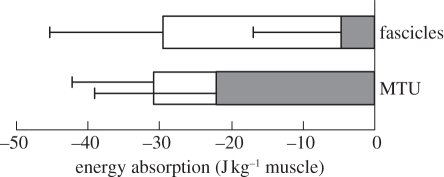
Measurements of total energy absorption (figure 4) summarize the difference in the timing of energy absorption by muscle fascicles as compared with the MTU. Most of the absorption of energy by the MTU happened during Frise, while the muscle fascicles dissipated energy (27 ± 18 J kg−1) almost exclusively during Fdecay.
Figure 4.
Tendon elasticity alters timing, but not the amount of energy absorbed by the muscle fascicles. Muscle mass-specific work during landing was calculated from muscle fascicle velocity and tendon force for the muscle fascicles, and from linear joint velocity and tendon force for the MTU. Energy absorption from the environment via joint flexion mainly happens during force rise (Frise, filled bars), but the muscle fascicles are effective energy sinks during force decay (Fdecay, unfilled bars). Bars are stacked averages, whiskers indicate 1 s.d.
4. Discussion
The spring-like properties of tendons serve a wide variety of functions in locomotion, from the amplification of muscle power during jumping and acceleration to the conservation of mechanical energy during steady-speed locomotion. Our results suggest another mechanism, in which energy storage and release in tendon elasticity both delay and slow the rate of energy dissipation by muscle fascicles during high-powered decelerations. We found that initially during landing, energy storage by tendon is rapid, while the subsequent release of this energy to the muscle fascicles is slower. As a result, power input to the muscle fascicles was attenuated relative to that of the whole MTU. The average rate of energy absorption by the MTU during Frise was approximately two times the average rate of energy absorption by the muscle fascicles during Fdecay. It is well established that muscles are vulnerable to damage during active lengthening [7,8]. We propose that the power-attenuating function of tendons acts as a protective mechanism that reduces the risk of muscle fascicle damage during lengthening.
A key feature in the power-attenuating mechanism of tendon elasticity is the decoupling of the timing of muscle lengthening from the timing of joint movement. In the turkey, two-thirds of ankle flexion happened during the first period of landing when force in the gastrocnemius was rising. The vast majority of muscle fascicle lengthening happened later in the event, when there was relatively little joint flexion. This decoupling of joint motion and muscle fascicle lengthening during an energy-absorption event has been observed in maximally stimulated muscles in situ [14,16], and in maximal voluntary contractions in human dynamometer studies [15]. A recent study of stair walking found a similar pattern in the human gastrocnemius: the muscle fascicles shortened early in the step as the MTU lengthened, followed by tendon shortening against lengthening of the muscle fascicles [28].
Decoupling of muscle fascicle strain from MTU strain during an energy-absorption event does not alter the total amount of muscle lengthening or energy absorption by the muscle. The key to the reduction in muscle-lengthening rates and power input is that tendon action alters the time course of muscle lengthening. In this way, power attenuation is similar to the familiar mechanisms of power amplification by elastic elements in jumping animals. In both cases, the tendon allows a separation in time of the muscular event and the movement event. In jumping, the work of muscle contraction can be stored in tendons prior to movement, followed by a rapid release of this energy during the jump [13,22,29–31]. Power is amplified because it is released from the tendon more rapidly than it is stored. We found that during energy absorption, most of the joint and body motion happens during an early and brief event associated with rapid energy absorption by tendon. The release of this energy to the muscle fascicles happens approximately 2.4 times slower and largely subsequent to movement (figure 3). Because rates of energy storage and release in tendon are less limited than in muscle, both power attenuation and amplification mechanisms may allow for movement that is beyond the mechanical range of muscle contraction alone [32,33].
Muscles are particularly susceptible to damage during active lengthening contractions [7,8,34–36]. It has been proposed that tendon elasticity could act as a buffer to protect muscles from the damaging effects of active lengthening [14,15] by stretching during the initial period of MTU lengthening. However, while this action can delay muscle lengthening, it can neither eliminate nor significantly reduce it if energy is to be dissipated. Our results point to several possible ways that tendon elasticity can protect muscles from damage. The rates at which muscle fascicles lengthen and absorb energy may be associated with the severity of damage [34–36]. Both of these parameters were reduced by the action of tendons in the turkey gastrocnemius. Because the tendon influences when muscle lengthening happens, it also influences the peak forces experienced by the MTU during an energy-absorbing event. The peak force experienced by the muscle in our study was a function of the level of muscle activation, as well as the force–velocity effects during Frise. During rapid stretches of an active isolated MTU, the peak force produced is directly proportional to the rate of length change in the muscle, with higher forces resulting as shortening velocities decrease or lengthening velocities increase [16]. Without the effects of the tendon during drop landings, the fascicles would presumably have undergone much more rapid lengthenings and thereby developed much higher forces. Reduction of muscle forces may protect not only the muscle fascicles, but also the associated musculoskeletal tissues from damage.
Acknowledgements
All animal use was approved by the Brown University Institutional Animal Care and Use Committee, and complied with state and federal legislation and regulations.
We thank E. Abbott, P. Konow and A. Matson for help with experiments, G. Sawicki for technical advice and N. Gidmark for Matlab scripting assistance. The manuscript benefited from comments made by H. Astley, E. Brainerd, A. Camp, S. Gatesy, N. Gidmark, A. Herrel, A. Horner and two anonymous colleagues. This work was funded by NIH grant AR055295 to T.J.R and F32AR054246 to E.A.
References
- 1.Abbott B. C., Aubert X. M., Hill A. V. 1950. The absorption of work when a muscle is stretched. J. Physiol. 111, 41–42 [PubMed] [Google Scholar]
- 2.Hill A. V. 1960. Production and absorption of work by muscle. Science 131, 897–903 10.1126/science.131.3404.897 (doi:10.1126/science.131.3404.897) [DOI] [PubMed] [Google Scholar]
- 3.Daley M. A., Biewener A. A. 2006. Running over rough terrain reveals limb control for intrinsic stability. Proc. Natl Acad. Sci. USA 103, 15 681–15 686 10.1073/pnas.0601473103 (doi:10.1073/pnas.0601473103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gabaldon A. M., Nelson F. E., Roberts T. J. 2004. Mechanical function of two ankle extensors in wild turkeys: shifts from energy production to energy absorption during incline versus decline running. J. Exp. Biol. 207, 2277–2288 10.1242/jeb.01006 (doi:10.1242/jeb.01006) [DOI] [PubMed] [Google Scholar]
- 5.McGowan C. P., Baudinette R. V., Biewener A. A. 2005. Joint work and power associated with acceleration and deceleration in tammar wallabies (Macropus eugenii). J. Exp. Biol. 208, 41–53 10.1242/jeb.01305 (doi:10.1242/jeb.01305) [DOI] [PubMed] [Google Scholar]
- 6.Carroll A. M., Lee D. V., Biewener A. A. 2008. Differential muscle function between muscle synergists: long and lateral heads of the triceps in jumping and landing goats (Capra hircus). J. Appl. Physiol. 105, 1262–1273 10.1152/japplphysiol.01316.2007 (doi:10.1152/japplphysiol.01316.2007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Proske U., Morgan D. L. 2001. Muscle damage from eccentric exercise: mechanism, mechanical signs, adaptation and clinical applications. J. Physiol. 537, 333–345 10.1111/j.1469-7793.2001.00333.x (doi:10.1111/j.1469-7793.2001.00333.x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lieber R. L., Friden J. 2002. Mechanisms of muscle injury gleaned from animal models. Am. J. Phys. Med. Rehabil. 81, 70–79 10.1097/00002060-200211001-00008 (doi:10.1097/00002060-200211001-00008) [DOI] [PubMed] [Google Scholar]
- 9.Roberts T. J., Azizi E. 2011. Flexible mechanisms: the diverse roles of biological springs in vertebrate movement. J. Exp. Biol. 214, 353–361 10.1242/jeb.038588 (doi:10.1242/jeb.038588) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cavagna G. A., Heglund N. C., Taylor C. R. 1977. Mechanical work in terrestrial locomotion: two basic mechanisms for minimizing energy expenditure. Am. J. Physiol. Regul. Integr. Comp. Physiol. 233, 243–261 [DOI] [PubMed] [Google Scholar]
- 11.Roberts T. J., Marsh R. L., Weyand P. G., Taylor C. R. 1997. Muscular force in running turkeys: the economy of minimizing work. Science 275, 1113–1115 10.1126/science.275.5303.1113 (doi:10.1126/science.275.5303.1113) [DOI] [PubMed] [Google Scholar]
- 12.Alexander R. M. 2002. Tendon elasticity and muscle function. Comp. Biochem. Physiol. A 133, 1001–1011 [DOI] [PubMed] [Google Scholar]
- 13.Astley H., Roberts T. J. 2009. Decoupling of muscle shortening and joint kinematics during frog jumping. Comp. Biochem. Physiol. A 153A, 128 [Google Scholar]
- 14.Griffiths R. I. 1991. Shortening of muscle fibres during stretch of the active cat medial gastrocnemius muscle: the role of tendon compliance. J. Physiol. 436, 219–236 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Reeves N. D., Narici M. V. 2003. Behavior of human muscle fascicles during shortening and lengthening contractions in vivo. J. Appl. Physiol. 95, 1090–1096 [DOI] [PubMed] [Google Scholar]
- 16.Roberts T. J., Azizi E. A. 2010. The series-elastic shock absorber: tendons attenuate muscle power during eccentric actions. J. Appl. Physiol. 109, 396–404 10.1152/japplphysiol.01272.2009 (doi:10.1152/japplphysiol.01272.2009) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ker R. F. 2007. Mechanics of tendon, from an engineering perspective. Int. J. Fatigue 29, 1001–1009 10.1016/j.ijfatigue.2006.09.020 (doi:10.1016/j.ijfatigue.2006.09.020) [DOI] [Google Scholar]
- 18.Maganaris C. N. 2002. Tensile properties of in vivo human tendinous tissue. J. Biomech. 35, 1019–1027 10.1016/S0021-9290(02)00047-7 (doi:10.1016/S0021-9290(02)00047-7) [DOI] [PubMed] [Google Scholar]
- 19.Fukunaga T., Kubo K., Kawakami Y., Fukashiro S., Kanehisa H., Maganaris C. N. 2001. In vivo behaviour of human muscle tendon during walking. Proc. R. Soc. Lond. B 268, 229–233 10.1098/rspb.2000.1361 (doi:10.1098/rspb.2000.1361) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Pollock C. M., Shadwick R. E. 1994. Relationship between body mass and biomechanical properties of limb tendons in adult mammals. Am. J. Physiol. 266, 1016–1021 [DOI] [PubMed] [Google Scholar]
- 21.Sousa F., Ishikawa M., Vilas-Boas J. P., Komi P. V. 2007. Intensity- and muscle-specific fascicle behavior during human drop jumps. J. Appl. Physiol. 102, 382–389 10.1152/japplphysiol.00274.2006 (doi:10.1152/japplphysiol.00274.2006) [DOI] [PubMed] [Google Scholar]
- 22.Bobbert M. F. 2001. Dependence of human squat jump performance on the series elastic compliance of the triceps surae: a simulation study. J. Exp. Biol. 204, 533–542 [DOI] [PubMed] [Google Scholar]
- 23.Basmajian J., Stecko G. 1962. A new bipolar electrode for electromyography. J. Appl. Physiol. 17, 849 [Google Scholar]
- 24.Otten E. 1987. A myocybernetic model of the jaw system of the rat. J. Neurosci. Methods 21, 287–302 10.1016/0165-0270(87)90123-3 (doi:10.1016/0165-0270(87)90123-3) [DOI] [PubMed] [Google Scholar]
- 25.Hedrick T. L. 2008. Software techniques for two- and three-dimensional kinematic measurements of biological and biomimetic systems. Bioinsp. Biomim. 3, 034001. 10.1088/1748-3182/3/3/034001 (doi:10.1088/1748-3182/3/3/034001) [DOI] [PubMed] [Google Scholar]
- 26.Azizi E., Brainerd E. L., Roberts T. J. 2008. Variable gearing in pennate muscles. Proc. Natl Acad. Sci. USA 105, 1745–1750 10.1073/pnas.0709212105 (doi:10.1073/pnas.0709212105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lutz G. J., Rome L. C. 1996. Muscle function during jumping in frogs. I. Sarcomere length change, EMG pattern, and jumping performance. Am. J. Physiol. 271, 563–570 [DOI] [PubMed] [Google Scholar]
- 28.Spanjaard M., Reeves N. D., van Dieen J. H., Baltzopoulos V., Maganaris C. N. 2007. Gastrocnemius muscle fascicle behavior during stair negotiation in humans. J. Appl. Physiol. 102, 1618–1623 10.1152/japplphysiol.00353.2006 (doi:10.1152/japplphysiol.00353.2006) [DOI] [PubMed] [Google Scholar]
- 29.Henry H. T., Ellerby D. J., Marsh R. L. 2005. Performance of guinea fowl Numida meleagris during jumping requires storage and release of elastic energy. J. Exp. Biol. 208, 3293–3302 10.1242/jeb.01764 (doi:10.1242/jeb.01764) [DOI] [PubMed] [Google Scholar]
- 30.Aerts P. 1998. Vertical jumping in Galago senegalensis: the quest for an obligate mechanical power amplifier. Phil. Trans. R. Soc. Lond. B 353, 1607–1620 10.1098/rstb.1998.0313 (doi:10.1098/rstb.1998.0313) [DOI] [Google Scholar]
- 31.Roberts T. J., Abbott E. M., Azizi E. 2011. The weak link: do muscle properties determine locomotor performance in frogs? Phil. Trans. R. Soc. B 366, 1488–1495 10.1098/rstb.2010.0326 (doi:10.1098/rstb.2010.0326) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Deban S. M., O'Reilly J. C., Dicke U., van Leeuwen J. L. 2007. Extremely high-power tongue projection in plethodontid salamanders. J. Exp. Biol. 210, 655–667 10.1242/jeb.02664 (doi:10.1242/jeb.02664) [DOI] [PubMed] [Google Scholar]
- 33.Bennet-Clark H. C., Lucey E. C. 1967. The jump of the flea: a study of the energetics and a model of the mechanism. J. Exp. Biol. 47, 59–67 [DOI] [PubMed] [Google Scholar]
- 34.Mccully K. K., Faulkner J. A. 1986. Characteristics of lengthening contractions associated with injury to skeletal-muscle fibers. J. Appl. Physiol. 61, 293–299 [DOI] [PubMed] [Google Scholar]
- 35.Katz B. 1939. The relation between force and speed in muscular contraction. J. Physiol. 96, 45–64 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Warren G. L., Hayes D. A., Lowe D. A., Armstrong R. B. 1993. Mechanical factors in the initiation of eccentric contraction-induced injury in rat soleus muscle. J. Physiol. 464, 457–475 [DOI] [PMC free article] [PubMed] [Google Scholar]