Evolving ecological networks and the emergence of biodiversity patterns across temperature gradients

Abstract

In ectothermic organisms, it is hypothesized that metabolic rates mediate influences of temperature on the ecological and evolutionary processes governing biodiversity. However, it is unclear how and to what extent the influence of temperature on metabolism scales up to shape large-scale diversity patterns. In order to clarify the roles of temperature and metabolism, new theory is needed. Here, we establish such theory and model eco-evolutionary dynamics of trophic networks along a broad temperature gradient. In the model temperature can influence, via metabolism, resource supply, consumers' vital rates and mutation rate. Mutation causes heritable variation in consumer body size, which diversifies and governs consumer function in the ecological network. The model predicts diversity to increase with temperature if resource supply is temperature-dependent, whereas temperature-dependent consumer vital rates cause diversity to decrease with increasing temperature. When combining both thermal dependencies, a unimodal temperature–diversity pattern evolves, which is reinforced by temperature-dependent mutation rate. Studying coexistence criteria for two consumers showed that these outcomes are owing to temperature effects on mutual invasibility and facilitation. Our theory shows how and why metabolism can influence diversity, generates predictions useful for understanding biodiversity gradients and represents an extendable framework that could include factors such as colonization history and niche conservatism.

1. Introduction

Mechanistically understanding large-scale biodiversity patterns is a major challenge in ecology and evolutionary biology. Species richness, one component of biodiversity, is correlated with myriad environmental variables [1–3], among which environmental temperature stands out [4–8]. Strong correlations between richness and temperature motivated the search for a causal link between them [9]. The ‘metabolic theory of biodiversity’ focuses on organismal metabolism as a link between temperature and the ecological and evolutionary factors controlling species richness. Rather than establishing causality, studies show that temperature-richness patterns vary in shape and directionality, casting doubt on the hypothesis of a causal link between metabolism and diversity [5,7]. Resolving this tension is difficult because no current theory integrates metabolic dependencies of key factors that regulate diversity: the ecological processes of basal resource supply and species interactions, the organismal processes of survival and reproduction, and the evolutionary processes of mutation and diversification.

Here, we work towards a more integrated theory linking metabolism to variation in ectotherm diversity across broad temperature gradients. Ectotherm metabolism is governed primarily by temperature and body size [10]. Thus, via metabolism, temperature and size can influence basal resource supply and trophic interactions (ecological processes) [11–13], individual resource use for survival and reproduction (organismal processes) [14–17], and the production of genetic variation and phenotypic divergence (evolutionary processes) [18–22]. Previous theory only accounts for subsets of these metabolic dependencies and does not incorporate feedbacks among key factors underlying ecological, organismal and evolutionary dynamics. Here, by building on the functional trait approach of Stegen et al. [23], we go beyond previous attempts to link metabolism to diversity by directly integrating metabolic dependencies of ecological, organismal and evolutionary processes in a dynamical theory of diversity. Where Stegen et al. [23] assumed a thermal dependence only for mutation rate, we build in additional thermal dependencies for basal resource supply and organismal feeding and mortality rates.

Our theory closes the eco-evolutionary feedback loop by linking genetically determined variation in body size with species interactions, which together drive ecological dynamics and evolutionary diversification of trophic networks. In this framework, the number of unique phenotypes (body sizes) that emerge through evolutionary time provides a measure of biodiversity similar to empirical characterizations of species richness. For simplicity, we use the general term ‘diversity’ to refer to the number of unique phenotypes within model networks. We avoid the more specific term ‘species richness’ owing to the asexual nature of our model organisms, for which precise species delineation can be difficult.

We initially generate predictions for dynamical patterns of diversity across a broad temperature gradient, and take two subsequent steps to assess the mechanistic basis of these predictions. First, we use the eco-evolutionary framework to evaluate the individual and interactive effects of all temperature dependencies. This is achieved by examining model predictions when only specific subsets of temperature dependencies are assumed. In order to gain a full understanding, we conducted a full factorial analysis, examining model predictions across all combinations of thermal dependencies. The second approach focuses on the ecological and organismal components of our framework, and examines how temperature influences coexistence between two phenotypes. This provides detailed characterization of the mechanisms responsible for the predicted, large-scale temperature–diversity patterns.

2. Material and methods

(a). Model development: temperature, size and ecological network dynamics

Our theory models the evolutionary dynamics of phenotypic (body size) diversity along temperature gradients in the ‘ecological theatre’ characterized by basal resource supply and trophic interactions. We build from Loeuille & Loreau [24], who developed and empirically validated a model of evolving size-structured trophic networks [23,25–27]. Loeuille & Loreau [24] found that only two parameters had a strong influence over food web topology: consumer niche breadth and the strength of interference competition. Stegen et al. [23] showed that diversity patterns generated by the model are qualitatively robust to changes in these parameters. Loeuille & Loreau [24] developed a robust and empirically supported eco-evolutionary model that allows one to use organismal traits to combine organismal, ecological and evolutionary processes. For these reasons, we build from their pioneering work.

In the model, phenotypes are linked ecologically: a given body size phenotype preys on smaller phenotypes and is eaten by larger phenotypes. Thus, the ecological function of a given phenotype depends on its own body size and the distribution of body sizes within a network. Each body size phenotype is effectively a distinct species or ‘node’ within an evolving network. Feeding rate is a Gaussian function (see below), whereby each phenotype preys on smaller phenotypes within a given body size range. The ecological network is tied to a basal resource, and heritable variation in body size fuels adaptive evolution.

Many organismal properties that determine vital rates, and thus fitness, scale with organismal size [10,28–30]. After body mass, temperature explains the largest amount of variation in biological rates [10,28,29], and previous models have begun addressing the joint effects of temperature and size in consumer–resource systems [15,23]. We build from this work and propose a trophic network model that integrates size and thermal dependencies of basal resource supply, consumer vital rates and mutation rate.

In a network containing n phenotypes with body sizes M₁, …, M_n, and a basal resource (subscript 0), the population biomass, N_i, of phenotype i is driven by biomass production owing to consumption of smaller phenotypes (at rate f_ijN_j, where j < i) and assimilation efficiency, ɛ; and biomass loss owing to consumption by larger phenotypes (rate f_jiN_j, where j > i), interference competition with phenotypes within a give size range (rate c_ijN_j) and intrinsic mortality (rate m_i). Dynamics of the basal resource depends on supply from outside the system (rate I), consumption by all phenotypes (rate f_i0N_i), recycling with efficiency ν and loss owing to extrinsic factors (rate μ). Hence, the ecological model of network dynamics:

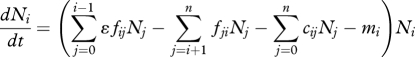2.1a

and

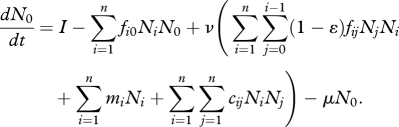2.1b

There is no size structure to the basal resource, which is taken to be inorganic nutrients derived from decomposition or weathering of allochthonous material (e.g. leaf litter, igneous fluorapatite) and recycling of autochthonous material. Recycled material is derived from three sources: less than complete assimilation of consumed prey (fraction 1 − ɛ), consumer death from intrinsic mortality (sum across all m_iN_i) and consumer death from interference (sum across all c_ijN_iN_j). It is assumed that a portion, 1 − ν, of this recycled material becomes biologically unavailable [23–27].

Our key assumption is that biological rates scale with metabolic rate [15–17,28–31]. We further assume that nutrients are made available through temperature-dependent biological or chemical processes. For example, nutrients derived from decomposing leaf litter are mineralized by microbes (which we do not directly model) and released to other organisms (which we do model) in a temperature-dependent manner [11–13]. Likewise, nutrient supply from chemical weathering has been shown to increase with temperature [32–34]. In turn, for basal nutrients derived from decomposition (or chemical weathering) of allochthonous materials, metabolic (and non-biological chemical reaction rate) scaling implies

2.2

where E is the mean activation energy of metabolic or chemical reactions and k is the Boltzmann's constant [10,32]. Note that a superscript asterisk denotes a normalization constant. For all consumers, i = 1, …, n in the network, mass-specific metabolic rate B_i scales with mass M_i and temperature T according to Therefore, feeding, f_ij, and mortality rates, m_i, scale as

2.3

and

2.4

Equation (2.3) indicates that besides metabolic rate, a consumer's feeding rate depends on the difference between its body mass and the body mass of a given prey item, M_j. For a consumer of a given size, increasing the size of prey increases ingested biomass but decreases the probability of successful attack. Thus, the feeding rate of a consumer is a function, f, of the size difference with its prey, and there is an optimal difference, d, at which feeding rate is maximized [15,24,35]. For consistency with previous theory, we assume f to be Gaussian with s.d. σ ([24,26,27,36], see Weitz & Levin [37] for alternative functions), such that the function f is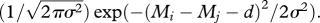

Interference competition is common in natural predator–prey interactions [38] and may be more intense among similar-sized organisms. For consistency with previous theory [24], c_ij is a stepwise function symmetrical around 0 with a cut-off size difference of β, i.e. c_ij = c* if |M_i − M_j| < β, and c_ij = 0 otherwise.

(b). Projecting the ecological network through evolutionary time

Diversification in consumer size is modelled by projecting the ecological network through evolutionary time. Variation in size generated by mutation is selected on by the current ecological network, and the network changes as successful mutants invade and previously established phenotypes go extinct. Thus, the ecological state of the network and the evolutionary fate of phenotypes are entangled in an eco-evolutionary feedback loop. The rate of genetic mutation is itself size-dependent [22], and proportional to metabolic rate [19,20]. For a given consumer i, the mutation rate, α_i, is given as [19–22]

2.5

It should be noted that when implemented, this mutation rate is effectively the mean probability of a mutant arising from phenotype i during each time step.

The eco-evolutionary model was evaluated at several temperatures through numerical integration, and parameters were set to values that generate realistic ecological networks [24] (see table 1, appendix A). Each simulation starts with a population of a single-consumer phenotype feeding on an initial pool of basal resources. New phenotypes can establish after a mutation in body size arises from an extant consumer. There are no a priori limitations on the range in body sizes (see electronic supplementary material, figure S1). The proportional difference between ancestor and mutant body size was randomly sampled from a uniform distribution ranging from 0.8 to 1.2, such that proportional changes in body size were less than 20 per cent. Mutant population growth is determined using equation (2.1a). While positive population growth establishes a new phenotype, negative growth leads to extinction. Extinction occurs when any population falls below a biomass threshold (equal to the initial biomass of a new mutant population). Although the production of mutants is a stochastic process, Stegen et al. [23] demonstrated and mathematical theory guarantees [39] that replicate simulations will be characterized by qualitatively and quantitatively similar dynamics.

Our model integrates the effects of three thermal dependencies on patterns of diversity in the context of ecological interactions: temperature-dependent resource supply (equation (2.2)), consumer vital rates (equations (2.3) and (2.4)) and mutation rate (equation (2.5)). In order to determine the influence of individual and combined thermal dependencies, we assessed our model in three steps. First, the ‘Full’ model (equations (2.1)–(2.5)) was evaluated via numerical integration at 17 temperatures using 2.5°C intervals from 5 to 45°C. Such a broad thermal range reflects a large geographical scale, and we assume no dispersal among networks. For each simulation, we measured phenotypic diversity through time as the number, S, of distinct body sizes in a network. Temperature–diversity patterns were examined by regressing ln(S) against inverse temperature (1/kT). Note that a negative relationship indicates an increase in diversity with temperature.

We also conducted in silico experiments where specific subsets of the thermal dependencies were assumed. These experiments used the same 17 temperatures as the Full model, and elucidate the influence of each thermal dependence. These in silico experiments also predict temperature–diversity patterns for natural systems in which specific thermal dependencies are not observed (e.g. endotherms).

In order to quantify temperature–diversity patterns through time, we used break-point regression which fits linear functions to either side of an inflection point [40] (see also Hawkins et al. [5] for a conceptually similar approach). For each point in time, a ratio of the two linear slopes was calculated with the shallowest slope in the numerator, constraining the ratio between +1 and −1. This ratio summarizes the shape of the ln(diversity)-to-1/kT relationship: a true linear relationship has a ratio of +1, a perfectly saturating relationship has a ratio of 0 and a perfectly symmetrical unimodal relationship has a ratio of −1. Intermediate ratios indicate intermediate patterns.

Our final step assessed the mechanistic basis of how each thermal dependence influences temperature–diversity patterns. For this, we retained only the ecological and organismal components of our model (equations (2.1)–(2.4)), and analytically solved for the coexistence criterion for two consumers of different body sizes. The coexistence criterion was used to compute the coexistence region at a given temperature and for a given thermal dependence. This is illustrated by numerical results at 5, 25 and 45°C.

3. Results and discussion

(a). Emergence and dynamics of temperature–diversity patterns

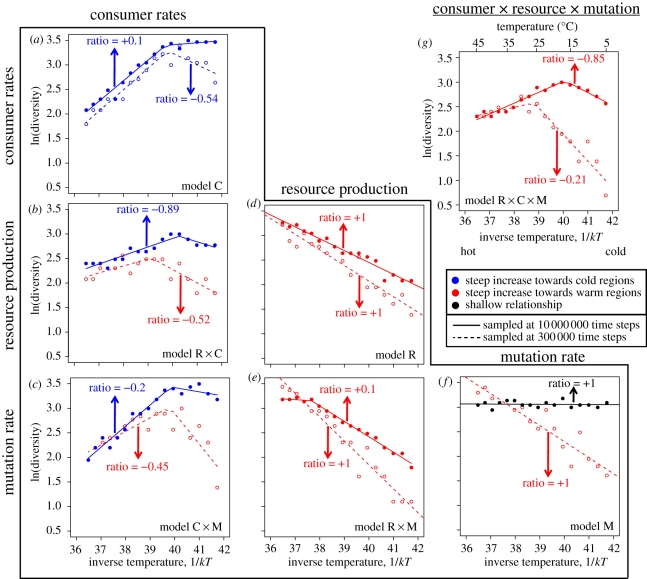
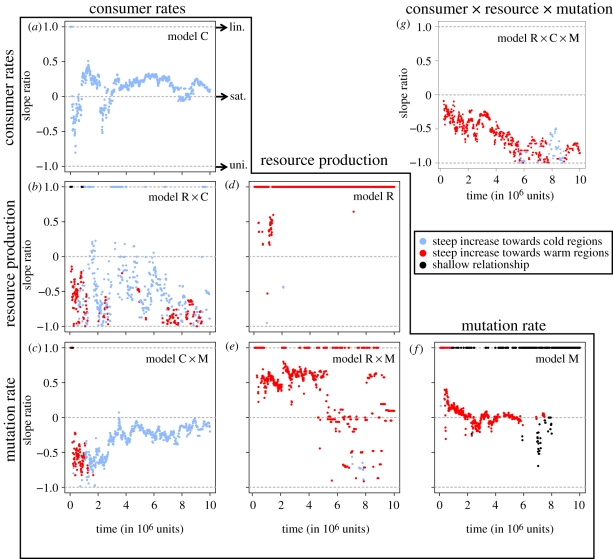
Our eco-evolutionary model predicts that the thermal dependencies of basal resource supply, consumer vital rates and mutation rate generate variation in phenotypic diversity across temperature (figures 1 and 2). The emergent patterns are dynamic, evolving through time. At the highest temperatures, diversification proceeded rapidly and then slowed as ecological niche space was filled. This resulted in a nonlinear, nearly saturating ln(S)-to-1/kT relationship (see dashed line in figure 1g and note data points from the early stages of diversification near the zero line in figure 2g). A distinctly unimodal ln(S)-to-1/kT relationship subsequently emerged and was maintained through time (see solid line in figure 1g and note trend through time towards −1 line in figure 2g).

Figure 1.

Temperature–diversity patterns sampled at two points in time (see inset) under different combinations of thermal dependencies. Vertical axes are the natural logarithm of diversity and horizontal axes are inverse temperature; in (g) degree-Celsius are also provided for reference. Lines represent break-point regression models, and ratios of the regression slopes are provided (see text). In order to characterize direction, data are colour-coded: red or blue, respectively, indicates that diversity increases most steeply towards warmer or colder temperatures, and black indicates there was no significant temperature–diversity relationship. Temperature dependencies and their combinations are indicated with unique letter combinations, where R, C and M refer to temperature-dependent resource supply, consumer vital rates and mutation rate, respectively. The temperature-dependence combinations are (a) consumer vital rates; (b) resource supply and consumer vital rates; (c) mutation rate and consumer vital rates; (d) resource supply; (e) resource supply and mutation rate; (f) mutation rate and (g) is the Full model with temperature-dependent resource supply, consumer vital rates and mutation rate. The model is given by equations (2.1)–(2.5). See table 1 for parameter values.

Figure 2.

Temporal dynamics of slope ratios from break-point regression of ln(diversity)-to-1/kT relationships across all combinations of thermal dependencies. Note that figure 1 shows the data and regression models underlying the slope ratios, but for only two points in time. The magnitude and colour of a given data point summarize the overall shape and direction of a temperature–diversity gradient at a given point in time under a given set of assumed thermal dependencies (refer to figure 1 and text for details). Abbreviations indicate ratio values for linear (lin.), saturating (sat.) and unimodal (uni.) relationships.

The emergent diversity patterns from the Full model are quite different from a previous model linking temperature to species richness [9], and from a recent elaboration in which the only assumed thermal dependence was on mutation rate [23] (our model M). In model M, diversity patterns were initially characterized by a linear, negative gradient (dashed line in figure 1f) that transitioned to a saturating relationship for a substantial period of time and eventually a flat relationship (note transition from red data on the +1 line to red data near the zero line to black data on the +1 line in figure 2f). Importantly, emergence of saturating temperature–diversity relationships from temperature-dependent mutation rate alone has not been previously demonstrated. Saturation of diversity with temperature is a common empirical pattern [5,7,41,42] that has appeared inconsistent with a strong influence of temperature-dependent mutation rate over diversity gradients. Our model M suggests that such a criticism is premature, and predicts that saturating relationships should be common. In order to understand mechanisms underlying the predominantly unimodal temperature–diversity patterns predicted by the Full model, however, we must examine ecological and organismal thermal dependencies.

To focus on interactive effects of ecological and organismal thermal dependencies, we modified the Full model by assuming temperature-independent mutation rate. This model (model R × C) predicts unimodal temperature–diversity patterns to be common throughout evolutionary time (figures 1b and 2b), similar to the Full model. There was, however, more variation in the shape of predicted temperature–diversity relationships under the R × C model, relative to the Full model: compare the consistent trend towards a ratio of −1 in the Full model (figure 2g) with the greater scatter in ratio values emerging from the R × C model (figure 2b). Temperature-dependent mutation rate may therefore reinforce a unimodal temperature–diversity relationship that ultimately emerges owing to ecological and organismal thermal dependencies. This influence of temperature-dependent mutation rate is maintained even when trophic networks are in an evolutionary steady state. By contrast, when mutation rate is the only thermal dependence, its effect on diversity is expected to be lost through evolutionary time. These model predictions suggest that interactions among thermal dependencies lead to emergent patterns that do not simply reflect the summed influences of individual thermal dependencies.

In order to better understand the details of how temperature-dependent ecology and organismal physiology interact, we evolved interaction networks with thermal dependencies assumed either for basal resource supply (equation (2.2); model R), or for consumer vital rates (equations (2.3) and (2.4); model C). Model R predicts a negative, linear ln(S)-to-1/kT relationship throughout all stages of diversification (note linear relationships in figure 1d and the predominance of red data points along the +1 line in figure 2d). This linear gradient strongly departs from the expectations generated by the Full and R × C models. Hence, decreased diversity observed at high temperatures is most likely owing to the thermal dependence of consumer vital rates. Indeed, model C predicts a positive ln(S)-to-1/kT relationship with diversity saturating towards low temperatures (see figure 1a and note blue data points near the zero line in figure 2a). Combining temperature-dependent consumer vital rates and mutation rate (C × M model) show that the thermal dependence of mutation rate can partially overcome the negative effects of temperature-dependent consumer rates (cf. dashed lines in figure 1a,c), but this effect of mutation is not maintained (note trend towards zero line in figure 2c).

We tested the robustness of these results to changes in underlying assumptions. First, basal resource supply rate (I) may influence network structure, and in model R, only I varies across networks, thereby examining model sensitivity to our baseline level of I. Model R predicts diversity to be a linear function of resource supply (i.e. ln(S) is a linear function of 1/kT) throughout evolutionary time (figure 2d). Thus, the baseline value of I should not influence the qualitative shape of temperature–diversity gradients. Second, we tested for an effect of the mutational step size distribution shape, and no qualitative differences emerged when using a normal distribution (mean 0, variance 0.2; electronic supplementary material, figure S2). Third, we assumed that all trophic networks were of the same evolutionary age. Owing to the large temperature gradient examined here, it is reasonable to instead assume different ages owing to later colonization of cooler areas [43]. Doing so did not result in qualitatively different predictions (electronic supplementary material, figure S3). Fourth, examining different levels of consumer specialization again showed the qualitative predictions to be robust (electronic supplementary material, figure S4). Note that the temperature above which diversity declines in the Full model increases with broader consumer niches (electronic supplementary material, figure S4), further suggesting that saturating ln(S)-to-1/kT relationships should be common, especially when consumers are generalists.

Comparing results across combinations of thermal dependencies shows that temperature–diversity patterns emerge from interactions among temperature-dependent resource supply, consumer vital rates and mutation rate. In the Full model, diversity peaks at an intermediate temperature owing to the positive effects of slowed consumer rates being offset by low resource supply and low mutation rate at cold temperatures, whereas the negative effects of faster consumer rates are offset by the positive effects of higher resource supply and higher mutation rate at hot temperatures. In the long run, diversity is held at relatively low levels by high consumer rates at higher temperatures, and by low rates of resource supply at lower temperatures. Within the Full model, diversity is thus maximized at intermediate temperatures where consumer vital rates are low enough and resource supply is high enough. Why does the thermal dependence of resource supply promote more diversity at higher temperature while the thermal dependence of consumer vital rates begets less diversity? To find out, we analysed the effect of each thermal dependence and their interactions on the coexistence of a pair of consumers.

(b). Understanding how temperature influences diversity

To dissect out mechanisms responsible for the predicted temperature–diversity patterns, we derived conditions for phenotype coexistence under different thermal dependencies (see the electronic supplementary material). Coexistence occurs either through mutual invasibility or facilitation. Mutual invasibility occurs when resident and mutant phenotypes form viable populations by themselves, and can each grow from rare when interacting with the other phenotype. Mutual invasibility is most relevant to competitors that both rely on the basal resource. Facilitation occurs when a phenotype does not form a viable population by itself, yet persists in the presence of the other phenotype. In our models, smaller bodied prey facilitate larger bodied predators, but the reverse is not true. Facilitation therefore arises owing to the size-structured nature of the trophic interactions: a large predator cannot persist without smaller bodied prey. The distinction between mutual invasibility and facilitation acquires special significance when evaluating the role of mutation rate: facilitation is a more effective mechanism of coexistence if novel, potential facilitators arise (by mutation) more frequently. For example, if a large consumer relies on one (smaller) prey phenotype that goes extinct, then the consumer's population will start to decline towards extinction. The higher mutation rate is, the higher the probability of the consumer's population being ‘rescued’ (i.e. facilitated) by emergence of a new prey phenotype that the consumer can efficiently use.

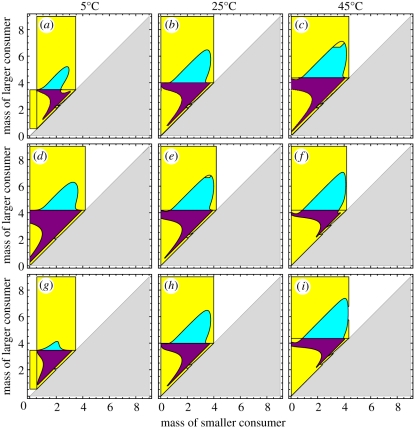
Analysis of a two-consumer submodel (n = 2 in equation (2.1)) shows how mutual invasibility and facilitation change with temperature. In the submodel, the two consumers have different body sizes, and the model is analysed across all body size combinations (see the electronic supplementary material). Trophic levels of the two consumers may therefore be very similar or different depending on the body size combination (figure 3). We examine only two-consumer phenotypes to maximize interpretability.

Figure 3.

Effects of temperature on coexistence in the two-consumer submodel (n = 2 in equation (2.1)). Temperatures are indicated above columns, and temperature dependence is (a–c) only on resource supply; (d–f) only on consumer vital rates; or (g–i) on both resource supply and consumer vital rates. Purple and cyan indicate coexistence by mutual invasibility and facilitation, respectively. Yellow indicates exclusion by one-way invasibility or no invasibility and white indicates no viability of either phenotype. A more detailed description of invasibility relations is reported in the electronic supplementary material, figure S11. Parameter values are those used in evolutionary projections (table 1). Note that near the diagonal line, the two consumers have the same trophic level, and the larger consumer has a higher trophic level than the smaller consumer above the diagonal.

When only resource supply is temperature-dependent, diversity should increase towards higher temperature owing to the regions of mutual invasibility and facilitation increasing with temperature (figure 3a–c; electronic supplementary material, figures S5a and S6a). The thermal dependence of mutation should thus increase the slope of the ln(S)-to-1/kT relationship (during early diversification) when coupled with temperature-dependent resource supply. This is indeed what the evolutionary simulations indicate (cf. dashed lines in figure 1d,e).

When only consumer vital rates are temperature-dependent, increasing temperature opposes mutual invasibility and slightly increases facilitation (figure 3d–f and electronic supplementary material, figure S5b), ultimately decreasing the total coexistence area (electronic supplementary material, figure S6b). Diversity is thus expected to decrease towards higher temperature, as it did in the evolutionary simulations of model C (figures 1a and 2a). The relatively large region of coexistence by facilitation and the slight increase in this region towards higher temperature allows temperature-dependent mutation to buffer the negative effects of temperature-dependent consumer rates. This explains the contrasting predictions of models C and C × M, where early on these models predict the steepest increase in diversity to be towards colder or warmer temperatures, respectively (note blue versus red data early on in figure 2a,c).

When thermal dependencies of both resource supply and consumer vital rates operate, the scope of mutual invasibility narrows towards higher temperatures, as it does under the thermal dependence of consumer vital rates, whereas the scope of facilitation expands, as it does under the thermal dependence of resource supply (figure 3g–i). The net effect is a saturating relationship between temperature and area of the coexistence region (electronic supplementary material, figure S6c). It is intriguing that the qualitative shape of the emergent diversity–temperature relationship under the R × C model varies through time (figure 2b). The influence of temperature over the total coexistence area must therefore change rapidly as trophic networks diversify, leading to an inconsistent influence of temperature over the net probability of invasion (electronic supplementary material, figure S5c). When the thermal dependence of mutation is taken into account, however, the influence of temperature is more predictable, and the expected saturating temperature–diversity relationship is observed during the early stages of diversification (figure 2g). Furthermore, the individual and combined effects of temperature-dependent resource supply and consumer vital rates are maintained across different levels of consumer specialization (electronic supplementary material, figures S7 and S8) and under non-quarter-power allometries (electronic supplementary material, figures S9 and S10). Examining the effects of temperature on coexistence between consumers has thus uncovered robust ecological mechanisms governing predicted temperature–diversity patterns.

(c). Comparisons with empirical temperature–diversity patterns

We are not aware of empirical analyses linking phenotypic diversity of whole trophic networks to environmental temperature (as in our model), but interesting comparisons can be made to analyses relating inverse temperature to species richness within taxonomic groups. Rather than a general gradient of richness increasing with temperature, recent analyses have demonstrated a variety of linear and nonlinear ln(species richness)-to-1/kT relationships across ectotherm groups [5,7,41,42]. From these empirical studies [5,7,41,42], significant ln(species richness)-to-1/kT patterns can be classified into five qualitative categories that we abbreviate parenthetically with symbols (+, −, 0) indicating the direction of a linear slope fit to either the warm or the cold range of the temperature axis (warm slope/cold slope). The five categories are negative linear (−/−), positive linear (+/+), saturation towards colder temperatures (+/0), saturation towards warmer temperatures (0/−) and unimodal (+/−).

Our model analyses captured all five categories and provided the following ‘coarse-grain’ predictions in terms of which diversity patterns should be associated with which thermal dependencies. (i) Globally positive relationships (+/+) are most likely when consumer vital rates and resource supply are both temperature-dependent (figure 2b); (ii) saturation towards low temperature (+/0) requires temperature-dependent consumer vital rates (figure 2a), which may be combined with temperature-dependent mutation (figure 2c); (iii) unimodal patterns (+/−) require multiple thermal dependencies and are most likely when resource supply, consumer vital rates and mutation rate are all temperature-dependent; (iv) globally negative relationships (−/−) are expected under temperature-dependent resource supply and/or mutation rate; and (v) saturation towards higher temperature (0/−) implies temperature-dependent mutation rate if the group is not in an evolutionary steady state (figure 2f). If evolutionary steady state has been reached, then saturation towards higher temperature implies full thermal dependencies if empirical samples do not cover the highest part of the temperature range or if the sampled taxonomic group reaches an upper temperature limit [44] below the maximum available temperature.

Although our model predictions qualitatively capture empirical patterns of temperature-richness, our theoretical framework should not be used to statistically fit temperature–diversity patterns. Statistical consistencies between empirical patterns and model expectations do not by themselves provide strong evidence for the hypothesis that temperature-dependent metabolism causally generates temperature–diversity gradients. We also suggest caution when comparing empirical species-richness patterns with our predictions. Phenotypic diversity and species richness will not always be strongly and positively correlated [45], and many empirical datasets analysed thus far do not represent multiple trophic levels. As large-scale functional trait datasets emerge, it will be possible to examine patterns of phenotypic diversity along temperature gradients. The influence of temperature-dependent metabolism over diversity gradients should then be gauged by the proportion of empirical systems showing patterns consistent with our predictions. We also encourage additional model analyses that develop system-specific predictions by building in empirically determined, system-specific assumptions that may deviate from the idealized thermal dependencies assumed here. We further envision direct experimental tests of our theory as experimental evolution is now well established [46]. By choosing or genetically engineering micro-organisms that differ in thermal dependencies, it should be possible to replicate our in silico experiments in vitro.

4. Conclusion and perspectives

The fact that inverse temperature-species richness data on ectotherms do not generally conform to a negative-linear relationship as predicted by the first generation of metabolic models of biodiversity [9] has been taken as evidence that metabolism may interact with other factors such as water availability [6]. While non-metabolic factors not already included in metabolic theory are certainly important, they are not required to explain observed departures from a negative, linear relationship. Instead, a decline in diversity at the highest temperatures can be explained by the thermal dependence of consumer vital rates acting alone or reducing the positive effect of increased resource supply at higher temperatures.

A major challenge for future work is to characterize the relative influences of metabolic and non-metabolic factors over diversity gradients. One approach for doing this would be to include non-metabolic factors into our theoretical framework that have been hypothesized to generate large-scale diversity gradients, such as niche conservatism and evolutionary age differentials [43]. Excitingly, the theory also shows that phenotypic diversity patterns can be mechanistically predicted, suggesting that more insight may be gained from empirical quantification of phenotypic diversity rather than species richness [47].

Our theory makes four important simplifying assumptions. First, we assume that networks are dispersed over a wide geographical scale. At such scales, networks may vary in evolutionary age owing to later colonization of cooler areas [43]. Factoring in the assumption that trophic networks are evolutionarily older in warmer regions allowed us to evaluate the sensitivity of temperature–diversity patterns to a range of age differentials, thus unifying our approach with the classical evolutionary age hypothesis of diversity gradients [1,2]. A key result is that a unimodal ln(S)-to-1/kT relationship is expected regardless of evolutionary age differences (electronic supplementary material, figure S3).

Second, our model assumes no dispersal among spatially discrete trophic networks, which is reasonable for a latitudinal distribution of networks. For more closely spaced networks (e.g. along an elevation gradient), dispersal may be an important factor influencing diversity patterns. Our approach, where invasibility plays a key role, is well suited for including dispersal. Predictions could be derived from the current model by examining how diversity (with no dispersal) correlates with invasibility (hence susceptibility of networks to dispersers).

Third, our model, like its progenitor [24], assumes that all consumers have the same degree of specialization. An interesting research direction allows for heritable variation in the degree of specialization [26]. Further pursuing this work will integrate two bodies of evolutionary theory (evolution of size, evolution of specialization) that have unfolded largely independently.

Finally, our theory primarily addresses ectotherms. By ‘turning off’ the thermal dependencies of consumer vital rates and mutation rate (yielding model R), our model also provides insight into endotherm diversity patterns. However, the theory can be extended to more explicitly model endotherms. The simplest approach would include a clade of temperature-insensitive endotherms alongside temperature-sensitive ectotherms. A more fundamental approach would allow adaptive evolution of the thermal dependence of metabolism. To do so, it will be important to account for seasonal and stochastic temperature fluctuations. In this extension of our theory, organismal thermal ecology will emerge through evolutionary time instead of being defined a priori. This will pave the way for investigating the origin and variation in temperature-dependent metabolism, and a better understanding of the consequences of that variation for the emergence of biodiversity patterns.

Appendix A

Table 1.

Parameter values and temperature-dependent functions used in model simulations. Examples of function implementation are provided using mass (M_i) of 5 (mass units), temperature (T) of 298 K, population biomass (N_i) of 1 (mass units) and prey population biomass (N_j) of 1 (mass units). Boltzmann's constant (k) is used, but for clarity its value (8.62 × 10⁻⁵ eV K⁻¹) is not written out in the table.

parameter or function	description and example function implementation	value (units)
α*	mutation rate normalization	14 722 190 (mutations mass−0.75 d−1)
(α*)(Mi−0.25)(e−E/kT)(Ni)	mutation rate = (α*)(5−0.25)(e−0.65/(298k))(1)	10−4 (mutations d−1)
ν	ecosystem nutrient retention efficiency	0.5 (unitless)
μ	nutrient loss rate	0.1 (d −1)
I*	nutrient influx rate normalization	432 819 544 708 (mass d−1)
(I*)(e−E/kT)	nutrient influx rate = (I*)(e−0.65/(298k))	4.44 (mass d−1)
β	interference competition max. body size difference	0.25 (mass)
c*	interference competition rate constant	0.1 (mass−1 d−1)
m*	mortality rate normalization	9 845 321 734 (mass0.25 d−1)
(m*)(Mi−0.25)(e−E/kT)(Ni)	mortality rate = (m*)(5−0.25)(e−0.65/(298k))(1)	0.067 (mass d−1)
f*	feeding rate normalization	117 081 266 560 (mass0.25 d−1)
(f*)(Mi−0.25)(e−E/kT)×(NiNj) (1/√(2πσ2))	max. feeding rate = (f*)(5−0.25)(e−0.65/(298k))×(1)(1/√(2π))	0.32 (mass d−1)
σ	feeding function standard deviation	1 (mass)
d	optimal body size difference	2 (mass)
σ2/d	consumer niche breadth	0.5 (mass)
ɛ	assimilation efficiency	0.25 (unitless)

*Normalization constant.