Abstract
Micro-CT is widely used in preclinical studies of small animals. Due to the low soft-tissue contrast in typical studies, segmentation of soft tissue organs from noncontrast enhanced micro-CT images is a challenging problem. Here, we propose an atlas-based approach for estimating the major organs in mouse micro-CT images. A statistical atlas of major trunk organs was constructed based on 45 training subjects. The statistical shape model technique was used to include inter-subject anatomical variations. The shape correlations between different organs were described using a conditional Gaussian model. For registration, first the high-contrast organs in micro-CT images were registered by fitting the statistical shape model, while the low-contrast organs were subsequently estimated from the high-contrast organs using the conditional Gaussian model. The registration accuracy was validated based on 23 noncontrast-enhanced and 45 contrast-enhanced micro-CT images. Three different accuracy metrics (Dice coefficient, organ volume recovery coefficient, and surface distance) were used for evaluation. The Dice coefficients vary from 0.45 ± 0.18 for the spleen to 0.90 ± 0.02 for the lungs, the volume recovery coefficients vary from for the liver to 1.30 ± 0.75 for the spleen, the surface distances vary from 0.18 ± 0.01 mm for the lungs to 0.72 ± 0.42 mm for the spleen. The registration accuracy of the statistical atlas was compared with two publicly available single-subject mouse atlases, i.e., the MOBY phantom and the DIGIMOUSE atlas, and the results proved that the statistical atlas is more accurate than the single atlases. To evaluate the influence of the training subject size, different numbers of training subjects were used for atlas construction and registration. The results showed an improvement of the registration accuracy when more training subjects were used for the atlas construction. The statistical atlas-based registration was also compared with the thin-plate spline based deformable registration, commonly used in mouse atlas registration. The results revealed that the statistical atlas has the advantage of improving the estimation of low-contrast organs.
Index Terms: Atlas registration, conditional Gaussian model, micro-CT, mouse atlas, statistical shape model
I. INTRODUCTION
SMALL animal in vivo imaging plays an important role in preclinical studies. Micro computed tomography (micro-CT) is an important technology that provides in vivo anatomy of the animal body [1]. Many small animal functional imaging modalities, such as positron emission tomography (PET) [2] and single photon emission computed tomography (SPECT) [3] use co-registered micro-CT images as an anatomical complement, and even optical imaging such as fluorescent molecular tomography (FMT) [4], [5] and bioluminescence tomography (BLT) [6] utilize micro-CT for anatomical reference. Based on the wide use of micro-CT for laboratory mice, it is necessary to segment internal organ structures from mouse micro-CT images and to facilitate the localization of abnormalities [7], the measurement of organ morphometry [8], the construction of anatomical models [4], and the determination of pharmacokinetic and pharmacodynamic parameters [9].
An important limitation of current in vivo micro-CT technology is the low soft tissue contrast. Due to a tradeoff between acquisition time, radiation dose and image quality, standard imaging protocols of in vivo micro-CT scans normally use low-dose X-rays and a limited number of projections, resulting in low soft tissue contrast [10]. Although contrast agents for soft tissues can be applied [11], the use of contrast agents increases study cost and complexity. Therefore, most preclinical studies still use noncontrast enhanced micro-CT images, and segmentation of soft organs from noncontrast micro-CT images remains problematic.
Since segmentation of mouse internal organs from conventional micro-CT images is problematic, several studies have used atlas-based registration methods to help estimate the internal organs instead of accurate segmentation. Most of these methods use high-contrast anatomical features (such as the body profile, skin, skeleton, and lungs) to register the atlas to individual subjects. Some studies acquire 2D silhouettes of the mouse body with optical cameras, and use these silhouettes to guide the atlas registration [12] or body surface alignment [13]. Other than 2D silhouettes, 3D body surface geometries are also acquired for atlas registration. Chaudhari et al. developed a skin-based atlas registration method with the assumption that the body surface is available from structured light measurements [14]. Joshi et al. proposed a finite-element-model-based elastic warping method to register the mouse atlas to 3D surface range data obtained from a laser scanner [15]. Besides the body surface, high-contrast organs in the CT image are also used for atlas registration. Baiker et al. used skin, skeleton, and lungs together as aligning features. They developed an articulated skeleton atlas for whole-body posture alignment, and used the aligned skeleton to initialize the skin and lungs. By registering the skin and lungs, a thin-plate spline (TPS) based transformation was obtained and used for atlas mapping [16]. Similarly, Xiao et al. registered skeleton, lungs, and skin using a 3D shape context based nonrigid registration method, and the whole-body organs of the atlas were mapped to the individual subject using the transformation obtained from the registration of skeleton, lungs, and skin [17]. In addition to the above methods that use geometrical alignment features, some methods also make use of intensity information from the CT image. Somayajula et al. registered the reference CT with the target CT using a mutual information-based approach [18]. Li et al. combined the skeleton geometrical features with image intensities for mouse CT image registration [19]. Although the use of intensity information could improve registration accuracy of low-contrast tissues, it may be more computationally expensive, making the method less efficient than geometrical feature-based approaches [16].
So far, most methods use a single subject atlas for registration. However, a single subject atlas is not sufficient for compensating the inter-subject anatomical variations which are caused by the differences of age, sex, strain, etc., among individuals. Although nonrigid transformations are commonly used in the existing methods, applying a global deformation to the whole body may not be sufficient for compensating the complex variations of individual organs. Kovacevic et al. [20] proposed a hierarchical piecewise affine registration scheme to cope with individual organ variations, but this method was specific to high-contrast micro-MR images rather than low-contrast micro-CT images, and it was based on the assumption that the morphological variations and posture differences are small enough between the reference and the target. Another solution to compensate for inter-subject differences is to use a multiple-subject atlas. By including more training subjects into the atlas, inter-subject variance is inherently included. Multi-subject atlases have already gained success in human image registration [21], [22] and mouse brain and kidney image analysis [23]–[25]. Based on our survey, no study has used a multi-subject atlas for the estimation of multiple mouse trunk organs.
In this paper we study the registration of a multi-subject statistical mouse atlas to noncontrast micro-CT images, aiming at estimating gross anatomy of major organs. We focus on the trunk region which includes most of the important organs for pre-clinical bio-distribution studies [26], [27]. Our statistical mouse atlas was constructed based on 45 training subjects to achieve better ability of compensating inter-subject anatomical variations than a single atlas. The statistical shape model (SSM) [28] was used to learn the inter-subject anatomical variations from the training sets. A conditional Gaussian model (CGM) [29] was used to capture inter-organ correlations of shapes and positions. For atlas registration, the statistical shape model was used to align the high-contrast organs, and the conditional Gaussian Model was used to estimate low-contrast organs from high-contrast organs. Section II below, describes the construction and registration of the statistical atlas and Section III provides the evaluation results of registration accuracy. Discussions and conclusions are made in Sections IV and V, respectively.
II. METHOD
A. Atlas Construction
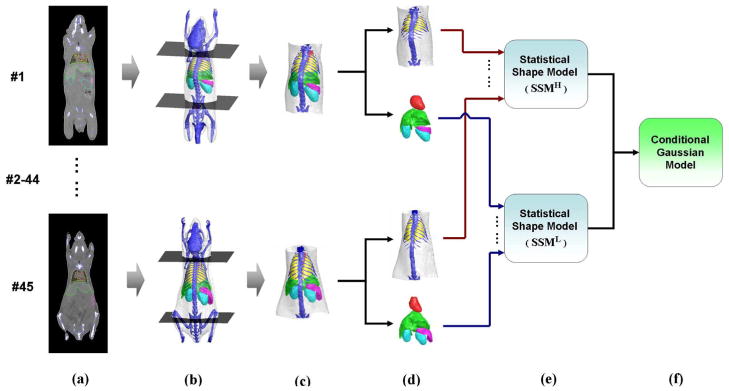
A schematic of the procedure of atlas construction is demonstrated in Fig. 1, and is further explained in the following subsections.
Fig. 1.
Construction of the statistical mouse atlas of the mouse trunk region. (a) Training set of 45 contrast-enhanced micro-CT images. Segmented organs are labeled with colored contours. (b) The two axial slices that pass the neck and pelvis. (c) Trunk region that is cut out between the two axial slices. (d) Segmented organs divided into two groups: high-contrast organs and low-contrast organs. (e) Two statistical shape models constructed for the high-contrast organs and low-contrast organs, respectively. (g) Conditional Gaussian model which is constructed based on the two statistical shape models.
1) Training Subjects
As shown in Fig. 1(a), 45 contrast-enhanced mouse micro-CT images from normal subjects were used for atlas construction. These images were selected from previously acquired datasets of contrast agent studies [30]. Healthy subjects of different sexes, strains, weights, and postures were acquired in vivo. Three of the most frequently used strains in preclinical studies [Nude, black C57, and severe-combined immunodeficient (SCID)] were included, with body weights ranging from 15 to 30 g. The subjects were imaged at prone positions inside a multimodality chamber that provided anesthesia and heating [31]. Although the imaging chamber restrained the possible postures of the subject, these were not strictly regularized and random flexing of bodies towards the left, right, and back directions was included in the dataset. The contrast agent used was Fenestra LC (ART, Montreal, QC, Canada) and the imaging system was a MicroCAT II small animal CT (Siemens Preclinical Solutions, Knoxville, TN). Exposure settings were 70 kVp, 500 mAs, 500 ms, and 360° rotation in 1° steps with 2.0 mm aluminum filtration. Images were reconstructed using a modified Feldkamp process to isotropic voxel size 0.20 mm, and a matrix size 256 × 256 × 496.
The major organs that were visible in the contrast-enhanced CT images were segmented by human experts using a semi-automatic segmentation software, which incorporated the tools of intensity thresholding, region growing, deformable simplex mesh [32] and graph cuts [33], [34]. The segmented organs included skin, skeleton, heart, lungs, liver, spleen, and kidneys. All the segmented organs were converted to triangular surface meshes using the Marching Cubes Algorithm [35]. To reduce the computational cost for the subsequent registration step, the triangular meshes were decimated [36] to fewer vertex numbers: 2500 for skin, 2000 for skeleton, 1000 each for lungs and liver, 700 each for the heart, spleen, and kidney. These numbers were selected as tradeoffs between reducing computation cost and maintaining organ shape features. To extract the trunk region, two axial slices were manually selected passing the neck bone and pelvis bone, respectively [Fig. 1(b)]. This extracted region between the two axial slices covers the biologically interesting areas where all the major organs other than brain are located [Fig. 1(c)]. To establish the vertex correspondence between different subjects, a reference subject of each organ was selected and registered to the rest of the training subjects (i.e., the correspondence of each organ was established separately) using the point set registration method based on Gaussian mixture models [37]. The accuracy (point distance) of the vertices correspondence for different organs is reported in the Appendix.
2) Statistical Shape Model
During the past decade, the statistical shape model (SSM) was widely used for modeling anatomical variations of biological structures [38]. It has been successfully used for registration and segmentation of human organs [28], [39], [40]. In our study, the statistical shape model was used to model the inter-subject anatomical variance of the major mouse trunk organs.
According to their visibility in noncontrast enhanced micro-CT images, the segmented organs were divided into two groups: high-contrast organs (skin, skeleton, and lungs) and low-contrast organs (heart, liver, spleen, and kidneys) [Fig. 1(d)]. Two statistical shape models, SSMH and SSML, were constructed for each group, respectively [Fig. 1(e)].
Before the construction of SSMH, the inter-subject differences of translation, scaling and rotation were eliminated using the Generalized Procrustes Analysis [41]. Let denote the mesh of high-contrast organs of the ith training subject index, the Generalized Procrustes Analysis was applied to the set of { } to obtain the similarity transformations { } that mapped each into the generalized shape space. If denotes the mesh after the Procrustes alignment, is represented as a 1-D vector which is lined up with the 3D coordinates of the mesh vertices
| (1) |
where
with ( ) being the 3D coordinates of the jth vertex of subject i, and Nskin being the total number of skin vertices. The same denotations also apply to skeleton and lungs. Therefore, is a 1-D vector of length 3×(Nskin+Nskeleton+Nlungs)
Principal component analysis (PCA) [42] was performed based on the training set of { }. This statistical analysis technique reduces data dimensionality of multivariate datasets. It linearly transforms the datasets into a new coordinate system where the first coordinate axis corresponds to the direction of greatest variance of data distribution, the second coordinate axis corresponds to the direction of second greatest variance, and so on. The directions of the new coordinate basis were defined as the eigenvectors of the covariance matrix of the datasets, with the eigenvalues as the energy of data variance in the corresponding directions. Each eigenvector was considered as a principal component of the original dataset. Using PCA, it is possible to simplify the representation of the datasets as a linear combination of the first few principal components. In our case, the principal components corresponded to the statistical variations of { }. By performing eigendecomposition to the covariance matrix of { }, the eigenvalues and eigenvectors were obtained. The first m̂ components that account for over 95% of the total variations (i.e., ) were grouped column-wisely into a matrix VH which satisfied (VH)TVH = I. The SSMH is represented as
| (2) |
where mH is an arbitrary instance of the model, m̄H is the mean value of { }, and bH is a m̂ component 1-D vector of the shape parameters. The shape parameters of each were computed as
| (3) |
The construction of SSML was the same as for SSMH, except for the Procrustes alignment step. In order to map { } and { } into the same shape space, { } was normalized using the similarity transformations of { }, i.e., . Therefore SSML was represented as
| (4) |
and the shape parameters for each were computed as
| (5) |
3) Conditional Gaussian Model
The conditional Gaussian model (CGM) is the mathematical tool for modeling the conditional distribution between two multivariate Gaussian variables. Iglesias et al. [29] used CGM to describe the correlations between sparse vertebrae landmarks and dense vertebrae edge points of human lateral X-ray spine images. In our case, the conditional Gaussian model was used to capture the shape correlation between SSMH and SSML [Fig. 1(f)]. Given that SSMH was matched to the micro-CT image, the conditional Gaussian model was used to estimate the conditional distribution of SSML. The basic assumptions were that the probabilistic distribution of SSMH and SSML could be modeled with Gaussian distributions, and there exist statistical correlations between SSMH and SSML. The feasibility of these assumptions is verified in the Appendix section, where we plotted the distributions of bH and bL, as well as the covariance matrix between different organs. Observations based on these plots confirmed that bH and bL roughly follow Gaussian distributions, and there were apparent correlations between different organs. While we do not deny the possible existence of better distribution models for describing the inter-organ correlations, the conditional Gaussian model works reasonably well in this application.
The construction of the conditional Gaussian model is described as follows. Based on the training subjects, the probabilistic distributions of bH and bL were modeled with multivariate Gaussian distributions, and the conditional distributions between bH and bL were modeled with a conditional Gaussian distribution
| (6) |
where b̄L | H and ΣL | H are the mean and covariance of the conditional distribution; b̄H, ΣH and b̄L, ΣL are the mean and covariance of bH and bL, respectively; ΣL,H and ΣH,L are the cross-covariance between bH and bL, respectively. The values of b̄H, ΣH, b̄L ΣL, ΣL,H and ΣH,L could be estimated from the training set { } and { }.
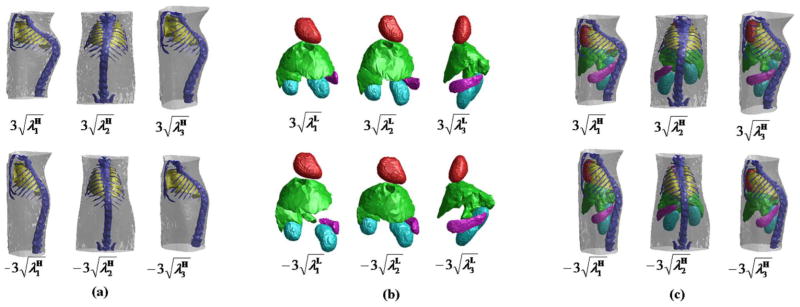
Fig. 2 demonstrates the shape variations generated from the statistical shape models and the conditional Gaussian model. Fig. 2(a) shows the shape variations of the first three principle modes of SSMH. The left column shows the variation of the largest eigenmode between and , the middle and right columns show the variations of the second and third largest eigenmode, respectively. Fig. 2(b) shows the shape variations of SSML in the same way. Fig. 2(c) shows the shape correlations generated from the conditional Gaussian model: both SSMH and SSML are displayed together, the shapes of SSMH are the same as Fig. 2(a), and the corresponding shapes of SSML are generated using the conditional Gaussian model, based on the shapes of SSMH as the conditions. It can be observed from Fig. 2(c) that the shape variations of SSML closely follow the shape variations of SSMH.
Fig. 2.
Shape variations generated from the statistical shape models and the conditional Gaussian model. (a) First three eigenmodes of the shape variations of SSMH. Each column shows the variation of one eigenmode, varying between (top) and (bottom). (b) First three eigenmodes of the shape variations of SSML, displayed in the same way of (a). (c) First three eigenmodes of the shape variations of SSMH coupled with the correlated variations of SSML estimated using the conditional Gaussian model.
B. Atlas Registration
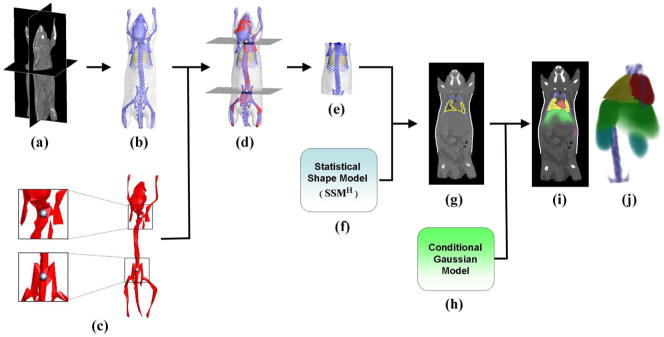
The registration of the statistical atlas is achieved in three steps: segmentation of high-contrast organs, registration of high-contrast organs, and estimation of low-contrast organs. Fig. 3 illustrates the process of atlas registration, which is explained below.
Fig. 3.
(a) Target micro-CT image. (b) High contrast organs segmented from the CT image. (c) Single-subject skeleton atlas used for trunk segmentation. The zoom-in regions show the two landmark points that are used for marking the trunk range. (d) Skeleton atlas registered with the segmented organs. Two axial slices are generated passing through the registered landmarks. (e) Trunk region of the segmented meshes, which is cut out by the two axial slices of (d). (f) Statistical shape model of high contrast organs(SSMH). (g) Result of fitting SSMH to the target subject. (h) Conditional Gaussian model. (i) Probability maps of the registered organs overlaid with the target CT image. (j) Volume rendering of the organ probability maps.
1) Segmentation of High-Contrast Organs
To obtain the alignment features for atlas registration, high-contrast organs were segmented from the micro-CT image [Fig. 3(a) and (b)]. The ISODATA clustering method [43] was used to group the voxels into clusters of different intensity levels. The cluster number was chosen as 8 to ensure good discrimination between the target organs. The resultant clusters were labeled from 1 to 8 based on the intensity level. Cluster 1 was classified as the background and was removed from the image, identifying the body region. Inside the body region, the cluster of the largest number of voxels (usually cluster 3 or 4) was recognized as soft tissue. Clusters brighter than soft tissue were classified as skeleton. Some subjects may have intestine regions as bright as the bones, in part due to bits of metal in the food. These intestine regions were recognized as small disconnected objects in the lower body region and were removed from the skeleton. The lungs were classified from the upper body region as large objects which were darker than the soft-tissue and brighter than cluster 2. Finally, the Marching Cubes Algorithm was used to create the triangular mesh of the skin, skeleton and lungs.
The trunk region of the target subject was extracted by registering a single-subject skeleton atlas (from an arbitrary subject of the training set) to the target skeleton. To reduce registration time, the mesh of the skeleton atlas was down-sampled to 400 vertices [Fig. 3(c)]. Two landmark points were defined on the neck and pelvis of the skeleton atlas, as shown in the zoomed-in boxes of Fig. 3(c). The skeleton atlas was registered to the target skeleton using the point set registration method based on Gaussian mixture models [37]. A TPS-based transformation was obtained from the registration and was used to map the two landmarks into the target subject. Two axial slices passing the mapped landmarks were generated [Fig. 3(d)], and the trunk region was cut out between the two axial slices [Fig. 3(e)].
2) Registration of High-Contrast Organs
In this step, SSMH [Fig. 3(f)] was registered to the segmented organs [Fig. 3(g)]. The initial correspondence between SSMH and the segmented organs was established by matching the mean shape m̄H to the segmented organs using the Robust Point Matching (RPM) method [44]. A minor adaption was made to the RPM method in order to register multiple organs simultaneously, i.e., the point correspondences between the source and target meshes were calculated only for the vertices belonging to the same organ. The RPM method resulted in a TPS-based transformation TPSinit (middot;). This transformation was applied to m̄H to obtain TPSinit (m̄H), which was the initial matching result. Based on the initial matching, SSMH was registered to the segmented organs via an iterative process:
Initialization: set b0 = 0, m0 = m̄H, y0 = TPSinit (m̄H), where b is the shape parameter, m is the model shape corresponding to b, and y is the target shape of model fitting.
FOR each iteration k = 0, 1, 2, …, +∞, DO
Use Generalized Procrustes Analysis to compute the similarity transformation SIM(·) that minimizes the summed squared distance ||yk − SIM(mk)||.
-
Calculate bk+1 with (3), i.e.,
Calculate mk+1 with (2): mk+1 = m̄H + VHbk+1.
IF ||SIM(mk+1) − SIM(mk)|| < ξ, THEN terminate the iteration and break out. The termination threshold was set as ξ = R · N, where R was the voxel size of the CT image, and was the total number of vertices of SSMH.
IF ||SIM(mk+1) − SIM(mk)|| ≥ ξ, THEN map mk+1 into the target subject via SIM(·). For each organ mesh of SIM(mk), do ray tracing along the normal directions of the vertices, find the nearest intersecting points of the rays with the surface of the same organ in the segmentation result. These intersection points compose the new target shape yk+1. If no intersection point is found for a specific vertex, use the vertex itself as the intersection point.
END FOR
The final value of bk+1 is used as the optimal shape parameter b̂H. The final value of SIM(·) is used as the optimal similarity transform SÎM(·). The model matching result is M̂H = SÎM(m̄H + VHb̂H).
-
Apply the RPM method again to register M̂H with the segmented organs. Let TPSfinal(·) be the transformation obtained from the RPM method, the final registration result of the high-contrast organs is
(7)
Note that the above method uses a strategy similar to the active shape model (ASM) approach [28]. The main difference between this method and the conventional ASM approach is that this method uses a TPS-based deformable registration after the SSM fitting, because combining SSM with deformable registration could achieve better accuracy than using each alone. The effect of combining SSM with deformable registration will be evaluated and discussed in Sections III and IV.
3) Estimation of Low Contrast Organs
After b̂H was obtained, the conditional distribution P(bL | b̂H) could be calculated using the conditional Gaussian model [according to (6)]. Let b̄L | H be the mean value of P(bL | b̂H), the estimation of low-contrast organs could be calculated as
| (8) |
where is the mean shape of the low-contrast organs.
4) Generation of Organ Probability Maps
P(bL | b̂H) gave the conditional distribution of low-contrast organs under the condition of high-contrast organs. Based on P(bL | b̂H), an arbitrary number of samples of bL could be randomly generated. Probabilistic maps of organ distribution could be created based on the random samples. Such probability maps are useful for probability-based image segmentation [21], [45] and quantification [46].
In practice, we generated Ns = 100 samples of bL. Let be the ith sample of bL, is converted to organ meshes using
| (9) |
where was the mesh union of the low-contrast organs (i.e., the heart, the liver, the spleen, and the kidneys). Let be the mesh of heart in , and { } be the set of all heart samples. For each sample i, was converted into a binary volume where the voxels inside the heart mesh were set to value 1, and the outside were set to 0. had the same matrix size as the CT image. Finally, the probability map of the heart was computed as the average of all s
| (10) |
where the voxel values of PMheart represented the probabilities of the heart’s existence at the locations of these voxels. Similarly, PMliver, PMspleen, PML Kidney, and PMR Kidney were computed.
Probability maps of the high-contrast organs were generated in a similar manner. Let be the mesh of lungs from [as in (7)]. PMlungs was created by filling the voxels inside with uniform probability 1. PMskeleton was created in the same way. Unlike the probability maps of low-contrast organs, the probability maps of high-contrast organs were uniform throughout the organ region, because they were registered with the segmentation results, rather than estimated using the conditional Gaussian model.
Fig. 3(i) shows the organ probability maps overlaid with the original CT image, Fig. 3(j) shows the volume rendering of the organ probability maps.
III. EVALUATION RESULTS
A. Experimental Setup
The statistical atlas-based registration was validated based on both noncontrast micro-CT images and contrast-enhanced micro-CT images. Note that the purpose of this study is to develop a method for organ estimation of noncontrast micro-CT images. However, noncontrast images do not offer good enough soft-tissue contrast for all the target organs. To evaluate the registration accuracy of all the target organs, we used the strategy borrowed from [16], i.e., high-contrast organs (the skin, skeleton, and lungs) were evaluated using the noncontrast images (because from noncontrast images, human experts can only define the high-contrast organs), while low-contrast organs (the heart, liver, spleen, and kidneys) were evaluated with the assistance of contrast agents, so that we could define reference standards of the low-contrast organ regions.
Twenty-three noncontrast images were randomly selected from the database of small animal images at the Crump Institute, UCLA [47]. The subjects in these images were healthy mice in prone positions. All the images were acquired with the same protocol as described in Section II-A, and reconstructed to isotropic voxel size 0.20 mm, matrix size 256 × 256 × 496.
The contrast-enhanced images were selected from the training sets of atlas construction. Leave-one-out test was performed to evaluate the registration accuracy, i.e., each time one of the 45 images used as a test image, the atlas was constructed from the rest 44 images. Therefore the test images were not included into the atlases.
The proposed method was applied to both noncontrast and contrast-enhanced images. Automatic registration was achieved for all the 23 noncontrast images. However, in 14 of the 45 contrast-enhanced images, the high-contrast organ segmentation step (Section II-B) yielded incorrect bone segmentation and manual correction was necessary. This is because the segmentation method was mainly designed for noncontrast images. For contrast-enhanced images, the high-intensity in the liver or spleen may interfere with bone segmentation. After this manual correction, the subsequent registration was completed automatically for the contrast-enhanced images.
The segmentation and registration algorithms were programmed with IDL 7.1 (ITT Visual Information Solutions, Boulder, CO) and were executed on a PC with a 3.05 GHz CPU and 5.99 GB RAM. The time requirements were ~16 s for automatic high-contrast organ segmentation (for image size 256 × 256 × 496), and ~5 min for atlas registration. Most of the registration time was spent on the generation of the probability maps (~4 min 15 s). The time spent on probability map generation was directly related to the number of random instances and the volume size of the probability map. In our experiment, we used 100 random instances and an image size of 256 × 256 × 496. Nevertheless, the necessity of probability map generation is optional and depends on user requirements. If the user decides to skip the generation of probability maps, the registration time could be less than 1 min.
B. Visual Assessment of Registration Results
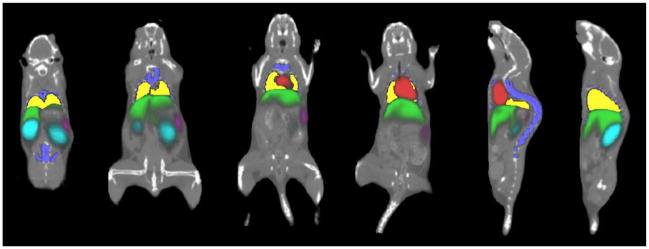
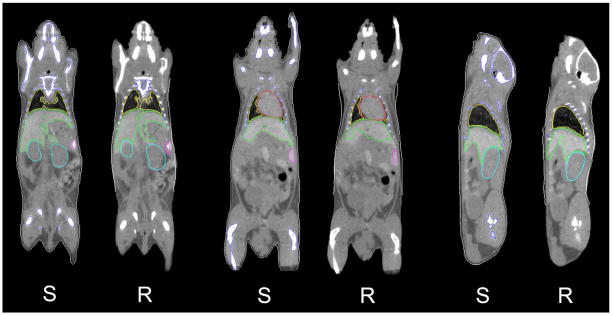
Fig. 4 shows the results of organ probability maps overlaid on noncontrast micro-CT images. Coronal and sagittal slices of different subjects are presented. The probability maps are color-coded, and the color brightness represents the probability value (brighter color means higher probability). Fig. 5 compares the mean shapes of registration results [ and in (7) and (8)] with the human segmentation results based on contrast-enhanced images. For every pair of comparison, “S” stands for human segmentation result, and “R” stands for registration result.
Fig. 4.
Registration result of organ probability maps, overlaid with noncontrast micro-CT images of different subjects. Different coronal and sagittal slices are demonstrated. The probability maps are color-coded. The brightness of color represents the probability value (brighter color means higher probability).
Fig. 5.
Visual comparison of the registration results with human segmentation results, based on contrast-enhanced micro-CT images. For every pair of comparison, “S” stands for human segmentation result, and “R” stands for registration result. The contours of the registration results demonstrate the mean shapes [ and in (7) and (8)] of the registered organs.
C. Registration Accuracy
As described above, for high-contrast organs (skin, skeleton, and lungs), the accuracy of atlas registration was evaluated based on 23 noncontrast images, and for low-contrast organs (heart, liver, spleen, and kidneys), the accuracy was evaluated based on 45 contrast-enhanced images, via the leave-one-out test. Registration accuracy was measured by comparing the mean shapes of registration results [ and in (7) and (8)] with the human segmentation results. Three different metrics, Dice coefficient, recovery coefficient of organ volume (RCvlm) and mean surface distance(Dsurf), were used for accuracy assessment
| (11) |
| (12) |
| (13) |
where RR and RS represent the organ regions of registration and segmentation, respectively; | · | denotes the number of voxels, ∩ indicates overlapping between two regions; uR and uS represent the surface vertices of the registered region and segmented region, respectively; and i and j denote the vertex index of the two meshes, respectively. The Dice coefficient reflects the estimation accuracy of shape, size and position, RCvlm reflect the estimation accuracy of organ volume, and Dsurf reflects the average distances between two organ surfaces.
For comparison, single-atlas-based registration was also applied to the test images. Two publicly available mouse atlases, the MOBY phantom [48] and DIGIMOUSE atlas [49], [50], were used for the comparison. Trunk regions of the two atlases were extracted in the same way as the statistical atlas (Section II-A). The registration on a single atlas was performed as follows: at first the high-contrast organs were registered using the RPM method [44], and then the low-contrast organs were mapped using the transformation obtained from the RPM method. The accuracy of the single atlas registration was also measured by the above three metrics.
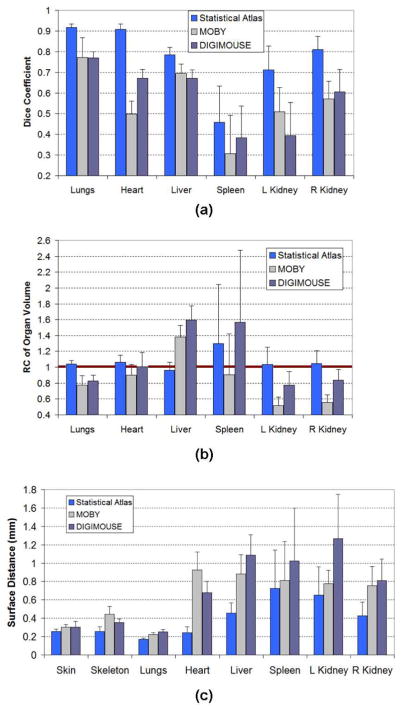
Fig. 6 demonstrates the comparison of registration accuracy of major organs between the statistical-atlas-based registration and the two single-atlas-based registrations. Both mean value and standard deviation are plotted. For the Dice coefficient and RCvlm, a mean value closer to 1 means better accuracy. For surface distance, mean value closer to 0 mm means better accuracy. It is clear that the statistical-atlas-based registration performs better than the two single-atlas-based registrations. Note that we did not calculate the Dice coefficient and RCvlm for skin and skeleton, because the skin and skeleton of the atlas are open meshes which are cut from the whole-body mesh. Opened surfaces cannot be filled into solid volumes for calculating volumetric metrics (Dice and RCvlm). Moreover, in the atlas, the skin and skeleton only cover the trunk range, while in the target image, the skin and skeleton cover the whole body range. Therefore it is not equitable to compute Dice and RCvlm based on different anatomical ranges.
Fig. 6.
Comparison of registration accuracies between statistical atlas-based registration and the two single atlas-based registrations. Two publicly available mouse atlases, the MOBY phantom [48] and DIGIMOUSE atlas [49], are used for the comparison. The skin, skeleton, and lungs are evaluated based on non-contrast images, while other organs are evaluated based on contrast-enhanced images. (a) Comparison results of Dice coefficient. (b) Comparison results of recovery coefficient of organ volume. (c) Comparison results of surface distance. In each comparison, both mean value and standard deviation across the target subjects are plotted.
To evaluate the significance of difference between the statistical atlas (SA)-based registration and the two single atlas-based registrations (MOBY and DIGI), the Wilcoxon signed-rank test was performed with each organ for each of the three accuracy values (i.e., Dice coefficient, RCvlm and surface distance) in Fig. 6. This paired different test was conducted for both “SA vs. MOBY” and “SA vs. DIGIMOUSE.” Most of the test yielded results of p < 0.0001, with only two exceptions: the results of the spleen Dice coefficients were p = 0.0011 for “SA vs. MOBY” and p = 0.0069 for “SA vs. DIGIMOUSE” and the results of the skin surface distances were p = 0.0386 for “SA vs. MOBY” and p = 0.1159 for “SA vs. DIGIMOUSE”. These results will be analyzed in Section IV.
D. Influence of the Number of Training Subjects
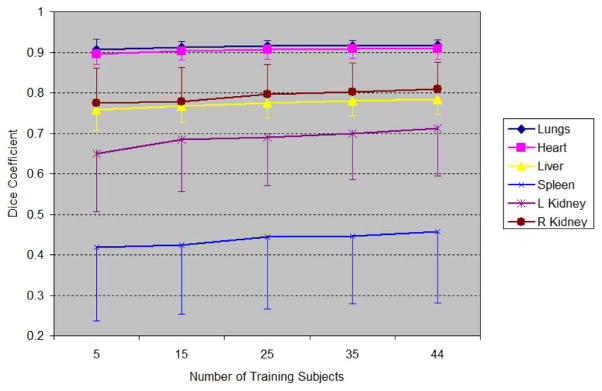
Since the statistical atlas is constructed based on multiple subjects, the number of training subjects should influence the accuracy of registration. A leave-many-out test of atlas registration was conducted to quantify this influence. Different numbers of training subjects, 5, 15, 25, 35, and 44, were used for the atlas construction. For 5, 15, 25, and 35 training subjects, the subjects were randomly selected from the total of 45 and the resulting atlas was registered to all the remaining number of subjects (40, 30, 20, and 10). This experiment was repeated five times to reduce the possible bias of random selection. For the case of 44 training subjects, the test was the same as the leave-one-out test. The means and standard deviations of the Dice coefficient for each training number were obtained and are plotted in Fig. 7. In order to give a clear demonstration, the standard deviations were plotted in different directions for different organs. It can be seen that with increasing training subject size, the mean Dice coefficients increase, and the standard deviations roughly decrease.
Fig. 7.
Influence of training subject number on registration accuracy. The numbers on the abscissa axis stand for the number of training subjects for atlas construction. Dice coefficient results of different organs are plotted for different training subject numbers. For clarity, the standard deviations of different organs are plotted in different directions.
E. Comparing Statistical Atlas Registration With TPS-Based Deformable Registration
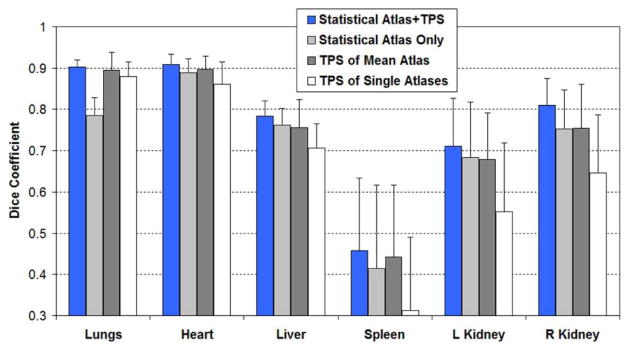
In this paper, we combined statistical atlas fitting with TPS-based deformation [see (7)]. To reveal the effect of this combination, we conducted an experiment to compare the accuracies of using each method alone with the accuracies of combing them together. Fig. 8 shows the comparison results in terms of Dice coefficients. Both mean values and standard deviations are reported. “Statistical Atlas+ TPS” means the combined method. “Statistical Atlas Only” means performing statistical atlas fitting without TPS-based registration [i.e., ignore TPSfinal in (7)–(9)]. “TPS of Mean Atlas” means using the mean shapes of SSMH and SSML as a single atlas, and register it with TPS-based deformable registration just as we did for the MOBY and DIGIMOUSE atlases. “TPS of Single Atlas” means using each of the 45 training subjects as a single atlas, register them with TPS-based deformable registration, and compute the means and standard deviations of the Dice coefficients for all the 45 single atlases. For all the four methods, the same test images were used as described in Section III-A. Leave-one-out tests were performed to avoid including the test images into the atlases.
Fig. 8.
Comparison of the organ registration accuracy (Dice coefficient) of statistical atlas registration and TPS-based deformable registration. “Statistical Atlas + TPS” means combining statistical atlas fitting with TPS-based registration. “Statistical Atlas Only” means performing statistical atlas fitting without TPS-based registration. “TPS of Mean Atlas” means TPS-based registration using the mean shapes of SSMH and SSML as a single atlas. “TPS of Single Atlas” means TPS-based registration using each of the 45 training subjects as a single atlas.
IV. DISCUSSION
A. Atlas Registration
From Fig. 4, we could see that the probability maps of low-contrast organs have fuzzy edges and bright centers. This means there is higher probability of the organs’ presence in the central regions than in the edge regions. In the probability map of the liver, the cranial part is better defined than the caudal part, because the cranial part is closer to the lungs, which are known as a deterministic condition. Similarly, we can explain why the probability map of the heart is better defined than other low-contrast organs, because the heart has good correlation with the location of the lungs. The spleen and the left kidney are two of the least well determined organs, since their positions are influenced to the varying size of the flexible stomach. The food content in the stomach influences its size, and consequently influences the positions of the spleen and left kidney. The same phenomenon is also observed from the quantitative results (Fig. 6), where the spleen and left kidney always have the worst accuracy.
As shown by Fig. 6(a), the two single subject atlases, MOBY and DIGIMOUSE, have similar levels of Dice coefficients. They outperform each other on different organs, but neither of the two prevails on all organs. The statistical atlas presented here yields larger Dice coefficients than both single atlases. Although a nonrigid deformation (the RPM method) is used for both the statistical atlas and the single atlas registrations, the statistical atlas outperforms the single atlases because it provides a good estimation of the individual anatomy before the final nonrigid deformation, just like generating an individual-specific single atlas which matches the subject better than any existing single atlas. Observing the results, it is promising that the statistical atlas-based registration obtains Dice coefficients >0.7 for the lungs, heart, liver and kidneys. The statistical atlas also produces small standard deviations for the lungs, heart, and liver, but not for the spleen and kidneys. The liver has smaller standard deviation because it is bigger in size and more stable in location. The spleen has the smallest mean Dice coefficient and the biggest standard deviation, because it suffers from both unstable position (affected by the flexible stomach) and problematic shape (banana-like long shape), which makes it very sensitive to small variances of position and direction. The kidneys also have suboptimal standard deviations, because their positions are unstable. It is interesting to see that the right kidney has larger Dice coefficient and smaller standard deviation than the left kidney, because the position of the right kidney is less flexible than the left kidney. The position of the right kidney is mainly affected by the liver, which is big and stable. In contrast, the position of the left kidney is mainly affected by the stomach, which is flexible in size and position.
From Fig. 6(b) and (c), the results of RCvlm and Dsurf reveal similar phenomena as the Dice coefficients. The RCvlm of the statistical atlas is close to 1 for almost all organs. This means that the statistical atlas is good at estimating organ volume. For the spleen, the statistical atlas tends to overestimate the spleen volume. The spleen of the MOBY atlas is even closer to 1 than the statistical atlas, but the MOBY atlas based registration tends to underestimate the spleen volume. In terms of surface distances, the statistical atlas has smaller distances for all organs than the single atlases. The surface distances of the high-contrast organs are significantly smaller than the low contrast organs, because the high-contrast organs are directly registered to the CT segmentation results. For the statistical atlas, the surface distances of the high-contrast organs are 0.26±0.02 mm for the skin, 0.26 ± 0.05 mm for the skeleton and 0.18 ± 0.01 mm for the lungs. The achievement of this accuracy is attributed to the combination of statistical atlas with the RPM registration method.
Judging from the results of Wilcoxon signed-rank test, the statistical atlas-based registration is significantly (p < 0.0001 for most organs with the three accuracy metrics) more accurate than the two single atlas-based registrations (MOBY phantom and DIGIMOUSE atlas). For the Dice coefficient, the spleen showed the least significant differences (p < 0.01), because the spleen is the most difficult organ to register, as explained above. For the surface distance, the skin showed weak significance (p < 0.05) for “SA vs. MOBY”, and is not significant (p > 0.1) for “SA vs. DIGIMOUSE”. This is because the skin has less complex shape than other organs, thus it is easier for the TPS-based method to get a good alignment, reducing the advantage of the statistical atlas. Moreover, the skin of the MOBY phantom is represented by the nonuniform rational B-spline (NURBS) surface which is less realistic than the DIGIMOUSE atlas, therefore the MOBY phantom showed more significant difference of skin accuracy than the DIGIMOUSE atlas.
Fig. 7 demonstrates the influence of training subject number on the Dice coefficient. It is clear that the Dice coefficient of every organ increases when more training subjects are used. This phenomenon again confirms the advantage of using more training subjects. It can also be observed that the improvement for low-contrast organs is faster than for high-contrast organs. This is because for high-contrast organs, the TPS-based registration [as in (7)] was used to capture more anatomical variations than the SSM captures, while for low contrast organs, no TPS-based registration can be directly applied thus we have to rely more on the improvement of SSM. From Fig. 7, we can also see that the Dice coefficients for all organs tend to increase slower when the subject number becomes larger, implying there might be an upper bound of Dice coefficient for each organ. The possible existence of the upper bounds reveals a limitation of the statistical-atlas-based approach: after all, we cannot expect to use statistical approach to model all possible inter-subject anatomical variations.
Fig. 8 reveals that combining the statistical atlas with deformable registration yields better accuracy than using each alone. Statistical atlas and deformable registration complement each other to achieve improved accuracy. By fitting the statistical atlas to the subject image, an individualized atlas is obtained and is then used as a good starting point of the deformable registration. On the other hand, the deformable registration serves as a compensation for the over-constrained SSM, since the training subject number is quite limited compared to the great inter-subject anatomical variations. Fig. 8 also demonstrates that “Statistical Atlas Only” and “TPS of Mean Atlas” have comparable accuracies with each other for low contrast organs, and both of them are more accurate than “TPS of Single Atlas”. However, for the lungs, “TPS of Mean Atlas” and “TPS of Single Atlas” are better than “Statistical Atlas Only”, because the lungs are directly registered by the TPS-based method. Concluding from these observations, TPS-based registration performs well for high-contrast organs, because the landmark points of the TPS deformation can be directly obtained from the segmentation of these organs. However, for low contrast organs, the statistical atlas is essential since it uses conditional Gaussian model to derive subject-specific estimation. It is also interesting to see that using the mean shape of the statistical atlas as a single atlas is more accurate than using an individual training subject as a single atlas, because the mean shape as a representation of the whole training set is less prone to the influence of the outlier subjects.
B. Atlas Construction
A direct question rising from Fig. 7 is how many training subjects are needed to approach the upper bound of registration accuracy. Although 45 training subjects is already a reasonably large number of subjects, the DICE data shows there is still room for improvement with more subjects, as 45 was not enough to model the tremendous anatomical variations of mice population. To achieve better accuracy, we should try either to increase the training sample number (by acquiring more training data) or to decrease the target population variations (by building and registering the atlas based on subgroups of the population, according to different ages, strains, sexes, and etc.), or both. The synthetic variation methods for statistical shape model construction [51] could also be used to artificially enlarge the variations of limited training sets.
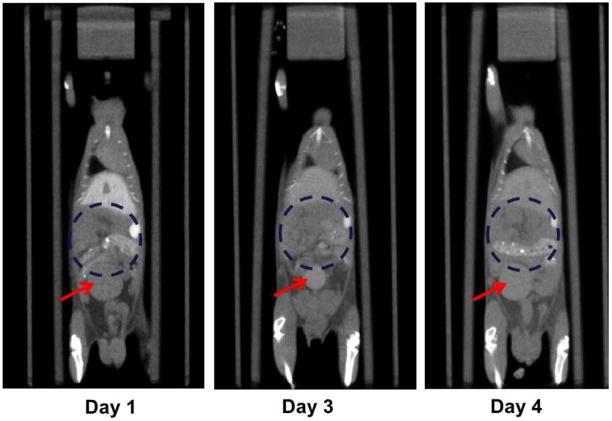
The statistical atlas is constructed based on the segmentation of Fenestra LC-enhanced CT images. Most trunk organs that are important for bio-distribution studies are included in the atlas. However, there are a few major trunk organs, such as the bladder and the gastrointestinal (GI) track, not included due to technical difficulties. The difficulties of including the bladder and the GI track are illustrated in Fig. 9, where the same subject is displayed at different time points. It is noticeable that the sizes and positions of the bladder vary between different time points, due to the influence of urine accumulation. Since the bladder has significant intra-subject variation, it is very difficult to model its inter-subject statistics. Therefore we consider the atlas registration strategy unsuitable to estimate the bladder. Instead it would be easier to extract the bladder via segmentation strategies, since the bladder normally presents good boundary contrast. As for the GI track, it is hard to clearly define the detailed boundaries from Fenestra enhanced images. To overcome this limitation, as well as to define other smaller organs like the gallbladder and pancreas, it might be necessary to try with multiple CT contrast agents [11], [52], intraperitonealy administrations or micro-MR images [53] in future studies.
Fig. 9.
Longitudinal micro-CT images of the same subject, demonstrating the instability of bladder position and size, as well as the difficulty of defining the region of the GI track. The subject is shown at similar coronal positions and at different time points after the injection of contrast agent. The red arrows point to the bladder, and the blue dashed circles delineate the rough GI regions. It can also be observed that the GI track has fuzzy boundaries in all images, making it difficult to accurately define it.
Another limitation of the current study is that the statistical atlas is constructed based on only healthy training subjects. It is difficult to include unhealthy training subjects because different diseases may affect the anatomy in unpredictable ways. However, many preclinical studies are conducted based on disease models. The registration of a healthy atlas to unhealthy subjects should be evaluated in future work.
C. Statistical Shape Model and Conditional Gaussian Model
In our work, the statistical shape models are constructed for groups of multiple organs. That is, instead of modeling each organ individually, we modeled a group of organs as a single object. The advantage of doing this is that the relative movements between adjacent organs can be inherently built into the model, therefore the chances of organ overlap are much reduced. However, group-wise modeling tends to over-constrain the model, making it difficult to capture delicate shape variations of single organs. For further improvement, multi-object statistical shape models [54]–[56] can be explored to model both inter-organ movements and single organ variations.
In this paper, the conditional Gaussian model was used in the estimation of low-contrast organs from high-contrast organs. Nevertheless, the value of the conditional Gaussian model can reach beyond this specific application. For example, for those applications that use the mouse body surface to estimate internal organs, the conditional Gaussian model is a good choice for capturing the correlation between internal organs and body surface. Furthermore, it can also be used in clinical image analysis, for the estimation of unknown organs based on the already segmented organs.
D. Comparison With Existing Methods
As mentioned in the introduction section, so far several single-subject atlas registration methods have been proposed. Most existing methods are used for whole-body registration. In contrast, our method focuses on trunk region because only this region is stable enough for inter-subject statistical modeling when imaged in our imaging chamber [31]. Otherwise if the head, the limbs and the tail are built into the model, they may introduce false statistical correlations caused by posture changing. By focusing on the trunk region, our method obtained better accuracy than single atlas-based registrations. Therefore, our statistical atlas is suitable for the trunk region, while a single-subject atlas could be used for whole-body registration. In fact, we already used a single-subject skeleton atlas in this paper for defining the trunk region based on spine and skull alignment, and this strategy can also be used for brain estimation if needed. However, this strategy is not accurate enough for aligning the limbs, especially for the front limbs which are too close to the thoracic bones. Khmelinskii et al. proposed some articulated skeleton atlases which are better at whole-body posture alignment [57]. Xiao et al. also developed a shape-context based non-rigid registration method which achieved posture alignment by piecewisely aligning the mouse skeleton [58], [59]. It could be a promising improvement if the statistical trunk atlas could be combined with articulated skeleton atlas or piecewise skeleton registration approach, to offer wider usability and better accuracy for mouse micro-CT image registration.
In this paper, a probabilistic atlas (PA) is generated for the abdominal organs. In the past decade, PA-based segmentation of human abdominal organs from clinical CT images has become a popular topic. Our method has a similar application purpose (for obtaining probability maps of abdominal organs) with the existing PA-based methods, but also has its own contribution in methodology. For the generation of the PA, existing methods firstly register the training subjects into a common space either by aligning the target organs themselves [60] or by establishing an external normalization space (such as the abdominal cavity [56], [61], [62] or TPS-based control points [21]), and then estimate the PA by computing the proportional fractions of the aligned binary organs. In our method, the PA is estimated by sampling the analytical distribution of SSML rather than by counting from aligned training subjects. In this way, the PA is related to the statistical shape model (SSM). The relationship of SSM and PA is not extensively studied in existing references of human abdominal CT. Okada et al. [62], [63] combined SSM and PA for the segmentation of human abdominal organs, but SSM and PA are constructed and applied separately. Shimizu et al. [64] correlated pancreas PA with the SSM of pancreas centerline, but each instance of the SSM had to be endowed with a different PA, making the optimization of individualized PA computationally expensive; hence they used only a limited number of pre-sampled SSM instances for the optimization. In this paper, since the conditional distribution of SSML is already individualized for the specific subject, it is straightforward to generate an individualized PA from SSML. Moreover, for localizing the PA into the individual subject, existing methods normally use the same normalization space of PA construction to map the PA into individual images, and some of these methods also utilize image intensity information for organ pose estimation [65] or atlas registration. [21]. In our method, the PA of low contrast organs is inherently localized according to the analytical anatomical correlation (conditional Gaussian model) with surrounding high contrast organs. The high contrast organs provide both shape condition [b̂H in (9)] and external spatial constraint [TPSfinal and SÎM in (9)] for the low contrast organs. Such a strategy might be useful not only for CT images, but also for other modalities where high contrast organs can help with the estimation of nearby low contrast organs, such as PET images, etc. Finally, unlike most existing human-oriented references, the PA obtained in this work is not used for segmentation, due to the imperfect soft-tissue contrast of in vivo micro-CT images (as discussed in Section I). Nevertheless, the PA generated here can be helpful for segmenting other modalities that are co-registered with the micro-CT images, such as micro-PET [2], micro-SPECT [3], and etc., which are beyond the scope of this paper but within the plan of future study.
V. CONCLUSION
In this study, we constructed a statistical atlas of the mouse trunk region, and registered this atlas to noncontrast mouse micro-CT images to estimate the major organs of trunk region. To our knowledge, this is the first time that a multi-subject mouse atlas has been proposed for multiple trunk organs. Moreover, differing from probabilistic atlases which are constructed by directly averaging multiple single-subject atlases, our atlas uses statistical models to analytically describe the inter-subject distributions and inter-organ correlations. Subject-specific organ probability maps are generated based on the registration of statistical shape models.
The strategy of combining statistical shape model with conditional Gaussian model could also enrich the methodologies of multi-subject atlas construction. The statistical shape model was used to compensate for inter-subject anatomical variations, and the conditional Gaussian model was used to capture inter-organ shape correlations. The evaluation results showed improvement of registration accuracy compared to single atlas-based registration, and the registration accuracy can be further improved with the increase of training subject number. Comparing the statistical-atlas-based registration with TPS-based deformable registration, the statistical atlas demonstrates advantage in improving the accuracy of low-contrast organs.
In future work, we still need to add more training subjects and include more organs into the atlas. We also need to incorporate the trunk atlas into a whole-body atlas, so as to widen the uses of the atlas.
Acknowledgments
This work was supported in part by SAIRP NIH-NCI 2U24 CA092865 and in part by the UCLA Chancellor’s Bioscience Core grant.
The authors would like to thank Dr. W. P. Segars for providing the MOBY phantom, and Dr. R. M. Leahy for providing the DIGIMOUSE atlas. The authors appreciate Dr. Y. Boykov for offering publicly available codes of graph cuts method, Dr. B. Jian for provding codes of point set Registration using mixture of Gaussians, and Dr. H. Chui and A. Rangarajan for providing the MATLAB codes for robust point matching (RPM) algorithm. The authors also appreciate the help of W. Ladno and D. Williams for acquiring micro-CT images, and acknowledge R. Taschereau, B. Berry Puzey, R. Lofstedt, and H. Herman for helpful suggestions on this project.
APPENDIX
As introduced in Section II-A, to build the statistical atlas, the point set registration method based on Gaussian mixture models [37] was used for establishing the organ vertex correspondence between training subjects. Using this method, a reference subject of each organ was selected and registered to the rest of the training subjects. The statistics of registration accuracy of each organ is reported in Table I. The accuracy is measured across the whole training set, using the surface distance defined in (13).
Table I.
Surface Distances for Vertex Correspondences of each Organ (Mean Value ± Standard Deviation, Unit: MM)
| Skin | Skeleton | Lungs | Heart | Liver | Spleen | L Kidney | R Kidney |
|---|---|---|---|---|---|---|---|
| 0.08 | 0.016 | 0.11 | 0.05 | 0.18 | 0.07 | 0.04 | 0.04 |
| ± | ± | ± | ± | ± | ± | ± | ± |
| 0.04 | 0.06 | 0.01 | 0.04 | 0.04 | 0.01 | 0.003 | 0.003 |
As reflected from Table I, different organs have different level of accuracy, the organs with simpler shapes (e.g., the heart and kidneys) tend to have better accuracy. Nevertheless, all the organs have accuracy of less than 0.2 mm, serving the purpose of this study. In future work, we will investigate possibilities to further improve the accuracy of vertex correspondence.
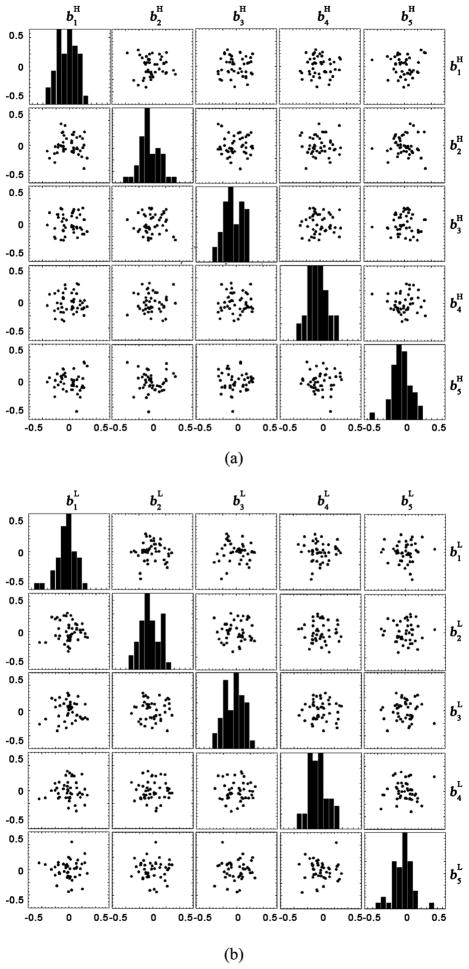
One basic assumption of the conditional Gaussian model is that both bH and bL follow multivariate Gaussian distributions. In order to verify this assumption, we inspected the distributions of the first five principal components of bH and bL in scatter plot matrices. Fig. 10(a) and (b) shows the scatter plots of bH and bL based on the 45 training subjects, respectively. In the nondiagonal blocks of the matrices, the joint distribution of two principal components is plotted. In the diagonal blocks, a histogram of each principal component is plotted. It can be observed that although the number of training subject is limited, the joint distributions and the histograms roughly follow 2D and 1-D Gaussian distributions, respectively. The plots also reveal that the number of training subjects is still not enough to support an obvious Gaussian distribution. Therefore, more training data is needed to improve the quality of the model.
Fig. 10.
(a) Distributions of the first five principal components of bH, based on the 45 training subjects. The non-diagonal blocks plot the joint distribution of every two principal components. The diagonal blocks plot the histogram of each principal component. (b) Distributions of the first five principal components of bL, plotted in the same way as (a).
Another assumption of the conditional Gaussian model is that there should be statistical correlations between the shapes of different organs. In order to verify this assumption, we plot the covariance matrix of different organs. Let v be the 1-D vector that lines-up the vertex coordinates of all organs
| (14) |
where
and similar for other organs. The correlation matrix of v was estimated based on the 45 training subjects and is plotted in Fig. 11. The pixels of the matrix stand for the correlations between every two elements of v. The bright diagonal line throughout the matrix means that every vertex has strong self-correlation. In order to mark the range of different organs, red lines are plotted to divide the matrix into sub-blocks. Each sub-block corresponds to the correlation between two organs. The brightness of the block represents the strength of inter-organ correlation. It can be observed that some sub-blocks demonstrate good inter-organ correlations, such as the heart vs. the lungs, and the spleen vs. the left kidney. Some organs correlate well with only part of other organs, such as the kidneys correlate well with part of the skeleton (the abdominal spine), and the right kidney correlates well with part of the liver (the right lobe). It is also interesting to see that the spleen and the kidneys have very strong self-correlations, meaning these organs have stronger inter-subject translations than the changing of sizes and shapes, because if a organ mainly performs translation without significantly changing the size or shape, the vertices of this organ will always move in similar directions and thus have strong correlations between each other.
Fig. 11.
Correlation matrix of the vertex coordinates of all organs. Each element of the matrix represents the correlation of two vertex coordinates (brighter element means higher correlation). The red lines are used to mark out the sub-blocks that represent the cross correlations of every two organs.
Footnotes
Color versions of one ore more of the figures in this paper are available online at http://ieeexplore.ieee.org.
Contributor Information
Hongkai Wang, Email: wang.hongkai@gmail.com, Crump Institute of Molecular Imaging, David Geffen School of Medicine, University of California, Los Angeles, CA 90066 USA.
David B. Stout, Crump Institute of Molecular Imaging, David Geffen School of Medicine, University of California, Los Angeles, CA 90066 USA.
Arion F. Chatziioannou, Email: archatziioann@mednet.ucla.edu, Crump Institute of Molecular Imaging, David Geffen School of Medicine, University of California, Los Angeles, CA 90066 USA.
References
- 1.Li H, Zhang H, Tang Z, Hu G. Micro-computed tomography for small animal imaging: Technological details. Prog Nat Sci. 2008 May;18:513–521. [Google Scholar]
- 2.Chow PL, Stout DB, Komisopoulou E, Chatziioannou AF. A method of image registration for small animal, multi-modality imaging. Phys Med Biol. 2006 Jan;51:379–390. doi: 10.1088/0031-9155/51/2/013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Franc BL, Acton PD, Mari C, Hasegawa BH. Small-animal SPECT and SPECT/CT: Important tools for preclinical investigation. J Nucl Med. 2008 Oct;49:1651–1663. doi: 10.2967/jnumed.108.055442. [DOI] [PubMed] [Google Scholar]
- 4.Schulz RB, Ale A, Sarantopoulos A, Freyer M, Soehngen E, Zientkowska M, Ntziachristos V. Hybrid system for simultaneous fluorescence and x-ray computed tomography. IEEE Trans Med Imag. 2010 Feb;29(2):465–473. doi: 10.1109/TMI.2009.2035310. [DOI] [PubMed] [Google Scholar]
- 5.Guo X, Liu X, Wang X, Tian F, Liu F, Zhang B, Hu G, Bai J. A combined fluorescence and microcomputed tomography system for small animal imaging. IEEE Trans Biomed Eng. 2010 Dec;57(12):2876–2883. doi: 10.1109/TBME.2010.2073468. [DOI] [PubMed] [Google Scholar]
- 6.Liu YWJ, Qu X, Li X, Ma X, Han R, Hu Z, Chen X, Sun D, Zhang R, Chen D, Chen D, Chen X, Liang J, Cao F, Tian J. In vivo quantitative bioluminescence tomography using heterogeneous and homogeneous mouse models. Opt Express. 2010;18:13102–13113. doi: 10.1364/OE.18.013102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Radu CG, Shu CJ, Nair-Gill E, Shelly SM, Barrio JR, Satyamurthy N, Phelps ME, Witte ON. Molecular imaging of lymphoid organs and immune activation by positron emission tomography with a new [18F]-labeled 2′-deoxycytidine analog. Nat Med. 2008 Jul;14:783–788. doi: 10.1038/nm1724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ritman EL. Micro-computed tomography of the lungs and pulmonary-vascular system,” in. Proc Am Thorac Soc. 2005 Dec;2:477–480. doi: 10.1513/pats.200508-080DS. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Garrison JC, Rold TL, Sieckman GL, Figueroa SD, Volkert WA, Jurisson SS, Hoffman TJ. In vivo evaluation and small-animal PET/CT of a prostate cancer mouse model using 64Cu bombesin analogs: Side-by-side comparison of the CB-TE2A and DOTA chelation systems. J Nucl Med. 2007 Aug;48:1327–1337. doi: 10.2967/jnumed.107.039487. [DOI] [PubMed] [Google Scholar]
- 10.Ford NL, Thornton MM, Holdsworth DW. Fundamental image quality limits for microcomputed tomography in small animals. Med Phys. 2003 Nov;30:2869–2877. doi: 10.1118/1.1617353. [DOI] [PubMed] [Google Scholar]
- 11.Willekens I, Lahoutte T, Buls N, Vanhove C, Deklerck R, Bossuyt A, de Mey J. Time-course of contrast enhancement in spleen and liver with Exia 160, Fenestra LC, and VC. Mol Imag Biol. 2009;11:128–135. doi: 10.1007/s11307-008-0186-8. [DOI] [PubMed] [Google Scholar]
- 12.Baiker M, Vastenhouw B, Branderhorst W, Reiber JHC, Beekman F, Lelieveldt BPF. Atlas-driven scan planning for high-resolution micro-SPECT data acquisition based on multi-view photographs: A pilot study. In: Miga MI, Wong KH, editors. Proc SPIE Medical Imaging 2009: Visualization, Image-Guided Procedures, and Modeling. 2009. pp. 72611L–8. [Google Scholar]
- 13.Wildeman MH, Baiker M, Reiber JHC, Lowik CWGM, Reinders MJT, Lelieveldt BPF. 2D/3D registration of micro-CT data to multi-view photographs based on a 3D distance map. Proc. 6th IEEE Int. Symp. Biomed. Imag.: From Nano to Macro; Boston, MA, USA. 2009. pp. 987–990. [Google Scholar]
- 14.Chaudhari AJ, Joshi AA, Darvas F, Leahy RM. A method for atlas-based volumetric registration with surface constraints for optical bioluminescence tomography in small animal imaging. In: Hsieh J, Flynn MJ, editors. Proc SPIE Medical Imaging 2007: Physics of Medical Imaging. 2007. pp. 651024–10. [Google Scholar]
- 15.Joshi AA, Chaudhari AJ, Li C, Dutta J, Cherry SR, Shat-tuck DW, Toga AW, Leahy RM. DigiWarp: A method for deformable mouse atlas warping to surface topographic data. Phys Med Biol. 2010 Oct;55:6197–6214. doi: 10.1088/0031-9155/55/20/011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Baiker M, Milles J, Dijkstra J, Henning TD, Weber AW, Que I, Kaijzel EL, Lowik CW, Reiber JH, Lelieveldt BP. Atlas-based whole-body segmentation of mice from low-contrast micro-CT data. Med Image Anal. 2010;14:723–737. doi: 10.1016/j.media.2010.04.008. [DOI] [PubMed] [Google Scholar]
- 17.Xiao D, Zahra D, Bourgeat P, Berghofer P, Tamayo OA, Green H, Gregoire MC, Salvado O. Mouse whole-body organ mapping by non-rigid registration approach,” in. Proc SPIE Medical Imaging 2011: Biomedical Applications in Molecular, Structural, and Functional Imaging. 2011:79650E–7. [Google Scholar]
- 18.Somayajula S, Joshi AA, Leahy RM. Mutual information based non-rigidmouse registration using a scale-space approach,” in. Proc IEEE Int Symp Biomed Imag. 2008:1147–1150. [Google Scholar]
- 19.Li X, Yankeelov TE, Peterson TE, Gore JC, Dawant BM. Automatic nonrigid registration of whole body CT mice images. Med Phys. 2008 Apr;35:1507–1520. doi: 10.1118/1.2889758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kovacevic N, Hamarneh G, Henkelman M. Anatomically guided registration of whole body mouse MR images. In: Ellis RE, Peters TM, editors. Proc Medical Image Computing and Computer-Assisted Intervention (MICCAI 2003) 2003. pp. 870–877. [Google Scholar]
- 21.Park H, Bland PH, Meyer CR. Construction of an abdominal probabilistic atlas and its application in segmentation. IEEE Trans Med Imag. 2003 Apr;22(4):483–492. doi: 10.1109/TMI.2003.809139. [DOI] [PubMed] [Google Scholar]
- 22.Isgum I, Staring M, Rutten A, Prokop M, Viergever MA, van Ginneken B. Multi-atlas-based segmentation with local decision fusion-application to cardiac and aortic segmentation in CT scans. IEEE Trans Med Imag. 2009 Jul;28(7):1000–1010. doi: 10.1109/TMI.2008.2011480. [DOI] [PubMed] [Google Scholar]
- 23.Ólafsdóttir H, Hansen M, Sjöstrand K, Darvann T, Hermann N, Oubel E, Ersbøll B, Larsen R, Frangi A, Larsen P, Perlyn C, Morriss-Kay G, Kreiborg S. Sparse statistical deformation model for the analysis of craniofacial malformations in the crouzon mouse. In: Ersbøll BK, Pedersen KS, editors. Proc Scandinavian Confe Image Anal (SCIA 2007) 2007. pp. 112–121. [Google Scholar]
- 24.Kovacevic N, Henderson JT, Chan E, Lifshitz N, Bishop J, Evans AC, Henkelman RM, Chen XJ. A three-dimensional MRI atlas of the mouse brain with estimates of the average and variability. Cereb Cortex. 2005 May;15:639–645. doi: 10.1093/cercor/bhh165. [DOI] [PubMed] [Google Scholar]
- 25.Barillot C, Haynor DR, Hellier P, Okuda H, Shkarin P, Behar K, Duncan JS, Papademetris X. Construction of a 3D volumetric probabilistic model of the mouse kidney from MRI,” in. Proc Medical Image Computing and Computer-Assisted Intervention (MICCAI 2004) 2004:1052–1054. [Google Scholar]
- 26.Kesner AL, Dahlbom M, Huang SC, Hsueh WA, Pio BS, Czernin J, Kreissl M, Wu HM, Silverman DHS. Semiautomated analysis of small-animal PET data. J Nucl Med. 2006 Jul;47:1181–1186. [PubMed] [Google Scholar]
- 27.Maroy R, Boisgard R, Comtat C, Jego B, Fontyn Y, Jan S, Dubois A, Trebossen R, Tavitian B. Quantitative organ time activity curve extraction from rodent PET images without anatomical prior. Med Phys. 2010 Apr;37:1507–1517. doi: 10.1118/1.3327454. [DOI] [PubMed] [Google Scholar]
- 28.Heimann T, Meinzer HP. Statistical shape models for 3D medical image segmentation: A review. Med Image Anal. 2009 Aug;13:543–563. doi: 10.1016/j.media.2009.05.004. [DOI] [PubMed] [Google Scholar]
- 29.Iglesias JE, de Bruijne M. Semiautomatic segmentation of vertebrae in lateral x-rays using a conditional shape model. Acad Radiol. 2007 Oct;14:1156–1165. doi: 10.1016/j.acra.2007.06.003. [DOI] [PubMed] [Google Scholar]
- 30.Suckow C, Stout D. MicroCT liver contrast agent enhancement over time, dose, and mouse strain. Mol Imag Biol. 2008;10:114–120. doi: 10.1007/s11307-007-0128-x. [DOI] [PubMed] [Google Scholar]
- 31.Suckow C, Kuntner C, Chow P, Silverman R, Chatziioannou A, Stout D. Multimodality rodent imaging chambers for use under barrier conditions with gas anesthesia. Mol Imag Biol. 2009;11:100–106. doi: 10.1007/s11307-008-0165-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Delingette H. General object reconstruction based on simplex meshes. Int J Comput Vis. 1999;32:111–146. [Google Scholar]
- 33.Kohli P, Torr PHS. Efficiently solving dynamic Markov random fields using graph cuts,” in. Proc IEEE Int Conf Comput Vis (ICCV 05) 2005:922–929. [Google Scholar]
- 34.Boykov Y, Kolmogorov V. An experimental comparison of min-cut/max- flow algorithms for energy minimization in vision. IEEE Trans Pattern Anal Mach Intell. 2004 Sep;26(9):1124–1137. doi: 10.1109/TPAMI.2004.60. [DOI] [PubMed] [Google Scholar]
- 35.William EL, Harvey EC. Marching cubes: A high resolution 3D surface construction algorithm,” in. Proc Comput Graphics Interactive Techn (SIGGRAPH 87) 1987:163–169. [Google Scholar]
- 36.Michael G, Paul SH. Surface simplification using quadric error metrics,” in. Proc Comput Graphics Interactive Tech (SIGGRAPH 97) 1997:209–216. [Google Scholar]
- 37.Bing J, Vemuri BC. A robust algorithm for point set registration using mixture of Gaussians,” in. Proc IEEE Int Conf Comput Vis (ICCV 2005) 2005:1246–1251. doi: 10.1109/ICCV.2005.17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bookstein FL. Shape and the information in medical images: A decade of the morphometric synthesis. Comput Vis Image Understand. 1997;66:97–118. [Google Scholar]
- 39.Bosc M, Heitz F, Armspach J-P. Statistical atlas-based sub-voxel segmentation of 3D brain MRI,” in. Proc IEEE Int Conf Image Process (ICIP 03) 2003 Sep;:1077. [Google Scholar]
- 40.Neumann A, Lorenz C. Statistical shape model based segmentation of medical images. Comput Med Imag Graph. 1998 Mar-Apr;22:133–143. doi: 10.1016/s0895-6111(98)00015-9. [DOI] [PubMed] [Google Scholar]
- 41.Bookstein FL. Landmark methods for forms without landmarks: Localizing group differences in outline shape,” in. Proc Math Methods in Biomed Image Anal (MMBIA 19 ) 1996:279–289. doi: 10.1016/s1361-8415(97)85012-8. [DOI] [PubMed] [Google Scholar]
- 42.Hotelling H. Analysis of a complex of statistical variables into principal components. J Educ Psychol. 1933;24:498–520. [Google Scholar]
- 43.Thresholding using the ISODATA clustering algorithm. IEEE Trans Syst Man Cybern. 1980 Nov;10(11):771–774. [Google Scholar]
- 44.Chui HL, Rangarajan A. A new point matching algorithm for non-rigid registration. Comput Vis Image Understand. 2003 Feb-Mar;89:114–141. [Google Scholar]
- 45.Lorenzo-Valdes M, Sanchez-Ortiz GI, Elkington AG, Mohiaddin RH, Rueckert D. Segmentation of 4D cardiac MR images using a probabilistic atlas and the EM algorithm. Med Image Anal. 2004 Sep;8:255–265. doi: 10.1016/j.media.2004.06.005. [DOI] [PubMed] [Google Scholar]
- 46.Casteels C, Vermaelen P, Nuyts J, Van Der Linden A, Baekelandt V, Mortelmans L, Bormans G, Van Laere K. Construction and evaluation of multitracer small-animal PET probabilistic atlases for voxel-based functional mapping of the rat brain. J Nucl Med. 2006 Nov;47:1858–1866. [PubMed] [Google Scholar]
- 47.Stout D, Chatziioannou A, Lawson T, Silverman R, Gambhir S, Phelps M. Small animal imaging center design: The facility at the UCLA Crump Institute for Molecular Imaging. Mol Imag Biol. 2005;7:393–402. doi: 10.1007/s11307-005-0015-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Segars WP, Tsui BMW, Frey EC, Johnson GA, Berr SS. Development of a 4-D digital mouse phantom for molecular imaging research. Mol Imag Biol. 2004 May-Jun;6:149–159. doi: 10.1016/j.mibio.2004.03.002. [DOI] [PubMed] [Google Scholar]
- 49.Dogdas B, Stout D, Chatziioannou AF, Leahy RM. Digi-mouse: A 3D whole body mouse atlas from CT and cryosection data. Phys Med Biol. 2007 Feb;52:577–587. doi: 10.1088/0031-9155/52/3/003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Stout D, Chow P, Silverman R, Leahy RM, Lewis X, Gambhir S, Chatziioannou A. Creating a whole body digital mouse atlas with PET, CT and cryosection images. Mol Imag Biol. 2002;4:S27. [Google Scholar]
- 51.Koikkalainen J, Tolli T, Lauerma K, Antila K, Mattila E, Lilja M, Lotjonen J. Methods of artificial enlargement of the training set for statistical shape models. IEEE Trans Med Imag. 2008 Nov;27(11):1643–1654. doi: 10.1109/TMI.2008.929106. [DOI] [PubMed] [Google Scholar]
- 52.Badea CT, Wetzel AW, Mistry N, Pomerantz S, Nave D, Johnson GA. Left ventricle volume measurements in cardiac micro-CT: The impact of radiation dose and contrast agent. Comput Med Imag Graph. 2008 Apr;32:239–250. doi: 10.1016/j.compmedimag.2007.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Driehuys B, Nouls J, Badea A, Bucholz E, Ghaghada K, Petiet A, Hedlund LW. Small animal imaging with magnetic resonance microscopy. Ilar J. 2008;49:35–53. doi: 10.1093/ilar.49.1.35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Gorczowski K, Styner M, Jeong JY, Marron JS, Piven J, Hazlett HC, Pizer SM, Gerig G. Multi-object analysis of volume, pose, and shape using statistical discrimination. IEEE Trans Pattern Anal Mach Intell. 2010 Apr;32(4):652–661. doi: 10.1109/TPAMI.2009.92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Tsai A, Wells W, Tempany C, Grimson E, Willsky A. Mutual information in coupled multi-shape model for medical image segmentation. Med Image Anal. 2004 Dec;8:429–445. doi: 10.1016/j.media.2004.01.003. [DOI] [PubMed] [Google Scholar]
- 56.Okada T, Yokota K, Hori M, Nakamoto M, Nakamura H, Sato Y. Construction of hierarchical multi-organ statistical atlases and their application to multi-organ segmentation from CT images. In: Metaxas D, Axel L, Fichtinger G, Székely G, editors. Proc Medical Image Computing and Computer-Assisted Intervention (MICCAI 2008) 2008. pp. 502–509. [DOI] [PubMed] [Google Scholar]
- 57.Khmelinskii A, Baiker M, Kaijzel EL, Chen J, Reiber JH, Lelieveldt BP. Articulated whole-body atlases for small animal image analysis: Construction and applications. Mol Imag Biol. 2011;13:898–910. doi: 10.1007/s11307-010-0386-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Xiao D, Zahra D, Bourgeat P, Berghofer P, Tamayo OA, Wimberley C, Gregoire MC, Salvado O. An accurate 3D shape context based non-rigid registration method for mouse whole-body skeleton registration. In: Dawant BM, Haynor DR, editors. Proc SPIE Medical Imaging 2011: Image Processing. 2011. pp. 79620V–10. [Google Scholar]
- 59.Xiao D, Zahra D, Bourgeat P, Berghofer P, Tamayo OA, Wimberley C, Gregoire MC, Salvado O. An improved 3D shape context based non-rigid registration method and its application to small animal skeletons registration. Comput Med Imag Graph. 2010 Jun;34:321–332. doi: 10.1016/j.compmedimag.2009.12.003. [DOI] [PubMed] [Google Scholar]
- 60.Linguraru MG, Sandberg JK, Li ZX, Shah F, Summers RM. Automated segmentation and quantification of liver and spleen from CT images using normalized probabilistic atlases and enhancement estimation. Med Phys. 2010 Feb;37:771–783. doi: 10.1118/1.3284530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Zhou XR, Kitagawa T, Hara T, Fujita H, Zhang XJ, Yokoyama R, Kondo H, Kanematsu M, Hoshi H. Constructing a probabilistic model for automated liver region segmentation using non-contrast X-ray torso CT images,” in. Proc Med Image Computing Computer-Assisted Intervent (MICCAI 2006) 2006;(Pt 2):856–863. doi: 10.1007/11866763_105. [DOI] [PubMed] [Google Scholar]
- 62.Okada T, Shimada R, Hori M, Nakamoto M, Chen YW, Naka-mura H, Sato Y. Automated segmentation of the liver from 3D CT images using probabilistic atlas and multilevel statistical shape model. Acad Radiol. 2008 Nov;15:1390–1403. doi: 10.1016/j.acra.2008.07.008. [DOI] [PubMed] [Google Scholar]
- 63.Okada T, Yokota K, Hori M, Nakamoto M, Nakamura H, Sato Y. Construction of hierarchical multi-organ statistical atlases and their application to multi-organ segmentation from CT images,” in. Proc Med Image Comput Computer-Assist Intervent (MICCAI 2008) 2008:502–509. doi: 10.1007/978-3-540-85988-8_60. [DOI] [PubMed] [Google Scholar]
- 64.Shimizu A, Kimoto T, Kobatake H, Nawano S, Shinozaki K. Automated pancreas segmentation from three-dimensional contrast-enhanced computed tomography. Int J CARS. 2010;5:85–98. doi: 10.1007/s11548-009-0384-0. [DOI] [PubMed] [Google Scholar]
- 65.Liu X, Linguraru M, Yao J, Summers R. Organ pose distribution model and an MAP framework for automated abdominal multi-organ localization. In: Liao H, Edwards P, Pan X, Fan Y, Yang G-Z, editors. Proc Medical Imaging and Augmented Reality (MIAR 2010) 2010. pp. 393–402. [Google Scholar]