Abstract
Recent whole-genome approaches to microbial phylogeny have emphasized partitioning genes into functional classes, often focusing on differences between a stable core of genes and a variable shell. To rigorously address the effects of partitioning and combining genes in genome-level analyses, we developed a novel technique called Random Addition Concatenation Analysis (RADICAL). RADICAL operates by sequentially concatenating randomly chosen gene partitions starting with a single-gene partition and ending with the entire genomic data set. A phylogenetic tree is built for every successive addition, and the entire process is repeated creating multiple random concatenation paths. The result is a library of trees representing a large variety of differently sized random gene partitions. This library can then be mined to identify unique topologies, assess overall agreement, and measure support for different trees. To evaluate RADICAL, we used 682 orthologous genes across 13 cyanobacterial genomes. Despite previous assertions of substantial differences between a core and a shell set of genes for this data set, RADICAL reveals the two partitions contain congruent phylogenetic signal. Substantial disagreement within the data set is limited to a few nodes and genes involved in metabolism, a functional group that is distributed evenly between the core and the shell partitions. We highlight numerous examples where RADICAL reveals aspects of phylogenetic behavior not evident by examining individual gene trees or a “‘total evidence” tree. Our method also demonstrates that most emergent phylogenetic signal appears early in the concatenation process. The software is freely available at http://desalle.amnh.org.
Keywords: cyanobacteria, concatenation, core, shell, emergent phylogenetic support
Introduction
In recent years, debates over the feasibility of the Tree of Life (TOL) have taken center stage in the phylogenetic research community (Ciccarelli et al. 2006; Bapteste et al. 2008). With respect to the prokaryotic portion of this tree, evidence for horizontal gene transfer (HGT) has polarized this debate (Bapteste et al. 2009; Degnan and Rosenberg 2009). One central issue is how best to combine information from individual genes that may have divergent histories or whether to combine them at all. The practice of concatenating gene alignments to generate a putative species tree (Lerat et al. 2003, 2005; Susko et al. 2006) has yielded important insights into microbial evolution, and many researchers agree that even in the face of HGT, prokaryotic data sets often have a “central tendency” (Bapteste et al. 2008).
A perceived drawback of the concatenation method is the expectation that the process yields a single definitive tree despite high levels of homoplasy and rampant incongruence among individual gene trees (Kubatko and Degnan 2007). This problem is exacerbated for large genomic data sets containing hundreds, or thousands, of genes (Rokas and Carroll 2006). Opponents of concatenation have pointed out that the concatenated tree could be spurious, unreflective of underlying diversity, and supported by inflated bootstrap values (Degnan and Rosenberg 2006). But concatenation is more than the sum of its parts. Proponents maintain that concatenated data can draw out mutually reinforcing (or conflicting) character states that amplify one another's historical signal in an emergent phenomenon known as hidden support (or conflict) (Gatesy et al. 1999; Gatesy and Baker 2005). This is especially important when a small gene size limits the amount of phylogenetic information available to resolve relationships among a large number of taxa (Castresana 2007; Rasmussen and Kellis 2007; Galtier and Daubin 2008). Overall, hidden support's signal amplification is expected to minimize the effects of HGT and noise. Methods that probe the dynamics of concatenation at intermediate stages may provide a perspective that illuminates the benefits of emergent support while avoiding the tyranny of “total evidence” (TE; Kluge 1997).
Another major question in concatenation analyses is which of the many genes in a genome should be concatenated. Numerous studies emphasize the need to find a stable core of genes with mostly congruent historical signal present in most or all taxa under investigation (Makarova et al. 1999; Charlebois and Doolittle 2004; Shi and Falkowski 2008; Tang et al. 2010). Pursuing core genes is expected to isolate vertical phylogenetic signal from the noise present in a set of shell genes that are more readily exchanged among bacteria. Some researchers have searched for the core by probing genomes for genes with similar or congruent information (Brochier et al. 2002; Ciccarelli et al. 2006), others have suggested that genes involved in complex cellular machinery, such as information processing genes that code for components comprising transcriptional and translational macromolecular complexes, are more likely to be refractory to HGT (Rivera et al. 1998; Jain et al. 1999; Daubin et al. 2002). Disparate approaches to identifying the core have arrived at the same or a similar set of genes dominated by ribosomal proteins. Thus, phylogenies from these techniques often agree. However, it is not clear what effect excluding shell genes has on phylogenetic inference, and the shell is rarely analyzed on its own.
Here, we introduce a technique called Random Addition Concatenation Analysis (RADICAL), a method that generates a library of trees along a set of random concatenation chains varying from one gene to whole-genome concatenation. RADICAL catalogs tree heterogeneity while allowing for emergent support through concatenation. Moreover, RADICAL monitors the dynamics of concatenation by calculating support statistics for candidate test topologies assessed against the library of trees.
To evaluate RADICAL, we chose the cyanobacterial clade, an ancient and diverse microbial phylum that through oxygenic photosynthesis was likely responsible for the oxidation of the early atmosphere (Blankenship and Hartman 1998; Whitton and Potts 2000). As with many microbial groups, phylogenetic relationships among the cyanobacteria are challenging because of substantial incongruence due in part to HGT (Ochman et al. 2000; Nakamura et al. 2004). In an attempt to overcome some of the difficulties presented by gene tree diversity, Shi and Falkowski (2008) conducted an analysis aimed at selecting genes with similar evolutionary histories. Using principle component analysis to differentiate congruent partitions, the authors identified 323 core genes of a total of 682 fully represented orthologs across 13 sequenced cyanobacterial genomes. Here, we show that when RADICAL is applied to genomic data from the cyanobacteria, random concatenation chains converge quickly on stable relationships for the majority of nodes. Moreover, with respect to the core versus shell distinction proposed by Shi and Falkowski (2008), we find that the shell genes recover the core topology with greater efficiency than the core itself. Examination of the concatenation path and associated statistics highlight examples where RADICAL reveals patterns not immediately obvious from either the individual gene tree or the TE approach. In addition, we explore gene partitions based on broad functional categories and show that these are mostly in agreement—with some notable exceptions. Finally, we present evidence that hidden support does emerge on concatenation and that this support builds early in the concatenation process.
Materials and Methods
Random Addition Concatenation Analysis
RADICAL creates a user-defined number of random partition concatenation paths. Each concatenation path consists of a chain of sequentially added gene partitions in which no gene is included more than once (fig. 1A). Every path ends with a total concatenation of all of the genes in the data set, which we refer to as the TE data set. At select points along these chains, RADICAL calculates trees representing the data concatenated to that point, creating a library of phylogenetic trees. The average level of topological agreement between this set of trees and a reference topology is calculated at each concatenation point and then plotted across the entire concatenation path. The resulting curve provides a summary of how topological support, relative to the reference topology, builds during the concatenation process. Because inference of large numbers of trees at numerous concatenation points can be computationally demanding (especially for phylogenetic reconstruction methods relying on probabilistic inference, such as maximum likelihood [ML] and Bayesian inference), RADICAL allows the user to sample along the concatenation path using a step function that corresponds to a set number of genes. For instance, if this function is set to one, then individual genes are added to each concatenation step, but if the function is set to ten, then ten genes are added to each concatenation point before a tree is recalculated. Stepping through the chains while controlling the total number of chains constructed gives the user the ability to sample the dynamics of concatenation with great depth in cases where tree inference is computationally easy or reduce the number of trees sampled for challenging data or demanding phylogenetic methods.
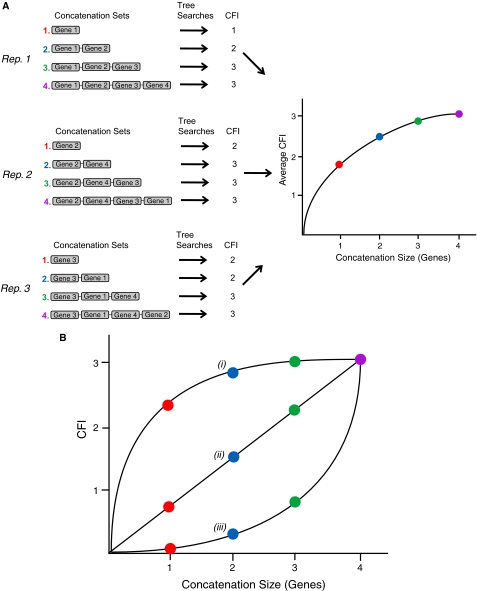
FIG. 1.—
RADICAL diagram. (A) A schematic of the RADICAL pipeline is shown for a hypothetical data set containing six taxa, four genes, and three concatenation randomizations. Starting with a single gene, concatenation sets are created by randomly adding a single gene to the existing data set. Each gene appears only once in any given randomization. Tree searches are conducted for each concatenation set. Therefore, for the three randomizations illustrated here, RADICAL produces a total of 12 trees. The Consensus Fork Index (CFI), which measures the number of nodes in common between the randomization tree and a reference topology, is calculated for all trees generated for each concatenation set. The CFI values across all randomizations for a concatenation set of a specific size (e.g., three genes) are averaged together and plotted relative to concatenation size. In this example, the concatenation interval is a single gene, but RADICAL can generate average CFI curves based on concatenation intervals of any size. For example, if the concatenation interval is five, then five genes are randomly added to the concatenation set in between each tree search step. (B) The RADICAL curve visualizes the conflict/agreement of the tree population with some reference tree. In this case, the reference tree is taken from TE. The population of trees at each concatenation point is compared with the TE tree using the CFI. In the case of a six taxa tree, once all four genes are concatenated, comparison to TE will yield a CFI value of three, the fixation point. However, the path to the fixation point will depend on the phylogenetic consistency of the data set. In (i), the tree library is highly consistent with TE: at the single-gene stage, over 2 TE tree nodes, on average, are already recovered in the tree population. However, in (iii) less than one TE node, on average, is recovered even after three random partition additions. By definition, curve (iii) accelerates to the fixation point because comparisons are being made to the TE tree. Curve (ii) illustrates intermediate RADICAL behavior. The area under the RADICAL curve (AUC) provides a convenient overall measure of the data set's support for the tree hypothesis in question. The concatenation point at which a given tree hypothesis either fixes in the population (fixation point) or disappears completely (degradation point), is also a useful measure of support/congruence.
For all the trees generated at each concatenation point, RADICAL compiles a list of all the unique topologies within that sample and calculates the average Consensus Fork Index (CFI) (Colless 1980) between this set of trees and a reference topology. The normalized CFI measures the number of identical nodes between any two topologies divided by the maximum number of nodes possible in either tree and provides a straightforward measure of concordance among all topologies created during the RADICAL process. It also is consistent with other common measures of tree support, such as the bootstrap (Felsenstein 1985) and jackknife (Farris et al. 1996), that express support as the percentage that a given node is present in a sample of trees. A normalized CFI varies between 0 and 1, where 0 indicates trees with no nodes in common and 1 where all nodes are identical. To create a “RADICAL curve,” the average CFI that is calculated at each concatenation point is then plotted along the entire concatenation path from individual gene trees to the TE tree (fig. 1). The RADICAL curve visualizes the dynamics of concatenation and can be used to measure the extent of agreement between the data matrix and a chosen topology. When a hypothesis is generally well supported by the data set, the RADICAL curve is convex, often quickly approaching a fixation point after which all subsequent trees mirror the reference topology. But if the data set is composed of numerous genes that are incongruent with the reference topology, the curve will be linear or even concave (fig. 1B).
Generating a RADICAL curve may require a large number of tree searches and considerable computational investment depending on the data set size and concatenation interval. In order to mitigate some of the computational burden, RADICAL is designed to terminate its tree searches once the trees have consistently converged on the reference topology. RADICAL monitors the percentage of randomizations that produce the maximum CFI among all the randomizations at a given concatenation point and will terminate the search when this percentage is above a user-specified amount for a user-specified number of consecutive concatenation intervals. For example, if the user sets the percentage cutoff at 95% for five concatenation intervals, then RADICAL will stop searching once 95% of the randomizations produce the TE tree for five consecutive concatenation intervals. Because CPU requirements related to tree searches increase linearly with concatenation size (supplementary fig. S1, Supplementary Material online), the tree searches for the largest concatenation points are the most computationally demanding. Therefore, even RADICAL runs that are terminated near the end of the complete concatenation path can substantially reduce the overall computational requirements of the analysis.
In addition to measuring overall topological similarity, RADICAL can assess the presence/absence of individual nodes in the concatenation trees and plot the frequency of a node's occurrence along numerous concatenation paths. RADICAL counts the number of times a given node appears in all the trees at a given concatenation point and calculates the average level of occurrence across all these randomizations. This value is then plotted on a graph in which the y axis represents the average frequency of occurrence on a scale of 0–1 (0: the node never appeared in any of the randomized data sets and 1: the node appeared in all the randomized data sets) and the x axis represents the concatenation path from smaller concatenation steps to TE.
Using these topology-based and node-based curves, RADICAL produces two measures of overall tree and branch support. First, the program estimates the total proportion of concatenation space occupied by a tree or node as the area under the RADICAL curve (AUC). RADICAL curves are transformed such that the number of partitions at each point is expressed as a fraction of the total available. For relationships strongly supported by the data, the theoretical maximum for the area under the RADICAL curve (AUC) is one. The theoretical minimum is zero. The integration procedure does not model mathematical functions because the concatenation dynamics can be complex and unpredictable. Instead we used the empirical data, approximating the AUC using trapezoidal integration. In cases where a large step function lowers the resolution of the chain sample, RADICAL employs a LOESS curve (Cleveland 1979) averaging technique in R (http://www.r-project.org) and infers points from a local nonlinear regression.
The second measure of support provided by RADICAL involves calculating the number of partitions at which a given topology or node either becomes fixed or disappears in the concatenation population: referred to here as fixation and degradation points, respectively. This measure can be computed either for the entire tree or for the individual nodes. A fixation point describes the minimum number of genes required to always recover that tree or node. For instance, if the fixation point for a tree or node is 30, then any combination of 30 genes randomly selected from the overall data set produces the tree or node of interest. Similarly, the degradation point describes the minimum number of genes needed to ensure that a given tree or node does not appear in any random selection of that size.
RADICAL is written in Perl and employs external phylogenetic reconstruction programs, such as RAxML (Stamatakis 2006), GARLI (Zwickl 2006), or PAUP (Swofford 2003). It is enabled for parallel handling of tree-building jobs across a cluster that uses the Sun Grid Engine for job scheduling and submission or on multicore architectures and can also be used serially on a laptop or desktop computer. The software is freely available under a GNU General Public License at http://desalle.amnh.org. Though we chose ML here, it is possible to use RADICAL with other phylogenetic optimality criteria, such as parsimony and Bayesian inference. Some of the computational requirements associated with a RADICAL analysis are presented in supplementary figure S1 (Supplementary Material online).
The Cyanobacterial Data Matrix
We conducted a RADICAL analysis using an alignment of 13 cyanobacterial genomes provided by Shi and Falkowski (2008). In their study, an all-against-all BLAST (Altschul et al. 1997) was mined for reciprocal best hits using an E value cutoff of 1 × 10−4. The final matrix is composed of 682 orthologous groups (192,464 characters) containing only one gene per genome and no missing data (supplementary data S1, Supplementary Material online). Throughout our analysis, we employed the core and shell gene supergroups as defined by Shi and Falkowski (2008) and maintained the Cluster of Orthologous Groups (COGs) (Tatusov et al. 2001) functions they assigned to the 682 genes.
In order to generate the RADICAL curves for the cyanobacterial data set, we ran 100 randomized chains. To assess the effect of sampling density, we also sampled from select concatenation points using 500 randomized chains (supplementary fig. S2, Supplementary Material online). We sampled at the first gene on the chain and every five partitions thereafter until reaching TE for a total of 13,800 trees. ML trees at each concatenation step were generated with the fine-grained parallel Pthreads (POSIX Threads Library) build of RAxML v7.2.6–7.2.8 (Stamatakis 2006; Stamatakis and Ott 2008) using the JTT amino acid substitution matrix (Jones et al. 1992), empirical amino acid residue frequencies, and among-site rate heterogeneity modeled with the Γ distribution and four discrete rate categories (Yang 1994) (exact RAxML search parameters: -T 1 -m PROTGAMMAJTTF -f d -N 1 -o GVI). Model parameters were chosen to be consistent with the analysis conducted by Shi and Falkowski (2008). We built RADICAL curves and calculated RADICAL statistics for seven data classes: all genes; core and shell as defined by Shi and Falkowski (2008); and the COG superclassifications' cellular processes, information processing, metabolism, and unknown. Using the CFI-based metrics, the concatenation dynamics of each data type were assessed relative to the core species tree specified in Shi and Falkowski (2008) A few alternative nodes that appear in a high proportion of individual gene trees were also used as reference nodes in the RADICAL analysis.
Bootstrap Support
Branch support was assessed with 500 nonparametric bootstrap pseudoreplicates (BS) (Felsenstein 1985) and 500 rapid nonparametric bootstrap pseudoreplicates (RBS) in the case of highly repetitive and time-consuming tasks, such as for all individual gene tree searches (Stamatakis and Ott 2008). We employed the so-called bootstrap convergence criteria of Pattengale et al. (2010) and found that in the vast majority of the data sets, more than 50 bootstrap pseudoreplicates would not alter branch support, that is, 50 would be enough, with the exception of core and metabolism partitions, where 250 and 450 pseudoreplicates would be the necessary. All ML tree searches started with an initial maximum parsimony tree built with a stepwise taxon addition process; in the case of the complete and function-partitioned data sets, we launched ten independent ML searches and chose the best for ML score and branch length refinement. The full data set was also subjected to a single-gene ML analysis, where each of the 682 protein partitions was allowed to evolve under a different among-site rate heterogeneity model and distinct branch lengths later proportionally averaged across all partitions for the full data set ML tree. Branch support is shown by filtering the tree topology of interest through the swarm of BS/RBS trees, thus displaying the percent proportion of BS/RBS trees that contain a given node.
Measuring Emergent Support
RADICAL is not limited to measuring topological congruence along the concatenation process but can also track changes in support and incongruence for different characters and partitions along the concatenation path. In this analysis, we examined the concatenation dynamics of a likelihood support (LS) (Lee and Hugall 2003) measure normalized by the size of the data set. LS calculates the difference in negative log-likelihood scores between a tree in which a given node is constrained to exist and a tree in which the same node is constrained not to exist. A large positive value indicates the node is well supported and a negative value indicates the node does not appear in the best-known ML tree. If all the genes in an analysis support a node the value of LS will likely increase as genes are concatenated together. In order to normalize LS by the size of the data set, we divided the measure by the maximum negative log-likelihood score for that data set. The maximum negative log-likelihood score scales linearly with concatenation size (supplementary fig. S3, Supplementary Material online). This normalized LS (LSn) score was used to evaluate the presence of emergent support during the concatenation process. If there is no emergent support, we expect LSn to remain unchanged during the concatenation process. However, if LSn increases as genes are concatenated this suggests there is emergent support for that node because support is increasing beyond what we would be expect as data set size increases. We used GARLI v1.0 (Zwickl 2006) in the calculation of this statistic because RAxML does not implement negative constraints. GARLI model parameters were identical to those used in our RAxML analysis. To front weight our calculation of support statistics, we used a base-two exponential sampling distribution: in addition to the initial state (1 partition), we sampled submatrices at 2, 4, 8, 16, 32, 64, and 128 partitions for our LS calculations. Beyond 128 partitions, deriving LS statistics is too computationally demanding.
Results and Discussion
RADICAL at the Tree Level: Is the Core Really a Core?
RADICAL is a technique that can be used to dissect complex phylogenomic patterns by probing the phylogenetic signal garnered through stepwise concatenation from the smallest data sets through the largest (fig. 1; for an in depth description, see Materials and Methods). We applied the method to a cyanobacteria data set comprised of 682 fully represented orthologs across 13 species (Shi and Falkowski 2008). Shi and Falkowski (2008) divided these genes into a stable core of genes that have similar phylogenetic signal and therefore could be combined to generate a species tree, and a variable shell containing the remaining genes that are characterized by increased HGT and more rapid rates of protein evolution. We conducted a combined ML analysis of all 682 genes that produced a topology (fig. 2A) identical to the core tree from Shi and Falkowski (2008; T3 in fig. 2). This tree (also referred to as T3 in this paper) was used as the reference topology for the RADICAL analysis.
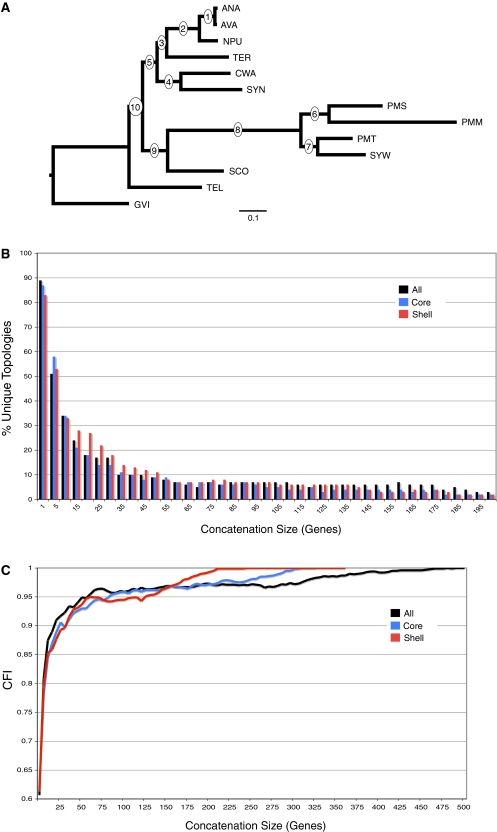
FIG. 2.—
RADICAL analysis of cyanobacterial data set. (A) T3 reference tree used as the basis for the CFI calculation. The ML tree was calculated from a concatenated data set of 682 genes, and the topology is identical to the T3 tree presented in Shi and Falkowski (2008). Circles at the nodes provide the reference numbers used throughout the text. Species abbreviations are as follows: ANA—Anabeana sp. PCC7120, AVA—Anabeana variabilis, NPU—Nostoc punctiforme, TER—Trichodesmium erythraeum, CWA—Crocosphaera watsonii, SYN—Synechocystis sp. PCC6803, PMS—Prochlorococcus marinus SS120, PMM—P. marinus MED4, PMT—P. marinus MIT9313, SYW—Synechococcus sp. WH8102, SCO—Synechococcus elongatus, TEL—Thermosynechococcus elongatus, GVI—Gloeobacter violaceus. (B) A histogram of the number of unique topologies among the 100 randomized concatenation sets at each concatenation size. Frequencies were calculated for all sets up to a concatenation size of 682, but only concatenation sets of 200 or less are displayed in the histogram. (C) RADICAL curves for data sets comprising all the data, the core genes and the shell genes. The CFI indicates the proportion of all the nodes in the T3 reference tree that occur in the concatenation set tree. At each concatenation size, 100 random sets of that size are generated to calculate an average CFI score. When a curve asymptotes at a CFI of 1, then all the trees in the randomized sets are identical to T3. All partitions maintained an average CFI of 1 for concatenation set sizes between 500 and 682.
Shi and Falkowski (2008) found a high degree of topological incongruence among the 682 gene trees generated in their study. Less than 2% of the gene trees were fully congruent with the T3 topology. Despite this high level of disagreement, RADICAL analysis reveals that the topological diversity rapidly diminishes during concatenation (fig. 2B). At the individual gene tree level, 89% of all genes have a unique topology. However, random concatenation sets comprised 20 genes yield only 20 unique trees, and this number drops to seven unique trees when 60 genes are analyzed together. The RADICAL curves also highlight that topologies for any combination of genes quickly approach the core topology during concatenation (fig. 2C). This trajectory is dramatically different than the behavior exhibited by randomly permuted data (supplementary fig. S4, Supplementary Material online). Individual gene trees share an average of 61% of their nodes with the T3 topology, but this value rises to 88% topological similarity for any combination of ten genes. Despite this rapid ascent, a substantial portion of the entire data set (490 genes) is required before the concatenation process fixes on T3.
The most striking pattern revealed by the RADICAL analysis is the similarity in concatenation dynamics between the core and shell genes. Contrary to the distinction made by Shi and Falkowski (2008), the shell genes converge on the T3 topology more rapidly than do the core genes. All 100 random combinations of 245 shell genes produced the T3 tree when combined, whereas 310 core genes are required to produce the T3 tree in all 100 randomizations. To establish whether this difference resulted from limited sampling of the concatenation space, we generated 500 additional randomizations at 100-gene concatenation intervals for the core, shell, and all partitions (supplementary file S3, Supplementary Material online). The average percent difference in CFI estimates between the 100 randomization and the 500 randomization sampling schemes was very small (0.5%), suggesting the difference in the concatenation dynamics of the shell and core genes is not an artifact of sampling effects. In terms of the number of phylogenetically informative characters (PICs), the shell genes (154 PICs) are slightly larger, on average, than the core genes (134 PICs), but if the RADICAL curves are plotted relative to the total number of PICs at each concatenation interval, the shell genes still reach fixation sooner than the core genes. The average AUC for 100 replicates in the shell is 0.966, whereas the average AUC for the core is 0.956. The distribution of unique topologies is also similar between the core and the shell genes (fig. 2B). T3 accounts for 76.2% of all shell topologies generated during RADICAL, whereas only 66.6% of the core topologies are identical to T3.
Branch Support
Given the large number of genes required to produce the T3 topology in all random concatenation paths, it is likely that a few nodes on the tree are characterized by weak support. Bootstrap resampling of the entire data set, however, produces strong support values (100%) for all the nodes on the tree (fig. 3A). RADICAL assesses nodal support by calculating the number of genes required to recover that node in all random concatenation paths and the percentage of total concatenation space in which a given node is recovered (AUC values). These values, and their associated RADICAL curves, are presented in figure 3 and reveal several instances in which RADICAL uncovers differences not evident from bootstraps or analysis of individual gene trees (supplementary data S2, Supplementary Material online). For instance, both nodes 5 and 3 occur in similar frequencies in the individual gene trees (0.356 and 0.361, respectively) and have bootstrap values of 100% but substantially different RADICAL support values. Node 5 becomes fixed for any concatenation set larger than 60 genes, whereas node 3 requires 225 genes before it occurs in all the concatenation paths. Similarly, node 7 appears in 57.8% of the individual gene trees and node 9 appears in 45.6% of the individual gene trees, but these values provide little indication of their support during concatenation. Node 9 reaches fixation quickly, occurring in every concatenation set larger than 35 genes, but node 7 requires 490 genes before becoming fixed. Overall, the RADICAL support values clearly identify nodes 3, 7, and 10 as problematic (fig. 3) and provide greater sensitivity for assessing relative branch support than do bootstraps or summation of gene tree occurrences.
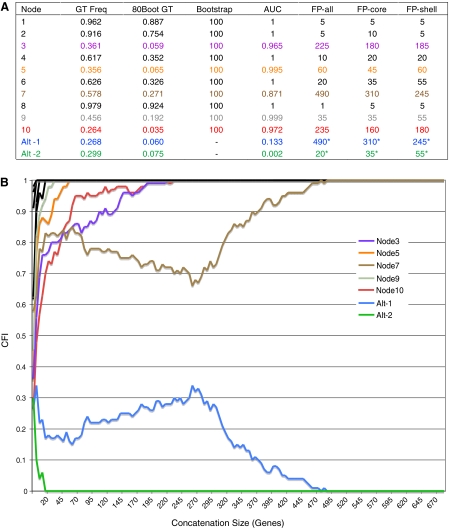
FIG. 3.—
RADICAL analysis of nodal support. (A) “GT Freq” provides the percentage of gene trees in which a given node occurs and “80Boot GT” provides the percentage of gene trees in which a given node occurs with greater than 80% bootstrap. The “Bootstrap” column indicates the bootstrap value at the node for an ML analysis of all 682 genes concatenated together. “AUC” measures the area under the RADICAL curves (for details, see Materials and Methods) and indicates the total proportion of concatenation space in which a given node occurs. The “FP” columns indicate the fixation points for each node measured as the concatenation size at which a given node appears in all 100 randomizations. The metric is calculated for all the genes, the core set and the shell set. Asterisks indicate a degradation point, which is defined as the gene size at which a node never occurs. Node numbers refer to number on the tree in figure 2A. Node Alt-1 defines a relationship uniting PMS, PMM, and PMT and node Alt-2 defines a relationship uniting PMS, PMT, and SYW. (B) RADICAL curves for each node on the T3 tree as well as the two alternative nodes. The occurrence of each node is derived from an average across 100 randomizations at each concatenation point. Concatenation sets are sampled at intervals of five genes. Only nodes that do not reach fixation in 20 genes or less are distinguished by a colored curve. The other nodes are shown in black.
Assessment of nodal support with RADICAL is not limited to the nodes in the best ML tree but can be evaluated for alternative nodes of interest. Because node 7 has the weakest signal throughout concatenation and is the primary reason that 490 genes are required to always recover the T3 topology, we focused on relationships that conflict with this grouping. Two other nodes—one uniting Prochlorococcus marinus MED4, P. marinus SS120, and P. marinus MIT9313 (Alt-1) and a second uniting P. marinus SS120, P. marinus MIT9313, and Synechococcus sp. WH8102 (Alt-2)—occur in relatively high frequency in the individual gene trees (0.268 and 0.299, respectively). Examination of the concatenation dynamics for these two nodes suggests that despite their similar frequency of occurrence in the gene trees, only one node represents a major source of conflict. The first alternative node (Alt-1) persists throughout much of the concatenation space and is only eliminated from all the randomizations when more than 490 genes are analyzed, whereas the second alternative node (Alt-2) does not appear in any trees constructed from more than 20 genes (fig. 3).
It is also clear from the RADICAL curves in figure 3B that there is a tug-o-war among the genes with respect to the resolution of node 7 and node Alt-1 as the curves for these two genes are mirror images of one another. It is possible that much of this conflicting signal results from HGT. Numerous studies on the evolutionary history of the Prochlorococcus and Synechococcus have identified abundant gene tree disagreement with respect to the monophyly of the Prochlorococcus, and HGT is believed to be particularly prominent among species in these genera (Palenik et al. 2003; Rocap et al. 2003; Beiko et al. 2005; Zhaxybayeva et al. 2006, 2009; Kettler et al. 2007; Shi and Falkowski 2008; Yerrapragada et al. 2009; Zhaxybayeva 2009). Although all Prochlorococcus species possess a unique light-harvesting system (Ting et al. 2002), most phylogenetic analyses using large data sets have failed to recover a monophyletic Prochlorococcus (Beiko et al. 2005; Zhaxybayeva et al. 2006, 2009; Dufresne et al. 2008; Shi and Falkowski 2008; Zhaxybayeva 2009; Gupta and Mathews 2010). Definitive determination of species level relationships and tests of genus-level monophyly requires more extensive taxon sampling than is available in this data set, but the RADICAL curves show that approximately 87% of the entire concatenation space supports a polyphyletic Prochlorococcus (fig. 3). Given that the genes in this data set are present in all species (and therefore do not represent any clade-specific gene acquisitions), this would appear to be a remarkably high level of HGT, if, in fact, that is the primary cause of the dominant phylogenetic signal. It is possible that the use of alternative ML models or the inclusion of additional species may shift the relative proportion of signal more in favor of a monophyletic Prochlorococcus. Regardless, RADICAL provides a valuable technique for assessing the distribution of support within the total concatenation space and should help assess the overall levels of HGT in a system.
Functional Subgroups and Conflicting Signal
In addition to identifying a core set of genes, many prokaryotic phylogenomic studies focus on the behavior of other functional groups of genes in order to illuminate possible sources of discordance and protein functions that are either refractory or susceptible to HGT (Beiko et al. 2005; Zhaxybayeva et al. 2006, 2009; Zhaxybayeva 2009). Here, we performed RADICAL analyses using gene subgroups based on the COG supercategories cellular processes (CELL), information processing (INFO), metabolism (METAB), and unknown (UNK). These categories exhibit strong agreement with the T3 topology with one notable exception (fig. 4A and supplementary fig. S5, Supplementary Material online). The metabolism category has a substantial proportion of genes that disagree with the T3 tree at node 3, node 7, and node 10. For the metabolism genes, both node 3 and node 10 stabilize only when 300 or more genes are concatenated together, whereas node 7 does not appear in the best ML tree for metabolism and fails to appear in any concatenation set larger than 300 genes. As with the nodal analysis of all the genes, examination of the concatenation dynamics provides information not immediately apparent from gene tree analysis. For instance, node 7 occurs in 57% of METAB gene trees but is slowly lost during concatenation, whereas node Alt-1, which specifies a contradictory relationship, occurs in only 29% of the METAB gene trees but occurs in the concatenation of all METAB genes (fig. 4B). Similarly, node 5 occurs in fewer gene trees than node 7 (34% vs. 57%) but reaches fixation relatively fast, occurring in all concatenation set larger than 90 genes (fig. 4).
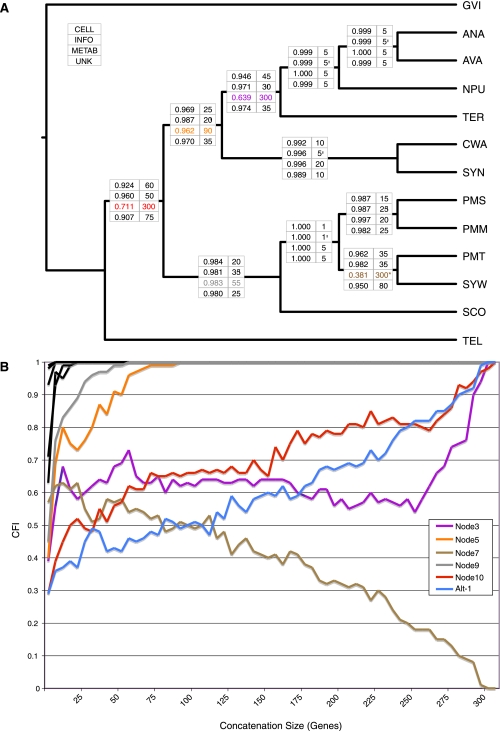
FIG. 4.—
RADICAL analysis of functional subgroups. (A) AUC values (left column) and fixation points (right column) are provided across all T3 nodes for the functional groups cellular processes (CELL), information processing (INFO), metabolism (METAB), and unknown (UNK). AUC values indicate the proportion of total concatenation space occupied by that node and the fixation point indicates the number of genes required before the node appears in all concatenation sets of that size. The asterisk indicates a degradation point, which is defined as the number of genes for which a node no longer occurs in any randomized concatenation set of that size or larger. (B) RADICAL curves for the metabolism genes. Node Alt-1 appears in the ML tree for all the metabolism genes and, therefore, is included in the figure. Only nodes that do not reach fixation in twenty genes or less are distinguished by a colored curve. The other nodes are shown in black.
Previous studies have identified elevated levels of incongruence for genes involved in metabolism (Beiko et al. 2005; Zhaxybayeva et al. 2006) and a similar result emerges from the RADICAL analysis. It is important to note that the distribution of metabolism genes is equivalent between the core set (45% of core genes are metabolism genes) and the shell set (44% of shell genes are metabolism genes). In fact, combination of the core and shell genes appears to reinforce the conflicting signal present in the metabolism genes more than it reinforces support for the T3 tree. For nodes 3, 7, and 10, the core and shell partition both reach fixation for these nodes faster when analyzed separately than does the combined data set that includes both core and shell genes (fig. 2C). The extent to which the phylogenetic signal provided by the metabolism genes is driven by HGT requires more detailed analysis of additional taxa as well as an evaluation of syntenic relationships among genes. However, it is noteworthy that the primary source of conflict between the metabolism genes and the rest of the data concerns the monophyly of the genus Prochlorococcus, with the metabolism genes being the only functional class of genes supporting this relationship. Therefore, if metabolism genes are disproportionately prone to HGT, there is virtually no support in this data set for a monophyletic Prochlorococcus.
Emergent Support
Several of the nodes on the T3 tree achieve rapid fixation during the concatenation process despite a substantial amount of incongruence among individual genes (fig. 3). For instance, node 4 appears in only 62% of the gene trees but occurs in all concatenation sets larger than ten genes. This rapid fixation may reflect the presence of emergent support, a situation in which the accumulation of nodal support is more rapid than would be predicted based on the levels of support on individual gene trees (Gatesy et al. 1999; Gatesy and Baker 2005). In this case, congruent phylogenetic signal is amplified as genes are combined together during concatenation, whereas divergent patterns of homoplasy specific to single genes or a small set of genes cancel each other out during concatenation.
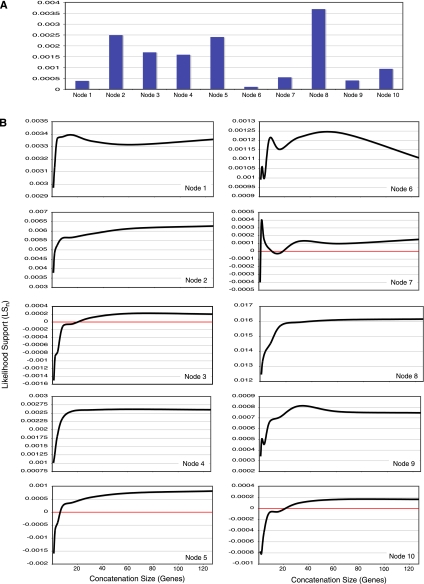
In this analysis, we evaluated the presence of emergent support by tracking the behavior of a LSn score during concatenation. If there is little emergent support, then LSn should remain constant as genes are combined, while increases in LSn as concatenation sets get larger suggest emergent support. Figure 5 plots the concatenation behavior of LSn for each node on the T3 tree, and in nearly, all cases shows clear evidence of emergent support. Four nodes (3, 5, 7, and 10) have a negative average LSn for individual gene analyses. In these cases, the average gene has more support for relationships that conflict with one of these nodes than for the nodes themselves. As genes are concatenated, however, this negative support quickly diminishes. For example, at node 5 (fig. 5B), the amount of negative LSn is reduced by more than half when two genes are combined together and disappears altogether (i.e., the average LS becomes positive) for all concatenation sets larger than eight genes. Similar trajectories exist for the other nodes, although node 7 exhibits a more haphazard behavior. Node 6 also exhibits a pattern that is more irregular than that for the other nodes. This, however, is largely due to the low amount of emergent support at this node (fig. 5A). The node exhibits a more stable trajectory when viewed on a scale comparable to the amount of emergent support present at other nodes.
FIG. 5.—
Emergent support during concatenation. Average LSn values (see Materials and Methods) are tracked across concatenation set sizes corresponding to 1, 2, 4, 8, 16, 32, 64, and 128 genes. Averages are calculated from 100 random concatenation sets at each step. (A) The total amount of emergent support for each node as measured by the difference in LSn values at the concatenation set size of 1 and 128. (B) LSn curves during concatenation for each node on the T3 tree. The red lines in the figures for nodes 3, 5, 7, and 10 indicate the threshold at which the average concatenation set shifts from not supporting the node to supporting the node.
Regardless of whether the LSn curves begin in negative territory or not, most of the curves exhibit a similar trajectory that is characterized by a rapid ascent during the early stages of concatenation followed by asymptotic leveling for the later stages of concatenation (fig. 5B). Averaged across all nodes, 86% of all the emergent support on the tree occurs by the time 16 genes have been concatenated, a data set size that comprises only 2% of the total gene space. The degree of emergent support is largely independent of the level of support for a node among the gene trees. For instance, node 1 and node 8 are both well supported among the gene trees (they occur in 98% and 96% of the gene trees, respectively), but node 8 has nearly ten times the total amount of emergent support as does node 1 (fig. 5A).
The dynamics of emergent support demonstrate that concatenation is not simply a “brute force” method that produces a definitive topology as a result of overwhelming data set size. A primary concern associated with concatenated phylogenomic studies is that many nodes will be strongly supported if enough data is analyzed together (Doolittle and Bapteste 2007; Bapteste et al. 2008). Rokas and Carroll (2006) point out that bootstrap support increases as a consequence of increasing the number of PICs analyzed without any changes in the relative distribution of homoplasy among these characters. In their example, a data set of 100 PICs produces a bootstrap of 72%, but when that same data is duplicated ten times to produce a data set of 1,000 PICs, the bootstrap value increases to 97%. RADICAL provides a technique to evaluate the relative impact of data set size on support and, for the cyanobacteria, demonstrates increases in nodal support are not simply a function of combining additional characters but reflect a disproportionate amplification of phylogenetic signal at the earliest stages of concatenation.
Concatenation Debate
RADICAL is fundamentally a concatenation method. Concatenation has recently been criticized as a source of bias (Edwards et al. 2007; Leigh et al. 2008). Simple concatenation of genome data in the context of incomplete lineage sorting may mislead species level inferences (Kubatko and Degnan 2007). But we have shown here that for the majority of the nodes in cyanobacterial genomic data, concatenation can lead to rapid convergence on well-accepted topologies. Indeed, not concatenating data may obscure the general agreement between genomic partitions, with the agreement between the core and the shell set of genes representing a prominent example. More importantly, concatenation may also increase the efficiency of a given gene's phylogenetic signal through the accumulation of hidden support (Gatesy et al. 1999; Gatesy and Baker 2005). The value of RADICAL derives from the fact that it attaches no special significance to the TE solution as it builds a topology library along multiple distinct concatenation paths. Therefore, researchers can distinguish situations in which nodes rapidly reach fixation in concatenation sets, often via emergent support, from situations in which internal conflicts persist throughout concatenation and are only resolved in the TE solution. As we demonstrate in this study, these dynamics may not be readily apparent using more traditional measures of support from either individual gene trees or TE trees and we suggest phylogenomic studies will benefit from an in depth exploration of the concatenation dynamics of large data sets using methods such as RADICAL.
Supplementary Material
Supplementary figures S1–S5, data S1 and S2, and file S3 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).
Acknowledgments
We thank John Gatesy for valuable discussion and comments on the manuscript. We acknowledge institutional support from the Lewis B. and Dorothy Cullman Program in Molecular Systematics at the American Museum of Natural History and the Korein Family Foundation. This work was supported by the National Science Foundation (DEB-0951816 to R.H.B., DBI-0421604 to R.D., A.N., S.O.K., DBI-0820757 to R.D., A.N., S.O.K., IOS-922738 to R.D., A.N., S.O.K.). S.O.K. was supported by the Defense Advanced Research Projects Agency (DARPA). P.J.P. is supported by the Pediatric Infectious Disease Society St Jude Basic Science Award and the Louis V. Gerstner Award.
References
- Altschul SF, et al. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bapteste E, et al. Alternative methods for concatenation of core genes indicate a lack of resolution in deep nodes of the prokaryotic phylogeny. Mol Biol Evol. 2008;25:83–91. doi: 10.1093/molbev/msm229. [DOI] [PubMed] [Google Scholar]
- Bapteste E, et al. Prokaryotic evolution and the tree of life are two different things. Biol Direct. 2009;4:34. doi: 10.1186/1745-6150-4-34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beiko RG, Harlow TJ, Ragan MA. Highways of gene sharing in prokaryotes. Proc Natl Acad Sci U S A. 2005;102:14332–14337. doi: 10.1073/pnas.0504068102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blankenship RE, Hartman H. The origin and evolution of oxygenic photosynthesis. Trends Biochem Sci. 1998;23:94–97. doi: 10.1016/s0968-0004(98)01186-4. [DOI] [PubMed] [Google Scholar]
- Brochier C, Bapteste E, Moreira D, Philippe H. Eubacterial phylogeny based on translational apparatus proteins. Trends Genet. 2002;18:1–5. doi: 10.1016/s0168-9525(01)02522-7. [DOI] [PubMed] [Google Scholar]
- Castresana J. Topological variation in single-gene phylogenetic trees. Genome Biol. 2007;8:216. doi: 10.1186/gb-2007-8-6-216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlebois RL, Doolittle WF. Computing prokaryotic gene ubiquity: rescuing the core from extinction. Genome Res. 2004;14:2469–2477. doi: 10.1101/gr.3024704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ciccarelli FD, et al. Toward automatic reconstruction of a highly resolved tree of life. Science. 2006;311:1283–1287. doi: 10.1126/science.1123061. [DOI] [PubMed] [Google Scholar]
- Cleveland WS. Robust locally weighted regression and smoothing scatterplots. J Am Stat Assoc. 1979;74:829–836. [Google Scholar]
- Colless DH. Congruence between morphometric and alloyzme data for Menidia species: a reappraisal. Syst Zool. 1980;29:288–299. [Google Scholar]
- Daubin V, Gouy M, Perriere G. A phylogenomic approach to bacterial phylogeny: evidence of a core of genes sharing a common history. Genome Res. 2002;12:1080–1090. doi: 10.1101/gr.187002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Degnan JH, Rosenberg NA. Discordance of species trees with their most likely gene trees. PLoS Genet. 2006;2:e68. doi: 10.1371/journal.pgen.0020068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Degnan JH, Rosenberg NA. Gene tree discordance, phylogenetic inference and the multispecies coalescent. Trends Ecol Evol. 2009;24:332–340. doi: 10.1016/j.tree.2009.01.009. [DOI] [PubMed] [Google Scholar]
- Doolittle WF, Bapteste E. Pattern pluralism and the Tree of Life hypothesis. Proc Natl Acad Sci U S A. 2007;104:2043–2049. doi: 10.1073/pnas.0610699104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dufresne A, et al. Unraveling the genomic mosaic of a ubiquitous genus of marine cyanobacteria. Genome Biol. 2008;9:R90. doi: 10.1186/gb-2008-9-5-r90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards SV, Liu L, Pearl DK. High-resolution species trees without concatenation. Proc Natl Acad Sci U S A. 2007;104:5936–59341. doi: 10.1073/pnas.0607004104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farris J, et al. Parsimony jackknifing outperforms neighbor-joining. Cladistics. 1996;12:99–124. doi: 10.1111/j.1096-0031.1996.tb00196.x. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. Confidence limits on phylogenies: an approach using the bootstrap. Evolution. 1985;39:783–791. doi: 10.1111/j.1558-5646.1985.tb00420.x. [DOI] [PubMed] [Google Scholar]
- Galtier N, Daubin V. Dealing with incongruence in phylogenomic analyses. Philos Trans R Soc Lond B Biol Sci. 2008;363:4023–4029. doi: 10.1098/rstb.2008.0144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gatesy J, Baker RH. Hidden likelihood support in genomic data: can forty-five wrongs make a right? Syst Biol. 2005;54:483–492. doi: 10.1080/10635150590945368. [DOI] [PubMed] [Google Scholar]
- Gatesy J, O'Grady P, Baker RH. Corroboration among data sets in simultaneous analysis: hidden support for phylogenetic relationships among higher level artiodactyl taxa. Cladistics. 1999;15:271–313. doi: 10.1111/j.1096-0031.1999.tb00268.x. [DOI] [PubMed] [Google Scholar]
- Gupta RS, Mathews DW. Signature proteins for the major clades of Cyanobacteria. BMC Evol Biol. 2010;10:24. doi: 10.1186/1471-2148-10-24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jain R, Rivera MC, Lake JA. Horizontal gene transfer among genomes: the complexity hypothesis. Proc Natl Acad Sci U S A. 1999;96:3801–3806. doi: 10.1073/pnas.96.7.3801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones DT, Taylor WR, Thornton JM. The rapid generation of mutation data matrices from protein sequences. Comput Appl Biosci. 1992;8:275–282. doi: 10.1093/bioinformatics/8.3.275. [DOI] [PubMed] [Google Scholar]
- Kettler GC, et al. Patterns and implications of gene gain and loss in the evolution of Prochlorococcus. PLoS Genet. 2007;3:e231. doi: 10.1371/journal.pgen.0030231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kluge AG. Testability and the refutation and corroboration of cladistic hypotheses. Cladistics. 1997;13:81–96. doi: 10.1111/j.1096-0031.1997.tb00242.x. [DOI] [PubMed] [Google Scholar]
- Kubatko LS, Degnan JH. Inconsistency of phylogenetic estimates from concatenated data under coalescence. Syst Biol. 2007;56:17–24. doi: 10.1080/10635150601146041. [DOI] [PubMed] [Google Scholar]
- Lee MS, Hugall AF. Partitioned likelihood support and the evaluation of data set conflict. Syst Biol. 2003;52:15–22. doi: 10.1080/10635150390132650. [DOI] [PubMed] [Google Scholar]
- Leigh JW, Susko E, Baumgartner M, Roger AJ. Testing congruence in phylogenomic analysis. Syst Biol. 2008;57:104–115. doi: 10.1080/10635150801910436. [DOI] [PubMed] [Google Scholar]
- Lerat E, Daubin V, Moran NA. From gene trees to organismal phylogeny in prokaryotes: the case of the gamma-Proteobacteria. PLoS Biol. 2003;1:e19. doi: 10.1371/journal.pbio.0000019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lerat E, Daubin V, Ochman H, Moran NA. Evolutionary origins of genomic repertoires in bacteria. PLoS Biol. 2005;3:e130. doi: 10.1371/journal.pbio.0030130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makarova KS, et al. Comparative genomics of the Archaea (Euryarchaeota): evolution of conserved protein families, the stable core, and the variable shell. Genome Res. 1999;9:608–628. [PubMed] [Google Scholar]
- Nakamura Y, Itoh T, Matsuda H, Gojobori T. Biased biological functions of horizontally transferred genes in prokaryotic genomes. Nat Genet. 2004;36:760–766. doi: 10.1038/ng1381. [DOI] [PubMed] [Google Scholar]
- Ochman H, Lawrence JG, Groisman EA. Lateral gene transfer and the nature of bacterial innovation. Nature. 2000;405:299–304. doi: 10.1038/35012500. [DOI] [PubMed] [Google Scholar]
- Palenik B, et al. The genome of a motile marine Synechococcus. Nature. 2003;424:1037–1042. doi: 10.1038/nature01943. [DOI] [PubMed] [Google Scholar]
- Pattengale ND, et al. How many bootstrap replicates are necessary? J Comput Biol. 2010;17:337–354. doi: 10.1089/cmb.2009.0179. [DOI] [PubMed] [Google Scholar]
- Rasmussen MD, Kellis M. Accurate gene-tree reconstruction by learning gene- and species-specific substitution rates across multiple complete genomes. Genome Res. 2007;17:1932–1942. doi: 10.1101/gr.7105007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivera MC, Jain R, Moore JE, Lake JA. Genomic evidence for two functionally distinct gene classes. Proc Natl Acad Sci U S A. 1998;95:6239–6244. doi: 10.1073/pnas.95.11.6239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rocap G, et al. Genome divergence in two Prochlorococcus ecotypes reflects oceanic niche differentiation. Nature. 2003;424:1042–1047. doi: 10.1038/nature01947. [DOI] [PubMed] [Google Scholar]
- Rokas A, Carroll SB. Bushes in the tree of life. PLoS Biol. 2006;4:e352. doi: 10.1371/journal.pbio.0040352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi T, Falkowski PG. Genome evolution in cyanobacteria: the stable core and the variable shell. Proc Natl Acad Sci U S A. 2008;105:2510–2515. doi: 10.1073/pnas.0711165105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stamatakis A. RAxML-VI-HPC: maximum likelihood-based phylogenetic analyses with thousands of taxa and mixed models. Bioinformatics. 2006;22:2688–2690. doi: 10.1093/bioinformatics/btl446. [DOI] [PubMed] [Google Scholar]
- Stamatakis A, Ott M. Efficient computation of the phylogenetic likelihood function on multi-gene alignments and multi-core architectures. Philos Trans R Soc Lond B Biol Sci. 2008;363:3977–3984. doi: 10.1098/rstb.2008.0163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Susko E, Leigh J, Doolittle WF, Bapteste E. Visualizing and assessing phylogenetic congruence of core gene sets: a case study of the gamma-proteobacteria. Mol Biol Evol. 2006;23:1019–1030. doi: 10.1093/molbev/msj113. [DOI] [PubMed] [Google Scholar]
- Swofford DL. PAUP*. Phylogenetic Analysis Using Parsimony (*and other methods). Version 4. Sunderland (MA): Sinauer Associates; 2003. Available from: http://paup.csit.fsu.edu. [Google Scholar]
- Tang K, Huang H, Jiao N, Wu CH. Phylogenomic analysis of marine Roseobacters. PLoS One. 2010;5:e11604. doi: 10.1371/journal.pone.0011604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tatusov RL, et al. The COG database: new developments in phylogenetic classification of proteins from complete genomes. Nucleic Acids Res. 2001;29:22–28. doi: 10.1093/nar/29.1.22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ting CS, Rocap G, King J, Chisholm SW. Cyanobacterial photosynthesis in the oceans: the origins and significance of divergent light-harvesting strategies. Trends Microbiol. 2002;10:134–142. doi: 10.1016/s0966-842x(02)02319-3. [DOI] [PubMed] [Google Scholar]
- Whitton BA, Potts M. The ecology of cyanobacteria. Dordrecht (the Netherlands): Kluwer Academic; 2000. [Google Scholar]
- Yang Z. Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: approximate methods. J Mol Evol. 1994;39:306–314. doi: 10.1007/BF00160154. [DOI] [PubMed] [Google Scholar]
- Yerrapragada S, Siefert JL, Fox GE. Horizontal gene transfer in cyanobacterial signature genes. Methods Mol Biol. 2009;532:339–366. doi: 10.1007/978-1-60327-853-9_20. [DOI] [PubMed] [Google Scholar]
- Zhaxybayeva O. Detection and quantitative assessment of horizontal gene transfer. In: Gogarten MB, Gogarten JP, Olendzenski LC, editors. Horizontal gene transfer: genomes in flux. New York: Humana Press; 2009. pp. 195–213. [DOI] [PubMed] [Google Scholar]
- Zhaxybayeva O, Doolittle WF, Papke RT, Gogarten JP. Intertwined evolutionary histories of marine Synechococcus and Prochlorococcus marinus. Genome Biol Evol. 2009;1:325–339. doi: 10.1093/gbe/evp032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhaxybayeva O, et al. Phylogenetic analyses of cyanobacterial genomes: quantification of horizontal gene transfer events. Genome Res. 2006;16:1099–1108. doi: 10.1101/gr.5322306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwickl DJ. Genetic algorithm approaches for the phylogenetic analysis of large biological sequence datasets under the maximum likelihood criterion [dissertation]. [Austin (TX)] University of Texas; 2006. [Google Scholar]