Atomistic simulation of lipid and DiI dynamics in membrane bilayers under tension

Abstract

Membrane tension modulates cellular processes by initiating changes in the dynamics of its molecular constituents. To quantify the precise relationship between tension, structural properties of the membrane, and the dynamics of lipids and a lipophilic reporter dye, we performed atomistic molecular dynamics (MD) simulations of DiI-labeled dipalmitoylphosphatidylcholine (DPPC) lipid bilayers under physiological lateral tensions ranging from −2.6 mN m⁻¹ to 15.9 mN m⁻¹. Simulations showed that the bilayer thickness decreased linearly with tension consistent with volume-incompressibility, and this thinning was facilitated by a significant increase in acyl chain interdigitation at the bilayer midplane and spreading of the acyl chains. Tension caused a significant drop in the bilayer's peak electrostatic potential, which correlated with the strong reordering of water and lipid dipoles. For the low tension regime, the DPPC lateral diffusion coefficient increased with increasing tension in accordance with free-area theory. For larger tensions, free area theory broke down due to tension-induced changes in molecular shape and friction. Simulated DiI rotational and lateral diffusion coefficients were lower than those of DPPC but increased with tension in a manner similar to DPPC. Direct correlation of membrane order and viscosity near the DiI chromophore, which was just under the DPPC headgroup, indicated that measured DiI fluorescence lifetime, which is reported to decrease with decreasing lipid order, is likely to be a good reporter of tension-induced decreases in lipid headgroup viscosity. Together, these results offer new molecular-level insights into membrane tension-related mechanotransduction and into the utility of DiI in characterizing tension-induced changes in lipid packing.

Introduction

Mechanical forces modulate cell growth, differentiation, signal transduction, transport, and migration, through biochemical signaling pathways¹ which may be related to membrane molecular organization and dynamics.^2,3 For example, lateral membrane tension causes conformational changes in integral membrane proteins,³ and affects membrane permeability,^4,5 lipid lateral diffusion,^2,6 and organization of lipid rafts.^7,8 These effects are believed to be mediated by bilayer thickness changes that result in lipid phase separation or hydrophobic mismatch between the lipid acyl chains and transmembrane region of proteins, leading to distortion of the lipid bilayer and concomitant protein conformational changes.^9–11

Despite the importance of lipid dynamics in cell signaling, to date the only experimental studies quantifying the relationship between lipid dynamics and force have been conducted in sheared endothelial cells^2,6,12 and in hair cells.^13,14 In these studies, a lipoid dye, such as 1,1′-dioctadecyl-3,3,3′,3′-tetramethylindocarbocyanine perchlorate (DiI), 9-(dicyanovinyl)-julolidine (DCVJ), or di-8-ANEPPS, was used to infer lipid dynamics from fluorescence intensity or fluorescence recovery after photobleaching (FRAP). Because these studies probed lipid dynamics indirectly and because the precise membrane tensions, at the molecular level, were unknown, there is a need to quantify directly the relationship between membrane tension and lipid dynamics.

The most prominent methods to assess lipid dynamics, including FRAP, fluorescence correlation spectroscopy (FCS), fluorescence anisotropy, and fluorescence lifetime imaging^15–17 probe membrane lipid dynamics by analyzing the dynamics of lipophilic fluorescent dyes (e.g. DiI, 1,6-diphenyl-1,3,5-hexatriene (DPH), and Laurdan). In particular, DiI is popular because of its structural similarity to phospholipids and its ability to selectively partition into different lipid phases (gel or fluid) depending on the matching between the length of its alkyl chains and the lipid acyl chain length.¹⁸ Spectroscopic investigations employing DiI have been used to study membrane organization and dynamics.^19,20 The fluorescence lifetime of DiI depends on the accessibility to water²¹ and on the viscosity of the local microenvironment,¹⁹ offering a useful tool to detect lipid rafts in cells and phase separation in model membranes. However, proper interpretation of these fluorescence measurements requires precise knowledge of location, orientation, and interactions of dye with lipids and water, which are difficult to obtain experimentally.^22,23 Examples of the utility of using molecular dynamics (MD) simulation as a tool to answer these questions include predictions of the location of drug-like small molecules in lipid bilayers along with validation by small-angle neutron scattering experiments.^24,25

The aim of this computational modeling study was to determine the effects of membrane tension on mechanotransduction-related structural and dynamical properties of the bilayer. In addition, we wished to understand the fidelity with which DiI, a popular membrane probe, reflects lipid dynamics, so that DiI photophysics could be used as a readout for tension effects on stressed membranes. To accomplish this goal, we performed a series of atomistic molecular dynamics (MD) simulations of fluid-phase dipalmitoylphosphatidylcholine (DPPC)/DiI bilayers under various physiological tensions. The main readouts from this study are as follows. First, we characterized the effects of tension on bilayer thickness, acyl chain packing, interdigitation, and electrostatic potential. Second, we determined the relationship between area-per-lipid and lipid lateral diffusion, and compared these results to predictions from free-area theory. Third, we compared the DiI probe dynamics to the dynamics of the native lipids, leading to an analysis of the relationship between lipid packing and fluorescence lifetime of DiI in terms of hydration and local viscosity.

Materials and methods

Simulation methodology

Force field parameters for DPPC and DiI-C₁₈ were identical to Berger et al.²⁶ Bond lengths and bond angles of the DiI's headgroup were obtained from X-ray crystallography data of a structurally similar carbocyanine dye.²⁷ Simple point charge (SPC) model was used for water.²⁸ The partial charges for the DPPC molecules were identical to those described by Chiu et al.,²⁹ whereas, the partial charges on the DiI molecule were obtained by performing ab initio quantum mechanical calculations using Gaussian 03 software package with the Hartree–Fock method and the 6–31G basis set using the charge partitioning scheme of Merz–Kollman.^22,29

A simulation box of well-equilibrated pure DPPC bilayer consisting of 128 DPPC molecules and 3655 water molecules was obtained from Tieleman and Berendsen.²⁸ The DiI-C₁₈ dye was incorporated in the DPPC bilayer by replacing two DPPC molecules with a single DiI-C₁₈, in each leaflet. To ensure electrical neutrality, two chloride ions were added to the system. To make sure that the equilibrium position of the dye was independent of its initial position, the dye headgroups were placed at random z-locations (above and below the lipid–water interface) and the system was equilibrated. Initial configurations of the simulation box with varied area-per-lipid (α) were constructed by scaling the original system, while maintaining constant volume, and the systems were equilibrated as described below. Membranes were simulated at seven different area-per-lipid values ranging from 0.635 to 0.750 nm², corresponding to tensions ranging from −2.6 to 15.9 mN m⁻¹. Final production runs were performed on NP_zAT ensemble. This ensemble was chosen in order to conveniently apply tension by prescribing area per lipid. Other ensembles such as NPT or NP_zgT ensembles could have been chosen and these would give equivalent structural and dynamical properties.^28,30

Molecular dynamics simulations were carried out using the GROMACS software package (version 3.3.2).^31,32 Pre-equilibration of energy minimized structures was performed under NVT conditions, at 323 K, for a simulation time of 1 ns, allowing for removal of any overlaps or defects caused by DiI placement and the application of tension. Subsequent equilibration of the structures was performed under NP_zAT conditions, at 323 K and 1 bar normal pressure, for a total simulation time of 100 ns. Final production runs were carried out under NP_zAT conditions for an additional 100 ns for each system configuration. Periodic boundary conditions were applied in all three coordinate dimensions. The temperature of the production runs was 323 K, which is above the gelto-liquid phase transition temperature, T_m, of DPPC (~315 K). Temperature and pressure were controlled using Berendsen's weak coupling method with the time constants set to 0.1 ps and 1.0 ps respectively.³³ Semi-anisotropic scaling was used for pressure coupling with zero compressibility in xy-plane to maintain the area constant. The LINCS algorithm was used to constrain the bond lengths, allowing for larger time steps than if the bonds were unconstrained.^31,32 The Particle-Mesh Ewald (PME) method was used for electrostatic interactions, with a direct-space cutoff of 1 nm,^34,35 and cubic interpolation (PME order = 4) for the calculation of long-range interactions in reciprocal space, with a Fourier transform grid of 0.12 nm maximum. Despite its computational cost, PME was chosen because it allows for proper electrostatics in systems with charged molecules and ions.^36,37 The Lennard-Jones interactions were cutoff (shifted and truncated) at 1.0 nm. A time-step of 2 fs was used with a leap-frog integration algorithm for the equations of motion, accommodating bond constraints and weak coupling to constant T and P baths.^31,32

Results and discussion

In this study, we addressed how membrane tension or, equivalently, how lipid packing affects structural and dynamical properties of a fluid-phase DPPC bilayer by performing a series of united-atom molecular dynamics (MD) simulations. Various physicochemical properties of the bilayer were analyzed as a function of area-per-lipid (α). We included DiI-C₁₈ in our simulations to facilitate the interpretation of lipid packing and dynamics from single-molecule fluorescence measurements of lateral and rotational diffusion, and fluorescence lifetime of DiI, a popular membrane probe. Perturbative effects of DiI on the lipid bilayer were studied previously by Gullapalli et al.²² Results are divided into five subsections: structural changes of lipid bilayer under tension, tension-induced changes in lipid order, electrostatic potential and lipid/water dipole ordering, lipid lateral diffusion and free-area theory, and sensitivity of DiI dynamics to membrane tension.

Tension induces bilayer thinning and interleaflet interdigitation

Surface tension was estimated from the pressure tensor, as described in ref. 38. As expected, the surface tension increased linearly with an increase in area, from −2.6 mN m⁻¹ at α = 0.635 nm² to 15.9 mN m⁻¹ at α = 0.750 nm², above which rupturing of the bilayer was observed (rupture data not shown). While this rupture tension is in good agreement with values from micropipette aspiration of lipid vesicles (ranging from 10 to 20 mN m⁻¹)⁵ MD simulated rupture and experimental rupture tensions often differ because rupture/pore tension depends strongly on the loading rate, which is inherently larger in MD simulations.³⁹ Thus within the range of tensions simulated in this study, pore formation or rupture cannot be observed in the size/time scales studied here.⁴⁰ Zero surface tension corresponded to α = 0.646 nm², close to the experimental value of 0.64 nm² for DPPC.⁴¹ In addition, the area compressibility modulus calculated from the tension–area plot³⁸ was 105 mN m⁻¹, in good agreement with the previous simulation value of 107 mN m⁻¹ for DPPC bilayer at 50 °C.³⁸ Experimentally, a compressibility modulus of 234 mN m⁻¹ was reported for DMPC lipid at room temperature.⁴² Using an identical force field to the current simulations, Lindahl and Edholm⁴³ reported a simulated value of 250–300 mN m⁻¹ for a larger membrane patch (1024 lipids), suggesting that the lower value in the current study is likely due to the finite-size effect.⁵ Considering the empirical nature of the force field parameters, these results indicate that the simulation methodology is sufficiently accurate in determining the microscopic and macroscopic properties of the lipid bilayer over an extended range of simulated tensions.

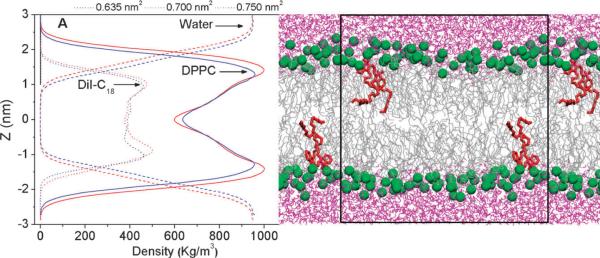
Bilayer thickness, defined as the distance between water and lipid density crossover points on either side of the bilayer, was directly computed from the mass density profiles (Fig. 1).²³ The bilayer thickness decreased linearly with increases in area-per-lipid, consistent with volume-incompressibility (Table 1). The density profile of the bilayer is highly reminiscent of a confined film^36,37—rather than a constant density bulk fluid—and thus changes in bilayer thickness are expected to result in structural reorientations within the bilayer.⁴⁴ In support of this interpretation, it was observed that increasing the surface area resulted in a decrease of the lipid density at the headgroup region and a concurrent increase in the local density at the mid-plane of the bilayer (Fig. 1). This indicates increased interdigitation of the acyl chains of the opposing leaflets due to extension of the chains beyond the bilayer mid-plane. Increased interdigitation has physiological implications; for example, acyl interdigitation has been proposed to result in the formation of membrane micro-domains.⁴⁵ Also, interdigitation of the acyl chains can alter the hydrophobic interactions and lateral pressure profile of the bilayer, which in turn can alter protein conformation.^46,47 Spreading of the acyl chains also takes place upon decrease in bilayer thickness (see below).

Fig. 1.

Mass density profiles of lipid (solid), water (dashed), and DiI-C₁₈ (dotted) across the lipid bilayer at selected values of area-per-lipid (the center of the bilayer was set at z = 0, DiI density is at 20× for clarity). A snapshot of the simulation box is also shown (DPPC—grey, DiI—red, water—purple, and DPPC phosphorous atoms are shown in green).

Table 1.

Summary of structural and dynamical properties of the lipid bilayer as a function of area-per-lipid

Bilayer property	Area-per-lipid, α/nm2
	0.635	0.650	0.675	0.687	0.700	0.725	0.750	S.E.a
Surface tension/mN m−1	−2.62	0.86	5.24	6.85	9.19	13.49	15.87	0.32
Volume per lipid/nm3	1.233	1.234	1.236	1.237	1.238	1.239	1.240	0.001
Bilayer thickness/nm	4.20	4.13	4.00	3.94	3.86	3.76	3.63	<0.01
Average trans fraction of chains (%)	76.8	76.5	76	75.9	75.7	75.4	75.2	0.2
End-to-end tail vector angle/°	36	40	43	48	50	53	57	1
Electrostatic potential/mV	615	614	596	608	605	597	589	10
Electrostatic potential barrier/mV	759	770	727	727	722	704	677	—
Mean square displacement (τ = 200 ps)/Å2	5.41	5.74	6.57	7.00	7.19	8.02	8.85	0.06
Lateral diffusion coefficient/10−12 m2 s−1	8.16	9.35	9.80	11.71	12.16	16.72	23.29	0.72
Rotational relaxation time τ1/ns	0.34	0.30	0.24	0.22	0.21	0.17	0.15	±0.01b
Rotational relaxation time τ2/ns	3.77	3.57	2.75	2.40	2.23	1.92	1.67	±0.03b

^aReported mean standard errors (S.E.) are upper limits of all the simulations.

^b95% confidence intervals obtained from curve-fitting.

Tension reduces lipid acyl chain packing and order

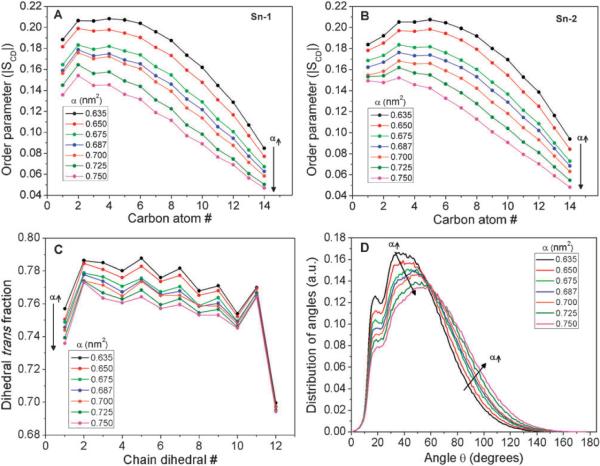
The effect of membrane tension on lipid chain order was determined by computing the order parameter of sn-1 and sn-2 chains separately, as a function of the chain carbon atom number, in accordance with our previous publication.²² The absolute value of the order parameter, |S_CD|, can vary from 0.5 (high ordering) to 0 (low ordering). Order parameter profiles for the sn-1 and sn-2 chain as a function of area-per-lipid are shown in Fig. 2A and 2B. For α = 0.635 nm², S_CD versus carbon chain number exhibited the typical trends with a plateau region near the headgroup (with an average order of 0.2 ± 0.02) which gradually dropped to near zero at the terminal methyl groups of the tails. These values are in good agreement with the values reported previously from experiments⁴⁸ and simulations.^26,35 Increasing the surface area caused a significant decrease in the order parameter values of both sn-1 and sn-2 chains throughout the length of the carbon chain. Changes in the order parameter with tension were smallest (~30%) near the headgroup region and largest (~50%) at the terminal tail region.

Fig. 2.

(A and B) Deuterium order parameter (S_CD) versus chain position for sn-1 and sn-2 acyl chains of the DPPC molecules for different values of area-per-lipid. (C) Dihedral trans fraction of the lipid acyl chain dihedrals, averaged over sn-1 and sn-2 chains. (D) Distribution of the end-to-end acyl–acyl angle of the DPPC lipids.

Changes in the S_CD order parameter resulted from the combined effect of tension on the acyl chain dihedrals and on the chain tilt angle.⁴⁹ To determine the relative magnitude of tension-induced changes in these parameters, we calculated the average trans fraction of the chain dihedrals, and the average angle between the end-to-end acyl chain vectors. In general, the average trans dihedral fraction was largest near the headgroup region and decreased towards the terminal tail region (a strong drop was observed in the last dihedral of both the acyl chains). Although measurable decreases in the average trans fraction of the chain dihedrals were observed with increased area-per-lipid, these changes were small (<3%, shown in Fig. 2C) and there was no change in the qualitative trend. This result strongly suggests that the acyl chain configuration is not markedly affected by the application of tension. On the other hand, when we analyzed the distribution of angles between the end-to-end sn-1 and sn-2 chain vectors, shown in Fig. 2D, the peak angle gradually increased from 36 degrees (for α = 0.635 nm²) to 57 degrees (for α = 0.750 nm²), with applied tension. This result clearly denotes that a significant “spreading” of the chains takes place with increases in the area-per-lipid. We can conclude that the tension-induced decrease in the S_CD order parameter is primarily due to an increase in the spreading of the acyl chains, i.e., changes in the acyl chain orientation within the bilayer, rather than due to any changes in the acyl chain conformations (i.e. trans and gauche fractions). Similar molecular shape changes of lipid were simulated previously in the outer leaflet of high curvature liposomes.⁵⁰

Tension reduces the electrostatic potential barrier through lipid/water dipole reordering

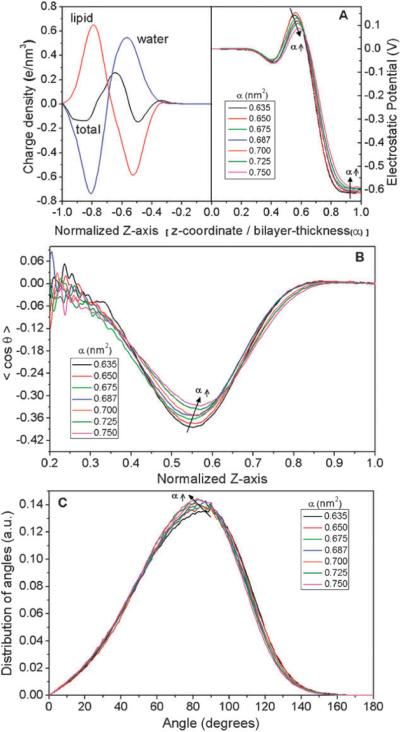
The electrostatic potential at the lipid–water interface results from the orientation of the water and lipid dipoles. To determine this electrostatic potential, the ensemble-averaged charge density along the z-axis was computed. Fig. 3A depicts the individual contributions of lipids and water to the total charge density. Due to symmetry, only half of the simulated membrane is shown in the figure. Compensation of the dipole potential of the lipid molecules by water resulted in a negative potential in the bulk water with respect to the bilayer interior. The corresponding electrostatic potential with respect to the center of bilayer was computed by double integration of the time-averaged charge density, ρ(z), using Poisson's equation:

$$V\left(z\right)=\phi \left(z\right)-\phi \left(0\right)=-\frac{1}{{\epsilon }_0}{\int }_0^z\mathrm{d}z\prime {\int }_0^{z\prime }\rho (z″)\mathrm{d}z″$$ (1)

where ϕ(z) and ρ(z) are the time-averaged dipole potential and the charge density, respectively, as a function of the distance normal to the bilayer, and ε₀ is the permittivity of vacuum. ϕ(0) is the dipole potential at the bilayer center that acts as a reference point. The resulting potential profiles for different values of the area-per-lipid, are shown in Fig. 3A. In the case of α = 0.635 nm², the potential difference between the center of the bilayer and water was −615 mV. This value is consistent with previous simulations of DPPC bilayers.²² Experimentally, values for the potential difference vary from −200 to −575 mV for various phosphocholine–water interfaces.³⁵ With increasing lateral tension, the following effects in the electrostatic potential profiles were observed (illustrated in Fig. 3A): First, the potential difference between the bilayer interior and bulk water decreased from 615 mV (for α = 0.635 nm²) to 588 mV (for α = 0.750 nm²). Similar results have been reported by Skibinsky et al., where lowering of surface tension by addition of trehalose induces an increase in electrostatic potential.⁵¹ Second, the positive potential barrier at the lipid–water interface, which originates from the strong ordering of water molecules around the phosphoryl groups of the lipids, was reduced in magnitude and shifted in position away from the bilayer center. The height of the potential barrier with respect to bulk water is shown in Table 1. The potential barrier reduced by ~80 mV at the highest tension simulated. These tension-induced changes in electrostatic potential at the lipid–water interface may have physiological significance, as a decrease in the electrostatic potential of ~30 mV can cause significant increase in ion transport across the lipid bilayer.^52,53

Fig. 3.

(A) Charge density profile of the lipid bilayer is shown on the left, including the contributions from lipid and water. On the right are the respective electrostatic potential profiles as a function of area-per-lipid. (B) Ordering of water dipoles with respect to bilayer normal at different area-per-lipid. (C) Angular distribution of DPPC P–N vector with respect to the normal of the bilayer. In (A) and (B) the abscissa is normalized by the size of the simulation box for each α, and only half of the simulation box is shown, due to symmetry (z = 0 denotes the center of the bilayer).

The ordering of the water dipole was quantified by calculating the time-averaged projection of the water dipole unit vector onto the interfacial normal (z-axis, Fig. 3B). A value of 〈 cos θ〉 = −0.5 corresponds to perfect ordering of the water dipoles parallel to the membrane normal, whereas a value of 〈 cos θ〉 = 0 corresponds to random water dipole orientation (disordered state). In general, high ordering of the water dipoles along the membrane normal is observed near the phosphorous atoms of the lipids.³⁵ Away from the interface, the ordering persists in the z-axis until the point where the lipid density becomes zero. Increasing the membrane tension resulted in decreased water dipole ordering around the lipids, as seen by an increase in the 〈cos θ〉 minimum. This decreased water dipole ordering correlatesi well with the reduced potential barrier at the lipid–water interface and explains the previously observed changes in the electrostatic potential profile at the lipid–water interface. Also, a slight shift was observed in the location of the water dipole where ordering towards the membrane surface was highest (Fig. 3B). This shift correlates well with the spatial shift observed in the electrostatic potential profile.

The ordering of the lipid dipoles at the lipid–water interface was quantified by calculating the angular distribution of the P–N vector with respect to the bilayer normal (Fig. 3C). In general, the peak of the P–N vector angle was around 90°, indicating that the P–N vector was aligned parallel to the lipid–water interface. Increasing the area-per-lipid resulted in a slight decrease of the peak angle value, as evidenced by the peak shifts of the P–N vector from 90° (for α= 0.635 nm²) to 82° for the largest tension simulated (for α = 0.750 nm²) (Fig. 3C). That is, increases in tension resulted in a tilt in the P–N vector towards the bilayer normal. Considering both the water and lipid dipole orientations, we can conclude that both water and lipid dipole reordering contribute to the observed changes in electrostatic potential profiles with tension. Based on these results we predict that mechanical stretching of the lipid bilayer can result in significant changes in small-molecule diffusion through the bilayer, due to reduced resistance to diffusion accompanying reductions in electrostatic potential. This novel mechanism of mechanosensitivity of cell membranes is worthy of further simulation and experimental testing.

Moderate tension increases lipid lateral diffusion by increasing free-area, but free-area theory does not hold for large tensions

Lateral diffusion coefficients (D) were computed from the mean-squared displacement (MSD) of the center-of-mass (COM) motion of the molecules. The MSD was ensemble averaged and calculated for multiple time-origins, and D was quantified through Einstein's equation:

$$D=\underset{t\to \infty }{\lim }\frac{1}{2\mathrm{d}t}\langle {[{\overrightarrow{r}}_1(t+t\prime )-{\overrightarrow{r}}_1(t\prime )]}^2\rangle$$ (2)

where, r_i are the x,y positions of the center of mass of a lipid i at a given time t′ and after a time interval t (i.e., at time t + t′); d is the dimensionality of the motion considered (here d = 2 for the in-plane lateral diffusion); the brackets denote ensemble average (over molecules and time) and also over multiple time origins t′. The MSDs were corrected for the COM motion of the membrane (i.e. removing any net leaflet translation). MSDs of DPPC at different area-per-lipid values are shown in Fig. 4A.

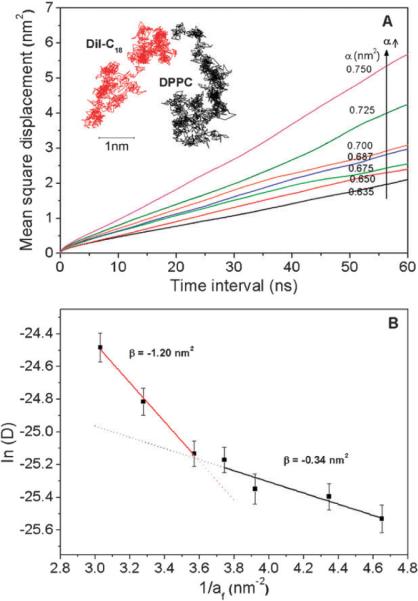
Fig. 4.

(A) Mean square displacements (MSD) of lipid molecules under different tensions. Representative xy-trajectories of DPPC and DiI molecules are shown in the inset (α = 0.635 nm²). (B) The plot of ln(D) vs. 1/a_f, where two different linear regimes were identified, represented by solid lines, with slopes β. Error bars represent standard errors, n = 124.

Lipids exhibit two different types of in-plane motion, a “rattling-in-cage” motion at short time-scales (<1 ns), and translation via “hopping” diffusion at longer time scales (>10 ns), as shown in the inset of Fig. 4A.⁵⁴ Long-time diffusion coefficients were quantified by fitting the MSD curves to a linear function at long times (10 to 70 ns). Experimental values of the lateral diffusion coefficient of lipids in fluid-phase membrane bilayers range from 1.5 × 10⁻¹² m² s⁻¹ to 6 × 10⁻¹² m² s⁻¹ depending on the method.²² The simulation-measured diffusion coefficient of DPPC at α = 0.635 nm² was 8.1 × 10⁻¹² m² s⁻¹, which is close to the values obtained using fluorescence correlation spectroscopy.²⁰ According to the free-area theory,⁵⁵ lipid hopping from one cage to another depends on the availability of a void space (larger than a critical size) next to the molecule. Opening up of a void space occurs occasionally due to random density fluctuations. Free-area theory of lipid lateral diffusion has been shown to fit well with experimental diffusion data obtained as a function of temperature and cholesterol concentration in lipid bilayers.^56,57 However, the predictive ability of the model has been challenged because of the large number of fitting parameters required.⁵⁸ Lipid lateral diffusion coefficient (D) according to free-area theory is given by the equation,

$$\text{ln}\left(D\right)=\text{ln}\left(\mathit{gdu}\right)-\frac{\gamma a_{\mathrm{c}}}{a_{\mathrm{f}}}$$ (3)

where, g is a geometric factor (~1/4), d is diameter of the cage, u is the gas kinetic constant, γ is the free area overlap factor (0.5 to 1), a_c is the critical area required for lipid diffusion, and a_f is the free area defined as the difference between average molecular area (α) and the van der Waals area of the lipid (a₀). Note that the critical area is not the same as the van der Waals area. Fitting parameters include maximum diffusion coefficient (i.e.D_max = gdu, from eqn (3)), critical area of the lipid, and free-area overlap factor (γ). Typical values of a₀ and a_c for phosphocholines are 0.42 nm² and 0.48 nm² respectively.⁵⁹ The D_max can be approximated by K_BT/f, where f is the friction coefficient given by 4πηR for a spherical particle of radius R in a medium of viscosity η.

According to eqn (3), free-area theory predicts a linear relationship between ln(D) and 1/a_f with a constant slope for lipid monolayers in the area-per-lipid range of 0.50 nm² to 0.90 nm².⁵⁹ From our simulations, however, the plot of ln(D) vs. 1/a_f (Fig. 4B) over the range of area-per-lipid tested, resulted in two distinct linear regimes. The slope of the curve, β = −γa_c, measured at smaller area-per-lipid (0.635 to 0.700 nm²) was −0.34, which is comparable to that measured in various fluid-phase lipid monolayers (summarized in Table 1 of ref. 59). However, the slope of the curve at larger area-per-lipid (0.700 to 0.750 nm²) was −1.2. Since there is no evidence of phase transition, explanation of a nonconstant slope must be due to changes in interleaflet friction and/or molecular shape. Indeed, experimental studies showing that lipid diffusion is substantially higher in monolayers (D ≈ 20 × 10⁻¹² m² s⁻¹) compared to bilayers (D ≈ 6 × 10⁻¹² m² s⁻¹), as measured using FCS^20,59 suggest that changes in interleaflet interactions explain discrepancies between low and high tension slopes.

We now explore the idea of non-constant friction and molecular shape further. First, fitting of diffusion data to free-area theory is typically done by assuming that the D_max is constant for a given lipid, i.e. the friction coefficient is assumed constant through the entire range of area-per-lipid values. However, D_max obtained from extrapolating the linear fits to 1/a_f = 0 in Fig. 4C shows that D_max is not constant and increases at high tensions. This suggests that the friction on the lipid molecules is decreased significantly at high tensions. This is supported by other observations in this study, namely, increase in disorder of the water molecules at the lipid headgroups (Fig. 3C) and increased disorder of terminal tail regions of lipid acyl chains (Fig. 2A and 2B). The decrease in headgroup and inter-leaflet friction might account for the dramatic increase in diffusion coefficient at higher tensions compared to the values predicted by free-area theory. Second, a significant increase in the slope of ln(D) vs. 1/a_f at high tensions also indicates an increase in critical area of the molecule and/or the free-area overlap factor. However, changes in these parameters are not sufficient to explain changes in diffusion. Specifically, although free-area theory can be used to fit the diffusion data at large tensions, the fits result in a β of −1.2. To obtain this slope either the overlap factor (γ) or the critical area (a_c) must be significantly greater than 1. But the overlap factor, by definition, lies between 0 (no overlap of free area) and 1 (complete overlap). Similarly, the critical area, the minimum area needed for diffusion, is normally held constant (at 0.48 nm²) but could increase if the molecular shape changes. Increase in critical area of the molecule at high tensions is evident from the observation that significant spreading of the acyl chains occurs at high tensions (Fig. 2D) but it will never increase sufficiently to yield a β of −1.2. Other local-density/free-area theoretical approaches, which have been developed for polymer and oligomer systems, can yield quantitative agreement with the D values obtained from the simulations,^60,61 however these models introduce additional adjustable parameters, which may be difficult to define properly for the lipid bilayer system. We conclude that a new theory for lipid diffusion is needed that takes into account changing friction and molecular shape with tension.

Changes in lipid packing are reflected in changes in DiI diffusion and rotation

Experimentally, membrane dynamics are often assessed using measurements of dynamics of fluorescent probe molecules.^15,17,19,20 Such spectroscopic measurements assume that the probe molecules faithfully reflect lipid dynamics. Interpretation of the obtained data necessitates knowledge of the microenvironment factors such as hydration and viscosity, which are dictated by the location and orientation of the chromophore. We discuss the sensitivity of fluorescence dynamics of DiI to lipid packing and compare DiI dynamics to the native lipid dynamics. Key properties pertaining to DiI are summarized in Table 2.

Table 2.

Location, orientation, hydration, and dynamics of DiI

				Rotational relaxation
α/nm2	DiI locationa/nm	DiI orientationc/degrees	MSD at τ = 200 ps/Å2	τ1/ns	τ2/ns	Hydration (molecules)
Standard error →	±0.01	±0.20	±0.06	±0.03d	±0.25d	—
0.635	0.62	4.74 (56.24)	3.73	1.09	9.69	4.7
0.650	0.54	5.5b	— b	— b	— b	5.4
0.675	0.57	2.14 (54.88)	4.34	0.95	8.07	4.7
0.687	0.62	−2.56 (55.14)	4.65	0.75	7.56	4.8
0.700	0.60	6.05 (56.71)	4.46	1.13	7.09	4.9
0.725	0.53	3.22 (61.08)	5.19	0.89	6.14	5.6
0.750	0.54	2.07 (52.90)	5.49	0.82	7.19	5.1

^aPositive values indicate DiI location below the lipid–water interface.

^bA bimodal distribution of dye orientation was observed, with one dye molecule temporarily trapped in a metastable configuration with an average orientation of around 60 degrees. For this reason, the lateral and rotational dynamics are not reported.

^cThe values in parenthesis indicate full width half maximum (FWHM) of the distribution.

^d95% confidence intervals obtained from curve-fitting.

The lateral diffusion coefficient of DiI has been shown to be in the same range but slightly lower than that of DPPC.²² In this study, we could not test the sensitivity of long-time lateral diffusion coefficient of DiI to lipid packing due to lack of sufficient statistics; there exist only two DiI molecules in the simulation box compared to 124 DPPC molecules. Alternatively, we computed the short-time diffusion (cage diffusion) of DiI and DPPC as a function of tension, and compared their MSDs at time t = 200 ps (Tables 1 and 2, respectively). The MSD of DiI was lower than that of DPPC at all tensions. The free area of the DPPC bilayer is smaller near the lipid headgroup region and increases considerably in the hydrophobic region of the bilayer.⁶² Despite the fact that DiI was located near the lipid acyl chain region (Table 2),²² DiI exhibited slower diffusion than DPPC. This is most likely due to the rigid and bulky structure of the DiI headgroup. Nevertheless, MSD of both DPPC and DiI scaled linearly with increases in tension and exhibited equal sensitivity. Considering that DiI exhibits hopping translation similar to DPPC at long time scales (inset of Fig. 4A), diffusion of DiI at longer times will likely also scale similarly to DPPC. Direct evidence for this would require simulating substantially larger systems, which is beyond the capabilities of our computational facilities. Nevertheless, based on the above observations, we conclude that the lateral diffusion mechanism of DiI is similar to that of the native lipid and that tension induces increases in DiI diffusion that are quantitatively similar to lipid diffusion.

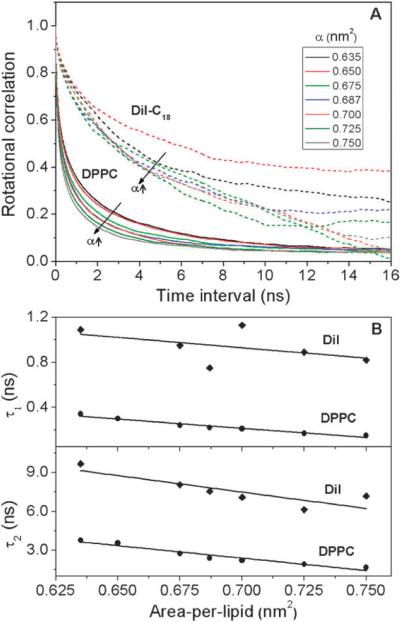
We further assessed the rotational dynamics of DiI and DPPC by computing the rotational autocorrelation function of DiI's orientation vector (vector joining the two indole rings) and of the P–N vector of DPPC, respectively (Fig. 5). On average, the orientation vector of DiI was parallel to the lipid–water interface to within a few degrees, and was independent of tension-induced changes in lipid packing (Table 2). The rotational correlation function, C(t), is defined as C(τ) = 〈P₂(cos(θ(τ)))〉, where θ(τ) is the angle between the orientation vectors separated by a time interval `τ', P₂ is the second Legendre polynomial, and 〈 〉 represents the ensemble average. Rotational autocorrelation curves of DPPC and DiI for different values of tension are shown in Fig. 5A. In most cases, the rotational correlation of DiI did not decay completely to zero suggesting that either DiI does not undergo isotropic rotation or, more probably, our simulation time was not sufficient to reach the asymptotic limit. A double-exponential function of the form $F\left(f_{\mathrm{t}}\right)=F_0+\sum _{i=1}^2{e}^{-\frac{t}{\tau }}$, commonly used to fit the experimental rotation data, was used here to determine the rotational relaxation times⁶³ (Table 2). The fast and slow relaxation times represent the wobbling motion and overall rotation, which were in the range of 0.8 to 1.1 ns and 6.1 to 9.7 ns, respectively, for DiI. These results are in good agreement with experimentally-determined rotational correlation times of DiI–C₁₂ (shorter chain length than DiI–C₁₈) in fluid-phase DOPC bilayer.⁶⁴ In comparison, the fast and slow relaxation times of DPPC were on the order of 0.1 to 0.3 ns and 1.7 to 3.8 ns, respectively (Table 1), and were smaller compared to DiI by a factor of 2 to 3. Both slow and fast relaxation times of DPPC and DiI decreased linearly with increased area-per-lipid with equal sensitivity, as inferred from the linear fits shown in Fig. 5B. These observations show that even though the rotational relaxation times of DiI do not match those of DPPC, their trend with membrane tension suggests they are a sensitive indicator of lipid packing.

Fig. 5.

(A) Rotational autocorrelation curves of DiI (dotted) and DPPC (solid) under different tensions. (B) The corresponding rotational relaxation times of DiI and DPPC, τ₁ (fast) and τ₂ (slow), obtained from fit with bi-exponential decay functions. Solid lines are linear fits of the data. 95% confidence interval of τ₁ and τ₂ of DiI are ±0.03 and ±0.25 ns respectively. 95% Confidence interval of τ₁ and τ₂ of DPPC are ∓0.01 and ±0.25 ns respectively.

DiI sensitivity to membrane tension may be revealed in fluorescence lifetime measurements

Although the present classical molecular dynamics simulations cannot simulate fluorescence, which is a quantum mechanical process, they do enable one to assess the local physical factors that govern fluorescence. In general, fluorescence lifetime of carbocyanine chromophores is sensitive to water accessibility and to the local microviscosity. Cyanine dyes exhibit weak fluorescence in water and a dramatic increase in quantum yield upon incorporation into lipid membranes.²¹ Viscosity-dependent fluorescence lifetime of cyanine dyes has been shown to be related to changes in the trans–cis photoisomerization dynamics of the central methine bridge.^65,66 Moreover, Packard and Wolf have shown that fluorescence lifetime of DiI increases with an increase in order of the lipid acyl chains.¹⁹

We assessed chromophore hydration by counting the average number of water molecules in the first shell of DiI's head-group. This hydration number can be accurately computed from the radial pair-distribution function of DiI-nitrogens and water-oxygens. Hydration of the chromophore under different membrane surface areas varied between 4.7 and 5.6 water molecules with no particular trend with tension (Table 2). This observation is in concert with the other trends observed here; namely, since the location of the dye with respect to lipid–water interface does not change with increased area-per-lipid (Table 2) and water does not penetrate appreciably beyond lipid headgroups (Fig. 1), no marked change in the DiI hydration is expected. On the other hand, measurable decreases in the rotational relaxation times of DiI were observed with increased tension, which is indicative of decreased viscosity near the DiI's headgroup region. These results indicate that changes in fluorescence lifetime of DiI due to membrane order¹⁹ are most likely due to changes in the viscosity near the headgroup, rather than due to changes in hydration. In summary, these results suggest that fluorescence lifetime of DiI may be a sensitive indicator of tension-induced decreases in lipid packing in membranes.

Conclusions

Lateral tension-induced changes in membrane organization and dynamics play an important role in transforming mechanical signals into biochemical signals at the cell surface. Despite the known significance of membrane tension, very little is known at a molecular level about the effects of tension on membrane organization. The goal of this study was to provide insights into the effects of membrane lateral tension on lipid structure and dynamics through atomistic molecular dynamics simulations of a fluid-phase lipid bilayer under a broad range of tensions (from zero to values just below rupture tension). Quantitative agreement of the simulation findings with available experimental values indicates that the simulation methodology used was robust and accurate in determining equilibrium properties of the lipid bilayer.

Key findings from the simulations are as follows. First, physiologically relevant tensions in the range of 0–15 mN m⁻¹ caused decreases in bilayer thickness in a linear fashion consistent with volume-incompressibility. Second, tension induced a significant increase in acyl chain interdigitation and a decrease in lipid order. Third, tension induces a significant decrease in electrostatic potential barrier (up to 80 mV at the highest tension), due to decreased ordering of both water and lipid dipoles. Fourth, the observed lateral diffusion coefficient of DPPC cannot be described satisfactorily using the free-area theory, across all tensions applied, due to a significant change in molecular shape and friction at high tensions. Finally, DiI has systematically lower lateral and rotational diffusion coefficients compared to DPPC, but the increase in each with tension is quantitatively similar for DiI and DPPC. Similarly, fluorescence lifetime of DiI, which depends on lipid order near the headgroups, appears to be a good indicator of tension in membranes.

These results have potential physiological implications. For instance, hydrophobic mismatch between lipids and proteins causes opening and closing of transmembrane stretch-activated ion channels.⁶⁷ Alternatively, forces may cause changes in the electrostatic potential of the bilayer, which in turn affects membrane channel conductance, ion and water transport through the lipid bilayer, protein conformation, and kinetics of membrane-bound enzymes.⁶⁸ For example, decrease in dipole potential leads to a decrease in dissociation of gramicidin channel dimers leading to increased sodium ion permeability.^53,69 Altered lipid mobility, due to force-induced changes in lipid packing, can also lead to changes in protein molecular mobility and change the kinetics of enzymatic reactions that require protein complex formation (e.g. dimerization).^70,71 Force-induced changes in lipid mobility are also associated with regulation of mitogen activated protein (MAP) kinase activity.^2,6 To explain the relationship between lipid mobility and membrane protein-mediated signaling, Nicolau et al.⁷² proposed that a local decrease in lipid viscosity, reflected in lipid mobility, temporarily corrals membrane proteins and increases their residence time and interaction kinetics leading to initiation of MAPK signaling pathways once a threshold residence time is reached.⁷³ Studies on model membranes have demonstrated that membrane tension promotes formation of large domains from micro-domains in order to minimize line tension developed at microdomain boundaries,^7,8 and there exists a critical pressure at which lipid phase separation into liquid-ordered and liquid-disordered domains is observed.⁷⁴ Taken together, these studies point to changes in bilayer structure and dynamics as a mechanism of force-induced biochemical signaling.

Future research will be needed to develop a new theory for tension-diffusion relationship that takes into account frictional and molecular shape changes. The current simulations not only provide additional quantitative insights into some of the well-studied bilayer properties (e.g. bilayer thickness, diffusion coefficient), but also lead to novel hypotheses related to membrane-mediated mechanotransduction in cells (e.g. interdigitation and electrostatic potential) that can be tested experimentally.

In addition, we tested which DiI fluorescence spectroscopic properties have potential as reporters of membrane tension effects on lipids. We observed that although DiI exhibited slower lateral and rotational diffusion compared to DPPC, its lateral and rotational diffusion increased with tension in a manner quantitatively similar to DPPC. This suggests that changes in DiI dynamics are good indicators of membrane tension. We also showed that hydration of the dye does not vary with packing, whereas the local viscosity experienced by the dye changes significantly. These results support the utility of DiI as a reporter of lipid packing and validate the use of DiI to label membrane cellular microdomains based on underlying heterogeneity in lipid order. Thus these findings offer new insights into the interpretation of fluorescence dynamics of DiI and lipids in lipid bilayer systems.