A filtered backprojection algorithm with characteristics of the iterative landweber algorithm

Abstract

Purpose: In order to eventually develop an analytical algorithm with noise characteristics of an iterative algorithm, this technical note develops a window function for the filtered backprojection (FBP) algorithm in tomography that behaves as an iterative Landweber algorithm.

Methods: Based on the formulation of the iterative Landweber algorithm, a frequency domain window function is derived for each iteration of the Landweber algorithm. The resultant window function has an index k, emulating the characteristics of the Landweber algorithm at the kth iteration. The window function is used to modify the ramp filter in the FBP algorithm.

Results: Computer simulations show that the windowed FBP algorithm with window function index k and the iterative Landweber algorithm iteration number k give similar reconstructions in terms of resolution and noise.

Conclusions: Analytical FBP algorithms are able to provide similar results to the iterative Landweber algorithm if the ramp filter in the FBP algorithm is modified by a set of specially designed window functions.

INTRODUCTION

The filtered backprojection (FBP) algorithm is simple and fast, and can be used to reconstruct images in nuclear medicine and x-ray CT.¹ However, without windowing, the FBP algorithm generally produces noisy images. An iterative algorithm (e.g., the iterative Landweber algorithm) that does not model the projection noise or does not model the projection noise correctly, can still outperform the FBP in terms of noise propagation control.^{2, 3} For this reason, the FBP algorithm has gradually been replaced by iterative image reconstruction algorithms.

The noise control strategies in an FBP algorithm and in an iterative algorithm are different. Usually, an analytic algorithm controls noise by selecting the filter’s cut-off frequency, while an iterative algorithm can control noise by selecting the iteration number.⁶ Another way to control noise in an iterative algorithm is to incorporate the noise model in the objective function and to use priors.^{4, 5, 6} As an initial step to improve the noise performance of the FBP algorithm, we link the FBP algorithm with an iterative reconstruction algorithm so that the FBP algorithm can “learn” from an iterative algorithm. Instead of selecting the cut-off frequency for the analytic filter function in the frequency domain, in Sec. 2, a shaping window function is designed for the FBP algorithm, according to each iteration of the iterative Landweber algorithm.

It turns out that the newly designed window function looks similar to the Metz filter,⁷ which has been shown by King et al. to be effective in controlling noise in SPECT images.⁸

METHODS

The Landweber algorithm solves a system of linear equations $\mathit{AX}=B$ by an iterative procedure

$$X^{(k+1)}=X^{(k)}+\alpha A^T(P-A{X}^{(k)}),$$ (1)

where A is the projection matrix, A^T is the backprojection matrix, P is the projection data vector, X is the image vector, X^(k) is the estimated image at the kth iteration, and α > 0 is the step size. Algorithm (1) is in the form of a gradient descent algorithm proposed as the solution to the unweighted (nonstatistical) minimum least squares problem, where A^T(P-AX) represents the gradient of the quadratic formulation (P-AX)^T(P-AX).

This recursive relation can be rewritten as a nonrecursive expression as

$$\begin{array}{c}\multicolumn{1}{c}{X^{(k+1)}=X^{(k)}+\alpha A^T(P-A{X}^{(k)})=\alpha A^{T}P+(I-\alpha A^{T}A)X^{(k)}=\alpha A^{T}P+(I-\alpha A^{T}A)[\alpha A^{T}P+(I-\alpha A^{T}A)X^{(k-1)}]=\alpha A^{T}P+(I-\alpha A^{T}A)\alpha A^{T}P+{(I-\alpha A^{T}A)}^2{X}^{(k-1)}=\alpha A^{T}P+(I-\alpha A^{T}A)\alpha A^{T}P+{(I-\alpha A^{T}A)}^2[\alpha A^{T}P+(I-\alpha A^{T}A)X^{(k-2)}]=\alpha A^{T}P+(I-\alpha A^{T}A)\alpha A^{T}P+{(I-\alpha A^{T}A)}^2\alpha A^{T}P+{(I-\alpha A^{T}A)}^3{X}^{(k-2)}=...=[I+(I-\alpha A^{T}A)+...+{(I-\alpha A^{T}A)}^k]\alpha A^{T}P+{(I-\alpha A^{T}A)}^{k+1}{X}^{(0)}=\left[\sum _{n=0}^k{(I-\alpha A^{T}A)}^n\right]\alpha A^{T}P+{(I-\alpha A^{T}A)}^{k+1}{X}^{(0)}.}\end{array}$$ (2)

If the initial image X⁽⁰⁾ is set to zero, the result from k iterations of the Landweber algorithm is

$$X^{(k)}=\alpha [\sum _{n=0}^{k-1}{(I-\alpha A^{T}A)}^n]A^{T}P.$$ (3)

This noniterative expression of the Landweber algorithm resembles a “backproject first, then filter” algorithm, in the sense that the projection data P are first backprojected by the operator A^T and then filtered by $\alpha [{\displaystyle \sum _{n=0}^{k-1}}{(I-\alpha A^{T}A)}^n]$. When the positive real number (i.e., step size) α is small enough, the Landweber algorithm will converge and we have

$$\alpha \left[\sum _{n=0}^{k-1}{(I-\alpha A^{T}A)}^n\right]\to {(A^{T}A)}^{-1}\mathrm{as}k\to \infty ,$$ (4)

if ${(A^{T}A)}^{-1}$ exists, otherwise ${(A^{T}A)}^{-1}$ is replaced by a generalized inverse. To guarantee convergence, the step size α should be chosen in the range of 0 < α < 2/σ_max, where σ_max is the largest singular value of A^TA. If the step size is too large, the algorithm will diverge. If the step size is too small, it will take too long for the algorithm to converge. In practice, the eigenvalue of is difficult to find, and the step size is empirically determined by testing different values of α. For a finite k, we have

$$\alpha \left[\sum _{n=0}^{k-1}{(I-\alpha A^{T}A)}^n\right]={(A^{T}A)}^{-1}[I-{(I-\alpha A^{T}A)}^k].$$ (5)

The proofs of the above equations are available in a review paper by Schafer et al.⁹

It is easy to see that the Landweber algorithm is a linear algorithm, but it may not be shift-invariant. The combined operator of projection-and-backprojection, A^TA, is almost shift-invariant in the central region of the image array, which can be verified by putting a point source in the image, and then performing the projection-backprojection operation. After the operation, the resultant blurred point source image is almost shift-invariant if the point source is close to the center of the image array. When the point source is close to the array edges, the blurred point source image is no longer shift-invariant.

The 1/r function is the theoretical point response function (PRF) for an ideal projection/backprojection pair. The matrix A^TA in the iterative Landweber algorithm uses a discrete projector and backprojector, which assume a finite pixel size and a finite image array. The PRF of A^TA is not 1/r everywhere due to the nonstationary property, and is not exactly 1/r due to the discretization effects. However, at the central region of the image array the PRF of A^TA can be accurately approximated by 1/r, which will be illustrated by computer simulations in the next section.

Another issue of consideration is where to compensate for this PRF: in the projection space or in the image space. As shown in image reconstruction textbooks,¹⁰ if the projection operator A is the line-integral (i.e., the Radon transform) in the two-dimensional (2D) space and A^T is the adjoint operator (i.e., the backprojection transform), the combined operator of projection-and-backprojection, A^TA, is the 2D convolution of the original image with a 2D kernel 1/r, where $r=\sqrt{x^2+y^2}$ in the x-y Cartesian coordinates. The 2D ramp filter is able to cancel the 1/r blurring effect.¹⁰ In this ideal situation, the (A^TA) operation is 1/r convolution, the (A^TA)⁻¹ operation is 2D ramp filtering, and $[I-{(I-\alpha A^{T}A)}^k]$ in Eq. 5 can be treated as a window function in the frequency domain

$$\begin{array}{c}\multicolumn{1}{c}{W_k({\nu }_x,{\nu }_y)=1-{(1-\frac{\alpha }{\Vert \nu \Vert })}^k,\text{with}\Vert \nu \Vert =\sqrt{{\nu }_x^2+{\nu }_y^2}.}\end{array}$$ (6)

where ν_x and ν_y are the frequencies with respect to x and y, respectively, and ν = (ν_x, ν_y) is the 2D frequency vector. Thus, the conceptual shift-invariant Landweber algorithm is equivalent to: first, backprojecting the data into the image domain; second, filtering the backprojected image with a 2D windowed ramp filter defined in Eq. 6.

In fact, a “backproject first, then filter” algorithm is equivalent to an FBP algorithm, which filters the projections first, then backprojects.¹⁰ The one-dimensional (1D) frequency domain filter in the FBP algorithm is the 1D profile of the 2D filter in the “backproject first, then filter” algorithm.¹⁰ The equivalence of the “backproject first, then filter” algorithm and FBP algorithm can be explained by using the central-slice theorem in tomography. The central slice theorem relates a 2D image with its 1D Radon transform in the Fourier domain. The 1D Fourier transform of the Radon transform at angle θ is equal to a slice (i.e., a 1D profile) with the angle θ through the origin of the 2D Fourier transform of the 2D image (see Fig. 1). Similarly, the backprojection of data at angle θ is to add a “central slice” of the 2D Fourier transform of the 2D image in the 2D Fourier space with the same angle θ. After backprjection is completed, the 2D Fourier space contains data that are nonuniformly distributed, looking like a bicycle wheel. At the center, the data are dense, and become less dense as the distance from center gets larger. The Fourier domain data density is proportional to the reciprocal of the distance. In order to make the density uniform, a 2D ramp filter can be used to weigh the data. The 2D ramp filter has a gain that is proportional to the distance to the center of the Fourier space. This is the “backprojection first, then filtering” algorithm. To achieve the same effect, one can preweigh the Fourier transform of the 1D Radon transform with a 1D ramp filter. After backprojection, the effective Fourier domain data density is uniform; this is the FBP algorithm. Therefore, ramp filtering can be either performed before or after backprojection. Therefore, an iterative-Landweber-equivalent FBP algorithm can be obtained, and the implementation steps are:

Figure 1.

Illustration of the 2D central slice theorem.

Step 1: Perform the 1D Fourier transform of the projection at each view.

Step 2: Filter the frequency domain data with a 1D windowed ramp filter

$$H_k({\nu }_t)=\left|{\nu }_t\right|·[1-{(1-\frac{\alpha }{\left|{\nu }_t\right|})}^k],$$ (7)

where ν_t is the frequency with respect to the linear variable on the 1D detector.

Step 3: Perform a 1D inverse Fourier transform of the filtered data.

Step 4: Perform the backprojection.

When k = ∞, Eq. 7 is the ramp filter in the conventional FBP algorithm. The idea of using window functions in the FBP algorithm is not new. Many window functions have been used by others, for example, the Hann window,¹¹ the Hamming window,¹² the Butterworth window,¹³ and so on. It is interesting to notice the similarity of the windowed ramp filter 6 and the Metz filter:

$$\mathit{Met}{z}_k({\nu }_x,{\nu }_y)=\frac{1-{(1-{\Vert \mathit{MTF}({\nu }_x,{\nu }_y)\Vert }^2)}^k}{\Vert \mathit{MTF}({\nu }_x,{\nu }_y)\Vert },$$ (8)

where MTF is a frequency domain modulation transfer function (i.e., the 2D Fourier transform of the image-domain point spread function(PSF)). King et al. showed that Metz filter performs well for nuclear medicine images in handling noise.^{7, 8} The main difference between the Metz filter and Eq. 6 is the square in the numerator of 8.

COMPUTER SIMULATION RESULTS

The Shepp-Logan head phantom¹ was used in computer simulation studies. A 1D parallel-hole detector was rotated over 180° with 120 views and 128 detector bins on the detector. The images were reconstructed in a 256 × 256 array, and the central 128 × 128 array was used for image display. Poisson noise was added to the projection data before image reconstruction. Two algorithms were used for image reconstruction: the iterative Landweber algorithm with α = 0.5 × 0.0000525 and the FBP algorithm with Eq. 7 as the frequency domain window function and α = 0.5. The values of the parameter α were selected independently for each algorithm by trial-and-error. A larger α value makes the algorithms converge faster, but can make the algorithms diverge if it is too large. The selection of the value of α is independent of the projection data noise. For the iterative algorithm, the upper limit of α is determined by the projection matrix A. For the FBP algorithm, the upper limit of α is determined such that the window function is always positive. Some computer simulation results are shown in Tables 1, TABLE II., where each image is displayed from its minimum image pixel value (black) to its maximum image pixel value (white). No post processing of the images was performed. The negative values in the images were not altered.

Table 1.

Comparison studies of the iterative Landweber algorithm and the windowed FBP algorithm. Noiseless data are used. The goal is to compare the image resolution for different index k.

Table 2.

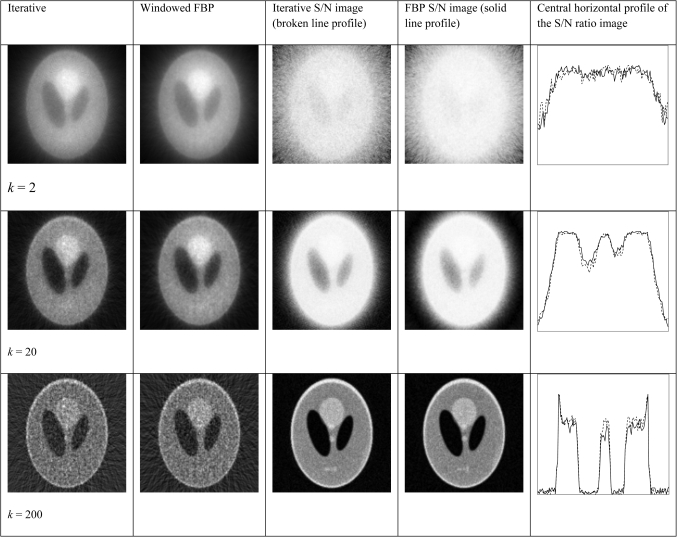
Comparison studies of the iterative Landweber algorithm and the windowed FBP algorithm. Noisey data are used. The goal is to compare the image noise for different index k. The signal-to-noise (S/N) ratio images use 100 noise realizations.

Images in Table TABLE I. used noiseless projections, and they are used to illustrate the resolution improvement as the index k gets larger. The profiles are drawn horizontally at the center of the images. The images are almost converged when k = 200. With the same index k, the iterative Landweber algorithm and the windowed FBP algorithm give almost the same resolution.

In Table TABLE II., Poisson noise was added to the projections. The average total count in the projections was 792 500 for each noise trial. Typical reconstructions are displayed in the left two columns. As the index k increases, the resolution improves, but the noise is more amplified. Signal-to-noise (S/N) ratio images were obtained by using 100 noise realizations and are displayed in the 3rd and 4th columns. In the S/N image each pixel represents the ratio of the mean value over the standard deviation. The S/N was calculated pixel-wise using the following formula:

$$\begin{array}{c}\multicolumn{1}{c}{\frac{S}{N}=\frac{\mathrm{True}\mathrm{image}\mathrm{pixel}\mathrm{value}}{\mathrm{Standard}\mathrm{deviation}\mathrm{of}\mathrm{the}\mathrm{reconstructed}\mathrm{image}\mathrm{pixel}\mathrm{value}}=\frac{\mathrm{True}}{\sqrt{\frac{1}{100}{\displaystyle \sum _{n=1}^{100}}{(\mathrm{Reco}{\mathrm{n}}_n-\mathrm{True})}^2}},}\end{array}$$ (9)

where n is the index of the noise realization.

As shown by the line profiles drawn horizontally across at the center of the S/N images, the iterative Landweber algorithm and the proposed FBP algorithm have almost the same noise property for the same index k. It is interesting to notice that when the algorithms are almost converged at k = 200, the S/N image is very similar to the density image itself.

CONCLUSIONS

In order to eventually develop an analytical algorithm with noise characteristics of an iterative algorithm, this paper derived an FBP window function with an index k that can emulate the iterative Landweber algorithm of k iterations. In deriving the windowed FBP algorithm, we assumed that the projector/backprojector PRF to be shift-invariant, while in an actual Landweber algorithm the PSF of the projector/backprojector is not exactly shift-invariant, especially at locations close to the image array edges. If the image array is much larger than the object (e.g., the image array size is twice as large as the object size) and the object is at the center of the array, the PRF of the matrix A^TA for an iterative algorithm in the image region can be considered shift-invariant and very closed to 1/r. Our computer simulations showed that the reconstructed images and noise textures are very similar with the same index k for the iterative Landweber algorithm and the proposed FBP algorithm. Since an analytical algorithm is much faster than an iterative algorithm, it is of significance to develop an analytic algorithm that can control noise as well as an iterative algorithm.

The proposed method is applicable to imaging geometries that have a shift-invariant PRF. It is expected that the proposed window function method can be extended to Feldkamp’s algorithm¹⁴ that is an approximate cone-beam reconstruction algorithm for the circular focal-point trajectory and to Katsevich’s algorithm¹⁵ that is an exact cone-beam reconstruction algorithm for the helical trajectory. In both Feldkamp’s and Katsevich’s algorithms, the PRF is shift-invariant. We are currently working on the extension of the current method to regulate noise propagation and to incorporate Bayesian prior information. The results are encouraging and will be reported in different publications. However, the proposed method has its limitations in the situations where the imaging PRF is shift-variant, for example, the projections are truncated, the view-angles are limited, or the attenuation (in emission tomography) is nonuniform.