Abstract
Purpose: Acquisition of laser range scans of an organ surface has the potential to efficiently provide measurements of geometric changes to soft tissue during a surgical procedure. A laser range scanner design is reported here which has been developed to drive intraoperative updates to conventional image-guided neurosurgery systems.
Methods: The scanner is optically-tracked in the operating room with a multiface passive target. The novel design incorporates both the capture of surface geometry (via laser illumination) and color information (via visible light collection) through a single-lens onto the same charge-coupled device (CCD). The accuracy of the geometric data was evaluated by scanning a high-precision phantom and comparing relative distances between landmarks in the scans with the corresponding ground truth (known) distances. The range-of-motion of the scanner with respect to the optical camera was determined by placing the scanner in common operating room configurations while sampling the visibility of the reflective spheres. The tracking accuracy was then analyzed by fixing the scanner and phantom in place, perturbing the optical camera around the scene, and observing variability in scan locations with respect to a tracked pen probe ground truth as the camera tracked the same scene from different positions.
Results: The geometric accuracy test produced a mean error and standard deviation of 0.25 ± 0.40 mm with an RMS error of 0.47 mm. The tracking tests showed that the scanner could be tracked at virtually all desired orientations required in the OR set up, with an overall tracking error and standard deviation of 2.2 ± 1.0 mm with an RMS error of 2.4 mm. There was no discernible difference between any of the three faces on the lasers range scanner (LRS) with regard to tracking accuracy.
Conclusions: A single-lens laser range scanner design was successfully developed and implemented with sufficient scanning and tracking accuracy for image-guided surgery.
INTRODUCTION
An ongoing problem in the field of image-guided neurosurgery is the measurement and compensation of intraoperative brain shift. It is well understood that there is often significant movement of brain tissue between the time of preoperative imaging and the time of resection of soft tissue.1, 2 As the most common strategy for image-guidance relies solely on registering preoperative tomograms with the physical intraoperative coordinate frame, brain shift reduces navigational accuracy.3, 4 Efforts to address the problem of brain shift have included methods to characterize intraoperative tissue deformation. Intraoperative imaging modalities are often utilized to provide updates to the pre-operative surgical plan derived from higher-resolution magnetic resonance (MR) or computed tomography (CT) images.5, 6, 7 There has also been a movement toward using intraoperative ultrasound for shift measurement, as in the SonoWand8 (Trondheim, Norway) and BRAINLAB (Ref. 9) (Munich, Germany) systems.10, 11 While these imaging systems do provide a quantitative measurement of brain movement, methods of compensating for shift in real-time for use in surgical guidance have not yet reached maturation.
Movement of the cortical surface is an attractive metric for brain shift, as it is readily observed and can provide intuition on the positions of internal structures of the brain. Any method which can capture and digitize the intraoperative surface of the patient could be used to provide quantitative measurements of shift. Once the surface has been acquired, it can be used to drive a number of shift compensation strategies. These strategies can include rigid or nonrigid registration of the surface to preoperative imaging to provide a corrective transformation to the guidance system.12, 13, 14 Another approach is to use the acquired surface to drive a biomechanical model of the brain, which provides displacement updates throughout the imaged tissue.15, 16 Sources of data may include intraoperative imaging modalities (such as intraoperative MR, CT, or ultrasound) or surface acquisition methods such as lasers range scanners (LRS). Each of these methods may be used to provide patient-specific boundary conditions for the mathematical model of the brain and thus present customized guidance to the surgeon. Regardless of the method used, real-time guidance requires that data acquisition be both fast and accurate.
LRS systems are traditionally used for geometric measurement of objects for which tactile means of measurement are either undesirable or infeasible.17, 18, 19 As soft tissue deforms when contacted, an LRS lends itself very well to surgical applications as a way of measuring geometry. Laser range scanners have been used for surface capture in a variety of procedures such as orthodontics, cranio-maxillofacial surgery, liver surgery, and neurosurgery. Table TABLE I. summarizes a list of publications that examine the integration of various LRS devices into image-guided procedures.
Table 1.
Recent examples of LRS integration into image-guided procedures.
| Year | Author | Procedure | Application |
|---|---|---|---|
| 2000 | Commer et al.31 | orthodontics | tooth position tracking |
| 2003 | Audette et al.32 | neurosurgery | registration, brain deformation tracking |
| 2003 | Cash et al.20 | liver surgery | registration of liver surface |
| 2003 | Marmulla et al.33 | cranio-maxillofacial surgery | face registration |
| 2003 | Meehan et al.34 | cranio-maxillofacial surgery | facial tissue deformation tracking |
| 2003 | Miga et al.35 | neurosurgery | cortical surface registration |
| 2005 | Cash et al.36 | liver surgery | liver deformation tracking |
| 2005 | Sinha et al.21 | neurosurgery | cortical surface deformation tracking |
| 2006 | Sinha et al.22 | neurosurgery | cortical surface registration |
| 2008 | Cao et al.29 | neurosurgery | comparison of registration methods |
| 2009 | Ding et al.23 | neurosurgery | semiautomatic LRS cloud registration |
| 2009 | Shamir et al.14 | neurosurgery | face registration |
| 2010 | Dumpuri et al.30 | liver surgery | liver deformation compensation |
Conventional LRS devices work by sweeping a line of laser light onto the object of interest, and the surface is digitized by capturing the shape of the laser line with a digital camera and using triangulation to form a point cloud. Calibration is done to determine how points detected by the digital camera are mapped to the physical location of the laser line. The digital camera may also be used to collect texture information from the surface and map it onto the geometry to form a textured point cloud.20, 21, 22 LRS systems are attractive for assisting image-guidance because they can provide relatively fast and accurate sampling of the entire exposed surface of the brain. Sun et al. have also used stereopsis via operating microscopes to capture the brain surface to address the problem of deformation.18 This intraoperative information can be used both to align image-to-physical space as well as to track deformations. Alignment can be facilitated by tracking a conventional LRS in 3D space via optical targets attached to the exterior enclosure. In addition to assisting with image-to-physical alignment, the role of an LRS in brain shift compensation is well defined by its ability to quickly acquire a series of scans over the course of surgery in order to track deformation. Work has also been done to use the texture associated with the point clouds to nonrigidly register a series of LRS scans, thus providing measurements of brain shift.21, 23 Although the accuracy of LRS data has been encouraging, efforts to improve LRS-driven model-updated systems have highlighted aspects of conventional LRS design which could be altered to increase system fidelity and ease of use.
We present two fundamental contributions in this paper: (1) a tracked single-charge-coupled device (CCD) LRS design and (2) an accuracy assessment of the new device. LRS devices which provide field-of-view colored point clouds are usually constructed from a two-lens design in which one lens captures geometric information from the laser line, and the other lens captures color information via a digital camera. The use of separate lenses unfortunately makes it necessary to create an additional calibration to map the 2D color information onto the 3D scanner point cloud. We present here a solution to this problem in the form of a single-lens system design. The novel LRS design was implemented and evaluated with the intent to use in cortical surface tracking; however, the LRS could be used to characterize any anatomy with sufficient surgical access.
MATERIALS AND METHODS
Sections 2, 2 describe the two production phases of the new LRS: (1) the design and development decisions which composed the final system, and (2) an analysis of its scanning and tracking accuracy.
Design and development
This work presents the results of a collaborative effort to design a new laser range scanner to capture both geometric and field-of-view color information without the need for two lenses. Working in conjunction with engineers at Pathfinder Therapeutics, Inc. (Nashville, TN, USA),24 we developed a single-lens solution which is unique in that existing commercial systems such as 3D Digital (Sandy Hook, CT, USA) (Ref. 25) or ShapeGrabber (Ottawa, ON, Canada) (Ref. 26) products capture both geometric and color information with two lenses and two CCDs, or do not collect color information at all. The older designs not only carry additional cost, but also require the overlay of color information onto the 3D point cloud. This process is another source of error, as each lens imparts a unique geometric distortion on the captured scene, and each lens also has a different line-of-sight to the target. One solution considered was to capture the field with a single-lens and feed the geometry and color to two CCDs via a beam splitter. Ultimately it was decided that this option was less attractive in terms of cost, size, and complexity compared to a single-CCD approach.
The novel single-CCD solution here utilizes a Basler Pilot camera (Basler Vision Technologies, Ahrensburg, Germany) running at 1920 × 1080 at 32 fps. This camera is part of a family of cameras with uniform physical dimensions and electrical interfaces, which enables other camera models to be swapped out to meet varying scanning accuracy or speed requirements. To capture the geometry of the field, a standard red laser with a wavelength of 635 nm and a uniform line generator was selected. This wavelength was selected because of the wide availability of diode modules as well as its known reflectivity on the organs of interest (primarily brain and liver). One drawback to using a red laser is that the Bayer color filter pattern (which filters pixels to record color as either red, green, or blue before interpolation generates the final image) used on the CCD only assigns one out of every four pixels to capture red light, which effectively reduces the resolution of the scanner. Since the Bayer filter pattern assigns two out of every four pixels to green light, there was some consideration to using a green laser. However, this would result in reduced contrast of the laser on the background image in some of our intended applications, such as scanning the liver surface, as a red-brown object would tend to absorb green light. The laser line is swept across the field-of-view using a mirror attached to a standard galvanometer. The galvanometer chosen can rotate over a 40° arc with approximately 15 bit precision and a settling time of about 0.1 ms. Using a video frame rate of 32 Hz, the maximum exposure length is 31.25 ms. The galvanometer is allowed to settle to its next resting position during the small window of time when the CCD is transferring data out to the frame buffer and is not actively collecting photons.
In order to maximize the scanning speed, the full frame rate of the CCD is used. At 8 bits per pixel, the CCD outputs data at a rate of 531 Mb/s. Conventionally, this high data rate would lead to a digital signal processor (DSP) based processing solution such that the point cloud could be calculated in the scanner and then transmitted to a host PC upon scan completion. However, by leveraging modern CPUs and high-speed communications links, the raw video frames are transferred to the host PC via gigabit ethernet for processing and calculation of the final textured point cloud.
The external enclosure of the LRS was designed to be as small as possible to accommodate the following hardware: camera, lens, white-light illuminator, galvanometer, galvanometer driver board, motherboard containing the microcontroller with support circuitry, and passive tracking targets (see Fig. 1). Within the enclosure, an internal structure was created to hold the camera, laser, and galvanometer perfectly rigid with respect to each other, as even slight changes in their relative positions would invalidate the scanner calibration. Although the calibration process and fixture are proprietary in nature, it can be stated that it is a semi-automated procedure in which the scanner is trained to measure distance, determine various optical parameters specific to the hardware used, and correct for geometric distortions.
Figure 1.
The novel LRS, showing the single CCD design from the front (top left picture) and the tracking marker configuration from the top of the scanner (top right picture). The bottom diagram shows the improved functionality of the single CCD system (right) in comparison with a dual-CCD system (left).
The tracking electronics were originally designed to be compatible with the NDI Certus position sensor (Northern Digital Inc., Waterloo, ON, Canada) (Ref. 27) for active optical tracking. This first design included active tracking infrared emitting diodes (IREDs) that were the same height as the scanner enclosure. However, initial testing indicated that the error in triangulating the position of these diodes was too great, which led to the design and construction of an alternate configuration of IREDs. The attachment design of the marker housings was chosen to be modular, such that they could be changed easily depending on the application without needing to modify the scanner enclosure itself. The initial marker geometry on the LRS was replaced due to preliminary problems with marker visibility in the operating room. The active marker housings were replaced with reflective spheres compatible with the NDI Polaris Spectra position sensor for passive tracking. Specifically, a passive target was added to the top face of the LRS to increase the number of viable poses in the tracking volume, as it was not always possible to position the LRS within the confines of normal OR workspace such that at least one of the rear targets was visible to the tracking system. Other tracking systems could also be used, such as the NDI Polaris Vicra, but the relatively large work volume of the Polaris Spectra allows for greater flexibility in positioning the equipment, as it is not always possible to position the tracking system close to the patient, in our specific application. The passive configuration is currently preferred in our work due to the ease of use of wireless tools and the existence of passive tracked surgical instruments and reference rigid bodies in the StealthStation (Fridley, MN, USA) (Ref. 28) workflow, currently used by our clinical colleagues at Vanderbilt University Medical Center. While the accuracy of active tracking was attractive, much consideration was given to the tradeoff between achievable accuracy and ease of integration (since the introduction of wired tools was intrusive to surgical workflow), and it was decided that passive tracking provided sufficient accuracy and minimized disruption in the OR.
Laser range scanner evaluation
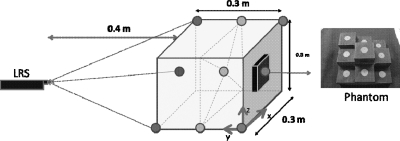
The LRS accuracy was characterized over the course of two tests. The first test was designed to evaluate the accuracy of the geometric range scans. A multilevel platform phantom (see Fig. 2) was scanned by a coordinate measurement machine such that the distances between disc centers were known to within a tolerance of 0.05 mm. The phantom was first used to determine the effective work volume of the scanner by the ability of the LRS to construct a geometric point cloud as it swept the laser across the phantom surface. Once the work volume was defined the geometric accuracy test was performed by mounting the LRS horizontally on an optical breadboard, facing the phantom. The LRS was held completely stationary, the phantom was moved systematically throughout the work volume, and the LRS scanned the phantom multiple times at each position. Nine positions in the work volume were used, consisting of three positions on each of three planes (see Fig. 2) such that at least six of the discs were visible in any scan (noncentral discs were occasionally outside of the LRS work volume due to field-of-view limitations). Ten scans were taken at each position for a total of 90 scans. From the acquired point clouds, the geometric centroids of each visible disc at each position were calculated. Then, the relative distances between centroids were compared to the known disc distances.
Figure 2.
Geometric accuracy test setup (left) showing the nine positions of the precision phantom (right).
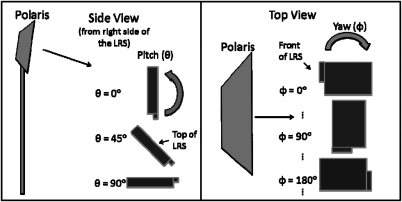
The second test was to characterize the ability of the LRS to be tracked with respect to a global coordinate system defined by the tracking system and a reference target. The first part of this test was to observe the tracking behavior of the scanner. A rigid body file describing the LRS passive sphere configuration was generated by characterizing the LRS as a passive three-face tool within the NDI software. Each face was composed of four of the twelve markers and was divided into the planes formed by the top panel and two posterior panels, respectively (see Fig. 1). The visibility of the spheres was tested by placing the camera and the LRS in “typical” operating room configurations. The camera was mounted horizontally at a height of approximately 2 m, whereas the LRS was mounted at a height of 1 m at a horizontal distance of 1.5 m directly in front of the tracking system. The relative positions of the tracking system and LRS were kept constant with respect to each other while the orientation of the LRS was incremented in its pitch (ψ) and yaw (θ) to simulate plausible orientations in the operating room (see Fig. 3). The pitch was varied between 0°, 45°, and 90° with respect to the floor, and at each pitch angle the yaw was incremented by 30° through a full 360° rotation. The number of spheres tracked at each orientation was recorded using software provided by the manufacturer of the tracking system.
Figure 3.
Orientations used in tracking visibility test. For reference, a pitch of 0° and a yaw of 0° denotes the orientation in which the top of the LRS is facing toward the camera, whereas a pitch of 90° and yaw of 180° denotes a horizontal orientation facing away from the camera.
The second tracking test was designed to observe the robustness of the rigid body file description for the passive targets attached to the LRS. A calibration was first performed to determine the transformation placing the raw point cloud into the coordinate frame of the tracked LRS rigid body.20 The calibration is performed by scanning the block phantom described above, and then calculating the geometric centroids of the discs in the point cloud. Using the tracked LRS rigid body as the reference coordinate system, the locations of the discs are also digitized with a tracked pen probe. The scan centroid points are then fitted to the probe points with a standard least-squares method to produce a 4 × 4 calibration matrix which transforms scan points into the space of the LRS. The navigation software then automatically transforms the point cloud into the space of the reference target as the LRS is tracked. This means that all scans of the patient will be in a common coordinate frame.
After the scanner was calibrated, the LRS was positioned horizontally facing the block phantom such that the phantom was in the center of the LRS work volume. The LRS, block phantom, and reference target were fixed in place as shown in Fig. 4. The Polaris camera was then moved between 30 positions distributed approximately 360° around the LRS such that the camera tracked each of the three faces of the LRS for ten of the scans. A scan of the phantom was acquired for each position of the camera, and the disc centroids were calculated in the coordinate frame of the reference target. In addition, the phantom discs were digitized with a tracked pen probe each time the phantom was scanned. These points were considered the gold standard positions for the discs, and the point cloud centroids were compared against them. While this gold standard was simple and convenient to create, it did inherently add error to the test, as there was tracking error associated with tracking the pen probe itself. There was also error in digitizing the discs, as placing the tip of the probe in the disc centers was a manual process. A more robust gold standard would entail a precision grid spanning the work volume of the tracking system throughout which the phantom and LRS setup could be stepped such that its position relative to the camera was known with higher precision than achievable with passive optical tracking. However, the pen probe method used above was deemed to be more practical for this study. The 30 scans were analyzed as a group and in the three subsets corresponding to the different faces to determine variability in tracking the LRS.
Figure 4.
Experimental setup used for the tracking accuracy test, showing the fixed phantom and LRS (left) and the Polaris Spectra optical tracking system (right).
RESULTS
The geometric accuracy test determined a mean error and standard deviation of 0.25 ± 0.40 mm, with an RMS error of 0.47 mm for the set of 90 scans acquired. The 95% confidence interval for this error was 0.24–0.27 mm. The maximum error encountered in this dataset was 1.6 mm.
The face visibility test indicated that in all of the tested LRS orientations except for one (in which the LRS was positioned vertically with its top face pointing away from the camera, i.e., a pitch of 0° and yaw of 180°) that the camera was able to track at least one of the faces. It should be noted that the NDI software (and navigation systems in general) only tracks a single face of a multiface tool at a time. As each face on the LRS contains four markers, four is the maximum number of usable markers at any particular position or orientation.
The second part of the tracking test resulted in a set of 30 scans such as the example in Fig. 5. The nine disc centroids in each scan were determined and compared to the corresponding points collected by the pen probe. The results of this comparison are shown in Table TABLE II., which shows the error across all 30 scans, as well as the error among just the ten scans acquired while tracking each of the respective faces on the LRS. The mean overall error (across all scans) was 2.2 ± 1.0 mm, with an RMS tacking error of 2.4 mm. The 95% confidence interval for this error across all 30 scans was 2.1–2.4 mm. When the data were examined per face, it was found that Face 1 (rear right face) had a mean error of 2.1 ± 1.2 mm with an RMS error of 2.4 mm. Face 2 (top face) had a mean error of 2.5 ± 1.1 mm with an RMS error of 2.7 mm. Face 3 (rear left face) had a mean error of 2.3 ± 1.0 mm with an RMS error of 2.5 mm.
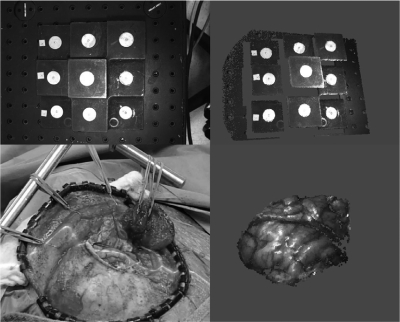
Figure 5.
Bitmap view of the phantom captured by the LRS (top left) and textured point cloud rotated slightly to show the 3D geometry of the data (top right). The bottom left shows an example of intraoperative data collection with the laser line sweeping across a brain surface. The corresponding LRS point cloud reconstructed from this scan is shown on the bottom right.
Table 2.
Comparison of the arithmetic and RMS tracking error over all 30 scans (total) and also over the separate groups of ten scans taken while tracking each face (Face 1 is the rear right face, Face 2 is the top face, and Face 3 is the rear left face). The errors were calculated by comparing the centroid points of the phantom discs against points collected with a tracked pen probe.
| Mean tracking error (mm) | RMS tracking error (mm) | |
|---|---|---|
| Total | 2.2 ± 1.0 | 2.4 |
| Face 1 | 2.1 ± 1.2 | 2.4 |
| Face 2 | 2.5 ± 1.1 | 2.7 |
| Face 3 | 2.3 ± 1.0 | 2.5 |
DISCUSSION AND CONCLUSIONS
The results of the geometric accuracy test show that the average geometric scanning error is about half a millimeter with submillimetric standard deviation, which is acceptable for the intended applications. A previous generation LRS using a dual-CCD design was reported to have a scanning accuracy of 0.3 mm at best, and its performance degraded outside of the center of the work volume at least in part due to the computational error in aligning the texture and geometric information from their respective CCDs.21 It is possible to increase the resolution of the point cloud through the scanner API by collecting more range points, at the cost of scanning speed.
The face visibility test showed that four markers were visible on average to the tracking system at virtually all of the tested positions, which provided enough markers to compute the LRS position and orientation in the reference frame. It was important to conduct this test in order to determine practical positioning limitations of the LRS with respect to the optical tracking system in the operating room. Equipment logistics are often beyond the control of research engineers in the operating room due to the requirements of normal surgical workflow, which necessitates flexibility in the positions in which the LRS can be tracked.
The second part of the tracking test showed that the error in LRS point cloud locations in the reference frame is on the order of normal optical tracking error for passive systems. The tracking accuracy of the previous generation scanner used by Sinha et al. was similar at 1.0 ± 0.5 mm.21 However, the LRS in that case utilized actively-emitting IREDs rather than the passively tracked solution used for the new LRS. The data in Table TABLE II. show the mean error in point cloud locations in the reference frame for all 30 scans and for each subset of 10 scans per tracked face. It is apparent that the error is approximately equivalent across all three faces, which implies that the accuracy of scan tracking is insensitive to the orientation in which the LRS is viewed by the optical tracking system (for configurations used in the OR).
CONCLUSIONS
The design goal of a single-CCD LRS capable of capturing both geometric and color information was met in terms of possessing submillimetric scanning accuracy and tracking accuracy that is typical of passive tracking systems (on the order of 2 mm). It was evaluated with regard to its scanning accuracy and tracking ability using a precision phantom and found to be appropriate for image-guided procedures. While the overall error in the system is approximately 2 mm (primarily contributed by the tracking of the LRS), this performance is similar to the 3D Digital LRS used by Dumpuri et al. to provide a TRE of 2–4 mm in liver phantom targets, and also used by Cao et al. to provide a TRE of about 2 mm for cortical targets.29, 30 We have integrated the LRS into our guidance software and are currently evaluating its contribution to our shift correction system.
ACKNOWLEDGMENTS
This work is funded by the National Institutes of Health: Grant Nos. R01 NS049251 of the National Institute for Neurological Disorders and Stroke and R01 CA162477 of the National Cancer Institute. Dr. Miga is a cofounder and holds ownership interest in Pathfinder Therapeutics Inc. which is currently licensing rights to approaches in image-guided liver surgery and has incorporated the reported laser range scanner within their product line.
References
- Nabavi A., Black P. M., Gering D. T., Westin C. F., Mehta V., R. S.Pergolizzi, Jr., Ferrant M., Warfield S. K., Hata N., Schwartz R. B., W. M.WellsIII, Kikinis R., and Jolesz F. A., “Serial intraoperative magnetic resonance imaging of brain shift,” Neurosurgery 48, 787–797; discussion 797–788 (2001). [DOI] [PubMed] [Google Scholar]
- Roberts D. W., Hartov A., Kennedy F. E., Miga M. I., and Paulsen K. D., “Intraoperative brain shift and deformation: A quantitative analysis of cortical displacement in 28 cases,” Neurosurgery 43, 749–758; discussion 758–760 (1998). 10.1097/00006123-199810000-00010 [DOI] [PubMed] [Google Scholar]
- Hill D. L. G., Maurer C. R., Maciunas R. J., Barwise J. A., Fitzpatrick J. M., and Wang M. Y., “Measurement of intraoperative brain surface deformation under a craniotomy,” Neurosurgery 43, 514–526 (1998). 10.1097/00006123-199809000-00066 [DOI] [PubMed] [Google Scholar]
- Nauta H. J., “Error assessment during “image guided” and “imaging interactive” stereotactic surgery,” Comput. Med. Imaging Graph. 18, 279–287 (1994). 10.1016/0895-6111(94)90052-3 [DOI] [PubMed] [Google Scholar]
- Black P. M., Moriarty T., E.AlexanderIII, Stieg P., Woodard E. J., Gleason P. L., Martin C. H., Kikinis R., Schwartz R. B., and Jolesz F. A., “Development and implementation of intraoperative magnetic resonance imaging and its neurosurgical applications,” Neurosurgery 41, 831–842; discussion 842–835 (1997). 10.1097/00006123-199710000-00013 [DOI] [PubMed] [Google Scholar]
- Butler W. E., Piaggio C. M., Constantinou C., Niklason L., Gonzalez R. G., Cosgrove G. R., and Zervas N. T., “A mobile computed tomographic scanner with intraoperative and intensive care unit applications,” Neurosurgery 42, 1304–1310; discussion 1310–1301 (1998). 10.1097/00006123-199806000-00064 [DOI] [PubMed] [Google Scholar]
- Lunsford L. D. and Martinez A. J., “Stereotactic exploration of the brain in the era of computed tomography,” Surg. Neurol. 22, 222–230 (1984). 10.1016/0090-3019(84)90003-X [DOI] [PubMed] [Google Scholar]
- www.mison.no.
- www.brainlab.com.
- Gronningsaeter A., Kleven A., Ommedal S., Aarseth T. E., Lie T., Lindseth F., Lango T., and Unsgard G., “SonoWand, an ultrasound-based neuronavigation system,” Neurosurgery 47, 1373–1379; discussion 1379–1380 (2000). 10.1097/00006123-200012000-00021 [DOI] [PubMed] [Google Scholar]
- Lindseth F., Kaspersen J. H., Ommedal S., Lango T., Bang J., Hokland J., Unsgaard G., and Hernes T. A., “Multimodal image fusion in ultrasound-based neuronavigation: Improving overview and interpretation by integrating preoperative MRI with intraoperative 3D ultrasound,” Comput. Aided Surg. 8, 49–69 (2003). 10.3109/10929080309146040 [DOI] [PubMed] [Google Scholar]
- Henderson J. M., Smith K. R., and Bucholz R. D., “An Accurate and Ergonomic Method of Registration for Image-Guided Neurosurgery,” Comput. Med. Imaging Graph. 18, 273–277 (1994). 10.1016/0895-6111(94)90051-5 [DOI] [PubMed] [Google Scholar]
- Raabe A., Krishnan R., Wolff R., Hermann E., Zimmermann M., and Seifert V., “Laser surface scanning for patient registration in intracranial image-guided surgery,” Neurosurgery 50, 797–801; discussion 802–793 (2002). 10.1097/00006123-200204000-00021 [DOI] [PubMed] [Google Scholar]
- Shamir R. R., Freiman M., Joskowicz L., Spektor S., and Shoshan Y., “Surface-based facial scan registration in neuronavigation procedures: A clinical study Clinical article,” J. Neurosurg. 111, 1201–1206 (2009). 10.3171/2009.3.JNS081457 [DOI] [PubMed] [Google Scholar]
- Roberts D. W., Miga M. I., Hartov A., Eisner S., Lemery J. M., Kennedy F. E., and Paulsen K. D., “Intraoperatively updated neuroimaging using brain modeling and sparse data,” Neurosurgery 45, 1199–1206 (1999). 10.1097/00006123-199911000-00037 [DOI] [PubMed] [Google Scholar]
- Škrinjar O. and Duncan J., Information Processing in Medical Imaging (Springer, Berlin/Heidelberg, 1999), pp. 42–55.
- Isheil A., Gonnet J. P., Joannic D., and Fontaine J. F., “Systematic error correction of a 3D laser scanning measurement device,” Opt. Lasers Eng. 49, 16–24. 10.1016/j.optlaseng.2010.09.006 [DOI] [Google Scholar]
- Sun H., Roberts D. W., Farid H., Wu Z., Hartov A., and Paulsen K. D., “Cortical surface tracking using a stereoscopic operating microscope,” Neurosurgery 56, 86–97; discussion 86–97 (2005) 10.1227/01.NEU.0000146263.98583.CC. [DOI] [PubMed] [Google Scholar]
- Van Gestel N., Cuypers S., Bleys P., and Kruth J.-P., “A performance evaluation test for laser line scanners on CMMs,” Opt. Lasers Eng. 47, 336–342. 10.1016/j.optlaseng.2008.06.001 [DOI] [Google Scholar]
- Cash D. M., Sinha T. K., Chapman W. C., Terawaki H., Dawant B. M., Galloway R. L., and Miga M. I., “Incorporation of a laser range scanner into image-guided liver surgery: Surface acquisition, registration, and tracking,” Med. Phys. 30, 1671–1682 (2003). 10.1118/1.1578911 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinha T. K., Dawant B. M., Duay V., Cash D. M., Weil R. J., Thompson R. C., Weaver K. D., and Miga M. I., “A method to track cortical surface deformations using a laser range scanner,” IEEE Trans. Med. Imaging 24, 767–781 (2005). 10.1109/TMI.2005.848373 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinha T. K., Miga M. I., Cash D. M., and Weil R. J., “Intraoperative cortical surface characterization using laser range scanning: Preliminary results,” Neurosurgery 59, ONS368–ONS376; discussion ONS376–ONS367 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding S. I., Miga M. I., Noble J. H., Cao A., Dumpuri P., Thompson R. C., and Dawant B. M., “Semiautomatic registration of pre- and postbrain tumor resection laser range data: Method and validation,” IEEE Trans. Biomed. Eng. 56, 770–780 (2009). 10.1109/TBME.2008.2006758 [DOI] [PMC free article] [PubMed] [Google Scholar]
- www.pathsurg.com.
- www.3ddigitalcorp.com.
- www.shapegrabber.com.
- www.ndigital.com
- www.medtronic.com.
- Cao A., Thompson R. C., Dumpuri P., Dawant B. M., Galloway R. L., Ding S., and Miga M. I., “Laser range scanning for image-guided neurosurgery: Investigation of image-to-physical space registrations,” Med. Phys. 35, 1593–1605 (2008). 10.1118/1.2870216 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumpuri P., Clements L. W., Dawant B. M., and Miga M. I., “Model-updated image-guided liver surgery: Preliminary results using surface characterization,” Prog. Biophys. Mol. Biol. 103, 197–207 (2010). 10.1016/j.pbiomolbio.2010.09.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Commer P., Bourauel C., Maier K., and Jager A., “Construction and testing of a computer-based intraoral laser scanner for determining tooth positions,” Med. Eng. Phys. 22, 625–635 (2000). 10.1016/S1350-4533(00)00076-X [DOI] [PubMed] [Google Scholar]
- Audette M. A., Siddiqi K., Ferrie F. P., and Peters T. M., “An integrated range-sensing, segmentation and registration framework for the characterization of intra-surgical brain deformations in image-guided surgery,” Comput. Vis. Image Underst. 89, 226–251 (2003). 10.1016/S1077-3142(03)00004-3 [DOI] [Google Scholar]
- Marmulla R., Hassfeld S., Luth T., Mende U., and Muhling J., “Soft tissue scanning for patient registration in image-guided surgery,” Comput. Aided Surg. 8, 70–81 (2003). 10.3109/10929080309146041 [DOI] [PubMed] [Google Scholar]
- Meehan M., Teschner M., and Girod S., “Three-dimensional simulation and prediction of craniofacial surgery,” Orthod Craniofac Res. 6(Suppl 1), 102–107 (2003). 10.1034/j.1600-0544.2003.242.x [DOI] [PubMed] [Google Scholar]
- Miga M. I., Sinha T. K., Cash D. M., Galloway R. L., and Weil R. J., “Cortical surface registration for image-guided neurosurgery using laser-range scanning,” IEEE Trans. Med. Imaging 22, 973–985 (2003). 10.1109/TMI.2003.815868 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cash D. M., Miga M. I., Sinha T. K., Galloway R. L., and Chapman W. C., “Compensating for intraoperative soft-tissue deformations using incomplete surface data and finite elements,” IEEE Trans. Med. Imaging 24, 1479–1491 (2005). 10.1109/TMI.2005.855434 [DOI] [PubMed] [Google Scholar]