Abstract
Purpose: The purpose of this study was to develop an automated lung segmentation method for computerized detection of lung nodules in digital chest tomosynthesis.
Methods: The authors collected 45 digital tomosynthesis scans and manually segmented reference lung regions in each scan to assess the performance of the method. The authors automated the technique by calculating the edge gradient in an original image for enhancing lung outline and transforming the edge gradient image to polar coordinate space. The authors then employed a dynamic programming technique to delineate outlines of the unobscured lungs in the transformed edge gradient image. The lung outlines were converted back to the original image to provide the final segmentation result. The above lung segmentation algorithm was first applied to the central reconstructed tomosynthesis slice because of the absence of ribs overlapping lung structures. The segmented lung in the central slice was then used to guide lung segmentation in noncentral slices. The authors evaluated the segmentation method by using (1) an overlap rate of lung regions, (2) a mean absolute distance (MAD) of lung borders, (3) a Hausdorff distance of lung borders between the automatically segmented lungs and manually segmented reference lungs, and (4) the fraction of nodules included in the automatically segmented lungs.
Results: The segmentation method achieved mean overlap rates of 85.7%, 88.3%, and 87.0% for left lungs, right lungs, and entire lungs, respectively; mean MAD of 4.8, 3.9, and 4.4 mm for left lungs, right lungs, and entire lungs, respectively; and mean Hausdorrf distance of 25.0 mm, 25.5 mm, and 30.1 mm for left lungs, right lungs, and entire lungs, respectively. All of the nodules inside the reference lungs were correctly included in the segmented lungs obtained with the lung segmentation method.
Conclusions: The method achieved relatively high accuracy for lung segmentation and will be useful for computer-aided detection of lung nodules in digital tomosynthesis.
Keywords: Digital tomosynthesis, computer-aided detection, lung segmentation, dynamic programming
INTRODUCTION
Chest radiography has been the most common imaging modality for the detection of lung nodules because of its advantages of low radiation dose and low cost. However, the detection sensitivity for lung nodules in chest radiography is relatively low, because normal anatomic structures such as ribs and heart may obscure lung nodules. Computed tomography (CT) is considerably more accurate in detecting lung nodules than chest radiography; however, CT has significantly higher radiation dose and higher cost. Digital chest tomosynthesis is an imaging modality that has some of the advantages of volumetric imaging, such as improving conspicuity of lung nodules, but with lower radiation exposure and cost than CT.1 In several clinical trials, digital chest tomosynthesis has shown a three-fold improvement in detection sensitivity for pulmonary nodules relative to conventional radiography,2, 3 and has been introduced commercially for chest imaging recently. Despite the advantage of improved sensitivity, radiologists must review many more images than with conventional radiography and the sensitivity for detection of nodules in chest tomosynthesis is about 30% less than with CT.3 Computer-aided diagnosis (CAD) systems have shown benefit to improve the detection performance of pulmonary nodules in radiography and CT.4, 5 White and his colleagues6 have indicated that a commercially available CAD scheme (OnGuard 3.0; Riverain Medical) has the ability to identify about 50% undetected nodules that were missed by radiologists in chest radiography. Therefore, we will develop a CAD system to detect lung nodules in digital chest tomosynthesis. In this paper, we present a novel method for a key step of the CAD approach: accurate segmentation of lungs in digital chest tomosynthesis.
An accurate lung segmentation method can remove irrelevant tissues surrounding lungs and thus can significantly reduce the computational cost and the false positive rate in nodule detection. The difference in intensity between lung parenchyma and surrounding tissue was often used for the segmentation of lungs in chest radiography. Xu et al.7 developed a method to accurately determine in chest radiography a ribcage that contains both left lung and right lung by identifying the lung top edges using vertical profiles of the images and the left and right ribcage edges using horizontal profiles of the images. Armato et al.8 segmented lungs in chest radiography by use of a thresholding method, in which the threshold was automatically determined by analyzing the histogram of images. Pietka et al.9 segmented lungs with thresholding technique as well but followed by a lung border smoothing routine using cubic spline interpolation and mathematical morphologic techniques. In lung segmentation method developed by Duryea et al.,10 the gray-scale of chest radiography was first remapped to improve the image contrast between the lung field and surrounding tissue, and the outlines of lungs were then determined by identifying the edge points with greatest contrast on the horizontal profiles. Carreira et al.11 and Brown et al.12 developed rule-based lung segmentation schemes, in which the image features and clinical information were combined and used for the identification of lung regions. In studies of McNitt-Gray et al.13 and Tsujii et al.,14 artificial neural network technique was employed for lung segmentation. The features of relative pixel address, pixel intensity, gray-level gradient, and local image texture were used for the classification of lung and nonlung pixels. van Ginneken et al.15 proposed a hybrid lung segmentation method that combined a rule-based scheme with a pixel classifier. The rule-based image segmentation system roughly identified the lung regions. A k-nearest-neighbor based pixel classifier was then employed to refine the segmentation results by correcting the incorrectly segmented pixels by the rule-based segmentation system. In Vittitoe et al.’s approach,16 a Markov random field (MRF) model was used to incorporate spatial and textural information of lung regions. An iterated conditional modes method17 was then used to determine the lung regions based on the MRF features. Li et al.18 developed a two-step method for lung segmentation. They first identified the obvious edges of lung and then applied an iterative edge-tracking algorithm to form a smooth lung boundary. Shi et al.19 first identified the lung regions by use of scale invariant feature transform and then refined lung boundary by use of longitudinal radiographies from the same patient. Deformable model-based methods, especially active shape models (ASM)-based techniques, were widely used in lung segmentation approaches developed by Xu et al.,20 Seghers et al.,21 Ginneken et al.,22, 23, 24 and Shi et al.25 These ASM-based approaches were able to accurately segment lungs and preserve the general topology of lungs.
In spite of many lung segmentation methods described above, lung segmentation in digital chest tomosynthesis is a new topic and has not been investigated adequately. Li and Dobbins26 were the first to segment ribcages in digital chest tomosynthesis. In their method, points on the ribcage border were determined on each row and each column at places where the differences in intensity between adjacent pixels were greater than a threshold. However, the segmented ribcages include some nonlung structures, such as the mediastinum.
We developed in this study, a novel method for accurate lung segmentation in digital chest tomosynthesis by use of a dynamic programming technique. In this method, we first estimated the centers of left lung and right lung in central slice of a tomosynthesis scan by use of a thresholding technique and used these centers of lungs to convert original slices into a polar coordinate space. Next, we segmented the lungs in the converted image of the central slice of a tomosynthesis scan with dynamic programming algorithm. The outlines of lungs obtained in the central slice were then employed to guide the segmentation of lungs in other slices. By use of information in adjacent slices, the lungs can be accurately segmented in all the slices of a tomosynthesis scan with a relatively stable shape.
MATERIALS AND METHODS
Database
This study was approved by the Institutional Review Board at Duke University. Forty-five digital chest tomosynthesis scans from a larger NIH-funded study were collected at Duke University Medical Center with a prototype chest tomosynthesis system built on a commercial-grade CsI/a-Si flat-panel detector (GE Healthcare, Milwaukee, WI).3, 26 The position of the detector was fixed with a source-to-image distance of 180 cm; a custom-built apparatus moves the x-ray tube vertically from − 10° to + 10°.3 For each subject, 71 projection images were acquired in 11 s at 120 kVp. Sixty-three slice images were reconstructed from the 71 projection images by use of a matrix inversion tomosynthesis algorithm.3 The reconstructed images had a 1024 × 1024 pixel matrix with a pixel size of 0.4 × 0.4 mm and a slice interval of 5 mm. The range of pixel values was between 0 and 600. A sliding average of seven adjacent slices was performed immediately after all slices were reconstructed to reduce noise and low-contrast tomosynthesis artifacts. Thus, the effective thickness of each slice was 35 mm and there was a 30 mm overlap between adjacent slices.
We used the first 20 scans of our database as the training dataset to adjust the parameters in the lung segmentation algorithm and the other 25 scans as the test dataset to evaluate the performance of the segmentation algorithm.
Lung segmentation in central slice
Our segmentation method was composed of two steps. In the first step, we segmented the lungs in the central slice (slice 32) of a digital tomosynthesis scan because of the absence of rib overlap. We then used the segmented lungs in the central slice to guide the segmentation of lungs in noncentral slices, in order to obtain accurate and consistent lung regions across slices. In each slice, the left lung and right lung were segmented separately.
Rescaling the original slice images
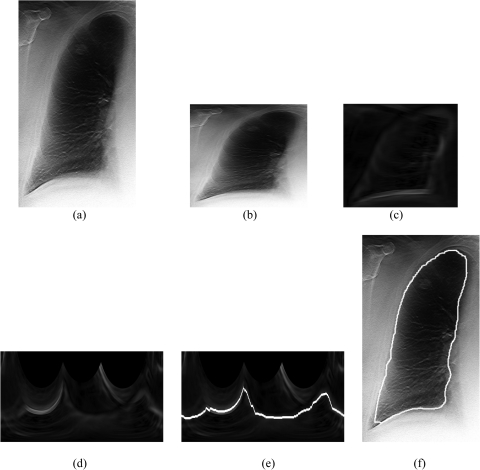
The first step in our lung segmentation method is to reduce the original slice of 1024 × 1024 pixels to a rescaled image of 512 × 256 pixels by use of the average value of 2 × 4 pixels in the original slice. Doing so can significantly save processing time and will have little negative impact on the accuracy of lung segmentation, as lung is a very large object. We reduced the image 4 times in vertical direction to make the width and height of a lung comparable, so that dynamic programming can be utilized appropriately. Figure 1a shows the right lung of a subject in the central slice of a digital tomosynthesis scan. The left lung was not shown in Fig. 1a. Figure 1b shows the rescaled lung. Please note that for clarity, Fig.1b was shown twice as large as its actual size. The rationale for rescaling the lungs will be further discussed in Sec. 4.
Figure 1.
(a) Original image of a right lung in a digital tomosynthesis slice, (b) rescaled image of the lung, (c) edge gradient image, (d) transformed edge gradient image in polar coordinate space, (e) the delineated outline of the lung in the transformed image, and (f) the segmented lung in the original image.
Generation of edge gradient images
We used the edge gradient of pixel intensities to identify outlines of lungs. We first designed two 11 × 11 kernels in Eq. 1 to calculate the edge in horizontal and vertical directions. In the kernel Kx for calculating the horizontal edge, the elements in the first two rows and the last two rows were assigned a value of +1 and −1, respectively, and those in other columns were assigned a value of 0. The kernel Ky for calculating vertical edge was designed similarly. Figure 1c shows the magnitude of the edge gradient for Fig. 1b by use of the two kernels. The magnitude was then used for determining lung outlines with dynamic programming. In this study, we tried using kernels of 5 × 5, 7 × 7, 9 × 9, 11 × 11, and 13 × 13 pixels for determining edge gradient and we found that the kernels of 11 × 11 pixels provided the highest accuracy for lung segmentation on the training dataset.
| (1) |
Transformation of lungs to a polar coordinate space
To make it easier for us to employ dynamic programming for delineation of lung outlines, we transformed each lung in edge gradient image to a polar coordinate space at an approximate center of the lung. The center of a lung was automatically estimated in the rescaled image Fig. 1b by use of an iterative thresholding method. The goal of this thresholding method is to determine a threshold that roughly separates the pixels inside lung regions and the pixels outside the lung regions. A binary image was created in the first iteration by use of an initial threshold of 300. A pixel was assigned a value of “1” in the binary image if the corresponding pixel value in the original image is less than the threshold. The initial lungs in the binary image represented only a part of the lung regions, because the threshold “300” is conservative for the segmentation of lung regions in chest tomosynthesis images. Subsequent iterations added more pixels to the initial lungs by incrementing the threshold by 10. To prevent lungs from merging with irrelevant regions, image border was checked at each iteration. If any pixels on the border of the image were included in the lung regions, the iterative thresholding routine was terminated and the lung regions obtained from the previous iteration were used to calculate the centroids of the lungs, which were used as the estimated centers of the lungs.
We then transformed a circular ROI at the estimated center of the lung to a polar coordinate space. The radius of the circular ROI was empirically set to 30 cm to include the lungs with a variety of sizes. We generated 360 radial lines originating from the center of the ROI and arranged the pixels on the radial lines column-by-column to generate a transformed image in Fig. 1d. Because a point on a radial line may not be located at the center of a pixel in Fig. 1c, the value of the point on the radial line was determined by a linear interpolation method using the four nearest pixels in Fig. 1c. The horizontal axis of the transformed image represents the angle of each radial line ranging from 0° to 360°, and the vertical axis represents the distance from a pixel to the center of the ROI. It is apparent in Fig. 1d that the outline of the lung extends roughly in horizontal direction and thus can be delineated conveniently by use of dynamic programming.
Delineation of lung outline using dynamic programming
We used dynamic programming for delineating the optimal outline of a lung in the transformed image. The optimal outline of a lung was defined as a “path” with a minimum cumulative cost; the path consisted of one and only one pixel (edge point) on each column from the leftmost column to the rightmost column of the transformed image Fig. 1d. Appendix defines the cumulative cost of a path and describes the dynamic programming algorithm to search for the path with the minimum cumulative cost. Figure 1e shows the outline of the lung in the transformed image determined by dynamic programming.27, 28
Reconstruction of the outline of a lung
The outline of a lung in the transformed polar coordinate space was then transformed back to the Cartesian coordinate space. By use of the angle of a radial line (the x-axis of the transformed image) and the distance between the center of the ROI and the edge point (the y-axis), each edge point on the radial line had a corresponding pixel in Cartesian space. We could thus obtain a series of points along the outline of a lung in the original image. We connected the adjacent points with a straight line to generate a closed outline of the lung. We then created a binary lung mask by filling the interior of the lung outline with “1” and by assigning a value of “0” to other pixels. We applied a morphological closing filter with a circular kernel (radius = 8 pixels) to the lung mask to smooth the outline of the lung. The contour of the smoothed lung mask was used as the final lung outline, as shown in Fig. 1f.
Lung segmentation in noncentral slices
The method for lung segmentation in noncentral slices is similar to that in the central slice, with two additional steps. In the first step, the centroid of a segmented lung in the central slice was used as the estimated center of the lung in an adjacent noncentral slice for polar coordinate transformation. In the second step, the outline of the segmented lung in the central slice was mapped to the transformed edge gradient image of the adjacent noncentral slice. The pixels on each column of the transformed edge gradient image were multiplied with a one dimensional Gaussian window function with a sigma of 4, which was centered at the “mapped outline point” of the central slice. We compared the accuracy of lung segmentation on the training dataset for different sigmas of 1, 2, 3, 4, 5, 6, and 7 and found that the Guassian window function with a sigma of 4 provided the highest accuracy. The mapped outline point was multiplied with a larger weighting factor and pixels far away from the mapped outline point had a smaller weighting factor. Therefore, the Gaussian window function could suppress the edge gradients in the noncentral slice that were far away from the mapped outline point of the central slice. It could also assure that the shape of the segmented lungs in all slices would remain relatively stable in spite of the effect of ribs and image noise. The above process of using the segmented lungs in the adjacent slice was applied iteratively from the central slice to the anterior and posterior slices.
Evaluation of lung segmentation
We created reference lungs to assess the accuracy of our lung segmentation method. The reference lungs were manually delineated by JW (4 years of experience in chest imaging) on an LCD screen and were confirmed (in all scans) and revised (in 6 scans) by QL (14 years of experience). The heart and diaphragm were excluded from the reference lungs. In order to make the manual delineation manageable, we delineated the lungs in every 8th slice. It should be noted that lung segmentation was applied to all slices; however, the evaluation of lung segmentation was applied to only selected slices. We employed an overlap rate of lung regions, a mean absolute distance (MAD) of lung borders, and a Hausdorff distance30, 31 of lung borders as performance metrics to measure the agreement between the segmented lung volume and the reference lung volume. The overlap rate was defined as the ratio of the intersection to the union between an automatically segmented lung and its corresponding reference lung. The value of the overlap rate ranges from 0%, no overlap between the segmented lung and the reference lung, to 100%, a perfect overlap. The MAD was calculated by measuring the average distance from all points on the border of the automatically segmented lung to the border of the reference lung. The smaller the MAD, the closer the points on the border of the segmented lung and the points on the border of the reference lung. To assess the local discrepancy between an automatically segmented lung and a reference lung, the Hausdorff distance between the border of the segmented lung and that of the reference lung was calculated. The mean value for each of the above three metrics for a tomosynthesis scan was defined as the average of the corresponding metric in the selected slices. Please note that, by definition, the mean Hausdorff distance for both lungs is greater than that of either left lung or right lung.
Because we will develop in the future a CAD system to detect lung nodules in digital chest tomosynthesis by use of this lung segmentation method, we employed the fraction of nodules included in the automatically segmented lungs as another performance metric. For this purpose, an independent chest radiologist with 24 years experience used CT examinations to identify and confirm all nodules in tomosynthesis as the reference standard of nodules. The chest radiologist identified 123 nodules from 45 patients in our database. Among the 123 nodules, 111 nodules were included in the reference lungs and 12 nodules were located in regions outside the referenced lungs, including the retrocardiac, mediastinal, and retrodiaphragmatic regions. The 111 nodules included in the reference lungs were employed to determine the fraction of nodules included in the automatically segmented lungs.
RESULTS
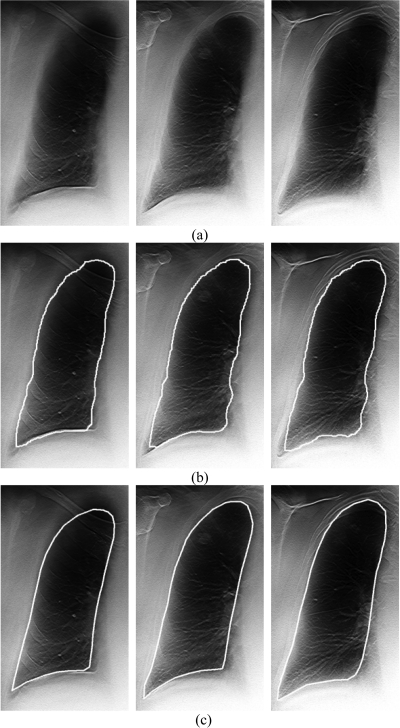
Our lung segmentation method achieved good segmentation results for the lungs in our database. Figure 2 shows (a) three slices of a lung in a digital tomosynthesis scan, (b) the segmented lung, and (c) the corresponding reference lung in the three slices. The image in the middle shows the lung in the central slice. The overlap rate, MAD, and Hausdorff distance for this lung were 90.3%, 3.3 mm, and 28.0 mm, respectively.
Figure 2.
(a) Three slices of a right lung in a digital tomosynthesis scan, (b) the segmented lung, and (c) the reference lung. The image in the middle shows the lung in the central slice, the image in the left shows the lung in the slice 40 mm above the central slice, and the image in the right show the lung in the slice 40 mm below the central slice. The overlap rate, MAD, and Hausdorff distance between the segmented lung and reference lung were 90.3%, 3.3 mm, and 28.0 mm, respectively.
Table TABLE I. shows the mean, standard deviation, and range of the overlap rates, MAD, and Hausdorff distance for the 25 test scans in our database. The mean overlap rate for left lungs, right lungs, and entire lungs were 85.7%, 88.3%, and 87.0%, respectively; the mean MAD for left lungs, right lungs, and entire lungs were 4.8, 3.9, and 4.4 mm, respectively; and the mean Hausdorff distances for left lungs, right lungs, and entire lungs were 25.0, 25.5, and 30.1 mm, respectively. By use of two tailed t-tests for unpaired data, we found that there was no significant difference in the mean overlap rate (p = 0.15), MAD (p = 0.30), and mean Hausdorff distances (p = 0.89) between the left lungs and right lungs.
Table 1.
The statistics of overlap rates, MAD, and Hausdorff distance for left lungs, right lungs, and entire lungs in the test dataset.
| Left lungs | Right lungs | Both lungs | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Overlap (%) | MAD (mm) | Hausdorff distance (mm) | Overlap (%) | MAD (mm) | Hausdorff distance (mm) | Overlap (%) | MAD (mm) | Hausdorff distance (mm) | |
| Mean | 85.7a | 4.8b | 25.0c | 88.3a | 3.9b | 25.5c | 87.0 | 4.4 | 30.1 |
| SD | 8.0 | 4.1 | 16.9 | 3.5 | 1.2 | 7.2 | 5.1 | 2.3 | 16.3 |
| Max | 90.8 | 24.3 | 101.4 | 93.5 | 8.0 | 39.0 | 92.0 | 15.2 | 101.4 |
| Min | 49.2 | 3.2 | 13.4 | 75.9 | 2.6 | 15.3 | 64.6 | 2.9 | 16.7 |
p = 0.15, two tailed t-test.
p = 0.30.
p = 0.89.
Table TABLE II. shows the overlap rate, MAD, and Hausdorff distance of lungs in anterior slices and posterior slices of the 25 test scans in our database. We used the first 32 slices (slice 1–32) of a scan as anterior ones and the last 32 slices (slice 32–63) as posterior ones. For lungs in anterior slices and posterior slices, the mean overlap rates were 87.9% and 86.0% (p = 0.05), respectively; the mean MAD were 4.0 and 4.7 mm (p = 0.10), respectively; and the mean Hausdorff distances were 24.3 and 28.9 mm (p = 0.30), respectively. Thus, there is no significant difference in the performance levels between lungs in anterior slices and posterior slices.
Table 2.
The overlap rates, MAD, and Hausdorff distance for lungs in the test dataset in anterior and posterior slices.
| Anterior | Posterior | |||||
|---|---|---|---|---|---|---|
| Overlap (%) | MAD (mm) | Hausdorff distance (mm) | Overlap (%) | MAD (mm) | Hausdorff distance (mm) | |
| Mean | 87.9a | 4.0b | 24.3c | 86.0a | 4.3b | 28.9c |
| SD | 5.1 | 2.4 | 16.8 | 5.1 | 0.9 | 16.7 |
| Max | 93.3 | 16.6 | 101.4 | 91.9 | 5.6 | 87.2 |
| Min | 62.0 | 2.4 | 13.8 | 64.3 | 2.9 | 28.9 |
p = 0.05, two tailed t-test.
p = 0.10.
p = 0.30.
Table TABLE III. shows the overlap rate, MAD, and Hausdorff distance of lungs in tomosynthesis scans of the 25 test scans with small (<30 mm) and large (≥30 mm) Hausdorff distances. For lungs with small Hausdorff distance and large Hausdorff distance, the mean overlap rates were 88.3% and 84.5% (p = 0.18), respectively; the mean MAD were 3.6 and 5.6 mm (p = 0.14), respectively; and the mean Hausdorff distances were 23.0 and 42.8 mm, respectively. Thus, for the segmented lungs with small and large Hausdorff distances, there is no significant difference in the mean overlap rate and mean MAD.
Table 3.
The overlap rates, MAD, and Hausdorff distance for lungs in the test dataset with small Hausdorff distance (<30 mm) and large Hausdorff distance (≥30 mm).
| Lungs with small Hausdorff distance (< 30 mm) | Lungs with large Hausdorff distance (≥30 mm) | |||||
|---|---|---|---|---|---|---|
| Overlap (%) | MAD (mm) | Hausdorff distance (mm) | Overlap (%) | MAD (mm) | Hausdorff distance (mm) | |
| Mean | 88.3a | 3.6b | 23.0 | 84.5a | 5.6b | 42.8 |
| SD | 1.8 | 0.4 | 3.4 | 7.8 | 3.6 | 22.2 |
| Max | 92.0 | 4.3 | 29.0 | 89.2 | 15.2 | 101.4 |
| Min | 85.9 | 2.9 | 16.7 | 64.6 | 3.8 | 30.0 |
p = 0.18, two tailed t-test.
p = 0.14.
We evaluated the performance levels of our method for segmentation of lungs without and with lung diseases other than lung nodules. One of the authors (Qiang Li, 14 years of experiences in computerized lung nodule detection) identified seven digital tomosynthesis scans with lung diseases other than nodules in the 25 test scans using both the CT examinations and digital tomosynthesis scans. Four scans contain interstitial lung disease (high attenuation) in a large section of lungs; two scans contain pleural effusion (high attenuation) that caused the overall distortion of lung boundaries, especially at the basal segment of the lungs; and one scan contains emphysema (low attenuation). Table TABLE IV. shows that for the lungs without and with other lung diseases, the mean overlap rates were 88.2% and 83.8% (p = 0.25), respectively; the mean MAD were 3.8 and 5.8 mm (p = 0.41), respectively; and the mean Hausdorff distances were 27.3 and 37.5 mm (p = 0.88), respectively. It is apparent from Table TABLE IV. that the segmentation performance level for lungs with other diseases was slightly lower than that without other lung diseases. This result is consistent with our expectation.
Table 4.
The overlap rates, MAD, and Hausdorff distance for lungs in the test dataset without and with lung abnormalities other than lung nodules.
| Lungs without lung abnormalities | Lungs with lung abnormalities | |||||
|---|---|---|---|---|---|---|
| Overlap (%) | MAD (mm) | Hausdorff distance (mm) | Overlap (%) | MAD (mm) | Hausdorff distance (mm) | |
| Mean | 88.2a | 3.8b | 27.3c | 83.8a | 5.8b | 37.5c |
| SD | 1.7 | 0.5 | 7.1 | 9.0 | 4.2 | 28.9 |
| Max | 92.0 | 4.7 | 38.8 | 90.3 | 15.2 | 101.4 |
| Min | 85.6 | 2.9 | 16.7 | 64.6 | 3.3 | 19.8 |
p = 0.25, two tailed t-test.
p = 0.41.
p = 0.88.
All of the 111 nodules inside the reference lungs were correctly included in the segmented lungs obtained with our lung segmentation method. Therefore, our lung segmentation method would be a reliable first step for automated detection of lung nodules in unobscured lung regions.
DISCUSSIONS
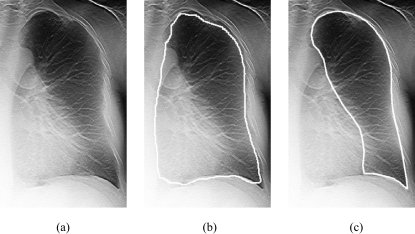
The primary reason for low segmentation accuracy in the left lungs is the presence of the heart. For most of the scans, the retrocardiac lung regions were excluded from the lungs segmented by our lung segmentation method. However, the retrocardiac lung was included as part of the left lung in one case as shown in Figs. 3a, 3b and led to the lowest overlap rate of 49.2%. The automated method actually more accurately determined the true lung area in this case by including the retrocardiac region, but in doing so gave an artificially poor overlap value with the manual segmentation method that did not include retrocardiac lung. In spite of this, we decided to exclude the heart from the reference lungs in this initial study for two reasons. First, trying to include the retrocardiac region in the segmented lungs may significantly increase the risk of including other irrelevant tissues, such as chest wall and mediastinum. Second, even if the heart is included, the detection of the nodules obscured by heart will be a more difficult task and will require a dedicated detection scheme, which is not our current goal. Nonetheless, it is clear that future work will need to be done to modify our algorithm to include true lung in retrocardiac and retrodiaphragmatic regions. A similar challenge also applied to all CAD method using conventional radiography.
Figure 3.
Segmentation result of a left lung with low overlap rate. (a) Original image, (b) the segmented lung, and (c) the reference lung. The overlap rate, MAD, and Hausdorff distance between the segmented lung and the reference lung was 49.2%, 24.3 mm, and 101.4 mm, respectively.
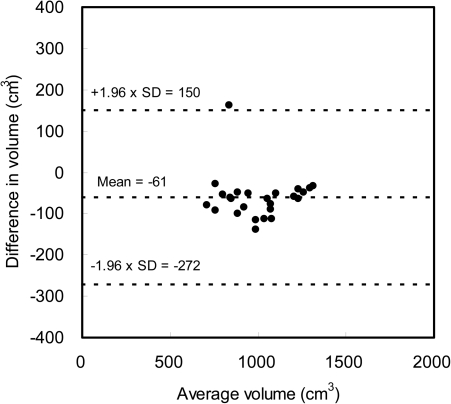
Under segmentation in costophrenic angle regions is a weakness of our lung segmentation method. Figure 4 illustrated a Bland-Altman scatter plot of the volume of reference lungs versus the difference of lung volume between automatically segmented lungs and reference lungs. Please note that the volume was calculated in selected slices, where the reference lungs were delineated. The mean difference was − 61 cm3, with the limits of agreement between −272 and 150 cm3. For most of the testing tomosynthesis scans, the lung volume of automatically segmented lungs is smaller than that of the reference lungs due to the under segmentation in costophrenic angle regions, except one including the retrocardiac lung regions in the segmented lungs (Fig. 3). The ASM-based approaches (Xu et al.,20 Seghers et al.,21 van Ginneken et al.,22, 23, 24 and Shi et al.25) may provide more accurate delineation of the lung boundary at costophrenic angle regions. However, we did not employ an ASM-based approach because (1) we did not have a large database to create accurate lung shape models, (2) in order to segment lungs in each slice of tomosynthesis scan using ASM, we need to create different shape models for different slices, which would make our segmentation scheme unmanageable and impractical, and (3) the under segmentation of costophrenic angle regions should have very limited effect on computerized nodule detection.
Figure 4.
Bland-Altman scatter plot for the volume of reference lungs and automatically segmented lungs.
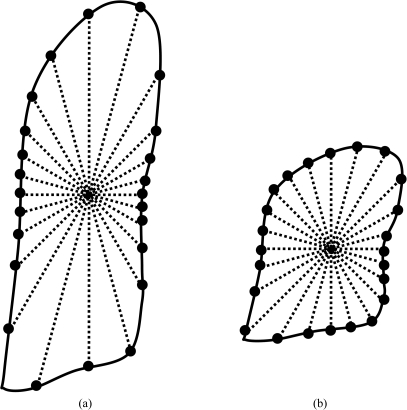
Before we transformed the lungs to polar coordinate space, we compressed the lungs by half in the vertical direction. If we did not compress the lungs, the intersection points between lung outlines and radial lines described in Sec. 2B3 would be denser on the two sides than on the top or bottom of the lung outline, as shown in Fig. 5a. This would affect the performance of dynamic programming algorithm. By compressing the original image by half in the vertical direction, the density of intersection points became approximately even on all segments of the lung outlines, as shown in Fig. 5b.
Figure 5.
Illustration of intersection points between the outline of a lung and radial lines in (a) a lung with original size and (b) a lung after compression in vertical direction. The intersection points in (b) are roughly evenly distributed on the lung outline.
The in-plane resolution of slice images in the digital tomosynthesis scans was high, whereas the image resolution across slices was low due to the limited angle of x-ray tube movement. In addition, the sliding average of seven adjacent slices blurred the border of lungs and led to overlapping of lungs and ribs in the first and last few slices of the lungs. Therefore, we first segmented the lungs in the central slice and then used the segmented lungs in the central slice to guide the lung segmentation in noncentral slices. This strategy made the shape of segmented lungs more stable and more consistent across slices than independent processing of each slice.
Our database contained only 45 digital tomosynthesis scans. A larger database may help us to improve, and reliably estimate, the performance of our lung segmentation method. Furthermore, we created the reference lungs in every 8th slice rather than every slice in each scan. Although we might more reliably estimate the performance of the segmentation algorithm by creating reference lungs in more slices, doing so would make it hard for us to manage our evaluation process; more importantly, the conclusion of this study would not likely change by use of more reference lungs in more slices than those we currently use. For example, the overlap rates for the segmented lungs in Fig. 2b were 90.9%, 91.4%, and 90.3%, respectively, when the reference lungs were delineated in every 2nd, 4th, and 8th slice.
CONCLUSIONS
Accurate lung segmentation is important for improving the performance of lung disease detection in digital chest tomosynthesis. Our automated lung segmentation method achieved good performance and would be useful for the development of CAD schemes in digital chest tomosynthesis.
ACKNOWLEDGMENTS
The authors thank Dr. H. Page McAdams for identifying nodules in the tomosynthesis scans. This work was supported by USPHS Grant No. R01 CA113870. Acquisition of the clinical images was supported by USPHS Grant No. R01 CA80490. Partial grant support for chest tomosynthesis research was also provided by GE healthcare. General Electric and Duke University jointly hold a patent on an element of tomosynthesis data acquisition. CAD technologies developed by Qiang Li and his colleagues have been licensed to companies including R2 Technologies, Riverain Medical Group, Median Technology, Mitsubishi Space Software Co., General Electric Corporation, and Toshiba Corporation. It is the policy of Duke University that investigators disclose publicly actual or potential significant financial interests that may appear to be affected by research activities.
APPENDIX: DYNAMIC PROGRAMMING FOR LUNG SEGMENTATION
Local cost
Dynamic programming is an optimization method and is often used for tracing object outlines and thin objects, such as road network in satellite photographs.27, 28, 29 In this study, we employed dynamic programming to determine an optimal outline with the lowest cumulative cost. The optimal outline of a lung consisted of one and only one edge point on each of the 360 columns of the transformed edge gradient image in Fig. 1d. The cumulative cost was defined as the sum of local costs of all edge points on the lung outline. The local cost of each pixel (edge point) on the outline was composed of two components, namely, an internal cost and an external cost. The internal cost measured the smoothness between edge points on adjacent columns and was given by
where xi and yi are the x- and y-coordinates of the ith edge point on the ith column of the transformed image; m and n are the width and height of the transformed image, respectively. The denominator was a normalization term. A curve with a relatively smooth shape would have a low internal cost.
The external cost of an edge point was determined by its edge strength. We used the negative value of edge gradient G (xi, yi) at each pixel (xi, yi) as its external cost,
where G (xi, yi) was determined by use of the kernels defined in Eq. 1. Thus, a pixel with stronger edge strength was assigned a lower external cost.
The local cost of an edge point (xi, yi) was defined as the weighted sum of the internal and external costs
where wint and wexe represent the weighting factors for the internal cost and external cost, respectively. We empirically selected a combination of wint = 1 and wext = 0.1, based on the accuracy of lung segmentation on the training dataset.
Cumulative cost
The cumulative cost of an outline was dynamically calculated on a column-by-column basis from the first column through the last column of the transformed image. First, the cumulative cost c(x1, y1) of each pixel (x1, y1) on the first column was initialized with its external cost only, because its previous pixel did not exist and its internal cost could not be defined.
The cumulative cost of a pixel (xi, yi) on other columns was then calculated by a recursive process,
Thus, the cumulative cost at a pixel on the ith column was defined as the minimum sum of the cumulative cost at the (i – 1)th column and the local cost at (xi, yi). The parameters t1 and t2 were used to control the searching interval in the vertical direction, so that a large “jump” between two edge points on adjacent columns was prevented. In this study, t1 = − 10 and t2 = + 10.
Backward searching of the optimal outline
After calculating the cumulative costs for all edge points on the last column, a backward searching strategy was used to determine the optimal outline path. We first selected in the last column a pixel with the lowest cumulative cost. This cumulative cost represents the total cost of the optimal “path” from the first to the last column. We then traced the path backward from the selected pixel on the last column m to find a pixel on the column (m − 1); this procedure was repeated to find the pixels on the optimal “path” on columns (m − 2), …, 1. The pixels on the optimal path were then connected together to form the outline of the lung.
References
- J. T.DobbinsIII and Godfrey D. J., “Digital x-ray tomosynthesis: Current state of the art and clinical potential,” Phys. Med. Biol. 48, R65–R106 (2003). 10.1088/0031-9155/48/19/R01 [DOI] [PubMed] [Google Scholar]
- Vikgren J., Zachrisson S., Svalkvist A., Johnsson A. A., Boijsen M., Flinck A., Kheddache S., and Bath M., “Comparison of chest tomosynthesis and chest radiography for detection of pulmonary nodules: Human observer study of clinical cases,” Radiology 249, 1034–1041 (2008). 10.1148/radiol.2492080304 [DOI] [PubMed] [Google Scholar]
- J. T.DobbinsIII, McAdams H. P., Song J. W., Li C. M., Godfrey D. J., D, DeLong, Paik S. H., and Martinez-Jimenez S., “Digital tomosynthesis of the chest for lung nodule detection: Interim sensitivity results from an ongoing NIH-sponsored trial,” Med. Phys. 35, 2554–2557 (2008). 10.1118/1.2937277 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doi K., “Overview on research and development of computer-aided diagnostic schemes,” Semin Ultrasound CT MR 25, 404–410, (2004). 10.1053/j.sult.2004.02.006 [DOI] [PubMed] [Google Scholar]
- Li Q., Li F., Suzuki K., Shiraishi J., Abe H., Engelmann R., Nie Y., MacMahon H., and Doi K., “Computer-aided diagnosis in thoracic CT,” Semin Ultrasound CT MR 26, 357–363, (2005). 10.1053/j.sult.2005.07.001 [DOI] [PubMed] [Google Scholar]
- White C., Flukinger T., Jeudy J., and Chen J., “Use of a computer-aided detection system to detect missed lung cancer at chest radiography,” Radiology 252, 273–281 (2009). 10.1148/radiol.2522081319 [DOI] [PubMed] [Google Scholar]
- Xu X. and Doi K., “Image feature analysis for computer-aided diagnosis: Accurate determination of ribcage boundary in chest radiographs,” Med. Phys. 22, 617–626 (1995). 10.1118/1.597549 [DOI] [PubMed] [Google Scholar]
- S. G.ArmatoIII, Giger M. L., and MacMahon H., “Automated lung segmentation in digitized posteroanterior chest radiographs,” Acad. Radiol. 5, 245–255 (1998). 10.1016/S1076-6332(98)80223-7 [DOI] [PubMed] [Google Scholar]
- Pietka E., “Lung segmentation in digital radiographs,” J. Digit Imaging 7, 79–84 (1994). 10.1007/BF03168427 [DOI] [PubMed] [Google Scholar]
- Duryea J. and Boone J. M., “A fully automated algorithm for the segmentation of lung fields on digital chest radiographic images,” Med. Phys. 22, 183–191 (1995). 10.1118/1.597539 [DOI] [PubMed] [Google Scholar]
- Carreira M., Cabello D., and Mosquera A., “Automatic segmentation of lung fields on chest radiographic images,” Comput. Biomed. Res. 32, 283–303 (1999). 10.1006/cbmr.1999.1510 [DOI] [PubMed] [Google Scholar]
- Brown M., Wilson L., Doust B., Gill R., and Sun C., “Knowledge-based method for segmentation and analysis of lung boundaries in chest x-ray images,” Comput. Med. Imaging Graph. 22, 463–477 (1998). 10.1016/S0895-6111(98)00051-2 [DOI] [PubMed] [Google Scholar]
- McNitt-Gray M., Huang H., and Sayre J., “Feature selection in the pattern classification problem of digital chest radiograph segmentation,” IEEE Trans. Med. Imaging 14, 537–547 (1995). 10.1109/42.414619 [DOI] [PubMed] [Google Scholar]
- Tsujii O., Freedman M., and Mun S., “Automated segmentation of anatomic regions in chest radiographs using an adaptive-sized hybrid neural network,” Med. Phys. 25, 998–1007 (1998). 10.1118/1.598277 [DOI] [PubMed] [Google Scholar]
- van Ginneken B., and ter Haar Romeny B., “Automatic segmentation of lung fields in chest radiographs,” Med. Phys. 27, 2445–2455 (2000). 10.1118/1.1312192 [DOI] [PubMed] [Google Scholar]
- Vittitoe N., Vargas-Voracek R., and C.Floyd, Jr., “Markov random field modeling in posteroanterior chest radiograph segmentation,” Med. Phys. 26, 1670–1677 (1999). 10.1118/1.598673 [DOI] [PubMed] [Google Scholar]
- Besag J., “On the statistical analysis of dirty pictures,” J. R. Stat. Soc. Ser. B (Methodol.) 48, 259–302 (1986). [Google Scholar]
- Li L., Zheng Y., Kallergi M., and Clark R., “Improved method for automatic identification of lung regions on chest radiographs,” Acad. Radiol. 8, 629–638 (2001). 10.1016/S1076-6332(03)80688-8 [DOI] [PubMed] [Google Scholar]
- Shi Y., Qi F., Xue Z., Chen L., Ito K., Matsuo H., and Shen D., “Segmenting lung fields in serial chest radiographs using both population-based and patient-specific shape statistics,” IEEE Trans. Med. Imaging 27, 481–494 (2008). 10.1109/TMI.2007.908130 [DOI] [PubMed] [Google Scholar]
- Xu T., Mandal M., Long R., and Basu A., “Gradient vector flow based active shape model for lung field segmentation in chest radiographs,” Proc. IEEE EMBS, 3561–3564 (2009). [DOI] [PubMed]
- Seghers D., Loeckx D., Maes F., Vandermeulen D., and Suetens P., “Minimal shape and intensity cost path segmentation,” IEEE Trans. Med. Imaging 26, 1115–1129 (2007). 10.1109/TMI.2007.896924 [DOI] [PubMed] [Google Scholar]
- van Ginneken B., Frangi A., Staal J., ter Haar Romeny B., and Viergever M., “Active shape model segmentation with optimal features,” IEEE Trans. Med. Imaging 21, 924–933 (2002). 10.1109/TMI.2002.803121 [DOI] [PubMed] [Google Scholar]
- van Ginneken B., Katsuragawa S., ter Haar Romeny B., Doi K., and Viergever M., “Automatic detection of abnormalities in chest radiographs using local texture analysis,” IEEE Trans. Med. Imaging 21, 139–149 (2002). 10.1109/42.993132 [DOI] [PubMed] [Google Scholar]
- van Ginneken B., Stegmann M., and Loog M., “Segmentation of anatomical structures in chest radiographs using supervised methods: A comparative study on a public database,” Med. Image Anal. 10, 19–40 (2006). 10.1016/j.media.2005.02.002 [DOI] [PubMed] [Google Scholar]
- Shi Y. and Shen D., “Hierarchical shape statistical model for segmentation of lung fields in chest radiographs,” Proceedings of MICCAI, pp. 417–424 (2008). [DOI] [PubMed]
- Li C. M. and J. T.DobbinsIII, “Preliminary assessment of the temporal subtraction of tomosynthesis images for improved detection of pulmonary nodules,” SPIE Proc. 6142, 61425C (2006). 10.1117/12.654540 [DOI] [Google Scholar]
- Aoyama M., Li Q., Katsuragawa S., Li F., Sone S., and Doi K., “Computerized scheme for determination of the likelihood measure of malignancy for pulmonary nodules on low-dose CT images,” Med. Phys. 30, 387–394 (2003). 10.1118/1.1543575 [DOI] [PubMed] [Google Scholar]
- Timp S. and Karssemeijer N., “A new 2D segmentation method based on dynamic programming applied to computer aided detection in mammography,” Med. Phys. 31, 958–971 (2004). 10.1118/1.1688039 [DOI] [PubMed] [Google Scholar]
- Wang J., Engelmann R., and Li Q., “Segmentation of pulmonary nodules in three-dimensional CT images by use of spiral-scanning technique,” Med. Phys. 34, 4678–4689 (2007). 10.1118/1.2799885 [DOI] [PubMed] [Google Scholar]
- Rockafellar R. and Wets R., Variational Analysis (Springer-Verlag, New York, 2005).
- Wang J., Li F., and Li Q., “Automated segmentation of lungs with severe interstitial lung disease in CT,” Med. Phys. 36, 4592–4599 (2009). 10.1118/1.3222872 [DOI] [PMC free article] [PubMed] [Google Scholar]