Abstract
To reduce the cost of algal biomass production, mathematical model was developed for the first time to describe microalgae growth, lipid production and glycerin consumption under photoheterotrophic conditions based on logistic, Luedeking–Piret and Luedeking–Piret-like equations. All experiments were conducted in a 2 L batch reactor without considering CO2 effect on algae’s growth and lipid production. Biomass and lipid production increased with glycerin as carbon source and were well described by the logistic and Luedeking–Piret equations respectively. Model predictions were in satisfactory agreement with measured data and the mode of lipid production was growth-associated. Sensitivity analysis was applied to examine the effects of certain important parameters on model performance. Results showed that S0, the initial concentration of glycerin, was the most significant factor for algae growth and lipid production. This model is applicable for prediction of other single cell algal species but model testing is recommended before scaling up the fermentation of process.
Keywords: Algae, Lipid, Chlorella minutissima, Mathematical model, Photoheterotrophic fermentation
1. Introduction
Biodiesel produced from vegetable oil, used frying oils, animal fats, soap-stocks, and greases is the first generation biodiesel (Banse et al. 2008). Since vegetable oils may also be used for human consumption, biodiesel produced from vegetable oils can lead to an increase in the food-grade oils price, causing the cost of biodiesel to increase and preventing its usage. Moreover, the amount of used frying oils, animal fats, soap-stocks, and greases is not sufficient to match today’s demands for biodiesel (Mata et al. 2010). The second generation biofuel–oil produced from microalgae is becoming a promising supplemental oil source (Mutanda et al. 2010). Although the microalgae lipid yield is strain-dependent, it is clearly advantageous because of algae’s higher biomass productivity and oil yield than those of other biofuel production crops. Microalgae may assume many types of metabolisms, such as autotrophic, heterotrophic, mixotrophic and photoheterotrophic (Brennan and Owende 2010). Compared to the other three different culture methods, the development of autotrophic culture for algae was very slow due to their low cell density of 0.01–0.06% (w/v) in lined and unlined ponds. Even with the use of on-line ultrafiltration unit to exchanges used with fresh growth medium and controlled CO2, the cell density of green algae Chlorella vulgaris was just 3% (w/v) (Javanmardian and Palsson, 1991). The highest dry biomass of Chlorella minutissima was 0.268 mg/L under 12 joules/m2 sec light intensity at 25 °C with 5% CO2 for 6 days (Seto et al. 1984). The biomass concentration and lipid content of Chlorella sp. cultivated in a medium containing 0.025–0.200 g L−1 urea with 2% CO2 for 6 days were 0.464–2.027 g L−1 and 0.661–0.326 g g−1, respectively (Hsieh and Wu 2009). Mixotrophic growth culturing was performed using photosynthesis as the main energy source, though both organic compounds and CO2 were essential (Berninger et al. 1992). Twenty different microalgae were tested on two different carbon sources, acetate and glucose. The results showed that Chlorella minutissima UTEX 2341 could not only live an autotrophic life, but also can grow using glucose and acetate as carbon and energy sources (Vazhappilly and Chen, 1998). Photoheterotrophic metabolism represents the metabolism in which light was required to use organic compounds as carbon source (Adolf et al. 2006). By using methanol as alternative carbon source to culture Chlorella minutissima, Kotzabasis et al. (1999) observed higher cell densities and faster growth with daily administration of 0.005 and 0.1% (v/v) methanol. In comparison to photoautotrophic cultivation, heterotrophic fermentation allows algae to accumulate much higher proportion of lipids within less time. The scale-up process is much easier and thus, it offers a potential pathway to produce lipids for diesel production in a large scale (Lee, 2001).
The price of algal biofuel ultimately depends on the substrate cost, lipid yield, and the quality of the products formed by the downstream process (Yang et al. 2006). Currently, the cost of biodiesel produced from algal oil is much higher than that of diesel derived from petroleum due to the lower culture process efficiency and higher cost of feedstock production. The cost of carbon source represents 50% of the cost of medium in algal cultivation (Cheng et al. 2009). With the aim of commercializing biodiesel from algae, a substantial effort has been devoted to the development of improved algal strains and more efficient fermentation process. Mathematical modeling of the fermentation process for biomass and lipid production is useful for optimizing the fermentation conditions and scaling-up for industrial production.
Many research studies focused on using models to analyze algae blooms and environmental factors, such as system-dynamic model, lake eutrophication model, parameter-sparse model, numerical model and many others. The system-dynamic model was established to evaluate the comptitive relationship between algae P. malaianus Miq. and Spirogyra sp. The model outputs showed that higher temperature, shading effect, improper nutrients, especially for algae Spirogyra sp. would result in biomass decrease of P. malaianus Miq. (Han et al. 2009). The lake eutrophication model helped in defining restoration policies for water quality (Estrada et al. 2009). The parameter-sparse model analyzed toxicological effects on algae under dynamic nutrient stress (Bontje et al. 2009). The numerical model simulated water quality and algae species composition in a deep lake and the model predicted that the concentrations of PO4–P, NH4–N, NO3–N, DO and pH throughout the water column had a significant influence on the growth of different algal species (Imteaz et al. 2009). There were also many other models applied to optimize photobioreator’s culture conditions. Barbosa et al. (2003) studied the effects of gas velocity, the ratio between the light period and the cycle time in an airlift photoreactor. The maximal volumetric productivity was 0.36 g L−1 per day at a dilution rate of 0.030 h−1. Pruvost et al. (2006) used computational fluid dynamics (CFD) to study the fluid of a torus photobioreactor with different impellers. But their research didn’t combine CFD with algal growth kinetics to analyze the relationship among inner structure parameters. Packer et al. (2010) developed a mathematical model to describe green algal growth parameters and lipid production in nitrogen limited and high light autotrophic conditions in batch culture, but the effect of C concentration and C/N ratio changes was ignored.
Culturing of Chlorella minutissima UTEX2341 in our lab was changed from traditional photoautotrophic to photoheterotrophic, and the cultivation time was reduced from more than 30 days to 7 days in a shaking flask. Algal the dry biomass reached 1.75 g L−1 from the original 0.2 g L−1 in a shaking flask under 35μE·m−2 s−1 light intensity. The fermentation process has also been studied using a 2 L fermentor and the optimal culture conditions were 10% inoculum, 1.5 ml min−1 aeration rate, 100 rpm agitation speed at 22 °C and 35 μE m−2 s−1 light intensity for 15 days. The feedback cost for photoheterotrophic production of Chlorella minutissima UTEX 2341 was reduced to no more than 30% of total cost. (unpublished results). The aim of this study was to establish a mathematical model that incorporated algae growth, lipids production and glycerin consumption under photoheterotrophic conditions. The model was applied to determine optimum values of the parameters that control the fermentation process. The accuracy of the model was then analyzed. A sensitivity study was also undertaken to examine the effect of important parameters on the model performance.
2. Methods
2.1. Experimental approach
Chlorella minutissima UTEX2341 was maintained in 500 mL flasks containing 200 mL medium and 0.1% (v v−1) micronutrient solution. The medium was composed of (g L−1) glycerin 2.05, case-in 1, yeast extract 0.1, KH2PO4 1.8, Na2HPO4 0.5, CaCl2.2H2O 0.013, FeNa EDTA 0.01, MgSO4 0.025. The micronutrient solution was composed of 3.58 g Al2(SO4)3.18H2O, 12.98 g MnCl2.4H2O, 1.83 g CuSO4.5H2O, 3.2 g ZnSO4.7H2O per liter of distilled water. Cultures were incubated at 22 °C for 7 days using an orbital shaker at 100 rpm. 10% inoculum was used to inoculate 2 L bioreactor containing 1500 mL medium with different concentrations of glycerin (9.02–25.2 g of C L−1) and the same casein concentration (8.13 g L−1) to form different C/N ratios. The bioreactor was aerated at rate of 1.5 ml min−1, and agitated at speed of 100 rpm under 35 μE m−2 s−1 light intensity at 22 °C for 15 days.
Dry biomass was determined by transferring cell suspension to a pre-weighed centrifuge tube at set intervals and then centrifuged at 5000 rpm, 20 °C for 10 min. The cell pellet was washed twice with distilled water, freeze dried overnight and weighed. The carbon concentration of the cultures was determined by UV-persulfate oxidation method (Teledyne–Tekmar Phoenix 8000) (Doane and Horwath 2010).
Lipids were extracted with chloroform–methanol–water system (Bligh and Dyer 1959). The extract was dried by N2 flushing, and then weighed (Bousquet et al. 1994).
2.2. Model development
Fig. 1 shows the glycerin consumption, biomass and lipid content changes along incubation time of strain Chlorella minutissima UTEX2341. It was noticeable that algae strain UTEX2341 had a short lag phase (no more than 1 day) at the beginning of the fermentation. When algal growth reached exponential phase, the accumulation of lipids increased quickly and the concentration of glycerin declined sharply. Then lipid content increase wasn’t significant and was following the trend of slow biomass increase before entering the stationary phase. After the point of highest biomass accumulation, the biomass and lipid content began to decline.
Fig. 1.
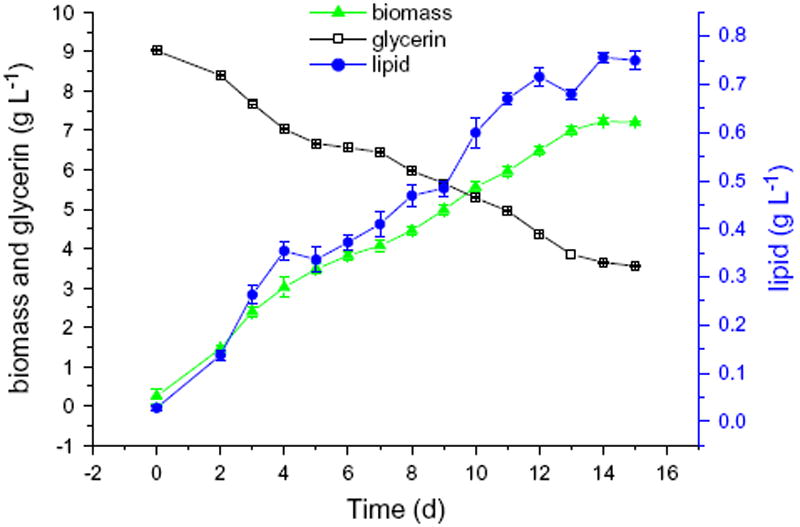
Microalgae growth, lipid content and glycerin consumption during the time of incubation.
2.3. Algae growth
Most microorganisms’ growth processes can be explained by Monod or Logistic equations. A Logistic equation allows simple calculation of fermentation parameters of biological and geometrical significance by sigmoid profiles independent of substrate concentration (Rao et al. 2009). Therefore, Logistic equation was selected for algae growth:
| (1) |
where is the rate of microalgae growth; μmax is the maximum specific growth rate of the microalgae; X is the concentration of microalgae in the medium; Xmax is the maximum value of the microalgal concentration.
At the beginning of fermentation, when t = 0, the algae concentration was given by the initial concentration value (X = X0). After integration, Eq. (1) becomes:
| (2) |
2.4. Lipids production
Product formation was described by Luedeking–Piret equation (Luedeking and Piret 1959). The product formation rate depends on both the instantaneous biomass concentration X and growth rate in a linear fashion:
| (3) |
Where is the lipid formation rate; α the lipid’s formation coefficient; β is a non-growth correlation coefficient.
Gaden (2000) classified the mode of product formation in terms of its relationship with microorganism growth as follows: Class 1, product formation was connected to microbial growth; Class 2, product formation was partially connected to microbial growth; and Class 3, product formation was unrelated to microbial growth. Consider Eq. (3): for α = 0 and β ≠ 0, the relationship between product formation and microbial growth was that of Class 3. For α ≠ 0 and β ≠ 0, the relationship between product formation and microbial growth was partial, and thus of Class 2. For α ≠ 0 and β = 0, there was a linear relationship between product formation and microalgal growth, and so was of Class 1. In this case, Eq. (3) may be integrated to give:
| (4) |
where P is the concentration of lipids, K is the constant of integration.
2.5. Glycerin consumption
The glycerin consumption kinetics may be expressed as substrate conversion to product and substrate consumption for maintenance (Yang et al. 2006).
| (5) |
Where is the total consumption rate of glycerin; t is fermentation time; Yx/s is the maximum microalgal growth coefficient; Yp/s is the maximum lipid yield coefficient; S is glycerin concentration; m is the maximum specific consumption rate for maintaining microalgae life (i.e. a maintenance coefficient).
As lipids are intracellular metabolism products, the glycerin is consumed mainly for microalgae growth, along with the accumulation of lipids, and the maintenance of microalgae. Upon these assumptions, Eq. (6) could be simplified as:
| (6) |
After substituting by Eq. (2) in Eq. (6), and integrating, the following expression for glycerin concentration was obtained:
| (7) |
Where S0 is the initial concentration of glycerin. The yield of coefficients for lipid production may be deduced from Eqs. (4) and (6), giving:
| (8) |
3. Sensitivity analysis and model calibration, results and discussion
The biomass growth-related (X0, Xm and μm), lipid production-related (Yp/s, K and α), and glycerin consumption-related (S0, Yx/s, m) parameters were measured during the experiment at different initial glycerin concentration. The data were used for model calibration using the proposed mathematic model Eq. (2), Eq. (4), Eq. (7) and Eq. (8). To calibrate the kinetic parameters in Eqs. (1)-(4) and (6)-(8), a general equation (named objective function) based on weighted model errors (difference between measured and predicted values) was formed (Eq. (9)). The calibration model was developed using Universal Inverse Modeling Code or UCODE (Poeter and Hill, 1998) whose sensitivity analysis capabilities and ability to estimate parameter values resulted in the best possible fit to our experimental observations.
| (9) |
where Xi, Pi, and Si are the measured values for biomass, lipid and glycerin concentration; , and are the corresponding predicted values; wi is the weighting factor for measured value defined in Eq. (10); and R is the objective function for the calibration which is based on the weighted sum of squares of differences between measured and predicted values. The weighting factors are defined to assign higher weights to the measured values that have less uncertainty (reflecting the accuracy of the measurements) and also to make the weighted residuals have the same units so that they can be squared and summed in the sum of the squared of equation. The weights for biomass, lipid and glycerin were defined in Eq. (10):
| (10) |
where σix is the standard deviation of the biomass measurement and λx is a scaling factor defined in Eq. (11) that normalizes each subset of objective function. Scaling factors could significantly improve calibration convergence properties (Poeter and Hill, 1998). wip and wis are defined likewise.
| (11) |
Sensitivity analysis of the kinetic terms on minimizing the objective function was performed by UCODE (Poeter and Hill, 1998). Sensitivity is usually a measure of whether provided observations are sufficient to estimate parameter values (Hill, 1998). In this study composite scaled sensitivity (CSS) was used to for the sensitivity analysis of model to the provided experimental data. CSS indicates the importance of measured data as a whole to a single parameter, compared with the accuracy on the observation. Eight parameters (X0, Xmax, S0, K, μmax, α, m, Yx/s) were used for sensitivity analyses. Results of parameter sensitivity assessments were presented in Fig. 2. The most significant parameters for calibrations were S0, Xmax, μmax, α, X0, Yx/s, K, and m, in descending order. It could be seen that initial glycerin concentration was the most significant factor in Chlorella minutissima UTEX2341’s growth and lipid production under the heterotrophic culture conditions.
Fig. 2.
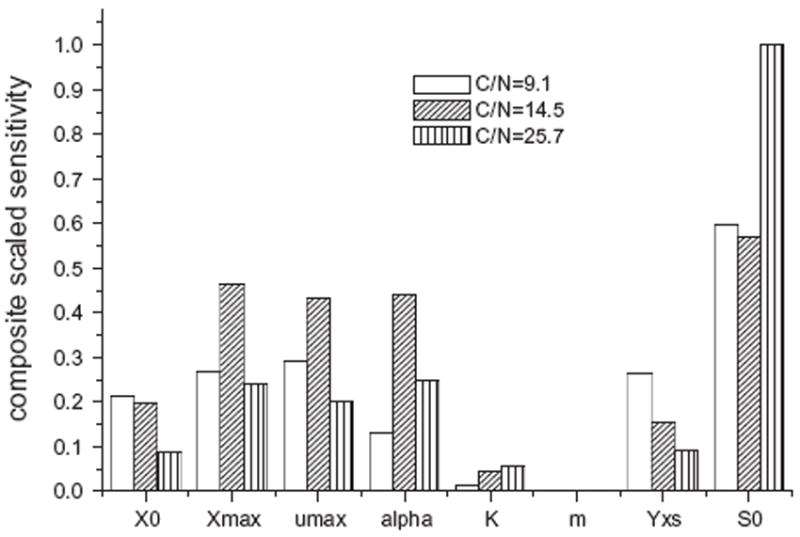
Composite scaled sensitivity analysis.
Calibration was carried out after the sensitivity analyses. Estimated parameters are presented in Table 1 whereas the experimental results and corresponding fits to the model equations were shown in Fig. 3. Fig. 3 compares the measured values of biomass and lipid concentration for C/N = 9.1, 14.5, and 25.2 treatment respectively with the corresponding simulated values.
Table 1.
Values of parameters used in the model.
| Parameter | Glycerin concentration (g L−1)
|
||
|---|---|---|---|
| 9.02 (C/N = 9.1) | 14.5 (C/N = 14.8) | 25.2 (C/N = 25.7) | |
| Biomass | |||
| μm (d−1) | 0.3469 | 0.364 | 0.408 |
| X0 (g L−1) | 0.7926 | 0.5947 | 0.3749 |
| Xm (g L−1) | 7.42 | 6.8 | 5.2 |
| Lipid | |||
| α | 0.1125 | 0.1057 | 0.1185 |
| K | −0.0316 | 0.0364 | 0.0891 |
| Yp/s (g g−1) | 0.0971 | 0.0885 | 0.1012 |
| Glycerin | |||
| S0 (g L−1) | 10.19 | 15.5 | 26.1 |
| Yx/s (g g−1) | 0.8629 | 0.8374 | 0.8543 |
| m (g g−1 d−1) | 0.0001 | 0.001 | 3.11E-07 |
| R2 | 0.9826 | 0.9830 | 0.9988 |
Fig. 3.
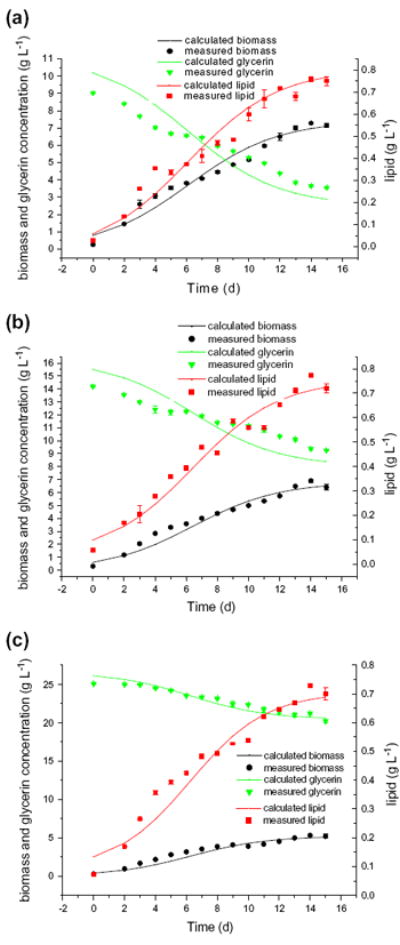
Comparison of experimental data and calculated values of biomass, lipid and glycerin consumption by UTEX2341. (■) experimental data of biomass, (▲) experimental data of glycerin, (▼) experimental data of lipid. The curves represent the fitted model equations proposed in this study. Fig. 3(a), Fig. 3(b), Fig. 3(c) corresponds to the three initial glycerin concentrations of 9.02, 14.5 and 25.2 g/L respectively.
Correlation coefficients (R2) for the model fits (Fig. 3) were 0.983, 0.983, and 0.999, respectively. The proposed calibrated mathematical model fitted the experimental data well. Overall, sensitivity analysis not only helped us find out the important parameters or factors to the process, it allowed to perform a more efficient calibration by including the most sensitive parameters and excluding parameters that are relatively not very sensitive.
Despite some reports that Chlorella minutissima could use organic carbon, such as glucose, acetate and methanol to live a heterotrophic life (Vazhappilly and Chen 1998; Kotzabasis et al. 1999), few studies about utilization of glycerin and its effect on Chlorella minutissima UTEX2341’s growth and lipid production have been reported (Lee 2001; Chen et al. 2010). In this research, the observed glycerin utilization pattern at different C/N ratios during fermentation indicated that with an increase of carbon concentration, the glycerin utilization decreased from 77.83% to 52.08% and then to 20.15% during the 15 days’ of fermentation. Furthermore, the yield factor for biomass (Yx/s) based on Eqs. (7) indicated that when C/N = 9.1, the efficiency of glycerin conversion into biomass was the highest. When C/N was beyond 9.1, inhibition of the further usage of glycerin was observed. A possible explanation is that the high glycerin concentration and accumulated biomass have inhibitory effects on algae growth as the kinetic model of biomass growth suggested (Altiok et al. 2006).
Compared with autotrophic cultures, under this photoheterotrophic incubation C. minutissima UTEX2341 reached 5.31, 6.9, and 7.28 g L−1 dry biomass at 25.7, 14.8, and 9.1 C/N ratio respectively on day 15th, which is more than 26 to 36 times as if it was cultured under autotrophic conditions (0.2 g dry biomass L−1). This result has greater outcome over most algae cultured under autotrophic condition. About 0.5 g L−1 cell concentration could be maintained when raceway-shape culture ponds were used in Israel, the United States of America, China and other countries (Richmond et al. 1990). In Yongmanitchai and Ward’s research (1991), the biomass of Chlorella minutissima UTEX 2219, Chlorella minutissima UTEX 2341, Dunaliella primolecta MBAUK 81, D. terriolecta MBAUK 83, Phaeodactylum trlcornutum UTEX 640, Porphyridium cruentum UTEX 161, Hetero-mastrix rotunda MBAUK 210, and Cricosphaera carteri MBAUK 17 were 0.48, 0.54, 1.39, 1.25, 2.49, 1.8, 0.17 and 0.18 g L−1 respectively, after 7 days’ of autotrophic growth under optimized conditions. Seto et al. (1984) optimized Chlorella minutissima’s culture conditions and found that the highest biomass produced was 0.39 g L−1.
Compared with other heterotrophic cultures, commercial heterotrophic cultivation of Chlorella sp. in conventional stirred tank fermentors was common (Lee 1997). Glucose and acetate were the most utilized carbons in this fermentation process. For example, Chlorella pyrenoidosa, Chlorella regularis, Chlorella vulgaris, and Nitzschia alba were selected and tested for their commercial heterotrophic growth ability (Gladue and Maxey, 1994). The highest cell density (45 g L−1) was achieved for Nitzschia alba, but the cost for heterotrophic production of Nitzschia alba was estimated at US$12 kg−1 dry biomass (Lee 2001), which was too expensive. In this research, the feedback cost for photoheterotrophic production of Chlorella minutissima UTEX 2341 account for no more than 30% of total cost (data not shown). If the cost for electricity could be reduced, this photoheterotrophic cultivation process would have great potential for future commercial algae production. Although the specific growth rate (μm) increased from 0.289 to 0.408 (d−1) with the increase of glycerin concentration from 9.02 to 25.2 g L−1, the maximum average biomass values were 7.28, 6.9, and 5.31 g L−1 at 9.1, 14.8, and 25.7 C/N ratio respectively. The results indicated that higher C/N ratio could promote the algae growth rate, but reduce the final total biomass. The observed substrate concentration-dependent biomass production suggests that glycerin concentration most likely regulates the growth pattern of UTEX2341 (Rao et al., 2009) and was confirmed by the model developed under this study.
The average lipid content of Chlorella minutissima varied between 7.1% and 23% of the dry biomass (Seto et al., 1984; Yongmanitchai and Ward 1991). Though the lipid yield in this research was relatively low, 13.1% of dry biomass, the total lipid content could reach 0.95 g L−1 because of the higher total biomass produced (dry weight). It could be seen from Fig. 1 that the lipid accumulation with time followed a similar trend to that of the biomass production. Lipids’ concentration (P) was plotted against algal biomass concentration (X) and a linear curve was fitted. The correlation coefficient (R2) was 0.99. Measured data showed a linear relationship between lipid accumulation and algae growth, in accordance with Eq. (4). It may therefore be concluded that the mode of lipid production was growth-associated. It is very useful for the practice to know when to harvest algae for lipid production and our study contributes significantly to this process. The model was applied to determine the optimum values of the parameters controlling fermentation process and this information is directly applicable for scaling up and optimization of algal oil production in bioreactors and industrial setups.
4. Conclusions
Microalgae metabolism is a complex process and varies in terms of light utilization. In order to harvest higher biomass and lipids as well as shorten the fermentation time, a photoheterotrophic fermentation was used in this study. Mathematical model was developed to understand the glycerin concentration-dependent Chlorella minutissima UTEX2341 biomass and lipids production. The presented model gave a satisfactory representation of the fermentation process and thus has a potential in optimizing UTEX2341 growth and lipid production kinetics in bioreactors. Sensitivity analysis helped us identify the important parameters in algal fermentation process which can be used to design an efficient experiment with higher growth and yield lower cost. The sensitivity analysis results showed that S0, the initial glycerin concentration, was the most significant factor for algae growth and lipid production. Model calibration results could successfully reproduce the experimental data at three different C/N ratio treatments with correlations coefficients of 0.983, 0.983 and 0.999 respectively. Furthermore, it was found for the first time that lipid production was growth-associated. This information will be useful in the process scaling up and commercial biofuel production.
Acknowledgments
This research was supported by Department of Water Resources Contract with UC Davis (08-002104, task oder 07-3, PI Dr. K. Hristova). Partial support was provided by the Project for Extramural Scientists of SKLAB (2010SKLAB06-8), the National Science Foundation of China (No. 30700010) and by Grant Number 5 P42 ES004699 (to Drs. K. Hristova and K. Scow) from the National Institute of Environmental Health Sciences (NIEHS), NIH and the contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIEHS, NIH. Thanks to Timothy A. Doane for the analysis of glycerin concentration in the fermentation process.
References
- Adolf JE, Stoecker DK, Harding LW. The balance of autotrophy and heterotrophy during mixotrophic growth of Karlodinium micrum (Dinophyceae) J Plankton Res. 2006;28:737–751. [Google Scholar]
- Altiok D, Tokatli F, Harsa S. Kinetic modeling of lactic acid production from whey by Lactobacillus casei (NRRL B-441) J Chem Technol Biotechnol. 2006;81:1190–1197. [Google Scholar]
- Banse M, Meijl HV, Tabeau AG, Will EU. Biofuel policies affect global agricultural markets? European Rev Agric Econ. 2008;35:117–141. [Google Scholar]
- Barbosa MJ, Hoogakker J, Wijffels RH. Optimisation of cultivation parameters in photobioreactors for microalgae cultivation using the A-stat technique. Biomol Eng. 2003;20:115–123. doi: 10.1016/s1389-0344(03)00033-9. [DOI] [PubMed] [Google Scholar]
- Berninger UG, Caron DA, Sanders RW. Mixotrophic algae in 3 ice-coverd lakes of the pocano mountains, USA. Freshw Biol. 1992;28:263–272. [Google Scholar]
- Bligh EG, Dyer WJ. A rapid method of total lipid extraction and purification. Can J Biochem Physiol. 1959;37:911–917. doi: 10.1139/o59-099. [DOI] [PubMed] [Google Scholar]
- Bontje D, Kooi BW, Liebig M, Kooijman SALM. Modelling long-term ecotoxicological effects on an algal popupation under dynamic nutrient stress. Water Res. 2009;43:3292–3300. doi: 10.1016/j.watres.2009.04.036. [DOI] [PubMed] [Google Scholar]
- Bousquet O, Sellier N, Legoffic F. Characterization and purification of polyunsaturated fatty-acids from microalgae by gas-chromatography mass-spectrometry and countercurrent chromatography. Chromatographia. 1994;39:40–44. [Google Scholar]
- Brennan L, Owende P. Biofuels from microalgae-a review of technologies for production, processing, and extractions of biofuels and co-products. Renew Sust Energ Rev. 2010;14:557–577. [Google Scholar]
- Chen CY, Yeh KL, Aisyah R, Lee DJ, Chang JS. Cultivation photobioreactor design and harvesting of microalgae for biodiesel production: A critical review. Bioresour Technol (2010) 2010 doi: 10.1016/j.biortech.2010.06.159. [DOI] [PubMed] [Google Scholar]
- Cheng Y, Lu Y, Gao C, Wu Q. Algae-based biodiesel production and optimization using sugar cane as the feedstock. Energy Fuels. 2009;23:4166–4173. [Google Scholar]
- Doane AD, Horwath WR. Eliminating interference from iron(III) for ultraviolet absorbance measurements of dissolved organic matter. Chemosphere. 2010;78:1409–1415. doi: 10.1016/j.chemosphere.2009.12.062. [DOI] [PubMed] [Google Scholar]
- Estrada V, Parodi ER, Diaz MS. Addressing the control problem of algae growth in water reservoirs with advanced dynamic optimization approaches. Comput Chem Eng. 2009;33:2063–2074. [Google Scholar]
- Gaden EL. Fermentation process kinetics. Biotechnol Bioeng. 2000;67:629–635. doi: 10.1002/(sici)1097-0290(20000320)67:6<629::aid-bit2>3.0.co;2-p. [DOI] [PubMed] [Google Scholar]
- Gladue RM, Maxey JE. Microalgal feeds for aquaculture. J Appl Phycol. 1994;6:131–141. [Google Scholar]
- Han H, Chen Y, Jørgensen SE, Nielsen SN, Hu W. A system-dynamic model on the competitive growth between Potamogeton malaianus. Miq and Spirogyra sp Ecol Modell. 2009;220:2206–2217. [Google Scholar]
- Hill MC. Methods and guidelines for effective model calibration. U S Geological Survey Water-Resources Investigations Report 98-4005. 1998:90. [Google Scholar]
- Hsieh CH, Wu WT. Cultivation of microalgae for oil production with a cultivation strategy of urea limitation. Bioresour Technol. 2009;100:3921–3926. doi: 10.1016/j.biortech.2009.03.019. [DOI] [PubMed] [Google Scholar]
- Imteaz MA, Shanableh A, Asaeda T. Modelling multi-species algal bloom in a lake and inter-algal competitions. Water Sci Technol. 2009;632:2599–2611. doi: 10.2166/wst.2009.632. [DOI] [PubMed] [Google Scholar]
- Javanmardian M, Palsson BO. High-density photoautotrophic algal cultures: Design, construction, and operation of a novel photobioreactor system. Biotechnol Bioeng. 1991;38:1182–1189. doi: 10.1002/bit.260381010. [DOI] [PubMed] [Google Scholar]
- Kotzabasis K, Hatziathanasiou A, Bengoa-Ruigomez MV, Kentouri M, Divanach P. Methanol as alternative carbon source for quicker efficient production of the microalgae Chlorella minutissima: Role of the concentration and frequence of administration. J Biotechnol. 1999;70:357–362. [Google Scholar]
- Lee YK. Commercial production of microalgae in the Asia-Pacific rim. J Appl Phycol. 1997;9:403–411. [Google Scholar]
- Lee YK. Microalgal mass culture systems and methods: Their limitation and potential. J Appl Phycol. 2001;13:307–315. [Google Scholar]
- Luedeking R, Piret EL. A kinetic study of the lactic acid fermentation: batch process at controlled pH. J Biochem Microbiol Technol Eng. 1959;1:363–394. doi: 10.1002/(sici)1097-0290(20000320)67:6<636::aid-bit3>3.0.co;2-u. [DOI] [PubMed] [Google Scholar]
- Mata TM, Martins AA, Caetano NS. Microalgae for biodiesel production and other applications: A review. Renewable Sustainable Energy Rev. 2010;14:217–232. [Google Scholar]
- Mutanda T, Ramesh D, Kathikeyan S, Kumari S, Anandraj A, Bux F. Bioprospecting for hyper-lipid producing microalgal strains for sustainable biofuel production. Bioresour Technol. 2010 doi: 10.1016/j.biortech.2010.06.077. [DOI] [PubMed] [Google Scholar]
- Packer A, Li Y, Andersen T, Hu Q, Kuang Y, Sommerfeld M. Growth and neutral lipid synthesis in green microalgae: A mathematical model. Bioresour Technol (2010) 2010 doi: 10.1016/j.biortech.2010.06.029. [DOI] [PubMed] [Google Scholar]
- Poeter EP, Hill MC. Documentation of UCODE: a computer code for universal inverse modeling. 116p: US Geological Survey Water-Resources Investigations Report. 1998:98–4080. [Google Scholar]
- Pruvost J, Pottier L, Legrand J. Numerical investigation of hydrodynamic and mixing conditions in a torus photobioreactor. Chem Eng Sci. 2006;61:4476–4489. [Google Scholar]
- Rao CS, Sathish T, Brahamaiah P, Kumar TP, Prakasham RS. Development of a mathematical model for Bacillus circulans growth and alkaline protease production kinetics. J Chem Technol Biotechnol. 2009;84:302–307. [Google Scholar]
- Richmond A, Lichtenberg E, Stahl B, Vonshak A. Quantitative assessment of the major limitations on productivity of Spirulina platensis in open raceways. J Appl Phycol. 1990;2:195–206. [Google Scholar]
- Seto A, Wang HL, Hesseltine CW. Culture condition affect eicosapentaenoic acid content of Chlorella minutissima. JAOCS. 1984;61(5):892–894. [Google Scholar]
- Vazhappilly R, Chen F. Eicosapentaenoic acid and docosahexaenoic acid production potential of microalgae and their heterotrophic growth. JAOCS. 1998;75(3):393–397. [Google Scholar]
- Yang JS, Huang JX, Ni JR. Mathematical modeling of batch fermentation of Zoogloea sp. GY3 used for synthesizing polyhydroxyalkanoates. J Chem Technol Biotechnol. 2006;81:789–793. [Google Scholar]
- Yongmanitchai W, Ward OP. Screening of algae for potential alternative sources of eicosapentaenoic acid. Phytochemistry. 1991;30(9):2963–2967. [Google Scholar]


