Static and Dynamic Error of a Biplanar Videoradiography System Using Marker-Based and Markerless Tracking Techniques

Short abstract

The use of biplanar videoradiography technology has become increasingly popular for evaluating joint function in vivo. Two fundamentally different methods are currently employed to reconstruct 3D bone motions captured using this technology. Marker-based tracking requires at least three radio-opaque markers to be implanted in the bone of interest. Markerless tracking makes use of algorithms designed to match 3D bone shapes to biplanar videoradiography data. In order to reliably quantify in vivo bone motion, the systematic error of these tracking techniques should be evaluated. Herein, we present new markerless tracking software that makes use of modern GPU technology, describe a versatile method for quantifying the systematic error of a biplanar videoradiography motion capture system using independent gold standard instrumentation, and evaluate the systematic error of the W.M. Keck XROMM Facility's biplanar videoradiography system using both marker-based and markerless tracking algorithms under static and dynamic motion conditions. A polycarbonate flag embedded with 12 radio-opaque markers was used to evaluate the systematic error of the marker-based tracking algorithm. Three human cadaveric bones (distal femur, distal radius, and distal ulna) were used to evaluate the systematic error of the markerless tracking algorithm. The systematic error was evaluated by comparing motions to independent gold standard instrumentation. Static motions were compared to high accuracy linear and rotary stages while dynamic motions were compared to a high accuracy angular displacement transducer. Marker-based tracking was shown to effectively track motion to within 0.1 mm and 0.1 deg under static and dynamic conditions. Furthermore, the presented results indicate that markerless tracking can be used to effectively track rapid bone motions to within 0.15 deg for the distal aspects of the femur, radius, and ulna. Both marker-based and markerless tracking techniques were in excellent agreement with the gold standard instrumentation for both static and dynamic testing protocols. Future research will employ these techniques to quantify in vivo joint motion for high-speed upper and lower extremity impacts such as jumping, landing, and hammering.

Introduction

Biplanar videoradiography systems that directly measure three-dimensional (3D) in vivo skeletal motion have been developed in-part to address the inherent limitations of optical motion capture systems that utilize skin-based marker sets [1–9]. Current skeletal tracking algorithms are classified as marker-based tracking [4,5,7,10,11] or markerless tracking [1,3,6,8,9,12]. Marker-based tracking methods require implantation of at least three radio-opaque spherical markers within each bone. The invasiveness of this technique severely limits its applicability for studying in vivo human joint motion. Markerless tracking makes use of algorithms designed to match 3D bone shapes to biplanar videoradiography data. Employing this technology to obtain quantitative data on human joint motion first requires an understanding of its systematic error, particularly in the dynamic setting.

The systematic error of specific biplanar videoradiography systems has been previously documented using markerless tracking algorithms [13–18]. These studies provide valuable information on existing biplanar videoradiography technologies and stress the importance of establishing error measures for specific joints and system configurations. However, these studies typically involve protocols where cadaveric bones undergo static, semi-static, or gravitational based pendulum-like motion that may not simulate high-speed lower and upper extremity impacts associated with activities like jumping, landing, or hammering. Additionally, previous methods for evaluating systematic error have compared markerless tracking to marker-based tracking using the same data set (intra-specimen). While this provides a convenient and acceptable measure of markerless tracking error, it is not ideal for independently assessing the overall systematic error of a biplanar videoradiography system for both marker-based and markerless tracking techniques.

Work from You et al. [13] and Bey et al. [15] has made significant contributions to 3D skeletal motion capture technology by describing and implementing robust markerless tracking algorithms. However, these algorithms require time consuming data processing [13] or expensive computational clusters [3]. Recent advancements in graphics processing unit (GPU) technology make it an ideal candidate for processing computer vision algorithms such as those developed by You et al. [13] and Bey et al. [15]. These markerless tracking algorithms can be efficiently implemented on the GPU of a single workstation, substantially reducing computational time [19] and equipment expenses.

The goals of this study are to (1) provide an outline of new markerless tracking software that makes use of modern GPU technology, (2) describe a versatile method for quantifying the systematic error of a biplanar videoradiography system using independent gold standard instrumentation, and (3) evaluate the systematic error of a biplanar videoradiography system using both marker-based and markerless tracking algorithms under static and dynamic motion conditions.

Methods

Description of XROMM Facilities and Resources

Hardware.

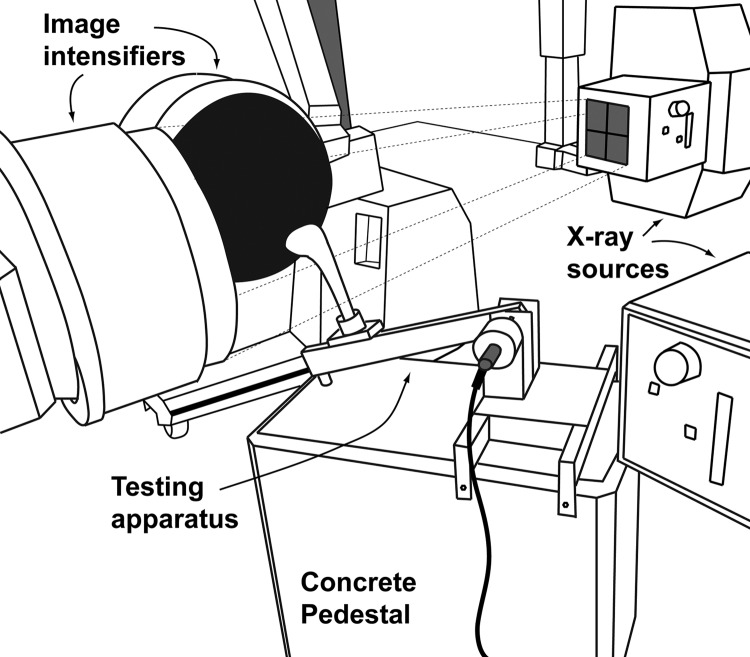
The biplanar videoradiography system in the W. M. Keck Foundation XROMM Facility at Brown University (Providence, RI, USA¹) consists of two Varian Medical Systems model G-1086 X-ray tubes (Palo Alto, CA, USA), two EMD Technologies model EPS 45-80 pulsed X-ray generators (Saint-Eustache, Quebec, Canada), two 16 in. Dunlee (Aurora, IL, USA) model TH9447QXH590 image intensifiers (IIs), and two Phantom v10 high-speed digital video cameras (Vision Research, Wayne, NJ, USA). The X-ray tubes are suspended from the ceiling by overhead tube cranes, and the IIs are mounted on mobile gantries (Fig. 1). The system can deliver pulsed X-ray generation up to 150 Hz and can record in continuous X-ray generation at up to 1000 frames-per-second (FPS). The system's pixel resolution is 1800 x 1800, and the overall resolution of the imaging chain is approximately 2 line pairs/mm.

Fig. 1.

Illustrated representation of the experimental testing environment within the W. M. Keck Foundation XROMM Facility. The dynamic testing apparatus is positioned within the field of view determined by the overlapping X-ray beams. A representative X-ray beam is illustrated with dotted lines projecting from one of the X-ray sources.

Image de-distortion and 3D space calibration for the biplanar XROMM facility have been described in detail previously and are available to the public [10]. Briefly, image distortion is addressed by imaging a patterned sheet of perforated metal (Part 9255T641, McMaster-Carr, Robinson, NJ, USA) and using a local weighted mean (LWM) distortion correction algorithm implemented in matlab (XrayProject, Brown University, Providence, RI, USA). To calibrate the 3D space, an acrylic calibration cube containing 64 steel beads is imaged. The markers are tracked in both planes using custom matlab software (XrayProject), and the calibration parameters are calculated using standard direct linear transform (DLT) techniques [20].

Software.

X-ray reconstruction of moving morphology (XROMM) is a computational process that combines motion data from X-ray video and shape data from 3D CT-based bone scans [10]. There are two fundamentally different ways to combine these data, marker-based XROMM and markerless XROMM.

Marker-based XROMM, also referred to as Dynamic Radiostereophotogrammetric Analysis [5], requires marker sets of three of more radio-opaque beads to be implanted into each rigid body. The 3D positions of the radio-opaque beads are reconstructed from the biplanar videoradiography data and then used to calculate frame-by-frame motion for each marker set and, therefore, the respective rigid body in which they are implanted. The development of marker-based XROMM has been built on previous work on canines [4,21] and humans [22]. Custom matlab software (XrayProject) has been developed to process all marker-based XROMM data using standard DLT techniques [20,23], as previously described by Brainerd et al. [10].

Markerless XROMM can be performed by auto-registration of a CT volume to biplanar videoradiography data. The following description of the auto-registration algorithm is built on previous work described by You et al. [13] and Bey et al. [15]. The auto-registration algorithm consists of four major components. First, a volume visualization technique is used to generate digitally reconstructed radiographs (DRRs) from a CT volume using a standard ray casting approach and the known orientation of the biplanar videoradiography system [24–26]. Second, both the radiographs and DRRs are processed to enhance features and detect edges [27]. Third, a normalized cross correlation is used to measure the similarity between the radiographs and DRRs [28]. Finally, a downhill simplex optimization algorithm iterates over the six degree-of-freedom (DOF) motion parameters until the desired correlation has been reached [29]. The entire autoregistration algorithm requires an initial guess of bone position and orientation. This can be manually assigned by a user or extrapolated from previously tracked frames.

There are several user defined parameters that control the creation of the DRRs. These include the sampling frequency of the ray casting, the intensity if the virtual X-rays, and a threshold density, which determines if a particular sample will contribute to the accumulated value along each ray. Once the DRRs have been generated there are additional filters available, such as contrast enhancement and Sobel edge detection. Contrast and edge detection filters can also be applied to the biplanar videoradiography sequence. These settings can enhance the algorithms ability to find a solution. For the purposes of this study, these parameters were selected by the user to provide the best visual match between the DRR and the biplanar videoradiography sequence (Fig. 2).

Fig. 2.

XROMM Autoscoper 3D software environment. This figure illustrates the before ((a) and (b)) and after ((c) and (d)) results obtained from the auto-registration algorithm using an initial guess that was extrapolated from the previous frames. Additionally, the constrained-axis rotation and translation manipulators are shown in (a) and (b) and (c) and (d), respectively. The Autoscoper software (executable and source) is publically available.

Once the user has fixed the above parameters, the objective function takes in the x-y-z position and x-y-z orientation of the CT volume as free parameters. It outputs a single scalar value representing the normalized cross correlation between the grayscale values of the DRR and radiograph. The correlation equation, adapted from You et al. [13], used in this study is

$$C_i(\stackrel{\wedge }{p})=\frac{\sum _{x,y}[r_i(x,y)-\overline{r_{\iota }(x,y)}][d_i(x,y,\stackrel{\wedge }{p})-\overline{d_{\iota }(x,y,\stackrel{\wedge }{p})}]}{\{\sum _{x,y}[r_i(x,y)-\overline{r_{\iota }(x,y)}]{}^2\sum _{x,y}[d_i(x,y,\stackrel{\wedge }{p})-\overline{d_{\iota }(x,y,\stackrel{\wedge }{p})}]{}^2\}{}^{1/2}}$$

where

$C_i$ is the correlation between the DRR and radiograph for camera i;

$\stackrel{\wedge }{p}$ is the vector containing the six DOF motion parameters of the CT bone model: xyz-position and xyz-rotation;

$r_i(x,y)$ is the radiograph from camera i after filtering with edges added;

$\overline{r_{\iota }(x,y)}$ is the mean of the radiograph from camera i after filtering with edges added;

$d_i(x,y,\stackrel{\wedge }{p})$ is the DRR from camera i generated from the CT bone model in position $\stackrel{\wedge }{p}$ after filtering with edges added;

and $\overline{d_{\iota }(x,y,\stackrel{\wedge }{p})}$ is the mean of the DRR from camera i generated from the CT bone model in position $\stackrel{\wedge }{p}$.

The final similarity measure for a biplanar videoradiography system is the product of the correlations from each camera,

$$C(\stackrel{\wedge }{p})=C_1(\stackrel{\wedge }{p})C_2(\stackrel{\wedge }{p})$$

The optimization routine searches the six DOF parameter space for the position and orientation values that maximize this correlation.

The solution space for the algorithm is noisy and has many local minima. To avoid local minima, the simplex is reset and run multiple times using the result of the previous optimization as the initial guess for the next. In general, this technique will not converge if the initial guess is too far away; however, the user-supplied initial guesses are generally close enough for quick convergence. Within dynamic data sets, initial guesses extrapolated from previous frames also converge quickly due to the high video frame rate and good frame coherence.

The described auto-registration algorithm for extraction of skeletal kinematics from markerless XROMM data has been implemented in an open source software package that is available to the public (Autoscoper, Brown University, Providence, RI, USA). The software provides a graphical interface for markerless bone tracking over a video sequence (Fig. 2). The images displayed in Figs. 2(a) and 2(b) show the DRRs and video sequences for the two X-ray sources before auto-registration. The DRR is displayed in orange and the videoradiography sequences are displayed in blue. The images displayed in Figs. 2(c) and 2(d) show the DRR and biplanar videoradiography sequence for the two X-ray sources after auto-registration is completed. The overlay of the DRR with the videoradiography sequence is represented in white. In addition to implementing the auto-registration algorithm, the software allows the user to rotate and translate the 3D CT volume to best match the DRRs to the biplanar videoradiography sequence. This can be done by using the constrained-axis rotation and translation manipulators shown in Figs. 2(a) and 2(b) and Figs. 2(c) and 2(d), respectively. All six position and orientation parameters can be plotted within the software to assist the user in identifying registration inconsistencies between video frames.

The implementation of the auto-registration algorithm makes significant use of general purpose computation on a GPU. Highly parallelized GPU implementations of this algorithm have shown significant speed improvements over the traditional central processing unit (CPU) implementations [19]. Specifically, the DRR generation, image processing, and similarity measure all take place on a single GPU with NVIDIA's Fermi architecture (GeForce GTX 480, EVGA, Brea, CA, USA). To generate the DRR, each ray was processed independently by a separate thread. The image processing was done in a similar manner, with each pixel processed independently by a separate thread. The normalized cross correlation similarity measure was also parallelized using a tree-based parallel sum, and the resulting output is read off the GPU. It was not necessary to parallelize the downhill simplex optimization algorithm as the bottleneck exists in DRR generation, image processing, and similarity measure calculation. As a result, the described auto-registration algorithm converges in less than one second for a single frame on a GPU equipped workstation (Precision T7400, Dell, Round Rock, TX, USA).

Systematic Error Testing Protocols

Static Testing Protocol.

Static error was evaluated by translating and rotating a set of human cadaver bones and a polycarbonate marker flag by known increments with high precision linear (NB4 Series, Newmark Systems, Mission Viejo, CA, USA) and rotary (RT-3 Series, Newmark Systems) positioning stages with accuracies of 0.001 mm and 0.002 deg, respectively (Fig. 3(a)). The bones used in this study include a distal femur, distal radius, and distal ulna (Fig. 4). The bones were manually stripped of soft tissue, cleaned using tergazyme in a hot water bath, disinfected with hydrogen peroxide, and dried at room temperature. The proximal end of each bone was rigidly fixed in a polyvinyl chloride pot using urethane resin (Smooth-Cast 300Q, Smooth-On, Easton, PA, USA). The marker flag was created by embedding 12 one-millimeter diameter tantalum markers into two cylindrical polycarbonate posts (Fig. 3(b)).

Fig. 3.

Static (a) and dynamic (b) testing apparatus. Both apparatuses were rigidly fixed to a concrete pedestal (Fig. 1) for all static and dynamic testing.

Fig. 4.

Images displaying the morphology of the three bones used in this study. Panels (a), (b), and (c) are the 3D CT models of the distal femur, distal radius, and distal ulna, respectively.

For each bone and the marker flag, twenty trials of 15 translational motion steps (0.000, 0.001, 0.010, 0.100, 1.000, 10.000, 10.100, 25.000, 25.100, 50.000, 50.100, 75.000, 75.100, 100.000, and 100.100 mm) and 15 rotational motion steps (0.000, 0.002, 0.010, 0.100, 1.000, 10.000, 10.100, 25.000, 25.100, 50.000, 50.100, 75.000, 75.100, 100.000, and 100.100 deg) were performed using the static testing apparatus shown in Fig. 3(a). An average reference position for the translational and rotational tests were determined from an additional twenty trials at 0.000 mm and 0.000 deg, respectively. All marker tracking was performed using the marker-based software discussed earlier.

Translational and rotational errors were determined as the difference between the computed rigid body translation or rotation and the true linear or rotary stage value.

Dynamic Testing Protocol.

Dynamic error was evaluated using the same bones and the marker flag employed in the static testing protocol. A specifically designed impact pendulum was fabricated (Fig. 3(b)). A computer-aided design of the impact pendulum is publically available. The fulcrum of the pendulum was attached to a high precision (±0.06 deg) angular displacement transducer (ADT: Series 600, Trans-Tek Inc., Ellington, CT, USA). This allowed the pendulum arm to spin along the same axis as the mechanical axis of the ADT. Angular displacement transducer data were collected at 5000 Hz and synchronized with the biplanar videoradiography system.

For each bone and the marker flag, five pendulum drop-impact trials were performed using the apparatus shown in Fig. 3(b). For each trial, the pendulum arm was dropped from a position held outside the field of view (FOV) of the XROMM system. As the arm fell, it entered the FOV and impacted a concrete pedestal. The motion of the arm and the attached bone or marker flag was recorded for all pendulum impacts until a stationary, steady state was achieved. Additionally, an average reference position for each bone and the marker flag were determined by collecting a stationary trial at the impact position. All markerless tracking was performed using the auto-registration software discussed earlier.

Rotational error was determined for each bone and the marker flag by calculating the difference between the computed rigid body rotation and true ADT value.

Imaging Parameters.

The X-ray tube voltage and current were set at 70 kVp and 200 mA, and the source to image distance (SID) was set to ∼140 cm for each testing protocol. For all static testing, the biplanar videoradiography system recorded in pulsed (4 ms) X-ray generation mode at 60 fps. During dynamic testing, the biplanar videoradiography system recorded in continuous X-ray generation mode at 250 fps. To optimize image quality and eliminate motion blur (dynamic protocol), each high-speed video camera was shuttered between 1/1300 and 1/2000 s depending on the bone or marker flag being imaged.

Clinical CT scans for each bone were acquired in the axial plane (Lightspeed, GE, Piscataway, NJ) at 80 kVp, using GE's SMART mA and Bone Plus reconstruction algorithm. The table speed and pitch were set at 0.562 deg and 5.62 mm/rotation for each scan. The image volumes contained 243 image slices for the distal femur and 218 image slices for the distal radius and distal ulna. In-plane image resolution was set at 512 × 512 pixels for a voxel size of 0.217 × 0.217 × 0.625 mm³. Each bone was isolated from its entire volume using thresholding and segmentation tools implemented in commercially available software (Mimics 14, Materialise, Ann Arbor, MI). These procedures follow well established techniques [30,31].

Data Analysis.

All analyses were performed on unfiltered data. Helical axis of motion rotation (HAM) rotation and translation variables were used to describe all rigid body kinematics obtained from the XROMM system. This permits a direct comparison of values without the need to define a common identical coordinate system in both the XROMM and testing apparatuses space. Systematic error, defined as the difference between the measured rigid body motion (XROMM) and the true value of the parameter being measured (stages or ADT), was determined for every static and dynamic data point. These data are summarized using sample median, 25–75 percentile, and range statistics. Absolute error data are summarized using sample mean and standard deviation (SD) statistics.

The distributions of angular velocities and angular accelerations were determined for the maker flag and each bone in order to highlight the motions being imaged during the dynamic protocol. Angular velocity was defined as the discrete derivative of the measured position data. Angular acceleration was defined as the discrete second derivative of the measured position data. Correlations between error, angular velocity, and angular acceleration were determined for all dynamic trials using standard linear regression techniques.

Results

The distributions of error values (minimum, 25th percentile, median, 75th percentile, and maximum) for the static rotational (Fig. 5(a)) and translational (Fig. 5(b)) movements were lower and more tightly clustered for the marker flag than for each bone tracked using the described markerless tracking software. For marker-based tracking of the marker flag, the mean static rotational and translational absolute errors were estimated to be 0.09 ± 0.08 deg (Fig. 5(c)) and 0.12 ± 0.08 mm (Fig. 5(d)), respectively. For markerless tracking, the mean static rotational absolute errors were 0.30 ± 0.18 deg, 0.39 ± 0.18 deg, and 0.44 ± 0.26 deg for the distal femur, distal radius, and distal ulna, respectively (Fig. 5(c)). The markerless tracking mean static translational absolute errors were 0.25 ± 0.16 mm, 0.33 ± 0.27 mm, and 0.30 ± 0.30 mm for the distal femur, distal radius, and distal ulna, respectively (Fig. 5(d)).

Fig. 5.

Static error results. (a) and (b). Box and whiskers rotational (a) and translational (b) plot displaying range, 25–75 percentile, and median static error for each specimen. (c) and (d). Mean (+1 SD) rotational (c) and translational (d) absolute static error for each specimen.

For the dynamic protocol, the minimum, 25th percentile, median, 75th percentile, and maximum angular velocity was 0.0, 47.2, 95.8, 172.7, and 6.2 × 10³ degrees/s, respectively (Figs. 6(a) and 6(b)). The minimum, 25th percentile, median, 75th percentile, and maximum angular accelerations was 0.0, 1.3 × 10³, 2.9 × 10³, 5.1 × 10³, and 1.6 × 10⁶ degrees/s [2], respectively (Figs. 6(c) and 6(d)). Approximately 50% of the velocities and accelerations were above 95 degrees/s and 2900 degrees/s [2], respectively.

Fig. 6.

Cumulative distributions of all velocities and accelerations tested during the dynamic protocols. The full cumulative distributions of velocities and accelerations are shown in (a) and (c), respectively. The majority of velocities and accelerations are shown in (b) and (d), respectively. These data are taken from the data windowed by the vertical dotted lines present in (a) and (c).

The distribution of dynamic rotational error values (minimum, 25th percentile, median, 75th percentile, and maximum) were similar for the marker flag and each bone tracked using the described markerless tracking software (Fig. 7(a)). However, the total range of error values was lower for the marker flag. For marker-based tracking, the mean dynamic absolute error was estimated to be 0.10 ± 0.06 deg (Fig. 7(b)). For markerless tracking, the mean dynamic absolute error was estimated to be 0.14 ± 0.09 deg, 0.10 ± 0.09 deg, 0.14 ± 0.12 deg for the distal femur, distal radius, and distal ulna, respectively (Fig. 7(b)). In addition, angular velocity and acceleration were found to be very poor predictors of systematic error for the marker flag and all bones (R²≤ 0.01). Furthermore, the change in error for a unit change in either angular velocity or acceleration was below 0.036 for the marker flag and all bones.

Fig. 7.

Dynamic error results. (a) Box and whiskers plot displaying range, 25–75 percentile, and median dynamic error for each specimen. (b) Mean (+1 SD) absolute dynamic error for each specimen.

Discussion

The goals addressed by this study were threefold. First, an outline of new markerless tracking software that makes significant use of modern GPU technology has been provided. Second, a versatile method for quantifying the systematic error of a biplanar videoradiography system using independent gold standard instrumentation was described. Finally, these methods were applied to evaluate the systematic error of a biplanar videoradiography system using marker-based and markerless tracking algorithms under static and dynamic motion conditions.

The results presented in this article indicate that the biplanar videoradiography hardware and Autoscoper software described here are capable of measuring sub-millimeter and sub-degree bone motion under the given testing conditions. The results were obtained using independent instrumentation as a gold standard, rather than an intra-specimen marker-based comparison. This provides two advantages: first, the systematic error of both marker-based and markerless tracking can be assessed independently; and second, eliminating the need to remove all marker signatures from the biplanar videoradiography data saves considerable preprocessing time and effort. The presented results are consistent with similar studies investigating errors associated with markerless bone tracking. A study by Bey et al. reports markerless tracking of the glenohumeral joint [15] to be within 0.5 mm of marker-based tracking. In another study, Bey et al. reports markerless tracking of the patellofemoral joint [16] to be within 0.455 mm and 0.987 deg of marker-based tracking. A study from Martin et al. [3] reports markerless tracking errors on a separate system to be within 0.25 mm of marker-based tracking for the distal femur and pelvis. Additional studies have shown similar markerless tracking results for the knee [6,18].

As anticipated, the systematic error of the biplanar videoradiography hardware and Autoscoper software system fell below 1 mm and 1 deg for both static and dynamic marker-based and markerless tracking. It was expected that the marker-based tracking would be equivalent for both the static and dynamic protocols because the W. M. Keck XROMM Facility is equipped with digital video cameras capable of capturing at high shutter speeds that effectively stop the motion at a given frame. Additionally, because spherical markers were being tracked, changes in marker flag orientation and location throughout the imaging FOV were not expected to affect tracking. The absolute error for the marker-based static and dynamic error were not statistically significant (P = 0.10) from each other.

Conversely, a surprising finding was the larger error observed for the static markerless tracking protocol compared to the dynamic markerless tracking protocol. The dynamic markerless tracking protocol showed lower error values for all bones tested (P < 0.01 for the distal femur, distal radius, and distal ulna). These findings may be associated with the initial guess required as input to the markerless tracking algorithm. During static testing, each frame is tracked independent of the previous and succeeding trial. During dynamic testing, each frame uses position and orientation information from the previous (or succeeding) frame or frames to determine the bone position and orientation at the current frame. The variation in error observed between different bones is thought to be a consequence of factors reported in previous studies [16]. Particularly, 3D bone shape, bone density, edge definition, and orientation within the FOV contribute to the observed measurement error. As an example, the relatively large errors observed for the distal ulna are thought to arise from a lack of bony features compared to the distal radius and distal femur. As a result of this deficiency, the 2D projection (radiograph and DRR) of the distal ulna appears similar for multiple 3D orientations. This highlights the need to conduct study specific error measurements on the system configuration being used and the bones being tracked. Establishing a method for testing the systematic error of a biplanar videoradiography system allows these measurements to be made consistently and relatively easily.

The described method for quantifying the systematic error of a biplanar videoradiography system allows for the independent assessment of marker-based and markerless tracking techniques under static and dynamic motion conditions. Specifically, the ability to assess errors at high speeds and during large accelerations such as highly dynamic impacts and direction changes is important for studying complex activities like jump-landing or hammering. Few studies have assessed markerless tracking error using independent “gold standards.” Li and colleagues [14] have evaluated the systematic error of a biplanar fluoroscope system using a high accuracy materials testing machine with favorable results; however, the low video capture frame rates ( ≤30 fps) limit the system's ability to measure highly dynamic joint motions [32]. The method described herein was successful in measuring the systematic error of a biplanar videoradiography system tracking bone motion during high-speed impact conditions.

Moreover, the versatility of this method allows it to be applied to diverse experiments and testing conditions that require different system configurations and bones. It has become increasingly evident that quantifying errors associated with different bones and system configurations is an important and recommended part of any biplanar videoradiography study [10,11,14–18,33,34]. The variation in error observed for the different bones reported herein as well as those reported in the literature further highlight the importance of quantifying study specific errors. Additional static measurements were performed where each bone was rotated about its long axis (axis through the diaphysis), and the results were consistent with those reported. The axis of rotation would most likely affect a bone with few distinguishing features. The bones tested in this study provided enough features for the algorithm to successfully converge for multiple orientations. For studies investigating specific rotations for a uniformly featured bone, the axis of rotation associated with the outcome measure would need to be validated. Both testing apparatuses allow for the attachment of specimens in any orientation and could be tailored to suit these study specific validation questions. These methods can be used in conjunction with the described auto-registration software to efficiently evaluate systematic error for the majority of biplanar videoradiography studies.

The XROMM Autoscoper software provides the user with an elegant interface (Fig. 2) for markerless bone tracking. Its use of GPU hardware significantly improves the speed over standard CPU implementations. You and colleagues [13] report total processing time to be 100 seconds per frame for two radiographic images. This can translate to hours of processing time for a single data set. Specifically, highly dynamic motions and impacts that occur during high-speed lower and upper extremity impacts require high video capture frame rates (>150 fps) [35–40]. These types of data sets produce hundreds of frames for a single motion capture trial. Bey et al. [15] and Martin et al. [3] have taken steps to reduce processing times by making use of multi-workstation computational clusters that allow the algorithm to parallelize its computations over many processors; however, this amount of computational power can be prohibitively expensive and may be impractical for many laboratories attempting to process biplanar videoradiography data. Making use of modern GPU technology significantly speeds up computation time without the need for large computational clusters. The current implementation of XROMM Autoscoper on one desktop workstation with a single GPU (480 processing cores) provides a substantial cost advantage. This particular configuration requires between 0.5 and 1.5 seconds per frame depending on the size of the CT volume and visualization parameters. These time estimates will vary with different GPU hardware. Overall, implementing auto-registration algorithms on GPUs successfully reduces processing time, financial commitments, and saves valuable laboratory space.

Previous studies have thoroughly documented the limitations of biplanar videoradiography technology. Compared to traditional optical motion capture technology, biplanar videoradiography technology is not as readily available. Additionally, the X-ray exposure increases risk to subjects, and the relatively small imaging volume (∼2,000 in³) limits the range of activities that can be studied when compared to traditional motion capture technology [37]. Furthermore, the registration algorithm presented herein does require at least one user-supplied initial guess that is visually close to the actual bone position and orientation. In practice, user input is typically required throughout data processing to assist the auto-registration algorithm converge on a final solution. The Autoscoper software requires different degrees of user input based on the quality of the collected data and the complexity of the joints and motions being processed. The results presented in this study are limited to idealized tracking situations. Only one bone was tracked during each test and no soft tissues were present. This eliminates bone and soft tissue overlap, which may increase processing time and measurement errors in vivo.

In summary, the results presented herein indicate that the biplanar videoradiography hardware and the publically available GPU-based markerless tracking software can be used to effectively track rapid bone motions to within 0.15 deg for the distal aspects of the femur, radius, and ulna. Future research will employ these techniques to quantify in vivo joint motion for high-speed upper and lower extremity impacts such as jumping, landing, and hammering. Furthermore, additional algorithms and image processing techniques will continue to be explored in hopes of further improving markerless tracking performance and efficiency.