Abstract
An unusual feature of the cerebellar cortex is that its output neurons, Purkinje cells, are GABAergic. Their high intrinsic firing rates1 (50 Hz) and extensive convergence2,3 predict that that target neurons in the cerebellar nuclei would be largely inhibited unless Purkinje cells pause their spiking, yet Purkinje and nuclear neuron firing rates do not always vary inversely4. A potential clue to how these synapses transmit information is that populations of Purkinje neurons synchronize their spikes during cerebellar behaviors5–11. If nuclear neurons respond to Purkinje synchrony, they may encode signals from subsets of inhibitory inputs7,12–14. Here we show in weanling and adult mice that nuclear neurons transmit the timing of synchronous Purkinje afferent spikes, owing to modest Purkinje-to-nuclear convergence ratios (~40:1), fast IPSC kinetics (τdecay=2.5 ms), and high intrinsic firing rates (~90 Hz). In vitro, dynamically clamped asynchronous IPSPs mimicking Purkinje afferents suppress nuclear cell spiking, whereas synchronous IPSPs entrain nuclear cell spiking. With partial synchrony, nuclear neurons time-lock their spikes to the synchronous subpopulation of inputs, even when only 2 of 40 afferents synchronize. In vivo, nuclear neurons reliably phase-lock to regular trains of molecular layer stimulation. Thus, cerebellar nuclear neurons can preferentially relay the spike timing of synchronized Purkinje cells to downstream premotor areas.
During cerebellar behaviors, on-beam Purkinje cells fire synchronous simple spikes with millisecond-scale precision5–8, and microbands of Purkinje cells fire synchronous complex spikes9–11. The extent to which cerebellar nuclear neurons respond to synchrony depends on the magnitude, convergence, and kinetics of Purkinje inputs. We therefore measured these properties before assessing the consequence of Purkinje synchrony on nuclear firing in vitro and in vivo.
We first recorded IPSC amplitudes evoked in nuclear neurons by stimulating Purkinje axons in mouse cerebellar slices (Fig. 1a,b). Maximal stimulation evoked IPSCs up to ~200 nS (mean ± s.e.m., 108.3±13.0 nS; n=17). Minimal stimulation evoked either failures or successes of 9.4±1.0 nS (n=30), whose amplitudes resembled TTX-sensitive spontaneous IPSCs15, consistent with activation of a single fiber. The high unitary amplitude suggests that individual Purkinje-to-nuclear contacts are quite strong16. The maximal-to-minimal conductance ratio indicates that functional convergence in the slice is about 12, or maximally ~22. Because both slicing and incomplete recruitment of afferents likely limit maximal IPSC amplitudes, this estimate represents a lower bound on functional convergence in the intact cerebellar nuclei.
Figure 1. Purkinje cell convergence and fast IPSCs in the cerebellar nuclei.
a, IPSCs evoked by maximal stimulation. Holding potential −57 mV (junction potential corrected). Top: 5 overlaid IPSCs. Middle: IPSC amplitudes as stimulus strength was reduced. Bottom: Maximal conductances calculated from measured IPSC reversal potentials (n=17, mean ECl=−75 mV). Bin width, 10 nS. b, IPSCs evoked by minimal stimulation (range 16–20 μA). Top: 20 overlaid IPSCs. Middle: Expansion of box in (a). Events near the zero line fell within the noise. Bottom: Minimal conductances (n=30). Bin width, 2 nS. c, Left: Scaled IPSCs in one cell at 22° and 36oC. Right: Temperature dependence of IPSC decay τ (n=7). d, Top: 50-Hz train of IPSCs at 36oC. Bottom: Depression of phasic IPSCs and absence of tonic current during train. In all figures, data are mean±s.e.m, unless noted.
We obtained a second convergence estimate by considering structural constraints on innervation (see Supplementary Discussion for calculations). In mouse, the Purkinje-innervated surface of a large nuclear cell with four dendrites (3130 μm2) maximally accommodates 1250 Purkinje boutons, each with a 2.5 μm2 surface area; comparable numbers (600–1200) are estimated for cat17. Multiple boutons must arise from a single Purkinje cell, however, because the quantal content of a unitary Purkinje IPSC15,16 is 12-18. Given a boutonal release probability18 of 0.5, each Purkinje cell must contribute ~24–36 boutons per target, predicting 34–52 Purkinje cells/nuclear cell.
A third estimate was derived from the maximal GABAAR conductance per nuclear neuron19, which yielded a mean convergence of ~20 (maximum, ~30) (Supplementary Discussion). The estimates from these three separate measures can be reconciled with classic histological measurements of 860 Purkinje cells per nuclear cell in the cat3, by the observation that each Purkinje bouton has 9–10 synaptic densities2,18. Correcting for this factor reduces the predicted convergence to 86–96, on the order of magnitude of the present estimates. Thus, multiple approaches suggest a functional convergence in the intact cerebellum of tens of Purkinje neurons per nuclear neuron, likely 20–50 in the rodent.
Additional determinants of the efficacy of inhibition are the intrinsic firing rates and IPSC kinetics. In P17-P26 mice, nuclear neurons fired spontaneously at 91.5±7.4 spikes/s, significantly faster than in P13 animals recorded under identical conditions15 (22.0 ± 5.0 spikes/s, Fig. S1), indicating a developmental increase in intrinsic firing rate. At near-physiological temperature (36°C), the τdecay of evoked IPSCs was 2.4 ± 0.2 ms (Fig. 1c), making corticonuclear IPSCs among the fastest known GABAA receptor- mediated currents20. This value is >5-fold briefer than the τdecay of 13.6 ms of IPSCs at room temperature21, which figures in previous corticonuclear models12–14. When unitary IPSCs were mimicked with dynamic clamp, the duration of inhibition of spontaneously firing nuclear cells varied directly with τdecay15,21,22, and the first post-inhibitory spike was well-timed relative to the stimulus23 (Fig. S2). Thus, brief IPSCs minimize inhibition.
When synchronous IPSCs were evoked at 50 Hz at 36°C, peak IPSCs depressed by 55% (n=6), but the current decayed fully between stimuli (Fig. 1d), resulting in no accumulation of “tonic” current15. Since tonic current is largely responsible for suppressing nuclear cell spiking, synchronous and asynchronous IPSCs may differentially modulate nuclear cell output. As a preliminary test of this idea, we delivered trains of dynamically clamped IPSPs (dynIPSPs) from eight afferents, each with an amplitude of 10 nS and a rate of 50 Hz, which were either desynchronized (equivalent to one non-depressing input at 400 Hz) or synchronized (Fig. 2a). Not surprisingly, desynchronized dynIPSPs strongly inhibited spontaneous firing. In contrast, upon synchronization of dynIPSPs, nuclear neuron firing rates jumped instantaneously, but only when τdecay was brief (Fig. 2b). Moreover, with physiological τdecay, nuclear cell spiking entrained to the synchronous input, evident as a match between the instantaneous firing rate and the stimulus rate (Fig. 2a). Likewise, IPSPs evoked by Purkinje stimulation nearly perfectly entrained nuclear neuron spiking between 60 and 80 Hz (Fig. 2c, 2d); in contrast, desynchronized dynIPSPs suppressed firing at all stimulus rates (Fig 2d). Thus, in the extreme case of low convergence, the output of nuclear neurons is determined by both the rate and synchrony of inhibition.
Figure 2. Entrainment of nuclear neuron spiking to synchronous IPSPs.
a, Top: Response to desynchronized and synchronized dynIPSPs from 8 inputs at 50 Hz, τdecay =2.5 ms. Bottom: Instantaneous firing rates of neuron in (a), showing entrainment during synchrony. Arrows, onset of desynchronized (left) and synchronized (right) dynIPSPs. Tall spikes reflect overlapping dynIPSPs and spikes. b, Firing rates during desynchronized and synchronized 50-Hz trains with different dynIPSP kinetics (τdecay=2.5, 5, 14 ms, n=25, 18, 10). c, Entrainment to corticonuclear IPSPs (36°C) between 60 and 80 Hz. Arrows, stimulation times. d, Median firing rates (±1 quartile) in response to evoked IPSPs (closed symbols) and desynchronized dynIPSPs (open symbols). From 50–100 Hz, evoked, n=8, 8, 8, 7, 3; simulated, n=25, 10, 10, 9, 14. Dashed line, unity.
Synchronous Purkinje firing occurs in vivo5–11, but the proportion of convergent Purkinje cells that synchronize is likely <100%. We therefore mimicked 40 Purkinje afferents with dynamic clamp, reflecting a realistic functional convergence, and tested whether synchronizing only a subpopulation of inputs can affect cerebellar nuclear output. To account for synaptic depression and mimic irregular spiking in vivo23,24, each input was 5 nS, and inter-IPSP-intervals were drawn from Gaussian distributions (CV=1), yielding a mean of 50 IPSPs/sec. After 1 sec of asynchronous inhibition, a fixed number of inputs (2–20, or 5%–50%) was synchronized at 20–125 Hz, while the remaining inputs continued to provide asynchronous inhibition, each at 50 IPSPs/sec (Fig. 3a, 3b). Asynchronous dynIPSPs greatly slowed nuclear cell firing. Firing rates, however, increased with fractional synchrony (Fig. 3a, 3c). The averaged voltage trajectories of synchronous dynIPSPs preceding and lacking a spike did not differ in the depth of hyperpolarization (Fig. S3). Thus, the action potentials are not low-threshold spikes that follow unusually large inhibitory stimuli.
Figure 3. The synchronous subpopulation of Purkinje inputs sets spike timing of nuclear neurons.
a, Nuclear neuron responses to dynIPSPs from 40 asynchronous or partially synchronized inputs, as labeled. b, Spike rasters during dynIPSP trains with 50–5% synchrony. c, Firing rates during 20–125 Hz trains with 0%–50% synchrony (“sync rates”). d, Normalized interspike interval distributions during 50% synchrony, from 40 to 100 Hz. Abscissa tick marks indicate multiples of the interstimulus intervals. Bin width, 2 ms. Black: no current injection. Blue: with 200 pA DC applied to increase spike number during inhibition. e, Black: Polar histograms of interspike intervals during 50–5% synchrony for 50, 55, 67, 83, 100, and 125 Hz input. Each cycle is one interstimulus interval (StimI). Red: Net vectors of interspike interval histograms. (For 50%, 25%, 10%, 5% synchrony, n=14, 9, 7, 7).
During trains of synchronous dynIPSPs, distinct temporal patterns of spiking emerged. For all frequencies tested, interspike interval distributions clustered at multiples of the interstimulus intervals of the synchronous dynIPSPs (Fig. 3d), reflecting phase-locking of spikes to the regular stimulus train. The data were combined across stimulus frequency by plotting interspike intervals as normalized polar histograms, with 0° representing multiples of the interstimulus interval (Fig. 3e). A net vector magnitude of 1 indicates perfect phase-locking, and 0 indicates randomly occurring spike patterns. For all fractions of synchrony, the net vector was oriented close to 0° (2°±2°) with a non-zero magnitude (0.18, 0.25, 0.45, and 0.52 for 5%, 10%, 25%, and 50% synchrony), illustrating the temporal restructuring of spikes according to stimulus interval.
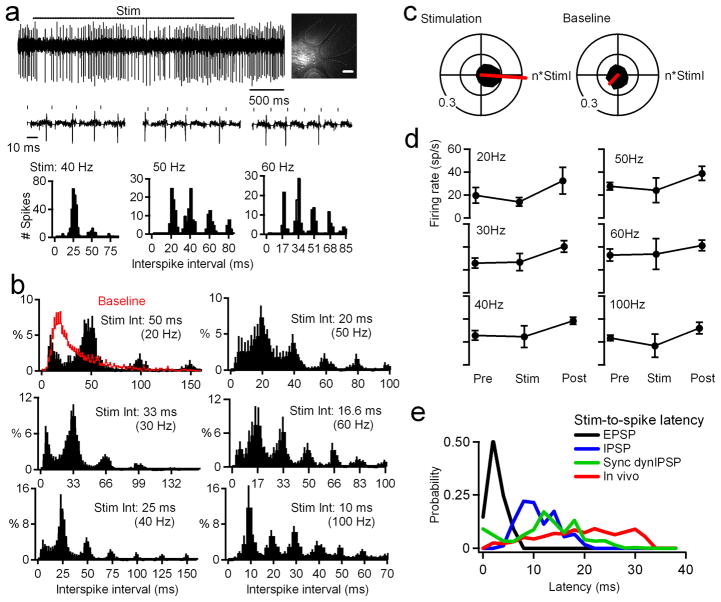
To test whether conditions in vivo permit phase-locking, we recorded single units from the cerebellar nuclei in anesthetized adult mice (Fig. 4a). Purkinje spiking was partially synchronized by stimulating the molecular layer23. Indeed, for stimuli from 20–120 Hz, phase-locking was robust in all neurons confirmed histologically to be within the nuclei (10 cells in 10 mice; Fig 4a, 4b). No phase-locking was apparent in two neurons located outside the nuclei. The net vector of the mean polar histogram combined across frequencies was oriented at −3° (Fig 4c). Its magnitude (0.33) was between those for 10% and 25% synchrony in vitro, and was greater than that of baseline (0.09, p<0.05, within-cell comparisons of vector magnitudes; direction 257°).
Figure 4. Nuclear neurons phase lock to molecular layer stimulation in vivo.
a, Upper trace, response of a nuclear neuron to 40-Hz molecular layer stimulation (bar). Inset, Recording site in the cerebellar nuclei recovered after focal Alexa 568 injection. Dashed lines demarcate cerebellar folia. Scale bar, 200 μm. Lower traces, expanded segments of spikes during 40, 50, and 60-Hz stimulation (ticks), showing the long stimulus-to-spike latency. Stimulus artifacts are zeroed. Plots, Interspike interval histograms for responses above. b, Mean normalized interspike interval distributions during molecular layer stimulation from 20–100 Hz for 4, 9, 9, 7, 5, and 7 cells respectively. Abscissa tick marks indicate multiples of the interstimulus interval. Red baseline histogram includes intervals before and after stimulation. Peaks at multiples of 8.3 ms were evident in 2/2 cells stimulated at 120 Hz (not shown). Bin width, 2 ms. c, Black: Polar histograms of interspike intervals during stimulation across rates (left) or during baseline periods. Red: Net vectors of polar histograms. d, Mean firing rates before (“pre,” 1 sec), during (“stim,” 3 sec) and after (“post,” 9 sec) stimulation. e, Stimulus-to-spike latencies for pharmacologically isolated EPSPs (black), IPSPs (blue), dynIPSPs during partial synchrony (green) and in vivo (red).
Stimulation modulated mean firing rates of individual neurons (p<0.05 vs. baseline, within-cell comparisons). Like the results for different fractional synchrony in vitro, however, spike rates decreased in some cells (n = 7) and increased in others (n =3; Fig. S4), yielding no net change across cells (p>0.05, Fig 4d). Thus, the firing rate of nuclear cells, which is likely affected by both basal excitation and the fractional synchrony induced by the stimulus, does not obviously encode information about the rate of inhibitory inputs.
To evaluate whether stimulation directly excited nuclear neurons, we compared stimulus-to-spike latencies across conditions. In vivo latencies were 20.2±2.2 ms, >5-fold greater than EPSP-to-spike latencies in vitro (3.5±0.5, inhibition blocked), making direct excitation seem unlikely. Instead, in vivo latencies were closer to IPSP-to-spike latencies (11.9±1.4 ms, excitation blocked) and synchronous dynIPSP-to-spike latencies with background inhibition (13.5±0.6 ms; Fig. 4e), consistent with sequential parallel fiber and Purkinje cell activation23. Given the similarity of phase-locking in vivo and in vitro with excitation blocked, these results suggest that the in vivo stimulation synchronizes Purkinje cell simple spikes, which in turn set the timing of nuclear cell spikes. The reliability of phase-locking to regular trains of inhibitory stimuli in vivo further suggests that the spike patterns of a synchronized Purkinje subpopulation can be transmitted with fidelity by cerebellar nuclear neurons.
These experiments address the long-standing question in cerebellar physiology of how nuclear neurons encode signals from convergent, inhibitory Purkinje cells firing at high basal rates1. Nuclear neurons’ intrinsic tendency to fire permits time-locked spiking during the transient reduction in inhibition after a few brief IPSCs overlap. Even synchrony of only 2 afferents (5%) can influence the timing of nuclear cell spiking. The results provide an alternative to the idea that nuclear cell firing requires pauses that permit low-threshold rebound spikes after prolonged Purkinje activity: Not only would such a mechanism discard information present in graded Purkinje firing rates, but it would also introduce ~100-ms delays in cerebellar processing that are not evident25.
The extent to which time-locking occurs during natural cerebellar processing will depend on the fractional synchrony of converging Purkinje cells, the precision of this synchrony, and the variance of ongoing excitation of nuclear neurons13. Supporting the idea that synchronized Purkinje neurons converge, simple spike synchrony is observed in neighboring on-beam Purkinje cells5,6, and closely spaced Purkinje cells likely converge on a common nuclear neuron26. Moreover, neighboring Purkinje cells are likely functionally related, since transsynaptic tracing from muscles labels discrete strips of Purkinje cells27.
A remaining question is how time-locked nuclear cell spikes are processed downstream. In the red nucleus, each interpositus axon makes parasagittally ramifying contacts28, and about 50 interpositus neurons converge onto each target, producing EPSPs with little short-term plasticity29. Therefore, summation of EPSPs in the red nuclei may drive spiking that follows the firing pattern of the synchronized Purkinje subpopulation. More generally, time-locking by cerebellar nuclear neurons may be a mechanism whereby the rate and timing of signals from varying groups of synchronized Purkinje cells are preferentially transmitted to premotor areas and other cerebellar targets.
Methods Summary
Procedures conformed to institutional guidelines for animal care and use.
In vitro electrophysiology
Parasagittal cerebellar slices from both sexes of C57/B6 13-29 day old mice mice were cut15 in ACSF (35°C). Recordings from large nuclear neurons were made15 at 35–37°C, unless noted, with a Multiclamp 700B amplifier and pClamp acquisition software. IPSCs were evoked in DNQX (5 μM), CPP (10 μM) and strychnine (2 μM) by 0.1 ms pulses delivered through a concentric bipolar electrode in the white matter surrounding the cerebellar nuclei. Evoked IPSCs were considered minimal when a fixed intensity stimulus elicited responses and failures with approximately equal likelihood, and maximal when increasing intensity produced no larger IPSCs. Dynamic clamp was implemented with an SM-2 (Cambridge Conductance) and a P25M real-time DSP board sampling between 10 and 25 kHz. Simulated IPSCs had a rise time and τdecay of 0.1 and 2.5 ms, 0.5 and 5 ms, or 1 and 14 ms, and reversed at −75 mV. Desynchronized inputs had dynIPSP intervals distributed uniformly. Asynchronous dynIPSP intervals were drawn from a Gaussian distribution, created off-line in IgorPro 5.05, with CV=1. Forty independent trains were merged.
In vivo electrophysiology
Adult C57/B6 mice were anesthetized with ketamine (80–100 mg/kg) and xylazine (5–10 mg/kg). A glass recording electrode containing 2M NaCl was targeted to the cerebellar nuclei. A bipolar stimulating electrode (~300 μm between poles) was placed stereo taxically in the molecular layer, flanking the recording electrode. Three-second stimulus trains were delivered once every 15 s, repeated 4–20 times per frequency. Data were analyzed in IgorPro.
Methods
Tissue Preparation
Parasagittal slices of the cerebellar nuclei were prepared as in Telgkamp and Raman15 in accordance with institutional guidelines for animal care and use. P13-P29 day old mice were deeply anesthetized with isofluorane and transcardially perfused with warm (35°C) artificial cerebrospinal fluid (ACSF) containing (in mM): 123 NaCl, 3.5 KCl, 26 NaHCO3, 1.25 NaH2PO4, 1.5 CaCl2, 1 MgCl2, 10 glucose and equilibrated with 95/5% O2/CO2. Mice were then rapidly decapitated and the brains removed into ACSF (35°C). Slices (300 μm thick) were cut on a Vibratome (Leica VT 100S) and incubated in warmed (35°C), oxygenated ACSF for at least 1 hour before recording.
Electrophysiological recording
Cerebellar slices were transferred to a recording chamber perfused continuously with warmed (35–37°C, unless noted), oxygenated ACSF at a flow rate of 2–4 ml/min. Slices were visualized with IR-DIC microscopy and recordings were made from large neurons (soma diameters >15 μm). Neurons all had fast decay constants (~2.5 ms at 36°C), resembling the <5 ms τdecay of GAD-negative large neurons at 34°C rather than the ~10 ms τdecay of GAD-positive neurons22. They are therefore likely to be excitatory projection neurons. Data were filtered at 6 kHz and sampled at 10–25 kHz.
Voltage- and current-clamp recordings were made with a Multiclamp 700B amplifier (Molecular Devices) and pClamp 10.0 data acquisition software (Molecular Devices). Borosilicate patch pipettes were pulled to tip resistances of 2–4 MΩ and filled with an internal solution containing (mM): 130 K-gluconate, 2 Na-gluconate, 6 NaCl, 10 HEPES, 2 MgCl2, 0.1 or 1 EGTA, 14 Tris-creatine phosphate, 4 MgATP, 0.3 Tris-GTP, and 10 sucrose. For experiments isolating GABAA receptor-mediated currents, DNQX (5 μM), CPP (10 μM) and strychnine (2 μM) were included in the bath solution and currents were evoked by stimulating the white matter surrounding the cerebellar nuclei with 0.1 ms current pulses (Isoflex Stimulus Isolation Unit; AMPI) delivered through a concentric bipolar electrode (FHC). Evoked IPSCs were considered minimal when a fixed amplitude stimulus strength elicited IPSCs or failures with approximately equal likelihood, suggesting stimulation was at threshold for a single input.
Dynamic clamp was implemented with a SM-2 system (Cambridge Conductance) with a P25M real-time DSP board (Innovative Integration) sampling between 10 and 25 kHz. Unitary conductances were set at either 10 or 5 nS and three kinetic profiles were used: 0.1 ms rise time and a single exponential τdecay of 2.5 ms; 0.5 ms rise and τdecay of 5 ms (Ref. 15); and 1 ms rise and τdecay 14 ms (Ref. 21), with a reversal potential of −75 mV, accounting for a 7 mV measured liquid junction potential. In experiments manipulating synchrony between 0 and 100%, eight 10-nS convergent units were simulated. Desynchronized inputs were designed to distribute IPSP-times uniformly during the inter-stimulus-interval, such that each ‘unit’ was activated at a given rate but offset in time by (inter-stimulus-interval/8) ms. Gaussian trains were created off-line in IgorPro 5.05 (Wavemetrics). Spike times were drawn from a Gaussian distribution with a CV of 1. Forty independent trains were merged to represent a population of corticonuclear IPSP arrival times and applied to trigger inhibitory conductances.
In vivo electrophysiology
Adult C57/B6 mice were anesthetized with a cocktail of 80–100 mg/kg ketamine and 5-10 mg/kg xylazine i.p. A small craniotomy above the cerebellum was made with a dental drill. A glass recording electrode containing 2M NaCl with 1% Alexa 568 10K dextran amine was targeted to the cerebellar nuclei (in mm: 2.6 –3.0 posterior to Lambda, 1.0 – 1.3 lateral, 2.2 – 3.1 depth). A bipolar stimulating electrode (~300 μm between poles) was placed stereotaxically in the cerebellar molecular layer, aligned approximately in the coronal plane (on-beam), flanking the recording electrode. Stimulus trains were 3 s, delivered once every 15 s, had pulse durations of 0.1 ms and amplitudes of 40 (n=1), 200 (n=6) or 360 μA (n=5), after other studies that used 100–200 μA23. A stimulus of 360 μA is expected to stimulate a sphere with <0.5 mm radius30. Each stimulus rate was delivered between 4 and 20 times to each unit. Following each recording, dye was pressure injected to mark the recording site. Only one cell was recorded from each mouse. Mice were transcardially perfused with physiological saline, brains were harvested and fixed in 4% paraformaldehyde. Brains were cryoprotected in 30% sucrose, sectioned to 40 μm on a freezing microtome, and visualized on a Leica laser scanning confocal microscope.
Data analysis
Data were analyzed offline in IgorPro 5.05 (Wavemetrics). Statistical analysis was done with paired or unpaired 2-tailed t-tests as noted in the text, with significance taken as p<0.05. Polar plots were constructed by binning interspike intervals with bin size = stimulus interval/12 for each stimulus frequency in each cell and averaging first across cells and then across frequencies. On each polar plot, one cycle is one interstimulus interval, such that a bar at 0° indicates spikes occurring at multiples of the interspike interval. Net vector magnitudes and directions were computed by summing the x and y values associated with the angle and radius values of the 12 vectors (histogram bars) that compose the mean polar plot. The null polar plot for the in vivo data was constructed from the interspike intervals of spikes occurring during non-stimulated periods, plotted with the same time bases as the stimulated interspike intervals. For statistical comparison of stimulated and null interspike intervals in vivo, vector magnitudes were calculated for data binned at 0.1 ms.
Supplementary Material
Acknowledgments
We are grateful to Dr. Jason R. Pugh for new analysis of data from Ref. 19 on whole-cell GABA conductances. We thank Drs. D. Ferster, D. McLean, and C. Woolley for comments on the manuscript. Supported by NIH grants R01-NS39395 (IMR) and F32-NS067831 (ALP).
Footnotes
Author contributions: ALP performed all experiments and analyses. ALP and IMR designed and interpreted experiments and wrote the manuscript.
References
- 1.Thach WT. Discharge of Purkinje and cerebellar nuclear neurons during rapidly alternating arm movements in the monkey. J Neurophysiol. 1968;31:785–97. doi: 10.1152/jn.1968.31.5.785. [DOI] [PubMed] [Google Scholar]
- 2.Chan-Palay V. Organization, cytology, and transmitters. Springer; Berlin: 1977. Cerebellar dentate nucleus. [Google Scholar]
- 3.Palkovits M, Mezeky E, Hamori J, Szentagothai J. Quantitative histological analysis of the cerebellar nuclei in the cat. I. Numerical data on cells and on synapses. Exp Brain Res. 1977;28:189–209. doi: 10.1007/BF00237096. [DOI] [PubMed] [Google Scholar]
- 4.McDevitt CJ, Ebner TJ, Bloedel JR. Relationships between simultaneously recorded Purkinje cells and nuclear neurons. Brain Res. 1987;425:1–13. doi: 10.1016/0006-8993(87)90477-x. [DOI] [PubMed] [Google Scholar]
- 5.Bell CC, Grimm RJ. Discharge properties of Purkinje cells recorded on single and double microelectrodes. J Neurophysiol. 1969;32(6):1044–1055. doi: 10.1152/jn.1969.32.6.1044. [DOI] [PubMed] [Google Scholar]
- 6.Heck DH, Thach WT, Keating JG. On-beam synchrony in the cerebellum as the mechanism for the timing and coordination of movement. PNAS. 2007;104:7658–63. doi: 10.1073/pnas.0609966104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.de Solages C, et al. High-frequency organization and synchrony of activity in the Purkinje cell layer of the cerebellum. Neuron. 2008;58:775–88. doi: 10.1016/j.neuron.2008.05.008. [DOI] [PubMed] [Google Scholar]
- 8.Wise AK, Cerminara NL, Marple-Horvat DE, Apps R. Mechanisms of synchronous activity in cerebellar Purkinje cells. J Physiol. 2010;588.13:2737–390. doi: 10.1113/jphysiol.2010.189704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Welsh JP, Lang EJ, Sugihara I, Llinas R. Dynamic organization of motor control within the olivocerebellar system. Nature. 1995;374:453–7. doi: 10.1038/374453a0. [DOI] [PubMed] [Google Scholar]
- 10.Ozden I, Sullivan MR, Lee HM, Wang SS. Reliable coding emerges from coactivation of climbing fibers in microbands of cerebellar Purkinje neurons. J Neurosci. 2009;29:10463–73. doi: 10.1523/JNEUROSCI.0967-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Schultz SR, Kitamura K, Post-Uiterweer A, Krupic J, Häusser M. Spatial pattern coding of sensory information by climbing fiber-evoked calcium signals in networks of neighboring cerebellar Purkinje neurons. J Neurosci. 2009;29:8005–15. doi: 10.1523/JNEUROSCI.4919-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gauck V, Jaeger D. The control of rate and timing of spikes in the deep cerebellar nuclei by inhibition. J Neurosci. 2000;20:3006–16. doi: 10.1523/JNEUROSCI.20-08-03006.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gauck V, Jaeger D. The contribution of NMDA and AMPA conductances to the control of spiking in neurons of the deep cerebellar nuclei. J Neurosci. 2003;23:8109–8118. doi: 10.1523/JNEUROSCI.23-22-08109.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kistler WM, De Zeeuw CI. Time windows and reverberating loops: a reverse-engineering approach to cerebellar function. Cerebellum. 2003;2:44–54. doi: 10.1080/14734220309426. [DOI] [PubMed] [Google Scholar]
- 15.Telgkamp P, Raman IM. Depression of inhibitory synaptic transmission between Purkinje cells and neurons of the cerebellar nuclei. J Neurosci. 2002;22:8447–57. doi: 10.1523/JNEUROSCI.22-19-08447.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pedroarena CM, Schwarz C. Efficacy and short-term plasticity at GABAergic synapses between Purkinje and cerebellar nuclei neurons. J Neurophysiol. 2003;89:704–15. doi: 10.1152/jn.00558.2002. [DOI] [PubMed] [Google Scholar]
- 17.Bengtsson F, Ekerot C-F, Jörntell H. In vivo analysis of inhibitory synaptic inputs and rebounds in deep cerebellar nuclear neurons. PLOS One. 2011;6(4):e18822. doi: 10.1371/journal.pone.0018822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Telgkamp P, Padgett DE, Ledoux VA, Woolley CS, Raman IM. Maintenance of high-frequency transmission at Purkinje to cerebellar nuclear synapses by spillover from boutons with multiple release sites. Neuron. 2004;41:113–26. doi: 10.1016/s0896-6273(03)00802-x. [DOI] [PubMed] [Google Scholar]
- 19.Pugh JR, Raman IM. GABAA receptor kinetics in the cerebellar nuclei: Evidence for detection of transmitter from distant release sites. Biophys J. 2005;88:1740–54. doi: 10.1529/biophysj.104.055814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bartos M, et al. Fast synaptic inhibition promotes synchronized gamma oscillations in hippocampal interneuron networks. PNAS. 2002;99:13222–7. doi: 10.1073/pnas.192233099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Anchisi D, Scelfo B, Tempia F. Postsynaptic currents in deep cerebellar nuclei. J Neurophysiol. 2001;85:323–31. doi: 10.1152/jn.2001.85.1.323. [DOI] [PubMed] [Google Scholar]
- 22.Uusisaari M, Knopfel T. GABAergic synaptic communication in the GABAergic and non-GABAergic cells in the deep cerebellar nuclei. Neuroscience. 2008;156:537–48. doi: 10.1016/j.neuroscience.2008.07.060. [DOI] [PubMed] [Google Scholar]
- 23.Hoebeek FE, Witter L, Ruigrok TJ, De Zeeuw CI. Differential olivo-cerebellar cortical control of rebound activity in the cerebellar nuclei. PNAS. 2010;107:8410–5. doi: 10.1073/pnas.0907118107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Goossens, et al. Simple spike and complex spike activity of floccular Purkinje cells during the optokinetic reflex in mice lacking cerebellar long-term depression. Eur J Neurosci. 2004;19:687–697. doi: 10.1111/j.0953-816x.2003.03173.x. [DOI] [PubMed] [Google Scholar]
- 25.Mauk MD, Buonomano DV. The neural basis of temporal processing. Annu Rev Neurosci. 2004;27:307–40. doi: 10.1146/annurev.neuro.27.070203.144247. [DOI] [PubMed] [Google Scholar]
- 26.Sugihara I, et al. Projection of reconstructed single Purkinje cell axons in relation to the cortical and nuclear aldolase C compartments of the rat cerebellum. J Comp Neurol. 2009;512:282–304. doi: 10.1002/cne.21889. [DOI] [PubMed] [Google Scholar]
- 27.Ruigrok TJH, Pijpers A, Goedknegt-Sabel E, Coulon P. Multiple cerebellar zones are involved in the control of individual muscles: a retrograde transneuronal tracing study with rabies virus in the rat. Eur J Neurosci. 2008;28:181–200. doi: 10.1111/j.1460-9568.2008.06294.x. [DOI] [PubMed] [Google Scholar]
- 28.Shinoda Y, Futami T, Mitoma H, Yokota J. Morphology of single neurons in the cerebello-rubrospinal system. Behav Brain Res. 1988;28:59–64. doi: 10.1016/0166-4328(88)90076-9. [DOI] [PubMed] [Google Scholar]
- 29.Toyama K, Tsukahara N, Kosaka K, Matsunami K. Synaptic excitation of red nucleus neurones by fibres from interpositus nucleus. Exp Brain Res. 1970;11(2):187–198. doi: 10.1007/BF00234322. [DOI] [PubMed] [Google Scholar]
- 30.Tehovnik EJ, Tolias AS, Sultan F, Slocum WM, Logothetis NK. Direct and indirect activation of cortical neurons by electrical microstimulation. J Neurophysiol. 2006;96:512–21. doi: 10.1152/jn.00126.2006. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.