A Role for Short-Term Synaptic Facilitation and Depression in the Processing of Intensity Information in the Auditory Brain Stem

Abstract

The nature of the synaptic connection from the auditory nerve onto the cochlear nucleus neurons has a profound impact on how sound information is transmitted. Short-term synaptic plasticity, by dynamically modulating synaptic strength, filters information contained in the firing patterns. In the sound-localization circuits of the brain stem, the synapses of the timing pathway are characterized by strong short-term depression. We investigated the short-term synaptic plasticity of the inputs to the bird’s cochlear nucleus angularis (NA), which encodes intensity information, by using chick embryonic brain slices and trains of electrical stimulation. These excitatory inputs expressed a mixture of short-term facilitation and depression, unlike those in the timing nuclei that only depressed. Facilitation and depression at NA synapses were balanced such that postsynaptic response amplitude was often maintained throughout the train at high firing rates (>100 Hz). The steady-state input rate relationship of the balanced synapses linearly conveyed rate information and therefore transmits intensity information encoded as a rate code in the nerve. A quantitative model of synaptic transmission could account for the plasticity by including facilitation of release (with a time constant of ~40 ms), and a two-step recovery from depression (with one slow time constant of ~8 s, and one fast time constant of ~20 ms). A simulation using the model fit to NA synapses and auditory nerve spike trains from recordings in vivo confirmed that these synapses can convey intensity information contained in natural train inputs.

INTRODUCTION

Information transmission in neural networks is partially determined by the rapid, activity-dependent alterations of synaptic strength in response to patterns of presynaptic action potentials, known as short-term synaptic plasticity (Abbott and Regehr 2004; Blitz et al. 2004; Schneggenburger et al. 2002; Trussell 2002; von Gersdorff and Borst 2002). Although some form of short-term synaptic plasticity has been observed in vitro at many different synapses, the functional consequences of this type of plasticity in vivo are still unclear (but see Chung et al. 2002 and Fortune and Rose 2000). Quantitative models of short-term depression and facilitation have been used to identify potential effects such as adaptation, change detection, and signal filtering (Abbott et al. 1997; Chance et al. 1998; Dittman et al. 2000; Tsodyks et al. 1998; Tsodyks and Markram 1997). In the chick, the auditory nerve synapses onto cochlear nucleus magnocellularis (NM) exhibit strong short-term depression (Zhang and Trussell 1994b), as do the mammalian auditory brain stem calyceal synapses (Oleskevich and Walmsley 2002; Schneggenburger et al. 2002; von Gersdorff and Borst 2002; Wang and Kaczmarek 1998; Wong et al. 2003). Nucleus laminaris (NL), a second-order nucleus of the brain stem responsible for encoding timing cues for sound localization, receives bouton-like synaptic input from NM. These synapses also express short-term depression (Cook et al. 2003; Kuba et al. 2002), suggesting that depression may characterize timing circuits.

Nucleus angularis (NA) also receives input from the auditory nerve and encodes intensity cues for sound localization (Takahashi et al. 1984). The nerve terminals in NA are bouton-like, unlike the calyceal synapses onto NM (Carr and Boudreau 1991). Because sound intensity information is encoded in the firing rate of the auditory nerve inputs, short-term synaptic depression, by dynamically adjusting the amplitude of the synaptic conductance inversely to the presynaptic firing rate, results in a loss of intensity information, as shown for the synapses onto NL (Cook et al. 2003; Kuba et al. 2002). We therefore investigated whether auditory nerve to NA synapses expressed short-term synaptic depression similar to NM and NL, or some other form of plasticity.

In chick embryonic brain stem slices, we observed radically different short-term synaptic plasticity in NA compared with the timing nuclei, in that many synapses in NA showed a mixture of short-term facilitation and depression. The particular balance of facilitation and depression maintained the synaptic amplitude at high firing rates (>100 Hz). Quantitative modeling showed that we could account for the plasticity with facilitation of release and a two-step recovery from depression. Simulations using model fits to data and natural auditory nerve spike trains showed that the intensity information contained in the nerve response is conveyed near-linearly across mixed facilitation-depression NA synapses. In a minority of synapses in NA that solely depressed, the postsynaptic response saturated at increasing intensities, limiting the range of intensity information conveyed. The short-term plasticity expressed at most NA synapses supports the encoding of intensity information in the auditory nerve firing rate. These results support the hypothesis that short-term synaptic plasticity in the brain may be specifically regulated based on the relationship between the filtering properties of the synapse and its function.

METHODS

Brain slice preparation

Chicken embryos were rapidly decapitated and an approximately 4 mm segment of the caudal skull containing the brain stem removed with a razor blade and quickly submerged in artificial cerebral spinal fluid (ACSF) (in mM: 130 NaCl, 26 NaH₂CO₃, 3 KCl, 2 CaCl₂, 2 MgCl₂, 1.25 NaH₂PO₄, and 10 dextrose). The majority of the chick embryos were E (embryo day)17, but spanned E16–E19 (mean ± SD, 17.3 ± 1.0 days in ovo). The brain stem segment was dissected out and transferred to a vibrating tissue slicer (Campden Instruments, Leicester, UK; Leica Microsystems, Nussloch, Germany) where it was mounted with cyanoacrylate glue, supported by a 4% agarose solution and cut in ACSF. Transverse slices (250–300 μm) containing NA and afferent fibers of the 8^th nerve were collected and maintained in a holding chamber at room temperature (22–24°C) in oxygenated (95% O₂-5% CO₂) ACSF. For recordings, slices were placed in a submersion-type recording chamber continuously perfused with oxygenated ACSF (1–2 ml min⁻¹) and heated with a Warner TC 324B inline heating device (Warner Instr., Hamden, CT). The bulk of the results in this paper come from stimulus train experiments which were performed in slices that were heated to 29.9 ± 0.9°C; the paired pulse results described in this context were from the train recordings, using the second pulse response in the train. Separate paired pulse experiments to test for sensitivity to changes in extracellular calcium were performed at room temperature.

Whole cell recordings

Whole cell patch-clamp recordings were made from visually-identified NA cells using IR/DIC (infrared/differential interference contrast) video microscopy (Stuart et al. 1993). Initial micropipette resistances were 3–7 MΩ with an internal solution of (mM): 120 potassium gluconate, 20 KCl, 0.1 EGTA, 2 MgCl₂, 2 Na₂ATP, 10 Hepes, and 0.1% biocytin. Electrical recordings were made using an AxoPatch 200B (Axon Instruments, Foster City, CA) in voltage-clamp mode with the series resistance corrected by 60–90%. Experiments were carried out in 20 μM bicuculline and 1–3 μM strychnine to eliminate measurement contamination by GABA/glycine inhibitory currents. Fast AMPA-receptor mediated excitatory synaptic currents were isolated by the application of 25–75 μM APV. Stimulation and recordings were controlled by a PC running custom software written in the programming software IGOR Pro programming environment (Wavemetrics, Lake Oswego, OR) with a National Instruments A/D board (National Instruments, Austin, TX). Stimuli biphasic waveforms passed through an analog, constant-current stimulus isolation unit (World Precision Instruments, Sarasota, FL) using metal bipolar electrodes.

Auditory nerve fiber stimulation

Synaptic stimulation was performed as previously described (MacLeod and Carr 2005). Extracellular stimulation of the 8^th (auditory) nerve fibers tracts was accomplished with a tungsten monopolar or bipolar electrode. As has been shown in a previous paper, each NA neuron receives synaptic input from multiple auditory nerve fibers (MacLeod and Carr 2005). Stimulation amplitude was carefully controlled by measuring a series of stimulation levels to find the response threshold and plateau region to isolate a response that evoked an EPSC typically between 50–300 pA in peak amplitude. The stimulation level was then set to a value in the center of the plateau region to avoid contamination of train responses by additional fiber recruitment. Experiments in which recruitment was suspected were discarded from our analysis. We evoked trains of 8–10 pulses with a constant interpulse interval (4, 5, 7, 10, 30, and 100 ms), which we report as stimulus “rate” (250, 200, 143, 100, 33, 10 Hz, respectively). An additional recovery test pulse was delivered 2 s after the last pulse in the train. For each cell, 4–6 different train rates were tested in interleaved trials. Intertrial intervals were 10–15 s for trains, and 5–10 s for the paired pulse experiments.

Analysis

Peak EPSC amplitudes were measured relative to a baseline calculated from the previous EPSC. Descriptions of the short-term plasticity changes are given as ratios relative to the initial EPSC amplitude (ratios >1 were enhanced; ratios <1 were depressed) or alternatively as an equivalent percentage (above 100% means synapses were enhanced; less than 100% were depressed). “Paired pulse ratio” was the ratio of the 2^nd EPSC to the 1^st EPSC, for both the trains and paired stimuli. “Steady state ratio” (trains only) was the ratio of the average of the last 3 EPSCs to the 1^st EPSC. While preliminary work that used longer trains (10–15) had suggested that the EPSCs reached steady state by the 7^th or 8^th response, analysis of the neurons here showed that this was not always the case, and therefore ‘steady state’ should be taken as “near steady state”. However, analysis of 10-pulse trains showed that there was generally <6% variation between pulses 8–10 than during pulses 6–8 (often due to variability; and only one case showed that the synapses had clearly not reached a steady state). No qualitative differences in the steady-state versus input rate functions were observed. Re-analysis using pulses 6–8 (ignoring 8–10) had no impact on the results.

Model and simulation of short-term synaptic plasticity

We simulated the effects of short-term plasticity on the EPSC amplitudes with a model similar to several previously published models (Brenowitz and Trussell 2001b; Dittman et al. 2000; Tsodyks and Markram 1997; Varela et al. 1997); a version of this model has been presented in abstract form (MacLeod and Horiuchi 2006). In this model, the presynaptic spike causes a readily releasable neurotransmitter vesicle pool, Q_ready, to release a fraction, F(t), of its resources in the synaptic cleft to produce a postsynaptic EPSC. We chose to represent the replenishment of the readily-releasable pool as a two-step process, in which Q_ready is replenished from a backup vesicle pool, Q_backup, which is itself replenished from a reserve pool (see Rizzoli and Betz 2005, for a discussion of vesicle pools). In the following equations, Q_ready(t) and Q_backup(t) represent the time-dependent fraction of their maximum sizes, Q_{ready_max} and Q_{backup_max}.

In the time interval between action potentials

$$\begin{array}{c}\frac{{\text{d}Q}_{\text{ready}}}{\text{d}t}=[Q_{\text{backup}}(t)-Q_{\text{ready}}(t)]·k1\\ \frac{{\text{d}Q}_{\text{backup}}}{\text{d}t}=[1-Q_{\text{backup}}(t)]·k2-[Q_{\text{backup}}(t)-Q_{\text{ready}}(t)]·\frac{k1}{\alpha }\end{array}$$

where α is the ratio of the relative maximum sizes of pools Q_ready and Q_backup (i.e., α = Q_{backup_max}/Q_{ready_max}.) To implement facilitation, each presynaptic spike causes F(t) to take a step increase toward its maximum value of 1, which subsequently decays with rate k_F toward its baseline value, F₀, between action potentials

$$\frac{\text{d}F}{\text{d}t}=-(F(t)-F_0)·k_{\text{F}}$$

At the time of an action potential, t_spike, an EPSC is generated, Q_ready is partially depleted, and the facilitation variable increases

$$\begin{array}{c}\text{EPSC}(t_{\text{spike}})=Q_{\text{ready}}(t_{\text{spike}}^{-})·F(t_{\text{spike}}^{-})\\ \mathrm{\Delta }{Q}_{\text{ready}}(t_{\text{spike}})=-Q_{\text{ready}}(t_{\text{spike}}^{-})·F(t_{\text{spike}}^{-})\\ \mathrm{\Delta }F(t_{\text{spike}})=(1-F(t_{\text{spike}}^{-}))·{\delta }_F\end{array}$$

where $t_{\text{spike}}^{-}$ represents the moment just before the incoming spike. The step increase in F(t) is proportional to parameter δ_F. This model describes neurotransmitter pool replenishment as a two-step process with a facilitating probability of release. F₀ may be interpreted as an initial average probability of release.

To fit the experimental data, we defined a fit error which quadratically penalized deviations of the model EPSC values from the normalized measured EPC values, scaled by the SD of the data

$$\text{Error}=\sum _{\text{ipi}=1}^6\sum _{n=2}^9{\left(\frac{{\text{EPSC}}_{\text{model}}(\text{ipi},n)-{\text{EPSC}}_{\text{data}}(\text{ipi},n)}{{\sigma }_{\text{data}}(\text{ipi},n)}\right)}^2$$

where ipi (“interpulse interval”) indicates the set of 6 different train input rates, and n indicates the pulse number within the trains. We used a gradient descent algorithm to find parameters (k₁, k₂, α, k_F, δ_F, F₀) whose initial values were constrained to lie within a broad range of physiological values. Global minima were estimated by running the algorithm using random initial conditions selected uniformly from each parameter range. We refer to the inverse of k₁, k₂, and k_F as time constants τ_k1, τ_k2, and τ_F.

The steady state synaptic transfer functions labeled “NM model” and “cortex model” plotted in Fig. 8 were the output of a simplified version of the model which used a single vesicle pool and no facilitation, using the following parameters: for NM, k₁ = 14.93/s (i.e., time constant of 67 ms), k₂ = 1000/s, α = 1, k_F = 1000/s, δ_F = 0, F₀ = 0.41; for cortex, k₁ = 2.63/s (i.e., time constant of 380 ms), k₂ = 1000/s, α = 1, k_F = 1000/s, δ_F = 0, F₀ = 0.60. The parameters for NM were determined by finding the best fit to the average NM steady state function, and the parameters for cortex were taken from the fast depression in Varela et al. (1997).

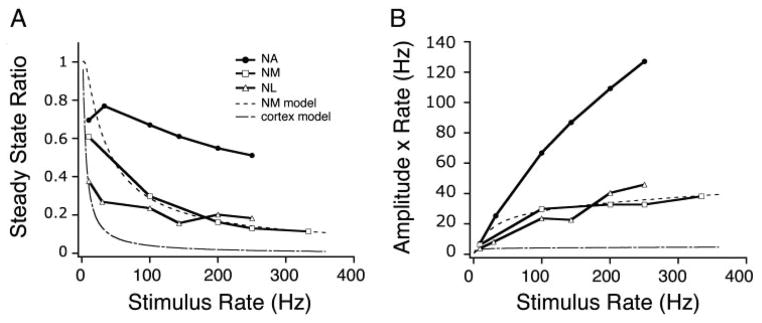
FIG. 8.

A: comparison of steady-state synaptic transfer functions for different auditory brain stem nuclei. ●, NA (from Fig. 6; n = 34); □, NM (n = 3); △, NL (n = 6). Also plotted are simplified, depression-only models using parameters from a fit to NM data (- - -) and from previously published cortical data (– · –; see METHODS). B: total postsynaptic conductance, per unit time (calculated as the product of the steady-state amplitude and stimulus rate) vs. stimulus input rate. Synaptic inputs to NA neurons transmit the presynaptic firing rate linearly and with a greater gain than depressing inputs to NM or NL. Symbols as in A.

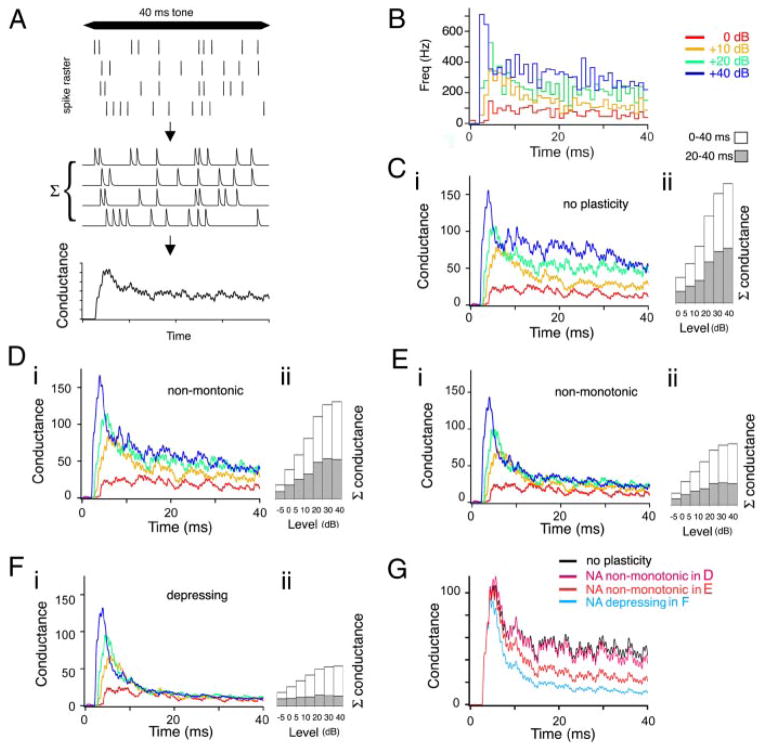
To determine the effects of the short-term plasticity on the coding of intensity, we constructed a simulation using natural auditory nerve spike trains, a generous gift of James C. Saunders (University of Pennsylvania). The auditory nerve data were recorded from juvenile (P24) chick under urethan anesthesia, in response to pure tone stimuli (40 ms; 2.5 ms ramp; CF, 1533 Hz) delivered at different intensities (from −5 to +40 dB relative to rate threshold). The data set consisted of 200 trials at each intensity, with ≤14 spikes per trial and firing rates that could transiently reach >500 Hz at the onset, but were between 0 and 300 Hz for the tonic component of the response. To construct the simulated postsynaptic response, each spike in a trial resulted in a postsynaptic “conductance”, whose amplitude was varied according to the plasticity model. The resulting responses were then summed for all trials of a given intensity (see Fig. 9A). The individual conductances were modeled as an alpha-like function whose rise and decay time matched the quantal EPSCs recorded in NA neurons (MacLeod and Carr 2005). Four sets of model parameters were used: one no-plasticity case (which represented a smoothed histogram of the original auditory nerve data); two fits of a nonmonotonic NA synapse: one that had enhancement: k₁ = 178.6/s, k₂ = 0.047/s, α = 9.3, k_F = 59.7/s, δ_F = 0.412, F₀ = 0.359, and another nonmonotonic without enhancement: k₁ = 88.2/s, k₂ = 0.36/s, α = 4.6, k_F = 32.8/s, δ_F = 0.20, F₀ = 0.389; and one fit of a purely depressing NA synapse: k₁ = 30.6/s, k₂ = 0.125/s, α = 2.12, k_F = 999.9/s, δ_F = 0.01, F₀ = 0.352. Note that in the first two NA synapses, the model contains a fast time constant of vesicle recovery (~6 ms and 11.3 ms), a slow time constant of vesicle recovery (~21 s and 2.8 s), and facilitation (time constant of decay, approximately 17 ms and 30.5 ms). In the “depressing” NA synapse, there was no facilitation (due to the nearly instantaneous decay of the facilitation variable) and two time constants of vesicle recovery, one fast (~32 ms) and one slow (~8 s).

FIG. 9.

Simulation of the effect of short-term plasticity in NA on the transmission of intensity information using natural auditory nerve input trains (nerve data trains courtesy of J. C. Saunders, University of Pennsylvania). A: illustration of the simulation process. Auditory stimuli result in auditory nerve spike train (rasters in top panel) were convolved with an alpha function to generate a “conductance” response for each trial (middle). The amplitude of the conductance response was altered according the model of short-term plasticity with respect to the interspike intervals present in each trial raster (shown is the “no plasticity” case, and thus all amplitudes are the same). These conductance responses were summed across all trials for a given stimulus intensity to generate the alpha-function convolved poststimulus histogram (αPSTH, bottom). B: standard PSTH of the firing responses of 1 auditory nerve fiber to a best-frequency tone stimulus at 4 acoustic intensities (0, +10, +20, and +40 dB relative to threshold; binning, 1 ms). C–F: effect of short-term synaptic plasticity on the αPSTHs for 4 different plasticity cases: no plasticity (C), NA nonmonotonic synapse (D; from Fig. 2), a 2nd NA nonmonotonic synapse (E; similar to Fig. 3 and the average for NA), depressing NA synapse (F; from Fig. 4). i: αPSTHs for each test synapse, summed over 200 different natural auditory nerve input trains at 4 different stimulus intensities. Note the convergence of the αPSTHs by 10–15 ms in F. ii: bar plots of the total summed conductance vs. the full range of auditory intensities (from −5 to +40 dB). □, summed conductance across entire 40-ms stimulus; , summed conductance for the last 20 ms, showing the intensity sensitivity of the tonic component. G: comparison of αPSTHs for the 20-dB input stimulus for each example in C–F.

RESULTS

To understand how auditory information is transmitted from the auditory nerve to the cochlear nuclei, we measured the short-term synaptic plasticity at the auditory nerve to nucleus angularis (NA) synapse. Whole cell patch-clamp recordings were made from NA neurons in chick embryonic (E16–E19) auditory brain stem slices in vitro, as described previously (MacLeod and Carr 2005). By this age, synapse development is largely complete, and hearing has begun in ovo (Kubke and Carr 2000; Rubel and Parks 1988). Synaptic responses were evoked by electrical stimulation of the 8^th (auditory) nerve with a metal bipolar electrode positioned medial to the nucleus, where nerve fibers enter the neuropil. We measured pharmacologically isolated AMPA-receptor mediated excitatory postsynaptic currents (EPSCs) under voltage-clamp in response to trains of stimuli. Stimulation consisted of 8–10 pulses in trains of a constant interpulse interval, and a recovery pulse delivered 2 s after the last pulse in the train. Six different interpulse intervals were used, corresponding to train frequencies of 10, 33, 100, 143, 200, and 250 Hz, which we refer to as input rate to avoid confusion with acoustic frequency. These input rates were chosen to span the range of firing rates observed in the auditory nerve of young hatchling and embryonic chicks, which have spontaneous rates of approximately 0–80 Hz and maximal average driven rates of approximately 250–300 Hz (see the example in Fig. 9; also: Jones and Jones 2000; Salvi et al. 1992; Saunders et al. 2002).

Short-term plasticity of auditory nerve synapses in NA is composed of a mixture of depression and facilitation

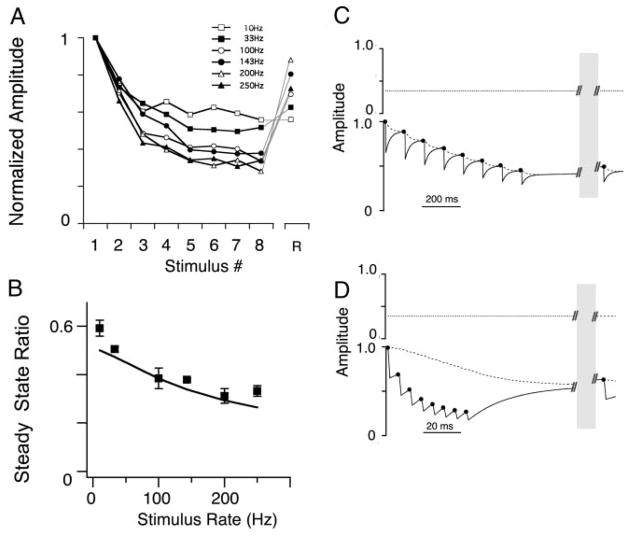
In contrast to the profound short-term depression uniformly expressed at synapses in the brain stem pathways that encode timing information, we found that the short-term synaptic plasticity recorded at the auditory nerve to NA neuron synapses was typically composed of a mixture of facilitation and depression (Fig. 1). In this paper, we use the term “enhancement” to describe the measured net increase in the EPSC amplitude and the term “facilitation” to refer to the putative underlying synaptic molecular mechanism, presumed to be a presynaptic increase in release probability. Enhancement of the EPSC amplitude (above a criterion of 10% greater than initial EPSC amplitude) was observed in a subset of NA recordings for at least one stimulus rate (n = 12/34; Fig. 1). For example, enhancement of the EPSCs recorded from one NA neuron during stimulus input trains of 100, 143, and 200 Hz is shown in Fig. 2. A maximal EPSC amplitude occurred on the 2^nd or 3^rd stimulus and some enhancement was sustained throughout the rest of the train (Fig. 2 A and B). For the 250 Hz input train, the EPSC amplitude declined after an initial enhancement back to the amplitude of the initial EPSC. In contrast, the EPSCs recorded during 10 Hz and 33 Hz input trains did not show any transient enhancement (Fig. 2A), but instead depressed in amplitude to a steady state ratio of 0.6 and 0.8, respectively (Fig. 2B, markers). In other recordings, the enhancement of EPSC responses was moderate, limited to less than a two-fold increase over the initial EPSC amplitude. The enhancement was often followed by a depression in the recovery EPSC in response to a stimulation delivered after a delay period (2 s after the end of the train; “R”, in Fig. 2A). This “anomalous” recovery response suggested that the EPSCs were the result of two competing mechanisms, one which facilitated the synaptic response and the other which depressed the synaptic response. In the case of enhancement during the train, the facilitating factor dominated. At the time of the recovery response, the facilitating factor had declined, and the depressing factor dominated. These effects could be reproduced with a quantitative model of synaptic plasticity, described below.

FIG. 1.

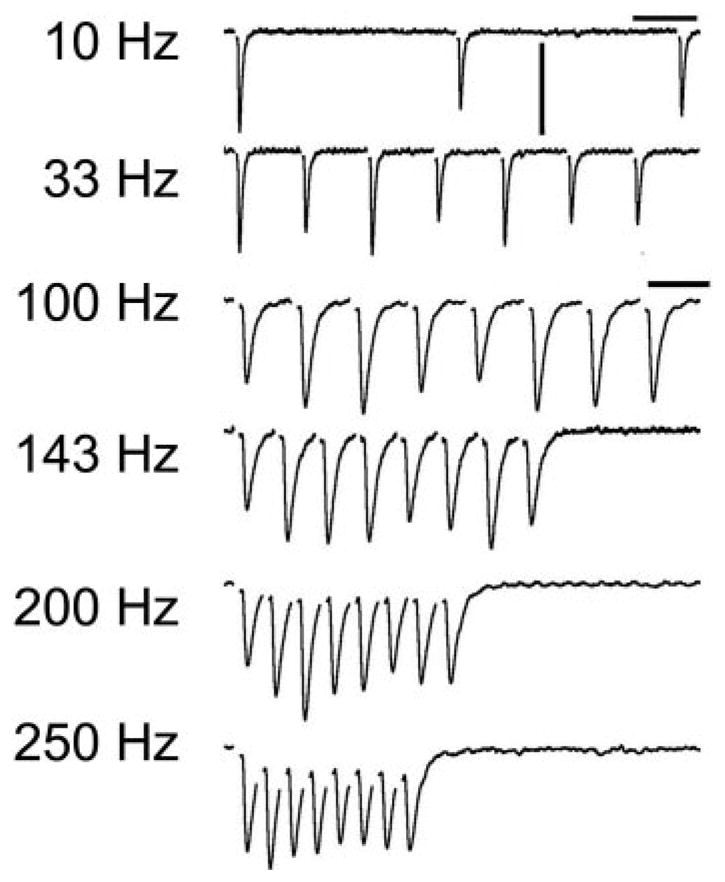
Excitatory postsynaptic currents (EPSCs) recorded in 1 nucleus angularis neuron in the chick auditory brain stem during stimulation of the auditory nerve fiber inputs. A: average traces in response to stimulus trains of 8 pulses at 6 different input stimulus rates. Stimulus artifacts have been digitally removed for clarity. Only the 1st 3 EPSCs are shown for the 10-Hz train. Horizontal scale bar is 25 ms for 10 Hz, 33 Hz, 10 ms for 100–250 Hz; vertical scale bar is 200 pA.

FIG. 2.

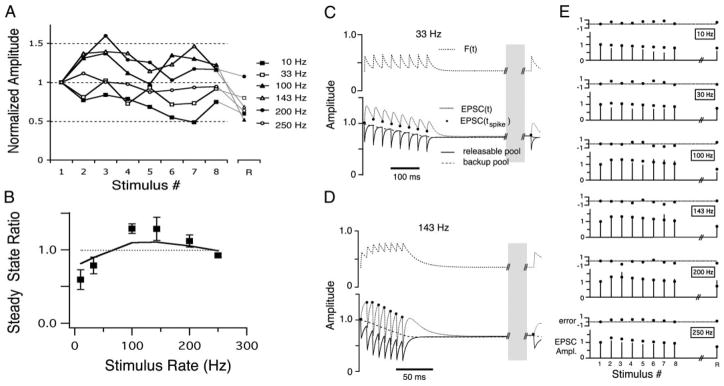
A: mean EPSC amplitudes, normalized to the initial EPSC plotted vs. stimulus pulse number in the train (1–8; R, EPSC response after a 2-s recovery period). Same data as in Fig. 1. B: steady-state amplitude ratio plotted vs. stimulus input train rate (mean ± SD). This nucleus angularis (NA) neuron’s steady-state profile showed a nonmonotonic function with stimulus rate (data are shown as markers; —, model fit result). C: short-term synaptic plasticity model variables vs. time during a 33-Hz train. Top: F(t), the facilitation variable. Bottom: readily releasable pool, Q_ready(t), —; backup pool, Q_backup(t), - - -; the product F(t) · Q_ready(t), which is equivalent to the normalized EPSC, · · ·. D: short-term synaptic plasticity model variables vs. time during a 143-Hz train. Traces are as in C. The parameters for this model fit were: τ_k1, 5.6 ms; τ_k2, 21.2 s; τ_F, 16.7 ms; F₀ (initial fraction release), 0.35; δ_F, 0.41; α, 9.3. See METHODS for an explanation of the parameters and fitting methods. Note the break in the traces in the time axis, due to the long delay during the recovery period. E: model fit to the data. Six pairs of panels in which the bottom panel show the normalized EPSC amplitude over trains at each stimulus rate, and the top panel shows the error of the fit. In the EPSC panel, sticks to 0 represent the data EPSC amplitude at each stimulus pulse (1–8 and recovery stimulus R), whereas markers represent the model EPSC output. Error was measured as the difference between model and data, normalized to the SD of the data (an error of 1 means the model fell 1 SD away from the data).

The relationship of the EPSC amplitude with train input rate was frequently nonmonotonic

To more easily compare the short-term plasticity across different synapses, we characterized the synaptic transfer function, defined as the relationship between the steady state amplitude and the input stimulus rate. A majority of synapses in NA (n = 18/34) had synaptic transfer functions that were nonmonotonic: they generally had a peak steady state amplitude for 33 or 100 Hz input trains. The example in Fig. 2B shows this nonmonotonic profile, a result of net enhancement of the EPSC during the train. Another example in Fig. 3, however, shows a synapse that also had a nonmonotonic profile, but in the absence of any net enhancement of the EPSC amplitude (Fig. 3A). In this case, a relative enhancement at the 33 Hz input rate also resulted in a nonmonotonic profile (Fig. 3B). To distinguish between the presence of an underlying facilitation that counterbalances the depression, or the simple lack of depression, we also measured the EPSC after a recovery period as in Fig. 2. In Fig. 3A, the amplitude of the recovery EPSC was reduced relative to the EPSCs at the end of the 33 Hz train, suggesting that during the train a similar competition between depression and facilitation was occurring as in the enhancement case, but with a balance in favor of net depression.

FIG. 3.

Recording in another NA neuron the synaptic inputs of which showed no transient or sustained facilitation. A: normalized EPSC amplitudes showed only net depression across all input rates. B: steady-state ratio profile showed a relative enhancement for the 33-Hz input and thus was also nonmonotonic. As in Fig. 2, markers represent data, — represents the model fit. C and D: short-term synaptic plasticity model variables vs. time during a 33-Hz train (C) and 200-Hz train (D). Traces are as in Fig. 2, B and C. The parameters for this model fit were: τ_k1, 21.5 ms; τ_k2, 1.7 s; τ_F, 60.7 ms; F₀ (initial fraction release), 0.30; δ_F, 0.14; α, 5.2.

For many synapses, the overall effect of these competing components was to maintain the unitary synaptic conductance across a broad range of input rates with little net enhancement or depression. For a minority of synapses, however, the synaptic transfer functions were similar to those found in the timing pathway: monotonically increased depression with increased input rate (n = 9/34; Fig. 4). The monotonically depressing synapses also showed an “anomalous” recovery, that is, the higher input rate trains appeared to recover more quickly than the low rate trains (note the crossover in the recovery amplitudes in Fig. 4A, in which the 200 Hz recovery EPSC amplitude exceeded that of the 10 Hz recovery EPSC). The classification of the remaining synapses (n = 8/34) was uncertain due to large variation in the responses or irregularity of the synaptic transfer function, but two had nonmonotonic, “bowl-shaped” transfer functions in which the intermediate input rates resulted in the greatest net depression. All synaptic transfer functions (n = 34) are shown in Fig. 6B.

FIG. 4.

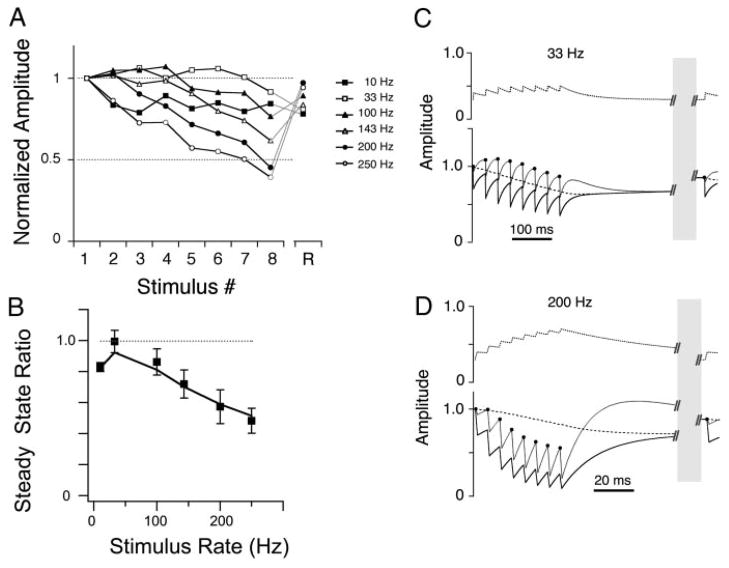
Recording from a 3rd NA neuron the synaptic inputs of which showed only simple depression. A: normalized EPSC amplitudes showed only net depression across all input rates. B: steady-state ratio profile showed monotonically increasing depression with stimulus rate. Markers represent data; —, model fit. C and D: short-term synaptic plasticity model variables vs. time during a 10-Hz train (C) and 200-Hz train (D). Traces are as in Fig. 3, C and D. The parameters for this model fit were: τ_k1, 32.6 ms; τ_k2, 7.9 s; τ_F, 1 ms; F₀ (initial fraction release), 0.35; δ_F, 0.01; α, 2.1.

FIG. 6.

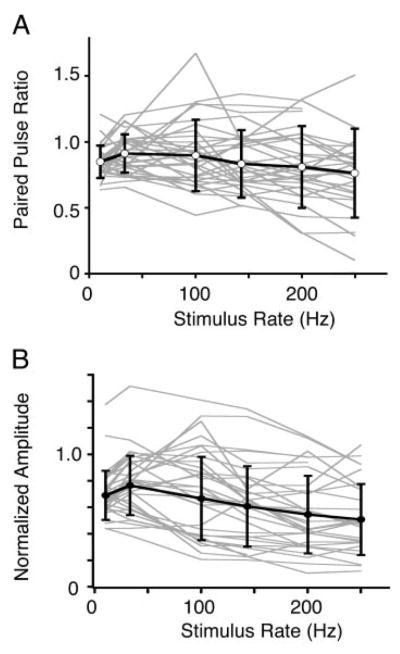
Summary of response profiles vs. stimulus input rate in NA. A: paired-pulse ratio, using the 2nd EPSC in the train. B: steady-state amplitude ratio as in Figs. 2–4. Thin gray lines represent response profiles from individual NA neurons; thick black lines and markers represent their average (mean ± SD). Both average paired-pulse and steady-state profiles show a nonmonotonic profile with input rate, with peaks around 33–100 Hz and flat from 100–250 Hz. Number of data points in averages: n = 34 for 10 and 33 Hz; n = 33 for 100, 143, and 200 Hz; n = 30 for 250 Hz.

Data were well fit by a model of short-term plasticity

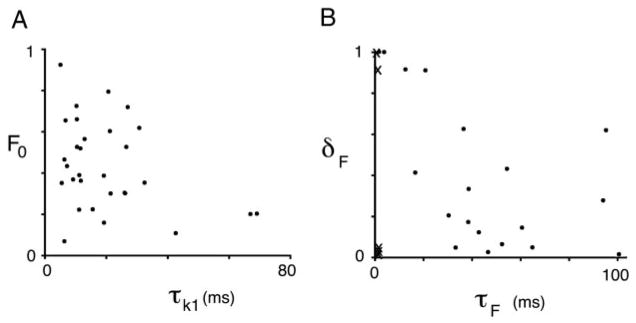
To determine whether the synaptic responses observed could be accounted for by a simple model of short-term plasticity, we fit each synapse individually with a dynamic model of synaptic release, similar to a class of models of plasticity published previously by a number of investigators (see METHODS; Abbott et al. 1997; Dittman et al. 2000; MacLeod and Horiuchi 2006; Tsodyks and Markram 1997). EPSCs were presumed to result from the fractional release of vesicles from a release-ready pool at the time of each presynaptic stimulation. The model contained both depression and facilitation. Depression resulted from a decrease in the size of the release-ready pool due to depletion, and recovery from depletion followed a two-step vesicle pool replenishment process. Facilitation was implemented by making the vesicle release fraction activity- and time-dependent. EPSCs were generated by the model for each stimulus in the train, and compared with the data for each individual neuron (Fig. 2E; see also Supplemental Figures S1 and S2¹). Using a randomly seeded gradient descent method to find the parameters, we were able to fit nearly all the NA cells (30 of 34; 4 were excluded due to data irregularity). The time-dependent variables in the model during the input trains are shown for fits to three NA synapses (panels C and D in Figs. 2–4; specific model parameters are given in the legend). In general, the data were well fit with a fast recovery time constant for the readily releasable pool (τ_k1 = 20.1 ± 16.0 ms, n = 30), and a slow recovery time constant for the backup pool (τ_k2 = 8.4 ± 9.3 s, n = 30; excluding one outlier at 80.9 s) (Table 1; Fig. 5). Many NA profiles were best fit with some degree of facilitation (average τ_F = 42.4 ± 30.0 ms, n = 20; excluding one outlier of 542 ms). Other NA profiles were best fit by minimizing the facilitation, including all those that were classified as monotonically depressing (the Xs in Fig. 5B clustered on far left). The initial release fraction (F₀, equivalent to an average probability of release) ranged from 0.07 to 0.92 (0.43 ± 0.21; n = 30). The fit was considered good if the error was low (compared with a zero-plasticity baseline error), and if several other qualitative criteria were met. Besides a good overall fit to the train data, model should fit the recovery response, especially the “anomalous” recovery. For example, the recovery responses in Fig. 2, C and D show that long after the facilitation parameter had relaxed to its initial value (top dashed line), the release-ready vesicle pool had not yet fully recovered (solid line). This resulted in a model recovery EPSC that was smaller than the EPSCs during the train (black dot late in the trace), matching the recovery EPSCs in the data. Finally, the model synapses should reproduce the profile of the steady state function (solid lines in panel B, Figs. 2–4). Reduced models in which a single pool was modeled, the relative pool sizes were held to be equal, or facilitation was eliminated (for those that required it) produced poorer fits, or failed to meet the criteria listed above. Thus we were able to account for the wide range of synaptic plasticity profiles in our data sample with a simple quantitative model of vesicle release, and a restricted parameter range (Fig. 5).

TABLE 1.

Model fits of the NA synapses

Parameter	All NA	Nonmonotonic, Other	Depressing
τk1 (ms)	20.1 ± 16.0	16.6 ± 13.3	28.3 ± 20.8
τk2 (s)	8.1 ± 9.3	9.2 ± 9.5	5.7 ± 9.4
F0	0.43 ± 0.21	0.44 ± 0.20	0.43 ± 0.26
τF (ms)	27.2 ± 29.4	42.4 ± 30.0	1.0 ± 0.1**
δF	0.35 ± 0.39	0.36 ± 0.35	0.34 ± 0.49
α	4.9 ± 2.8	5.7 ± 2.6	2.9 ± 2.2**

All nucleus angularis (NA), n = 30; nonmonotonic, other, n = 21; depressing n = 9, except for τ_k2 and τ_F which each exclude one outlier, see text.

^**P < 0.001 between nonmonotonic, other and depressing groups.

FIG. 5.

Parameters of the model fit of all NA neurons. A: depression parameters F₀, the initial fraction of release, vs. τ_k1, the time constant of recovery of the readily releasable vesicle pool. B: facilitation parameters, δ_F, the fractional increase in F(t), vs. τ_F, the time constant of recovery from facilitation.

Population and average profiles

Summary data for all the train data obtained from NA recordings are shown in Fig. 6. Because there were no differences observed related to the cell types within NA (defined by their firing responses to current injection; see supplementary Fig. S3), the data are pooled here. The paired pulse ratios (i.e., the ratio of the 2^nd EPSC in the train to the 1^st EPSC) plotted in Fig. 6A demonstrated that for most NA neurons, there was either enhancement (in 11/34 neurons) or generally weak paired pulse depression, in contrast to the strong paired pulse depression seen in NM and NL neurons (see following text, Fig. 7). The average paired pulse ratio remained about 0.80–0.90 across all rates, with a slight maximum at 33–100 Hz (Fig. 6A). The average steady state ratio profile with input rate was also nonmonotonic, similar to many individual steady state profiles, with a maximum at 33 Hz (0.77 ± 0.23, mean ± SD; Fig. 6B). The average steady state ratio decreased to 0.70 ± 0.18 at 10 Hz, and was minimal at 250 Hz at 0.52 ± 0.26.

FIG. 7.

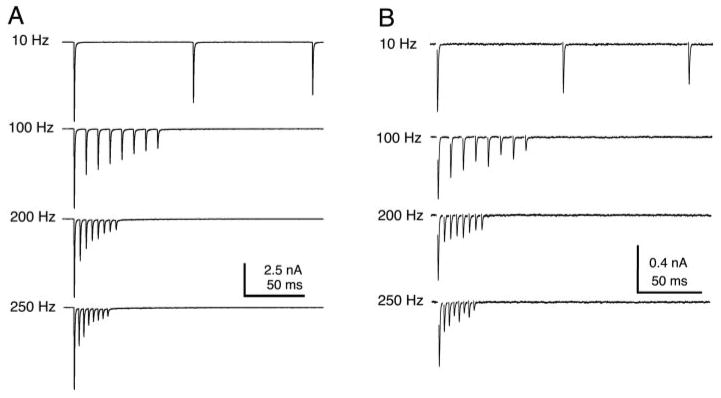
EPSCs recorded in nucleus magnocellularis (NM, A) and nucleus laminaris (NL, B) in response to trains of stimuli showed simple, strong depression and a monotonic relationship to input rate (see also Fig. 8). Synaptic responses in laminaris were evoked by electrical stimulation of the NM afferents that project to NL.

Relationship with initial EPSC size

The average initial EPSC amplitude recorded in the NA neurons was 232.3 ± 212.4 pA, and ranged from 30.7 pA to 1113.3 pA (n = 34). There was no correlation between the amplitude of the initial EPSC with the paired pulse or steady state ratio at any frequency. Thus smaller EPSC recordings were no more or less likely to demonstrate depression, or facilitation, than those of larger EPSCs. The size of the EPSC reflects of the number of inputs recruited with a given stimulus intensity, and is unrelated to release probability (MacLeod and Carr 2005).

External calcium levels alters the paired pulse ratio

Although the paired pulse ratio was not related to initial EPSC amplitude, the ratio could be altered by changes in the external calcium concentration. We investigated the calcium dependence of the paired pulse ratio with a 10 ms interval. Application of an elevated calcium ACSF (4 mM) shifted the paired pulse ratio toward more depression with a ratio of 0.70, compared with 1.02 in control calcium (2 mM; n = 6; P < 0.01). Elevated calcium also slightly increased the amplitude of the average initial EPSC, from 114.9 pA to 143.2 pA (n = 6; P = 0.113). Under decreased calcium conditions (1 mM), the paired pulse ratio shifted toward greater enhancement, from 1.01 to 1.58 (n = 5; P < 0.01) and decreased the amplitude of the initial EPSC, from 152.9 pA to 58.4 pA (n = 5; P = 0.055). During individual recordings, paired pulse ratios could change from net enhancement to depression and vice versa.

Comparison with timing nuclei in the brain stem

To compare the short-term plasticity found in NA recordings with those in the timing nuclei, we made recordings from neurons in the cochlear nucleus magnocellularis (NM) and nucleus laminaris (NL). Synaptic responses recorded in NM neurons showed profound depression at this age, as has been shown previously (Fig. 7A) (Zhang and Trussell 1994b). The steady state amplitude monotonically decreased with input stimulus rate (Fig. 8A; open squares, n = 3 NM neurons). These experimental results are similar to that predicted by a model of simple depression in NM (dashed line; see METHODS). The synapses onto NM neurons showed significantly more depression on average than those onto NA neurons at input rates 200 Hz and 250 Hz (P < 0.05). NL neurons receive synaptic input from NM, and these synapses also show profound short-term depression (Cook et al. 2003; Kuba et al. 2002). We found that NM to NL synapses expressed significantly more depression than auditory nerve to NA synapses for all rates (Fig. 7B; Fig. 8A, open triangles; n = 5 NL neurons; P < 0.05). Although NA synaptic responses often showed net depression at steady state, they nevertheless showed much less depression on average than the synaptic responses recorded in NM or NL neurons, and had a distinctly different steady state synaptic transfer function.

Information transmission

To understand how the short-term plasticity expressed at the auditory nerve to cochlear nucleus synapse affects the transmission of spike rate information, we analyzed how the total steady state synaptic conductance is related to the input rate (Abbott et al. 1997; Markram et al. 1998b; Tsodyks and Markram 1997). We used as an approximation of total conductance the product of the steady state amplitude with the presynaptic spike rate (Fig. 8B). This calculation provides an estimate of the net impact on the postsynaptic neuron per unit time, assuming linear summation of the input conductance. For depressing synapses such as those in NM, the relationship of the total conductance with input rate is a nonlinear, saturating curve (Fig. 8B, symbols as in Fig. 8A). This is because the decreasing steady state amplitude offsets the increase in input stimulus rate, keeping the total conductance nearly constant. The curve for NA was linear (Fig. 8B; linear fit, slope = 0.50, R² = 0.98), implying that changes in the input stimulus rate would result in a proportional change in total postsynaptic conductance.

Simulation using in vivo spike patterns shows that short-term synaptic plasticity in NA can help maintain the rate code for intensity

To better understand how short-term synaptic plasticity may affect sound coding, we simulated the synaptic driving conductance in response to input trains that had been recorded from auditory nerve fibers in vivo in hatchling chick (nerve data provided courtesy of Dr. James C. Saunders, University of Pennsylvania). The auditory nerve data consisted of spike trains recorded in response to a 40 ms tone stimulus at best frequency, across a range of sound levels (−5 to +40 dB relative to threshold), with 200 trials per level. The simulations used synaptic model parameters from fits to three representative NA synapses: two nonmonotonic (one of which is the synapse shown in Fig. 2, and one which had a steady-state profile similar to the average NA profile), and one monotonically depressing (synapse shown in Fig. 4).

As illustrated in Fig. 9A, each presynaptic spike (top panel) was assumed to result in a postsynaptic conductance, simulated as an alpha-like function (middle panel) with a time course similar to a quantal EPSC in NA (MacLeod and Carr 2005). The amplitude of the conductance was varied according to the output of the short-term plasticity model driven by the inter-spike intervals present in the input trains. We summed the simulated conductances across the set of in vivo trials for each sound level, creating an alpha-function-smoothed poststimulus time histogram (αPSTH; bottom panel). The αPSTH thus represents the input conductance versus time, summed over multiple sequential trials, or large numbers of inputs. The αPSTHs that resulted from the simulation using each representative synapse are plotted in Fig. 9, Ci-Fi. To compare across intensities, the total summed conductance versus stimulus intensity (“Level” was calculated (bar plots in Fig. 9, Cii-Fii), either over the whole stimulus (white bars, “0–40 ms”), or just during the tonic component (gray bars, “20–40 ms”). The spike frequency PSTHs of the original auditory nerve trains show the primary-like profile (phasic and tonic components) which is characteristic of all auditory nerve responses (Fig. 9B). In the absence of facilitation or depression (“no plasticity”), the αPSTH is a smoothed version of the spike frequency PSTH (Fig. 9Ci). Increasing sound levels produced increasing summed conductance, reflecting the increasing pre-synaptic firing rates (Fig. 9Cii). The simulated nonmonotonic NA synapse in Fig. 9D shows that this NA synapse produced an αPSTH very close to the “no plasticity” case, and preserved most of the intensity-related range in the total conductance during the tonic component (gray bars, Fig. 9Dii). In contrast, for the purely depressing synapse the αPSTHs converge within 10–15 ms (Fig. 9Fi). The phasic component still contains intensity information (white bars, Fig. 9Fi), but there is no information in the tonic component (gray bars, Fig. 9Fii). The results for a third NA synapse showed intermediate behavior and maintenance of some degree of intensity information during the tonic component (Fig. 9Ei,ii). The synaptic plasticity observed in NA can clearly influence how the sound level information of sound stimuli is transmitted. While depressing synapses can convey intensity information at the onset of the stimulus, the intensity of ongoing stimuli can only be conveyed by synapses that maintain the amplitude of the synaptic conductance by enlisting facilitation to balance the depression.

DISCUSSION

The synaptic properties of auditory nerve inputs onto their postsynaptic targets in the cochlear nuclei are fundamental to the transformation of auditory information. Short-term synaptic plasticity dynamically regulates the synaptic amplitude in response to activity patterns, and have profound effects on what components of the presynaptic pattern are transmitted to the postsynaptic neuron. Previous work suggested that most auditory brain stem synapses were characterized by strong short-term depression. In nucleus angularis, however, the auditory nerve synaptic inputs were characterized instead by a combination of facilitation and depression. The short-term plasticity was notable for two reasons. First, the auditory nerve to NA synaptic connections showed much less net depression at steady state for high stimulus frequencies (100–250 Hz) than has been shown at most other synapses in the brain, including calyceal and noncalyceal synapses in the brain stem. Second, the particular balance of short-term facilitation and short-term depression mechanisms meant that steady state amplitudes converged to approximately the same value regardless of the input rate. This allows the synapses to linearly transmit rate information in the presynaptic firing activity, and maintain intensity information encoded as a rate code (in decibels) in the auditory nerve. Future work will reveal the implications of short-term synaptic plasticity for dynamic stimuli, such as during AM, which is an important component of auditory processing of speech and birdsong.

Importance of nucleus angularis in auditory coding

Intensity is one of the primary dimensions of sound: overall loudness is a fundamental percept, interaural differences in intensity are useful cues for localizing sounds, and relative intensity across frequency defines the spectral content of environmental sounds. Evidence strongly suggests that nucleus angularis is the gateway for intensity-related auditory processing, and is thus critical to our understanding of localization and nonlocalization auditory tasks in birds. Nucleus angularis is required for intensity-dependent elevational sound localization in barn owls (Takahashi et al. 1984). NA projects to the superior olivary nucleus (SON), the posterior area of the ventral nucleus of the lateral lemniscus (VLVp), and the inferior colliculus (Burger et al. 2005; Mogdans and Knudsen 1994; Takahashi and Konishi 1988). Neurons in VLVp are binaural, tuned sigmoidally to ILD (Adolphs 1993; Manley et al. 1988), and project to the inferior colliculus, where ILD and ITD information converges into a space-specific map (Takahashi 1989). The NA projection to SON could contribute to a mechanism for intensity-dependent gain control by providing inhibitory feedback to NA, NM, and NL (Burger et al. 2005; Lachica et al. 1994; Yang et al. 1999).

NM is morphologically and physiologically homogeneous and appears specialized for encoding timing cues with tightly phase-locked action potentials, suggesting a critical, but circumscribed, role in auditory coding. NA, on the other hand, is heterogeneous and is composed of ≥4–5 cell types, suggesting a broader range of function, including both localization and nonlocalization tasks, such as sound recognition and discrimination (Köppl and Carr 2003; Soares et al. 2002). A range of cell types have been classified based on morphological and in vitro physiological characteristics (Häusler et al. 1999; Soares and Carr 2001; Soares et al. 2002). A distinct classification of NA cell types has been described based on in vivo sound responses (Hotta 1971; Köppl and Carr 2003; Sachs and Sinnott 1978; Sullivan and Konishi 1984; Warchol and Dallos 1990). Such neuronal heterogeneity suggests that NA is not a single-purpose processor of intensity, but has a range of functions related to intensity cues. It is not yet known whether the different response types in vivo correlate with physiological types defined in vitro, or whether they represent different processing streams in the auditory brain stem.

Differential filtering of intensity information within NA

Individual NA neurons received synaptic inputs that expressed varying degrees of facilitation and depression, with some expressing primarily depression. This variability suggests the intriguing speculation that differential filtering may occur within NA. We have demonstrated how short-term plasticity may contribute to maintaining intensity information (in the case of the nonmonotonic NA synapse); a purely depressing synapse, on the other hand, could signal changes in intensity, a potentially important cue in many auditory signals, such as speech and birdsong. Computational studies suggest that a synaptic filter can have numerous effects on the signal. Depending on the properties of the synaptic filter, it can implement low- or band-pass filtering (Chance et al. 1998; Fortune and Rose 2002; Fuhrmann et al. 2002), shift the phase of the firing activity (Chance et al., 1998), selectively transmit changes in stimulus magnitude (Abbott et al. 1997; Markram et al. 1998a), and differentiate between bursts of presynaptic behavior or tonic input (Matveev and Wang 2000; Tsodyks and Markram 1997). In the data presented here, no differences were observed between the different cell types, in terms of the shape of the steady-state functions with input rate (i.e., simple depressing versus nonmonotonic) or quantitatively across input rates. The conclusion that plasticity and cell type have no relationship may be confounded by two factors: variations in age and position within NA. A developmental reduction in short-term depression has been well documented at the synapses in NM (Brenowitz and Trussell 2001a). We did not observe any effects by age, but nearly all the recordings were carried out at E17 or E18, and further work in more mature chicks will be needed to determine how development may affect the plasticity expressed in NA. Furthermore, we observed differences across recordings within the same slice, although we cannot completely exclude the possibility that variation in plasticity reflects variation in the rates of maturity at individual synapses. Interestingly, if maturity results in similar changes at NA synapses as those in NM (less depression, perhaps due to improved vesicle cycling or recruitment), many NA information transfer profiles (i.e., plot in Fig. 6B) may more closely approximate linearity, further improving the transmission of intensity information.

Short-term depression in brain stem timing circuits

The auditory brain stem is characterized in part by large, calyceal-type synapses, not only in the NM of birds, but also in the mammalian anterior ventral cochlear nucleus (endbulb of Held) and the medial nucleus of the trapezoid body (calyx of Held). The axosomatic contact and large number of active zones of the calyceal synapse result in very large synaptic currents and appear highly specialized for extremely precise encoding of timing information for sound localization (Carr et al. 2001; Jhaveri and Morest 1982; Parks 2000; Trussell 1999; Zhang and Trussell 1994a; Zhang and Trussell 1994b). Calyceal synapses experience profound depression due to presynaptic vesicle depletion and postsynaptic AMPA receptor desensitization (Barnes-Davies and Forsythe 1995; Bellingham and Walmsley 1999; Oleskevich et al. 2000; Schneggenburger et al. 2002; von Gersdorff and Borst 2002; Wong et al. 2003; Zhang and Trussell 1994b). Both depletion and desensitization depend in part on the high probability of release; in NM, if release probability is reduced, there is a paradoxical enhancement of the steady state amplitude during trains (that is, less depression), due to the relief of desensitization as well as reduced depletion (Brenowitz et al. 1998; Brenowitz and Trussell 2001b). An activity-dependent acceleration of recovery from depression may help to limit the effects of depression at the calyx of Held (Wang and Kaczmarek 1998).

However, the synapses in NL, which are noncalyceal, also uniformly express short-term depression. This indicates that depression is a characteristic of the timing pathways, and that the determining factor is the functional role of a particular synapse, rather than the physical size of the terminal or amplitude of the EPSC. In NL, short-term depression may enhance ITD tuning by scaling synaptic amplitudes to maintain the inputs within the range suitable for coincidence detection (Cook et al. 2003; Kuba et al. 2002). When one ear was driven more strongly than the other, due to interaural intensity differences, the more strongly activated inputs were reduced relatively more in amplitude, favoring binaural coincidence detection, and reducing the drive that might result from high monaural firing rates. In this system, synaptic depression acts as an adaptive mechanism which maintains interaural timing information and may account for the insensitivity of NL ITD tuning to sound intensity (Pena et al. 1996). In ILD computation, however, where absolute intensity is the feature that is being compared, short-term depression would be detrimental because it would eliminate precisely the intensity information required. Thus one would predict that throughout the intensity pathways of both avians and mammals, wherever intensity is encoded in the rate, short-term depression will be minimized or balanced by facilitating mechanisms.

Mechanisms

Our data and the model fits suggests that several overlapping, frequency- and time-dependent mechanisms may be at work in NA, including facilitation of release and depression due to depletion or other suppression of release. The model was especially useful in identifying the facilitation in cases where no net enhancement occurred, and estimating the underlying rates of the intertwined mechanisms that would have been difficult to isolate experimentally. The model also provides an explanation for the “anomalous” recovery responses we observed in the purely depressing case. One hypothesis for this behavior is the presence of an activity-dependent acceleration of recovery from depression, as has been proposed at the calyx of Held and several other areas (Dittman and Regehr 1998; Stevens and Wesseling 1998; Wang and Kaczmarek 1998). However, our model of short-term plasticity accounted for the responses in NA without implementing such a mechanism; instead, a two-step replenishment process, which consisted of a slow kinetic step (with a time constant of ~7 s) followed by a fast kinetic step (time constant of ~20 ms), was able to explain most of the data.

The vesicle recovery time constants generated by our model fits are in close agreement with the two-component fits obtained during depression recovery experiments in NM (Brenowitz and Trussell 2001b), MNTB (Wang and Kaczmarek 1998), and a slow time constant of recovery in the calyx of Held (Weis et al. 1999). Also, the time constant of the recovery from facilitation in our model (~40 ms) is similar to the measured time constants for facilitation of release in other systems (40 ms; Atluri and Regehr 1996), or the intracellular calcium levels that probably underlie facilitation (~100 ms). This suggests that the model found parameter values that were in a reasonable range to represent physiological events, such as calcium flux in the terminal. The model results do not completely exclude the possible presence of other mechanisms, such as postsynaptic receptor desensitization and metabotropic glutamate-receptor or GABA-B receptor mediated feedback, which remain to be tested.