Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2011 Dec 14;28(3):441–443. doi: 10.1093/bioinformatics/btr684

MTBindingSim: simulate protein binding to microtubules

Julia T Philip 1,*, Charles H Pence 2,*, Holly V Goodson 1
PMCID: PMC3268247  PMID: 22171336

Abstract

Summary: Many protein–protein interactions are more complex than can be accounted for by 1:1 binding models. However, biochemists have few tools available to help them recognize and predict the behaviors of these more complicated systems, making it difficult to design experiments that distinguish between possible binding models. MTBindingSim provides researchers with an environment in which they can rapidly compare different models of binding for a given scenario. It is written specifically with microtubule polymers in mind, but many of its models apply equally well to any polymer or any protein–protein interaction. MTBindingSim can thus both help in training intuition about binding models and with experimental design.

Availability and implementation: MTBindingSim is implemented in MATLAB and runs either within MATLAB (on Windows, Mac or Linux) or as a binary without MATLAB (on Windows or Mac). The source code (licensed under the GNU General Public License) and binaries are freely available at http://mtbindingsim.googlecode.com.

Contact: jphilip@nd.edu; cpence@nd.edu

1 INTRODUCTION

The investigation of protein–protein interactions is a critical issue in biochemistry, and many different models have been proposed to account for the various binding behaviors that have been observed. This wide array of possible models makes it difficult for both students and researchers to predict the binding data expected from these different models. This can make the interpretation of experimental data for an interaction without an established model particularly difficult (e.g. Zhu et al., 2009). In addition, it is difficult to design experiments that can conclusively determine which model is best if one does not have a solid understanding of the behaviors expected from the different models.

We have written MTBindingSim to assist with these challenges. MTBindingSim provides researchers and students with an environment in which they can easily and rapidly visualize protein–protein interactions under a variety of models and experimental designs. While MTBindingSim was written specifically with microtubule (MT) binding proteins in mind, all models except one apply to binding to any polymer, and four of the models can be used in any protein binding system. We are confident that MTBindingSim can therefore be useful for understanding protein binding in a wide variety of contexts, within both research and education.

2 IMPLEMENTATION

MTBindingSim is written in MATLAB and distributed under the GNU General Public License. It can therefore run on any platform on which MATLAB is supported, including Windows, Mac OS X and Linux. We also provide installation files that enable MTBindingSim to be run on both Windows and Mac OS X systems that do not have MATLAB installed. MTBindingSim allows users to model predicted binding data in a variety of situations, as described below.

2.1 Binding models

MTBindingSim allows users to simulate protein binding curves for seven different binding models. For detailed information on the mathematics used to calculate the binding curves, see the MTBindingSim documentation, available at http://mtbindingsim.googlecode.com. We have chosen this set of models because they include most of those that have been proposed for MT binding proteins (Sandblad et al., 2006; Zhu et al., 2009).

As is conventional in the MT field, we treat the concentration of polymerized tubulin dimers as the concentration of MT. All models allow the user to set the binding ratio of a microtubule-associated protein (MAP), symbolized by A, to MT. The binding ratio assumes that each tubulin dimer is an available binding site for A and that when the binding ratio of A to MT is not 1, a single bound A takes up more or less than one binding site. A key aspect of the program is that the user specifies the values for all binding constants.

While Models 1–4 are described in terms of binding between an arbitrary protein A and MT subunits, they are not limited to MT binding and can be used to simulate interactions between any arbitrary proteins A and B (simply replace MT by B in the descriptions). Models 5 and 6 are limited to polymer systems. Model 7 alone is MT-specific. Additional information beyond these brief descriptions is provided in the User Manual.

  1. First-order binding: this model calculates binding curves for a simple binding interaction where protein A binds to MT with Kd (dissociation constant) KAMT.

  2. Two independent binding sites: in this model, there are two separate first-order binding sites for A on each MT subunit, each with its own Kd.

  3. MAPs bind MT-bound MAPs: this model assumes that when one A is bound to the MT, a second A can bind the MT-bound A without taking up another MT binding site. The user specifies the dissociation constants for the A-MT binding and the A-A binding. This model simulates a situation where binding to the MT opens up an A-A binding site on a bound A.

  4. Two MAPs bind MT-bound MAPs: this model is identical to the one described above except that two As can bind to the first MT-bound A. Both A-A binding interactions have the same dissociation constant.

  5. MAPs dimerize (a polymer-specific model): in this model, A dimerizes, and both A and A-A can bind to the MT, but do so with different dissociation constants.

  6. Pseudocooperativity (a polymer-specific model): due to the complexity of filamentous structures, cooperative binding of protein A to MTs cannot be easily modeled by the standard cooperative binding model. Given this, we have implemented a pseudocooperativity model, in which the binding of one A to any MT site creates an MT* site, which has a dissociation constant for A of KAMT*. This model approximates a situation where protein binding causes changes to the overall polymer structure, changing the binding affinity for subsequent proteins.

  7. Seam and lattice binding (an MT-specific model): this model allows users to investigate the significance of the fact that the binding surface at the MT seam is different from that on the rest of the lattice (Kikkawa et al., 1994; Sandblad et al., 2006). In this model, protein A binds to the MT seam (1/13 of the MT surface) with a dissociation constant of KAS and lattice (12/13 of the MT surface) with a dissociation constant of KAL.

2.2 Types of experiments simulated

MTBindingSim allows users to simulate data from three different kinds of experiments. The experimental methods are based on data collected using cosedimentation assays, the most common method of testing protein-MT binding (e.g. Ackman et al., 2000; Zhu et al., 2009). However, the binding curves computed by MTBindingSim will be valid for experiments using any method of measuring protein binding, including surface plasmon resonance, fluorescence anisotropy and tryptophan fluorescence. The experimental methods and plotting options were chosen to mimic common data collection and plotting practices in protein binding experiments. MTBindingSim allows users to save the generated graphs and data in a variety of image formats, including .csv (data), PDF, Adobe Illustrator and JPEG (graphs). In the descriptions below, it is assumed that an arbitrary protein A is binding to MT subunits, but MT could symbolize any binding partner.

Vary [MT]: in this experiment, the concentration of the MT-binding protein A is held constant and the concentration of MT is varied. This is a ‘standard’ binding experiment. For this experimental method, the y-axis of the graph is the fraction of A bound to MT, and the user can choose to plot concentration of total MT or the concentration of free MT on the x-axis. This experimental method yields the familiar Langmuir binding isotherm.

Vary [A]: in this experiment, the concentration of MT is held constant and the concentration of A is varied. The concentration of A bound to MT is graphed on the y-axis, and the user determines whether the x-axis is the concentration of free or total A. This method of investigating binding is often used to determine the level at which A will saturate the MT (Ackman et al., 2000). These data also can be graphed as a Scatchard plot, which can be useful because the graph will be linear for a standard first-order interaction and curved if cooperativity or other non-first-order interactions exist.

Competition: this experiment examines the binding of two MT-binding proteins, A and B. The concentration of A and MT is held constant and the concentration of B is varied. The fraction of A bound to MT is graphed on the y-axis and the total concentration of B is plotted on the x-axis. Both A and B are assumed to bind to the MT using the first-order model.

2.3 Examples

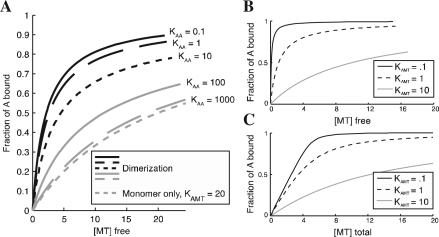
As a first example of how MTBindingSim might be used, we present here an investigation of the effect of dimerization on protein binding to MT. Figure 1A shows binding curves for a protein where the monomer binds to MT with a significantly weaker affinity than the dimer. The curves generated by MTBindingSim demonstrate the dramatic effect that even weak dimerization can have on protein binding. This effect is relevant for experiments with GFP fusion proteins because GFP has a weak dimerization affinity of ~ 100 μ M (Tsien, 1998), which, as shown in Figure 1, can be enough to cause a clear (and to many people, surprising) change in behavior. This suggests that researchers should be cautious in drawing conclusions from data collected with GFP-tagged proteins.

Fig. 1.

Fig. 1.

Open in a new tab

(A) Curves demonstrating the effect of dimerization on MT binding behavior. For all curves, the total amount of A is 10 μM, the dissociation constant for monomer binding to MT is 20 μM, and the dissociation constant for dimer binding to MT is 2 μM. The monomer-only curve is calculated using the first-order model with a dissociation constant of 20 μM. (B) Illustration of simple first-order binding behavior at different Kd values, with [A] total of 5 μM. (C) Curves for systems identical to those in (B), showing the effect of plotting binding as a function of [total ligand] instead of [free ligand] as in (B). Examination of the curves shows that the difference between (B) and (C) becomes significant when [A] > Kd. All graphs were made in MTBindingSim and edited in Adobe Illustrator.

As a second example, more relevant in an educational context, we use MTBindingSim to illustrate standard first-order binding behaviors. Figure 1B shows how binding curves shift with different Kd values, while comparison of Figure 1C to Figure 1B shows how the appearance of the curves (and the position of 50% saturation) can change dramatically when binding is plotted as a function of total ligand (C) instead of free ligand (B). It is important for educators to highlight this behavior, because it frequently causes misinterpretations in binding experiments.

3 CONCLUSION

We here introduce a program, MTBindingSim, which provides an environment for the simulation and comparison of protein binding curves. This program is an excellent resource for students learning about binding as well as researchers both training their intuition and designing experiments to investigate different binding models.

ACKNOWLEDGEMENTS

We thank Brian Baker for helpful discussions about the binding model mathematics. We are grateful to Jill Voreis, Abigail Weaver, Emily Ottenweller, Ben Paulson, Aranda Slabbekoorn and Eric Bunker for program testing.

Funding: National Science Foundation (grant 0951264 to H.V.G.); fellowship from the University of Notre Dame Chemistry, Biochemistry, Biology Interface Program (NIH T32GM075762 to J.P.).

Conflict of Interest: none declared.

REFERENCES

  1. Ackman M., et al. Nonsaturable binding indicates clustering of tau on the microtubule surface in a paired helical filament-like conformation. J. Biol. Chem. 2000;275:30335–30343. doi: 10.1074/jbc.M002590200. [DOI] [PubMed] [Google Scholar]
  2. Kikkawa M., et al. Direct visualization of the microtubule lattice seam both in vitro and in vivo. J. Cell. Biol. 1994;127:1965–1971. doi: 10.1083/jcb.127.6.1965. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Sandblad L., et al. The Schizosaccharomyces pombe EB1 homolog Mal3p binds and stabilizes the microtubule lattice seam. Cell. 2006;127:1415–1424. doi: 10.1016/j.cell.2006.11.025. [DOI] [PubMed] [Google Scholar]
  4. Tsien R. The green fluorescent protein. Annu. Rev. Biochem. 1998;67:509–544. doi: 10.1146/annurev.biochem.67.1.509. [DOI] [PubMed] [Google Scholar]
  5. Zhu Z., et al. Interactions between EB1 and microtubules: Dramatic effect of affinity tags and evidence for cooperative behavior. J. Biol. Chem. 2009;284:32651–32666. doi: 10.1074/jbc.M109.013466. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES