Hydration of highly charged ions

Graphical abstract

Highlights

►Concise treatment of highly charged ions with very different properties. ► Performed by ab initio simulations with the recent QMCF-MD methodology. ► Treating hydrates with extreme stability, labile hydrates and instable systems with (sub-)picosecond proton transfer reactions.

Abstract

Based on a series of ab initio quantum mechanical charge field molecular dynamics (QMCF MD) simulations, the broad spectrum of structural and dynamical properties of hydrates of trivalent and tetravalent ions is presented, ranging from extreme inertness to immediate hydrolysis. Main group and transition metal ions representative for different parts of the periodic system are treated, as are 2 threefold negatively charged anions. The results show that simple predictions of the properties of the hydrates appear impossible and that an accurate quantum mechanical simulation in cooperation with sophisticated experimental investigations seems the only way to obtain conclusive results.

1. Introduction

Highly charged metal ions, i.e. those with a formal charge of +3 and +4 are of increasing relevance and interest concerning their behaviour in an aqueous environment. Their properties range from extreme inertness of the hydrates – Ir(III) exchanges a ligand every 300 years [1] – to hydrolysis on the femtosecond scale as As(III) [2]. In the latter case experimental access to the dynamics is almost impossible. On the other hand, the presence of such ions in industrial waste water and their toxicological effects upon incorporation into an organism make it highly desirable to gain detailed information on their physical and chemical behaviour in aqueous solution.

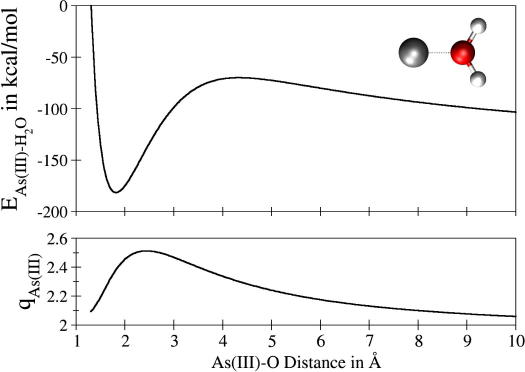
The progress of theoretical approaches and computational facilities has made simulations a practical alternative to access the desired data, in particular after quantum mechanical simulation methods have provided the necessary methodical flexibility and accuracy of results. This approach is of particular importance in the case of highly charged ions, which not only lead to very strong polarization and charge transfer effects, but can – in the course of hydrolysis processes – invoke cleavage and formation of chemical bonds, which require a quantum mechanical description. The polarisation and charge transfer effects also make the construction of classical interaction potentials from 2- or 3-body gas phase quantum chemical calculations almost impossible due to a ‘Coulombic catastrophe’ at larger distances (Figure 1 ).

Figure 1.

Example of the Coulomb catastrophe in the case of an As(III)–${\text{H}}_2\text{O}$ potential energy scan.

Quantum mechanical simulations, in particular of the molecular dynamics (MD) type, can provide a large variety of data relevant to the chemistry of the highly charged ions. Structure and stability of the hydrates and ligand exchange dynamics can be extracted from the simulation trajectories and the strength of the ion–water bond is accessible via the simulated vibrational spectra, which also offer good comparison with experimental data of (stable) hydrates. In those cases where ultrafast hydrolysis reactions take place, the simulation enables the observation of these processes on a sub-picosecond scale and as well as the associated mechanisms.

A recently developed QM/MM hybrid method, namely the quantum mechanical charge field molecular dynamics (QMCF MD), has numerous advantages for the treatment of highly charged ions in solution, which will be outlined.

2. Method

An alternative approach to experimental techniques are theoretical methods, in particular statistical simulation techniques such as Monte-Carlo and molecular dynamics [3–5]. These approaches are based on statistical thermodynamics and employ a microscopic description to investigate the properties of chemical systems. In order to successfully apply these techniques an accurate description of the potential energy surface of the system is required, which can either be achieved by empirical molecular mechanical approaches [6,7] or via quantum chemical methods [8–10].

In the first case, the interactions within the system are described based on pre-parametrized (i.e. empirical) potential functions. The main advantage of this approach, known as molecular mechanics (MM) of force fields (FF) [6,7], is its computational efficiency, which is strongly dependent on the considered interaction types (e.g. bonding, non-bonding, polarisation, many-body effects, etc.) and the functional form employed to model the respective contributions. The development and balancing of a reliable parameter set for a particular chemical system is a challenging, tedious and time-consuming task and in many cases, limitations in the applicability, accuracy and transferability are encountered. A further severe limitation of MM approaches results from the harmonic approximation. Many force fields model bonding interactions such as bonds and angles via a harmonic approximation, which prevents the description of the formation and cleavage of chemical bonds.

Quantum mechanical (QM) [8–10] approaches on the other hand do not rely on empirical parameters. These methods employ numerical solutions of Schrödinger’s equation to obtain a quantitative description of the electronic structure, i.e. the electron density surrounding the nuclei. These approaches are more accurate than force field methods, as polarisation, charge-transfer and polarisation effects are automatically taken into account. As no empirical parameters are utilized, these approaches are very general and can be applied to a broad range of chemical systems. The accuracy of quantum chemical approaches is in some cases limited due to an inaccurate treatment of the correlation of electrons. While this may become significant in the case of weakly interacting systems, it was found to be less pronounced when strong interactions are present, as for example in the case of solvated ionic species and hydrogen bonded systems. A hierarchy of corrective treatments [10] (such as perturbative approaches or so-called coupled cluster methods) enabling an increasingly accurate treatment of the electron correlation are available. Although the associated computing times prevent the application of these methods in chemical simulations as of yet, preliminary computations of representative systems enable the assessment of the error associated with the inaccurate treatment or, respectively, neglect of correlation of the electrons.

Due to the complexity of quantum chemical approaches the associated computing time is orders of magnitude larger than the effort required to treat the system with a molecular mechanical ansatz and a compromise between accuracy and computational effort has to be sought. In the Car-Parinello molecular dynamics (CPMD) framework [11], this balance is achieved by reducing the system size to a critical minimum (typically to the solute and about 30–100 water molecules) and the application of approximate quantum chemical schemes, typically density functional theory (DFT) at the generalised gradient approximation (GGA) level [12]. Although this approach has become quite popular due to the comparatively low computational demand, recent data for pure water have revealed a number of method-inherent shortcomings leading to an inaccurate description of hydrogen bonded systems. In this framework, the melting point of water was estimated as approximately 410 K and it was concluded, that the description of water at room-temperature shows the characteristics of a supercooled liquid [13,14].

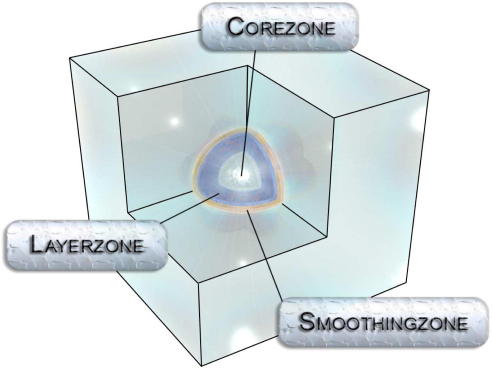
An alternative approach exploiting the advantages of quantum chemical and molecular mechanical methodologies are hybrid approaches [15–18]. In this framework, the system is partitioned into two sub-regions. The chemically most relevant part is treated via a suitable quantum mechanical approach, and molecular mechanical potential functions are considered to be sufficiently accurate to describe the remaining part of the system. While the computation of energies and forces within the respective sub-regions result from the straightforward application of the associated theoretical method, the coupling of the two zones is not trivial and a large number of coupling protocols have been developed [19]. An improved simulation technique known as Quantum Mechanical Charge Field (QMCF) ansatz was recently developed [20,21] and successfully applied in investigations of various hydrated systems [22]. Due to the use of an enlarged quantum chemical region the coupling between particles located in the center of the QM region (QM core; cf. Figure 2 ) and MM atoms requires only the application of Coulombic potentials, because the contribution of the non-Coulombic interactions are negligibly small. This does not apply in the case of particles located in the layer part of the QM region where both Coulombic and non-Coulombic coupling potentials have to be applied.

Figure 2.

Definition of QM regions (core and layer) and MM region in QMCF MD simulations.

The sizes of all regions have to be set to avoid the occurrence of discontinuities of energies and forces. As solvent molecules are assigned as a whole to either the QM or the MM region, water molecules are never fragmented by the QM/MM interface. To ensure a continuous change of forces upon particle migration to/from the quantum mechanical region a smoothing procedure is invoked to gradually shift the force from the QM to the MM contribution [21–25]. The elimination of the requirement of coupling potentials for the solute located in the QM core enabled QMCF simulations studies of systems showing anisotropic hydration [26–29], in which case the formulation of appropriate interaction potentials is even more difficult.

A significant increase in the accuracy of the QMCF methodology was achieved by employing quantum mechanically derived partial charges in the QM–MM Coulombic coupling. This approach incorporates the influence of polarisation, charge-transfer and many-body effects occurring in the QM region into the QM–MM coupling. These QM partial charges are re-evaluated in each step of the simulation, accounting for the influence of all geometrical changes within the QM region. Similarly, the incorporation of all MM partial charges as a perturbational potential into the quantum chemical treatment [30,31] leads to an improved description of the electron density.

The latter two improvements were found to effectively eliminate all coupling artifacts close to the QM/MM interface [20–22] that have been observed in QM/MM simulation studies employing a conventional coupling scheme, which almost always implies the use of solute–solvent potentials with formal charges. It was demonstrated that the application of the QMCF approach improves the accuracy of the simulations significantly, whereas the increase associated to the computational effort is minor.

One particularly challenging application is the study of hydrolysis phenomena. In order to assess the capabilities of the QMCF approach, as a first example a solute was chosen that cannot be observed in neutral aqueous environment: the As(III) ion is known to hydrolyse rapidly, for instance if ${\text{AsCl}}_3$ is dissolved in water. Indeed, hydrolysis was observed within a very short simulation period [2], confirming the capability of quantum chemical approaches to describe the formation and cleavage of chemical bonds.

3. Protocol of simulations

For all QMCF simulations presented here a similar protocol was employed, based on a cubic box containing the solute and 1000 water molecules. The density of the system was fixed at $0.997{\text{g/cm}}^3$, which coincides with the density of pure water at the simulation temperature of 298.15 K. The flexible BJH-CF2 water model [32,33] was employed to describe the solvent in the molecular mechanical region. Since the QM treatment as well as the water model enable intramolecular hydrogen motion, a time step of 0.2 fs was chosen. A second-order predictor corrector algorithm of the Adams-Bashforth family was applied to integrate the equations of motion. All simulations were carried out in the canonical (NVT) ensemble employing the Berendsen weak-coupling thermostat [34] with a relaxation time of 0.1 ps. A general cutoff of 12–15.0 Å was employed. The O–H and H–H non-Coulombic contributions were truncated at 5.0 and 3.0 Å, respectively, and to account for the error of the Coulombic cutoff, the reaction field method was employed.

Dunning DZP basis sets [35] were assigned to oxygen and hydrogen. For the solutes a number of basis sets have been tested. The results of gas-phase energy minimizations (binding energies and minimum geometries) for various ion–water clusters were utilised to compare the performance of the different basis sets, enabling the choice of the most suitable one. Similarly, comparisons of different levels of theory were routinely performed to assess performance and quality of the respective approaches. As correlated ab initio methods, such as Møller–Plesset perturbation theory or coupled cluster approaches, are too demanding for application in QMCF simulations, the level of theory is limited to the single determinantal level, i.e. density functional theory or ab initio Hartree–Fock. In all studies the latter was found to yield results in better agreement with correlated methods than DFT methods. Therefore, the Hartree–Fock approach was the method of choice in all simulations.

The size of the quantum mechanical region was set to include the solute and its first and second hydration shells. Thus, the number of solvent molecules included in the QM region ranged from 18 to 25 water molecules. Due to the enormous computational demand of the quantum chemical treatment, the computation of the energy and forces in the QM region was executed in parallel. Depending on the number of processors and the size of the QM region, the computing time for energy and forces ranges from 90 s to more than four minutes per time step. If a total simulation time of 10 ps is envisaged plus a 2 ps period of equilibration (assuming that a properly pre-equilibrated starting geometry is employed), a total number of 60 000 MD steps is required leading to simulation times between 3 and 8 months. In some cases a longer trajectory was required, leading to even longer computation times.

To generate starting geometries either purely classical (i.e. MM) simulations can be employed if suitable solute–solvent interaction potentials are available or geometries of simulations of similar systems can be adopted, e.g. a simulation cube containing Al(III) in aqueous solution can be utilised as starting geometry for hydrated Fe(III).

4. Results and discussion

The computational effort for a QMCF MD simulation of a trajectory between 10 and 30 ps at ab initio Hartree–Fock level with double zeta plus polarisation basis set (and relativistically corrected ECP basis sets for the heavier atoms) is considerable, amounting to 6–12 months of CP time with 8–16 processors on a high-performance computer cluster. The use of more processors does not improve the performance automatically as the parallelizability of the ab initio calculation of the energies and forces is limited, depending on the QM software used. For these reasons, results are available only for a selection of ions which, however, represent a good sampling of the different characteristics of highly charged ions. In principle, they can be classified as ‘stable’ and ‘instable’ ions, where ‘stability’ means that they do not undergo hydrolysis within the simulation period and are also mostly reported as observable in experiment. As will be shown, the size of the ions and their position in the periodic table of the elements determines their properties, and the selection made thus includes a variety from small and medium sized main group metal to different transition metal ions including lanthanoid examples. Two anions have been selected as examples of stable and instable highly negatively charged systems.

5. Stable ions

5.1. Trivalent ions

This category includes a number of threefold charged cations, whose structural hydration characteristic are summarised in Table 1 and whose dynamical data are collected in Table 2 .

Table 1.

Structural parameters of hydrated trivalent metal cations, $r_1$ and $r_2$ are the mean distances of first and second hydration shell, $N_1$ and $N_2$, the (average) number of ligands in these shells.

Ion	$r_1$ (Å)	$r_2$ (Å)	$N_1$	$N_2$	Ref.
Al(III)	1.90	4.1	6	11.8	[37]
Sb(III)	2.18/2.70	4.3	4 + 4	8 + 5	[38]
Fe(III)	2.03	4.1	6	13.6	[39]
V(III)	2.03	4.3	6	13.5	[40]
Ir(III)	2.06	4.2	6	13,5	[41]
La(III)	2.62	4.8	9.5	25.0	[42]
Ce(III)	2.63	5.0	9	24.2	[42]

Table 2.

Dynamical parameters of hydrated trivalent metal cations, ${\text{MRT}}_1$ and ${\text{MRT}}_2$ are the mean ligands residence times of water ligands in the first and second hydration shell, ${\text{K}}_{\text{I}0}$, the force constant for the ion–O bond.

Ion	${\mathrm{MRT}}_1$ (ps)	${\mathrm{MRT}}_2$ (ps)	${\text{K}}_{I0}(\text{N/m})$	Ref.
Al(III)	n.o.	17.7	194	[37]
Sb(III)	5.9	1.7	n.a.	[38]
Fe(III)	n.o.	3.1	193	[39]
V(III)	n.o.	4.7	203	[40]
Ir(III)	n.o.	3.6	260	[41]
La(III)	13.4	2.4	96	[42]
Ce(III)	n.o.	2.7	73	[42]

n.o.: no exchange processes observed during simulation time; n.a.: not available.

Al(III) is a small main group ion, which forms a very stable octahedral first hydration shell and a second shell binding in an almost ideal way via hydrogen bonds to the first shell ligands, thus amounting to ∼12 water molecules. Within the simulation time no hydrolysis of a first shell ligand was observed. An indication of a third shell could be recognised in the radial distribution function (RDF) [36,37], and the mean residence time (MRT) of second shell ligands of over 17 ps is the highest observed among all ions presented here. The force constant obtained from the vibrational spectrum calculated via Fourier transformation of the velocity autocorrelation functional (VACF) amounts to nearly 200 N/m, which belongs to the upper segment of these values and explains, why no first shell ligand exchange was observed in the simulation.

A completely different system is the main group ion Sb(III) with its lone electron pair destabilising the hydrate [38]. As this electron pair occupies a considerable space, it induces the formation of two different hydration hemispheres, one with four tightly bound ligands at a distance of ∼2.2 Å and another one on the opposite side with four much more loosely bound water molecules located ∼2.7 Å far from the ion. The latter are responsible for frequent exchanges between first and second hydration sphere, leading to an MRT value of 6 ps for first shell ligands.and a very low MRT $(<2\text{ps})$ for those of the second shell, which is equally unsymmetric as the first shell, with ∼5 plus ∼8 ligands.

Fe(III) [39] and V(III) [40] are good representatives for trivalent first row transition metal ions, with very stable octahedral first hydration shells showing no exchange processes, and rapidly exchanging second shells whose coordination numbers vary between 10 and 16, with a mean value deviating from the ‘ideal’ 2:1 ratio based on hydrogen bonding. The force constants for the ion–O bonds of the first shell are of the same magnitude as that of Al(III) [37] with values of 193 (Fe) and 203 (V) N/m.

Ir(III) has been selected as representative of the heavier transition elements for two reasons: first, it forms the hydrate with the highest ever measured MRT value for first shell ligands as ∼300 years [1], and second for its completely different behaviour from divalent platinum metal ions Pd(II) and Pt(II) [27,28], characterised by 4 very stable ligands in a square planar arrangement and 2 loosely bound axial ligands. Ir(III) [41] forms an enormously stable octahedral arrangement with 6 water molecules and the ion–O force constant resulting from our simulation amounts to 260 N/m, which is the highest one among all reported here and thus in good agreement with the experimentally observed inertness of this hydrate complex.

The lanthanoids are a special class of elements, apparently also with regard to their hydrated ions. Their peculiarity can be easily recognised from the simulation results for La(III) [42] and Ce(III) [42] reported here. Both of them form a first coordination sphere with an average of nine ligands with dominating capped prismatic geometry. The MRT value for La(III) ligands is only ∼13 ps, while no ligand exchange was observed in the first shell of Ce(III), indicating the influence of the remaining valence electron in the latter ion. In both cases the simulation time was extended to >20 ps in order to obtain a reasonable statistics for possible exchange processes. The second shell MRT values, slightly above 2 ps differ only marginally from that of bulk water (1.7 ps [43,44]). The force constants evaluated for the ion–O bonds reflect the relative lability of the hydration shells, with values below 100 N/m and are certainly related to the higher coordination number and thus larger ion–O distances compared to the other trivalent metal cations.

5.2. Tetravalent ions

Not many of the tetravalent metal ions are present as ${\text{M}}^{4+}$ in aqueous solution. Some of them immediately form oxonium ions ${\text{H}}_3{\text{O}}^{+}$ and are thus reduced to a lower charge state (vide infra), others are present as oxo-ions, e.g. ${\text{TiO}}_2^{+}$ [45]. There is experimental evidence, however, that zirconium, hafnium. cerium and uranium (IV) exist [46,47], at least under suitable acidic conditions, as ${\text{M}}^{4+}$, and for these ions QMCF MD simulations have been carried out.

Although the hydration characteristics are not so different as in the case of trivalent ions, some surprising results have been obtained, which seem relevant for the chemical behaviour of these ions in water. A summary of the results is given in Tables 3 and 4 .

Table 3.

Structural parameters of hydrated tetravalent metal cations, $r_1$ and $r_2$ are the mean distances of first and second hydration shell, $N_1$ and $N_2$, the (average) number of ligands in these shells.

Ion	$r_1$ (Å)	$r_2$ (Å)	$N_1$	$N_2$	Ref.
Ce(IV)	2.44	4.7	9	17.4	[42]
Zr(IV)	2.25	4.5	8	17.8	[46]
Hf(IV)	2.26	4.5	8	17.2	[47]
U(IV)	2.46	4.8	9	17.4	[53]

Table 4.

Dynamical parameters of hydrated tetravalent metal cations ${\text{MRT}}_1$ and ${\text{MRT}}_2$ are the mean ligands residence times of water ligands in the first and second hydration shell, ${\text{K}}_{\text{I}0}$, the force constant for the ion–O bond.

Ion	${\text{MRT}}_1$ (ps)	${\text{MRT}}_2$ (ps)	${\text{K}}_{I0}$ (N/m)	Ref.
Ce(IV)	n.o.	6.0	149	[42]
Zr(IV)	n.o.	5.5	188	[46]
Hf(IV)	n.o.	15.4	212	[47]
U(IV)	n.o.	13.6	157	[53]

n.o.: no exchange processes observed during simulation time.

The coordination number of all ions is either 8 or 9 [46,47] and the observed basic structure of the hydrates is either a (single capped) square antiprism or a tri-capped trigonal prism, in good agreement with available experimental findings. Sometimes conversion between both geometrical arrangements occurs without any inter-shell exchange process: the first hydration shell does not exchange ligands with the second shell within the simulation time in any case. The lability of second shell ligands shows considerable differences: as expected, the fastest exchanges are observed for Ce(IV), and the MRT value for Zr(IV) is much lower than those for the heavier ions U(IV) and Hf(IV). The strength of the ion–O bonds is similar for Ce(IV) and U(IV), namely ∼150 N/m, and increases for Zr(IV) with ∼190 and Hf(IV) with ∼210 N/m. All of these values are considerably below the value for Ir(III), in good agreement with the experimental characterisation of the Ir(III) hydrate as the most stable one. The strength of the ion–ligand bonds is also a consequence of the coordination number, and the higher coordination number of the tetravalent ions implies for steric reasons, a larger ion–O distance than in the predominantly octahedral aquo-complexes of the trivalent ions.

At this point, the stability of the ion–water bonds can be summarised by ordering them according to their ion–O force constants:

$$\text{Ir}(\text{III})\gg \text{Hf}(\text{IV})>\text{V}(\text{III})>\text{Al}(\text{III})\approx \text{Fe}(\text{III})>\text{Zr}(\text{IV})>\text{U}(\text{IV})>\text{Ce}(\text{IV})\gg \text{La}(\text{III})>\text{Ce}(\text{III})$$

As the MRT value of La(III) demonstrates, these bond strength are not always directly related to the exchange dynamics. In Figures 3 and 4 typical examples of tri- and tetravalent hydrates are shown.

Figure 3.

Typical example of a highly charged metal cation in aqueous solution: Ir(III).

Figure 4.

Typical example of a highly charged metal cation in aqueous solution: Ce(IV).

5.3. Unstable ions

As mentioned in the introductory remarks, some highly charged ions react immediately with first-shell water molecules as soon as a quantum mechanical treatment is invoked, forming oxonium ions ${\text{H}}_3{\text{O}}^{+}$ and binding one or more ${\text{OH}}^{-}$ groups instead of water ligands, thus reducing the hydrate’s charge.

A typical trivalent ion of this sort is As(III), whose immediate hydrolysis in aqueous solution is also known from experiment, for instance when ${\text{AsCl}}_3$ is dissolved in water. Within the first picoseconds of the simulation, it transforms in 2 steps to As ${(\text{OH})}^{2+}$ and then As ${(\text{OH})}^{2+}$ [1], the final stable form hydrated by a few more water molecules. A video clip illustrating this process is available at our web page www.molvision.com under ‘videos’. In the case of this smaller group V cation, the effect of the lone pair is apparently strong enough to cause an immediate hydrolysis, while in the heavier analogue Sb(III) it only leads to a strongly distorted hydration structure (vide supra). Figure 5 shows the result of the hydrolysis process of As(III).

Figure 5.

Typical example of a highly charged metal cation in aqueous solution: As(III) after the first hydrolysis event.

The group IV cations ${\text{Ge}}^{4+}\text{,}{\text{Sn}}^{4+}$ and ${\text{Pb}}^{4+}$ [48] are other examples of metal ions unstable in water, as they undergo hydrolysis on the picosecond scale, observable in the simulation. While with ${\text{Ge}}^{4+}$ this process produces 3 oxonium ions, leading to the tetracoordinated species $\text{Ge}{(\text{OH})}_3{({\text{H}}_2\text{O})}^{+}$ both ${\text{Sn}}^{4+}$ and ${\text{Pb}}^{4+}$ form ions of the type ${\text{M(OH)}}_{\mathit{aq}}^{+}$ which hexacoordinated in the case of Sn(IV) and heptacoordinated with Pb(IV), respectively. These reactions have been visualised on a video clip accessible at www.molvision.com. Figure 6 shows the result of the hydrolysis process of Ge(IV).

Figure 6.

Typical example of a highly charged metal cation in aqueous solution: Ge(IV) after hydrolysis.

With the present QMCF MD code, these simulations can only be performed to the point, where the oxonium ions are leaving the QM region, as the classical water force field is not capable of describing these ions. The planned inclusion of a dissociative reactive force field will overcome this problem. However, the present results already give a good impression of the mechanistic progress of the hydrolysis reactions of these instable cations.

5.4. Anions

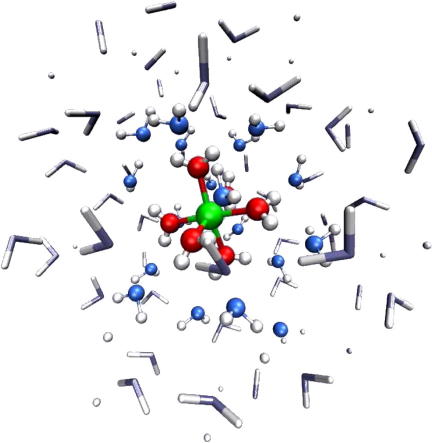
Some anions carrying a high negative charge are stable in aqueous solution, at least at high pH values. The most representative example is probably the phosphate ion ${\text{PO}}_4^{3-}$ for which we summarise the results of a QMCF MD simulation [49] here.

Binding of water molecules to phosphate is based on hydrogen bonds between water hydrogens and phosphate oxygens. Due to the high charge, each of the 4 oxygens binds on average to 3 water molecules, and the total average coordination number of the first shell is 13.4. These hydrogen bonds are considerably shorter than those between solvent molecules and the stronger binding is reflected in a MRT value of these ligands of 3.6 ps, which is more than double the value for water in the bulk (1.7 ps [43,44]). However, even this value indicates a quite rapid exchange of ligands, many orders of magnitude faster than for ions with a threefold positive charge.

How sensitive hydration can be also in the case of anions is best demonstrated by going up in the periodic system from P to As. The analogous anion to phosphate is the arsenate ${\text{AsO}}_4^{3-}$, which in contrast to phosphate, undergoes hydrolysis and thus represents an instable ion in the sense of this presentation. This process takes place in the first picoseconds of the simulation [50,51], and the arsenate captures one proton from a first shell water ligand, releasing an ${\text{OH}}^{-}$ ion into the solution. The resulting species ${\text{As(OH)O}}_3^{2-}$ remained stable in the further course of the trajectory. No such process has been observed in the case of anions carrying two negative charges, e.g. sulfate [52].

6. Conclusions

The results presented here demonstrate that contemporary simulation methods are a suitable tool for the investigation of solvation processes, elucidating not only structure and composition of ion solvates, but also their dynamics and stability in solution. In particular in the cases where ultrafast, i.e. picosecond structural changes or solvolysis reactions take place, the theoretical simulation approach can be advantageous or even superior to experimental methods which can reach this timescale only in exceptional cases to date. On the other hand, the data presented here also demonstrate how important it is to include a sufficiently large region with full ab initio quantum chemical treatment and a much larger MM region for an appropriate embedding in bulk in the simulation protocol. Only this approach ensures the necessary accuracy and the possibility to describe reactions involving formation and cleavage of bonds.

Although only a limited number of highly charged ions could be presented here, this selection already gives quite some insight, how different the behaviour of such ions can be when they are embedded in water, ranging from extreme inertness until a hydrolytic conversion to new species within picoseconds. Computational facilities will enable to increase the quantitative accuracy of this description by the use of correlated ab initio methods in the simulations in a not too distant future, and the inclusion of counterions as well as the simulation of more concentrated solutions. This will further facilitate the already very fruitful collaborations with experimental research and thus open new horizons for investigations in solution chemistry.

Biographies

Ass.-Prof. Dr. Thomas Sebastian Hofer Born 1978 in Innsbruck, Austria. Ph.D. from University of Innsbruck in 2006. Since 2006 assistant professor in theoretical chemistry, promoted to associate professor in 2011. Main research fields are the development, implementation and application of advanced QM/MM methodologies, approaches to probe potential energy landscapes and simulations of biophysical systems.

Mag. Alexander Kurt Hermann Weiss Born 1986 in Rum, Austria. Graduted from University of Innsbruck in 2010. Currently working at University of Innsbruck as a PhD student.

Dr. Bernhard Rudolf Randolf Born 1975 in Vienna, Austria. Ph.D. from University of Innsbruck in 2006. Currently working as senior scientist at the University of Innsbruck. Teaching in the field of computational materials science.

Professor Dr. Dr.h.c.mult. Bernd Michael Rode Born 1946 in Innsbruck, Austria, Ph.D. from University of Innsbruck in 1973. Associate professor in 1976, professor in 1979 at University of Innsbruck. Research stays in Germany, Greece, Japan, Thailand and Indonesia. Main research fields are quantum mechanical simulations of liquids and solutions and prebiotic chemical evolution (experimental).