Multifactor Dimensionality Reduction as a Filter-Based Approach for Genome Wide Association Studies

Abstract

Advances in genotyping technology and the multitude of genetic data available now provide a vast amount of data that is proving to be useful in the quest for a better understanding of human genetic diseases through the study of genetic variation. This has led to the development of approaches such as genome wide association studies (GWAS) designed specifically for interrogating variants across the genome for association with disease, typically by testing single locus, univariate associations. More recently it has been accepted that epistatic (interaction) effects may also be great contributors to these genetic effects, and GWAS methods are now being applied to find epistatic effects. The challenge for these methods still remain in prioritization and interpretation of results, as it has also become standard for initial findings to be independently investigated in replication cohorts or functional studies. This is motivating the development and implementation of filter-based approaches to prioritize variants found to be significant in a discovery stage for follow-up for replication. Such filters must be able to detect both univariate and interactive effects. In the current study we present and evaluate the use of multifactor dimensionality reduction (MDR) as such a filter, with simulated data and a wide range of effect sizes. Additionally, we compare the performance of the MDR filter to a similar filter approach using logistic regression (LR), the more traditional approach used in GWAS analysis, as well as evaporative cooling (EC)-another prominent machine learning filtering method. The results of our simulation study show that MDR is an effective method for such prioritization, and that it can detect main effects, and interactions with or without marginal effects. Importantly, it performed as well as EC and LR for main effect models. It also significantly outperforms LR for various two-locus epistatic models, while it has equivalent results as EC for the epistatic models. The results of this study demonstrate the potential of MDR as a filter to detect gene–gene interactions in GWAS studies.

Introduction

Advances in genotyping technology have led to an explosion of information for human geneticists, and genome wide association studies (GWAS) have now become the preferred method for studying complex diseases such as diabetes, hypertension, cancer, asthma, etc. So far the majority of these studies have focused on finding main effects and though many studies have had some success with this strategy (Burton et al., 2007; Hakonarson et al., 2007; Helgadottir et al., 2007; Hunter et al., 2007; Plenge et al., 2007), their results still suggest that main effects do not totally account for all the genetic variation associated with these phenotypes (Frazer et al., 2009; Manolio et al., 2009; Eichler et al., 2010). It is now generally accepted that one potential explanation for this “missing heritability” are epistatic effects (gene–gene interactions), as well as gene–environment interactions that may be contributing to the disease phenotype (Frazer et al., 2009; Manolio et al., 2009; Eichler et al., 2010). Additionally, such epistatic interactions are a potential explanation for the inability of many univariate signals to replicate in independent, replication studies. This explanation is further validated by studies showing evidence of the possibility of the existence of epistatic interactions without any associated marginal effects (Culverhouse et al., 2002; Hu et al., 2010). This has resulted in an increasing number of researchers including the search for interactions as part of their analysis for GWAS. Concerns with high false positive rates associated with GWAS and the reproducibility of genetic association signals has prompted the use of a replication sample as a standard in the study designs of GWAS (Moore and Williams, 2002; Calle et al., 2008; Kraft et al., 2009), highlighting the need to be able to investigate potential interactions in the discovery stage of GWAS, which could then be further evaluated in replication sample(s).

In order to find the most promising candidates for replication, a broad number of methods have been developed, using a range of variable selection and statistical modeling techniques (Hoh and Ott, 2003; Culverhouse, 2007; Brinza et al., 2010). While the majority of these approaches have been applied to candidate gene studies, the potential of a few methods have been investigated at a genome-wide level (Brinza et al., 2010). Encouragingly, using traditional logistic regression (LR) analysis with a multistage approach has been evaluated in simulation studies, with the general conclusion that even after correcting for the large number of tests associated with searches for interactions in high-throughput data, there is high power to detect interactions (Burton et al., 2007).

These previous studies used a variety of multistage filters including: (1) filtering for significant main effects and then testing for interactions amongst loci with main effects (Hoh et al., 2001); (2) filtering for significant main effects, then testing for interactions between these significant markers and all other (non-univariately associated) markers (Evans et al., 2006); and (3) filtering out markers that have significant main effects and then testing for interactions amongst all the other non-univariately associated markers. These approaches can be successful for particular types of genetic etiologies of disease. The first approach can find interactions that involve significant main effects for all loci involved in the interaction, but will fail to detect interactions involving markers without significant marginal effects. The second approach will only be able to detect interactions with at least one-locus having a significant main effect, but will fail to detect purely epistatic effects (interactions with no marginal effects). The third approach will only be able to detect interactions with no main effects and will fail to characterize interactions with marginal effects. More recently, the idea of using filters that incorporate some prior biological knowledge such as biochemical pathways in order to limit the subset of variants considered in the initial analysis or as a means of prioritizing results have started to gain traction (Moskvina et al., 2011; Ritchie, 2011), and are being used in some combination with the filtering approaches mentioned above. The specific performance characteristics of these approaches motivate the use of a method that can inclusively detect interactions with a range of stringency: a method needs to filter both purely epistatic effects, and main effects with interactions. Multifactor dimensionality reduction (MDR) is a highly successful method that was designed to detect gene–gene and gene–environment effects, and is capable of detecting a wide range of epistatic models (Ritchie et al., 2001; Hahn et al., 2003). It has shown high power to detect a range of effect sizes and genetic models in a broad range of simulation studies (Ritchie et al., 2003; Motsinger and Ritchie, 2006; He et al., 2009) and real data applications (Ritchie et al., 2001; Park et al., 2007). The main limitation to the application of MDR to GWAS was originally computation time (since it uses an exhaustive combinatoric search approach), but recent parallel applications and GPU implementations (Greene et al., 2010) make this a reasonable approach to investigate two-locus interactions in GWAS studies.

In traditional applications of MDR, model selection within a cross-validation framework is used to select a single best model that is associated with disease status. Given the commonality of two-stage study designs, with the use of discovery and replication cohorts to identify and then replicate models, we evaluate the potential of MDR as a filter-based approach, using MDR modeling to evaluate and rank all univariate effects and two-locus epistatic effects. We compare the use of MDR as a filter approach, to evaporative cooling (EC), another machine learning filtering method (McKinney et al., 2009), which we use in conjunction with the Genetic Association Interaction Network (GAIN) first proposed by McGill (1954) to find multivariate epistatic models. We also compare our approach to a more traditional filter approach using LR modeling, the de facto standard in genetic association studies. We compare these approaches in simulations with a range of genetic main effects and interaction effects, and show the better performance of MDR for filtering gene–gene interactions.

Materials and Methods

In brief, to evaluate our ranking approach, we simulated case–control SNP data for single locus main effects, two-locus interaction effects, and two-locus combinations of both main and interaction effects. The simulations were done using varying penetrance functions, created with heritabilities close to 1 and 5%, “odds ratios” from 1.2 to 3.0, and minor allele frequencies of 0.2 and 0.4 separately (details of the penetrance functions are given in Tables A1–A6 in Appendix), giving us a wide range of effect sizes to analyze. For the one-locus models, we use MDR, EC, and LR modeling as filters for ranking and prioritizing models for follow-up in replication studies. We also use MDR, LR, and GAIN to find the important interactions for the two-locus models. For the one-locus models, all possible main effects were tested, and all possible interactions effects were also analyzed for the two-locus models. For each distinct model the marginal locus or multi-locus combinations (for two-locus models) were then ranked according to classification error (for MDR), p-values (for LR) and significance scores (for GAIN) separately. Additionally, error rates were calculated for the two-locus interactions analyzed with MDR to assess the false positive rates and reliability of our filter.

Data Simulations

Three types of disease models (one-locus main effect, two-locus epistatic effects, and two-locus models with joint epistatic and main effects) were simulated to include the disease causing SNP or SNPs for main effects and interaction effects. All simulations were done assuming SNPs are biallelic. All the models were simulated with specific penetrance functions (where the penetrance is the risk of disease given a genotype) to reflect the “odds ratios” and heritabilities desired. For the single locus models, a classical definition of an odds ratio was used. The odds ratios were calculated as the ratio of the odds of being affected to the odds of being unaffected, with the reference allele being the minor allele, e.g., for the dominance model and minor allele “A” the odds ratio is calculated by

$$\underset{\text{Affected}}{\underbrace{\left(\text{(oddsAA + oddsAa)/2}\right)\text{/}}}\underset{\text{Unaffected}}{\underbrace{\text{oddsaa}}}$$

For the two-locus models found using software described below, the use of the term “odds ratio” is specific to the data simulation, and is meant to capture the effect size between low-risk and high-risk penetrance values. The heritabilities (the proportion of trait variation that is due to genetics) were calculated as described in by Culverhouse et al. (2004).

The GenomeSim software (Dudek et al., 2006) package was used for all data simulations. A null model with no disease causing SNP was also simulated to be used for assessing the false positive rates of the filter. While our study involves relatively small datasets, other studies have shown that the results of large GWAS studies analyzed with MDR are highly consistent, regardless of the number of noise SNPs simulated (Edwards et al., 2009), so our results hopefully should also apply to GWAS data. Unfortunately, computational limitations prevent a large-scale simulation experiment with extremely large numbers of SNPs (at a true GWAS level).

One-locus main effect models

We simulated additive, recessive and dominant genetic effects for the main effects models. Odds ratios for the simulations ranged from 1.2 to 3.0 and heritabilities of 1 and 5%, as well as minor allele frequencies of 0.2 and 0.4 for the disease causing SNP. The penetrance functions with targeted odds ratios, heritabilities and allele frequencies were then used to simulate case–control data. The penetrance functions used are shown in Tables A1–A3 in the Appendix for each genetic inheritance mode. For each specific disease model within each of the three genetic inheritance structures (additive, recessive, and dominant), there were two groups of data simulated, each with eight models: One group for the data simulated with minor allele frequencies of 0.2 and the other for those simulated with minor allele frequencies of 0.4 for the disease causing SNP. One hundred replicate datasets were simulated for each model, with each dataset having 250 cases, 250 controls, and 100 independent SNPs [no recombination or linkage disequilibrium (LD) between SNPs]. This process created a combined total of 4,800 datasets of one-locus (univariate) models (1,600 within each inheritance mode).

Two-locus interaction (epistatic) models

We simulated a total of 16 two-locus epistatic models, with each model having a distinct penetrance function used for its dataset simulation. The penetrance functions were generated with “odds ratios” ranging from 1.2 to 3.0 (in increments of 0.2), heritabilities close to 1 and 5%, and minor allele frequencies of 0.2 and 0.4 for the disease causing SNPs separately (shown in Tables A4 and A5 in Appendix). This resulted in two sets of two-locus models, one with minor allele frequencies of 0.2 and the other with 0.4. Penetrance functions, with purely epistatic effects (with no marginal main effects for either SNP) were found using a genetic algorithm implemented in the SimPen software (Moore et al., 2002). SimPen uses a genetic algorithm that minimizes marginal penetrance variance to find penetrance functions with minimal to no main effects. The program accepts specified user parameters including heritability, “odds ratio,” marginal penetrance, allele frequency, etc., and gives the function with the best fitness. For each penetrance model 100 replicate datasets were simulated, with each dataset having 250 cases, 250 controls, and 100 independent SNPs (no recombination or LD between SNPs). This process created a total of 1,600 two-locus datasets.

Two-locus models with main effects

The modifying effect model previously described by Li and Reich (2000) was used as the template for estimating the penetrance functions for interaction effects that include both a main effect and an interaction effect between the main effect and another SNP. In this model, an individual is affected if they are homozygous for the disease allele (in this case the minor allele) from the main effect locus regardless of what alleles they carry at the second locus, or if they are heterozygous at the main effect locus and heterozygous or homozygous for the minor allele at the secondary locus. As with the purely epistatic models, two sets of disease models were simulated, one with minor allele frequency of 0.2 and the other with 0.4. Each set had eight models for a total of 16 models, with 100 replicates within each model. As with previous models, the penetrance functions were estimated with “odds ratios” varying from 1.2 to 3.0 (in increments of 0.2), but with heritabilities ranging from 0.02 to 8.4% using the modifying effect model as a template (Table A6 in Appendix). There were 100 replicate datasets for each model, each with 250 cases, 250 controls, and 100 SNPs per dataset, which were also independent (no recombination or LD between SNPs).

Null model

In addition to the disease model simulations, a null model was also simulated, with 100 replicate datasets having 250 cases, 250 controls, and 100 independent SNPs. The model was simulated with no penetrance function or heritability, as well as no main or interaction effect loci, such that all loci are noise loci with no disease status association.

Data analysis

Multifactor dimensionality reduction

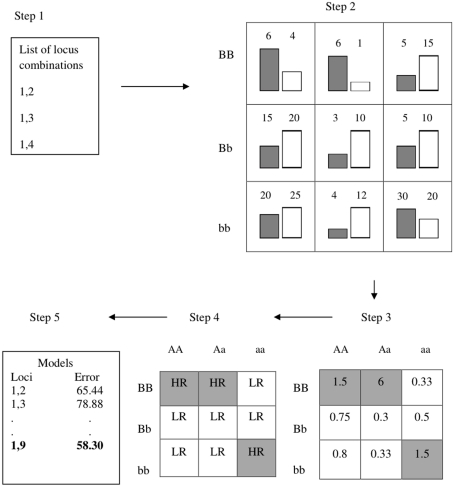
Traditional applications of MDR have previously been described in detail (Ritchie et al., 2001; Hahn et al., 2003), and we implemented MDR similarly, except for our exclusion of cross-validation. Briefly, the MDR algorithm performs an exhaustive search of all possible main effects (for one-locus models) or all two-way interactions (for the two-locus models), and for our filter implementation we saved and ranked all models (as opposed to selecting the top single model as traditionally done). For the one-locus models this yields 100 possible main effects for each replicate within each model and 4,950 two-way models within each replicate for the two-locus interaction models. For each locus within each dataset a contingency table (1 by 3 for one-locus and 3 by 3 for two-way interactions) of all possible genotypes for that locus/locus combination is made and the number of cases and controls within each cell in the table (genotype combination) is counted. The ratio of cases to controls is taken and compared to a threshold, which was set to 1 as is the standard for MDR when using balanced data where there are an equal number of cases and controls (Velez et al., 2007). Each cell was then classified as high-risk if the ratio is greater than 1 and low-risk if less than 1. The classification error for each model is based on the number cases in cells that were classified as low-risk and the number of controls in those that were classified as high-risk. Figure 1 illustrates the MDR method for two-locus combinations. The classification error of each model was used to rank the models, where lower error was given a better rank (with a rank of 1 representing the top model).

Figure 1.

Summary of MDR implementation. Step 1: list of multi-locus combinations is generated. Step 2: number of cases/controls is counted (gray bars are cases, white bars are controls). Step 3: ratio of cases to controls is counted. Step 4: Cells are labeled as high-risk (HR) or low-risk (LR). Step 5: the classification error is calculated.

Logistic regression

For the one-locus main effect models, association analysis using LR was done, as implemented in PLINK version 1.06 (Purcell et al., 2007)¹ Dummy encoding was used for each genotype, such that two terms were entered into the regression model for each SNP, for a more fair comparison to the model free encoding (categorical) of MDR. By default, the genotype that was homozygous for the major allele was used as the reference. Loci were ranked from lowest to highest p-value (taking the lowest p-value from testing the two parameters for the dummy encoding), where lower p-values resulted in higher ranks. For testing the two-locus interaction models, terms for each dummy variable were entered as terms in the model, and terms for the interaction effects of each combination of variables were also entered.

The specific LR model used for the two-locus models is:

$$\begin{array}{rcll}log\left[\text{y}∕1-\text{y}\right]& =\alpha +{\beta }_1{\text{x}}_{\text{1}i}+{\beta }_2{\text{x}}_{\text{1}j}+{\beta }_3{\text{x}}_{\text{2}i}+{\beta }_4{\text{x}}_{\text{2}j}+{\beta }_5{\text{x}}_{\text{1}i}{\text{x}}_{\text{2}i}& & \\ & +{\beta }_6{\text{x}}_{\text{1}i}{\text{x}}_{\text{2}j}+{\beta }_7{\text{x}}_{\text{1}j}{\text{x}}_{\text{2}i}+{\beta }_8{\text{x}}_{\text{1}j}{\text{x}}_{\text{2}j}+\text{e}& & \end{array}$$

where: y = 1 if case; 0 if control.

α = intercept.

β₁ = main effect of SNP 1, dummy variable i.

β₂ = main effect of SNP 1, dummy variable j.

β₃ = main effect of SNP 2, dummy variable i.

β₄ = main effect of SNP 2, dummy variable j.

β_5–8 = interaction effects of the dummy encoded variables of SNPs 1 and 2.

This model was applied to all SNP pairs and the SNP pairs were then ranked based on the most significant p-values. The p-values were from the joint test of the overall LR model. The two-locus LR analysis was implemented in R software package version 2.8.1²

Evaporative cooling

The EC algorithm is motivated by the statistics of the thermodynamic process of cooling a gas through evaporation (Hess, 1986), and was adapted by McKinney et al. (2007) for selection of variants involved in interactions. It is based on a linear combination (coupling) of transformations using Relief-F (Kononenko, 1994), as well as random forests (RF; Breiman, 2001), and it works by integrating and optimizing the importance scores from Relief-F and RF in order to find the most relevant variants to the phenotype.

In brief, it optimizes F = E − TS, where (F) is the free energy which is analogous to relevance of a group of SNPs to the phenotype (in our study this is case/control status). E is determined by statistical interactions (the Relief-F score). Independent/main effects are S (RF score) and the noise variants are T which are also used as a coupling constant. Since EC is designed to find the SNPs with the highest potential for interaction and not the specific interactions themselves, we expected it to give the main effect SNP a high rank in both the one-locus and two-locus datasets. We use EC to analyze the one-locus models as well as the two-locus models to see if the main effect locus (in the one-locus model) or both the main effect locus and the secondary interacting locus (in the two-locus joint main and interaction effect models) would rise to the top in the rankings, as these would have been the SNPs that may have been considered for further tests of interaction in a real study. We expect that the most significant interaction models would contain the main effect SNP especially for the two-locus joint main and interaction effect models, and as such should rank high in the EC results. The software package provided by the McKinney et al. (2009) was used for this analysis.

Genetic association interaction network

Genetic association interaction network (GAIN) calculates the pair-wise interaction information (I), which quantifies interaction gains between the variants and case/control status. It works based on the following model:

$$I_{i,j,y}=I_{i,j,y}-I_{i,y}-I_{j,y}$$

where I_i,j,y = interaction information between SNPs i and j, and the phenotype (case/control) y.

I_ij,y = information gained about y when considering loci i and j jointly.

I_i,y = information gained about y when locus i is measured.

I_j,y = information gained about y when locus j is measured.

We performed a GAIN search for the two-locus datasets to rank all possible two-way interactions and compare the results to the MDR and LR analysis. The GAIN tool software package was used for this analysis (McKinney et al., 2009).

Ranking filter

For each simulated model, MDR, EC, and LR analysis was performed, using the level of interaction (one or two-way interactions) simulated for each model, and the rank was calculated. The average rank of the simulated model was calculated across the 100 replicates of each model. For the single locus model, the possible ranks ranged from 1 (highest) to 100 (lowest). For the two-locus models, the possible ranks range from 1 (highest) to 4,950 (lowest). The average ranks for the non-causal loci were also calculated across each model for comparative purposes, and to get a feeling for the distribution of ranks expected by chance. These experiments were performed to compare how the “signal” raises out of the “noise” for the two methods.

Power analysis for the MDR filter

To evaluate the “power” of the MDR filter, we evaluated the number of times across the 100 replicates that the true, simulated model would pass through a filter using different cut-offs. We evaluated a range of cut-off values based on classification error, from 45% (a very loose filter) to 35% (a more stringent filter). The number of times the classification error score of our disease locus combination, passed through the filter for all 100 replicates was counted and converted to percentage points to estimate power.

False positive rate of the MDR filter

We then estimated the false positive rate of the two-locus epistatic models for the MDR method. To find this rate we calculated the frequency of noise (the non-disease two-locus combinations) passing through the classification error filter. For each replicate within each purely epistatic model the number of non-disease locus combinations that passed through the filter at the six different levels of the filter from 35 (the most stringent) to 45 (a score that could be expected by chance), was counted. The average for each error filter level, within each model was then calculated by averaging over the counts collected from the 100 replicates in that model; these scores were then converted to percentage points.

Large dataset analysis

In order to get a an idea of how well our filter may perform in the presence of thousands of noise SNPs, we ran an EC analysis and a one-way and two-way MDR analysis on a simulated dataset of 50,000 SNPs, with 1,000 cases, and 1,000 controls. The simulated dataset includes four interacting loci with 1 two-locus XOR model with heritability of 2% and 2 one-locus dominant models with heritability of 0.9 and 2%. All models had the minor allele frequencies set at 0.5. The whole four-way penetrance function had heritabilities ranging from 0 to 2% for all the individual two-way interactions contained within it (Table A7 in Appendix). This additional analysis was performed to evaluate how well the results seen in the simulation experiment might extrapolate to larger data, with a GWAS number of SNPs.

Implementation

Multifactor dimensionality reduction was implemented in C++, the two-locus LR was implemented in R, and the EC and GAIN algorithms are both implemented in JAVA. All simulations and analysis were run on quad-core Core2 Xeon processors (8 processors, each at 3 GHz and with 4 GB of memory). A java implementation of MDR software is publicly available through www.epistatis.org and an R implementation is available through http://cran.r-project.org/ (Winham and Motsinger-Reif, 2010). Java implementations of EC and GAIN were used from software provided by (McKinney et al., 2009).

Results were tested for significance using a mixed model analysis of variance approach. The analysis of variance model used checked for effects of allele frequency, analysis method (MDR, EC, or LR), models (effect sizes), and effect of association between allele frequency and analysis method on ranks. Note that the p-values reported from the ANOVA are raw (uncorrected for multiple comparisons) since these tests are meant to help interpret the results and not meant as strict statistical hypotheses.

Results

One-locus (main effect) models

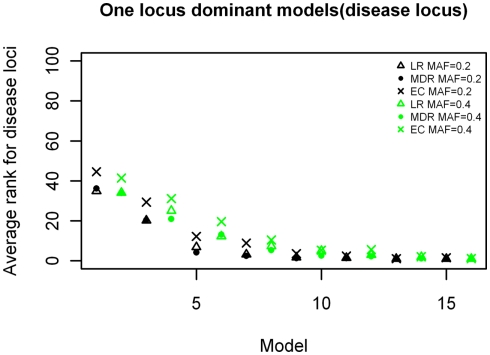
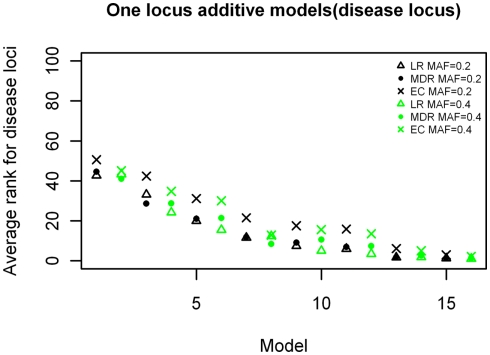
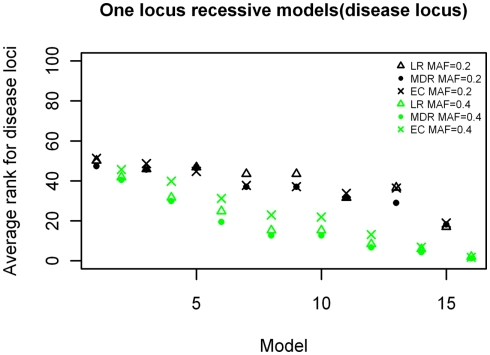
The ranking results for the disease causing SNP in the one-locus models based on the MDR, EC, and LR analyses are shown in Figures 2–4, for the dominant, additive, and recessive models. The ranks are shown for all 16 models (in order of increasing effect size on the x-axis) for all methods, and for both minor allele frequencies models. As expected, the average rank of the causal locus model improves as the effect sizes increase. There was not a significant difference between the average ranks of LR and MDR for the additive, dominant, or recessive models (p = 0.609, p = 0.748, and p = 0.117 respectively). There was also no significant difference between the MDR and EC results for the dominant and recessive models (p = 0.818 and p = 0.062 respectively), however there was a difference in the results for the recessive model (p = 3.83 × 10⁻⁶). Also, though not shown, the average ranking for the noise loci (non-disease causing) ranged between 45 and 55 on a scale of 1–100 for all models (data not shown).

Figure 2.

Ranking of the simulated disease locus for the one-locus dominant main effect model. Δ: LR analysis for models with MAF of 0.2; : LR analysis for models with MAF of 0.4; •: MDR analysis for models with MAF of 0.2; : MDR analysis for models with MAF of 0.4. : EC analysis for models with MAF of 0.2; ×: EC analysis for models with MAF of 0.4. See Table A1 in Appendix for model descriptions.

Figure 4.

Ranking of the simulated disease locus for the one-locus additive main effect model. Δ: LR analysis for models with MAF of 0.2; : LR analysis for models with MAF of 0.4; •: MDR analysis for models with MAF of 0.2; : MDR analysis for models with MAF of 0.4. : EC analysis for models with MAF of 0.2; ×: EC analysis for models with MAF of 0.4. See Table A3 in Appendix for model descriptions.

Figure 3.

Ranking of the simulated disease locus for the one-locus recessive main effect model. Δ: LR analysis for models with MAF of 0.2; : LR analysis for models with MAF of 0.4; •: MDR analysis for models with MAF of 0.2; : MDR analysis for models with MAF of 0.4. : EC analysis for models with MAF of 0.2; ×: EC analysis for models with MAF of 0.4. See Table A2 in Appendix for model descriptions.

EC ranks for interacting loci for two-locus models

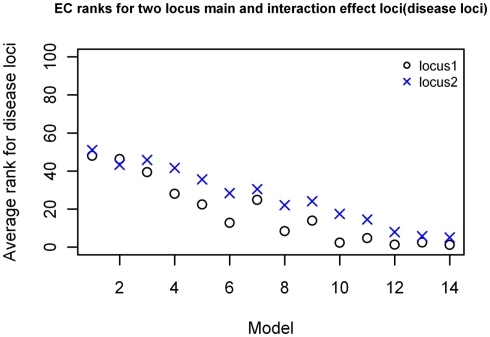
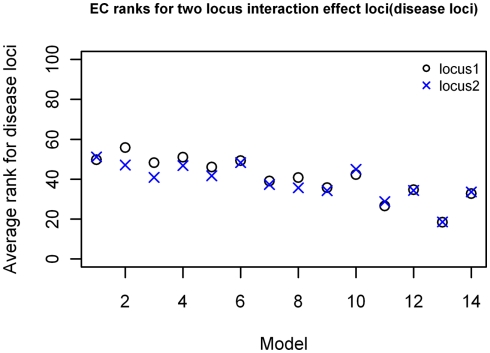
For the two-locus joint main and interaction effect models, the two disease loci were ranked in the top 20% for the models with “odds ratios” greater than 2.0 (Figure 5). The main effect locus was in the top 20 for 57% of the total models while the second locus was in the top 20 for about 28% of the models. For the purely epistatic models, there was only one model in which EC ranked the 2 interacting loci in the top 20%. The ranks were generally between 40 and 50 for most models in this group (Figure 6).

Figure 5.

EC Ranking of the simulated disease locus combination for the two-locus joint main and interaction effect model. ○: Locus 1 (main effect locus); : Locus 2 (secondary interacting locus).

Figure 6.

EC Ranking of the simulated disease locus combination for the two-locus pure interaction effect model. ○: Locus 1 (main effect locus); : Locus 2 (secondary interacting locus).

Two-locus interaction (purely epistatic) models

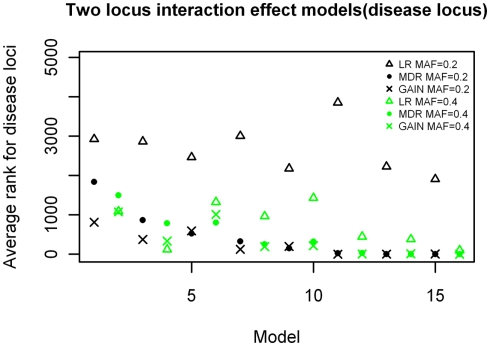
The results of the rankings for the purely epistatic models are shown in Figure 7. Again the models are ranked in order of increasing effect size on the x-axis. For all 16 epistatic models, the non-disease locus combinations had rankings expected by chance, ranging between 2,000 and 3,000 on a scale of 1–4,950 (not shown). These results demonstrate a marked difference between the rankings produced by MDR and LR. MDR had better rankings than LR for most of the models and especially so for the larger effect sizes (p = 3.046 × 10⁻⁸). The comparison between the MDR and GAIN results were better for GAIN when the effect sizes were smaller, but were about the same for both methods when the effect sizes were larger. The analysis of variance showed a significant difference between the two methods (MDR and EC) for this analysis (p = 0.0005). There was also a significant difference between the rankings for the models with minor allele frequencies of 0.2 and those of 0.4 for the LR method (p = 1.267 × 10⁻⁵) but there was no significant difference between effects of allele frequency on ranks for the MDR and GAIN analysis. The results show a strong trend of improving ranks as effect sizes increases for MDR and GAIN, but it is clear that there is little improvement in rank for the LR results. The average rankings for the models with allele frequency of 0.2, for the LR analysis were not better than what could be expected by chance as they had similar rankings as those for the null model.

Figure 7.

Ranking of the simulated disease locus for the two-locus pure interaction effect model. Δ: LR analysis for models with MAF of 0.2; Δ: LR analysis for models with MAF of 0.4; •: MDR analysis for models with MAF of 0.2; •: MDR analysis for models with MAF of 0.4. ×: GAIN analysis for models with MAF of 0.2; : GAIN analysis for models with MAF of 0.4. See Tables A4 and A5 in Appendix for model descriptions.

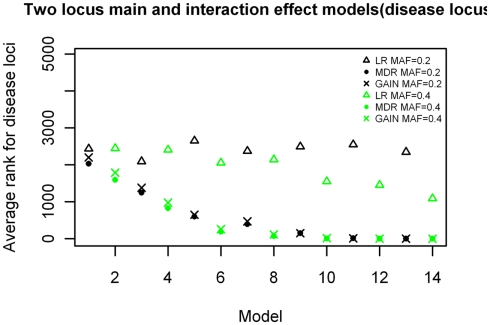
Two-locus main effect and interaction models

The ranking results for the two-locus models with significant main effects are shown in Figure 8, again arranged based on effect size of the models simulated. The results are similar to those shown in Figure 5, with MDR having better rankings than LR (p = 4.916 × 10⁻¹¹), and about the same rankings for the comparison with GAIN. The ranking improves as effect size increases, with the MDR and GAIN results. There was again a significant difference in results with respect to minor allele frequency for the LR results (p = 0.01774) but not the MDR or GAIN results (p = 0.562 and p = 0.51 respectively). For the MDR and GAIN analysis the results show that for all 16 models within this group, the average rankings for locus combinations not including the disease SNPs were spread around the center (ranking between 2,000 and 3,000) as expected, except for those locus combinations that included the main effect SNP or the secondary interaction effect SNP (which had better than average rankings), however, the locus combination with both disease SNPs ranked highest in all models for both MDR and EC (results not shown). The LR analysis ranked the actual disease locus combination has highest only for the models with the larger minor allele frequency of 0.4 and did not rank the other combinations that included either the main effect locus or secondary disease locus any better than the average (Figure 6). Again, the improvement of ranks in the LR analysis for those locus combinations was not much different from the null model.

Figure 8.

Ranking of the simulated disease locus combination for the two-locus main and interaction effect. Model Δ: LR analysis for models with MAF of 0.2; : LR analysis for models with MAF of 0.4; •: MDR analysis for models with MAF of 0.2; : MDR analysis for models with MAF of 0.4. : GAIN analysis for models with MAF of 0.2; ×: GAIN analysis for models with MAF of 0.4. See Table A6 in Appendix for model descriptions.

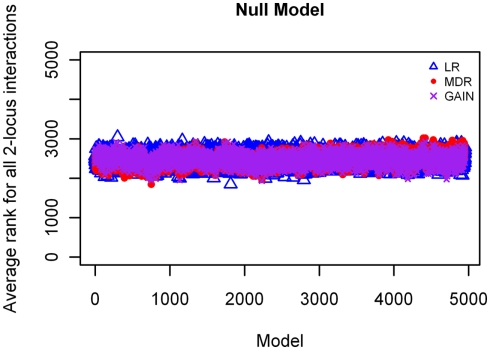
Null model

The results from analyzing the null model using MDR, GAIN, and LR, showed all loci with rankings ranging between 2,000 and 3,000, which is to be expected by chance, and are accurate for this model as no disease loci were simulated for this model (rankings shown in Figure 9).

Figure 9.

Ranking of LR, GAIN and MDR on the null model. : LR analysis; : MDR analysis; : GAIN analysis.

Power analysis of MDR results

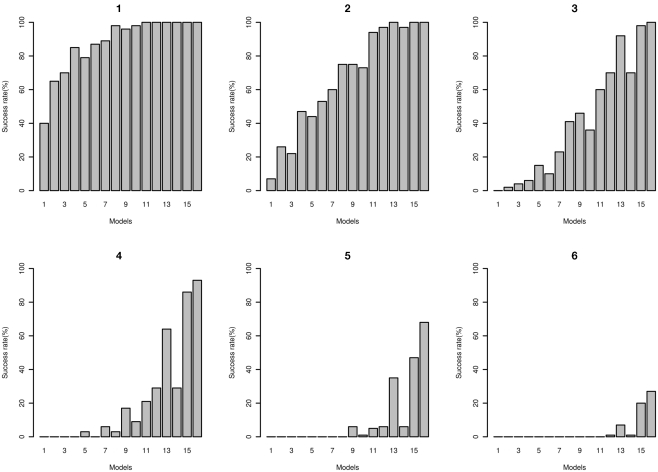
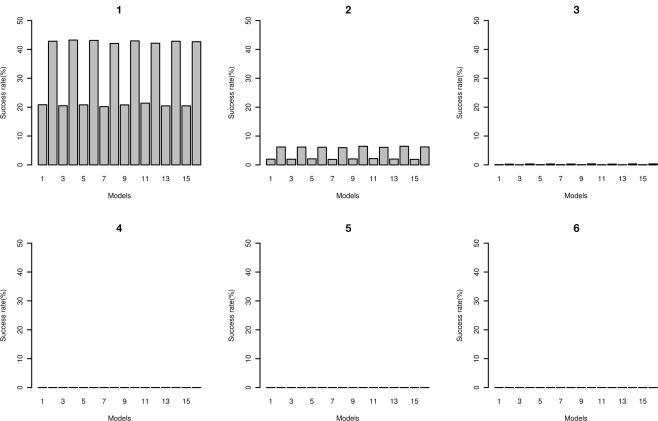
The number of times that the correct disease model passed through the MDR filter with a range of filter cut-offs is shown in Figure 10. As expected, with lower cut-offs the “power” for the model to pass through is higher, and as the cut-off is lower (more stringent), the power is lower. At the more stringent cut-off, only the higher effect size models pass through. The false positive rates are shown in Figure 11; the increased power for the lower cut-off is at the cost of a much higher false positive rate. The disease locus combination for the smallest effect model was only able to pass the threshold of 43 at a 7% rate, however for the same effect size but with MAF of 0.4 it was able to pass the threshold of 41 at a rate of 2%. For the largest effect model, even at the most stringent classification error threshold of 35, the disease locus combination was able to pass through the filter at a rate of 27% while no false positive could pass below the threshold of 39, with the rate for that threshold being 0.006%.

Figure 10.

Power of MDR for detecting correct disease loci. Plots: 1, 2, 3, 4, 5, and 6 show power of detecting true interacting loci using filter based on classification error rates of 45, 43, 41, 39, 37, and 35 respectively for two-locus interaction effects only models 1 through 16 (see Tables A4 and A5 in Appendix).

Figure 11.

False positive rate of MDR as filter. Plots: 1, 2, 3, 4, 5, and 6 show rates in percentages of false positives based on classification error rates of 45, 43, 41, 39, 37, 35 respectively for two-locus interaction effects only models 1 through 16 (see Tables A4 and A5 in Appendix).

Large dataset results

For both the one-way MDR and EC analysis the four simulated interacting disease SNPs were the highest ranked variants, with both methods ranking them in the top 5 (MDR having them as the best one-locus models and EC as the SNPs most enriched for interactions). The two-way analysis of MDR showed the highest ranked interaction to be the interaction between the two-locus XOR model we had simulated into the data, and among the top interactions were locus combinations including one of those two SNPs. The two-locus exhaustive search done by MDR yielded interactions involving the same SNPs that were ranked as having the highest potential for interactions (in the top results) as the iterative search of EC. When looking at the overall results, MDR also ranked the interactions in which at least one of the disease SNPs was involved higher than other interactions. As EC results are a set of SNPs that have the most potential for interactions with each other, and not the specific interactions themselves, a GAIN analysis or perhaps a further MDR analysis of that result set would be needed to find those interactions, but due to computational resources and time constraints, this was not included in this analysis. The results here show that even in the presence of noise both MDR and EC should be able to find the SNPs with the most potential for interactions in real data, with MDR being able to further elucidate what the specific interactions may be.

Discussion

It is now widely accepted that multiple genes may be responsible for many complex diseases and as such in the study of such diseases, emphasis is now been placed on finding these interactions. However, with the large amounts of data collected for these studies, there are still few methods available to study all possible interactions (Ritchie et al., 2001; Hahn et al., 2003; Hu et al., 2010; Steffens et al., 2010; Wan et al., 2010) between these variants on a GWAS scale. Another obstacle may be the computational time required for these methods to process all these interactions, although BOOST (Wan et al., 2010) seems to do this in a reasonable amount of time and with hardware requirements available to most researchers. The issue here however is how are the results from these preliminary analysis prioritized for replication and biological and functional validation. As such, just being able to analyze all possible interactions may not be enough, and methods also have to ensure that the most significant interactions, rise to the top, making filtering an important step for more success with GWAS results replication, and useful health outcomes. We simulated datasets of SNPs for both main effect and epistatic effect models, with varying effect sizes and allele frequencies, with the goal of analyzing the data and ranking the outcomes, using MDR, EC, and LR separately. As stated earlier there are several methods that have been put forward as filters for GWAS (Moore et al., 2002; Hoh and Ott, 2003; Moore and Ritchie, 2004; Wang et al., 2006; Culverhouse, 2007; Calle et al., 2008; Saccone et al., 2008). Our study compares ranking methods based on significance scores (LR, EC) and classification errors (MDR) derived from the SNPs and combinations of SNPs within our data without adding any extra information.

The analysis of the one-locus main effect datasets for the three different inheritance models show that the three methods have comparable performance in detecting the disease locus for the dominant and additive models. The ranking results for both types of data follow a similar pattern with the ranks improving as the effect sizes increased regardless of the minor allele frequency. The recessive model showed an almost identical pattern with the exception that there were separate curves according to minor allele frequencies, with those having MAF of 0.4 having better ranks than those with 0.2 for the same effect sizes and this followed for all three methods (note here that the minor allele is our disease causing allele). This disparity of the recessive model as compared with the other two models may be due to the nature of the recessive model itself; since the disease locus is homozygous for the minor allele and as such the smaller minor allele frequency (0.2), produces a smaller genotype frequency for the disease genotype thereby creating fewer cases of this genotype to select from for these datasets than for the datasets with the larger minor allele frequency (0.4). The analysis here mainly showed that for main effect models, MDR, EC, and LR worked comparably well with similar results using our ranking system.

The two-locus purely epistatic models show a significant difference between the ranks estimated by MDR and EC from that of LR. The results showed that when the minor allele frequency was small (0.2), LR was unable to rank the interacting disease loci better than it would by chance, even as the effect sizes increased, but for the datasets with MAF of 0.4, LR rankings were better than would be expected by chance, and ranging between 4,950 and 1. In contrast the rankings from MDR and EC were always better than what could be expected by chance regardless of allele frequency and there was consistent improvement in ranking as the effect sizes increased. These results show that for higher-order interactions LR may fail to find the disease locus. This supports findings from other studies showing that sparse contingency table cells can result in biased coefficient estimates and large SE estimates with LR analysis (Concato et al., 1993; Peduzzi et al., 1996; Hosmer and Lemeshow, 2000) The MDR and GAIN comparisons however, were about the same when finding the disease loci and even when finding other loci that are associated with either of the disease loci. Although GAIN may be used to exhaustively find all possible two-way interactions (which is how our two-way interaction analysis was done), it has been used by others (McKinney et al., 2009) as a second step after selection of SNPs by some other method such as EC and is designed for finding interactions and not for selection of SNPs enriched for interactions. The results of using it after filtering with EC will depend greatly on how well EC selected the SNPs most enriched for interactions.

The models with main and interaction effects show that MDR and GAIN were able to find both loci at both minor allele frequencies. Again, LR was unable to give a ranking that would have been better than chance for the lower allele frequency. Another important observation here was that MDR and GAIN also ranked all loci interacting with the secondary locus much higher than those that were not and further still, it ranked loci interacting with the main effect locus even higher. The EC ranks of the two separate interacting loci showed that their average rank was in the top half of all SNPs and the ranks got better and were among the top 20 as the effect sizes became larger.

It has been shown in a previous study using LR to analyze genome wide data using different strategies (Marchini et al., 2005) that searches that allowed for interactions are generally more powerful than single locus searches alone for genome wide datasets even after accounting for multiple testing. It was also shown that the information gathered from multiple loci simultaneously is greater than that from single locus analysis. This is important in the context of the current study, since based on the increased performance of MDR in ranking correct signals and on previous study results, MDR has a better performance than LR, such that if a more formal hypothesis testing approach was used instead of just a ranking approach, it is expected that MDR would have improved performance compared to LR.

Our power analysis of the MDR results reveal that even at stringent thresholds of classification error, the rate of false positives passing the filter was relatively low, with 0.001% false positive rate at a threshold of 39 for the model with the smallest effect size (MAF = 0.2, “odds ratio” = 1.2, h² = 1%) and a rate of 0.005 at the same threshold for the model with the largest effect size (MAF = 0.4, “odds ratio” = 3.0, h² = 5%). Within this same threshold, the disease loci also passed through the filter at a rate of 93% for the model with the largest effect size and at a rate of 0% for the model with the smallest effect size. It is important to note here that even with this low rate, the disease loci combination was still ranked highest in this model, as the rank is based on the average classification error for each locus combination, not on single occurrences. At the most stringent threshold of 35 in our filter, the disease loci combination passed through the filter at a rate of 27% for the largest effect size model with no false positive passing through, while for the smallest effect size model, no locus combination passed through the threshold.

The findings from these simulations suggest that MDR, EC, and LR perform favorably in detecting main effects, but MDR and GAIN perform better than LR in detecting epistatic effects especially when the effect sizes are small. Even though we performed our MDR analysis without cross-validation our analysis still produced powerful results, supporting other studies that have used MDR without cross validation (Mei et al., 2005). Our method is non-parametric as no models are implied, and can be used to rank any number of interactions computationally feasible; it is also clear from our results that MDR has an advantage over LR in finding very small effects. As it is now being suggested that combinations of these tiny effects may be very important in manifesting the disease phenotype, methods such as MDR may assist in giving more clues as to the pathophysiology of these diseases, which could become important factors in designing drug targets for their treatment.

Overall the results of the current study demonstrate the potential of the use of the MDR method as a filter in large-scale genetic association studies. The study demonstrates that as a ranking procedure, the “signal” emerges from the noise for even very small effect sizes, and this signal emerges more readily using MDR modeling compared to LR modeling. Additionally, it demonstrates the ability of MDR to detect both purely epistatic models, as well as models with main effects. This is in contrast to the filter approaches that have previously been proposed (Hoh et al., 2001; Evans et al., 2006), that make assumptions about the etiology of the interaction in their model search.

It is important to note here that while our analysis showed MDR to be a successful filter, the SNPs analyzed were all independent of each other as LD was not included as a factor in the simulations, however the effects of LD on MDR have been investigated (Grady et al., 2011), and they found that loci not in direct association with the disease SNP, but in LD with it, may be good predictors of disease risk and can help in singling out actual risk alleles, but there is also the danger of those indirect associations coming up as the best models. This is similar to the results we obtained for the two-locus joint main and interaction effect models where loci in association with the main effect locus are ranked higher than those not in association. This allows us to believe that the locus combinations that rank high in our filter may also be used as predictors of disease risk alleles, if there is some correlation between them. Related to this, it would also be important in future studies to evaluate the impact of current imputation methods (based on LD patterns and reference genomes) on the performance of MDR and other machine learning methods on the performance of the filter.

Additionally, the models themselves were not tested for significance; although the results of our joint main and interaction effect models suggest that the correct model may still rise to the top. All p-values shown are raw p-values and were not corrected for multiple testing and as such are intended mostly for interpretation. There was not a rigorous method to threshold selection in our filter, but care was taken to use threshold intervals that allowed for a range of liberal inclusion of false positives to more stringent threshold.

Another consideration here is that although this analysis is intended for genome wide association data our simulations were not done on a GWAS scale. Although our large dataset consisted of 50,000 SNPs it cannot be considered genome wide. This part of the analysis was done primarily to show that even in the presence of noise, MDR is capable of finding the best candidates for interaction, and can act as a filter. We also expect that it should be able to do so with data on a genome wide scale. While the exhaustive search approach is ideal for detecting purely epistatic effects, the most immediate limitation of this approach for GWAS is the computation time required for higher-order interactions. Currently, two-way interaction searches are feasible for GWAS scale data (Greene et al., 2010) and improving the computation time for the approach is an active area of research for MDR, hopefully making searches for higher-order interactions feasible in large studies.

In thinking toward this goal, it is important to remember that model over fitting could become a concern. Computational limitations limit concerns with over fitting with the current filtering approach, but it must be remembered that classification error will always decrease as the order of interaction increases (Motsinger and Ritchie, 2006), and in the traditional application of MDR, internal model validation is used to control over fitting. By removing the cross-validation step for this filter, this characteristic of classification error as a metric must be kept in mind. Using this filter approach for discovery only, within a study design that includes a validation set would be important to limit false positives. If models are over fit, false positive loci should be removed in the validation stage of the study.

While this study has shown MDR’s utility as a filter, this is still a preliminary analysis, and is only the beginning stage of applying MDR as a filter approach, there is still more that can be done to improve its utility as a filter for GWAS studies. Future directions aim to address issues that were not addressed in this study, which include the incorporation of significance testing for the models before ranking is performed. The current study simulated various effect sizes and various classification thresholds were tested. An analysis of a more rigorous approach to better determine classification error thresholds for more reasonable effect sizes that may be encountered in real data also needs to be done. While this method filters models based on ranks, it has not been tested for optimization of power to detect associations for a two-stage analysis in which case the selected models from the first stage (one partition of all data) are further tested on another partition of the data, as has been done with other two-stage or two-phase joint analysis methods for main effects (Satagopan and Elston, 2003; Satagopan et al., 2004; Wang et al., 2006; Zuo et al., 2006; Skol et al., 2007; Yu et al., 2007; Kwak et al., 2009; Pan et al., 2011). Also as mentioned earlier, it may be important to include prior biological information as part of an overall filter strategy, as it would be expected that results from such analysis should prove to be true biologically. However there is currently no consensus on if inclusion of some of these pathways as factors in analysis actually improves the chances of finding true associations, and there has been at least one study (Moskvina et al., 2011) showing evidence of genetic interaction among products with seemingly unrelated function. The same study also shows that such a filter also suffers from the same problems of previous methodologies, such as high false positive associations. It is thought that these inflated false positive rates may be due to incomplete pathways, or a lack of true understanding of how these pathways or other genomic interactions work.

In thinking about the application of such a filter approach in real data, there are a couple of important points to consider. First, while in the simulations studies performed we knew the correct number of SNPs to be found (whether the real disease model was due to single locus effects or interactions), of course in real data this is unknown. Hopefully the results of the current study encourage testing for both single locus and interaction models. As computational capabilities advance, higher-order interactions may be computationally feasible as well. Second, in real data, when a two-locus model is found by MDR (ranked very highly), to really understand how these loci confer risk, post hoc analysis should be considered to better understand the model. A high rank of two loci could be because of two strong main effects, or by interactive effects. A high rank alone does not necessarily indicate an interaction effect, and the development of methods to help dissect the underlying etiology of complex genetic models is an active research area.

While we have done a comparison with one of the other prevailing filtering approaches, this method may still need to be compared with other filter approaches designed for the analysis of epistatic interactions without main effects (Kooperberg, 2008; Hu et al., 2010) to further evaluate its strengths, weaknesses, and to make it more efficient.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Appendix

Table A1.

Penetrance functions for one-locus dominant main effect models.

One-locus dominance models
OR	Models (#)	MAF = 0.2			Models (#)	MAF = 0.4
		AA	Aa	Aa	AA	Aa	Aa
1.2	(1) h2 = 1.05%	0.0155	0.0155	0.012916	(2) h2 = 1.07%	0.0155	0.0155	0.012916
1.4	(3) h2 = 1.01%	0.0159	0.0159	0.011349	(4) h2 = 1.07%	0.0155	0.0155	0.01108
1.6	(5) h2 = 1.04%	0.017	0.017	0.010625	(6) h2 = 1.1%	0.016	0.016	0.009999
1.8	(7) h2 = 1.02%	0.017	0.017	0.009444	(8) h2 = 1.09%	0.016	0.016	0.008879
2.0	(9) h2 = 1.013%	0.017	0.017	0.0085	(10) h2 = 1.03%	0.015	0.015	0.0075
2.0	(11) h2 = 5.00%	0.083	0.083	0.041489	(12) h2 = 5.007%	0.072	0.072	0.035989
2.5	(13) h2 = 5.03%	0.0833	0.0833	0.03332	(14) h2 = 5.066%	0.072	0.072	0.0288
3.0	(15) h2 = 5.07%	0.08233	0.08233	0.02744	(16) h2 = 5.07%	0.071	0.071	0.02366

(#), Model numbers; OR, odds ratio; MAF, minor allele frequency; h², heritability; values in the center of the table represent the probability of disease given the genotype.

Table A2.

Penetrance functions for one-locus recessive main effect models.

One-locus recessive models
OR	Models (#)	MAF = 0.2			Models (#)	MAF = 0.4
		AA	Aa	Aa	AA	Aa	Aa
1.2	(1) h2 = 1.06%	0.016766	0.01396	0.01396	(2) h2 = 1.09%	0.016766	0.01396	0.01396
1.4	(3) h2 = 1.088%	0.019766	0.014118	0.014118	(4) h2 = 1.077%	0.018366	0.013118	0.013118
1.6	(5) h2 = 1.027%	0.020966	0.0131	0.0131	(6) h2 = 1.05%	0.019366	0.0121	0.0121
1.8	(7) h2 = 1.028%	0.023126	0.012847	0.012847	(8) h2 = 1.08%	0.021126	0.01173	0.01173
2.0	(9) h2 = 1.068%	0.02607	0.013031	0.013031	(10) h2 = 1.077%	0.0218	0.010891	0.010891
2.0	(11) h2 = 5.006%	0.120806	0.06029	0.06029	(12) h2 = 5.03%	0.100806	0.05029	0.05029
2.5	(13) h2 = 5.002%	0.140558	0.05622	0.05622	(14) h2 = 5.003%	0.105106	0.04204	0.04204
3.0	(15) h2 = 5.08%	0.015791	0.052618	0.052618	(16) h2 = 5.038%	0.106906	0.035595	0.035595

(#), Model numbers; OR, odds ratio; MAF, minor allele frequency; h², heritability; values in the center of the table represent the probability of disease given the genotype.

Table A3.

Penetrance functions for one-locus additive main effect models.

One-locus additive models
OR	Models (#)	MAF = 0.2			Models (#)	MAF = 0.4
		AA	Aa	Aa	AA	Aa	Aa
1.2	(1) h2 = 1.02%	0.01559	0.01429	0.012991	(2) h2 = 1.02%	0.015	0.01375	0.0125
1.4	(3) h2 = 1.1%	0.019008	0.016254	0.0135	(4) h2 = 1.2%	0.019008	0.016254	0.0135
1.6	(5) h2 = 1.004%	0.018501	0.015031	0.01156	(6) h2 = 1.08%	0.018001	0.014626	0.01125
1.8	(7) h2 = 1.06%	0.020995	0.016329	0.011663	(8) h2 = 1.05%	0.018031	0.014024	0.010016
2.0	(9) h2 = 1.028%	0.020995	0.015746	0.010496	(10) h2 = 1.02%	0.018005	0.013503	0.009002
2.0	(11) h2 = 5.1%	0.104091	0.078059	0.052027	(12) h2 = 5.02%	0.087	0.06525	0.0435
2.5	(13) h2 = 5.01%	0.11091	0.077637	0.044364	(14) h2 = 5.03%	0.09051	0.06335	0.036199
3.0	(15) h2 = 5.02%	0.116091	0.077391	0.03869	(16) h2 = 5.03%	0.092	0.061333	0.030667

(#), Model numbers; OR, odds ratio; MAF, minor allele frequency; h², heritability; values in the center of the table represent the probability of disease given the genotype.

Table A4.

Penetrance functions for two-locus interaction (epistatic) effect models with minor allele frequency of 0.2.

Interaction effect models (MAF = 0.2)
Model (#)	AABB	AaBB	aaBB	AABb	AaBb	aaBb	AAbb	Aabb	Aabb
(1) OR = 1.2, h2 = 1.02%	0.795	0.043	0.241	0.357	0.194	0.193	0.082	0.21	0.2
(3) OR = 1.43, h2 = 1.09%	0.029	0.324	0.151	0.001	0.255	0.187	0.31	0.165	0.21
(5) OR = 1.61, h2 = 1.1%	0.202	0.148	0.227	0.075	0.133	0.246	0.265	0.24	0.178
(7) OR = 1.82, h2 = 1.1%	0.519	0.926	0.995	0.945	0.936	0.966	0.986	0.963	0.946
(9) OR = 2.0, h2 = 1.12%	0.043	0.088	0.11	0.059	0.166	0.068	0.125	0.069	0.117
(11) OR = 2.03, h2 = 5.05%	0.706	0.533	0.003	0.535	0.063	0.247	0.002	0.246	0.191
(13) OR = 2.5, h2 = 5.13%	0.202	0.218	0.339	0.032	0.112	0.403	0.43	0.392	0.236
(15) OR = 3.02, h2 = 5.1%	0.438	0.223	0.176	0.389	0.368	0.105	0.092	0.115	0.252

(#), Model numbers; OR, odds ratio; MAF, minor allele frequency; h², heritability; values in the center of the table represent the probability of disease given the genotype.

Table A5.

Penetrance functions for two-locus interaction (epistatic) effect models with minor allele frequency of 0.4.

Interaction effect models (MAF = 0.4)
Model (#)	AABB	AaBB	aaBB	AABb	AaBb	aaBb	AAbb	Aabb	aabb
(2) OR = 1.24, h2 = 1.0%	0.166	0.407	0.498	0.454	0.402	0.371	0.436	0.394	0.396
(4) OR = 1.448, h2 = 1.07%	0.255	0.081	0.054	0.083	0.104	0.102	0.052	0.099	0.117
(6) OR = 1.62, h2 = 1.14%	0.087	0.176	0.267	0.276	0.172	0.193	0.139	0.234	0.168
(8) OR = 1.81, h2 = 1.1%	0.062	0.115	0.091	0.15	0.102	0.065	0.045	0.081	0.145
(10) OR = 2.0, h2 = 1.17%	0.022	0.146	0.072	0.07	0.11	0.099	0.172	0.061	0.114
(12) OR = 2.0, h2 = 5.04%	0.678	0.281	0.098	0.129	0.254	0.38	0.307	0.309	0.227
(14) OR = 2.5, h2 = 5.04%	0.202	0.189	0.479	0.188	0.391	0.212	0.481	0.213	0.322
(16) OR = 3.05, h2 = 5.03%	0.34	0.106	0.267	0.236	0.142	0.27	0.101	0.324	0.084

(#), Model numbers; OR, odds ratio; MAF, minor allele frequency; h², heritability; values in the center of the table represent the probability of disease given the genotype.

Table A6.

Penetrance functions for two-locus interaction (epistatic) and main effect models.

Interaction and main effect models
OR	Models (#)	AABB	AaBB	aaBB	AABb	AaBb	aaBb	AAbb	Aabb	aabb
1.2	(1) h2 = 1.02%	0.37	0.37	0.3074	0.37	0.37	0.3074	0.37	0.3074	0.3074
	(2) h2* = 1.02%
1.4	(3) h2 = 1.99%	0.37	0.37	0.2636	0.37	0.37	0.2636	0.37	0.2636	0.2636
	(4) h2* = 3.3%
1.6	(5) h2 = 1.3%	0.37	0.37	0.2309	0.37	0.37	0.2309	0.37	0.2309	0.2309
	(6) h2* = 2.3%
1.8	(7) h2 = 1.99%	0.37	0.37	0.2055	0.37	0.37	0.2055	0.37	0.2055	0.2055
	(8) h2* = 3.3%
2.0	(9) h2 = 2.68%	0.37	0.37	0.1846	0.37	0.37	0.1846	0.37	0.1846	0.1846
	(10) h2* = 4.3%
2.5	(11) h2 = 4.3%	0.37	0.37	0.1479	0.37	0.37	0.1479	0.37	0.1479	0.1479
	(12) h2* = 6.5%
3.0	(13) h2 = 5.9%	0.37	0.37	0.1229	0.37	0.37	0.1229	0.37	0.1229	0.1229
	(14) h2* = 8.4%

(#), Model numbers; OR, odds ratio; h², heritability scores for datasets with minor allele frequency of 0.2; h²*, heritability scores for datasets with minor allele frequency of 0.4; values in the center of the table represent the probability of disease given the genotype.

Table A7.

Four-way penetrance function for large dataset.

		CC				Cc		cc
		BB	Bb	bb	BB	Bb	bb	BB	Bb	bb
	AA	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003
DD	Aa	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003
	aa	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003
	AA	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003
Dd	Aa	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003
	aa	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003
		(1)			(2)				(3)
	AA	0.055	0.055	0.055	0.095	0.095	0.095	0.01	0.0634	0.01
dd	Aa	0.055	0.055	0.055	0.095	0.095	0.095	0.0634	0.01	0.0634
	aa	0.01	0.01	0.01	0.0095	0.0095	0.0095	0.01	0.0634	0.01

MAF = 0.5; (1) h² = 0.9%; (2) h² = 2.0%; (3) h² = 2.0%.

Total h² = 5.0%.

(#), Embedded penetrance functions for the 2 one-locus and the XOR two-locus models respectively are shaded in gray; h², heritability scores; MAF, minor allele frequency; values in the center of the table represent the probability of disease given the genotype.