Abstract
Identifying the genetic basis of human adaptation has remained a central focal point of modern population genetics. One major area of interest has been the use of polymorphism data to detect so-called “footprints” of selective sweeps – patterns produced as a beneficial mutation arises and rapidly fixes in the population. Based on numerous simulation studies and power analyses, the necessary sample size for achieving appreciable power has been shown to vary from a few individuals to a few dozen, depending on the test statistic. And yet, the sequencing of multiple copies of a single region, or of multiple genomes as is now often the case, incurs considerable cost. Enard et al. (2010) have recently proposed a method to identify patterns of selective sweeps using a single genome – and apply this approach to human and non-human primates (chimpanzee, orangutan, and macaque). They employ essentially a modification of the Hudson, Kreitman, and Aguade test – using heterozygous single nucleotide polymorphisms from single individuals, and divergence data from two closely related species (human–chimpanzee, human–orangutan, and human–macaque). Given the potential importance of this finding, we here investigate the properties of this statistic. We demonstrate through simulation that this approach is neither robust to demography nor background selection; nor is it robust to variable recombination rates.
Keywords: selective sweeps, demography, adaptation, statistical inference
Introduction
When a new beneficial mutation increases in frequency and fixes in the population, linked neutral and nearly neutral mutations will similarly increase in frequency on the selected haplotype (Smith and Haigh, 1974). This results in a number of well-described patterns – including a reduction in local variation, a skewed site frequency spectrum, and spatially elevated levels of linkage disequilibrium (see review of Nielsen, 2005). This phenomenon is known as a selective sweep. Many methods have been proposed utilizing these patterns to detect beneficial fixations, using both polymorphism and divergence data in a variety of statistical frameworks. One of the biggest problems confronting all such methodologies is the challenge of distinguishing these patterns from those produced under neutral non-equilibrium conditions (e.g., population size change and population structure) – a problem that different approaches grapple with to varying degrees of success (see review of Thornton et al., 2007). And yet, despite these differences between approaches – one commonality of polymorphism based test statistics is indeed the need for polymorphism data from multiple sequenced individuals.
Thus, owing to the inherent difficulty and cost of generating data appropriate for existing methods of statistical inference, the recent claims of Enard et al. (2010) have attracted considerable attention. Using a whole-genome shotgun sequence of a single human, they argue that they have sufficient power to identify swept regions of the genome. Extending this analysis to chimpanzee, orangutan, and macaque, they focus upon “sweep hotspots” shared among apes, and argue for the long-term adaptive significance of these genomic regions.
The authors use a method inspired by the Hudson, Kreitman, and Aguade (HKA) test (Hudson et al., 1987). This statistic employs intra-specific polymorphism data and inter-specific divergence data to test for deviations from the Standard Neutral model. Enard et al. (2010) derive their polymorphism data from a single heterozygous individual, and the divergence information from comparison with a single chimp, orangutan, or macaque genome. This approach is termed “K–estimation,” where the corrected level of heterozygosity is indicated by the value of a statistic K (0 ≤ K ≤ 1).
They assess two single human individuals, the Venter and Watson genomes. They use a co-occurrence test to find the difference between the expected and observed values for the K-statistic among orthologous genes. Numerous other recent studies have sought to identify and describe genome-wide positive selection in humans using various aspects of polymorphism and divergence data (e.g., Sabeti et al., 2006, 2007; Voight et al., 2006; Williamson et al., 2007) – mostly using single nucleotide polymorphisms (SNP) data from HapMap (Frazer et al., 2007) or Perlegen (Hinds et al., 2005). Enard et al. (2010) find essentially no overlap with the candidate gene sets generated using these other methodologies. Enard et al. (2010) perform forward-time population simulations to validate their method using fregene. However, they only consider two models – an equilibrium model and a single bottleneck model. Here we further evaluate their method and assertions using simulations under several models of positive and negative selection, variable recombination and mutation, and a variety of non-equilibrium models.
A possible complication with the K-statistic is its ability to differentiate between patterns produced by a selective sweep, relative to other neutral processes. Given the essence of the statistical design, significant regions will be those that have reduced heterozygosity relative to flanking genomic sequence. Thus, we investigate whether this approach is robust to: (1) non-equilibrium demographic models, which may greatly increase the variance in heterozygosity across the genome, (2) varying levels of selective constraint across the genome, and (3) simple variation in recombination rate.
Materials and Methods
Simulations
All simulations were performed using the program SFS_CODE (Hernandez, 2008). This is a generalized Wright–Fisher forward population genetic simulation for finite-site mutation models with selection, recombination, and demography. The program and documentation are available for download at: http://sfscode.sourceforge.net/SFS_CODE/SFS_CODE_home/SFS_CODE_home.html
The parameters used are human specific and rescaled for computational efficiency. The mutation rate (μ) is 2.35*10−8 per site per generation, considering human–chimp divergence to be ~1.13%, divergence time is ~6 mya, and a generation time of 25 years (Gutenkunst et al., 2009). For expediency, the effective population size, Ne, is 500. To account for the estimated Ne = 10,000 for humans, a rescaling factor of 20 was used. Thus, θ = 0.00094 for all simulations. Similarly, the scaled recombination rate 4Nr = ρ = 0.00074 (Nielsen et al., 2005). The selection coefficient, s, is evaluated at 0.1, 0.01, and 0.001. All simulations were conducted both in the presence and absence of recombination. Additionally, models of recurrent positive and negative selection were modeled with a fraction 0.01, 0.001, and 0.0001 of sites under selection.
Population bottlenecks are modeled in the following way: a population of constant size N is reduced to size Nb at time tb (in units of 4N generations) in the past and then exponentially increases back to size N. Population bottlenecks are simulated for various times since the reduction (tb = 0.1, 0.54, and 1, in 4N generations), and severities (0.02, 0.1, and 0.722).
Enard et al. (2010) chose the size of test region (L) depending on the level of heterozygosity across the genome, and thus it varies by species. We simulate a test region of 100 kb with adjacent 2000 kb genomic flanking regions. For this test region, a ratio rl is calculated, which is the ratio of polymorphism to divergence for the L region. A similar ratio rg is calculated for the adjacent genomic region (G) and then a final ratio Robs of rl/rg. If Robs is less than 1, then there is said to be a local reduction in heterozygosity. Similarly, a ratio R is computed for 5,000 additional windows of size q, that are randomly sampled within G, but at a distance at least five times q from L. The Robs for test region is ranked among the R values for the adjacent regions. K is the proportion of random windows with R lower than Robs.
K values < 0.05 are statistically significant, and thus reject the model (i.e., are consistent with positive selection). Simulations under models of positive selection were performed in order to characterize the true positive rate; while a variety of simulations under alternative models characterize the false positive rate. These two measures thus describe the performance of the K-statistic.
Results
The standard neutral model, with variable rates of recombination
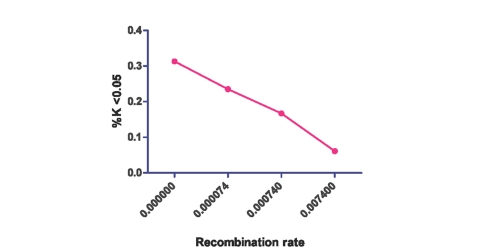
To account for the effect of recombination rate on patterns of selective sweeps, we simulated with and without recombination. Under the equilibrium neutral model (for θ = 0.00094), the false positive rate is 0.167 (ρ = 0.00074) and 0.313 (ρ = 0), with and without recombination respectively (Table 1). The performance under this Standard Neutral model (where the standard false positive rate may be expected to be 0.05), should be taken as the baseline performance of this statistic. Considering the known genomic variation in recombination rate (Broman et al., 1998; Lenzi et al., 2005), this result suggests a strong bias toward false positive signatures being detected in low recombination rate regions (Figure 1).
Table 1.
K value for region containing varying recombination rates (θ = 0.00094).
| Recombination rate | %K < 0.05 |
|---|---|
| 0 | 0.313 |
| 0.000074 | 0.235 |
| 0.00074 | 0.167 |
| 0.0074 | 0.061 |
Figure 1.
K value for region containing varying recombination rates (θ = 0.00094).
Non-equilibrium neutral models, the effect of population size change
A tremendous amount of literature has focused upon the ability of test statistics to distinguish between patterns produced under selective vs. demographic models – and distinguishing these models has often proven difficult (see review of Kelley et al., 2006; Thornton et al., 2007). Here, we examine the performance of the K-statistic under a variety of bottleneck models of varying timing and severity – models of the sort that are commonly estimated for non-African human populations (e.g., Gutenkunst et al., 2009).
For population bottlenecks the false positive rate ranges from 0.12 to 0.153 in presence of recombination and 0.311–0.344 in absence of recombination (Table 2). While there are some common trends – such as the duration of the bottleneck (i.e., the extent of diversity reduction) correlating with an increased false positive rate – it is significant to note that performance is not much worse (relatively) than under the Standard Neutral model itself. Thus, the inherent low power and high false positive rate under simple models of variable recombination rates appears to remain the primary factor.
Table 2.
K value for population bottleneck duration (θ = 0.00094).
| Bottleneck duration (4N gen) | Bottleneck severity | %K < 0.05 (ρ = 0.00074) | %K < 0.05 (ρ = 0) |
|---|---|---|---|
| 0.1 | 0.02 | 0.119 | 0.319 |
| 0.1 | 0.133 | 0.33 | |
| 0.722 | 0.146 | 0.344 | |
| 0.48 | 0.02 | 0.144 | 0.34 |
| 0.1 | 0.135 | 0.311 | |
| 0.722 | 0.136 | 0.339 | |
| 1 | 0.02 | 0.153 | 0.336 |
| 0.1 | 0.132 | 0.313 | |
| 0.722 | 0.12 | 0.328 |
Models of positive and negative selection
When the target region is evolving under purifying selection, the false positive rate ranges from 0.117 to 0.143 in presence of recombination, and 0.313–0.344 in the absence of recombination (Table 3). As with the demographic models – the primary factor again appears to be the inherent poor performance in the presence of variable recombination rates. However, because this is also a diversity-reducing model, the addition of constrained sites results in an elevated false positive rate – with the effect similarly being more pronounced in regions of low recombination (Begun and Aquadro, 1992).
Table 3.
K values for region under negative selection (θ = 0.00094).
| Selection coefficient | Proportion of sites under negative selection | %K < 0.05 (ρ = 0.00074) | %K < 0.05 (ρ = 0) |
|---|---|---|---|
| 0.1 | 0.0001 | 0.129 | 0.322 |
| 0.001 | 0.117 | 0.324 | |
| 0.01 | 0.136 | 0.334 | |
| 0.01 | 0.0001 | 0.126 | 0.313 |
| 0.001 | 0.119 | 0.313 | |
| 0.01 | 0.143 | 0.344 | |
| 0.001 | 0.0001 | 0.127 | 0.334 |
| 0.001 | 0.143 | 0.313 | |
| 0.01 | 0.128 | 0.323 |
Finally, under the true model (i.e., the target region is under positive selection), the true positive rate ranges from 0.115 to 0.142 in presence of recombination, and 0.296–0.332 in absence of recombination (Table 4). Thus, while there is some power to identify positively selected genomic regions, power does not exceed even the baseline false positive rate under the Standard Neutral model – making all models of true and false positives indistinguishable.
Table 4.
K values for region under positive selection (θ = 0.00094).
| Selection coefficient | Proportion of sites under positive selection | %K < 0.05 (ρ = 0.00074) | %K < 0.05 (ρ = 0) |
|---|---|---|---|
| 0.1 | 0.0001 | 0.129 | 0.329 |
| 0.001 | 0.138 | 0.313 | |
| 0.01 | 0.131 | 0.332 | |
| 0.01 | 0.0001 | 0.142 | 0.33 |
| 0.001 | 0.132 | 0.323 | |
| 0.01 | 0.115 | 0.33 | |
| 0.001 | 0.0001 | 0.127 | 0.322 |
| 0.001 | 0.123 | 0.296 | |
| 0.01 | 0.127 | 0.33 |
Discussion
From our simulated tests of the K-statistic of Enard et al. (2010), a variation of the HKA test designed for detecting positive selection using a single genome, we find that the method is not able to distinguish between models of positive selection, negative selection, or population size change, nor is it robust to local variation in rates of recombination. Indeed, the true and false positive rates under the examined models are roughly similar.
Indeed, the largest determinant in dictating the fraction of rejecting loci is the rate of recombination. While a decrease in the rate of recombination increased the true positive rate, it equally corresponded to an increase in the false positive rate under most models examined. This is owing to the diversity-reducing potential of all of the models examined, with the size of the reduction being dictated by local recombination rates. While the false positive rate was not well explored by Enard et al. (2010) the low power of the statistic is consistent with their results. These results suggest a strong bias toward preferentially identifying low recombination rate regions of the genome – under any true underlying model. And while there is indeed evidence of differences in fine-scale recombination rates between humans and chimps (Ptak et al., 2005; Winckler et al., 2005), results suggest that any overlap between species in selective constraint or rate of crossover will result in false positives in even inter-species comparisons.
The poor performance of this statistic is consistent with the poor overlap with other human genomic scans (Carlson et al., 2005; Voight et al., 2006; Tang et al., 2007; Williamson et al., 2007; Pickrell et al., 2009), with the fraction of overlapping genes varying between 6 and 15%. Thus, despite the novelty of the initial claim, these results strongly suggest that the single genome approach to sweep detection is not robust to any local diversity-reducing model. Thus, the variety of polymorphism based test statistics (see review of Nielsen, 2005; Thornton et al., 2007) for distinguishing the above models using patterns in linkage disequilibrium and the site frequency spectrum appear to be the most promising avenue forward – continuing to necessitate the sampling and sequencing of consistently sampled population data.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Begun D. J., Aquadro C. F. (1992). Levels of naturally occurring DNA polymorphism correlate with recombination rates in D. melanogaster. Nature 356, 519–520 10.1038/356519a0 [DOI] [PubMed] [Google Scholar]
- Broman K. W., Murray J. C., Sheffield V. C., White R. L., Weber J. L. (1998). Comprehensive human genetic maps: individual and sex-specific variation in recombination. Am. J. Hum. Genet. 63, 861–869 10.1086/302112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlson C. S., Thomas D. J., Eberle M. A., Swanson J. E., Livingston R. J., Rieder M. J., Nickerson D. A. (2005). Genomic regions exhibiting positive selection identified from dense genotype data. Genome Res. 15, 1553–1565 10.1101/gr.4326505 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enard D., Depaulis F., Roest Crollius H. (2010). Humans and non-human primate genomes share hotspots of positive selection. PLoS Genet. 6, e1000840. 10.1371/journal.pgen.1000840 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frazer K. A., Ballinger D. G., Cox D. R., Hinds D. A., Stuve L. L., Gibbs R. A., Belmont J. W., Boudreau A., Hardenbol P., Leal S. M., Pasternak S., Wheeler D. A., Willis T. D., Yu F., Yang H., Zeng C., Gao Y., Hu H., Hu W., Li C., Lin W., Liu S., Pan H., Tang X., Wang J., Wang W., Yu J., Zhang B., Zhang Q., Zhao H., Zhao H., Zhou J., Gabriel S. B., Barry R., Blumenstiel B., Camargo A., Defelice M., Faggart M., Goyette M., Gupta S., Moore J., Nguyen H., Onofrio R. C., Parkin M., Roy J., Stahl E., Winchester E., Ziaugra L., Altshuler D., Shen Y., Yao Z., Huang W., Chu X., He Y., Jin L., Liu Y., Shen Y., Sun W., Wang H., Wang Y., Wang Y., Xiong X., Xu L., Waye M. M., Tsui S. K., Xue H., Wong J. T., Galver L. M., Fan J. B., Gunderson K., Murray S. S., Oliphant A. R., Chee M. S., Montpetit A., Chagnon F., Ferretti V., Leboeuf M., Olivier J. F., Phillips M. S., Roumy S., Sallée C., Verner A., Hudson T. J., Kwok P. Y., Cai D., Koboldt D. C., Miller R. D., Pawlikowska L., Taillon-Miller P., Xiao M., Tsui L. C., Mak W., Song Y. Q., Tam P. K., Nakamura Y., Kawaguchi T., Kitamoto T., Morizono T., Nagashima A., Ohnishi Y., Sekine A., Tanaka T., Tsunoda T., Deloukas P., Bird C. P., Delgado M., Dermitzakis E. T., Gwilliam R., Hunt S., Morrison J., Powell D., Stranger B. E., Whittaker P., Bentley D. R., Daly M. J., de Bakker P. I., Barrett J., Chretien Y. R., Maller J., McCarroll S., Patterson N., Pe’er I., Price A., Purcell S., Richter D. J., Sabeti P., Saxena R., Schaffner S. F., Sham P. C., Varilly P., Altshuler D., Stein L. D., Krishnan L., Smith A. V., Tello-Ruiz M. K., Thorisson G. A., Chakravarti A., Chen P. E., Cutler D. J., Kashuk C. S., Lin S., Abecasis G. R., Guan W., Li Y., Munro H. M., Qin Z. S., Thomas D. J., McVean G., Auton A., Bottolo L., Cardin N., Eyheramendy S., Freeman C., Marchini J., Myers S., Spencer C., Stephens M., Donnelly P., Cardon L. R., Clarke G., Evans D. M., Morris A. P., Weir B. S., Tsunoda T., Mullikin J. C., Sherry S. T., Feolo M., Skol A., Zhang H., Zeng C., Zhao H., Matsuda I., Fukushima Y., Macer D. R., Suda E., Rotimi C. N., Adebamowo C. A., Ajayi I., Aniagwu T., Marshall P. A., Nkwodimmah C., Royal C. D., Leppert M. F., Dixon M., Peiffer A., Qiu R., Kent A., Kato K., Niikawa N., Adewole I. F., Knoppers B. M., Foster M. W., Clayton E. W., Watkin J., Gibbs R. A., Belmont J. W., Muzny D., Nazareth L., Sodergren E., Weinstock G. M., Wheeler D. A., Yakub I., Gabriel S. B., Onofrio R. C., Richter D. J., Ziaugra L., Birren B. W., Daly M. J., Altshuler D., Wilson R. K., Fulton L. L., Rogers J., Burton J., Carter N. P., Clee C. M., Griffiths M., Jones M. C., McLay K., Plumb R. W., Ross M. T., Sims S. K., Willey D. L., Chen Z., Han H., Kang L., Godbout M., Wallenburg J. C., L’Archevêque P., Bellemare G., Saeki K., Wang H., An D., Fu H., Li Q., Wang Z., Wang R., Holden A. L., Brooks L. D., McEwen J. E., Guyer M. S., Wang V. O., Peterson J. L., Shi M., Spiegel J., Sung L. M., Zacharia L. F., Collins F. S., Kennedy K., Jamieson R., Stewart J. (2007). A second generation human haplotype map of over 3.1 million SNPs. Nature 449, 851–861 10.1038/nature06258 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutenkunst R. N., Hernandez R. D., Williamson S. H., Bustamante C. D. (2009). Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genet. 5, e1000695. 10.1371/journal.pgen.1000695 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernandez R. D. (2008). A flexible forward simulator for populations subject to selection and demography. Bioinformatics 24, 2786–2787 10.1093/bioinformatics/btn522 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinds D. A., Stuve L. L., Nilsen G. B., Halperin E., Eskin E., Ballinger D. G., Frazer K. A., Cox D. R. (2005). Whole genome patterns of common DNA variation in three human populations. Science 307, 1072–1079 10.1126/science.1105436 [DOI] [PubMed] [Google Scholar]
- Hudson R. R., Kreitman M., Aguadé M. (1987). A test of neutral molecular evolution based on nucleotide data. Genetics 116, 153–159 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelley J. L., Madeoy J., Calhoun J., Swanson W., Akey J. (2006). Genomic signatures of positive selection in humans and the limits of outlier approaches. Genome Res. 16, 980–989 10.1101/gr.5157306 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenzi M. L., Smith J., Snowden T., Kim M., Fishel R., Poulos B. K., Cohen P. E. (2005). Extreme heterogeneity in the molecular events leading to the establishment of chiasmata during meiosis in human oocytes. Am. J. Hum. Genet. 76, 112–127 10.1086/427268 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen R. (2005). Molecular signatures of natural selection. Annu. Rev. Genet. 39, 197–218 10.1146/annurev.genet.39.073003.112420 [DOI] [PubMed] [Google Scholar]
- Nielsen R., Williamson S., Kim Y., Hubisz M. J., Clark A. G., Bustamante C. D. (2005). Genomic scans for selective sweeps using SNP data. Genome Res. 15, 1566–1575 10.1101/gr.4252305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickrell J. K., Coop G., Novembre J., Kudaravalli S., Li J. Z., Absher D., Srinivasan B. S., Barsh G. S., Myers R. M., Feldman M. W., Pritchard J. K. (2009). Signals of recent positive selection in a worldwide sample of human populations. Genome Res. 19, 826–837 10.1101/gr.087577.108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ptak S. E., Hinds D. A., Koehler K., Nickel B., Patil N., Ballinger D. G., Przeworski M., Frazer K. A., Pääbo S. (2005). Fine-scale recombination patterns differ between chimpanzee and humans. Nat. Genet. 37, 429–434 10.1038/ng1529 [DOI] [PubMed] [Google Scholar]
- Sabeti P. C., Schaffner S. F., Fry B., Lohmueller J., Varilly P., Shamovsky O., Palma A., Mikkelsen T. S., Altshuler D., Lander E. S. (2006). Positive natural selection in the human lineage. Science 312, 1614–1620 10.1126/science.1124309 [DOI] [PubMed] [Google Scholar]
- Sabeti P. C., Varilly P., Fry B., Lohmueller J., Hostetter E., Cotsapas C., Xie X., Byrne E. H., McCarroll S. A., Gaudet R., Schaffner S. F., Lander E. S., International HapMap Consortium. Frazer K. A., Ballinger D. G., Cox D. R., Hinds D. A., Stuve L. L., Gibbs R. A., Belmont J. W., Boudreau A., Hardenbol P., Leal S. M., Pasternak S., Wheeler D. A., Willis T. D., Yu F., Yang H., Zeng C., Gao Y., Hu H., Hu W., Li C., Lin W., Liu S., Pan H., Tang X., Wang J., Wang W., Yu J., Zhang B., Zhang Q., Zhao H., Zhao H., Zhou J., Gabriel S. B., Barry R., Blumenstiel B., Camargo A., Defelice M., Faggart M., Goyette M., Gupta S., Moore J., Nguyen H., Onofrio R. C., Parkin M., Roy J., Stahl E., Winchester E., Ziaugra L., Altshuler D., Shen Y., Yao Z., Huang W., Chu X., He Y., Jin L., Liu Y., Shen Y., Sun W., Wang H., Wang Y., Wang Y., Xiong X., Xu L., Waye M. M., Tsui S. K., Xue H., Wong J. T., Galver L. M., Fan J. B., Gunderson K., Murray S. S., Oliphant A. R., Chee M. S., Montpetit A., Chagnon F., Ferretti V., Leboeuf M., Olivier J. F., Phillips M. S., Roumy S., Sallée C., Verner A., Hudson T. J., Kwok P. Y., Cai D., Koboldt D. C., Miller R. D., Pawlikowska L., Taillon-Miller P., Xiao M., Tsui L. C., Mak W., Song Y. Q., Tam P. K., Nakamura Y., Kawaguchi T., Kitamoto T., Morizono T., Nagashima A., Ohnishi Y., Sekine A., Tanaka T., Tsunoda T., Deloukas P., Bird C. P., Delgado M., Dermitzakis E. T., Gwilliam R., Hunt S., Morrison J., Powell D., Stranger B. E., Whittaker P., Bentley D. R., Daly M. J., de Bakker P. I., Barrett J., Chretien Y. R., Maller J., McCarroll S., Patterson N., Pe’er I., Price A., Purcell S., Richter D. J., Sabeti P., Saxena R., Schaffner S. F., Sham P. C., Varilly P., Altshuler D., Stein L. D., Krishnan L., Smith A. V., Tello-Ruiz M. K., Thorisson G. A., Chakravarti A., Chen P. E., Cutler D. J., Kashuk C. S., Lin S., Abecasis G. R., Guan W., Li Y., Munro H. M., Qin Z. S., Thomas D. J., McVean G., Auton A., Bottolo L., Cardin N., Eyheramendy S., Freeman C., Marchini J., Myers S., Spencer C., Stephens M., Donnelly P., Cardon L. R., Clarke G., Evans D. M., Morris A. P., Weir B. S., Tsunoda T., Johnson T. A., Mullikin J. C., Sherry S. T., Feolo M., Skol A., Zhang H., Zeng C., Zhao H., Matsuda I., Fukushima Y., Macer D. R., Suda E., Rotimi C. N., Adebamowo C. A., Ajayi I., Aniagwu T., Marshall P. A., Nkwodimmah C., Royal C. D., Leppert M. F., Dixon M., Peiffer A., Qiu R., Kent A., Kato K., Niikawa N., Adewole I. F., Knoppers B. M., Foster M. W., Clayton E. W., Watkin J., Gibbs R. A., Belmont J. W., Muzny D., Nazareth L., Sodergren E., Weinstock G. M., Wheeler D. A., Yakub I., Gabriel S. B., Onofrio R. C., Richter D. J., Ziaugra L., Birren B. W., Daly M. J., Altshuler D., Wilson R. K., Fulton L. L., Rogers J., Burton J., Carter N. P., Clee C. M., Griffiths M., Jones M. C., McLay K., Plumb R. W., Ross M. T., Sims S. K., Willey D. L., Chen Z., Han H., Kang L., Godbout M., Wallenburg J. C., L’Archevêque P., Bellemare G., Saeki K., Wang H., An D., Fu H., Li Q., Wang Z., Wang R., Holden A. L., Brooks L. D., McEwen J. E., Guyer M. S., Wang V. O., Peterson J. L., Shi M., Spiegel J., Sung L. M., Zacharia L. F., Collins F. S., Kennedy K., Jamieson R., Stewart J. (2007). Genome wide detection and characterization of positive selection in human populations. Nature 449, 913–918 10.1038/nature06250 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith J. M., Haigh J. (1974). The hitch-hiking effect of a favourable gene. Genet. Res. 23, 23–35 10.1017/S001667230001466X [DOI] [PubMed] [Google Scholar]
- Tang K., Thornton K. R., Stoneking M. (2007). A new approach for using genome scans to detect recent positive selection in the human genome. PLoS Biol. 5, e171. 10.1371/journal.pbio.0050171 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton K. R., Jensen J. D., Becquet C., Andolfatto P. (2007). Progress and prospects in mapping recent selection in the genome. Heredity 98, 340–348 [DOI] [PubMed] [Google Scholar]
- Voight B. F., Kudaravalli S., Wen X., Pritchard J. K. (2006). A map of recent positive selection in the human genome. PLoS Biol. 4, e72. 10.1371/journal.pbio.0040072 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williamson S. H., Hubisz M. J., Clark A. G., Payseur B. A., Bustamante C. D., Nielsen R. (2007). Localizing recent adaptive evolution in the human genome. PLoS Genet. 3, e90. 10.1371/journal.pgen.0030090 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winckler W., Myers S. R., Richter D. J., Onofrio R. C., McDonald G. J., Bontrop R. E., McVean G. A., Gabriel S. B., Reich D., Donnelly P., Altshuler D. (2005). Comparison of fine-scale recombination rates in humans and chimpanzees. Science 308, 107–111 10.1126/science.1105322 [DOI] [PubMed] [Google Scholar]