Multiscale Finite Element Modeling of the Lamina Cribrosa Microarchitecture in the Eye

Abstract

In this paper, we describe a new method for constructing macro-scale models of the posterior pole of the eye to investigate the role of intraocular pressure in the development and progression of glaucoma. We also describe a method and present results from micro-scale finite element models of the lamina cribrosa microarchitecture that are derived from parent macro-scale continuum models using a novel multiscale substructuring approach. The laminar micro-scale models capture the biomechanical behavior of the laminar trabeculae in a way that cannot be estimated using macro-scale techniques, and predict much higher stresses and strains than those calculated within macro-scale models of the coincident region in the same eye.

I. INTRODUCTION

Glaucoma is the second leading cause of blindness in the US and is usually associated with elevated intraocular pressure (IOP). The principal site of glaucomatous damage is believed to be within the optic nerve head (ONH) where the retinal ganglion cell axons pass through an opening in the back of the eye wall on their path to the brain. This opening, known as the scleral canal, is spanned by the lamina cribrosa, a three-dimensional fenestrated connective tissue meshwork that provides structural and nutritional support for the axons as they pass through the eye wall.

Elevated IOP is the most common risk factor for glaucoma and IOP-lowering remains the only proven clinical treatment for the disease. However, there is no agreement on the role of IOP in the development or progression of glaucoma, and the mechanism through which IOP is related to glaucomatous damage is unknown. The purpose of the present study was to explore the regional biomechanical response of the lamina cribrosa microarchitecture to IOP elevations using multiscale anatomical finite element (FE) models, which are derived from parent macro-scale continuum FE models. Results were compared for the superior (S), inferior (I), nasal (N), and temporal (T) regions in the mid-periphery of the lamina in normal monkey ONHs.

II. Methods

Three-dimensional reconstructions of the ONH connective tissues were generated for a normal eye of three rhesus monkeys. The reconstruction data was compiled using a microtome-based serial sectioning technique, wherein high-resolution images of the manually connective tissue-stained, embedded tissue block-face were consecutively captured, aligned and stacked into a volume, at a voxel resolution of 2.5×2.5×3.0 μm [1].

Once acquired, these histologic 3D ONH reconstructions can be sliced, viewed, and their structures 3D delineated interactively using custom software [2]. Once the neural canal wall, and anterior and posterior scleral and laminar surfaces have been fully 3D delineated, the region of the ONH containing the lamina cribrosa can be isolated. The 3D point cloud of delineated points is imported into Geomagic Studio 9 software (Geomagic, Research Triangle Park, NC) and each structure is surfaced, then combined using Boolean operations to isolate the laminar volume. The lamina cribrosa connective tissues are then three-dimensionally segmented (Figure 1) using a diffusion-filtering, coherence-enhancing, anisotropic, Markov random field algorithm that has been optimized for this task [3].

Figure 1.

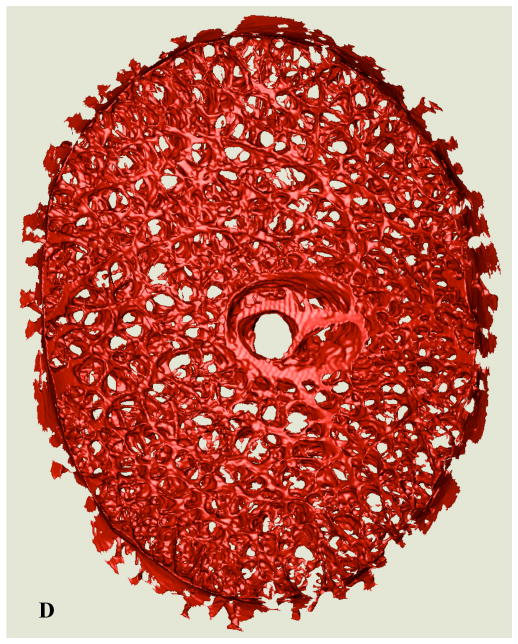
(A) A single raw serial section block-face image from a representative normal monkey ONH showing the ONH, with connective tissues stained red and a highlighted region of the lamina. (B) A close up view of the highlighted region showing the laminar beams stained in red; (C) the same image as seen in (B), with blue borders indicating the edges of the lamina cribrosa connective tissues as 3D-segmented by our algorithm. (D, Next Page) Anterior view of the full 3D-segmented lamina cribrosa microarchitecture of a normal monkey ONH. Note that the laminar trabeculae insert into the sclera at the periphery, and the central retinal vessels are seen in the center of the reconstruction. The retinal ganglion cell axons that transmit visual signals from the eye to the brain pass through the pores in the lamina. Note that the laminar microstructure shows tremendous regional variation in pore size, laminar beam thickness, connective tissue volume fraction, and connective tissue volume, all of which should affect regional laminar biomechanics. The region to the right of the central retinal vessels (temporal) has small laminar beams and small pores, while the region to the left of the vessels (nasal) has large laminar beams and large pores. Interestingly, these regions have similar connective tissue volume fractions.

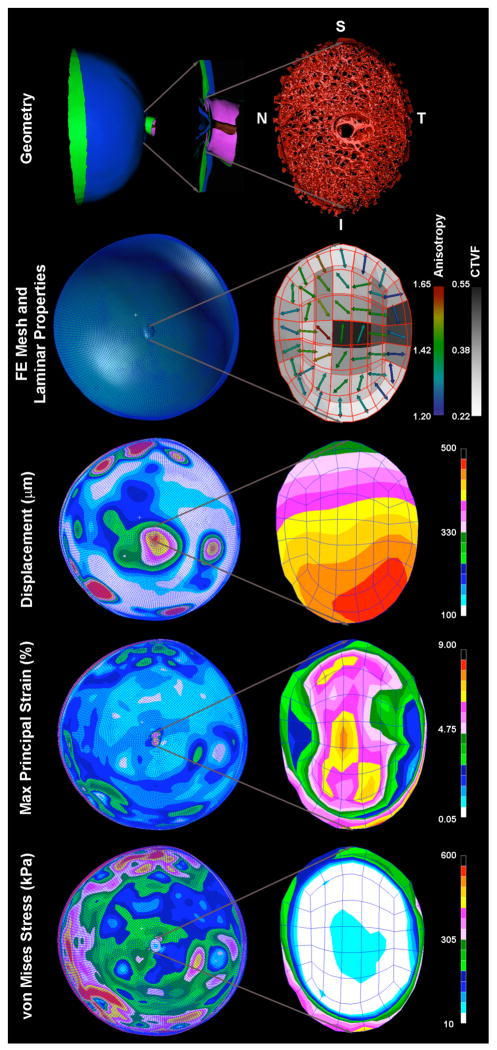
Macro-scale biomechanical modeling of the posterior pole and ONH (Figure 2)

Figure 2. Construction and results from a continuum FE model of the posterior pole.

To construct the model geometry, the 3D-delineated lamina cribrosa and surrounding peripapillary sclera are incorporated into a generic anatomic scleral shell that reflects average regional thickness variations mapped from histologic measurements [9]. The ONH-scleral shell complex is used to define the geometry (Top) for a finite element model of the posterior pole using the PATRAN (MSC Software, Santa Ana, CA) pre-processing software. The models are meshed using quadratic, 20-noded hexahedral elements (FE Mesh, above). The porous, load-bearing lamina cribrosa tissue of the ONH is modeled using a continuum approach, with linear elastic orthotropic material properties defined using a combination of the connective tissue volume fraction and the predominant laminar beam orientation (direction and degree of anisotropy; Laminar Properties above) [4]. Macro-scale displacement, strain, and stress induced in the lamina and sclera of an eye subjected to an IOP elevation from 10 to 45 mmHg are contour plotted on the posterior pole model (left column) with a close-up view of the ONH shown in the right column. Note that in this eye, the model predicts that the ONH tilts inferiorly, the strains are highest along the superior-inferior axis of the ONH, and that the sclera bears most of the IOP-related stress.

We have developed a novel modeling method to explore the biomechanical response of the connective tissues of ONH and posterior scleral shell to IOP. These models use anatomical, 3D, macro-scale finite element (FE) models that incorporate characterization of the porous microstructure of the lamina cribrosa into the models’ material property description [4]. Each model geometry (Figure 2, top) is constructed from the 3D histomorphometric measures of an individual eye. The porous, load-bearing lamina cribrosa tissue of the ONH was modeled using a continuum approach, with the element size chosen so that each element would contain a sufficient volume of the microstructure to satisfy the continuum assumption [5]. Linear elastic orthotropic material properties for each element in the nerve head were defined as:

$$E_i=A{\rho }^2{H}_i^3$$ (1)

where E = Young’s modulus; A = laminar material constant; ρ = connective tissue volume fraction; H = normalized eigenvalue of the mean intercept length (MIL) tensor (degree of orthotropic anisotropy); and i = 1, 2, 3 represent each of the three orthotropic material directions [6]. Poissons’ ratios were defined as:

$$v_{13}=0.45;v_{12}={({\text{E}}_2/{\text{E}}_1)}^{\ast }0.45;v_{23}={({\text{E}}_3/{\text{E}}_2)}^{\ast }0.45$$ (2)

The scleral shell of each model was assigned linear elastic material properties calculated from scleral mechanical testing [7]. Nodes along the equatorial boundary of the hemispherical model were constrained to allow for radial displacement. An IOP load of 35 mmHg was applied to the interior surface of all elements to analyze the posterior pole’s response to an acute IOP elevation from 10 to 45 mmHg (note that all model geometries were obtained from eyes pressure fixed at an IOP of 10 mmHg, which is our reference condition). Static analyses were performed using ABAQUS 6.5 (Simulia, Providence, RI). The laminar material constant, A, was adjusted iteratively until the average posterior displacement of the internal laminar surface of the FE model agreed with histologically measured displacement data obtained from a previous experiment [8].

In this way, we can estimate the biomechanical behavior of eyes based on their individual scleral and ONH connective tissue morphology. We use these models to estimate the macro-scale biomechanical behavior of the posterior scleral shell, determine the deformations that the peripapillary sclera imposes on the contained ONH, and predict the overall patterns of stress and strain in the ONH of each eye modeled (Figure 2). While these macro-scale models offer tremendous insight into the biomechanical behavior of the scleral and ONH as a whole, they do not inform the biomechanical environment of the individual laminar beams. We have therefore developed the micro-FE models presented below to investigate laminar beam biomechanics in individual eyes.

Biomechanical modeling of the lamina cribrosa microarchitecture

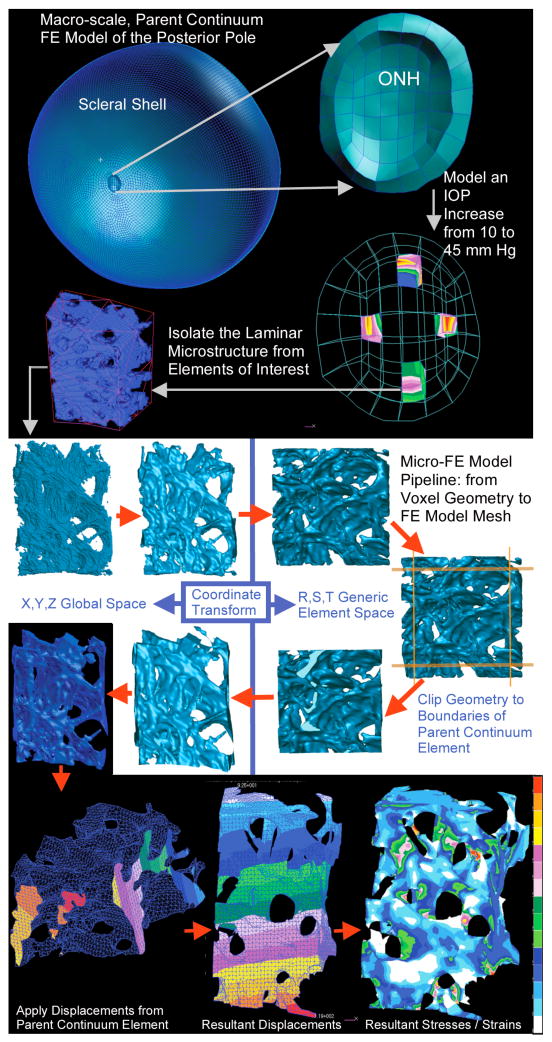
The purpose of the micro-scale modeling is to explore the regional biomechanical response of the lamina cribrosa microarchitecture to IOP elevations using anatomic FE models, which are derived from parent macro-scale continuum FE models (see Figure 3, right). In the following example, stress and strain are compared for the superior (S), inferior (I), nasal (N), and temporal (T) regions in the mid-periphery of the lamina for a monkey eye subjected to an IOP increase from 10 to 45 mm Hg.

Fig. 3.

Micro-FE pipeline showing substructuring, model geometry creation, mesh generation, boundary condition assignment, and resulting displacement and maximum principal strain fields.

The parent continuum model was loaded with an internal pressure of 35 mm Hg (representing an IOP increase from 10 to 45 mm Hg) and the resulting nodal displacement, stress and strain noted. The 3D-segmented laminar microstructure [3] within four parent continuum elements from the superior (S), inferior (I), nasal (N), and temporal (T) mid-periphery of each ONH (Figure 3, right) model was isolated. A super-region of the voxelated laminar geometry associated with each continuum element was surfaced and smoothed (Figure 2, top left) using a volume neutral method in Geomagic Studio, transformed into generic r-, s-, t- element space using the nodal locations of the parent element and the quadratic shape functions for 20-noded hexahedral elements, then cut down to a unit-2 cube (Figure 3, middle left). The resulting geometry was transformed back into x-, y-, z- global space and meshed with 10-noded tetrahedral finite elements using Harpoon meshing software (CEI, Apex, NC) to form micro-scale FE models of the laminar microarchitecture precisely coincident with the parent continuum element (Figure 3). All laminar elements in each micro model were assigned homogeneous, isotropic, linear elastic material properties derived from the parent continuum model. In the laminar micro-scale models, the laminar connective tissue is solid, and the directional stiffness associated with the conformation of the microarchitecture is inherent in the model geometry. Hence, for the micro-FE models, all elements were assigned a Young’s modulus of E = A(1²)(1/3)³ = A/27, which corresponds to micro-FE models wherein the laminar connective tissue volume fraction, ρ, is 1 and there is no preferred trabecular orientation, i.e., H_i = 1/3 for i=1,2,3).

The displacements calculated for each parent continuum element (Figure 3, bottom left) were interpolated using the quadratic shape functions for 20-noded hexahedral elements, and applied as displacement boundary conditions to nodes on the cut faces of the underlying laminar micro models (Figure 3, middle) and analyzed using ABAQUS 6.5. Resultant maximum principal strains (Figure 3, bottom right) in each micro-FE model were sorted by magnitude, separated into 20 bins of equal volume, and plotted for comparison (Figure 4). Volume-averaged maximum principal strain was also calculated for each region and overall.

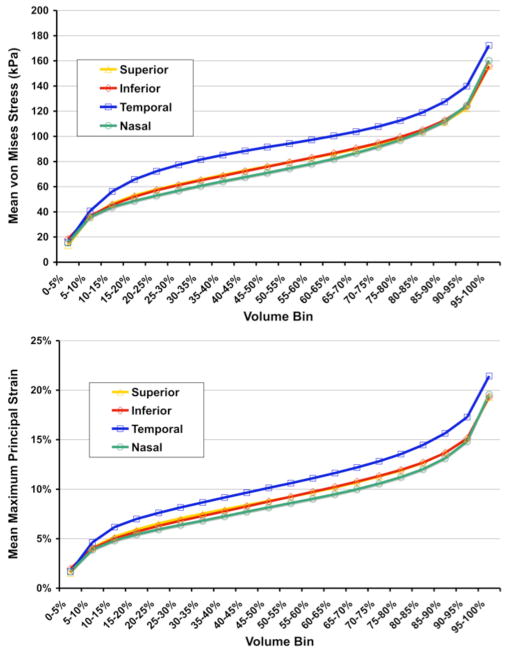
Fig. 4.

Results from a set of micro-FE models of the laminar microarchitecture from the mid-periphery of the 4 quadrants of a normal monkey eye. Von Mises stress (a scalar measure of force per unit area) and maximum principal strain (local % stretch), sorted by magnitude, separated into 20 bins of equal volume, and plotted for the 4 micro-FE models from the 4 quadrants of the ONH. Stress and strain vary substantially within individual laminar beams, and by quadrant. Note that in this eye, the models predict that the stresses and strains are highest in the temporal quadrant of the lamina, and that the peak volumetric stress and strains are much higher in these micro-scale FE models than predicted in their parent macro-scale continuum FE models (approximately a factor of 4–5 larger).

III. RESULTS

Results show that this substructuring scheme produces precisely the same displacements for points at the continuum element’s boundary for the micro model (as expected), but reveals a complexity of strains and stresses in the microarchitecture of the lamina cribrosa that is not available in their parent macro-scale continuum models.

FE analysis of the lamina cribrosa microarchitecture of pairs of monkey eyes showed that the laminar micro-scale FE models consistently exhibited higher stresses and strains than coincident regions in their parent continuum models. Volume-averaged mean maximum principal strain in the lamina ranged from 3.5 to 9.6% in the 3 normal eyes from 3 different monkeys for which results were compiled.

IV. Discussion

Our substructuring technique yields estimates of the biomechanical response of the lamina cribrosa microarchitecture under elevated IOP at low computational cost. If IOP-related axonal damage co-localizes with predicted regional concentrations of high stress and strain in modeled eyes, this technique will prove useful in elucidating the role of ONH biomechanics glaucoma.

It should be noted, however, that this interpretation of the results is subject to the limitations of the methodology currently employed. First, we used linear elastic material properties, which could lead to errors in the stress and strain magnitudes predicted. Second, we have ignored the collagen and elastin fibril structure and the associated material anisotropy inherent in the laminar beams. In future models, we will incorporate anisotropic hyperelastic properties that should improve model accuracy. Finally, all model constants were fit using averaged displacement data taken from a previous histological study on different eyes. A more desirable validation scheme would. Once imaging modalities allow the measurement of animal–specific IOP-displacement data in an in-vivo setting, a more refined validation of model behavior (including the incorporation of a more complex constitutive model) will be possible.