The Nature of Belief-Directed Exploratory Choice in Human Decision-Making

Abstract

In non-stationary environments, there is a conflict between exploiting currently favored options and gaining information by exploring lesser-known options that in the past have proven less rewarding. Optimal decision-making in such tasks requires considering future states of the environment (i.e., planning) and properly updating beliefs about the state of the environment after observing outcomes associated with choices. Optimal belief-updating is reflective in that beliefs can change without directly observing environmental change. For example, after 10 s elapse, one might correctly believe that a traffic light last observed to be red is now more likely to be green. To understand human decision-making when rewards associated with choice options change over time, we develop a variant of the classic “bandit” task that is both rich enough to encompass relevant phenomena and sufficiently tractable to allow for ideal actor analysis of sequential choice behavior. We evaluate whether people update beliefs about the state of environment in a reflexive (i.e., only in response to observed changes in reward structure) or reflective manner. In contrast to purely “random” accounts of exploratory behavior, model-based analyses of the subjects’ choices and latencies indicate that people are reflective belief updaters. However, unlike the Ideal Actor model, our analyses indicate that people’s choice behavior does not reflect consideration of future environmental states. Thus, although people update beliefs in a reflective manner consistent with the Ideal Actor, they do not engage in optimal long-term planning, but instead myopically choose the option on every trial that is believed to have the highest immediate payoff.

Introduction

Effective decision-making often requires a delicate balance of exploratory and exploitative behavior. For example, consider the problem of choosing where to dine out from a set of competing options. The quality of restaurants changes over time such that one cannot be certain which restaurant is currently best. In this non-stationary environment, one either chooses the best-experienced restaurant so far (i.e., exploit) or visits a restaurant that was inferior in the past but now may be superior (i.e., explore). The actions a diner should take in a series of choices is a non-trivial problem as optimal decision-making requires factoring in the uncertainty of the environment and the impact of the current action on one’s future understanding of restaurant quality.

How humans and artificial agents balance and structure exploratory and exploitative actions is an important topic in reinforcement learning (RL) research (Sutton and Barto, 1998; Cohen et al., 2007; Lee et al., 2011). Exploring when one should exploit and, conversely, exploiting when one should explore both incur costs. For example, an actor who excessively exploits will fail to notice when another action becomes superior. Conversely, an actor who excessively explores incurs an opportunity cost by frequently forgoing the high payoff option.

In deciding whether to explore or exploit, an agent should consider its uncertainty about the environmental state. In the dining example above, the agent’s decision to explore or exploit should depend on the volatility of the environment (e.g., the rate at which restaurant quality changes over time) and how recently the agent has explored options observed to be inferior in the past. For example, an agent should exploit when it has recently confirmed that alternative restaurants remain inferior and the environment is fairly stable (i.e., restaurant quality does not rapidly change). On the other hand, an agent should explore when alternatives have not been recently sampled and the environment is volatile. Between these two extremes lie a host of intermediate cases.

In this contribution, we examine how people update their belief states about the relative superiority of actions. In one view, reflective belief updates incorporate predictions of unobserved changes in the environment. For example, a reflective belief-updater would be more likely to believe that an inferior restaurant has improved as time passes since its last visit to the restaurant. In contrast, a reflexive model of choice is only informed by direct observations of rewards and, therefore, does not fully utilize environmental structure to update beliefs and guide actions. This distinction closely echoes contemporary dual-system frameworks of RL in which a reflexive, computationally parsimonious model-free controller putatively competes for control of behavior with a reflective and model-based controller (Daw et al., 2005).

For reflexive models, exploratory choices are the result of a purely stochastic decision process. Thus, reflexive accounts do not predict sequential structure in humans’ patterns of exploratory choice (cf. Otto et al., 2010). Perhaps because of their simplicity and unexamined intuitions about the “randomness” of exploratory behavior, reflexive approaches are commonly adopted to model human behavior (Daw et al., 2006; Worthy et al., 2007; Gureckis and Love, 2009; Pearson et al., 2009; Jepma and Nieuwenhuis, 2011). Reflexive approaches are also prominent in the design of artificial agents (Sutton and Barto, 1998).

The Leapfrog variant of the classic bandit task

To understand how people balance exploration and exploitation given uncertainty about the state of the environment, we developed a variant of the commonly used n-armed bandit task, as the restaurant example given above can be formally described. In the classic n-armed bandit task, there are multiple actions (i.e., bandits) with unknown payoffs associated with them. Crucially, the payoffs at each time point are not explicitly revealed to decision-makers but instead must be determined by repeated sampling of actions. In restless bandit tasks, the actions’ payoffs change over time, necessitating the aforementioned balancing of exploratory and exploitive actions.

Previous studies of exploratory choice have utilized n-armed bandit tasks in which the payoff distributions associated with the actions noisily drift over the course of decision-making (Daw et al., 2006; Pearson et al., 2009; Jepma and Nieuwenhuis, 2011). Although these tasks assess how people behave in changing environments, one major drawback of existing tasks is that there is no accompanying formal analysis of what decisions people should ideally make. In particular, existing work does not specify a statistically optimal process for updating estimates of action payoffs, and the action selection methods posited ignore the informational value of exploring. The failure of existing tasks to prescribe optimal choice behavior makes it difficult to assess how people differ from an optimal agent. In part, these shortcomings reflect that formulating ideal agents for existing tasks is an intractable problem (e.g., Daw et al., 2006).

In this contribution, we develop and use a novel laboratory task that is sufficiently constrained to allow for formal specification of the ideal agent. This formulation will be used to assess human behavior (e.g., Are people reflective or reflexive belief updaters? Do they act optimally given their beliefs?). In our Leapfrog task, the rewards for two possible actions continually alternate in their superiority, “leapfrogging” over each other. The underlying state of the environment – that is, which option currently has the higher payoff – is only partially observable to the decision-maker. This class of problems is referred to as a partially observable Markov decision process (POMDP) in the Artificial Intelligence literature (Kaelbling et al., 1998). Choosing the best-observed action (“exploiting”) generally provides little information about the underlying state while exploration can resolve the underlying state but potentially incurs opportunity costs.

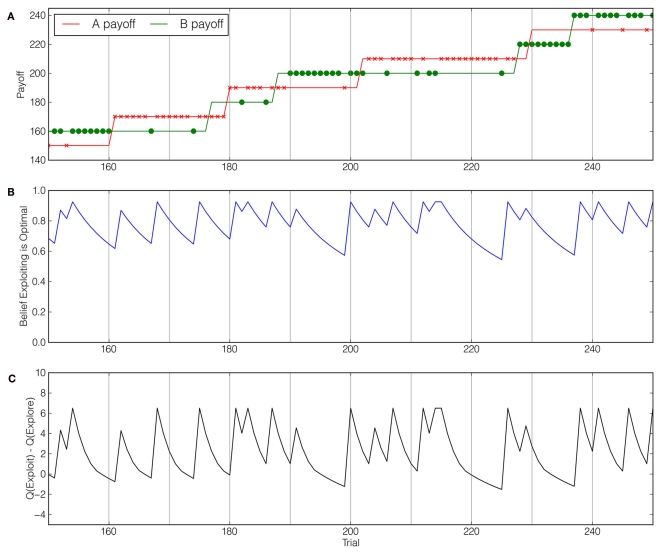
An example instantiation of the Leapfrog task is depicted in Figure 1A. In the Leapfrog task there are two actions, A and B, with different payoffs. The participants’ task is to try to choose the higher payoff option as often as possible (this proportion, not total points, is the key metric). Option B’s payoff is initially higher (at 20 points) than option A’s payoff (10 points). On each trial, there is a fixed probability, which we refer to as volatility, that the inferior action increases its payoff by 20 points, “leapfrogging” the other option to give higher payoff. In summary, jumps are subject to three constraints: they occur at a fixed volatility unknown to the decision-maker, the two actions alternate in making jumps, and a jump always increases an action’s point payoff by 20. Critically, instructions make clear to participants that they will be rewarded at the end of the experiment based on the proportion of “correct” choices (i.e., choices for which the option with the higher true payoff was chosen) as opposed total points earned. Jumps are not explicitly made known to the decision-maker, but rather must be inferred indirectly from observing choice payoffs.

Figure 1.

Choice behavior and model-inferred beliefs and values in the Leapfrog bandit task. At each trial, there is a fixed probability, which we refer to as volatility or P(flip), that the inferior action increases its point payoff by 20 points. After the first “jump,” Action A “pays” 30 points, superior to Action B’s 20 points. After this jump, Action B’s payoff will increase by 20 points with the same probability. (A) An example participant’s sequence of choices over 100 trials in an environment with volatility rate P(flip) = 0.075. The two solid lines indicate the true payoffs for each option, and the × and • marks indicate the participant’s choices among these options. (B) The Ideal Observer’s belief that the exploitative options will yield larger the higher payoff – and thus the higher immediate reward – at each trial in the task instantiation at top. Note that the subject’s certainty about the options’ relative payoffs generally decreases during exploitation-only runs. (C) The relative long-term value of the exploitative option at each trial as determined by the Ideal Actor, using the beliefs from (B) and an optimal valuation function. Also note that changes in the relative value follow changes in belief in a non-linear fashion.

Consistent with previous frameworks (Daw et al., 2006), we define exploitation as choosing the action with the highest observed payoff. A decision-maker must explore to detect when the alternative action has leapfrogged over the action presently being exploited. The Leapfrog task has only two actions, and all possible underlying environment states can be mapped to the number of unobserved jumps. For example, when there are no unobserved jumps, the exploitative option still yields the higher payoff. On the other hand, when there is one unobserved jump, the exploratory option has the higher payoff. Consequently, unlike previously studied bandit tasks, the prescription for optimal choice behavior in the Leapfrog task is tractable, though non-trivial. Our task also affords a straightforward manipulation of the rate at which decision-makers should explore. Namely, across conditions, we vary the volatility of the environment to examine whether subjects in low and high volatility conditions differ in their balance of exploratory and exploitative choice. Intuitively and in accord with the Ideal Actor, we expect that subjects should explore more frequently in more volatile environments.

Models evaluated

A number of model variants are evaluated to shed light on human choice behavior in the Leapfrog task. In addition to examining whether choice is better described by reflexive versus reflective strategies, the second main question we ask is whether people plan ahead optimally, taking the value of the information gained through exploration into account when acting, or myopically choose the action expected to receive the larger reward, regardless of the action’s impact on later reward. We compare human data from the Leapfrog task to three models: a reflexive and myopic model we term the “Naïve RL” model, which expects payoffs (or rewards) to be as they were last experienced; a reflective and myopic model we call the “Belief model,” which directly acts on the basis of its beliefs about current payoffs; and a model that plans optimally from reflective beliefs, the “Ideal Actor.” For full algorithmic descriptions of the models we refer the reader to the Appendix.

Both reflective models employ an “Ideal Observer,” which optimally updates beliefs based on past actions and observed payoffs. Figure 1B depicts beliefs as determined by the Ideal Observer for the actions and observations in Figure 1A. Similar Ideal Observer models have been employed in task domains such as visual search (Najemnik and Geisler, 2005) and prediction and change point detection (Steyvers and Brown, 2005). Of the two reflective models, only the Ideal Actor builds upon its optimal beliefs by considering the effect of exploration on reducing uncertainty in its future beliefs. Optimal beliefs about current payoffs and correct assessments of each action’s informational value together yield a numeric expression of each action’s overall value – expressed as Q-values – determining optimal choice behavior. The Ideal Actor’s Q-values are calculated by converting the task to a POMDP and solving it in this form. In Figure 1C, the options’ relative Q-values are shown as a function of the beliefs in Figure 1B and the number of remaining trials.

Because people may act noisily, in all three models we make choice a stochastic function of action values using the Softmax choice rule (Sutton and Barto, 1998), parameterizing the extent to which the choice rule is sensitive to value differences using the inverse temperature parameter (henceforth the “Softmax parameter”). This constitutes the Naïve RL model’s only free parameter, while the two reflective models have an additional parameter, P(flip), which represents the model’s estimate of the environment volatility.

We rely on two complementary results to assess the belief-directed nature of subjects’ choices in the Leapfrog task. First, we define a hazard rate metric elucidating the increasing likelihood of exploratory choice over time, for which reflective and reflexive models make clear and divergent predictions. Second, these qualitative results in turn motivate quantitative comparison of the extent to which these models characterize human choice. To foreshadow, we find that humans are best described by the reflective, but myopic, Belief model, suggesting that exploratory choice is not necessarily directed by a planning process that takes into account the value of future information yielded by actions. Finally, we analyze people’s choice latencies in terms of the Ideal Actor’s action prescriptions, observing that people exhibit larger latencies when they act suboptimally, demonstrating the Ideal Actor’s potential as a tool for online, process-oriented analysis of exploratory choice behavior.

Materials and Methods

Subjects

A total of 139 undergraduates at the University of Texas participated in this experiment in exchange for course credit and a small cash bonus tied to proportion of trials for which the higher payoff option was chosen. The sample from which our sample was drawn is 54.3% female and 42.5% male, with 3.2% who declined to report their gender. The ages of participants in this pool ranged from 18 to 55 (M = 19.08, SD = 1.76). Participants were randomly assigned to three volatility level conditions, defined by the probability at each trial that the payoff ordering of options would flip, P(flip): low volatility [P(flip) = 0.025], medium volatility [P(flip) = 0.075], and high volatility [P(flip) = 0.125]. There were 51, 41, and 47 subjects in the low, middle, and high volatility conditions respectively.

Materials and procedure

The task instructions explained that one option was always worth 10 more points than the other option, that the superiority of the two options alternated over time, and that options always changed values by 20 points. Subjects were informed that their payment was tied to the number of times they chose the higher payoff option. Additionally, they were told at the outset which option, A or B, was initially superior at the start of the experiment and that the experiment consisted of 500 choices in total. The bandit task interface consisted of two buttons on a computer screen marked “OPTION A” and “OPTION B.”

Prior to the main bandit task, subjects completed a number of training trials intended to familiarize them with the procedure and the volatility rate. In these training trials, participants first completed a passive viewing task in which they viewed 500 trials of the bandit task whose payoffs were randomly generated as previously described in the section on the Leapfrog task. To focus subjects’ attention on the volatility rather than the true payoffs in the volatility-training phase, the payoffs for each option either read “SAME” or “CHANGED.” Before each block of 100 trials, participants then provided an estimate of the number of flips they expected in the next block.

Following training, participants completed 500 trials of the main bandit task. On each trial, subjects saw the word “CHOOSE” and had 1.5 s to make a choice using the using the “Z” or “?” keys for the left and right options respectively. Following each choice, numerical feedback was provided for 1 s, indicating the number of points that resulted from the choice. When a response deadline was missed, the computer displayed the message “TOO SLOW” accompanied by a large red X for 1 s and the participant repeated that trial. Payoffs for options A and B started at 10 and 20 respectively and, as described above, alternated jumping by 20 points with probability governed by P(flip). An example instantiation of the payoffs is depicted in Figure 1A along with an example subjects’ sequence of choices.

Results

Choice behavior

The primary dependent measure is whether subjects explored or exploited on a trial. We classified each choice made by a participant as either exploratory or exploitative based on their experienced payoffs up to that choice point: when the decision-maker chose the option with the highest-seen payoffs, that choice was considered an exploitative choice, and when they chose the other option, that was considered an exploratory choice (cf. Daw et al., 2006).

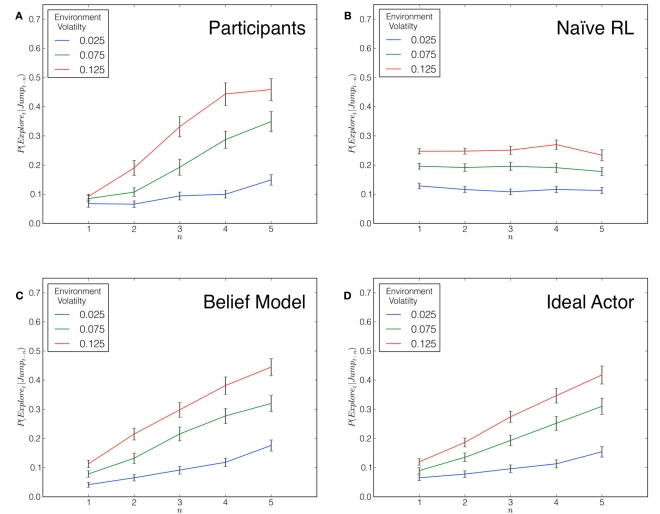
Figure 2A depicts the hazard rates of subjects’ exploratory choice across the three conditions, calculated as the probability that an exploratory choice is made on trial t given that a payoff jump was observed on trial t − n, restricted to a five-trial window. In other words, this hazard rate is the probability of making an exploratory choice as a function of the number of consecutive exploitative choices. These hazard rates are calculated from 139 simulations – one for each subject in the experiment – of each model allocated across the three volatility conditions. Each model was “yoked” to a subject’s particular instantiation of the Leapfrog payoff structure and, consequently, their environment volatility rate. To determine model choice behavior, we used the average of participants’ best-fitting parameter values for each volatility condition and model (see Table 1; procedure described below). For each model, we calculated the hazard rate of exploration in the same way as subjects and report these rates in Figures 2B–D. It can be seen that subjects’ rate of exploration increased monotonically over time, F(1,137) = 5.96, p < 0.05, contrasting with the predictions of the purely reflexive Naïve RL model but in accordance with the qualitative predictions of the reflective Belief and Ideal Actor models. Further, subjects in more volatile environments explored more frequently, F(2,137) = 31.50, p < 0.001, which is an intuitive result as beliefs about the relative expected payoffs of the options should change more rapidly in more volatile environments. There was a significant interaction between volatility and run length of exploitive trials, F(2,137) = 4.47, p < 0.001.

Figure 2.

“Hazard rate of exploration” for participants (A) and the three models under consideration (B–D), defined as the probability of exploring as a function of the number of consecutive exploitative choices after observing a payoff jump. Thus, for example, n = 4 refers to a situation where, beginning with the observation of a jump, three exploitative choices are made before an exploratory choice. Critically, the reflective nature of the Belief model and the Ideal Actor results in a monotonically increasing hazard rate as the models’ certainty about the relative optimality of the options decays over time.

Table 1.

Best-fitting parameter values by model and condition.

Condition	P(flip) (SD)	Softmax parameter (SD)	Total BIC
NAÏVE RL
P(flip) =  0.025		1.9 (0.04)	16365
P(flip) =  0.075		1.4 (0.03)	16730
P(flip) =  0.125		1.1 (0.03)	21134
BELIEF MODEL
P(flip) =  0.025	0.046 (0.033)	3.87 (1.40)	14757
P(flip) =  0.075	0.103 (0.059)	4.78 (2.02)	13668
P(flip) =  0.125	0.134 (0.069)	4.90 (2.28)	16807
IDEAL ACTOR
P(flip) =  0.025	0.01 (0.01)	0.58 (0.23)	16535
P(flip) =  0.075	0.04 (0.05)	0.55 (0.23)	13995
P(flip) =  0.125	0.07 (0.07)	0.59 (0.25)	16914

Model fits

Having specified the three models computationally, we determined which model(s) best characterized participants’ choices across the three volatility conditions. We used maximum likelihood estimation to find the set of parameters that maximized the likelihood of each model for each subject. To compare goodness of fit across models, we used the Bayesian information criterion (BIC: Schwartz, 1978) as the models have differing numbers of free parameters. Note that lower BIC values indicate better fit.

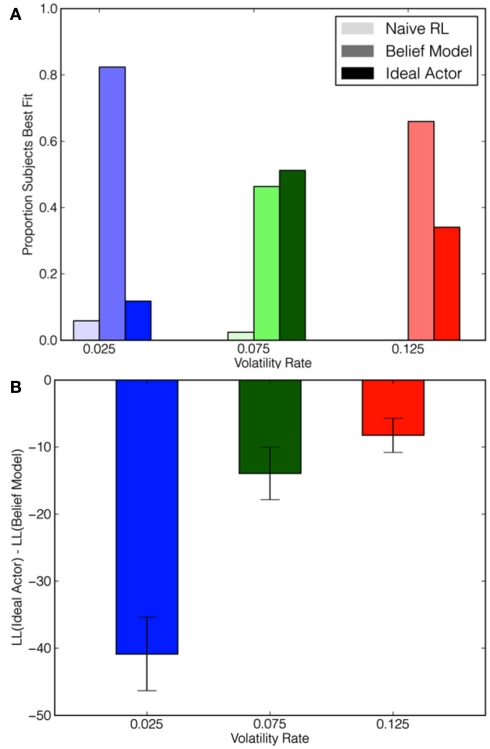
Across all three conditions, subjects were best fit by the Belief model as judged by log-likelihood scores (see Figure 3A). Though the Ideal Actor model fit worse overall (see Figure 3B), it provided the best fit for a considerable number of subjects. Very few subjects were best fit by the Naïve RL model. These results suggest that subjects’ exploration manifests a reflective belief-updating rather than a reflexive process, but they do not appear to be optimally using these beliefs to conduct long-term planning.

Figure 3.

Model goodness of fit measures as a function of model and volatility condition. (A) The proportion of participants that were best fit by each model in each condition. (B) Log-likelihood ratios comparing the Ideal Actor and the Belief model. Negative values indicate that participants were better described by the Belief model.

Choice latency

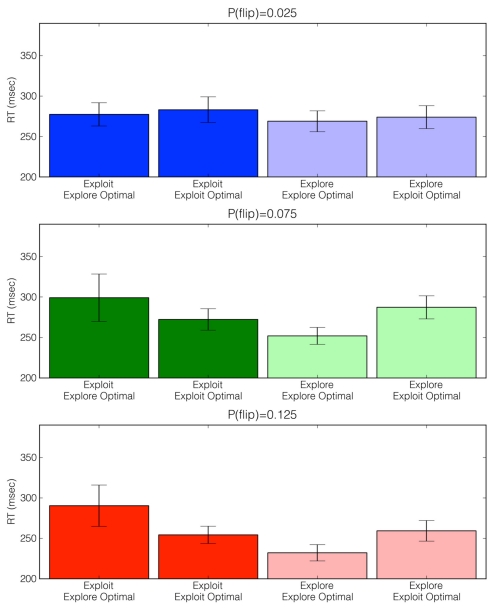
We also hypothesized that choice latencies (as measured by RTs) would provide an online assessment of a reflective and belief-driven decision process. We intuited that RTs would be larger in situations in which participants acted against their beliefs about the currently optimal action – that is, people would exhibit larger choice latencies when they made errors. Supporting this conjecture and following the data pattern of most studies of speeded choice in which response bias is minimal, leading models of choice predict that errors are associated with larger response times than are correct responses (cf. Ratcliff and Rouder, 1998). Accordingly, we factorially examined exploratory and exploitative choice RTs, classifying them as “explore optimal” or “exploit optimal,” defining the two bins based on the Ideal Actor’s choice prescription. To ensure that any effects of choice RT observed were not attributable to sequential effects such as response repetitions or switches (Walton et al., 2004) – which may be confounded with exploratory choices – we first performed a regression to partial out these effects. This model assumed that choice RTs were a linear function of the response repetitions and switches (in relation to the present response) of the previous 10 trials. We then performed the analysis of interest on the resultant residual RTs. Figure 4 depicts the average median reconstructed RTs across the three volatility conditions in the four unique situations described above.

Figure 4.

Adjusted choice reaction times (RTs) across volatility conditions as a function of choice type (exploratory versus exploitative) and Ideal Actor choice prescription (exploit optimal versus explore optimal). For example, the far right bars represent situations in which participants explored when the Ideal Actor prescribed exploiting. Of note is that across the medium [P(flip) = 0.075] and high [P(flip) = 0.125] volatility conditions, participants exhibited larger RTs when they acted against the prescription of the Ideal Actor. See main text for analysis details.

It is apparent that, in the medium [P(flip) = 0.075] and high [P(flip) = 0.125] volatility conditions, participants exhibited larger choice latencies when they acted against the prescription of the Ideal Actor. A mixed-effects linear regression (Pinheiro and Bates, 2000) conducted on these residual RTs (random effects over subjects) revealed a significant interaction between chosen action (explore versus exploit, mirroring non-human primate results reported by Pearson et al., 2009) and prescribed optimal action (exploration-optimal versus exploitation-optimal), β = −8.90, SE = 3.41, p < 0.01. A full list of regression coefficients are provided in Table 2. It is important to note that these effects are prevalent even when explanations such as switch costs are taken into consideration. These patterns did not appear to vary significantly with volatility condition, F = 0.18, p = 0.67.

Table 2.

Choice latency regression coefficients.

Coefficient	Estimate (SE)	p-Value
Volatility	−367.13 (185.93)	0.054
Choice type	5.96 (3.74)	0.1
Optimal choice	3.14 (4.26)	0.24
Volatility × choice type	0.06 (42.21)	0.76
Volatility × prescribed choice	35.06 (48.17)	0.4
Choice type × optimal choice	−8.87 (3.42)	0.006
Volatility × choice type × prescribed choice	7.89 (37.99)	0.71

Model performance

To examine the importance of optimal planning (as opposed to myopic choice) in reflective belief models, we simulated deterministic versions of the Ideal Actor and the Belief model on 10,000 independent instantiations of the Leapfrog task. Rather than use a Softmax choice rule, these models act deterministically: the deterministic Ideal Actor always chooses the highest-valued action and the deterministic Belief model always exploits when the model’s belief that the exploitative option yields higher payoff is greater than 0.5. Both models also employ optimal belief-updating by the Ideal Observer, using the condition’s true P(flip) value. To examine how the addition of stochasticity might improve the Belief model’s performance in this task, we simulated a Softmax variant of the Belief model using the true P(flip) values and Softmax parameters that were optimized to give the best performance. The results reported in Table 3 confirm the importance of planning in the Leapfrog task and the benefit the Belief model derives from an element of stochastic (i.e., random) choice.

Table 3.

Choice performance relative to deterministic Ideal Actor.

Condition	Deterministic Belief model	Stochastic Belief model
P(flip) = 0.025	0.854	0.988
P(flip) = 0.075	0.943	0.978
P(flip) = 0.125	0.946	0.954

Discussion

We examined whether human decision-makers approach exploratory choice in a reflective and belief-directed fashion as opposed to a stochastic and undirected fashion. Using a novel task that allowed for unambiguous identification of the two candidate strategies, we found that decision-makers appeared to be updating their beliefs about relative payoffs in a reflective manner – including knowledge about possible unseen changes in the task structure – but did not seem to be fully utilizing these beliefs by planning ahead with assessments of the informational value of actions. Indeed, for both subjects and reflective models, hazard rates reveal that the probability of exploratory choice increases with the number of immediately previous consecutive exploitive choices (see Figure 2). This quality is not predicted by the reflexive Naïve RL model.

Given the reflexive and reflective models’ qualitatively different predictions of sequential dependency, this comparison yields a strong test for determining which type of belief-updating better matches human behavior. Furthermore, our quantitative model comparisons revealed that the two reflective models clearly provide better fits than the purely reflexive Naïve RL model (see Figure 3A). These results suggest that people do exhibit marked sequential dependency and that their belief updates are reflective. Further, these results give credence to previous usage of reflective models of human choice behavior in bandit tasks (Daw et al., 2006; Boorman et al., 2009), which until now has not been empirically justified.

A number of related contributions dovetail with our reflexive versus reflective distinction. However, the tasks used in these studies differ in important ways. Recent work has sought to identify the contributions of model-based (i.e., reflective) and model-free (i.e., reflexive) strategies of choice in a multistep decision task (Daw et al., 2011). However, model-based behavior in Daw et al.’s study did not entail updating beliefs about option payoffs across trials as uncertainty grew. Instead, a forward model of the environment was used to prospectively evaluate option values in accordance with the environment’s transition structure. Related, Biele et al. (2009) found that a model prescribing use of higher-level strategies in a series of exploration–exploitation problems better predicted the patterns of sequential dependency in human behavior than a naïve sampling model that shared qualities with the Naïve RL model presented here

Critically, participants’ differing levels of exploration across conditions could not be explained by the stochasticity with which they made choices: the best-fitting Softmax parameters did not decrease with environment volatility in either of the two models. Rather, the differences in rates of exploratory choice appear to be accounted for by the best-fitting P(flip) rates.

Notably, we also found that when decision-makers in medium and high volatility environments made sub-optimal decisions (insofar as the choices did not accord with the Ideal Actor’s prescription), they exhibited larger choice RTs compared to when they made optimal choices. Since the Ideal Actor’s choice prescriptions are a function of subjects’ inferred trial-by-trial beliefs, these choice RTs provide another window into the belief-directed and reflective nature of their choices. Indeed, previous experimental work revealed that decision-makers exhibit greater choice latency when choosing options that will result in increased cognitive costs (Botvinick and Rosen, 2009) or when perceived logical conflict – and thus, the potential for making erroneous responses – is high (De Neys and Glumicic, 2008).

Quantitative comparison of the two reflective models – the Belief model and the Ideal Actor – favors the Belief model as a characterization of human choice behavior. Both models employ an Ideal Observer to maintain optimal beliefs about the expectation of immediate reward. However, the Ideal Actor also considers how an exploitative or exploratory action would inform its beliefs and precisely calculates the expected benefit of this information on future reward. Adding this value of information to the Ideal Observer’s expectation of immediate reward, as the Ideal Actor does, decreases the model’s ability to fit participants’ choice behavior (shown in Figure 3B). Thus, it appears that people do not fully utilize these beliefs in a forward-planning way but, rather, appear to use the beliefs in a myopic fashion, in accordance with the Belief model.

In addition to providing a qualitative characterization of the structure of human exploratory choice, this paper contributes two tools for the study of exploratory decision-making. First, we present a task that allows us to disentangle reflective and belief-directed exploration from stochastic and undirected exploration, a feature absent in previous tasks used to examine exploratory choice (Worthy et al., 2007; Jepma and Nieuwenhuis, 2011). Further, the task is also sufficiently constrained to prescribe a statistically optimal pattern of choice, yielding the Ideal Actor. In turn, this model’s belief-updating mechanism provides powerful tools for characterizing human choice behavior in this task, and its choice prescriptions afford the revelation of nuanced patterns of choice latencies that would be undetectable without such a model.

These formal models offer new ways of understanding what exploration is. The definition of exploratory choice depends on how one views the relationship between the actor and the structure of the environment or, even more abstractly, the relationship between the action and the hierarchical structure of the actor (Levinthal and March, 1993). In this paper, we define the exploitative action as a choice of the option that has yielded the highest-experienced payoff up to the time of choice. An alternative trial classification scheme could define an exploitative action as a choice of the option believed – according to a specific model – to give the highest payoff at the time of choice. However, we chose our definition because it avoids commitment to a particular model of choice; a choice is exploitative or exploratory regardless of any model under consideration. Under the alternative definition, exploration in our models could only arise from a purely stochastic process.

Simulations of the Ideal Actor and Belief model suggest an intriguing hypothesis, namely that stochastic behavior may be an adaptation to cognitive capacity limitations in long-range planning. As detailed in Table 3, performance of the Belief model (which does not plan) approaches that of the Ideal Actor (which does plan optimally) when stochasticity is incorporated into the Belief model’s action selection. Consequently, we hypothesize that stochasticity in human decision-making may arise from a sub-optimal valuation process; the knowledge gained from potential exploration is not explicitly incorporated in valuation but is still obtained by random behavior. This hypothesis warrants further investigation through tasks and models that afford requisite discrimination.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Appendix

The Leapfrog task

Here we give a more technical description of the Leapfrog task, using the framework of reinforcement learning (RL). We then briefly introduce partially observable Markov decision processes (POMDPs) and map the Leapfrog task to a highly compacted POMDP task, which we use in the following section to formulate the Ideal Observer, the belief-maintaining component of our reflective models, and the Ideal Actor itself.

We now describe the Leapfrog task more formally within the RL framework. Our task consists of two actions, A and B, two corresponding state variables, s_a or s_b, and reward is 1 for one action and 0 for the other. Given an action X, the reward is 1 if s_X > s_Y and 0 otherwise. s_a = 10 and s_b = 20 when the task starts. At each trial, there is a fixed probability that the lower s_a and s_b increases by 20, switching the two actions’ rewards and, consequentially, which action is optimal (thus the name Leapfrog). We call this probability volatility or P(flip). To create uncertainty that propagates from trial to trial – thus motivating exploration – the agent is not shown its reward. Rather, the agent only observes the value of the state variable that is tied to its action, s_a or s_b. The benefit of showing only s_a or s_b is that the lower-valued state variable can “jump” by 20 points and the agent will not know that the optimal actions are switched until it explores.

The task has a finite horizon (i.e., a set number of trials), and an agent’s performance is evaluated by how much reward it accumulates. Note that, because of the limited observability and stochastic nature of the task, no decision-maker can guarantee to always choose the correct action. Therefore the Ideal Actor, in addition to its use as a model of the human, provides an upper bound on expected performance that facilitates assessment of how well people perform with various volatilities (and consequently, various difficulty levels).

Partially observable Markov decision processes

If the dynamics of a task are determined by a Markov decision process (see Sutton and Barto, 1998; for an introduction to MDPs), but the state cannot be directly observed by the agent – as is the case with the Leapfrog task – the task can often be modeled as a partially observable Markov decision process (POMDP).

To illustrate, consider a navigation task through a maze with a known map. When the decision-maker knows its exact location state at any time (e.g., via GPS), the task maps naturally to an MDP. On the other hand, a decision-maker without such global knowledge must use local features, such as corridors and corners, to localize itself. In this case, more than one location could share the same local features, and the decision-maker must use these observations along with its knowledge of recent movements and previous estimates of location to probabilistically estimate its location. In this case, the task maps well to a POMDP, as Stankiewicz et al. (2006) did for a similar navigation task.

More formally, a POMDP is defined by the set of variables {S, A, T, R, Ω, O} (Kaelbling et al., 1998). S and A are respectively the sets of states and actions. Given an action a_t and a current state s_t at time t, the state transitions to s_t + 1 at time t + 1 with probability T(s_t, a_t, s_t + 1) [i.e., P(s_t + 1 | s_t, a_t)]. At each time step, the agent also receives a real-valued reward, r = R(s, a), and an observation O from the set Ω of possible observations. The probability of an observation o_t can be modeled equivalently as either O(a_t + 1, s_t, o_t) or O(a_t, s_t, o_t) (Kaelbling et al., 1998). In the undiscounted case such as the Leapfrog task, an agent’s goal in a POMDP is to choose actions that maximize return, defined as $E\left[{\sum }_{t=0}^{\infty }{r}_t\right]$.

Within a POMDP, optimal actions are determined not only by expectations of immediate reward and transitions to next states (as in MDPs), but also by the value of knowledge that actions yield. Therefore, an optimal action can have the sole purpose of gathering information about the true state. Note that a POMDP is a formal description of a task and is separate from a model of choice within the task.

Specifying the Leapfrog task as a three-state POMDP

As described, the leapfrog task can be specified as a POMDP with two state variables; s_A and s_B can respectively take values in {10, 30, …, 10 + 10n} and {20, 40, …, 20 + (10n)}, where n is the number of trials.

However, we can specify the task much more compactly, reducing the belief space to three dimensions (one per state) from the n² dimensions it would otherwise have, making the Leapfrog task tractable to solve exactly. To justify this more compact representation, we first let s_H be the action-tied state variable (s_A or s_B) with the Highest observed number, which we call o_H, and s_¬H be the other action-tied state variable; H and ¬H are their corresponding actions. Thus H frequently changes its mapping between the two possible actions in the task. Consequently, according to the definitions in the main text, choosing H would constitute an exploitative choice and choosing ¬H would constitute an exploratory choice. At any trial, the agent knows the minimal states for (s_H, s_¬H) are (o_H, o_H − 10), based on the leapfrogging nature of the task.

For a trial with o_H, there are three possible action-tied state pairs (s_H, s_¬H). The pairs (o_H, o_H − 10) and (o_H, o_H + 10) occur when there are zero and one unobserved jumps, respectively. When there are two unobserved jumps, resulting in the pair (o_H + 20, o_H + 10), the agent is guaranteed to observe at least one jump regardless of its action. Since there is at most one new jump per trial, this guarantee of observing a jump makes it impossible to have more than two unobserved jumps. Note that action H (i.e., exploiting) receives a reward of 1 only when there are zero or two unobserved jumps. Therefore, the three possible states of our compacted POMDP are 0, 1, or 2 unobserved jumps. Additionally, a belief within this compacted POMDP is a vector of the probabilities that there are 0, 1, or 2 jumps, which necessarily sum to 1. Following this, the compacted observations are the number of previously unobserved jumps seen in a trial (0, 1, or 2), where payoffs o_H − 10 and o_H yield the same observation of 0 previously unseen jumps. In summary, the compacted POMDP has three states, three observations, two actions, and two possible rewards values.

Models of human behavior and the Ideal Observer

This section gives a full technical description of the Ideal Observer, which optimally maintains a distribution over possible state, and the Ideal Actor, the model that reflectively incorporates optimal beliefs along with an exact assessment of the information-based value of actions. On the explicative path to the Ideal Actor, we comment on the other two models of human behavior used in our evaluations, Naïve RL and Belief.

All models choose options based on a Softmax choice rule that takes a model’s valuation of each action as input. The probability of choosing option A at time t with payoff belief b_t, is

$$P_t\left(A\right)=\frac{e^{\gamma Q_t\left(b_t,A\right)}}{e^{\gamma Q_t\left(b_t,A\right)}+e^{\gamma Q_t\left(b_t,B\right)}}.$$

Here, Q_t(b_t, ·) is the model’s assessed value of option A or B, and γ is the Softmax inverse temperature parameter, the determination of which is described in the Model Fits section of this paper’s body.

Naïve RL model

The simplest model reflexively maintains beliefs about payoffs based only on what it has seen. In other words, it believes the point payoffs for each action are those most recently observed. Therefore, the Naïve RL model assumes that action H and ¬H respectively give rewards of 1 and 0. Its expectation of each action’s reward, Q(·), is input into a Softmax action selector, giving it a constant probability of exploring or exploiting:

$$P\left(H\right)=\frac{exp\left[\gamma Q\left(H\right)\right]}{exp\left[\gamma Q\left(H\right)\right]+exp\left[\gamma Q\left(\neg H\right)\right]}=\frac{exp\left[\gamma \right]}{exp\left[\gamma \right]+1}.$$

Here, γ is the Softmax inverse temperature parameter. In Softmax action selection, as this parameter rises, the probability that the highest-valued action (i.e., the greedy action) will be chosen increases. When the Softmax parameter approaches infinity, actions become deterministically greedy; at zero, the parameter creates uniformly random action selection. As mentioned in the main text, the Naïve RL model is equivalent to a memory-based RL agent, with a memory size of one, which is appropriate given the deterministic nature of the payoffs and that payoffs never return to previous values; a larger memory would not yield useful information for a reflexive model performing the Leapfrog task. Algorithmically, this model is equivalent to the Softmax model used in Worthy et al. (2007) and Otto et al. (2010), with a learning rate of 1.

Ideal observer

An Ideal Observer uses past actions and observations optimally to update its belief distribution over the set of states. The Ideal Observer – agnostic to action selection – is used as a component of the belief and Ideal Actor models described below, providing correct beliefs at each time step. Because POMPDs by definition satisfy the Markov property (Kaelbling et al., 1998), belief updates can be performed with only the past belief, the last action, and the last observation, given knowledge of the observation and transition functions. In other words, the Ideal Observer can dispense with the remainder of its history of actions, beliefs, and observations.

Below, we show the derivation of our optimal Bayesian belief-updating procedure, which is specific to the case of POMDPs where observation o_t is a function of s_t and a_t, not the more typical s_t and a_t − 1,¹ since the number of unobserved jumps and the action determine the number of newly observed jumps. The final line of this derivation, a function of known distributions, is used to calculate the next state belief. In this notation, we put a_t and b_t after a “;” because they are fixed and known and are thus considered to parameterize the probability distributions.

$$\begin{array}{l}P\left(s_{t+1}=i|o_t;a_t,b_t\right)=\frac{P\left(s_{t+1}=i|o_t;a_t,b_t\right)}{P\left(o_t;a_t,b_t\right)}\\ P\left(s_{t+1}=i|o_t;a_{t,}{b}_t\right)\alpha P\left(s_{t+1}=i,o_t;a_t,b_t\right)\\ b_{t+1}\left(i\right)\alpha P\left(s_{t+1}=i,o_t,s_t=j;a_t,b_t\right)\\ b_{t+1}\left(i\right)\alpha {\displaystyle \sum _{j}P\left(s_{t+1}=i,o_t,s_t=j;a_t,b_t\right)}\\ b_{t+1}\left(i\right)\alpha {\displaystyle \sum _{j}P\left(o_t|s_{t+1}=i,s_t=j;a_t\right)P\left(s_{t+1}=i,s_t=j;a_t,b_t\right)}\\ \left(o_t\text{\hspace{0.17em}is\hspace{0.17em}contd.\hspace{0.17em}indep.\hspace{0.17em}of\hspace{0.17em}}{s}_{t+1}\text{\hspace{0.17em}given\hspace{0.17em}}{s}_t\right)\\ b_{t+1}\left(i\right)\alpha {\displaystyle \sum _{j}P\left(o_t|s_t=j;a_t\right)}P\left(s_{t+1}=i|s_t=j;a_t\right)P\left(s_t=j:b_t\right)\\ b_{t+1}\left(i\right)\alpha {\displaystyle \sum _{j}P\left(o_t|s_t=j;a_t\right)P\left(s_{t+1}=i|s_t=j;a_t\right)}{b}_t\left(j\right)\end{array}$$

Belief model

We can easily specify a model that values actions by their expected immediate rewards according to the Ideal Observer, creating a more sophisticated action selection technique than simply always choosing H. More precisely, this more sophisticated Belief model is more likely to choose action H than ¬H when b_t + 1(0) + b_t + 1(2) > 0.5 – that is, when it believes that there are probably 0 or 2 unobserved jumps and thusly action H is expected to yield the higher immediate reward.

If the Belief model chooses the action deterministically, the model is optimal with respect to maximizing immediate reward. However, this model would not be fully optimal in the long-term because its choices fail to take into account the informational benefit of each action.

Ideal actor model

An Ideal Actor uses beliefs reflectively provided by its Ideal Observer component to consider expected immediate reward, but it also evaluates an action’s effect on its longer-term expectation of return caused by the change in its belief distribution. In other words, the Ideal Actor sometimes chooses actions with lower immediate rewards to increase its knowledge about the true state, facilitating more informed decisions in future trials. To implement the Ideal Actor, we employed the Incremental Pruning algorithm (using the POMDP-Solve library, Cassandra et al., 1997), an exact inference method that calculates action-value functions (i.e., Q-functions) for each time horizon (i.e., number of trials remaining).² We used the implementation of Incremental Pruning from the POMDP-Solve library. This action-value function Q_t, where t is the horizon, takes as input a belief b_t and an action H or ¬H and outputs a real-number value. The belief vector input to Q_t comes from the Ideal Observer’s belief, making the Ideal Actor a reflective model. If acting optimally, the Ideal Actor deterministically chooses argmax_a Q_t(b_t, a), where a ∈ {H, ¬H}. Unlike other actor models examined in this paper and in previous work, the Ideal Actor chooses actions based on both its belief about the immediate reward and the expected benefit from the knowledge gained by choosing each action. Figure 1A illustrates the trial-by-trial relative Q-values – that is, Q_t(b_t, H) – Q_t(b_t, ¬H) – which are a function of the Ideal Observer’s trial-by-trial belief (shown in Figure 1B).

Model-fitting procedure

For each model, we sought parameter estimates that maximized the likelihood of each participant’s observed choices given their previous history of choices and outcomes:

$$L_{\text{model}}=\prod _t{P}_{c,t}$$

where c,t reflects the choice made on trial t and P_c,t is the probability of the model choosing c,t, informed by participant's choice and payoff experience up to trial t. We conducted an exhaustive grid search to optimize parameter values for each participant. To compare models, we utilized the Bayesian information criterion (BIC: Schwartz, 1978), which is calculated by

$$\text{BI}{\text{C}}_{\text{model}}=-2\times 1\text{n}\left(L_{\text{model}}\right)+k_{\text{model}}\cdot 1\text{n}\left(n\right)$$

where k is the model’s number of free parameters and n is the number of trials being fit (500 in all cases).