Resolution limit for DNA barcodes in the Odijk regime

Abstract

We develop an approximation for the probability of optically resolving two fluorescent labels on the backbone of a DNA molecule confined in a nanochannel in the Odijk regime as a function of the fluorescence wavelength, channel size, and the properties of the DNA (persistence length and effective width). The theoretical predictions agree well with equivalent data produced by Monte Carlo simulations of a touching wormlike bead model of DNA in a high ionic strength buffer. Although the theory is only strictly valid in the limit where the effective width of the nanochannel is small compared with the persistence length of the DNA, simulations indicate that the theoretical predictions are reasonably accurate for channel widths up to two-thirds of the persistence length. Our results quantify the conjecture that DNA barcoding has kilobase pair resolution—provided the nanochannel lies in the Odijk regime.

INTRODUCTION

DNA barcoding is emerging as a key tool for high-throughput, single-molecule analysis of the genome at the kilobase pair level, representing an important complement to DNA sequencing.¹ As illustrated in Fig. 1a , specific sequences (the DNA barcodes) are fluorescently labeled by either binding the probes to the chain^{2, 3, 4, 5} or inserting labeled nucleotides via nick extension.^{6, 7} The backbone is fluorescently labeled with a second color through an intercalating dye such as YOYO-1. To determine the genomic distance between barcode markers, the DNA needs to be stretched from its equilibrium, coiled conformation. Several competing technologies have arisen to accomplish this task: using a receding contact line and subsequent binding to the surface (molecular combing),^{8, 9, 10} extensional flow (direct linear analysis),^{11, 12, 13} and nanochannel confinement.^{5, 6, 7, 14, 15} The genomic distance between neighboring barcodes is then determined by first locating the centers of the sequence-specific labels and then integrating the total backbone fluorescence intensity between these two locations. Nanochannels provide a particularly attractive approach to make such measurements since a confined chain fluctuates about its equilibrium extension; making multiple, statistically independent measurements of the distance reduces the sampling error.^{5, 16}

Figure 1.

(a) Principle of DNA barcoding. If the linear distance in the focal plane between barcodes does not exceed the diffraction limit, λ/2, for light of wavelength λ, then the two fluorophores cannot be resolved. (b) Illustration of the chain extension in different regimes of confinement. The configurations were generated using the simulation method in Sec. 3 with a chain with an approximate size of 27.7 kilobase pair (kbp). Only part of the chain is shown in the figure. The persistence length is l_p = 53 nm (Ref. ¹⁷) and the effective width¹⁸ is w = 4.6 nm, appropriate for TBE 5x buffer.¹⁹, ²⁰ The two blue spheres in each snapshot are shown to illustrate barcodes with one of the barcodes located at the end of the chain and the other barcode at 2 kbp.

A fundamental question related to DNA barcoding in nanochannels is the ability to resolve two nearby barcodes on the DNA backbone. If we consider a sequence-specific probe that emits light with wavelength λ = 573 nm (Ref. ¹⁴) and a completely extended DNA molecule with a rise of 0.34 nm per base pair (bp), then two probes would have to be separated by at least 843 bp if we take λ/2 as an estimate of the resolution limit for diffraction limited optics. However, as we can see from simulation data in Fig. 1b, the semi-flexible nature of the DNA leads to incomplete stretching, even in very small channels lying in the Odijk regime.²¹ In this paper, we develop an approximation for the probability of resolving two nearby barcodes as a function of the nanochannel size and the properties of the DNA (persistence length and effective width), which themselves depend intimately on the ionic strength of the buffer.^{18, 22, 23, 24} Our results apply to the Odijk regime, which is the most desirable regime for DNA barcoding.^{6, 15}

THEORY

The equilibrium two-point distribution function ${\Psi }_{\mathit{ij}}(r_{\mathit{ij}})$ quantifies the probability density for segment i and j, corresponding to a genomic distance |j − i|, being separated by a linear distance $r_{\mathit{ij}}=|{\overrightarrow{r}}_i-{\overrightarrow{r}}_j|$ in the focal plane of the image. In our theoretical analysis, we envision the “segments” to be base pairs of the chain, whereupon the contour length per segment is given by the rise of DNA, r. In our simulations, we will consider a slightly coarser model where the characteristic length scale is the effective width of the chain, w. Owing to the symmetry of the square channel, we only need to assume that focal plane is parallel to one of the walls of the channel but we do not need to specify which wall.²⁵ While Ψ_ij is known for a confined Gaussian chain,²⁶ there are no results for more complicated cases,²⁷ such as the wormlike chain in a good solvent we need here. However, we do not need to compute this distribution function to determine the probability of resolving two barcodes. Rather, we can define the probability

$$\psi (j|i)={\int }_{\lambda /2}^{\infty }{\Psi }_{\mathit{ij}}(r_{\mathit{ij}})\mathrm{d}{r}_{\mathit{ij}}$$ (1)

that, given a barcode marker at some point i along the chain, we are able to resolve a second marker at some different point j. The average probability of resolving a pair of barcode markers on a chain of N base pairs separated by n = |j − i| base pairs is then

$$p(n)=\frac{1}{N-n}\sum _{i=1}^{N-n}\psi (i+n|i).$$ (2)

We are interested in computing p(n) for the Odijk regime,²¹ which applies to nanochannel widths much smaller than the chain persistence length, l_p. The width of the channel accessible to the centerline of the DNA backbone is D_eff = D − w in the limiting case of steric interactions only, where w is the effective width of the DNA.¹⁸ While the inequality $D_{\mathrm{eff}}\ll l_p$ may appear to be so restrictive as to exclude all reasonable nanochannel sizes that allow easy insertion of DNA,²⁸ we will see that our final result is a reasonable approximation out to $D_{\mathrm{eff}}\cong l_p$. In the Odijk regime, a chain of total length L consists of a series of deflection segments with the mean span

$$〈R_{\parallel }〉=L[1-2\alpha {(D_{\mathrm{eff}}/l_p)}^{2/3}],$$ (3)

where α = 0.09137 ± 0.00007.²⁵ The variance of the extension in this regime is

$$〈R_{\parallel }^2〉-{〈R_{\parallel }〉}^2=2\beta {\mathit{LD}}_{\mathrm{eff}}^2{l}_p^{-1},$$ (4)

where β = 0.00478 ± 0.00010.²⁵

We can construct an approximate model for p(n) in the Odijk regime through the following ansatz. We assume the chain is long compared with the distance n between barcodes and that the barcodes are not located too close to the end of the chain, whereupon Ψ_ij ≈ Ψ_n and ψ(i + n|i) ≈ p(n). If we further neglect the contribution of lateral fluctuations between the two barcode points, ${\Psi }_{\mathit{ij}}(r_{\mathit{ij}})\approx {\Psi }_n(x)$, where x is the distance down the channel axis and Ψ_n(x) is interpreted as the distribution function for the distance in the x-direction between segments on the chain separated by a genomic length n. Equation 1 then reduces to

$$p(n)\approx {\int }_{\lambda /2}^{\infty }{\Psi }_n(x)\mathrm{d}x.$$ (5)

In a high ionic strength buffer, the diffraction limit is long compared with the size of a deflection segment. Neglecting prefactors of order unity, but retaining the definition of the diffraction limit, this corresponds to²¹

$$\lambda /2>>D_{\mathrm{eff}}^{2/3}{l}_p^{1/3}.$$ (6)

Provided we satisfy Eq. 6, then the integral in Eq. 5 always involves many deflection segments. It is thus reasonable to assume that the average distance, $\overline{x}$, and variance, σ², between the two barcodes separated by a contour length L = r|i − j| > λ/2, where r is the rise of double stranded DNA, are given by Eqs. 3, 4, respectively. If we further assume a normal distribution for the distance between these barcodes,

$${\Psi }_n(x)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp [-\frac{{(x-\overline{x})}^2}{2{\sigma }^2}],$$ (7)

then Eq. 5 leads to

$$p(n)=\frac{1}{2}\mathrm{erfc}\left(\frac{\lambda -2\overline{x}}{2^{3/2}\sigma }\right),$$ (8)

where $\mathrm{erfc}(\mathrm{x})=(2/{\pi }^{1/2}){\int }_x^{\infty }\exp (-t^2)\mathit{dt}$ is the complementary error function. Equation 8 is the key result of our analysis.

SIMULATION METHOD

The logic leading to Eq. 8 involves a number of assumptions. We tested these assumptions by using Monte Carlo simulations to directly compute p(n) from Eq. 2 in square nanochannels of width D. The “touching bead” simulation model²⁹ we used here, illustrated in Fig. 2, is a modification of the model we used previously²⁰ to study the different regimes of confined DNA. The chain consists of N = 2048 beads of size w = 4.6 nm. All beads interact by a hardcore excluded volume with one another and with the walls, whereupon we identify w as both the coarse-graining size (in the direction along the backbone) and the effective width of the DNA chain (in the direction perpendicular to the backbone). The value of 4.6 nm is the Stigter effective width^{18, 30} for DNA in TBE 5x buffer.^{19, 20} To provide a connection with experiments, we will ultimately convert the simulation data (in terms of the beads) into the experimentally relevant genomic distances using the conversion factor w/r. We take r = 0.34 nm/bp as the rise of DNA. Since intercalating dyes can introduce an increase in the rise of DNA,³¹ this conversion should be considered approximate and our results for the resolution limit are likely conservative estimates. Neighboring beads also experience a bending potential given by the discretized wormlike chain model³²

$$U_{\mathrm{bend}}\approx k_{B}T(l_p/w)\sum _{k=1}^{N-2}(1-{\overrightarrow{u}}_k·{\overrightarrow{u}}_{k+1}),$$ (9)

where l_p = 53 nm is the persistence length¹⁷ and ${\overrightarrow{u}}_j=({\overrightarrow{r}}_{j+1}-{\overrightarrow{r}}_j)/l$, j ∈ [1, N − 1] is the unit vector between beads j and j + 1.

Figure 2.

Schematic illustration of the touching bead model. The “segments” of the chain, numbered from k = 1 to k = N, are spherical beads of size w that experience hardcore bead-bead and bead-wall interactions. The bending energy is computed from the discrete wormlike chain model in Eq. 9 using the vectors $\overrightarrow{u}$ pointing between bead centers. For calculations of p(n), we compute the distance x between each pair (i,j) in the direction of the channel axis.

Chain configurations were generated using reptation and crankshaft moves in the Metropolis scheme. Simulations for each channel size were performed in 12 replicates. The simulations for a channel of size D were initialized using a configuration generated from preceding simulations of a slightly smaller channel to guarantee acceptance of the initial configuration. Upon increasing the channel size, we first waited for the mean extension to stabilize around the average value in the larger channel, and then added an additional 2.048 × 10⁷ equilibration steps before starting the production run. This approach introduces a slight bias against hairpin configurations, which are difficult to form in the smallest channels. However, the long equilibration time and the small change in channel width between simulations minimizes this bias.

To determine an appropriate sampling time for computing the chain statistics, we calculated the auto-covariance of the extension,³³

$$C_{R_{\parallel }}(n)=\frac{{〈R_{\parallel }(m)R_{\parallel }(m+n)〉}_m-{〈R_{\parallel }〉}^2}{〈R_{\parallel }^2{〉-〈R_{\parallel }〉}^2}.$$ (10)

Figure 3 shows the decay of the auto-covariance with the number of Monte Carlo steps. On average, the auto-covariance is sufficiently attenuated after approximately 2.048 × 10⁸ trial moves. In what follows, we used sampling rates of 4.096 × 10⁸ trial moves for the 10 nm and 20 nm channels and 2.048 × 10⁸ trial moves for the 30 nm and 40 nm channels, which produces 10 statistically independent configurations per replicate.

Figure 3.

Auto-covariance of the chain extension as a function of the number of Monte Carlo steps normalized with the size of the chain. Symbols are averaged results over the 12 independent runs.

In our prior work,²⁰ we used a bead-rod model with a Weeks-Chandler Anderson (WCA) potential³⁴ to provide bead-bead excluded volume. With our code for this model, we were able to reach a long chain (2048 beads, 9.42 μm contour length, 27.7 kbp) without sacrificing the spatial resolution. In free solution, this model produces a root-mean-square end-to-end distance of 1.06 μm, a root-mean-square radius of gyration of 0.43 μm, and a mean span dimension of 0.88 μm. All of these values agree well with our prior simulations,²⁰ which themselves match experimental results. Likewise, the results for the fractional extension of this chain exhibit the same scaling laws as simulations of our prior model.²⁰

RESULTS AND DISCUSSION

In Eq. 7, we assumed that the distance between barcodes is normally distributed, with the mean and variance given by those for the mean span of a chain in the Odijk regime.^{21, 25} In Fig. 4, we compare this assumption to the simulation data for two barcodes separated by 1001 base pairs. Using a rise of 0.34 nm/bp and a persistence length of 53 nm, these data correspond to barcodes separated by 6.4 persistence lengths. The normal distribution appears to be an excellent model for the simulation data in Fig. 4. Nevertheless, there is reason to be cautious about assuming a normal distribution in Eq. 7, since it permits unphysical stretching of the chain. Explicitly, the normal distribution is supported over x ∈ (−∞, +∞), so there is a finite probability that two barcodes separated by a contour length l will be separated by a linear distance x > l. For n = 1001 bp, the maximum distance between barcodes is approximately 340 nm. Fortunately, for all of the cases plotted in Fig. 4, the relatively small variance in the chain extension given by Eq. 4 leads to the normal distribution being strongly attenuated near x = l. As a result, Ψ_ij(x > l) makes a negligible contribution to the integral in Eq. 5. The normal distribution also permits a nonsensical probability that x < 0. Since the probability distribution decays quickly enough at the upper bound x = l and the mean of the distribution is closer to x = l than x = 0, then the probability distribution is exponentially small at the other physical limit, x = 0. While the data in Fig. 4 give us confidence in the validity of using a normal distribution, we will return to this issue after evaluating the corresponding theoretical predictions for p(n).

Figure 4.

Comparison between Monte Carlo simulation data for the probability distribution Ψ_n and the assumed form in Eq. 7 for two barcodes separated by n = 1001 base pairs for λ = 573 nm, l_p = 53 nm, and w = 4.6 nm. The different curves correspond to Eq. 7 for channel sizes D between 10 and 40 nm, and the symbols are the values of the binned data.

We thus turn our attention to the second key assumption of our theory, namely, that the distance between barcodes on the interior of the chain obeys the statistics for a long chain in the Odijk regime. Naturally, this can only be the case if the chain as a whole, which contains a large number of deflection segments, also obeys the statistics for the Odijk regime. As we can see in Fig. 5, the prediction of Eq. 3, which contains no adjustable parameters,²⁵ is an excellent fit for our smallest channel. As the effective channel size increases, there is a systematic deviation between the predictions for the Odijk regime and the simulation data. The origin of the deviation is apparent in Fig. 1b, where the chain is beginning to form hairpins.¹⁹ However, the deviation from the theoretical prediction is quite small, ranging from 0.1% to 3.2% over the range D = 10 nm to D = 40 nm.

Figure 5.

Comparison between the extension of the chain and the predictions from the Odijk regime with no adjustable parameters given by Eq. 3. The simulations correspond to 2048 touching wormlike beads with l_p = 53 nm and w = 4.6 nm. The channel width accessible to the chain is D_eff = D − w. The error bars correspond to the standard deviation over the 12 independent replicas.

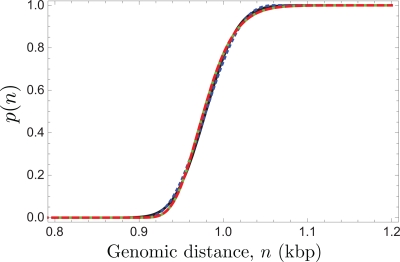
Figure 6 compares the predictions of Eq. 8 to our simulation data. Since we already confirmed in Fig. 4 that the probability distribution p(n) is reasonably Gaussian for all of these channel sizes, we can conclude that the deviation between the theory and simulation in Fig. 6 is due to a gradual breakdown in the Odijk regime (Fig. 5) as the chain begins to form hairpins (Fig. 1). Indeed, the agreement between the theoretical prediction and the simulation data for p(n) in Fig. 6 mirrors the phenomenon we observed in Fig. 5. Nevertheless, the approximate theoretical result given by Eq. 8 appears to be a quite good description for all of these channels. Although the numerical results for the mean span and its variations in Eqs. 3, 4 are only valid in the limit $D_{\mathrm{eff}}\ll l_p$, it seems that they provide a reasonable approximation for the configuration of an internal segment of the chain up to D_eff ≈ 2l_p/3.

Figure 6.

Comparison between Monte Carlo simulation data for the probability of resolving two barcodes separated by a genomic distance n, p(n), and the prediction from Eq. 8 for λ = 573 nm, l_p = 53 nm and w = 4.6 nm. The different curves correspond to Eq. 8 for channel sizes D between 10 and 40 nm, and the symbols are the values of the simulation data.

We also investigated the effect of relaxing the assumption of a normal distribution in Eq. 7 by considering other “Gaussian-like” distributions. A natural alternative is the inverse Gaussian distribution (also called the Wald distribution).³⁵ In the large L limit, the inverse Gaussian distribution limits to the normal distribution, making it an appropriate choice for proximate barcodes separated by a handful of deflection segments. We also considered distributions that would remove the unphysical features of the normal distribution. The log-normal distribution is supported on x ∈ (0, ∞), removing the possibility for a “negative” extension, and the raised cosine distribution has a finite support, which further removes the possibility of overextension. As we can see in Fig. 7, the results for the resolution limit in a 40 nm channel, which has the broadest distribution for Ψ_n, are effectively unchanged by the choice of any of these “Gaussian-like” probability distributions. The results in Fig. 7 support our choice of the normal distribution to describe the probability distribution even though its limits are not physical; the normal distribution gives essentially the same results for p(n) as a more realistic model, such as the raised cosine distribution, while permitting the simple expression for p(n) given by Eq. 8.

Figure 7.

Comparison of the predictions for p(n) in the 40 nm channel corresponding to different probability distributions for Ψ_n(x), using the statistics for a chain in the Odijk regime given by Eqs. 3, 4. The various curves correspond to the normal distribution for R_‖ (black, solid), a raised cosine distribution for R_‖ (blue, dots), a log-normal distribution for L − R_‖ (red, dashed) and an inverse Gaussian distribution for L − R_‖ (green, solid).

All of our simulation data and discussion thus far focused on the configurations of confined DNA in a high ionic strength buffer, where DNA-DNA and DNA-wall electrostatic interactions are screened. In this case, the inequality given by Eq. 6 holds and the diffraction limit corresponds to many deflection segments. As the ionic strength of the solution is decreased, the electrostatic interactions become sensible and lead to an increase in both the persistence length of the DNA^{22, 23, 24} and the effective width.¹⁸ Schwartz and coworkers^{6, 15} have advocated the use of low ionic strength buffers to permit DNA barcoding in relatively wide nanochannels (nanoslits). By increasing the persistence length, these nanochannels still satisfy the criteria for the Odijk regime, $D_{\mathrm{eff}}\ll l_p$, especially when we recall that D_eff = D − w and the effective width w also increases as the ionic strength decreases. We can make a crude estimate for the bounds of our theory by assuming that these systems operate in a regime D_eff ≈ l_p, corresponding to the edge of the Odijk regime in Fig. 5. In such circumstances, our theory would only be valid for $\lambda /2>>l_p$, corresponding to ionic strengths down to around 0.1–1 mM.³⁶ This value is similar to the most recent low ionic strength experiments aimed towards DNA barcoding,¹⁵ so our results represent a conservative estimate for the maximum barcode density for these experiments. However, we should use caution in applying the results for square nanochannels to nanoslits.³⁷

CONCLUDING REMARKS

In the present contribution, we have developed an approximation for the probability of resolving two nearby barcodes on a DNA molecule confined in a nanochannel as a function of the channel size, the wavelength of the fluorescence, and the properties of the DNA (persistence length and effective width). Although the final result in Eq. 8 required assuming that (i) the linear distance between barcodes is normally distributed and (ii) that the statistics for these short, internal sections of the chain are equivalent to an infinitely long chain, we found that the theory leads to a reasonable description of the simulation data. While we chose to use a normal distribution for algebraic simplicity, the results for the probability of resolving two barcodes are essentially unchanged when we use more realistic probability distributions (and the concomitantly more difficult algebra.) Our results provide a theoretical basis for claims that the resolution of DNA barcoding in nanochannels is around 1 kbp.^{16, 38}

Our conclusions are based exclusively on the equilibrium chain statistics. Such an analysis tacitly assumes that we can actually measure the instantaneous chain configuration or, in the case of barcoding, the instantaneous location of the two barcodes. While the fluorophores used for DNA barcodes are bright enough to image before they photobleach, the rate of photon emission relative to the fluctuations in the chain extension is probably low. As a result, the photons need to be collected over a period of time to increase the signal-to-noise ratio to an acceptable level. The imaged fluorophore “position” is then a smeared value of the instantaneous positions corresponding to each photon emission. Our results likely correspond to a theoretical lower bound on the minimum distance between fluorophores.

While we had success in determining the resolution limits in the Odijk regime, we have less confidence that this approach can be extended easily into other regimes of confinement.^{20, 37, 39, 40} As the channel size increases, the size of the statistical segment increases as well. For example, in the so-called “extended de Gennes” regime,²⁰ which is more representative of the confinement regime in recent DNA barcoding experiments,^{5, 7} the chain consists of anisometric compression blobs with a characteristic size $H\cong {(D_{\mathrm{eff}}{l}_p)}^{2/3}{w}^{-1/3}$.³⁹ For a 250 nm nanochannel with l_p = 53 nm and w = 4.6 nm, the blob size (neglecting prefactors of order unity) is commensurate with the diffraction limit and it is no longer appropriate to adopt a resolution model that requires an assumption similar to Eq. 6. While we can certainly compute the probability of resolving two nearby barcodes using Monte Carlo simulations of the type employed here, developing the corresponding theoretical model remains challenging.