Ion selectivity and current saturation in inward-rectifier K⁺ channels

Abstract

We investigated the features of the inward-rectifier K channel Kir1.1 (ROMK) that underlie the saturation of currents through these channels as a function of permeant ion concentration. We compared values of maximal currents and apparent K_m for three permeant ions: K⁺, Rb⁺, and NH₄⁺. Compared with K⁺ (i_max = 4.6 pA and K_m = 10 mM at −100 mV), Rb⁺ had a lower permeability, a lower i_max (1.8 pA), and a higher K_m (26 mM). For NH₄⁺, the permeability was reduced more with smaller changes in i_max (3.7 pA) and K_m (16 mM). We assessed the role of a site near the outer mouth of channel in the saturation process. This site could be occupied by either permeant ions or low-affinity blocking ions such as Na⁺, Li⁺, Mg²⁺, and Ca²⁺ with similar voltage dependence (apparent valence, 0.15–0.20). It prefers Mg²⁺ over Ca²⁺ and has a monovalent cation selectivity, based on the ability to displace Mg²⁺, of K⁺ > Li⁺ ∼ Na⁺ > Rb⁺ ∼ NH₄⁺. Conversely, in the presence of Mg²⁺, the K_m for K⁺ conductance was substantially increased. The ability of Mg²⁺ to block the channels was reduced when four negatively charged amino acids in the extracellular domain of the channel were mutated to neutral residues. The apparent K_m for K⁺ conduction was unchanged by these mutations under control conditions but became sensitive to the presence of external negative charges when residual divalent cations were chelated with EDTA. The results suggest that a binding site in the outer mouth of the pore controls current saturation. Permeability is more affected by interactions with other sites within the selectivity filter. Most features of permeation (and block) could be simulated by a five-state kinetic model of ion movement through the channel.

INTRODUCTION

In addition to K⁺ itself, inward-rectifier K⁺ channels conduct other ions including Rb⁺, Tl⁺, and NH₄⁺. In Kir1.1 (ROMK), Rb⁺ behaves similarly to K⁺ but has a lower conductance and permeability. NH₄⁺ is the only other physiologically important cation besides K⁺ that is conducted by these channels. The selectivity properties of NH₄⁺ are interesting because the relative permeability P_NH4/P_K measured under bi-ionic conditions is 0.1, whereas the relative conductance g_NH4/g_K is approximately one (Chepilko et al., 1995; Choe et al., 2000). This suggests that NH₄⁺ ions can pass through the channels easily but have weaker binding interactions within the pore. K⁺ could then readily displace NH₄⁺ from the pore, accounting for the low NH₄⁺ permeability under bi-ionic conditions.

Inward-rectifier K channels have a high affinity for K⁺ ions as assessed by the concentration dependence of conduction. In both Kir1.1 and Kir2.1, currents saturate at low concentrations, with apparent K_m values on the order of 10 mM (Lu and MacKinnon, 1994a; D’Avanzo et al., 2005). In the present study, we investigated the relationship between Kir1.1 cation affinity and permeability. In general, Kir1.1 had lower affinities for less permeable cations. However, the relationship between conductance, permeability, and K_m is complex and appears to involve interactions with different parts of the channel. Permeability depends on binding affinities within the selectivity filter, whereas K_m is strongly influenced by sites outside the filter.

MATERIALS AND METHODS

Expression of Kir1.1 in Xenopus laevis oocytes

Oocytes were harvested from Xenopus according to the guidelines of, and with the approval of, the Institutional Animal Care and Use Committee of Weill Cornell Medical College. The animals were anesthetized through immersion in 1 liter of tap water containing 1.9 g L⁻¹ tricaine methanesulphonate and HEPES (adjusted to pH 7.4) for 5–10 min. Once the animals were anesthetized, a small incision was made in the abdomen and part of the ovary was removed. The oocytes were then dissociated through incubation in OR2 solution (in mM: 82.5 NaCl, 2.5 KCl, 1 MgCl₂, 1 Na₂HPO₄, and 5 HEPES, pH 7.4) supplemented with 2 mg ml⁻¹ collagenase type II (Worthington) and 2 mg ml⁻¹ hyaluronidase type II (Sigma-Aldrich) for 1 h.

pSport plasmids containing Kir1.1b (ROMK2) were linearized with NotI restriction enzyme, and cRNAs were transcribed with T7 RNA polymerase using mMESSAGE mMACHINE T7 kit (Invitrogen). cRNA pellets were dissolved in nuclease-free water and stored at −70°C before use. The oocytes were injected with 10 ng RNA and incubated overnight in L-15 solution supplemented with HEPES, pH 7.4, 63 mg L⁻¹ penicillin, and 145 mg L⁻¹ streptomycin at 18°C. All chemicals were from Sigma-Aldrich unless otherwise noted.

Patch clamp

Before use, the vitelline membranes of the oocytes were mechanically removed in a hypertonic solution containing 200 mM sucrose. Patch-clamp pipettes were prepared from hematocrit capillary glass (VWR International) using a vertical puller (David Kopf Instruments). They had resistances of 2–8 MΩ when filled with 110 mM KCl. For measurements in inside-out patches, pipette and bath solutions contained Cl⁻ salts of K⁺, Rb⁺, and NH₄⁺, as indicated, plus 5 mM HEPES buffered to pH 7.4. In addition, bath solutions contained 0.5 mM EDTA. Currents from cell-attached and excised inside-out patches were recorded with a patch-clamp amplifier (EPC-7; HEKA), digitized with an interface (Digidata 1332A; Axon Instruments). Data were filtered at 1 kHz and analyzed with pCLAMP9 software (Axon Instruments).

Data analysis

Currents were measured from selected recording intervals normally containing a single active channel using all-points histograms. Histograms were fit with double Gaussian functions, and the current amplitude was defined as the distance between the two peaks.

Single-channel currents (i) were analyzed according to the equation:

$$\text{i}={\text{i}}_{\text{max}}/\left(1+{\text{K}}_{\text{m}}/\left[{\text{C}}^{+}\right]\right),$$ (1)

where [C⁺] is the concentration of the permeant ion.

The effects of external blocking ions were analyzed according to the equation:

$$\text{i}\left(\text{B}\right)=\text{i}\left(0\right)/\left(1+\left[\text{B}\right]/{\text{K}}_{\text{i}}\right),$$ (2)

with

$${\text{K}}_{\text{i}}\left(\text{V}\right)={\text{K}}_{\text{i}}\left(0\right)·\text{exp}\left(\text{z}\delta \text{FV/RT}\right),$$ (3)

where [B] is the blocker concentration, z is the blocker valence, V is the transmembrane voltage, and δ is the effective valence or fraction of the electric field at the blocking site. K_i(0) and δ were estimated from linear regression analysis of a linearized form of Eq. 2:

$$\text{ln}\left(\text{i}\left(0\right)/\text{i}\left(\text{B}\right)-\text{1}\right)=\text{ln}\left(\left[\text{B}\right]/{\text{K}}_{\text{i}}\left(0\right)\right)-\text{z}\delta \text{FV/RT}.$$

Kinetic modeling

The kinetic model shown in Fig. 10 was evaluated using Matlab 7.8.0 as described previously (Edvinsson et al., 2011). Rate constants were calculated based on the values set for binding energies, energy barriers, and electrical distances. The values for the fractional electrical distances δ₁, δ₂, and δ₃ were 0.07, 0.113, and 0.233, respectively, as used in previous studies (Kutluay et al., 2005). The model was fitted to the appropriate experimental data using the lsqcurvefit function in Matlab.

Figure 10.

Kinetic model for permeation through Kir1.1 channels. (A) Kinetic scheme with six ion-binding sites and five states. (B) Fits of i-V relationships with symmetrical [K⁺]. (C) Fits of i-V relationships with symmetrical [NH₄⁺]. (D) Fits of i-V relationships with fixed internal [K⁺] and variable external [NH₄⁺]. (E) Saturation of K⁺ and NH₄⁺ currents in the simulated channel. (F) Energy profile for K⁺ and NH₄⁺ movement through the pore of Kir1.1. The major differences are in the well depths of S1 and S2.

Online supplemental material

Online supplemental material shows the effects of external Na⁺ on K⁺ currents in the presence of the divalent cation chelator EDTA (Fig. S1). Figs. S2 and S3 illustrate the sensitivities of the measurable parameters of conductance, apparent K_m, and bi-ionic reversal potentials simulated by these models to changes in the binding energies to the different sites. Table S1 lists the kinetic parameters of the permeation model based on fits to experimental data. Figs. S1–S3 and Table S1 are available at http://www.jgp.org/cgi/content/full/jgp.201110727/DC1.

RESULTS

Conductance–concentration relationships

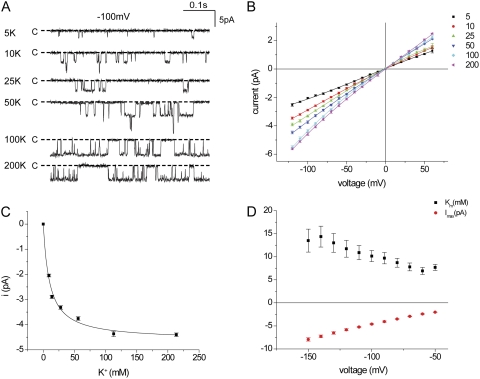
We first confirmed the relationship between K⁺ concentration and inward currents in Kir1.1 channels. Channels were expressed in Xenopus oocytes, and excised inside-out patches were formed with identical K⁺ concentrations, ranging from 5 to 200 mM, on both sides of the membrane. K⁺ was increased by the addition of KCl to the basic medium without cation substitution. Typical inward current traces for a membrane potential of −100 mV are shown in Fig. 1 A, and the corresponding i-V relationships are plotted in Fig. 1 B. At low K⁺ concentrations, the open probability decreased sharply. Decreased open times, together with decreased currents, determined the lower limit of [K⁺] at which currents could be resolved. The i-V relationships were approximately linear over the range of −20 to −100 mV at all concentrations. Plotting the current as a function of ion concentration at −100 mV indicated a hyperbolic relationship with a maximal inward current (i_max) of −4.6 pA and an apparent K_m of 10.2 mM (Fig. 1 C). The K_m value decreased mildly with depolarization of the membrane voltage, suggesting different voltage dependencies of rates of entering and exiting the channel (Fig. 1 D). Outward currents were less reliably measured as a result of faster kinetics and increased noise levels.

Figure 1.

Conduction through Kir1.1 channels in inside-out patches with symmetrical K⁺ concentrations. (A) Inward currents with −100 mV across the patch at different [K⁺]. (B) i-V relationships for different [K⁺]. Lines through the data points have no theoretical meaning. (C) Single-channel currents at −100 mV as a function of ion concentration. The line represents the best fit of Eq. 1 to the data, with i_max = 4.6 ± 0.1 pA and K_m = 10.2 ± 1.2 mM. (D) i_max and K_m, measured as in C, as a function of voltage.

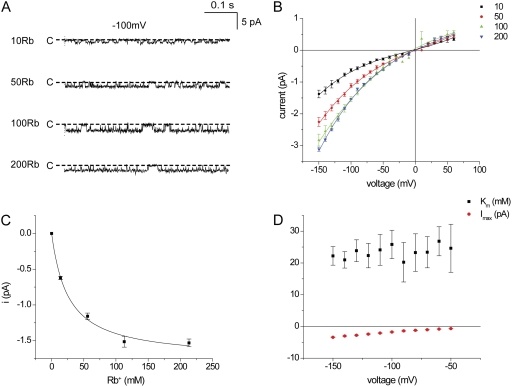
We repeated these experiments using Rb⁺ as the conducted ion. Fig. 2 A shows inward currents at −100 mV in inside-out patches with various Rb⁺ concentrations from 10 to 200 mM on both sides of the membrane. Fig. 2 B shows i-V relationships for these concentrations. Rb⁺ currents were lower than those for K⁺, confirming previous findings (Chepilko et al., 1995; Choe et al., 2000). At −100 mV, i_max was 1.8 pA, whereas the apparent K_m was 26 mM, higher than that for K⁺ (Fig. 2 C). The i-V relationship for Rb⁺ was less linear than that for K⁺; inward currents increased more rapidly with hyperpolarization. In contrast, the voltage dependence of the apparent K_m for Rb⁺ conduction was less than that for K⁺ (Fig. 2 D). The lower affinity for conduction correlates with the reduced permeability for this ion relative to K⁺, estimated from bi-ionic reversal potentials (Chepilko et al., 1995; Choe et al., 2000).

Figure 2.

Conduction through Kir1.1 channels in inside-out patches with symmetrical Rb⁺ concentrations. (A) Inward currents with −100 mV across the patch at different [Rb⁺]. (B) i-V relationships for different [Rb⁺]. Lines through the data points have no theoretical meaning. (C) Single-channel currents at −100 mV as a function of ion concentration. The line represents the best fit of Eq. 1 to the data, with i_max = 1.8 ± 0.1 pA and K_m = 26 ± 4 mM. (D) i_max and K_m, measured as in C, as a function of voltage.

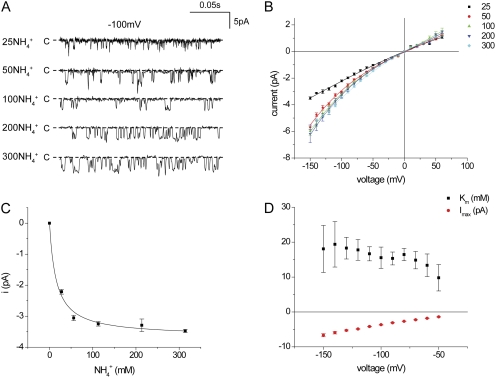
We also examined the concentration–conductance relationships for NH₄⁺. Handling of this ion is unusual in that it has a permeability ratio P_NH4/P_K of only ∼0.1, determined from reversal potential measurements, but its conductance is comparable to that of K⁺ (Chepilko et al., 1995; Choe et al., 2000). We hypothesized that the low permeability might be explained if NH₄⁺ interacted less strongly (i.e., were bound less tightly) than K⁺ as it traversed the channel, predicting a higher apparent K_m for conduction. Current traces for NH₄⁺ are shown in Fig. 3 A, and i-V relationships are shown in Fig. 3 B. As found previously (Choe et al., 2000), the channel kinetics change when NH₄⁺ is conducted, with much briefer openings and lower open probability. With low NH₄⁺ concentrations, the open times were further decreased, limiting the lower end of the usable concentration range to 25 mM. As shown in Fig. 3 C, the maximal inward current for NH₄⁺ was 3.7 pA at −100 mV, whereas the apparent K_m value was 16 mM, higher than but not strikingly different from that for K⁺. The voltage dependence of K_m was small, at least between −60 and −150 mV (Fig. 3 D). However, outward NH₄⁺ currents were virtually independent of NH₄⁺ concentration over this range (Fig. 3 B), implying that the K_m for conduction in this direction was well below those for inward currents. However, as with K⁺, these currents were more difficult to measure accurately.

Figure 3.

Conduction through Kir1.1 channels in inside-out patches with symmetrical NH₄⁺ concentrations. (A) Inward currents with −100 mV across the patch at different [NH₄⁺]. (B) i-V relationships for different [NH₄⁺]. Lines through the data points have no theoretical meaning. (C) Single-channel currents at −100 mV as a function of ion concentration. The line represents the best fit of Eq. 1 to the data, with i_max = 3.7 ± 0.1 pA and K_m = 16 ± 3 mM. (D) i_max and K_m, measured as in C, as a function of voltage.

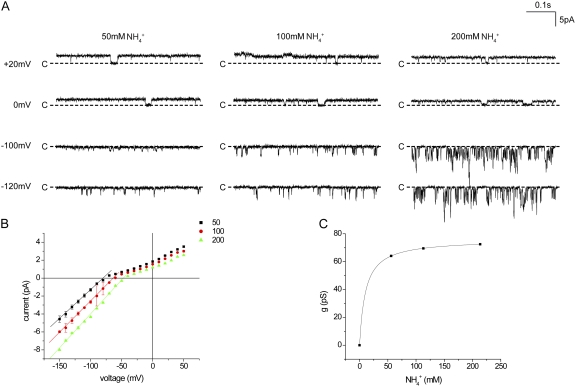
To see if the saturation of NH₄⁺ currents is affected by the presence of K⁺ on the opposite side of the membrane, we investigated inside-out patches in which NH₄⁺ was varied only in the pipette (extracellular) solution with constant 110 mM K⁺ in the bath. Because the reversal potential changes under these conditions, we analyzed inward NH₄⁺ slope conductances, rather than currents, over the concentration range of 50–200 mM (Fig. 4). These conductances (60–80 pS) were larger than those measured under symmetrical conditions for K⁺ or NH₄⁺. There was little change in conductance over this concentration range, again indicating high-affinity interactions with the channel.

Figure 4.

Conduction through Kir1.1 channels in inside-out patches with 110 mM K⁺ in the bath solution and different [NH₄⁺] in the pipette. (A) Currents at different voltages and [NH₄⁺]. (B) i-V relationships for different [NH₄⁺]. Lines through the data points have no theoretical meaning. (C) Inward single-channel conductance measured as the slope of the i-V plots between −60 and −150 mV. The line represents the best fit of Eq. 1 to the data, with g_max = 76 ± 1 pS and K_m = 10.4 ± 0.1 mM.

Occupancy of an outer binding site

One possible site of interaction of permeant ions with the channel that could contribute to saturation of currents is the outer mouth of the pore, just external to the selectivity filter. This could contain an obligatory binding site for ions that controls the rate of movement into the channel. Analysis of a multi-ion pore with simplified association–dissociation kinetics showed that the presence of such a site could lead to Michaelis–Menten-type kinetics of permeation (Nelson, 2011). Similar results are presented below for a more complex kinetic scheme.

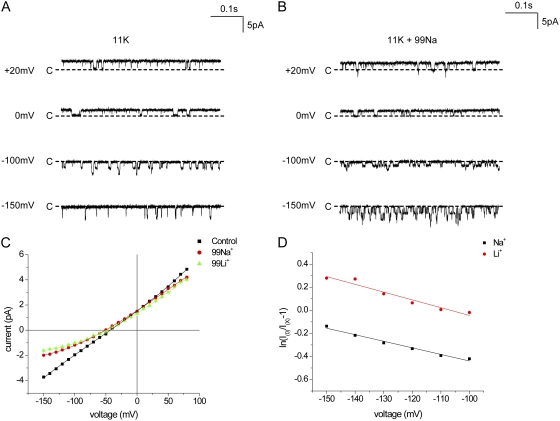
Because such a site might not be as strongly ion selective as those of the filter itself, we examined whether the smaller alkali metal cations Na⁺ and Li⁺ could reduce K⁺ conductance through the channel by competing for occupancy. Fig. 5 (A and B) shows traces and i-V relationships in inside-out patches with 110 mM K⁺ on the cytoplasmic side and either 11 mM K⁺ alone or 11 mM K⁺ plus 99 mM Na⁺ on the extracellular side of the membrane. The effects of Na⁺ were modest but clear. Outward currents were virtually unaffected, whereas inward currents were reduced by 50% or more.

Figure 5.

External Na⁺ and Li⁺ block K⁺ currents through Kir1.1 channels. (A) Currents at different voltages in the presence of 11 mM K⁺ in the pipette solution and 110 mM K⁺ in the bath solution. (B) Currents under the same conditions as in A but with 99 mM Na⁺ in the pipette solution. (C) i-V relationships in the absence of blockers and in the presence of 99 mM Na⁺ or Li⁺ in the external solution. (D) Analysis of block by external Na⁺ and Li⁺ according to Eqs. 2 and 3. The lines represent best fits to the data, with K_iNa = 272 mM and zδ_Na = 0.15, and K_iLi = 203 mM and zδ_Li = 0.17.

We analyzed these results using a simple Woodhull-type model (see Eqs. 2 and 3 in Materials and methods) that assumes a blocking site at a fixed point within the transmembrane electric field. The results of this analysis are shown in Fig. 5 D, in which the equation for fractional block is linearized with respect to voltage. The apparent K_I(0) obtained by extrapolating the linear regression line to V = 0 was 272 mM, whereas the slope of the line gave an effective valence of the blocking reaction of 0.15. That is, the voltage dependence of block could be explained by Na⁺ blocking at a site that senses 15% of the transmembrane electric field. In this interpretation, the effects of Na⁺ appear as a reduction in single-channel current rather than a decreased open time because the blocking kinetics are too fast to resolve.

Very similar results were obtained with Li⁺ (Fig. 5, B and C). In this case, the estimated K_I(0) was 203 mM and the effective valence was 0.17. The voltage dependence of the reduction suggests that Na⁺ and Li⁺ also bind weakly but specifically within the permeation pathway.

Divalent cations interact with an outer binding/blocking site

We next asked whether divalent cations could block the channel in a similar manner. Fig. 6 (A and B) shows traces and i-V relationships with 11 mM K⁺ (and 99 mM Na⁺) in the pipette in the absence of divalents and in the presence of Ca²⁺ or Mg²⁺. Both Ca²⁺ and Mg²⁺ produced a voltage-dependent decrease in current, but the Mg²⁺-dependent block was stronger. Fig. 6 C shows the analysis of the voltage dependence; the K_i(0) for Ca²⁺ was about threefold higher than that for Mg²⁺, whereas the effective valences were similar. These values of 0.17 to 0.18 are close to those measured for Na⁺ and Li⁺, despite the fact that these blockers carry twice the positive charge. The voltage dependence of the block as well as the selectivity between these two divalent cations for block provides further evidence for a specific interaction with the pore.

Figure 6.

External Mg²⁺ and Ca²⁺ block K⁺ currents through Kir1.1 channels. (A) Currents at different voltages in the presence of 11 mM K⁺ plus 99 mM Na⁺ in the pipette solution and 110 mM K⁺ in the bath solution. (B) Currents under the same conditions as in A but with 10 mM Mg²⁺ in the pipette solution. (C) i-V relationships in the absence of divalents and in the presence of 10 mM Mg²⁺ or 10 mM Ca²⁺ in the external solution. (D) Analysis of block by external Mg²⁺ and Ca²⁺ according to Eqs. 2 and 3. The lines represent best fits to the data, with K_iMg = 13 mM and zδ_Mg = 0.18, and K_Ca = 31 mM and zδ_Ca = 0.17.

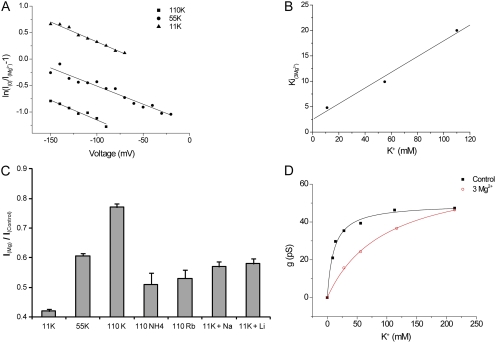
We extended these results by examining block by 3 mM Mg²⁺ at different extracellular K⁺ concentrations. The effects of Mg²⁺ are similar in each case, but the magnitude of current reduction increases as K⁺ decreases. This is shown quantitatively in Fig. 7 A. The K_i(0) values, interpolated with 11 mM K⁺ and extrapolated with 55 and 110 mM, increase with K⁺ concentration, whereas the slopes of the plots are similar. The Ki(0) values are plotted as a function of K⁺ in Fig. 7 B. The approximately linear relationship is consistent with a competitive interaction between K⁺ and Mg²⁺, with an estimated K_i for Mg²⁺ in the absence of K⁺ of 2.5 mM and a dissociation constant of 15 mM for K⁺ binding to the Mg²⁺-blocking site. This is similar to the apparent K_m for conduction (11 mM) in the absence of blocking ions, suggesting that this site may well contribute to conductance saturation.

Figure 7.

External K⁺ competes with Mg²⁺ block of Kir1.1 currents. (A) Analysis of block of K⁺ currents by 3 mM Mg²⁺ at three different external [K⁺] according to Eqs. 2 and 3. Lines represent K_Mg(0) = 4.6 mM and zδ_Mg = 0.19 (11 mM K⁺); K_Mg(0) = 9.9 mM and zδ_Mg = 0.18 (55 mM K⁺); and K_Mg(0) = 20 mM and zδ_Mg = 0.19 (110 mM K⁺). (B) K_Mg(0) plotted versus [K⁺]. The straight line represents a linear regression fit of the data. The intercept on the ordinate implies that K_Mg = 2.5 mM in the absence of K⁺, and the slope provides an estimate of 15 mM for the dissociation constant for K⁺ displacement of Mg²⁺. (C) Ratios of currents at V_m = −100 mV in the presence and absence of 3 mM Mg²⁺ with different ions in the external solution. (D) External Mg²⁺ decreases the apparent affinity for K⁺. g is plotted as a function of [K⁺] for no added divalents (black) and with 3 mM Mg²⁺ in the external solution (red). Lines represent the best fits to Eq. 1, with g_max = 50 ± 1 pS and K_m = 11.0 ± 1.3mM (control), and g_max = 67 pS ± 1 and K_m = 96 ± 4 mM (+3 mM Mg²⁺).

We assessed the selectivity of this site by comparing the ability of different monovalent cations to relieve Mg²⁺ block. This was assessed as the ratio of currents at −100 mV with and without 3 mM Mg²⁺ and is plotted in Fig. 7 C. For Rb⁺ and NH₄⁺, external K⁺ was completely replaced by these ions. For Na⁺ and Li⁺, 99 mM of the test ion was added to a solution containing 11 mM K⁺. These results indicate that the site is somewhat selective for K⁺; the other ions tested had similar abilities to displace Mg²⁺, with Na⁺ and Li⁺ being slightly more effective than Rb⁺ or NH₄⁺.

If this outer binding site determines saturation of currents, competition between K⁺ and Mg²⁺ in the outer part of the permeation path predicts that Mg²⁺ should shift the apparent affinity of the channel for K⁺. To test this, we repeated the measurements of concentration–conductance relationships for K⁺ in the presence of 3 mM Mg²⁺ (Fig. 7 D). Under these conditions, the apparent K⁺ affinity decreased markedly, with apparent K_m values increasing from 11 to 96 mM. This is consistent with the idea that saturation of K⁺ conductance involves K⁺ occupancy of the outer binding/blocking site, at least when Mg²⁺ is present in the external solution.

Role of fixed negative charges in saturation and block

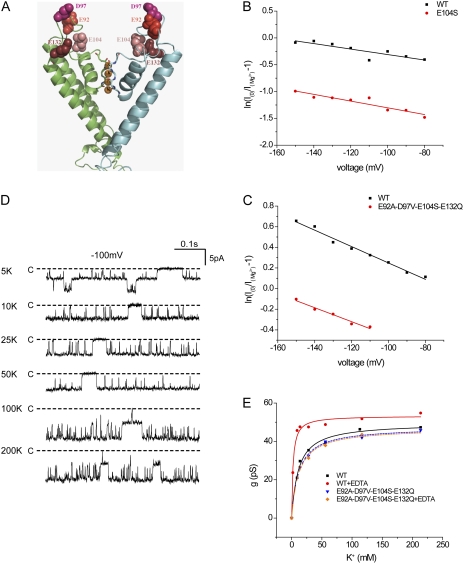
Affinities for ions at the outer mouth of the pore should be affected by the presence of fixed negative charges in the extracellular domain of the channel protein (D’Avanzo et al., 2005; Chang et al., 2010). To test this, we mutated several aspartate and glutamate residues in the outer mouth of the pore (E92, D97, E104, and E132) to eliminate their negative charges. The largest effect was observed with alterations at the E104 position; this side chain is situated just above the outer aspect of the selectivity filter (Fig. 8 A). The E104S mutant significantly reduced the efficacy of Mg²⁺ block without changing the voltage dependence (Fig. 8 B). We also studied a quadruple mutant in which all four negatively charged amino acids in the extracellular domain were neutralized. Again, the affinity for Mg²⁺ was decreased modestly but significantly, whereas the voltage dependence remained constant (Fig. 8 C).

Figure 8.

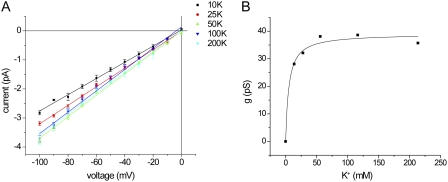
Removal of external fixed negative charges reduces affinity for Mg²⁺ block and K⁺ permeation. (A) Homology model of the outer mouth of Kir1.1b showing the positions of four negatively charged amino acid side chains, E92, D97, E104, and E132, relative to the conduction pathway. (B) Analysis of block by 3 mM Mg²⁺ of wild-type (WT) ROMK and the mutant E104S. The internal solution contained 110 mM K⁺. The external solution contained 11 mM K⁺ plus 99 mM Na⁺. Lines represent fits to Eqs. 2 and 3, with K_Mg(0) = 3.9 mM and zδ_Mg = 0.16 (WT), and K_Mg(0) = 20 mM and zδ_Mg = 0.16 (E104S). (C) Analysis of block by 3 mM Mg²⁺ of WT ROMK and the quadruple mutant E92A/ D97V/ E104S/E132Q. The internal solution contained 110 mM K⁺. The external solution contained 11 mM K⁺ and no Na⁺. Lines represent fits to Eqs. 2 and 3, with K_Mg(0) = 5.2 mM and zδ_Mg = 0.20 (WT), and K_Mg(0) = 9.3 mM and zδ_Mg = 0.17 (E92A/ D97V/ E104S/E132Q). (D) Current traces for WT Kir1.1b in excised inside-out patches with different K⁺ concentrations on both sides of the membrane and 0.5 mM EDTA in the pipette solution. (E) Conductance as a function of concentration for WT and E92A/ D97V/ E104S/E132Q in the presence and absence of 0.5 mM EDTA. Lines represent best fits to Eq. 1, with g_max = 50 pS ± 1 and K_m = 11.0 ± 1.3 mM (WT); g_max = 53 ± 1 pS and K_m = 2.2 ± 0.4 mM (WT + EDTA); g_max = 47 ± 1 pS and K_m = 12 ± 1 mM (E92A/ D97V/ E104S/E132Q); and g_max = 47 ± 2 pS and K_m = 12 ± 2 mM (E92A/ D97V/ E104S/E132Q + EDTA).

The elimination of negative charges did not have much effect on the apparent affinity for K⁺ (Fig. 8 D). This result did not support the idea that the K_m reflects binding to the outer mouth. However, we considered the possibility that the charges might be screened, particularly by trace metal cations in the solutions. Indeed, inclusion of 0.5 mM EDTA to chelate divalent cations significantly decreased the apparent K_m to values too low to measure accurately (Fig. 8 D). The chelator did not change the K_m in mutant channels lacking the negative charges in the outer mouth, consistent with the idea that the charges do affect affinity but are partially screened by residual divalent cations under most conditions. EDTA also modestly increased the block of the channels by extracellular Na⁺ (Fig. S1).

In some Kir channels, fixed negative charges in the transmembrane cavity enhance the affinity for block by Mg²⁺ and polyamines (Lu and MacKinnon, 1994b; Taglialatela et al., 1995; Yang et al., 1995). To see if such charges on the other side of the selectivity filter could also influence current saturation, we used the Kir1.1b mutant N152D, in which an aspartate is inserted in the second membrane-spanning segment at the position corresponding to D172 of IRK1. Indeed, there was a significant decrease in the apparent K_m for K⁺ conductance, from 10.2 ± 1.2 (Fig. 1) to 4.7 ± 1.4 mM (Fig. 9). The effect is in the same direction as, but much smaller than, the increase in affinity for block by Mg²⁺ or spermine block from the cytoplasmic side of the pore (Lu and MacKinnon, 1994b; Taglialatela et al., 1995; Yang et al., 1995).

Figure 9.

Fixed charges in the transmembrane cavity increase affinity for K⁺ permeation. (A) i-V relationships for Kir1.1b N152D in inside-out patches with different symmetrical [K⁺]. (B) Conductance as a function of concentration for N152D. Lines represent the best fits to Eq. 1, with g_max = 39 ± 2 pS and K_m = 4.7 ± 1.4 mM.

Kinetic modeling

To examine if the saturation properties of the Kir1.1 channel could be accounted for with standard models of K⁺ channel permeation, we used a five-state scheme used previously to describe KcsA channels (Kutluay et al., 2005) and Kir4.1 channels (Edvinsson et al., 2011). The model can be formulated in terms of rate constants between the states of the channel as described in Fig. 10 A. This scheme is based on known properties of the selectivity filter of K⁺ channels. Because Kir1.1 and other inward rectifiers contain a cytoplasmic domain that may provide an additional resistance to ion flow (Choe et al., 2000), the step between the cavity and the internal solution would include movement through this part of the pore.

The model could fit data for i-V relationships with symmetric K⁺ or NH₄⁺ concentrations, but many different parameter sets gave equally good fits. We then attempted to simultaneously fit data from symmetrical K⁺, symmetrical NH₄⁺, and bi-ionic K⁺ versus NH₄⁺ conditions. We assumed the same kinetic scheme with the same number of sites and barriers with the same placement within the electric field for the two ions. Only the rates of transitions among the states were allowed to vary. A parameter set that gave satisfactory results is illustrated in Fig. 10 (B–E). The pseudo-energy profiles for NH₄⁺ and K⁺ along the pore for this set are shown in Fig. 10 F. These values are plotted as “rate-constant representation” (RCR) units (Andersen, 1999), arbitrarily assuming a frequency factor for the Eyring transition-state reaction rates of 6 × 10¹⁰ s⁻¹. The actual rates used are given in Table S1.

These parameters were able to reproduce the basic properties of K⁺ conduction as well as several of the remarkable features of the NH₄⁺ data, including the near independence of outward currents on ion concentration, the high conductance to NH₄⁺ despite the low bi-ionic permeability, and the increased inward NH₄⁺ conductance with K⁺ on the inside of the membrane. One prediction of the model that is different from the experimental observations is the slight decline in currents at high NH₄⁺ concentrations. The main features of the parameter set for NH₄⁺ are decreased depths of energy wells for NH₄⁺ compared with K⁺, particularly at sites S1 and S2. Although other parameter sets could also successfully fit the data, all of them involved similar changes at these sites. Thus, this simplified model of ion permeation can largely account for movements of K⁺ and NH₄⁺ through the channel.

We also performed a sensitivity analysis to examine the influence of model parameters on the predicted observables of apparent K_m, conductance, and reversal potentials. When the binding sites were altered by simultaneously changing the energies of the well and adjacent barriers, the apparent K_m values were most sensitive to increases in S0; increases of 1.3 RCR increased K_m by nearly 10-fold (Fig. S2 A). Changes in S1 had smaller effects, whereas K_m values were almost independent of S2-binding energies. This may reflect the nature of the kinetic scheme, as the model is constrained such that the S1–S4 sites’ selectivity filter is occupied by two ions at all times. In contrast, inward conductance through the channel was most sensitive to changes in S1 (Fig. S2 B).

Under bi-ionic conditions, with the parameters for the internal ion fixed (to those estimated for K⁺) and those for the external ion varied, reversal potentials were inversely related to the binding energy at each of the sites. When all sites were raised or lowered simultaneously, an increase of 1 RCR produced a reversal potential of −60 mV (Fig. S3 A). These changes also reduced the open-channel conductance by ∼50% (Fig. S3 B).

The decreased energy wells for NH₄⁺ account for the decreased P_NH4/P_K ratio because under bi-ionic conditions, the sites will be preferentially occupied by K⁺. The concomitant high inward NH₄⁺ conductance is a distributed property of the various energy barriers and is not so simply accounted for by any one parameter. We have not explored in depth the basis for other properties, such as the higher inward NH₄⁺ conductance in the presence of internal K⁺ or the low apparent K_m for outward NH₄⁺ currents.

DISCUSSION

The main conclusions of this study are: (a) Currents through Kir1.1 channels carried by NH₄⁺ saturate with a low apparent K_m only modestly higher than that for K⁺, despite a reduced NH₄⁺ permeability. (b) Saturation of inward currents partly reflects occupancy of an outer binding site that is selective for K⁺ but also accepts other monovalent and divalent cations. (c) The unusual permeation properties of the NH₄⁺ ion can be accounted for by conventional kinetic models of ion transport through Kir1.1. These topics are discussed in more detail below.

Saturation of K⁺ currents

We found that currents through Kir1.1 channels saturated at low K⁺ concentrations, with apparent K_m values of ∼10 mM. This is in general agreement with previous results on Kir1.1 (Lu and MacKinnon, 1994a) and Kir2.1 (Lopatin and Nichols, 1996; D’Avanzo et al., 2005; Chang et al., 2010), although the analyses of the concentration dependence varied. At very high K⁺ concentrations (>300 mM), conductances through Kir1.1 channels can actually decline from maximal values (Lu and MacKinnon, 1994a). These results contrast with the concentration dependence seen in other K⁺ channel types. Maxi-K channels have apparent K_m values of 50–140 mM (Latorre and Miller, 1983). For Shaker channels, the value is even higher, around 300 mM (Heginbotham and MacKinnon, 1993). KcsA channels show a more complex biphasic concentration dependence with a linear increase in conductance at high concentrations of K⁺ (Morais-Cabral et al., 2001).

In evaluating the K⁺ concentration dependence, we did not substitute other ions for K⁺. If fixed negative charges attract K⁺ to the outer mouth of the channels (D’Avanzo et al., 2005; Chang et al., 2010), the change in ionic strength would alter the screening of these charges, making the measured K_m values artificially low. On the other hand, if there is a relatively nonspecific binding site for cations in the outer mouth, the presence of other ions that might compete for this site would make the measured K_m values artificially high. We believe, based on our measurements and as discussed below, that the latter artifact is more important, so we used a protocol without ion substitution.

We focused our attention on concentrations between 5 and 200 mM, where the channels behave as a pseudo–single-ion system:

$${\text{K}}_{\text{o}}+\text{C}\leftarrow \to \text{K}·\text{C}\leftarrow \to {\text{K}}_{\text{i}}+\text{C},$$

where C is the channel, and K_o, K • C, and K_i refer to the K⁺ ions in the outer solution, bound to the channel and in the inner solution, respectively. In such as system, ion movement through the channel saturates with an apparent K_m value of k_d/k_a that reflects the (voltage-dependent) rates of association to (k_a) and dissociation from (k_d) the binding site. Maximal inward currents are determined by the rate of dissociation to the inner solution. Under bi-ionic conditions, the relative permeability will reflect channel occupancies by the two species; these occupancies will be inversely related to K_m. Such a model is clearly an oversimplification, as both physiological and structural measurements indicate that the channels are multi-ion pores. However, as shown recently (Nelson, 2011), permeation through multi-ion pores can under some conditions still be considered a two-step association–dissociation process that follows Michaelis–Menton kinetics.

In any case, the scheme provides some simple approximations. From the single-channel currents of 5 pA at −100 mV, k_d must be at least 3 × 10⁷ s⁻¹ at this voltage. If K_m = 10 mM, the value of k_a would be >3 × 10⁹ M⁻¹ • s⁻¹. This is close to the maximum rate of ion capture by diffusion for a pore with an outer mouth of ∼10-Å radius (Hille, 2001). Cation capture rates by the channel may be accelerated by electrostatic attraction to fixed negative charges in the channel mouth.

Rb⁺ and NH₄⁺ currents

The apparent K_m value for Rb⁺ conduction was 24 mM, significantly larger than that for K⁺. Rb⁺ also has a lower maximal conductance than does K⁺ (Fig. 2), and the permeability ratio P_Rb/P_K based on bi-ionic reversal potentials is 0.4–0.6 (Chepilko et al., 1995; Choe et al., 2000). This indicates that channel occupancy by K⁺ is favored over Rb⁺. As channel occupancy would in turn be inversely related to K_m, as discussed above, the higher K_m for Rb⁺ is in agreement with the lower permeability. The lower maximal currents indicate a lower rate of dissociation from the channel.

NH₄⁺ is a more complicated case. It has a maximal inward conductance similar to that of K⁺, but the permeability ratio is ∼0.1 (Chepilko et al., 1995; Choe et al., 2000). This could be explained if permeation barriers for NH₄⁺ and K⁺ were similar, but that NH₄⁺ interacted more weakly than K⁺ with binding sites within the channel. Our naive prediction was that the apparent affinity of the pore for NH₄⁺ would be lower than that for K⁺. Consistent with this notion, the measured K_m value for NH₄⁺, 14 mM, is indeed higher than that for K⁺. However, the ratio of K_m values (K_m(NH₄)/K_m(K) of <2) is much smaller than that for permeability (P_K/P_NH4 of ∼10). Outward NH₄⁺ currents apparently saturated at lower concentrations. Although these observations are difficult to explain with a simple permeation model, they can be accommodated by a more realistic (and more complex) formalism, as shown in Fig. 10 and discussed below.

Outer binding site for cations

The outer mouth of the pore represents one possible location of saturable cation binding. Occupancy of a site in this part of the channel could be rate limiting for conduction, particularly for inward currents. To explore this possibility, we first examined the abilities of impermeant ions to block the channel from the outside. Small divalent cations (Mg²⁺, Ca²⁺) blocked Kir1.1 channels with a small but significant voltage dependence (zδ of ∼0.2), consistent with a blocking site within the transmembrane electric field. The affinity of these divalents for the blocking site, assessed as apparent K_i value at constant voltage, was higher for Mg²⁺ than for Ca²⁺. A similar block of Kir2.1 channels was reported previously (Murata et al., 2002). The impermeant monovalent cations Na⁺ and Li⁺ also blocked the channels with lower apparent affinity but with a voltage dependence similar to that of Mg²⁺ or Ca²⁺. Although this could indicate that the monovalent ions penetrate deeper into the electric field, it is also consistent with the idea that monovalents and divalents block at the same site, with the voltage dependence attributable mainly to the movement of K⁺ ions within the field consequent to block. Such a scenario was suggested for external TEA⁺ interactions of Shaker K⁺ channels (Thompson and Begenisich, 2003).

Competition between monovalents and divalents indicates that these ions occupy the same outer site, or at least that their binding is mutually exclusive. Based on the ability to relieve Mg²⁺ block, the monovalent cation selectivity for this site is K⁺ > Na⁺ ∼ Li⁺ > Rb⁺ ∼ NH₄⁺. In particular, the estimated K_d for K⁺ displacement of Mg²⁺ was 14 mM, a value not too different from the apparent K_m for conduction. In addition, 3 mM Mg²⁺ added to the outer solution increased the apparent K_m for K⁺ conductance substantially. These findings are consistent with the idea that saturation of K⁺ conductance involves interaction with this outer binding site. The ability of the other permeant ions, Rb⁺ and NH₄⁺, to displace Mg²⁺ was less than that of K⁺, in qualitative agreement with their lower permeabilities and higher K_m.

The S0 site, lying just outside the selectivity filter of K⁺ channels, is a likely structural locus for this outer binding site. This site has been identified in crystal structures of KcsA channels (Zhou et al., 2001) as well as through computational modeling (Bernèche and Roux, 2001). Ions associated with the channel at this location are probably partially dehydrated (Bernèche and Roux, 2001). Occupancy and dehydration may be stabilized by electrostatic interactions with negatively charged amino acid side chains (Zhou et al., 2001). If this identification is correct, this site exhibits a significant though modest selectivity for K⁺ over Na⁺. Another site, termed S_ext, was also identified as a locus of ion accumulation in KcsA channels external to S0 (Bernèche and Roux, 2001; Zhou et al., 2001). Blocking at this site is less likely to show an appreciable voltage dependence. The blockers are unlikely to bind deeper within the pore, as this would predict a stronger voltage dependence, at least for divalent cations. If the S1 site senses 25% of the electric field, block at that site by external Mg²⁺ would have a zδ value of at least 0.5, and probably more because K⁺ would be displaced toward the cytoplasm during occupancy of the site by a blocker. The measured was ∼0.2. On the other hand, the binding of permeant cations to the S1 site selectivity filter could contribute to the ability of monovalent cations to inhibit Mg²⁺ block at S0, especially in the case of K⁺.

The apparent K_m for inward currents was weakly voltage dependent, at least for K⁺ and NH₄⁺, with a higher K_m estimated when the membrane was hyperpolarized. This could arise if the forward rate of exit from the outer binding site had a higher voltage dependence than the rate of entry onto the site.

We mutated anionic amino acids in the outer mouth that might increase Mg²⁺ and/or K⁺ affinities for the channel through favorable electrostatic interactions. As reported previously (Sackin et al., 2011), the elimination of four of these charges (or 16 negative charges per tetramer) still resulted in a functional channel with conductance and kinetics similar to those of the wild-type channel. Mutation of the negatively charged side chain closest to the site, E104S, did indeed decrease the affinity of the channel for Mg²⁺ block; the apparent K_i(0) increased from 4 to 20 mM. The elimination of a negative charge at an adjacent residue in Kir2.1 had a similar effect on Mg²⁺ affinity in Kir2.1 channels (Murata et al., 2002). The removal of the other three negative charges did not further decrease Mg²⁺ affinity of the Kir1.1. The apparent K_m for K⁺ conductance did not change significantly either with the single E104S mutation or the quadruple mutation. In part, this reflects the lower valence of K⁺, relative to Mg²⁺, making binding less sensitive to the electrostatic potential. In addition, however, elimination of the screening of the negative charges by trace divalent cations by chelation with EDTA revealed their impact on K_m.

Inner cation-binding site

We also examined the effects of adding negative charges just inside the selectivity filter within the transmembrane cavity. This N152D mutation mimics the natural anionic side chain in Kir2.1 that contributes to the strong block of this channel by intracellular Mg²⁺ and polyamines (Lu and MacKinnon, 1994b; Taglialatela et al., 1995; Yang et al., 1995). The apparent K_m for conductance through this mutant was about half that of the wild-type channel. Thus, this site can also contribute to the saturation behavior of inward rectifiers.

A kinetic model

Our simulations addressed the question of whether standard models of permeation through K⁺ channels with designated ion-binding sites identified by x-ray crystallography could explain the observed behaviors. We could identify a set of kinetic parameters that accounted for many of the channel properties, including the low K_m values for both K⁺ and NH₄⁺, the high K⁺/NH₄⁺ permeability ratio despite similar maximal conductances, and the increase in inward NH₄⁺ conductance with K⁺ on the opposite side of the membrane. The model is based on discrete-state kinetics and contains a minimal number of sites consistent with structural information. We do not claim that it is unique in describing the experimental results. However, we believe that the simulations show that our data can be explained without postulating any new or unusual features of the channel or a qualitatively different interaction of NH₄⁺ and K⁺ ions with the channel.

Analysis of this model helps to explain a major conclusion from experimental findings: two observable parameters related to the strength of interaction of permeant ions with the pore—bi-ionic permeability and apparent affinity—can be dissociated. The relative permeability of ions depends on the energy of binding to all the sites within the multi-ion pore. Saturation of inward conduction through the channels reflects the occupancy of a cation-binding site outside the selectivity filter and is not necessarily correlated with permeability. The similar K_m values for permeant cations reflect the relatively nonspecific cation binding to this part of the channel.