Investigation of the isoplanatic patch and wavefront aberration along the pupillary axis compared to the line of sight in the eye

Abstract

Conventional optical systems usually provide best image quality on axis, while showing unavoidable gradual decrease in image quality towards the periphery of the field. The optical system of the human eye is not an exception. Within a limiting boundary the image quality can be considered invariant with field angle, and this region is known as the isoplanatic patch. We investigate the isoplanatic patch of eight healthy eyes and measure the wavefront aberration along the pupillary axis compared to the line of sight. The results are used to discuss methods of ocular aberration correction in wide-field retinal imaging with particular application to multi-conjugate adaptive optics systems.

1. Introduction

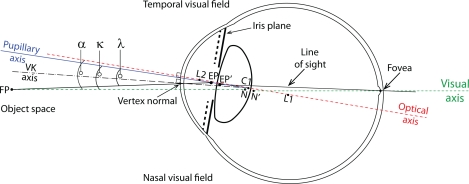
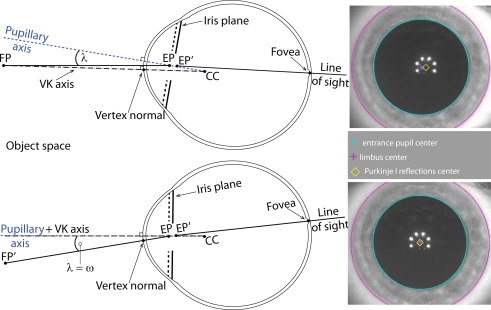
Most man-made optical systems employ rotationally symmetric components with the reflecting and refracting surfaces aligned and centered with respect to each other. A unique line joining the centres of curvatures of these surfaces exists: the optical axis. The eye is a non-centered and non-rotationally symmetric optical system without a uniquely defined optical axis. Small decentrations and tilts of its various surfaces give rise to a collection of different ocular axes used when performing ocular measurements. A complete discussion of these axes can be found elsewhere [1, 2, 3]. Each axis has specific advantages suited to different purposes; no single axis is universally more important than another and the usefulness and suitability of an axis should be determined according to the measurement task being considered. Figure 1 shows a selection of the ocular axes and the angles formed by their intersections. Bradley and Thibos [4] present a useful tutorial on practical methods for locating the ocular axes and associated angles. Ordinarily optical systems are designed to provide best optical image quality when operating with on-axis conditions, where the object of regard is centered on the optical axis. The isoplanatic patch defines the angular field (ω) within which the variation of image quality is considered negligible (below a certain level [5]). For purposes of retinal imaging it is useful to characterise the isoplanatic patch and aberration distribution along different ocular axes. This information can assist optical design of imaging systems and may influence aberration correction methods to benefit more from prevailing conditions and to maximize the field of view. In this study we compare the wavefront aberration of the eye along the pupillary axis (PA) and the line of sight (LOS). In the second part of this study we report an investigation of the isoplanatic patch of the eyes of 4 subjects by sampling the wavefront aberration over 129 field points (14 degrees × 11.6 degrees).

Fig. 1.

Schematic sketch of a selection of ocular axes and angles formed by these axes. The axes are indicated by the following lines; solid black (line of sight), solid blue (pupillary axis), dashed green (visual axis), dashed red (optical axis), and dashed black (videokerato-scope axis). The center of curvature of the posterior cornea C2 is omitted for the sake of clarity. The exit pupil is also omitted for clarity although its center EP’ is shown.

The line of sight (LOS) is commonly used to report and analyse ocular monochromatic aberrations with measurements typically performed in the plane optically conjugated to the pupil [6, 7]. Figure 1 depicts the LOS as the line connecting the fixation point FP with the center of entrance pupil EP, the center of exit pupil EP’, and the fovea. The LOS defines the centre of a beam of light (i.e. the principal ray) entering the fixating eye; however it is not statically fixed as the pupil center typically varies with asymmetric fluctuations in the diameter of the iris opening [8, 9].

The optical axis of the eye is estimated by a ‘line of best fit’ through the centres of curvature of each refracting surface (L2,C2,C1,L1) [3]. The pupillary axis (PA) is defined as the line normal to the anterior cornea passing through the center of the entrance pupil (EP) and the anterior corneal center of curvature (C1). Even in the ideal case of perfectly aligned and centered corneal and lenticular surfaces, the optical axis does not coincide with the PA because the pupil of a real eye is usually decentred nasally, often being displaced by up to 0.5 mm relative to the visual axis [10], and moreover, the center of the pupil may be shifted up to 0.6 mm in the nasal or temporal direction following pupil dilation [11]. Pupil decentration occurs to a lesser extent in the vertical direction.

The anterior corneal surface is aligned with the PA but it may be tilted with respect to other axes. Navarro et al. showed in a sample of 123 young eyes the anterior corneal surface is tilted by 2.3 degrees midway between optical axis and the LOS [12]. Small tilts are likely in the retinal surface as well as each of the corneal and lenticular surfaces. The angle from the PA to the LOS is usually denoted as lambda (λ). Earlier work reported average angle λ values of +1.4 degrees [13] and +9 degrees [14] in the horizontal direction, where the PA is temporal to the LOS in object space as conventionally defined [3]. Purkinje I reflection is typically displaced slightly nasally from the center of the entrance pupil.

The visual axis connects the fixation point FP to the fovea and passes through the first nodal point N and the second nodal point N’. A ray directed towards the nodal point undergoes no angular deviation by the system and therefore the visual axis is a reference axis for unit angular magnification. The visual axis defines the direction of gaze and a pencil of rays traveling along this axis undergoes no transverse chromatic aberration for a given reference wavelength. The angle from the optical axis to the visual axis is called angle alpha (α) and is often assumed to be about +5 degrees horizontally [15] (i.e. the fovea is shifted from the optical axis to the temporal retina). The visual axis is typically nasal to the optical axis in object space. Bradley and Thi-bos [15] report a typical range of +17 degrees (nasal object space) to −2 degrees (temporal object space), however Marcos et al. measured smaller variation, from +1.8 to +7.4 degrees [16]. Vertically the visual axis is declined relative to the optical axis by 2 to 3 degrees [3, 12]. The angle between pupillary axis and visual axis is denoted as the angle kappa (κ).

Usually corneal topographers are designed such that the fixation target, the object (the keratometry mires), and the detection/observation systems are all coaxial with each other. In this arrangement the videokeratometric (VK) axis aligns the instrument’s axis normal to the anterior cornea (consequently passing through the corneal center of curvature C1) while the subject is fixating [17]. The VK axis intercepts the anterior corneal surface at the vertex normal. Commonly, the vertex normal is used as the origin of reference coordinate systems for measuring, reconstructing and presenting topography maps of the cornea. Mandel et al. emphasised the vertex normal is not an intrinsic corneal reference landmark and is distinguished from the apex (region of greatest curvature) and the corneal sighting center (interception of the anterior cornea by the LOS) [1].

2. Instrumentation

Hartmann-Shack aberrometers have been widely used to measure the monochromatic aberrations of the eye since the efficiency of the technique was first demonstrated for the eye by Liang et al. [18]. A combination of laboratory techniques and some other more mature technologies are available to perform aberrometry; curvature sensing [19], pyramid sensors [20, 21], laser-ray tracing [22, 23, 24], spatially resolved refractometers [25, 26], wavefront analyzers [27, 28] based on Tscherning’s aberroscope [29], and skiascopy [30], which is essentially a retinoscopy application of the Foucault knife-edge test [31]. Corneal topography in recent decades has been dominated by use of Placido disc technology [32], although ultrasound, scanning slit techniques, rotating Scheimpflug cameras and anterior segment Optical Coherence Tomography (OCT) [33, 34] offer alternative modalities for corneal topography measurements [35].

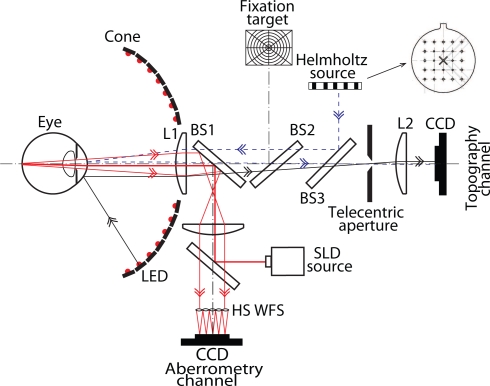
The following investigation used an iDesign^TM (Abbott Medical Optics) instrument which combines aberrometry and corneal topography measurements. Figure 2 depicts its optical layout in a simplified form. The wavefront sensor component is a Hartmann-Shack (HS WFS) type, which has been extensively described in literature [36, 37, 38]. It uses a 840 nm wavelength superluminescent diode (SLD) source which reduces the effects of speckle compared to a laser source. The lenslet array has a square geometry with a 109.2 microns pitch (center to center) and a 100 % fill factor. The system magnification results in a sampling density of 177 microns square geometry at the ocular pupil plane. The fixation target is generated by a microdisplay presenting a rectangular field of view ±7 degrees horizontally and ±5.8 degrees vertically. Although this investigation does not heavily utilise the topography data we present the principles of the instrument operation here for completeness.

Fig. 2.

Optical layout of the iDesign^TM combined wavefront aberrometer and corneal topographer.

The corneal topographer component of the system is based on measuring the position of Purkinje I reflections of an array of light sources appropriately spaced on a cone-like surface. The optical arrangement creates a grid of rectangularly and uniformly spaced Purkinje I reflec-tions observed by the CCD detector (topography channel) when a calibration surface of average corneal dimensions is measured. The cone-like surface is back illuminated by a Lambertian reflectance screen using 780 nm LEDs. This uniform light field is then masked by an optically thick screen with appropriately spaced and angled fenestrations. This produces sources with a narrow forward emission primarily directed towards the focal plane of the anterior cornea and improves photometric efficiency of the instrument. The corneal gradient at each sample point is determined by analysing the translation of the spot position in two (x and y) directions. Translation of the spot position allows calculation of the ray angle with respect to the surface normal at the sample location. As the ingoing ray angle is known from the instrument geometry, the gradient of the corneal surface is measured. Integration and an iterative search algorithm (based on Fermat’s principle) allows reconstruction of the elevation data. This technique differs from Placido disc patterns which can only determine the magnification of a mire in the radial direction at each sample location [39, 40, 41].

The distance between the eye under measurement and the first optical element in the system must be measured accurately in order to determine the correct radius of curvature. This is due to the scale-ambiguity, in which a flatter, more distant cornea has the same appearance as a steeper, closer cornea. In the instrument, the distance is measured by noting that the radius of curvature calculated from the Helmholtz spots (HHS) is independent of the eye position (since the light is projected through the collecting lens). For the corneal topography (CT) cone spots the pattern depends on both: the radius of curvature and the eye position. The position where the HHS pattern matches the CT pattern yields the correct distance.

The measurement of the corneal gradient in two directions is a continuation of previous concepts [42, 43, 44]. The corneal topography measurement data is mapped onto the same axis as used for the aberrometry measurement (LOS), and the results are presented to the operator following this mapping process. Sampling at the cornea is 215 microns square (for an 8 mm radius of curvature cornea), although the sampling pattern is slightly less dense in the central corneal region. The aberrometry and the corneal topography measurements are not exactly simultaneous, although the time separation between these measurements is generally less than a tenth of a second. Each measurement consists of four images: wavefront spot image, corneal topography spot image, scotopic iris (SI), and photopic iris (PI). The later three images are recorded with the same camera but with different illumination. The CT, SI and PI images are recorded with the same camera, but with different illumination. Both the aberrometry and topography systems use a prerecorded reference to subtract any small residual errors in the optical systems.These were optically recorded using ideal wavefront and cornea surface standards.

The instrument’s software maps the aberrometry and topography data sets onto a mutual coordinate system, however by exporting the raw corneal elevation data we retain the CT data in a format with its coordinate system centered along the VK axis.

3. Repeatability

Intrasession and intersession repeatability of aberrometry and corneal topography data was investigated to characterize the instrument. Test-retest measurements were performed on a single surface, spherical, glass artificial eye and also on both eyes of subject 1. Subject 1 details are given in Table 3 and both eyes were cyclopleged with one drop of 1% cyclopentolate. At each session, 10 measurements were performed with re-alignment of the eye/instrument between each single measurement. Note that for each measurement the instrument’s internal software performs single-frame evaluations of aberrometry and corneal topography data, which is then combined and displayed to the operator. This ensures a high temporal resolution of measurements but without any peremptory smoothing across multiple frames. Each session was completed within 20 minutes and measurements were repeated at 3 different sessions (day 0, day 4, day 38). The wavefront phase was fitted with Zernike polynomials according to standards [6, 7] using 28 modes (up to 6^th order) over a 6 mm pupil diameter. Using the same standards (although conjugate to the corneal plane), the corneal elevation data was fitted with Zernike polynomials using 28 modes over a 10 mm diameter.

Table 3.

Subject details. OD - right eye, OS - left eye.

Subject details
Subject	Age	Gender	Automated refraction (6 mm pupil diameter)		Dominant eye
1	31	male	OD −0.29/−0.11 x 25	OS −0.30/−0.38 × 67	OS
2	33	male	OD +0.14/−0.40 × 149	OS +0.48/−0.80 × 15	OD
3	28	male	OD −1.04/−0.50 × 160	OS −0.18/−0.44 × 17	OD
4	26	female	OD −0.02/−0.28 × 80	OS −0.08/−0.25 × 62	OS

Repeatability of both the topography and aberrometry data was analysed as follows. To quantify typical intrasession repeatability the variance of the coefficients for each Zernike mode was calculated over the 10 measurements. This ‘intrasession variance’ calculation was repeated for each real eye/session combination and the mean of all ‘intrasession variance’ values (n_eye · n_session = 6) gives the ‘mean intrasession variance’ for each Zernike mode. Finally the square root of the ‘mean intrasession variance’ gives the ‘mean intrasession standard deviation’. The same analysis was used for the artificial eye (n_eye · n_session = 3).

To quantify typical intersession repeatability the mean coefficients for each Zernike mode of each real eye was calculated over the 10 measurements. This ‘intrasession mean’ calculation was repeated for each session. The variance in the ‘intrasession mean’ values over all sessions (n_session = 3) is the ‘intersession variance’ for each Zernike mode. This ‘intersession variance’ value is calculated for each eye, and finally the mean of the ‘intersession variance’ values for both real eyes gives the ‘mean intersession variance’ (n_eye = 2). Finally the square root of the ‘mean intersession variance’ gives the ‘mean intersession standard deviation’. The same analysis was used for the artificial eye (n_session = 3 and n_eye = 1).

The mean intrasession mean variance and mean intersession mean variance for real and artificial eyes is reported in Table 1 for wavefront aberrometry data and Table 2 for corneal elevation topography data. The variance of artificial eye measurements gives an indication of the noise within the instrument and including the alignment and measurement technique. The variance of the real eye values gives an indication of the consistency of measurements including the underlying biological variation of the eye. Noise sources of a short time scale (such as tear film dynamics or eye movements) influence the intrasession repeatability, whereas medium term natural evolution in axial length and corneal shape influence the intersession repeatability. Like all devices reliant on Purkinje I reflections, the topography results are particulary sensitive to the tear film quality and stability.

Table 1.

Repeatability of iDesign wavefront aberrometry measurements on real and artificial eyes. SD is the standard deviation. See text for comments on the proportionally significant tip/tilt values for the artificial eye repeatability.

Mode	Mean intrasession SD (μm)		Mean intersession SD (μm)
$Z_n^m$	Real	Artificial	Real	Artificial
$Z_1^{-1}$	0.146	0.239	0.074	0.326
$Z_1^1$	0.207	0.085	0.046	0.128
$Z_2^{-2}$	0.049	0.020	0.027	0.023
$Z_2^0$	0.057	0.049	0.188	0.033
$Z_2^2$	0.047	0.018	0.040	0.012
$Z_3^{-3}$	0.034	0.008	0.015	0.002
$Z_3^{-1}$	0.025	0.019	0.009	0.016
$Z_3^1$	0.030	0.010	0.012	0.020
$Z_3^3$	0.032	0.010	0.014	0.002
$Z_4^{-4}$	0.027	0.004	0.012	0.002
$Z_4^{-2}$	0.020	0.008	0.011	0.006
$Z_4^0$	0.019	0.012	0.013	0.003
$Z_4^2$	0.020	0.007	0.011	0.003
$Z_4^4$	0.020	0.008	0.007	0.001
$Z_5^{-5}$	0.008	0.002	0.006	0.001
$Z_5^{-3}$	0.007	0.002	0.003	0.001
$Z_5^{-1}$	0.006	0.002	0.005	0.001
$Z_5^1$	0.009	0.002	0.003	0.002
$Z_5^3$	0.007	0.002	0.002	0.000
$Z_5^5$	0.007	0.003	0.002	0.002
$Z_6^{-6}$	0.005	0.001	0.002	0.001
$Z_6^{-4}$	0.006	0.001	0.002	0.000
$Z_6^{-2}$	0.005	0.001	0.002	0.001
$Z_6^0$	0.005	0.003	0.002	0.000
$Z_6^2$	0.005	0.001	0.003	0.001
$Z_6^4$	0.005	0.001	0.003	0.000
$Z_6^6$	0.006	0.002	0.002	0.001

Table 2.

Repeatability of iDesign topography corneal elevation measurements on real and artificial eyes. SD is the standard deviation.

Mode	Mean intrasession SD (μm)		Mean intersession SD (μm)
$Z_n^m$	Real	Artificial	Real	Artificial
$Z_1^{-1}$	1.106	0.285	0.810	0.016
$Z_1^1$	0.916	0.079	0.290	0.054
$Z_2^{-2}$	1.095	0.532	0.654	0.054
$Z_2^0$	3.537	0.665	1.189	0.268
$Z_2^2$	0.966	0.794	1.064	0.224
$Z_3^{-3}$	0.704	0.209	0.166	0.027
$Z_3^{-1}$	0.833	0.179	0.371	0.040
$Z_3^1$	0.630	0.030	0.278	0.013
$Z_3^3$	0.756	0.193	0.218	0.045
$Z_4^{-4}$	0.668	0.112	0.419	0.080
$Z_4^{-2}$	0.669	0.068	0.348	0.039
$Z_4^0$	0.670	0.401	0.189	0.173
$Z_4^2$	0.524	0.446	0.526	0.205
$Z_4^4$	0.741	0.397	0.637	0.212
$Z_5^{-5}$	0.313	0.056	0.240	0.006
$Z_5^{-3}$	0.284	0.062	0.092	0.006
$Z_5^{-1}$	0.288	0.053	0.114	0.022
$Z_5^1$	0.283	0.012	0.113	0.003
$Z_5^3$	0.279	0.020	0.131	0.006
$Z_5^5$	0.428	0.033	0.145	0.011
$Z_6^{-6}$	0.291	0.036	0.081	0.022
$Z_6^{-4}$	0.257	0.022	0.135	0.014
$Z_6^{-2}$	0.238	0.017	0.162	0.012
$Z_6^0$	0.221	0.108	0.069	0.045
$Z_6^2$	0.185	0.119	0.120	0.051
$Z_6^4$	0.259	0.103	0.202	0.051
$Z_6^6$	0.385	0.116	0.131	0.063

In Table 1 the real eyes measured were almost emmetropic (with a sphero-cylinder dioptric refractive error of OD (right eye) +0.14/ – 0.40 × 19, OS (left eye) +0.48/ – 0.80 × 15) and therefore, the ocular refraction of the ingoing 1^st pass pencil creates an optimally positioned retinal beacon and only modest amounts of tip and tilt aberration are generated in the backscattered wavefront. Accordingly the measurement variance of the tip/tilt coefficients is quite small. Conversely, the artificial eye measured had large myopic refraction (−6.9 Diopters) and so in its case the angular deviation of the ingoing 1^st pass pencil is excessive (with respect to eye length) and creates a retinal beacon that is not positioned on the optical axis but is transversally displaced. Thereby, apart from generating a defocus refractive error, the artificial eye also generates other aberrations (particularly tip and tilt aberration) in the back-scattered wavefront. Accordingly, measurement variance is higher for the artificial eye than one may initially expect from casual inspection of Table 1. Any small misalignment of the artificial eye mounting additionally produced a much greater tip/tilt wavefront aberration. Therefore it is reasonable to expect greater variation (both intrasession and intersession) for the c(1,−1) and c(1,1) aberrometry values. As tip/tilt wavefront correction is often delegated to a plane mirror on a gimbal mount, the c(1,−1) and c(1,1) coefficients are often unreported by researchers using wavefront sensors for the eye.

Comparing Table 1 and 2, it is expected to observe a greater variation in coefficients fitted to the corneal topography elevation (Table 2) compared to the wavefront phase (Table 1) as the fitting diameter is much greater (10 mm compared to 6 mm) and the corneal surface itself departs from a flat plane much greater than the wavefront phase does, even for a highly ametropic eye.

4. Aims and protocol

Wavefront aberrometry and corneal topography were measured on 8 healthy eyes from 4 young subjects (1 female, 3 male). The subjects age ranged between 26 and 33 years (mean 29 years) and further details are given in Table 3. All subjects were experienced observers and none had undergone ocular surgery. Each subject practiced fixating the target to ensure accuracy of ocular alignment during measurements. All measurements were performed in a darkened room and to paralyse accommodation, one drop of cyclopentolate 1 % was instilled to both eyes of each subject 20 minutes before performing measurements. Cycloplegia was confirmed subjectively by inability to clear a −0.50 Diopter lens combined with the distance correction when viewing a distance Snellen chart, although it is possible that some accommodative ability remained after only 20 minutes and increased the variability in the early measurements of a session.

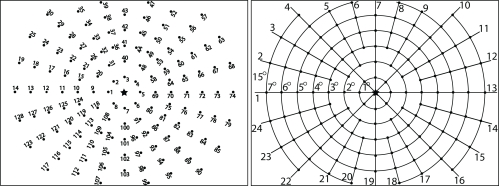
The microdisplay was used to present a fixation target as shown in Fig. 3 consisting of white field points numbered on a black background. The target presented a fixation point at every 1 degree radially and along 24 semi-meridians. Essentially this gave meridional targets every 15 degrees (azimuthal). The only exception occurred in the ±1 and ±2 degrees field points where crowding restricted the display to only 4 meridians for clarity. The wavefront aberrometry data is reported according to the ophthalmic standards [6, 7]. The pupil size exceeded 6 mm diameter for all eyes, so to allow comparison between eyes, the wavefront data was fitted using a 6 mm pupil diameter. The data was fitted with 28 Zernike polynomial terms (6th order including a piston term), but as the 6^th order results showed very little aberration structure, for the sake of being succinct we elect to only display up to 5^th order (18 coefficients, piston c(0,0), tip c(−1,1), and tilt c(1,1) removed) Zernike polynomials in Fig. 5.

Fig. 3.

Fixation target with 129 field points used in experiment. There are 24 semi-meridians with 1 degree radial increments. Note that the actual target used was a negative of this figure with white fixation points and labels on a black background.

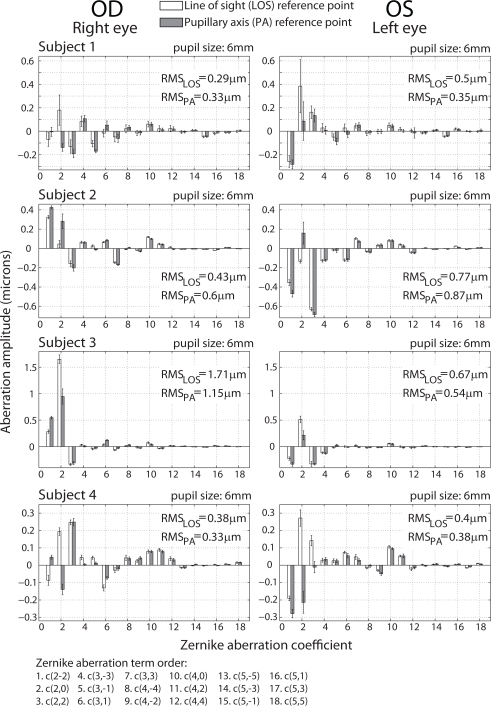
Fig. 5.

Comparison between Zernike wavefront aberration coefficients measured at two reference axes: line of sight (LOS) and pupillary axis (PA), given in microns. Error bars are ± 1 standard deviation. Eight eyes of four subjects are shown with wavefront abberations evaluated over a 6 mm pupil diameter. Data was fitted to 6^th order but the 6^th order is omitted from display.

5. Wavefront aberration of the eye along the line of sight compared to the pupillary axis

In this section we compare wavefront aberrations measured along the line of sight (LOS) to that measured along the pupillary axis (PA). The LOS as a reference axis for aberrometry is convenient since it joins a fixation point and the fovea through the center of the entrance pupil EP (see Fig. 4). All wavefront measurements on the LOS were performed while subject was fixating on the central star of the fixation target (see Fig. 3). For each eye in the study, 10 consecutive measurements were recorded for this field point. The bottom of Fig. 4 shows alignment of the PA measurements. In order to obtain such arrangement subjects were asked to fixate at different field positions. The field angle ω, at which the center of the entrance pupil superimposes the Purkinje I reflection, indicated alignment on the pupillary axis. As before, 10 consecutive wavefront measurements were performed along the PA of each eye. The angle λ between the LOS (central fixation point) and the PA (field fixation point) was measured as the field angle ω required to align the instrument along the PA.

Fig. 4.

Pupillary (PA), videokeratometric (VK) axes and the line of sight (LOS). On the right: the actual view of a measured eye that correspond to the sketched cases from the left side.

Figure 5 presents amplitude of Zernike wavefront aberration coefficients of each eye truncated to the first 18 terms (c(0,0), c(−1,1), and c(1,1) omitted). The mean Zernike coefficients of the 10 measurements along the LOS and along the PA and total RMS wavefront error is shown for each eye. The overall trend shows the expected dominance of low order aberrations along both the LOS and the PA for all eyes. The higher order coefficients are very similar for measurement along the LOS and the PA of an individual eye, whereas the 2^nd order coefficients show significant variation between the LOS and the PA of an individual eye. Not surprisingly, for the small sample size in the study, some inter-subject variability was detected. Subjects 3 and 4 show a greater amount of total wavefront aberration on the LOS compared to the PA for both eyes. It can be seen that the defocus term c(2,0) on the LOS has the greatest impact on the total RMS wavefront error. Furthermore, for subjects 3 and 4, the horizontal/vertical astigmatism coefficient c(2,2) contributes modestly to the total amount of aberrations. Typically astigmatism c(2,2) wavefront aberration arises when the maximum and minimum curvature fall on the vertical/horizontal meridians of the corneal surface. It has been reported that ’with the rule’ astigmatism (negative magnitude of c(2,2)) is likely to appear in eyes from a young population [45, 46].

Subject 2 represents the opposite case, where the wavefront aberration is much greater along the PA compared to the LOS for both eyes. For subject 2 there is a significant difference between the c(2,0) coefficient measured along LOS and PA. This may be an indication of a strong presence of field curvature for this subject. Subject 1 exhibits mixed results comparing the total wavefront aberration along the LOS to the PA. The aberration is slightly greater along the PA for the right eye whereas the aberration is greater along the LOS for the left eye. Like subject 3, the defocus term on the LOS for subject 1 dominates the aberration distribution. In undilated conditions the difference between aberrations measured along LOS and PA may be smaller.

Our measured values of angle λ range from 3 degrees to 7 degrees (Table 4) with a mean value of 5.5 degrees, which is comparable to previous mean values of 1.4 degrees and 9 degrees reported by Loper [13] and von Noorden [14]. Our results show the tendency for bilaterally symmetry for angle λ between the eyes. Furthermore, for all eyes in the study the PA was found close to the horizontal meridian (semi-meridian 1 in Fig. 3) indicating a smaller vertical component of angle λ compared to its horizontal component. During measurements the operator took notice that estimating the PA location was a predictable task due to consistency between subjects and bilateral symmetry. Figure 6 shows the field angle ω of the PA relative to the LOS (origin of the map). Note for all eyes the PA is located in the temporal visual field (object space) with a high bilateral symmetry between eyes.

Table 4.

RMS wavefront error measured on the line of sight (LOS) compared to the pupillary axis (PA). OD - right eye, OS - left eye. The dominant eye of each subject is indicated with a (*) symbol.

Wavefront aberrations measured along the line of sight and along the pupillary axis
Eye	Axis	Root Mean Square Aberration (μm)				Angle λ (degrees)
		2nd order	3rd order	4th order	Total
Subject 1 OD	LOS	0.23	0.14	0.07	0.29	5
	PA	0.24	0.22	0.07	0.33
Subject 1 OS*	LOS	0.49	0.08	0.06	0.50	3
	PA	0.32	0.11	0.05	0.35
Subject 2 OD	LOS	0.36	0.18	0.01	0.43	6
	PA	0.55	0.20	0.11	0.60
Subject 2 OS*	LOS	0.74	0.21	0.11	0.77	4
	PA	0.85	0.19	0.11	0.87
Subject 3 OD*	LOS	1.70	0.10	0.08	1.71	7
	PA	1.13	0.13	0.07	1.15
Subject 3 OS	LOS	0.65	0.12	0.07	0.67	7
	PA	0.52	0.13	0.06	0.54
Subject 4 OD	LOS	0.33	0.15	0.13	0.38	6
	PA	0.29	0.08	0.13	0.33
Subject 4 OS*	LOS	0.36	0.10	0.13	0.40	6
	PA	0.35	0.80	0.12	0.38

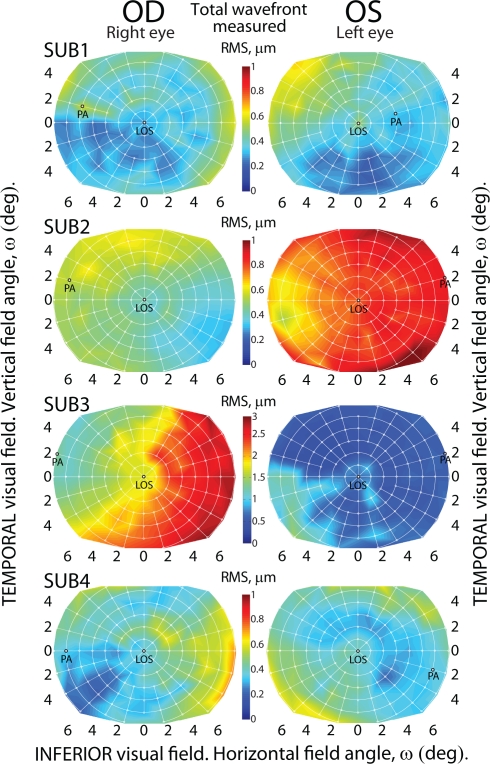
Fig. 6.

Total RMS wavefront error for 6 mm pupil diameter of all eyes measured across field angle ω with the origin centred on the line of sight (LOS). The position of the pupillary axis (PA) is also indicated. Note that maps for subject 3 use a separate color scale.

Table 4 presents more details regarding ocular aberration distribution along the line of sight and the pupillary axis. Zernike wavefront RMS of 2^nd order, 3^rd order, 4^th order and a total RMS is presented, together with an angle λ distance between the two reference axes. The overall trend suggests that the total RMS is similar between the LOS and the PA measurements for the emmetropic eyes. Only one eye of the subjects could be classified as ametropic (subject 3, right eye (OD)) and this eye indeed shows a more distinct difference of RMS along the LOS compared to the PA. Considering the contributions of specific orders, subject 1 illustrates higher-order RMS dominance on the PA with a very strong influence from the 3^rd order aberration terms, while subject 4 represents the opposite case with stronger impact from higher-order terms along the LOS. Subjects 2 and 3 show mild differences of higher-order RMS measured along two reference axes. In regard to eye dominance, the results indicate no association between the eye of minimal wavefront aberration and eye dominance for this group of subjects. Subject 2 is the only subject with ocular dominance coinciding with the eye of minimal wavefront aberration.

6. Isoplanatic patch of the eye

Knowledge about how aberrations of the ocular components of the eye are distributed across the visual field, leads to an important topic: the isoplanatism of the human eye. This topic is relevant for the performance of conventional adaptive optics (AO) systems. The first complete AO system for the eye was built in 1997 by Liang et al. [47]. Although the AO technique enables high-resolution retinal imaging, it can only be implemented over a small field called the isoplanatic patch [48]. In astronomy, this area is usually defined as a region of the field where the variation of the RMS wavefront error between any two points does not exceed 1 rad [5]. Following this definition, as previously discussed in the work of Goncharov et al. [49], this is equivalent to λ/2π = 0.13 μm RMS (considering λ = 840 nm). Therefore, we shall consider the isoplanatic patch as an area in the visual field, where the RMS wavefront error does not exceed 0.13 μm with respect to the central value at the origin of the field. This is equivalent to a Strehl ratio being reduced to 0.37 [50, 51]. This boundary value of the RMS is a more realistically achievable criterion over a 6 mm pupil, compared to the Maréchal criterion (0.8 Strehl), which would require a value of the RMS wavefront error below λ/14. Such a strict criterion is the classical measure of diffraction limited systems.

Ocular AO systems are therefore inherently limited in field of view, since a clear image of the retina can only be obtained over a narrow field angle for which AO correction is implemented. With increasing distance from the reference point on the retina, we move beyond the isoplanatic patch of relatively constant amounts of aberrations and enter regions of different aberration magnitudes and their combinations. Thus the image quality is degraded. Only a few studies have been conducted on the isoplanatism of the human eye. In 2008 Bedggood and colleagues reported the isoplanatic patch to be approximately 0.8 degrees at the fovea [52]. The same year Dubinin et al., reported the angular size of the zone of constant wavefront aberrations varies from 1.5 to 2.5 degrees [51].

Having defined the boundary limit of RMS wavefront error, the isoplanatic region for each eye was obtained by subtracting the reference wavefront coefficients from wavefronts coefficients for each field angle ω. Rotationally symmetric optical systems exhibit symmetric distribution of field aberrations that can be characterized in annular zones of the field [53], whereas for optical systems that lack any type of symmetry, e.g. the human eye, the characterization of image quality requires measurements of a larger number of field points. Hence aberrations were measured over a 14 × 11.6 degrees field of view at 129 sampling points. For each field point the subject was asked to fixate at the relevant target. Each measurement session lasted approximately 2 hours per eye and both eyes were cyclopleged regardless of which eye was undergoing measurement.

Figure 6 presents the field maps of distribution of the total RMS wavefront error for each eye over the central 11.6 degrees (and extending in the horizontal meridian to 14 degrees). Each field distribution map was centred on the line of sight and for additional information the location of the pupillary axis is also shown. Since the latter is closely associated with the optical axis of the eye, it is interesting to compare the size of isoplanatic patch for both the line of sight and pupillary axis. Before presenting this comparative analysis, it is worth giving a brief overview of the distribution of aberrations observed in the central field. For all field maps the wavefront data was fitted to 28 Zernike polynomials over a 6 mm diameter pupil and the total wavefront aberration RMS was calculated as the square root of the sum of the squared coefficients (omitting c(0,0), c(−1,1) and c(1,1)). Due to the high inter-subject variability the plots of total RMS required a separate color scale for subject 3. The plots in Fig. 6 are overlaid with a white grid and each grid intersection indicates a measured field location.

Comparing the right and left eyes of subject 2, the left eye displays a greater value of total wavefront error over the field, which can be attributed to the stronger presence of astigmatism in this eye. Comparing the fellow eyes of subject 3, the left eye shows a lower wavefront aberration, which is relatively uniform across the field. Whereas the right eye shows a distinct vertical demarcation of the total RMS field distribution. For this eye the optical quality appears to be significantly better in the temporal visual field (object space) compared to the nasal visual field. The central point indicating measurement along the LOS interestingly creates a notch within the generally vertical demarcation. For the left eye of subject 3 a similar island of lower wavefront aberration occurs at the map origin (corresponding with the LOS). Subjects 1 and 4 present mild amounts of aberration over the field, with the plots for both subjects using the same color scale. There is an irregular field aberration pattern, for each eye (subjects 1 and 4) with relatively low magnitude total RMS. This is in good agreement with the expected features of typical, young and healthy emmetropic eyes [54].

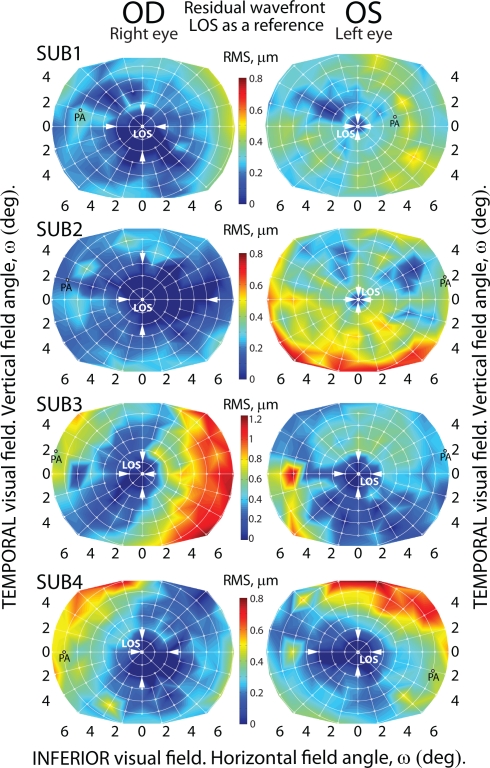
To further investigate wavefront aberration over the visual field and implications for aberration correction over the field (e.g. wide field retinal imaging), we analysed the aberration data with two alternative methods. In the first case the line of sight wavefront (LOS WF) is used as the reference and in the second case the pupillary axis wavefront (PA WF) is used as the reference wavefront. The method of subtracting the reference wavefront coefficients from field data has previously been described [50, 55, 56, 57]. Figure 7 shows the classical adaptive optics (AO) approach where the wavefront aberration measured along the LOS is used as the reference. Subtracting the LOS WF reference we simulate a perfect AO correction, where the corrector (e.g. deformable mirror) is conjugated to the pupil and assuming no intrinsic aberrations in the imaging system. It can be seen in Fig. 7 that eyes differ in their results of applying AO correction on the LOS. For clarity in displaying the isoplanatic patch of the eye, field points in Fig. 7 and Fig. 8 with a residual RMS value less then our criterion (0.13 μm corresponding to a Strehl ratio of 0.37) are displayed with the zero default of the color scale (dark blue in color).

Fig. 7.

Residual wavefront for 6 mm pupil diameter of all eyes across field angle ω. Obtained by subtracting the wavefront along the line of sight from each field point. Note that maps for subject 3 use a separate color scale.

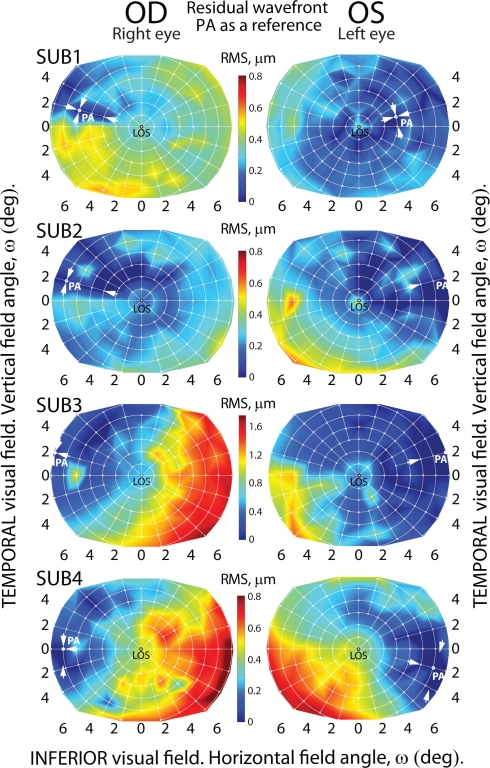
Fig. 8.

Residual wavefront for 6 mm pupil diameter of all eyes across field angle ω. Obtained by subtracting the wavefront along the pupillary axis from each field point. Note that maps for subject 3 use a separate color scale.

To simplify estimation of the angular size of the isoplanatic patch and due to the irregularity in its shape, only the edges along the horizontal and vertical meridians of patches centered on the LOS are marked with white arrows. The left eyes of subjects 1 and 2 in Fig.7 show a limited area of optimal correction with respect to field angle (ω) when simulating a conventional AO strategy of sensing and correcting aberrations using the LOS as the reference axis. These eyes have a small isoplanatic patch, whereas the fellow right eyes of subjects 1 and 2 show larger fields of potentially well-corrected wavefront aberrations up to angular size of 6 degrees horizontally and 5 degrees vertically (subject 2). This method of subtracting the LOS WF from field aberrations (simulating a deformable mirror operating on the LOS) gave different outcomes for subjects 3 and 4 resulting in a comparable correction requirement over the field for both eyes of subjects 3 and 4. Figure 7, subject 4 shows significant bilateral symmetry in the size, shape and position of the isoplanatic patch. In contrast, subject 2 shows no tendency towards bilateral symmetry regarding the isoplanatic patch. The right eye of subject 2 depicts the largest isoplanatic patch and indicates using the LOS wavefront reference arrangement would be suitable for wide field imaging in this eye.

Now consider the second case where wavefront aberrations are analysed by subtracting the pupillary axis wavefront (PA WF) from each field point. This simulates an AO system with the corrector operating on the PA. For clarity in Fig.8 the edges of the isoplanatic area are marked by white arrows along the radial meridian upon which the PA location was detected and also perpendicular to this meridian. Comparing Fig.8 with Fig.7, it could be argued that applying the LOS WF reference produces a better correction over the field with larger isoplanatic areas observed for nearly all eyes measured. Figure 8 shows in the case of PA WF reference the isoplanatic region was relatively asymmetric and often fragmented, which is in agreement with previous studies [55, 57]. Applying such a method to an AO system may result in the isoplanatic patch breaking up from one contiguous region into multiple islands. This unsatisfactory effect of field correction may be attributed to the irregular pattern of ocular aberrations near the PA. In Fig.8 some eyes we were unable to define the boundary of the isoplanatic patch as it fell outside the measurement area. It is important to note that irregular isoplanatic patches with island formation may also be observed in the classical case of LOS WF reference. In simulating correction of aberrations using the LOS as the reference axis, the isoplanatic patch size varies among subjects with a typical angular extent of approximately 2 degrees. This is in line with theoretical predictions of the eye model based on reverse ray-tracing [49].

7. Discussion and limitations

From Table 4 it can be seen that the dominant contribution to the total RMS wavefront error are the lower-order aberrations, namely the 2^nd order of the Zernike terms (astigmatism and defocus). These results are in accordance with the observations made in previous studies [58, 59, 49]. From Fig. 5 we observe that it is these same lower order aberrations which undergo greatest change in magnitude with the field angle change between the LOS and the PA. The field dependent component of lower-order aberration terms manifest themselves off-axis as field curvature and classical Seidel primary astigmatism. This means that correcting these field-dependent terms can significantly help to improve retinal imaging over the central retinal field without necessitating multiple adaptive elements within an adaptive optics system. Single-conjugate AO correction would be beneficial for a small region on the retina (1 – 2 degrees), but it is unlikely to be effective over a field larger than the isoplanatic patch [60]. Using additional deformable mirrors or spatial light modulators would complicate the instrument design and might not give sufficient correction over large fields. Our results suggest that correction of field-dependent astigmatism and field curvature by traditional optics of the instrument is a promising option. A dedicated optical system with components producing variable amounts of astigmatism and field curvature could help to eliminate the lower-order ocular aberrations over a larger central field. Using a variable low-order field aberration corrector in conjunction with an adaptive optics system might be an alternative to the multi-conjugated AO system proposed recently [61, 62]. Assuming such a system is well corrected for the lower-order field-dependent aberrations (field curvature and field-dependent astigmatism) one may imagine the possibility of incorporating static elements in the pupil conjugate plane which correct typical values of spherical aberration c(4,0), which is field-independent.

For multi-conjugated adaptive optics systems with only one deformable mirror (DM) or spatial light modulator, it might be an efficient design to use a conventional optics approach with a field flattener lens to correct curvature of field. Such a relatively inexpensive field flattener might successfully negate the average variation in defocus with field angle and relaxes the demands for the stroke on the DM to be dedicated to higher-order aberrations correction. As Bedggood and Metha [62] point out it is logical that the conjugation plane of the DM is not necessarily optimal to conjugate it to the pupil, and indeed a field flattener element would be conjugate to the retina.

It is known that tear film fluctuations can influence wavefront aberration measurement [63, 64, 65]. To reduce measurement noise due to tear film fluctuations we used a waiting period following the blink with the aim of capturing data once the tear film distribution had stabilised. Measurements were performed approximately 2 seconds following a single blink ensuring avoidance of tear film break up. Another potential noise source affecting ocular aberration measurements is the accommodation system [66]. Fluctuations in the accommodation state were minimised by using strong cycloplegic agents and experienced subjects. The cyclopentolate also ensured all pupil diameters were greater than 6 mm.

8. Conclusions

Our experiment took advantage of some of the unique features of the instrument being both an aberrometer and corneal topographer. This instrument helped establish the orientation of the line of sight with respect to pupillary axis. The aberrometer featuring Hartmann-Shack wavefront sensor allowed us to consecutively measure the field aberrations (wavefront error) at 129 field points in the central visual field (14 × 11.6 degrees) for 8 young healthy eyes. This information about the aberration distribution across the field was used to calculate the size of isoplanatic patch using the line of sight as well as pupillary axis as references. We considered two cases: a perfect adaptive optics (AO) correction applied along LOS and PA. In both cases the AO simulation featured a single adaptive element conjugated to the pupil. Our results show that the shape of the isoplanatic region applying the LOS reference is more regular and typically larger than that by applying the PA reference. Suggesting that for a single corrector, it may be better to use the LOS as a reference as is the norm. We also confirmed that the field-dependent component of lower-order aberrations (defocus and astigmatism) accounts for the largest contribution to the total wavefront error for each field point, as previously observed [67, 68]. We suggest that as an alternative to multi-conjugated AO system one could use a classical approach to aberration correction by utilizing variable optics to reduce the average amount of defocus off-axis and field astigmatism in the eye. It is hoped that this statistical data would aid future designs for wide-field ocular adaptive optics systems to achieve high-resolution retinal images over a wider field. This is beneficial since it reduces the amount of montage image stitching required to create a wide-field retinal image with single-conjugate AO.

As previously pointed out, the PA is likely to be located near the optical axis of the eye and therefore, one may expect lower wavefront aberration along this axis compared to the LOS. This is true for some eyes measured in this study however, in order to maximize the size of the isoplanatic patch with a single-conjugated AO system, the goal is to apply the reference wavefront correction that is closest to average or median over a field of interest. There is no requirement to locate the ocular axis along which the wavefront aberration is minimal, provided that the required correction along the selected axis does not exceed the capability of the DM. Our observations indicate the LOS reference provides wavefront aberrations that are closer to the median wavefront aberrations over the central field in most eyes. As is often the case regarding the human eye, significant inter-subject variability exists and aberrations correction methodologies may benefit from consideration of individual aberration pattern across the field.