Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2012 Feb 1.
Published in final edited form as: Nanotechnology. 2008 Apr 8;19(19):195702. doi: 10.1088/0957-4484/19/19/195702

Molecular dynamics simulation study on trapping ions in a nanoscale Paul trap

Xiongce Zhao 1,*, Predrag S Krstic 2
PMCID: PMC3269946  NIHMSID: NIHMS349250  PMID: 21825720

Abstract

We found by molecular dynamics simulations that a low energy ion can be trapped effectively in a nanoscale Paul trap in both vacuum and aqueous environment when appropriate AC/DC electric fields are applied to the system. Using the negatively charged chlorine ion as an example, we show that the trapped ion oscillates around the center of the nanotrap with the amplitude dependent on the parameters of the system and applied voltages. Successful trapping of the ion within nanoseconds requires electric bias of GHz frequency, in the range of hundreds of mV. The oscillations are damped in the aqueous environment, but polarization of water molecules requires application of higher voltage biases to reach improved stability of the trapping. Application of a supplemental DC driving field along the trap axis can effectively drive the ion off the trap center and out of the trap, opening a possibility of studying DNA and other charged molecules using embedded probes while achieving a full control of their translocation and localization in the trap.

1. Introduction

A possibility to trap free charged particles in an electric field “bottle”, preventing their interaction with the walls has become a reality in recent decades, opening opportunities for trapping and measurement on a single atom or molecule level. Atomic ions can be confined by particular arrangements of electromagnetic fields. For studies of ions at low energy, two types of trap are typically used - the Penning trap, which uses a combination of static electric and magnetic fields, and the Paul or radiofrequency (rf) trap which confines ions primarily through ponderomotive forces generated by inhomogeneous oscillating fields (Paul, 1990).

A three-layer crossing metal/insulator structure, with a nanopore (20-50 nm) etched through from top to bottom by reactive ion etching (RIE) and appropriate AD/DC voltages applied to the metal electrodes, constitutes a nanoversion of a quadrupole Paul ion trap, whose fabrication becomes a reality (Reed). The detailed modeling could be done to optimize the planar geometry, thus enabling consideration of various electrode configurations. The goal of the present work is to show by molecular dynamics (MD) simulations that, if fabricated, such Paul-type nanotrap could be an efficient tool for trapping and filtering of single atomic and molecular ions. Of particular interest is the effect of polarizable aqueous environment that would potentially fill the trap. Such environment might be crucial for supporting the trap functions for bio-molecular ions like DNA. Other effects, emerging from the trap's nanodimensions, could be expected in the presence of the Van der Waals force from the trap walls, in a need for confinement of the ion oscillations to the nano-volumes, in effects of thermal fluctuations, polarization of the medium and walls, and in their inhomogenities. These all might suppress predictive powers of the common “analytic” approach to the motion of an ion in the trap. Atomistic molecular dynamics simulation which would take into account majority of these dimension and medium effects is a reasonable alternative. We choose a model of electrodes following a hyperbolic shape, which corresponds to the conventional Paul trap (Paul, 1990), a simplification which is not essential in providing a proof of principle for functionality of the Paul nanotrap. This allows the application of analytical expressions for the resulting quadrupole electric field in the modeling, which significantly speeds up the algorithms involved for numerically intensive MD simulations performed here, without loss of generality. Quite analogous simulations are possible using a numerical calculated electric field of the realistically shaped electrodes, upon knowing the parameters of a fabricated nanotrap.

An excellent review of the functions and applications of the conventional Paul ion traps is given by Leibfried et al (Leibfried et al 2003). The idea to store a single atomic ion was discussed by Dehmelt (Dehmelt, 1973), while the first single-particle trapping experiments were done by Wineland et al (Wineland et al., 1973) using a Penning trap to confine electrons. The first experiments with a single atomic ion (Ba) in a rf trap was done by Nauhauser et al (Nauhauser et al., 1980), followed by Wineland and Itano (Wineland and Itano, 1981) with a single magnesium ion in a Penning trap. Currently, a large number of research groups are capable of confining single ions in the rf traps. The recent applications of the rf ion traps are for quantum information processing (Vant et al., 2006; Seidelin et al., 2006), for coherent quantum-state manipulation of trapped atomic ions (Wineland et al., 1998), for functional studies with fluorescent proteins (Rothbauer et al., 2007), for laser sideband cooling of the motion (Abichet al., 2004), for formation of ordered structures of trapped ions (Schiffer, 2003; Shi et al., 1999; Itano et al., 1995; Walther, 1995; Edwards et al., 1994), etc. A wide spectrum of applications relies on the use of the quadrupole ion trap as a mass spectrometer (Paul, 1990).

Much research attention has been focused recently to the possibility of sequencing genome by measuring the base-type specific properties of each nucleotide as it migrates through a nanoscale pore (Chan, 2005; Fredlake et al., 2006; Healy, 2007; Kricka et al., 2005; Nakane et al., 2003; Rhee and Burns, 2006, 2007; Ryan et al., 2007). However, it has been realized that repeatable measurements of the base specific signature of each nucleotide depends critically on the relative geometry of the bases to the pore during the DNA sequencing (Lagerqvist et al., 2007; Tabard-Cossa et al., 2007). For example, it is found that the variation in the conductance due to the geometry of the base relative the electrode can easily overwhelm the difference between different types of nucleotide (Zhang et al., 2006; Zikic et al., 2006). Therefore, control of the orientation and position of the nucleotide as it threads the nanopore becomes a primary concern for such kind of DNA sequencing techniques (Trepagnier et al., 2007; Tsai and Chen, 2007; Chen and Peng, 2003). One of the proposed approaches to enhance the controllability of a migrating DNA segment through a nanopore is to use the Paul type ion trap such as quadrupole ion trap (Arnott et al., 1998; Oberacher et al., 2004). The idea is based on the concept that negatively charged DNA segments can be trapped in the device while it is driven through the trap by an electric field. Due to the strong trapping effect, each nucleotide on the DNA could be maintained with a specific orientation or a stable average geometry, far from the walls and with a defined position to the appropriate probes, which might critically increase certainty of the measured electronic or mechanical properties including the genome sequencing. This application sets two restrictions to the trap parameters. One is the size of the trap that should be small enough to establish a confinement of a DNA within its characteristic, nanometer dimension. The second one is the aqueous nature of the trap, since water is a natural environment for a stable DNA molecule. The presence of water in the trap is a big challenge, which requires consideration of the polarization of water molecules, the thermal effects, the damping forces to the ion motion, and the inhomogenity effects. We include these effects in our MD simulations of the trap, considering the interaction of a large number of water molecules in the trap at a given temperature and forces from external electrical fields. We note that a “vacuum” nanotrap could also potentially have significant applications. For example, fabrication of the surface arrays of the Paul-type nanotraps can serve as a basis for a high spatial resolution detector of charged particles, which is of importance in studies of nuclear reactions.

Quadrupole trap types are those that lead to an electric potential F(x, y, z, t) of approximately quadrupolar spatial shape in the center (Leibfried et al., 2003). Their functionality emerges from the assumption that the particles are bound to an axis of the system if a binding force which acts on them increases linearly with their distance (F = –cr ). Cylindrically symmetric electrical potential is assumed in the form of

Φ(r,z,t)=Φ02r02(αx2+βy2+γz2). (1)

The condition that this potential has to fulfill the Laplace equation ∇2Φ = 0 at every instant in time leads to a constraint α + β + γ = 0 of the three geometric factors, which can be achieved in various ways, thus defining various possible geometries and types of quadrupole traps (Paul, 1990). From this constraint it is obvious that no local three-dimensional minimum in free space can be generated, so the potential can only trap charges in a dynamical way. The driving frequency and voltages can be chosen in such a way that the time-dependent potential will give rise to a stable, approximately harmonic motion of the trapped particles, in all or chosen directions. This can easily be demonstrated by a mechanical analogue. The equipotential lines form a saddle surface in a trap. A small, still ball set on the saddle is not in a stable equilibrium and will roll down the saddle. But if one sets the saddle into rotation with an appropriate frequency the ball motion will become stable in form of small oscillations which can be positioned on the saddle for an extended time (Paul, 1990).

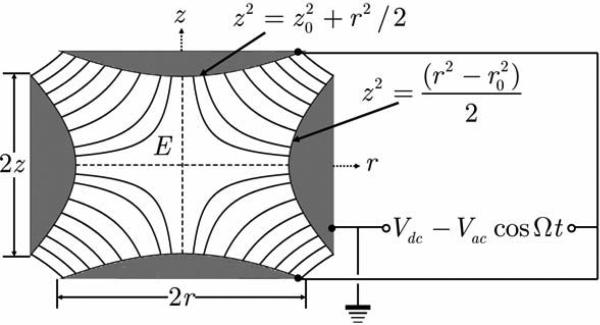
Both classical and quantum approaches have been applied to the motion of a charged particle in such a trap, and stability was reached for a range of parameters. One of the most popular trap configurations is the 3D radio-frequency (rf) Paul trap, with α = β = 1, γ = –2 (Paul, 1990; Leibfried et al., 2003). This trap is composed of one ring-shaped metal electrode and two cap-shaped metal electrodes, whose internal surfaces are defined as hyperbolic surfaces shown schematically in Figure 1. The surfaces coincide with equipotential surfaces. The hyperbolic ring electrode is halfway between the other two electrodes, i.e. r02=2z02. The ions are trapped in the space between these three electrodes by AC (rf oscillating, non-static) and DC (non oscillating, static) electric fields. Such devices in a macroscopic scale have been widely fabricated in laboratory and been proven to be a powerful tool in storage and detection of a single ion (Winter and Ortjohann, 1991). Their typical dimensions are 100 μm to 1 cm, with voltages Vac in the range of 100 to 300 V, Vdc in the range of 0 to 50 V and the AC frequencies f = Ω/2π in the range of 100 kHz to 100 MHz. We will study in next sections the effects of reduction of the trap in Figure 1 to nanometer dimensions, under both vacuum and aqueous filling environment.

Figure 1.

Figure 1

Open in a new tab

Schematic sketch of a Paul trap (section of z – r plane).

If an electric bias of Φ0 = Vdc – Vac cosΩt is applied to the system in Figure 1, the resulting azimuthally symmetric electric field is given by its components (Paul, 1990)

Ez=Vdc−VaccosΩtz02z,Er=Vdc−VaccosΩt2z02r. (2)

Due to periodic change in the sign of the electric force, one gets focusing and defocusing in both the r and z directions alternating in time. The equations of motion of a particle with mass M and charge Q in this field is given by Mathieu differential equations (Paul, 1990), even in the presence of a damping force (Nasse and Foot, 2001; Hasegawa and Uekara, 1995) that is emerging in our case from viscosity of aqueous environment. If such viscosity force is modeled by F =–Dν, where v is the instantaneous velocity of the ion in the trap, and D is a constant proportional to the viscosity constant and g eometrical features of the particle, the Mathieu equations of the damped motion of the particle, u = wexp(–kτ), are

d2wdτ2+(a−k2−2qcos(2τ))w=0 (3)

where u stands for either r or z coordinate, k = D/MΩ τ = Ωt/2 and

a=4QMVdcz021Ω2,q=2QMVacz021Ω2. (4)

Here az = –2ar, qz = –2qr. The stability of the solutions to the equations, defining the confining functions of the trap, is dependent on the values of parameters a and q (Winter and Ortjohann, 1991), i.e. the stability depends on the magnitudes of both AC and DC components of the applied bias, on the angular frequency Ω, on the trap dimensions, as well as on the ion charge Q and its mass M. In the presence of a damping force, the regions in (a, q) plane of the stable confinement are both enlarged and shifted in comparison to those with no damping. The solutions u may be bounded (stable) even if w is unbounded (unstable), due to the damping factor exp(–kτ). The effect of the collisions between ion and background particles will change the stable orbit of the ion, statistically increasing or decreasing the ion energy, which depends on the relative mass of the particles. In our case the ion mass (chlorine) is about twice larger than that of the background water molecule, and this results in a damping force. The solution generally oscillates with a system “secular” frequency ω=βΩ2, where

β=[a−k2+q2∕21−3q2∕8]1∕2, (5)

on which it is superimposed micromotion (of much higher frequency Ω and 2Ω).

In this paper, we report a series of molecular dynamics studies on trapping an ion in a quadrupole 3D Paul trap of nanometer scale, in vacuum and in aqueous environment. Modeling of DNA/ion/nanopore systems using MD method had been reported by different groups in recent years. (Chen, 2005; Aksimentiev et al., 2004a; Aksimentiev et al., 2004b; He et al., 2007; Lu et al., 2006; Gracheva et al., 2006; Zhao et al., 2007) The method we employed here is similar to the one used previously by us and by other groups. The specific details of our MD method applied are given in Section 2. The results of the simulations are presented in Section 3, while Section 4 contains our conclusions.

2. MD Simulation Method

It is certainly interesting to consider the nanotraps of dimensions of order of a few nm, with respect to anticipated applications. However, present fabrication capabilities of the nanotraps might be limited to a few tens of nm, in which case it is important to know both ion confinement capabilities and sizes of the ion oscillation amplitudes, which might determine the applicability of the trap. Thus, in our simulations we consider Paul-type traps (Figure 1) of two different dimensions, 2r0 = 5 nm, 2z0 = 5/√2 nm (nanotrap A), and 2r0 = 50 nm 2z0 = 50/√2 nm (nanotrap B). We choose the parameters a and q in the middle of the stable region as defined for a conventional Paul trap (Winter and Ortjohann, 1991), i.e. a = 0.25 and q = 0.4. In applications of nanoscale Paul trap, prevention of the electric breakdown is an additional constraint to the applied voltages, and this certainly depends on the trap dimensions (Hirata et al., 2007).

The nanoscale Paul traps used in simulations were “built” from a cuboid FCC gold lattice with a dimensions of 7.9×7.7×5.6 nm3 in case of trap A and 60×60×42nm3 for trap B. The internal part of the lattice was removed to create hyperbolic surfaces, consistent with the surfaces in Figure 1. A nanopore of 2 nm in diameter is created in each cap to mimic the device proposed. A chlorine ion was placed randomly inside the trap at the beginning of each simulation, with random initial momentum conforming to a chosen system temperature. For simulations with solvent, the trap is wrapped in box of explicit water molecules. Periodic boundary conditions are applied in all three directions.

The ions were modeled by the AMBER force field 1999 version (Case et al., 2005). The gold atoms composing the trap electrodes were modeled by the universal force field potentials (Rappe et al., 1992). Water molecules were modeled by the TIP3P potential (Jorgensen et al., 1983) based on previous successful modeling of biomolecules and ions using this model (Cheatham and Young, 2000). The polarization interaction between ion/water and the gold atoms were calculated by the Electrode Charge Dynamics (ECD) (Guymon et al., 2005). The ECD accounts for the polarization effects of finite size metal surfaces and gives a reasonable representation of ion-metal interactions (Payne et al., 2008). The Lennard-Jones interaction between different species were calculated by the standard Lorentz-Berthelot mixing rules with a 0.9 nm spherical cutoff without long range corrections. The particle-mesh Ewald method (Darden et al., 1993) with a fourth order interpolation and direct space summation tolerance of 10–6 was applied to evaluate the electrostatic interactions. The force to the charged ion due to the trapping fields applied can be included in each MD step by adding the force

f=QE (6)

to the equations of motion of the ion, where the three dimensional field E is defined by Eqs. (2).

The MD simulations in vacuum were performed within the NVT (constant number of particles, constant volume, and constant temperature) ensemble. For simulations including solvent, preliminary simulation under NPT (constant number of particles, constant pressure, and constant temperature) ensemble with pressure of 1 bar was performed to equilibrate the solvent before NVT simulations. The temperature and pressure were kept constant where necessary using the method in literature (Berendsen et al., 1984). The NAMD (Phillips et al., 2005) software package was employed to integrate the equations of motion. The gold atoms were kept “frozen” thus neglecting metal-atoms vibrations and thermal fluctuations during the simulation (Zhao et al., 2007). This assumes that amplitude of the vibrational oscillations of the atoms in the electrode (gold) crystal lattice is much smaller than the typical dimension of the trap, at the considered system temperatures (3 - 300 K). A typical simulation run at 300 K include 20000 steps of energy minimization using a conjugate gradient algorithm, followed by gradual heating from 0 to 300 K in three ps, 40 ps of MD solvent equilibration where appropriate, and 3 to 12 ns of production. The timestep used to integrate the equations of motion was two fs. The electric fields used to trap the ions were turned on at the beginning of production run. In simulations with explicit solvent molecules, a 400 ps equilibration was performed after the electric fields were turned on and before the production began. The SHAKE (Ryckaert et al., 1977) algorithm was applied to constrain the bonds involving hydrogen bonds for simulations involving water molecules. The structural configurations were collected every ps for subsequent analysis. Finally, visualization and trajectory analysis were performed using the VMD software package (Humphrey et al., 1996).

3. Results and Discussion

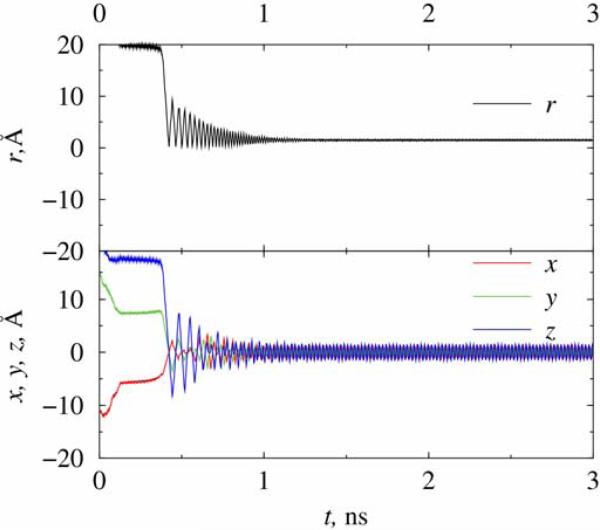
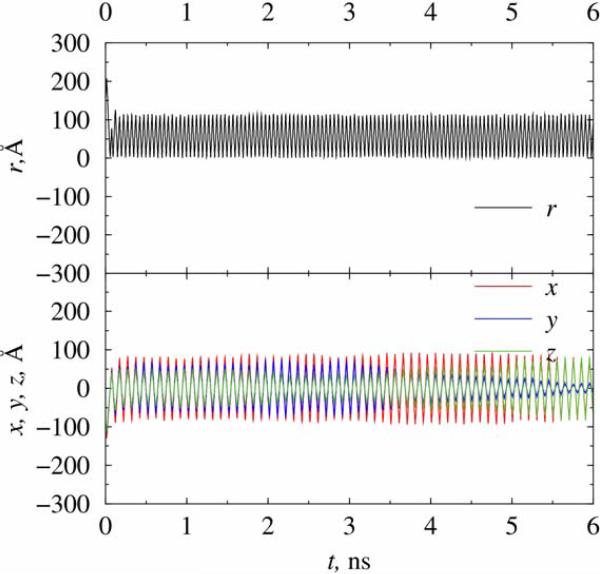
Since modeling of the aqueous nanotrap is much more numerically demanding than the vacuum case due to the presence of large number of “active” particles (water molecules) in the former case, most of our results are on trapping of a chlorine ion in both traps A and B under vacuum conditions. In Figure 2 we show coordinates of the ion as function of time in trap A at temperature of 3 K (corresponding to the ion energy of 2.5×10-4 eV). Shown initial coordinates have values (-12, 15, 24) Å relative to the geometric center of the trap, which were randomly set at the beginning of simulation. The initial momentum of the ion was randomized following a Gaussian distribution but conformed to the system temperature. The needed trapping field is Vdc = 200mV and Vac = 600mV estimated from Eqs. (4), with the chosen frequency of AC voltage being 318 GHz. The trajectory of the ion was monitored for up to 3 ns of simulation. As can be seen in Figure 2, the chlorine ion is driven to the center of the trap and rotated in a circular motion with its stabilized distance to the trap center being about 1.5 A. The time of 1.2 ns is elapsed before the stabilization is reached. The oscillation frequency of the trajectory is about 50 GHz, which is quantitatively consistent with the estimated “secular” frequency ω according to Eq. (5), for the given values of (a,q,k = 0,Ω). The simulations were repeated for at least five times by changing the initial random number seeds that were used to generate the initial positions and momenta of the ion. However, we only present figures calculated from one chosen trajectory in the present and the following cases of this section. The repeated runs lead to the same quantitative conclusions as the one shown, contributing to a statistical weight of the results.

Figure 2.

Figure 2

Open in a new tab

Simulation of a chlorine ion in nanotrap A at T=3 K in vacuum. The frequency of the AC field applied is 318 GHz.

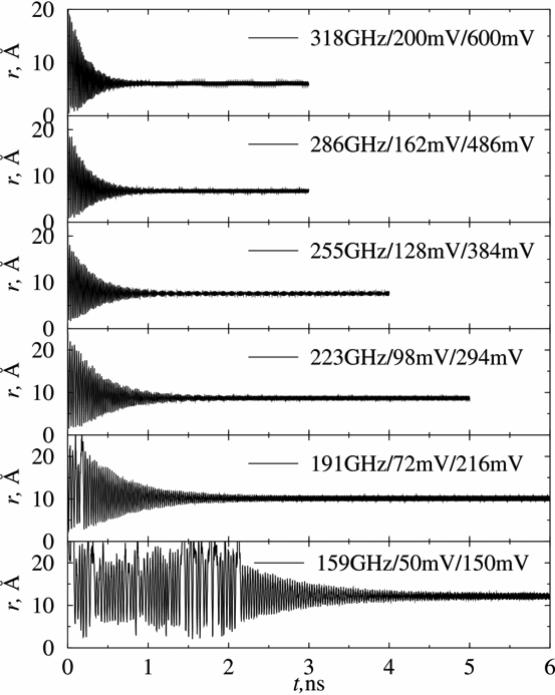
We have performed a series of simulations varying the driving fields from (Vdc = 0.5mV, Vac = 1.5mV ) to (Vdc = 200mV, Vac = 600mV ), and with frequencies ranging from 16 to 318 GHz. The AC voltage with a frequency in tens-to-hundreds of GHz range is required in order to trap the charged ions within a timescale of nanoseconds. Increase in the frequency, which also implies an increase in the magnitude of the voltage according to Eqs. (4) for given a and q, results in a faster establishment of stabilization. In Figure 3 we show simulations with AC voltage frequencies in the range of 159 to 318 GHz, which require voltages of Vdc = 50mV, Vac = 150mV to Vdc = 200mV, Vac = 600mV, under constant temperature of 50 K (i.e. equivalent ion energy of 4.3×10-3 eV). The stabilization time for these systems ranges from 4.5 ns to 1 ns. However, the amplitude of the stabilized ion “secular” oscillations ranges from 12 Å to 6 Å, well below the dimensions of the trap.

Figure 3.

Figure 3

Open in a new tab

Dependence of stabilization time on the magnitude of applied voltages and the frequency of AC voltages at 50 K. The simulation parameters are given by the legend in each figure.

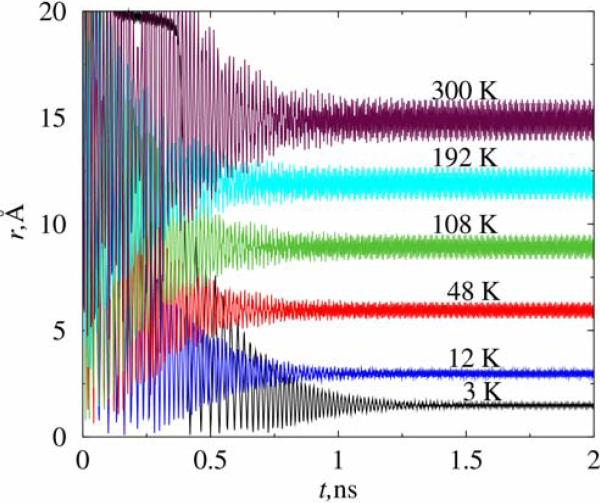
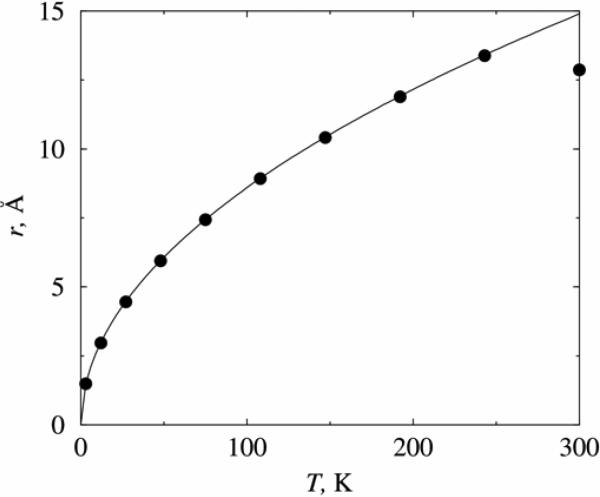
The stabilization time is dependent on the temperature, i.e. on the initial ion kinetic energy. Figure 4 shows such variation of the initial ion energy in the range of 3 to 300K in trap A for Vdc = 200mV, Vac = 600mV, and f = 318 GHz. Remarkably, we find that there is an optimal temperature which yields the shortest stabilization time. For a chlorine ion under the above conditions the shortest stabilizing time occurs at 50 K, differing by almost a factor of 2 to the values at 3 K and 300 K. Presently, we do not have a viable explanation of this phenomenon. Furthermore, the oscillation amplitude of the ion inside the trap is also strongly dependent on the temperature. For example, at 300 K the ion is orbiting with a radius of 15 Å, whereas at 3 K the orbiting radius is only about 1.5 Å. A simple relationship can be derived to describe the dependence of the orbiting radius and temperature. Assuming that the confining centripetal force is proportional to the distance between the particle and the trap axis, compatible with quadrupole potential, we have mv2 = rFc ∝ r2 and mv2 = kT, which yields r2 ∝ T. From simulations we can conveniently estimate the orbiting radius of the trapped ion at each different temperature. We can also fit the simulated results using a simple relationship r = α√T. The results are plotted in Figure 5. It can be seen that r2 ∝ T fits excellently with the simulated data. The regressed prefactor α is about 0.86 for the above defined system. We notice that the simulated data point at 300 K does not overlap with the curve, simply because of the confinement effect of trap A. That is, the ion was not able to move beyond the trap cap along the z axis. Therefore, the effective circulating orbit of the ion at 300 K is depressed below 0.86√T. In the 300 K case, we also observe that the orbiting trajectory of trapped ion is changed slightly to adapt to the inner shape of the trap, although the circular nature of the orbit was not changed. In other words, the motion of the ion will depend on the trap size. This phenomena will not be present for a macroscopic Paul trap but becomes significant when the trap scales down to nanometer size. We deem this as one of the main limitations of a nanoscale trap in confining a charged particle. On the other hand, this effect also implies that larger trap will tolerate an input ion with a higher energy, therefore higher temperature, without disturbing its orbiting motion in the z direction.

Figure 4.

Figure 4

Open in a new tab

The stabilization time and circulation radius of a chlorine ion inside trap A at various temperatures. All the simulation were performed at Vdc = 200mV, Vac = 600mV, and the frequency of AC voltage is 318 GHz.

Figure 5.

Figure 5

Open in a new tab

Temperature dependence of the orbiting radius of a chlorine ion inside trap A. The simulation parameters: Vdc = 200mV, Vac = 600mV, f = 318 GHz, The symbols are calculated from simulations, and the curve is a fitting using equation r = 0.86√T.

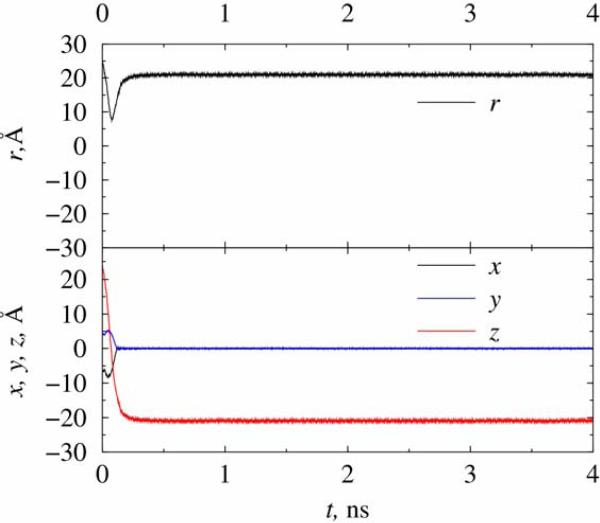
Our next simulation studies the trapping of a chlorine ion in trap B, which is about 10 times larger in dimensions than trap A. This simulation is numerically much more demanding than the one with trap A, due to larger number of atoms in the electrodes, and in case of aqueous environment because of significant number of explicit water molecules to be included in the dynamics. Thus, trap B was simulated only in vacuum. However, the increased dimensions of the trap allowed for lower (and more realistic) trapping field frequencies, here chosen to be 20 GHz, and larger electric biases before a possible breakdown occurs. The ion was initially positioned at (-110, -100, 88) Å and the initial kinetic energy of the ion conforms to a system temperature of 300 K. The trapping fields were Vdc = 80mV, Vac = 240mV, which were turned on at t=0. As shown in Figure 6, the ion was trapped to the center of the trap after a short time, with the orbital radius of about 6.5 nm. The overall behavior of the ion motion is similar to that observed in trap A, only with much bigger orbiting amplitudes.

Figure 6.

Figure 6

Open in a new tab

Trapping of a chlorine ion inside trap B at 300 K. The trapping fields are Vdc = 80mV, Vac = 240mV, f = 20 GHz.

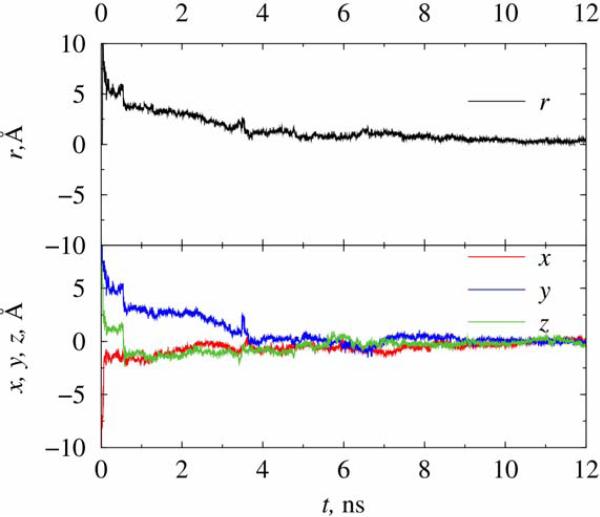
Simulations were also performed for trapping of a chlorine ion in trap A with an additional driving DC field along the z axis (see Figure 1) ranging from 10 mV/nm to 150 mv/nm, in order to study the impact of this additional field to the trapping process. We again study this with a negatively charged chlorine ion, noting that this might be relevant to driving a charged DNA molecule into (the holes in the caps), through and out the trap. Initially the ion was placed at the entrance of one of the cap holes with its coordinate as (5, -7, 22) Ǻ relative to the trap center, with initial momentum of the ion set to conform to the system temperature as before. The z-direction driving field and the trapping fields were turned on simultaneously when the simulation starts, and the trajectory of the ion was monitored for 3 to 12 ns. An example of such simulations is presented in Figure 7. Near zero temperature of 3 K is used to get a clear picture on how the ion wil l move along each direction under the influence of the additional z-direction field. As seen in Figure 7, the ion migrates through the central region from one entrance, while orbiting around the trap center in the x-y plane. In this example, the ion was finally stabilized at a position of about (0, 0, -21) Å, with the orbiting radius of about 2.1 nm. That is, the ion is trapped similarly like that without the z-direction DC field although its position is now significantly shifted along the z axis. We have carried out simulations with driving fields of various strength and found the expected shift of the ion orbit along the z-axis varies with the strength of the field. Additional simulations indicate that the ion is stably trapped when the z field is below 110 mV/nm, while a field of 125 mV/nm would drive the ion all the way through the trap within one ns, without reaching the stabilization. This suggests that for trap A the threshold driving DC field for moving the ion through the whole trap along z direction lies in 110 to 125 mV/nm. Attractive is also a possibility, emerging from this case to drive the ion back and forth along the z-axis through the trap, by changing the polarity of the driving DC field, possibly increasing a measurement certainty by the probes embedded in the trap. Apparently the shift of ion from the trap center along the z direction when the field is under 110 mV/nm would depend on the magnitude of the field, but we could not establish a simple relationship between them like that in Fig. 5.

Figure 7.

Figure 7

Open in a new tab

Trapping of a chlorine ion inside trap A with a biased voltage along the axis through the two holes in the caps. The simulation was performed at near zero temperature (3 K) with Vdc = 200mV, Vac = 600mV, f = 318 GHz,. The driving field along the z axis is 75 mV/nm.

It is now evident that the mathematical relationships such as those defined by equations in the Introduction are valid in predicting the stable trapping parameters of the system, at least under vacuum condition. These predictions are not as certain in the presence of a dense background such as explicit solvent (water), which is relevant to applications of, for example, DNA trapping and sequencing. The presence of random noise from solvent would render the system to a Mathieu system that can be described by a stochastic Mathieu equation, where some of the terms are random quantities (Casademunt and Vinals, 2001; Rong et al., 2002). The random fluctuations of the equation parameters may cause unexpected effects such as stochastic resonance, stabilization by noise, etc. Nonlinear and damped models of Mathieu equation could be introduced to describe viscosity, curvature and inhomogenuous effects of parameteric waves in solvent (Kumar, 1999; Robinson et al., 2002; Tian and Zoller, 2004). The least demanding approach to the inclusion of the solvent effects in MD modeling is to use implicit solvent models. For an analysis of macro-sized traps filled with water, this could be a good choice since one can include the dielectric properties of the bulk water into the simulation. However, in a nanoscale trap filled with solvent, there could be significant dielectric inhomogenities through the Paul trap volume, requiring explicit inclusion of the solvent molecules in the MD simulations.

In Figure 8 we show one set of simulation for trapping a chlorine ion inside trap A filled with water, under the condition of 300 K, Vdc = 4V, Vac = 12V, f = 80 GHz, with values estimated from Eqs.(4) rescaled to the dielectric constant of water. The solvent polarization effects as well as impact from the collisions and thermal fluctuations of water molecules were treated through explicit atomistic MD simulations, using 5108 water molecules filling the volume of the trap. From the trajectory of the ion we see that the stabilization process takes much longer time than the one in vacuum with even stronger trapping electric fields. It takes about 12 ns for the ion to be trapped stably to the center of trap A. On the other hand, it is found that the ion experiences much less fluctuations in the movement during the stabilizing process along any of the directions, with the much smaller final oscillation amplitude of the ion in comparison to that for the same ion trapped in a vacuum trap under the same temperature. One possible reason for such effect is that the motion of the ion was effectively thermalized by water molecules around it due to strong collision force from the electrostatic interactions. This is in qualitative agreement with the discussion in the Introduction showing the effects of the background damping to the ion motion in the trap, suggesting that the addition of the solvent to the trap can help to stabilize the ion motion although the time required to reach stabilization might be significantly longer than in the vacuum trap.

Figure 8.

Figure 8

Open in a new tab

Trapping of a chlorine ion inside solvated trap A at 300 K. The trapping fields are Vdc = 4V, Vac = 12V, f = 80 GHz.

We also observe that the presence of explicit solvent relaxes the parameter choices defined by Eqs. (4), as discussed in the Introduction. The range of stabilization defined by parameters a and q is widened in the presence of the damping with water. This is supported by a series of simulations performed using the system shown by Figure 8, but with various combinations of trapping fields and frequencies, such as Vdc = 2V, Vac = 6V, f = 20 GHz, Vdc = 1V, Vac = 3V, f = 20 GHz. Some of these parameters do not satisfy strictly the stable region defined by Eqs. (4) (with or without correction to the water dielectric constant). Interestingly, in all these cases we could still observe the trapping and stabilization process, qualitatively similar to that shown in Figure 8.

4. Conclusions

Our molecular dynamics simulations show that trapping of low-energy charged ions in nanoscale Paul traps is feasible both under vacuum and solvated conditions. The trapping of an ion in such Paul trap occurs within a timescale of nanoseconds if an AC field of tens to hundreds of GHz is applied. The trapped ion oscillates around the center of the vacuum trap when the ion energy is low enough to prevent collisions with the trap walls (<300 K for a trap with characteristic dimension of 5 nm). The stabilization time required and the orbiting radius of ion trapped are dependent on the system temperature, magnitude and the frequency of the trapping AC and DC fields.

In order to extend the applicability of the proposed Paul-type nanotrap to the biological molecules, in particular to the DNA sequencing, it is important to stabilize the orientation of the molecule. Our simulations indicate that the charged particle would rotate inside the trap and would stay stable in the trap center if solvent is present. This suggests that control of DNA in a Paul trap is possible if appropriate fields are applied. Application of a driving field along the z direction can effectively translocate the ion through the trap, which indicates the step-by-step motion of a negatively charge DNA segment could be controlled along the z-axis. However, the average amplitude of oscillatory motion of DNA inside the trap will depend on many parameters, such as temperature, voltage magnitude and frequency, trap size, etc. A series of detailed study has to be carried out to optimize the relevant parameters along with the fabrication of the proposed trap device.

Acknowledgement

The authors are grateful to Mark A. Reed and Peter T. Cummings for insightful discussions. This research was supported by the U.S. National Human Genome Research Institute of the National Institutes of Health under grant No. 1 R21 HG003578-01, by the Center for Nanophase Materials Sciences (XCZ), which is sponsored at Oak Ridge National Laboratory by the Division of Scientific User Facilities, and by the Office of Fusion Energy Sciences (PK) of U.S. DOE, at ORNL managed by a UT-Battelle for the U.S. DOE under contract No. DEAC05-00OR22725. This research used resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the U.S. DOE under Contract No. DE-AC02-05CH11231.

References

  1. Abich K, Keil A, Reiss D, Wunderlich C, Neuhauser W, Toschek PE. Thermally activated hopping of two ions trapped in a bistable potential well. Journal of Optics B-Quantum and Semiclassical Optics. 2004;6:S18–S23. [Google Scholar]
  2. Aksimentiev A, Heng JB, Timp G, Schulten K. Microscopic kinetics of DNA translocation through synthetic nanopores. Biophysical Journal. 2004a;87:2086–97. doi: 10.1529/biophysj.104.042960. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Aksimentiev A, Schulten K, Heng J, Ho C, Timp G. Molecular dynamics simulations of a nanopore device for DNA sequencing. Biophysical Journal. 2004b;86:480A–A. [Google Scholar]
  4. Arnott D, Henzel WJ, Stults JT. Rapid identification of comigrating gel-isolated proteins by ion trap mass spectrometry. Electrophoresis. 1998;19:968–80. doi: 10.1002/elps.1150190612. [DOI] [PubMed] [Google Scholar]
  5. Berendsen HJC, Postma JPM, Vangunsteren WF, Dinola A, Haak JR. Molecular dynamics with coupling to an external bath. Journal of Chemical Physics. 1984;81:3684–90. [Google Scholar]
  6. Casademunt J, Vinals J. Stochastic modeling of the residual acceleration field in a microgravity environment. Astrophysics and Space Science. 2001;276:123–33. [Google Scholar]
  7. Case DA, Cheatham TE, Darden T, Gohlke H, Luo R, Merz KM, Onufriev A, Simmerling C, Wang B, Woods RJ. The Amber biomolecular simulation programs. Journal of Computational Chemistry. 2005;26:1668–88. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Chan EY. Advances in sequencing technology. Mutation Research-Fundamental and Molecular Mechanisms of Mutagenesis. 2005;573:13–40. doi: 10.1016/j.mrfmmm.2005.01.004. [DOI] [PubMed] [Google Scholar]
  9. Cheatham TE, Young MA. Molecular dynamics simulation of nucleic acids: Successes, limitations, and promise. Biopolymers. 2000;56:232–56. doi: 10.1002/1097-0282(2000)56:4<232::AID-BIP10037>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
  10. Chen CM. Driven translocation dynamics of polynucleotides through a nanopore: off-lattice Monte-Carlo simulations. Physica a-Statistical Mechanics and Its Applications. 2005;350:95–107. [Google Scholar]
  11. Chen CM, Peng EH. Nanopore sequencing of polynucleotides assisted by a rotating electric field. Applied Physics Letters. 2003;82:1308–10. [Google Scholar]
  12. Darden T, York D, Pedersen L. Particle mesh Ewald - an Nlog(N) method for Ewald sums in large systems. Journal of Chemical Physics. 1993;98:10089–92. [Google Scholar]
  13. Dehmelt HG. Proposed 1014 Dv < v Laser Fluorescence Spectroscopy on Tl+ Mono-Ion Oscillator. Bull. Am. Phys. Soc. 1973;18:1521. [Google Scholar]
  14. Edwards CS, Gill P, Klein HA, Levick AP, Rowley WRC. Laser-cooling effects in few-ion clouds of YB+ Applied Physics B-Lasers and Optics. 1994;59:179–85. [Google Scholar]
  15. Fredlake CP, Hert DG, Mardis ER, Barron AE. What is the future of electrophoresis in large-scale genomic sequencing? Electrophoresis. 2006;27:3689–702. doi: 10.1002/elps.200600408. [DOI] [PubMed] [Google Scholar]
  16. Gracheva ME, Xiong AL, Aksimentiev A, Schulten K, Timp G, Leburton JP. Simulation of the electric response of DNA translocation through a semiconductor nanopore-capacitor. Nanotechnology. 2006;17:622–33. [Google Scholar]
  17. Guymon CG, Rowley RL, Harb JN, Wheeler DR. Simulating an electrochemical interface using charge dynamics. Condensed Matter Physics. 2005;8:335–56. [Google Scholar]
  18. Hasegawa T, Uekara K. Dynamics of a single-particle in a Paul trap in the presence of the damping force. Applied Physics B-Lasers and Optics. 1995;61:159–63. [Google Scholar]
  19. He YD, Qian HJ, Lu ZY, Li ZS. Polymer translocation through a nanopore in mesoscopic simulations. Polymer. 2007;48:3601–6. [Google Scholar]
  20. Healy K. Nanopore-based single-molecule DNA analysis. Nanomedicine. 2007;2:459–81. doi: 10.2217/17435889.2.4.459. [DOI] [PubMed] [Google Scholar]
  21. Hirata Y, Ozaki K, Ikeda U, Mizoshiri M. Field emission current and vacuum breakdown by a pointed cathode. Thin Solid Films. 2007;515:4247–50. [Google Scholar]
  22. Humphrey W, Dalke A, Schulten K. VMD: Visual molecular dynamics. Journal of Molecular Graphics. 1996;14:33. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
  23. Itano WM, Bergquist JC, Bollinger JJ, Wineland DJ. Cooling methods in ion traps. Physica Scripta. 1995;T59:106–20. [Google Scholar]
  24. Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. Journal of Chemical Physics. 1983;79:926–35. [Google Scholar]
  25. Kricka LJ, Park JY, Li SFY, Fortina P. Miniaturized detection technology in molecular diagnostics. Expert Review of Molecular Diagnostics. 2005;5:549–59. doi: 10.1586/14737159.5.4.549. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kumar S. Parametrically driven surface waves in viscoelastic liquids. Physics of Fluids. 1999;11:1970–81. [Google Scholar]
  27. Lagerqvist J, Zwolak M, Di Ventra M. Influence of the environment and probes on rapid DNA sequencing via transverse electronic transport. Biophysical Journal. 2007;93:2384–90. doi: 10.1529/biophysj.106.102269. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Leibfried D, Blatt R, Monroe C, Wineland D. Quantum dynamics of single trapped ions. Reviews of Modern Physics. 2003;75:281–324. [Google Scholar]
  29. Lu DY, Aksimentiev A, Shih AY, Cruz-Chu E, Freddolino PL, Arkhipov A, Schulten K. The role of molecular modeling in bionanotechnology. Physical Biology. 2006;3:S40–S53. doi: 10.1088/1478-3975/3/1/S05. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Nakane JJ, Akeson M, Marziali A. Nanopore sensors for nucleic acid analysis. Journal of Physics-Condensed Matter. 2003;15:R1365–R93. [Google Scholar]
  31. Nasse M, Foot C. Influence of background pressure on the stability region of a Paul trap. European Journal of Physics. 2001;22:563–73. [Google Scholar]
  32. Nauhauser W, Hohenstatt M, Toshcek PE, Dehmelt HG. Localized visible Ba+ monoion oscillator. Phys. Rev. A. 1980;22:1137. [Google Scholar]
  33. Oberacher H, Parson W, Oefner PJ, Mayr BM, Huber CG. Applicability of tandem mass spectrometry to the automated comparative sequencing of long-chain oligonucleotides. Journal of the American Society for Mass Spectrometry. 2004;15:510–22. doi: 10.1016/j.jasms.2003.12.002. [DOI] [PubMed] [Google Scholar]
  34. Paul W. Electromagnetic traps for charged and neutral particles. Reviews of Modern Physics. 1990;62:531–40. [Google Scholar]
  35. Payne CM, Zhao XC, Vlcek L, Cummings PT. Molecular dynamics simulation of ss-DNA tranlocation through a copper nanoelectrode gap. J. Phys. Chem. B. 2008 doi: 10.1021/jp077483e. In press. [DOI] [PubMed] [Google Scholar]
  36. Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. Scalable molecular dynamics with NAMD. Journal of Computational Chemistry. 2005;26:1781–802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Rappe AK, Casewit CJ, Colwell KS, Goddard WA, Skiff WM. UFF, a full periodic-table force-field for molecular mechanics and molecular dynamics simulations. Journal of the American Chemical Society. 1992;114:10024–35. [Google Scholar]
  38. Reed M. 2007. Private communication.
  39. Rhee M, Burns MA. Nanopore sequencing technology: research trends and applications. Trends in Biotechnology. 2006;24:580–6. doi: 10.1016/j.tibtech.2006.10.005. [DOI] [PubMed] [Google Scholar]
  40. Rhee M, Burns MA. Nanopore sequencing technology: nanopore preparations. Trends in Biotechnology. 2007;25:174–81. doi: 10.1016/j.tibtech.2007.02.008. [DOI] [PubMed] [Google Scholar]
  41. Robinson JA, Bergougnou MA, Castle GSP, Inculet II. A nonlinear model of AC-field-induced parametric waves on a water surface. Ieee Transactions on Industry Applications. 2002;38:379–88. [Google Scholar]
  42. Rong HW, Meng G, Wang XD, Xu W, Fang T. Invariant measures and Kyapunov exponents for stochastic Mathieu system. Nonlinear Dynamics. 2002;30:313–21. [Google Scholar]
  43. Rothbauer U, Zolghadr K, Muyldermans S, Schepers A, Cardoso MC, Leonhardt H. A versatile nanotrap for biochemical and functional studies with fluorescent fusion proteins. Molecular & Cellular Proteomics. 2007 doi: 10.1074/mcp.M700342-MCP200. In press. [DOI] [PubMed] [Google Scholar]
  44. Ryan D, Rahimi M, Lund J, Mehta R, Parviz BA. Toward nanoscale genome sequencing. Trends in Biotechnology. 2007;25:385–9. doi: 10.1016/j.tibtech.2007.07.001. [DOI] [PubMed] [Google Scholar]
  45. Ryckaert JP, Ciccotti G, Berendsen HJC. Numerical-integration of cartesian equations of motion of a system with constraints - molecular dynamics of n-alkanes. Journal of Computational Physics. 1977;23:327–41. [Google Scholar]
  46. Schiffer JP. Order in confined ions. Journal of Physics B-Atomic Molecular and Optical Physics. 2003;36:511–23. [Google Scholar]
  47. Seidelin S, Chiaverini J, Reichle R, Bollinger JJ, Leibfried D, Britton J, Wesenberg JH, Blakestad RB, Epstein RJ, Hume DB, Itano WM, Jost JD, Langer C, Ozeri R, Shiga N, Wineland DJ. Microfabricated surface-electrode ion trap for scalable quantum information processing. Physical Review Letters. 2006;96:253003. doi: 10.1103/PhysRevLett.96.253003. [DOI] [PubMed] [Google Scholar]
  48. Shi L, Zhu XW, Feng M, Fang XM. Ordered structures of a few ions in the Paul trap. Communications in Theoretical Physics. 1999;31:491–6. [Google Scholar]
  49. Tabard-Cossa V, Trivedi D, Wiggin M, Jetha NN, Marziali A. Noise analysis and reduction in solid-state nanopores. Nanotechnology. 2007;18:305505. [Google Scholar]
  50. Tian L, Zoller P. Coupled ion-nanomechanical systems. Physical Review Letters. 2004;93:266403. doi: 10.1103/PhysRevLett.93.266403. [DOI] [PubMed] [Google Scholar]
  51. Trepagnier EH, Radenovic A, Sivak D, Geissler P, Liphardt J. Controlling DNA capture and propagation through artificial nanopores. Nano Letters. 2007;7:2824–30. doi: 10.1021/nl0714334. [DOI] [PubMed] [Google Scholar]
  52. Tsai YS, Chen CM. Driven polymer transport through a nanopore controlled by a rotating electric field: Off-lattice computer simulations. Journal of Chemical Physics. 2007;126:144910. doi: 10.1063/1.2717187. [DOI] [PubMed] [Google Scholar]
  53. Vant K, Chiaverini J, Lybarger W, Berkeland DJ. Photoionization of strontium for trapped-ion quantum information processing. arXiv:quant-ph. 2006:0607055. [Google Scholar]
  54. Walther H. From a single-ion to a mesoscopic system - crystallization of ions in Paul traps. Physica Scripta. 1995;T59:360–8. [Google Scholar]
  55. Wineland DJ, Ekstrom P, Dehmelt HG. Monoelectron Oscillator. Phys. Rev. Lett. 1973;31:1279. [Google Scholar]
  56. Wineland DJ, Itano QM. Spectroscopy of a Single Mg+ Ion. Phys. Lett. A. 1981;87:75. [Google Scholar]
  57. Wineland DJ, Monroe C, Itano WM, Leibfried D, King BE, Meekhof DM. Experimental issues in coherent quantum-state manipulation of trapped atomic ions. Journal of Research of the National Institute of Standards and Technology. 1998;103:259–328. doi: 10.6028/jres.103.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Winter H, Ortjohann HW. Simple demonstration of storing macroscopic-particles in a Paul trap. American Journal of Physics. 1991;59:807–13. [Google Scholar]
  59. Zhang XG, Krstic PS, Zikic R, Wells JC, Fuentes-Cabrera M. First-principles transversal DNA conductance deconstructed. Biophysical Journal. 2006;91:L4–L6. doi: 10.1529/biophysj.106.085548. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Zhao XC, Payne CM, Cummings PT, Lee JW. Single-strand DNA molecule translocation through nanoelectrode gaps. Nanotechnology. 2007;18:424018. doi: 10.1088/0957-4484/18/42/424018. [DOI] [PubMed] [Google Scholar]
  61. Zikic R, Krstic PS, Zhang XG, Fuentes-Cabrera M, Wells J, Zhao XC. Characterization of the tunneling conductance across DNA bases. Physical Review E. 2006;74:011916. doi: 10.1103/PhysRevE.74.011919. [DOI] [PubMed] [Google Scholar]

RESOURCES