AN OVERVIEW OF ELASTOGRAPHY – AN EMERGING BRANCH OF MEDICAL IMAGING

Abstract

From times immemorial manual palpation served as a source of information on the state of soft tissues and allowed detection of various diseases accompanied by changes in tissue elasticity. During the last two decades, the ancient art of palpation gained new life due to numerous emerging elasticity imaging (EI) methods. Areas of applications of EI in medical diagnostics and treatment monitoring are steadily expanding. Elasticity imaging methods are emerging as commercial applications, a true testament to the progress and importance of the field.

In this paper we present a brief history and theoretical basis of EI, describe various techniques of EI and, analyze their advantages and limitations, and overview main clinical applications. We present a classification of elasticity measurement and imaging techniques based on the methods used for generating a stress in the tissue (external mechanical force, internal ultrasound radiation force, or an internal endogenous force), and measurement of the tissue response. The measurement method can be performed using differing physical principles including magnetic resonance imaging (MRI), ultrasound imaging, X-ray imaging, optical and acoustic signals.

Until recently, EI was largely a research method used by a few select institutions having the special equipment needed to perform the studies. Since 2005 however, increasing numbers of mainstream manufacturers have added EI to their ultrasound systems so that today the majority of manufacturers offer some sort of Elastography or tissue stiffness imaging on their clinical systems. Now it is safe to say that some sort of elasticity imaging may be performed on virtually all types of focal and diffuse disease. Most of the new applications are still in the early stages of research, but a few are becoming common applications in clinical practice.

I. INTRODUCTION

The number of papers on elasticity imaging (EI) has grown enormously during the last two decades. Novel technical approaches and systems continue to be proposed. Areas of applications of EI in medical diagnostics and treatment monitoring are steadily expanding. A wealth of data published in recent years indicates that the shear elasticity modulus of tissue is one of the most wide ranging physical parameters of tissue. It is also highly sensitive to tissue structural changes accompanying physiological and pathological processes. It is surprising that this understanding came only about two decades ago. It is especially surprising because qualitative assessment of tissue elasticity by manual palpation has been widely used since ancient times and is still in use today. In characterizing non-biological materials, elastic moduli are considered to be among the most fundamental parameters. It is impossible to imagine an engineer designing a machine, or any other structure, without a quantitative assessment of the mechanical characteristics of the components and materials used. Meanwhile, until the 1990s, hardly any biomedical engineer would have been able to answer the simple question: is the Young’s modulus of muscle (or liver, kidney and any other soft tissue) on the order of (a) 1kPa, (b) 10kPa, or (c) 100kPa?

II. HISTORICAL ROOTS

A. Ultrasonic Elasticity Imaging

Until the late 1980s, biomechanics of soft tissues was not a part of any branch of acoustics. In a comprehensive book on biomechanics [1], Fung wrote 415 pages, but the propagation of acoustic waves was mentioned on only two pages that are related to the pulse waves in blood vessels governed by the Moens-Korteweg equation. In physics, acoustics and mechanics always go hand in hand because acoustics is actually a branch of mechanics. However, acoustics started to appear in biomechanical studies only in the last two decades.

John Ferry did pioneering studies on the relationship between viscoelastic properties and the macromolecular structure of polymers such as rubbers and a naturally occurring biological polymer of interest to the medical science. But, his classic book “Viscoelastic Properties of Polymers” first published in 1961 [2] did not discuss acoustic wave propagation parameters and their relation with mechanical properties of macromolecular systems.

Practically all literature on acoustic properties of soft tissue published prior to the 1990s was related to bulk compressional waves and had few links to biomechanics. The first publications on propagation of shear waves and surface waves (which like shear waves are predominantly dependent on shear viscoelastic properties) in soft tissues, started to appear after the 1950s [3–23], However, these publications did not get much feedback from the scientific community. It was hard to accept the fact that mechanical waves in soft tissues can propagate with speed 100 times slower than the speed of sound in air.

Most of the early work on the use of acoustic methods for assessment of elastic properties of soft tissues was related to studies of skin. The reasons for that were twofold. First, the main function of the skin is mechanical and a close relationship between the state of the skin and its viscoelastic properties is quite apparent. Many dermatologic diseases are manifested in the changes of the skin mechanical properties. Second, skin is the most accessible soft tissue so the possibility of assessing its mechanical properties using acoustic means, such as surface acoustic waves is apparent. Numerous publications addressed the issue of use of surface waves in assessment of skin [10–21]. However, there has been limited research in the area of using surface waves for assessment other types of tissues such as human lung [22, 23].

Some of the first studies, most closely related to the current understanding of what elasticity imaging is, were conducted at the Royal Marsden Hospital, UK, by Kit Hill and his students in the late 1970s and in 1980s. Previous experience of Hill in the radar application to moving target indication gained in the 1950s during his service in the Army and in the Canadian General Electric Company led him to an idea to extract tissue movement information from the ultrasound echoes. In about 1976, Hill gave a graduate student - Rob Dickinson - the task of trying to develop an ultrasonic method of analyzing tissue motion. Tissue movement was characterized by determining the time rate of decorrelation between successive, collinear A-scans taken through the tissue volume of interest. Results of this work were published in several papers [24–26].

In the book “Physical Principles of Medical Ultrasonics” published in 1986 [27], Hill had written a chapter entitled “Telehistology”, where he briefly introduced some of the ideas which are currently among those forming the basis of Elasticity Imaging. He defined “telehistology” as “the description of a defined region of a target tissue or organ in terms of ‘features’…that can be quantified by remote means – in this case ultrasound.” One of such feature mentioned by Hill was the tissue motion. Remarkably, Hill accurately defined all principal techniques used in current modes of elasticity imaging for inducing the strain necessary for elasticity assessment. He had written: “Tissue movements can be considered to be of four kinds: primary (e.g. cardiac or fetal limb movement), secondary (e.g. movement of liver tissue in response to pulsation of a neighboring major blood vessel), fluid flow (particularly blood flow), and externally induced movement.” Then he continued: “The interest in characterizing secondary and externally induced movement is that it may yield information features of the bulk mechanical properties tissues (e.g. bulk, and possibly shear, elastic moduli): features which already have a long-established value in the clinical technique of manual palpation.” Further he introduced the term ‘remote palpation’ which he defined as detection of “response of tissues to externally induced movement.” Ultrasonic studies of tissue movement were further continued in the Hill’s group by Maria Tristam and Jeff Bamber who showed that the time rate of decorrelation between successive A-mode scans may be a useful discriminator between hard and soft tissues subjected to either secondary or externally induced movement [28, 29]. Tristam and coworkers moved Hill’s ideas to more practical implementation. They were able to discriminate normal liver parenchyma from hepatic metastasis using a multidimensional evaluation of Fourier coefficients associated with the cross correlation [29].

In a letter sent recently by Kit Hill to one of the authors of this paper (A.S.) he had written: “It is gratifying to find that some of these ideas eventually turn out to be worthwhile.”

A major surge in development of ultrasonic methods and devices for elasticity imaging started in the late 1980s and early 1990s [30–37]. Practically every aspect of current ultrasonic elasticity imaging has roots originating in the studies initiated in that period. The means employed in the early elasticity imaging systems for generating stress in the tissue included static loading and external vibrators. Beginning in the late 1990s several laboratories developed an alternative approach for remote probing tissue elasticity using acoustic radiation force [38–44]. Acoustic radiation force is the time-average force exerted on an object by an acoustic wave. Radiation force is produced by a change in the ultrasonic wave energy density of an incident acoustic field.

Notably, the fraction of the radiation force related modes of ultrasound elasticity imaging is constantly increasing. Numerous elasticity imaging modalities based on the use of acoustic radiation has been developed and tested in various clinical applications. Analytical equations describing the spatial and temporal behavior of the radiation force induced shear displacement and waves in tissue-like media have been derived [38, 45, 46].

B. Magnetic Resonance Elastography (MRE)

The first MR elasticity experiments, described in detail in [47], were conducted at the University of California at San Diego in 1989 and at the University of Michigan, Ann Arbor, in 1992. Experiments in San Diego were performed by R. Buxton and A. Sarvazyan on a phantom mimicking soft tissue with inclusions. The phantom was a disposable ultrasound standoff gel pad in which three liquid-filled capsules (common Vitamin E capsules) had been inserted randomly in the pad through small incisions. This phantom was placed in a non-ferrous clamp which allowed planar deformation of the phantom normal to its longitudinal central axis while it was inside a standard bird-cage coil designed for head imaging. The whole assembly was then placed into the bore of a 1.5T whole body imaging MRI system (General Electric, Milwaukee) and was imaged with a standard spin echo sequence at different levels of compression. Mathematical analysis of MRI data on deformation of the inclusions showed that the liquid-filled capsules with their complex structure provide local deformation effects similar to homogeneous inclusions having Young’s moduli values two times smaller than the Young’s modulus of the surrounding material.

MRE studies, dated from 1992 conducted at the University of Michigan, Ann Arbor, used similar static loading of tissue mimicking phantoms [47, 48]. MRE using dynamic loading from the surface of the tissue has been pioneered by researchers at the Mayo Clinic, Rochester, MN, and by several other laboratories starting in 1995 [49–51].

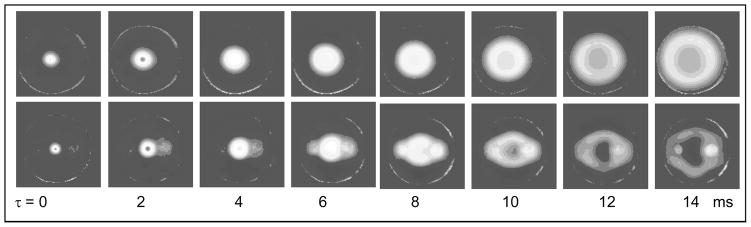
The first demonstration of the use of MRI to record shear wave propagation was made in the collaborative study of the University of Michigan and Artann Laboratories [38] conducted in 1995–1996. In that study, an ultrasound transducer was mounted to rubber phantoms which were either homogeneous or contained two cylindrical inclusions. Remote displacement of 20 microns was achieved by a single 555 kHz ultrasound pulse with a duration of 1.5ms. The displacement was measured by phase sensitive MRI using a pair of opposite polarity gradient pulses. Figure 1 shows the time evolution of the shear wave induced by the radiation force of focused ultrasound pulse. The top set of images is from the homogeneous phantom and the bottom set from the phantom with the two hard inclusions. Propagation of the shear wave in the homogeneous phantom is cylindrically symmetric, radiating outward from the initial displacement. Propagation in the phantom with the two inclusions starts the same as the in the homogeneous phantom, but when the shear wave reaches the inclusions in the phantom, it passes through much faster due to the difference in elastic modulus in the two media.

Figure 1.

Propagation of shear wave induced by the radiation force impulse in homogeneous phantom (top row) and phantom with two inclusions (bottom row) recorded by MRI.

C. Mechanical Imaging (MI)

Mechanical Imaging (MI) most closely mimics manual palpation and therefore is also called ‘tactile imaging’. In contrast to other elasticity imaging techniques, which are based on estimating static or dynamic strain in the tissue, i.e. are “strain imaging”, MI uses estimates of the surface stress pattern to reconstruct tissue mechanical structure and therefore is “stress imaging”. Early attempts to visualize the ‘sense of touch’ date back to the 1970s and 1980s [52–54].

One of the first published elastographic images has been obtained by tactile imaging. Figure 2 shows an elasticity image of a breast phantom with two simulated lumps published by CR Gentle in 1988 in the paper entitled “Mammobarography: a possible method of mass breast screening” [54]. The image was obtained using an optical technique employing frustrated total internal reflection to convert a pressure distribution into a brightness distribution over the region of contact with the tested object. Extensive studies on imaging tissue mechanical structure using a pressure sensor array to measure stress patterns on the surface of compressed tissue were conducted in the 1990s at Harvard University in applications related to robotics and documentation of breast masses [55–60]. Similar studies were conducted at Artann Laboratories in applications related to prostate and breast cancer detection [61–68].

Figure 2.

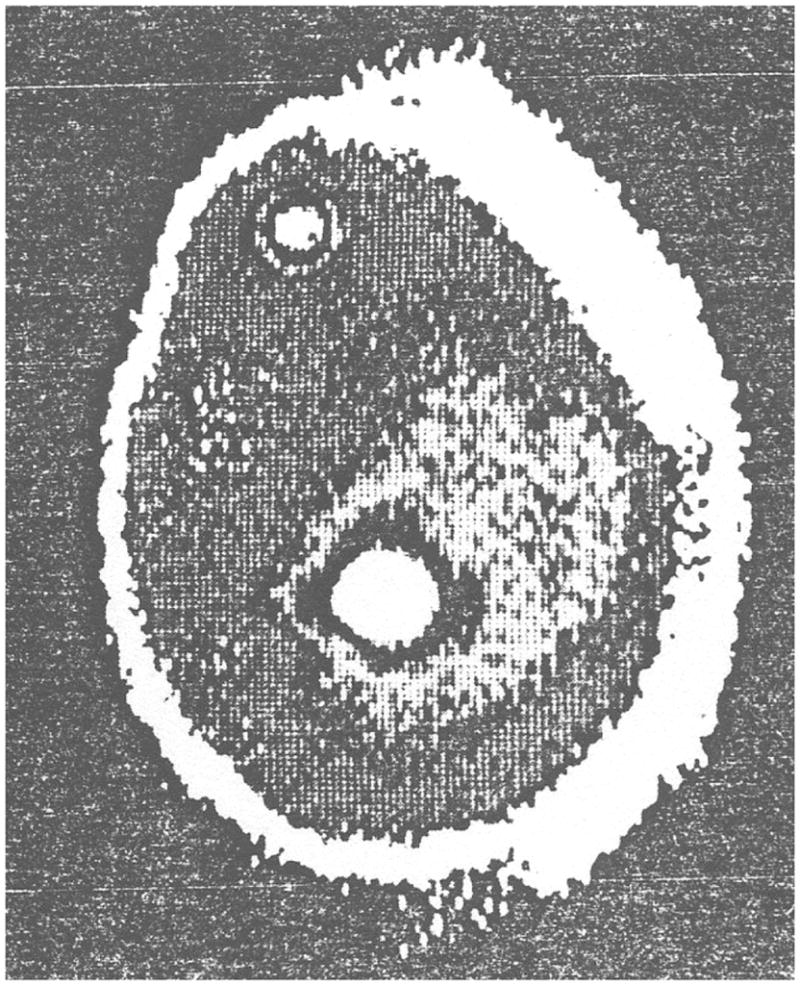
One of the first elastographic images published in 1988: a stress pattern recorded on the surface of compressed breast phantom (rubber prosthesis filled with silicone rubber gel) containing two lumps (nylon balls of diameters 25 mm and 6 mm). Reproduced with permission from [54].

III. BIOPHYSICAL BASIS OF ELASTICITY IMAGING: RELATIONSHIP BETWEEN MECHANICAL PROPERTIES AND STRUCTURE AND COMPOSITION OF SOFT TISSUE

To fully characterize tissue as a mechanical system a great number of parameters are needed including the shear and Young’s moduli, bulk compressional modulus, frequency dependencies of these moduli, nonlinearity, Poisson’s ratio, viscosity, poroelastic parameters, anisotropy and heterogeneity indices, etc. However, in most practical cases, there is no need to have a comprehensive mechanical characterization of the tissue of interest and even just one elasticity parameter, such as Young’s modulus, may be sufficient to address some diagnostic tasks. Though such grossly simplified mechanical characterization might be quite adequate in most cases, one should bear in mind that the level of appropriate simplification in characterizing a biomechanical system must be carefully estimated.

The term “elasticity” and similar common terms “hardness” and “stiffness” correspond most closely to a rigorous physical parameter – Young’s modulus, E. The significant dependence of the Young’s modulus on structural changes in the tissue is the basis for the palpatory diagnosis of various diseases, such as detection of cancer nodules in the breast or prostate. Detection of a mechanical heterogeneity by manual palpation is based exclusively on sensing the variations of the Young’s modulus of tissue (or shear elasticity modulus, μ, which is approximately equal to E/3 for soft tissues).

Soft tissues are called “incompressible” because their bulk compressional modulus, K, is generally several orders of magnitude larger than the shear modulus. As a result, a short external stress applied to soft tissues causes mainly a change in the shape of the stressed tissue, while the volume remains constant with a high degree of precision. If a soft tissue is deformed, the relationship between the stress and strain patterns is completely defined by the Young’s modulus only, regardless of the K value for the tissue, and whether it is infinitely large or is only a few orders of magnitude higher than E.

Bulk compressibility and shear elasticity are dependent on different features of tissue. Bulk compressibility modulus depends on short range molecular interactions and is defined mainly by tissue molecular composition while shear elasticity is defined by structural peculiarities of tissue, its cellular and higher level of architecture [69].

Water is the most abundant constituent of soft tissues. Consequently, the major contribution to bulk modulus of tissues comes from hydration, that is the interaction of polar, charged, and hydrophobic atomic groups of organic substances with molecules of water. Therefore, the bulk modulus for all the soft tissues is close to that of water and varies within only about 10% [69]. In contrast to that, the range of variability of structural features of tissues, such as geometrical parameters of cells in different tissues and the degrees of heterogeneity and anisotropy, are incomparably greater. Therefore, the shear elasticity for different soft tissues vary over four orders of magnitude and, even within one tissue, may change by hundreds of percent during such process as development of a tumor or an ordinary muscle contraction [30].

IV. THEORETICAL BASIS OF ELASTICITY IMAGING

Evaluation of the mechanical properties of tissues from data obtained using various elastographic techniques is often based on modeling tissue as a linearly viscoelastic and incompressible medium. Viscoelastic models assume that soft tissue is a solid (single phase) medium and does not consider the fluid motion in the tissue. Alternatively, tissue can be treated as being composed of porous solid phase and fluid phase that inhabits the pores of the solid matrix. Such an approach in elastography, called poroelastography [70–77], is based on the poroelastic model developed by Biot [78, 79]. Poroelastic material may be compressible even if it consists of an incompressible solid and fluid. However, for time scales shorter than the characteristic time of fluid motion, the model of a viscoelastic and incompressible medium is a good first approximation which is sufficient to address most of the biomechanical problems arising in elasticity imaging.

In cases where a solution is to be obtained without considering the object as linearly elastic, one can also use nonlinear solutions which are much more elaborate [80–82]. However, the results obtained with the use of nonlinear solutions often do not alter qualitatively the answers obtained under the linear elastic model. The literature on the theoretical physics of elasticity imaging is quite limited but a comprehensive analysis of the problem of reconstruction of 3D elastic modulus distribution is given in the book by A.R. Skovoroda [83]. This problem was analyzed by several authors [51, 84–96], however, in the following discussion we will closely follow the logic and concepts developed by Skovoroda.

A. Elasticity equations

The general linear equations of dynamic equilibrium describing the motion of a mechanical body in Cartesian coordinates x₁, x₂ and x₃ are [96, 97]:

$$\sum _{j=1}^3\frac{\partial {\sigma }_{ij}}{\partial x_j}+f_i=\rho \frac{{\partial }^2{u}_i}{\partial t^2},i=1,2,3,$$ (1)

where: σ_ij are components of stress tensor, u_i are components of displacement vector, f_i is the body force per unit volume acting on the body in the x_i direction, ρ is density of media, and t is time. The components of the stress tensor in an isotropic compressible medium are given by the following equation [98]:

$${\sigma }_{ij}=\lambda \theta {\delta }_{ij}+2\mu {\epsilon }_{ij}+{\lambda }^{\ast }\frac{\partial \theta }{\partial t}{\delta }_{ij}+2{\mu }^{\ast }\frac{\partial {\epsilon }_{ij}}{\partial t},$$ (2)

where, λ and μ are Lame coefficients, λ* and μ* are the coefficients of viscosity, ε_ij are the components of the strain tensor, δ_ij is the Kronecker delta symbol and θ is the divergence of the displacement vector:

$$\theta =\mathit{div}\overrightarrow{u}=\frac{\partial u_1}{\partial x_1}+\frac{\partial u_2}{\partial x_2}+\frac{\partial u_3}{\partial x_3}={\epsilon }_{11}+{\epsilon }_{22}+{\epsilon }_{33}.$$ (3)

The relationship between the components of the (infinitesimal) strain tensor and displacement vector is:

$${\epsilon }_{ij}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right).$$ (4)

B. Tissue incompressibility

In general, an isotropic mechanical body can be characterized by the spatial distribution of its viscoelastic parameters. In viscoelastic tissue, there is a time delay between force application and any displacement that occurs. In a dynamic mode where force is applied in time, the development of stresses in time provides information on viscosity. This requires knowledge of the relationship between the time course of stress application and the time constants of the tissue response. If the body is deformed more slowly, only static deformation needs to be considered. For static deformation the right part of (1) is zero and time-dependent terms in (2) vanish. Therefore, for static deformation the mechanical properties of the medium are completely characterized by the Lame parameters. The Lame parameters can be written in terms of two other independent parameters, such as Young’s modulus E and Poisson’s ratio ν[85]:

$$\mu =\frac{E}{2(1+\nu )},\lambda =\frac{E\nu }{(1+\nu )(1-2\nu )}.$$ (5)

For incompressible media like most tissues or other water based systems, Poisson’s ratio is close to 0.5. As a result, for static deformations, a single elastic parameter – the shear modulus μ (or Young’s modulus E = 3μ) – fully describes the static mechanical properties of the tissue. In addition to (1) we have the equation of incompressibility which shows that the divergence of the displacement vector equals zero:

$$\theta =\frac{\partial u_1}{\partial x_1}+\frac{\partial u_2}{\partial x_2}+\frac{\partial u_3}{\partial x_3}=0.$$ (6)

This last equation represents the condition that when force is applied to an object with Poison’s ratio equal to 0.5, all the deformation is related to changes of the shape but not the volume of the object. For the static case and under this condition (6), the stress-strain relation (2) reduces to:

$${\sigma }_{ij}=p{\delta }_{ij}+2\mu {\epsilon }_{ij},$$ (7)

where p is an internal pressure defined as:

$$p=\underset{\lambda \to \infty ,\theta \to 0}{lim}(\lambda \theta ).$$ (8)

Therefore, by combining equations (1), (4), (6–7), the forward problem is formulated as a system of four equations containing three components of displacement vector u_i and the unknown pressure p. The boundary conditions for these equations can be described in terms of displacements or stress on the surface of object. Techniques for solving such boundary problems are well developed and can be used to obtain the solution to the forward problem [99].

C. Inverse problem

Elastic modulus reconstruction in an inhomogeneous material can be posed in a number of ways [51, 83–95, 100–102]. These approaches can be generally grouped into two categories: direct and indirect (model-based) reconstruction techniques. If all necessary components of the internal displacement vector and strain tensor are available at any point within the object, then reconstruction algorithms based on the equilibrium equations can be used to describe the unknown distribution of Young’s modulus - these techniques, therefore, belong to direct reconstruction methods.

The term λθ for a compressible medium, or the internal pressure p for the incompressible case, is the source of instability for solving the inverse problem and it should be eliminated from the equilibrium equations (1), (4), (6–7). Combining these equations the pressure gradient can be expressed as [98]:

$$p_{,i}=-2\mu {\epsilon }_{ij,j}-2{\mu }_{,j}{\epsilon }_{ij}(i,j=1,2,3).$$ (9)

Here, we imply summation over repeated index j, and the lower index after a comma means differentiation with respect to the corresponding spatial coordinate. Now, the pressure term can be excluded after differentiation of (9):

$$({\mu }_{,jn}{\epsilon }_{mj}-{\mu }_{,jm}{\epsilon }_{nj})+[({\mu }_{,n}{\epsilon }_{mj,j}-{\mu }_{,m}{\epsilon }_{nj,j})+{\mu }_{,j}({\epsilon }_{mj,n}-{\epsilon }_{nj,m})]+\mu ({\epsilon }_{mj,n}-{\epsilon }_{nj,m}),j=0n,m=1,2,3,n\ne m.$$ (10)

If all components of the strain tensor ε_ij are known, equations (10) are the system of three equations for the unknown spatial distribution of shear elastic modulus μ. Note here that (10) is valid for both compressible and incompressible cases. The boundary conditions for (10) could be defined on the areas of medium homogeneity, where μ does not depend significantly on spatial coordinates. For special cases, for example plane strain deformation, equations (10) can be simplified and reduced to single equation.

Alternatively, the internal pressure p could be eliminated by integrating the first of these equations along x₁, the second along x₂ and third along x₃, and combining resulting expressions afterward [82]. Such an approach permits avoiding additional differentiation of noisy displacement components and improves the stability of the inverse problem. The major advantage of the direct reconstruction method is that this procedure permits local reconstruction of the elastic modulus within a body without knowledge of global boundary conditions for the forward problem.

D. Model-based approaches

Unfortunately, in direct reconstruction methods, it is often difficult to formulate and solve the inverse problem for an arbitrary geometry and elasticity distribution. However, if any prior knowledge or assumptions about the geometry of the object and boundary conditions can be made, the inverse problem can be solved by using repeated solutions of forward problems (1), (4), (6–7) with adjusted elasticity parameters [102, 103]. Using an analytic or numerical solution to the forward problem and having experimentally measured the displacement (or strain) distribution, the unknown elasticity modulus can be estimated by minimizing the error function δ, that is, the difference between experimentally measured and theoretically predicted data. For instance, if axial components of the strain tensor ${\epsilon }_{22}^{exp}$ are measured in the region of interest S and the model forward problem solution ${\epsilon }_{22}^{\mathit{theor}}(\mu )$ is calculated, the error function could be defined as:

$$\delta (\mu )=\underset{S}{\int }{({\epsilon }_{22}^{exp}-{\epsilon }_{22}^{\mathit{theor}}(\mu ))}^{2}dS.$$ (11)

Therefore, the elasticity reconstruction reduces to a minimization of the error function of (11) with respect to the unknown elasticity distribution μ(x). If elasticity variations of the object within the region of interest can be modeled based on the object geometry or any other assumptions, then a model-based reconstruction can be performed.

E. [104]Acoustic radiation force

One of the major problems in the model-based reconstructive approaches is the need to incorporate boundary conditions to solve the forward problem. In practice, boundary conditions in tissue could be very complicated and the error in the definition of boundary conditions could significantly reduce the quality of reconstruction. A possible solution to this problem was suggested in [38] where acoustic radiation force of the focused ultrasound wave was used to induce the motion of the tissue. The dynamics of this highly localized motion is defined by the parameters of acoustic excitation and the mechanical properties of tissue, and only weakly depends on the boundary conditions. Analytical equations describing the spatial and temporal behavior of the radiation force induced shear displacement and waves in tissue-like media have been derived in [38, 45, 46]. Figures 3 and 4 adapted from [38] illustrate the calculated tissue response to acoustic radiation force generated by a focused ultrasonic wave.

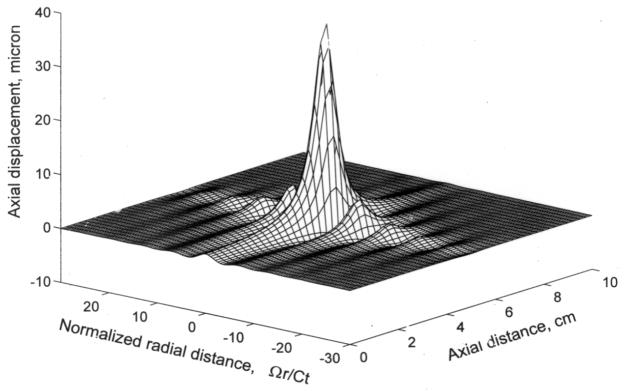
Figure 3.

Typical distribution of the axial (i.e., shear) displacement induced by sinusoidally modulated radiation force of focused ultrasound. Reproduced with permission from [38].

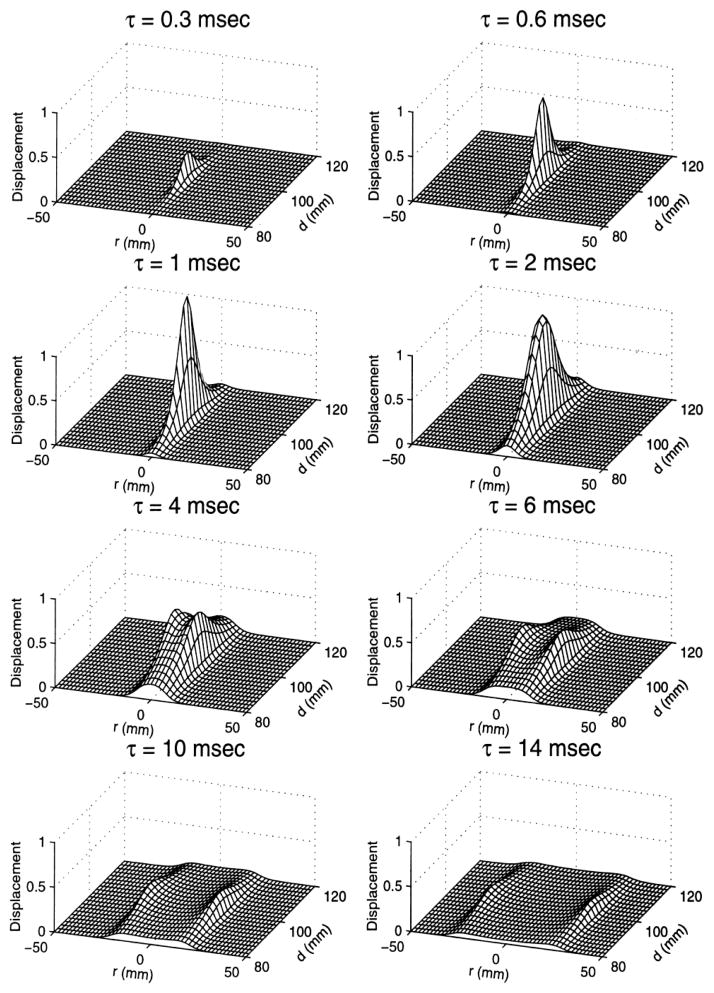
Figure 4.

Generation and propagation of the shear wave shown at different times after transmission of the acoustic pulse. Reproduced with permission from [38].

Figure 3 shows the distribution of axial displacement induced by a focused ultrasonic beam with a 3 MHz carrier frequency modulated with a 1 kHz sinusoid and spatial- and temporal-peak intensity of 10 W/cm². The parameters of tissue were chosen close to those of liver. The spatial distribution of axial displacement at an arbitrarily chosen time is shown. The absolute maximum of the displacement is near the geometric focus on the axis of the ultrasound beam. Neighboring local minima and maxima are about a half wavelength from each other. Figure 3 shows only axial displacement, however, that radial displacement is an order of magnitude smaller than axial displacement [38].

Figure 4 illustrates the temporal behavior of the axial displacement in the focal plane, i.e., in the plane near the geometric focus of the transducer and parallel to the beam axis. A rectangular 100 μs duration acoustic pulse and a tissue with shear wave speed 5.2 m/s were used in this simulation. Initially, displacement magnitude along the beam axis increases with time. This increase continues due to inertia for some time after the acoustic pulse is terminated. Displacement reaches its maximum at the time needed for the shear wave to travel the distance equal to the depth of the focal region. After reaching the maximum, the displacement starts to decrease, due the absorption of the shear wave as well as due to the formation of a diverging cylindrical wave propagating away from the axis. At that stage, the distance between the wavefront and the axis of the beam linearly increases as in accordance with the speed of shear wave, which is proportional to the square of shear elasticity modulus (in an infinite, isotropic and homogeneous medium).

Local viscoelastic properties of tissue may also be evaluated from the data on tissue motion induced by a radiation force impulse in the focal region of the focused ultrasound beam, which is the basis of Acoustic Radiation Force Impulse (ARFI) imaging [41, 105–107]. Here, we consider an example of the model-based reconstructive approach based on a semi-analytical solution for focused ultrasound loading [82]. In the case of the tissue response to the focused ultrasound radiation force impulse, the problem is symmetrical with respect to the direction of the ultrasound beam. Therefore, the problem could be considered in a cylindrical coordinate system (r,φ,z), where z-axis is aligned with the acoustic radiation force F. Displacements and force depend only on coordinates r and z. In cylindrical coordinates the equations of dynamic equilibrium (1) has a form:

$$\begin{array}{l}\frac{\partial {\sigma }_{rr}}{\partial r}+\frac{\partial {\sigma }_{rz}}{\partial z}+\frac{({\sigma }_{rr}-{\sigma }_{\phi \phi })}{r}=\rho \frac{{\partial }^2{u}_r}{\partial t^2},\\ \frac{\partial {\sigma }_{rz}}{\partial r}+\frac{\partial {\sigma }_{zz}}{\partial z}+\frac{{\sigma }_{rz}}{r}+F=\rho \frac{{\partial }^2{u}_z}{\partial t^2},\end{array}$$ (12)

where u_r, u_z and σ_rr, σ_zz, σ_φφ, σ_rz are components of displacement vector and stress tensor in the cylindrical coordinate system. An incompressible medium with zero volume viscosity was assumed in (2). Using the Hankel transform of the force F, displacements u_r, u_z and the pressure p, equations (12) are reduced to a single differential equation for function W:

$$\frac{{\partial }^2({\alpha }^{2}W-W^{″})}{\partial t^2}+\frac{\mu L(W)}{\rho }+\frac{{\mu }^{\ast }}{\rho }\frac{\partial L(W)}{\partial t}-\frac{{\alpha }^{2}f}{\rho }=0,$$ (13)

where L(W) = W^IV − 2α²W″ + α⁴W, primes mean differentiation with respect to z, W and f are the Hankel transforms of the displacement u_z and the force F, respectively, and α is the variable of integration:

$$F(r,z,t)=\underset{0}{\overset{\infty }{\int }}\alpha f(\alpha ,z,t)J_0(\alpha r)d\alpha ·u_z(r,z,t)=\underset{0}{\overset{\infty }{\int }}\alpha W(\alpha ,z,t)J_0(\alpha r)d\alpha$$ (14)

The boundary conditions for (13) assume that W and W′ are zero away from the focus. If the dependence f(α,z,t) is known, or can be evaluated, equation (13) can be solved numerically using, for example, a three level difference scheme. Thereby, the general 3D problem is reduced to a 1D problem, which can be solved fast and with high accuracy.

Figures 5a and 5b present the time dependence of the axial displacement u_z at the focal point for various elastic and viscous properties of the medium. In the calculations the load was distributed over the focal spot as an ellipsoid of rotation (for details, see [82]).

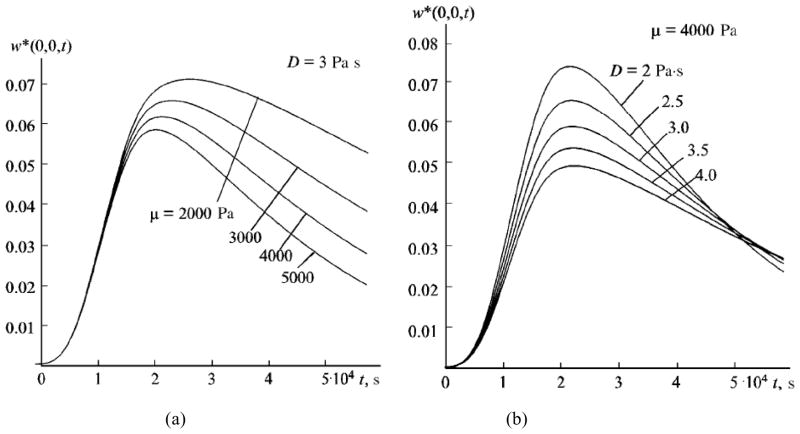
Figure 5.

Displacement at the focal point in response to ultrasound radiation force impulse for different (a) shear elasticity μ (b) shear viscosity D (Adapted from [82].)

The results show that the time dependence of the displacement is sensitive to changes in the mechanical properties of the medium. An increase in elasticity of the medium leads to decrease in both displacement magnitude and time needed for the displacement to reach the maximum. High viscosity reduces the displacement amplitude and increases the relaxation time.

Using the solution to this forward problem, the inverse problem can be solved by minimizing the error function (11).

V. ELASTICITY IMAGING METHODS

Over the last two decades, there has been significant development in different methods to perform elasticity measurements. However, every elasticity imaging method involves two common elements: the application of a force or stress and the measurement of a mechanical response. The force or stress source can be generated at least four different ways (see Sec II. A). For EI, the most common types of stress have been from external sources such as compression devices, external vibrators, or acoustic radiation force. The primary (physiological sources of motion), particularly cardiac motion, secondary, and fluid flow have been used but to lesser degrees.

The measurement method can be performed using differing physical principles including magnetic resonance imaging (MRI), ultrasound imaging, X-ray imaging, optical and acoustic signals.

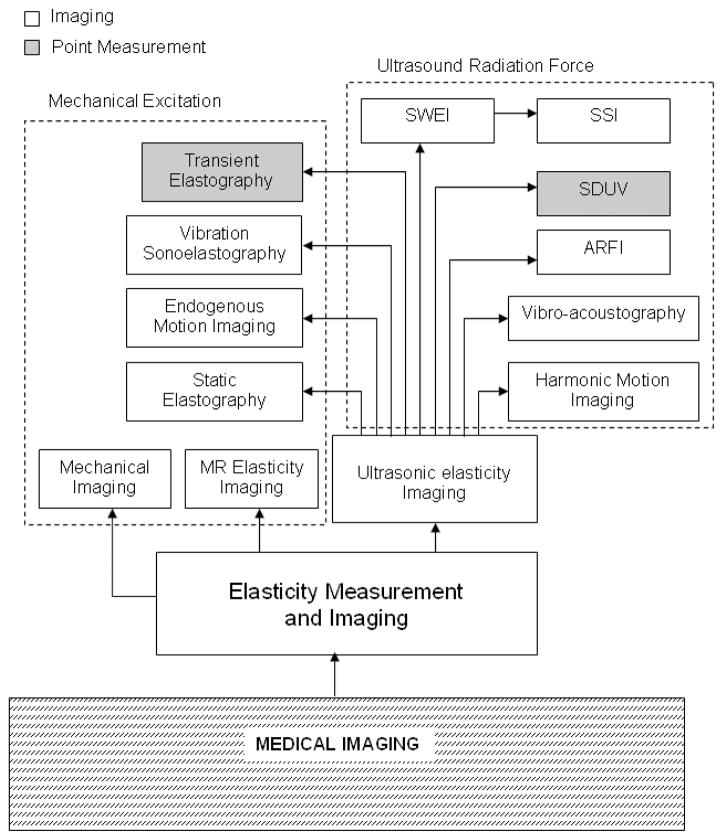
Each elasticity imaging method can be characterized by the methods used for force excitation and measurement of the tissue response. Figure 6 provides a block diagram of elasticity measurement and imaging techniques which will be detailed below. The techniques are categorized by their excitation method, mechanical or ultrasound radiation force. Also, a classification is made between point measurement methods and imaging methods.

Figure 6.

Block diagram of elasticity measurement and imaging and different methods included within this imaging modality. The techniques are categorized by their excitation method, mechanical or ultrasound radiation force. Also, a classification is made between point measurement methods and imaging methods. Ultrasonic elasticity imaging methods are expanded to illustrate the broad range of approaches. A similar expansion of the MR techniques, as well as other approaches such as optical or X-ray methods, is excluded for brevity. [Acronyms: SWEI: Shear wave elasticity imaging; SSI: Supersonic shear imaging; SDUV: Shearwave dispersion ultrasound vibrometry; ARFI: Acoustic radiation force impulse imaging]

A. Sonoelastography

A method called sonoelasticity or sonoelastography involves mechanical generation of harmonic shear waves and measurement of the wave propagation with Doppler or ultrasound imaging techniques. The first studies utilized external actuators in contact with the skin to induce motion into the tissue [30, 32, 35, 49]. These actuators were driven with a harmonic signal to induce shear waves in tissue so that shear wave speed could be measured and used to obtain estimates for the shear modulus. In the study reported by Krouskop, et al., [30] a motorized actuator was placed on the medial side of the thigh to induce shear waves into the muscle tissue and an ultrasound transducer was coupled to the lateral side of the thigh to measure the induced motion using Doppler techniques. The elastic modulus of the muscle was measured in different contraction states using this system. Lerner, et al. used an acoustic horn to generate wave motion in phantoms and excised tissue and used a color Doppler system to measure the resulting motion [31]. Yamakoshi, et al., proposed using a mechanical actuator coupled to the surface of a phantom or a subject’s skin to induce vibration [32]. An ultrasound transducer was placed in proximity to the actuator to insonify the vibrating region and measure the induced shear waves.

In recent years, sonoelastography has been modified to incorporate two mechanical actuators. The piezoelectric actuators are placed on opposite sides of the object and driven at frequencies ω and ω + Δω. The shear waves interfere in the medium resulting in an apparent wave called a “crawling wave” [108]. The speed of the crawling wave interference pattern travels at

$$c_{\mathit{pattern}}\approx \frac{\mathrm{\Delta }\omega }{2\omega }{c}_s,$$ (15)

where c_s is the shear wave speed and assuming that Δω ≪ ω. In practice Δω is in the range of ω/200 to ω/100 so that the crawling wave can be imaged with the ultrasound scanner’s frame rate (typically less than 50 frames/s).

Sonoelastography has been used to make images of the distribution of shear wave velocities in phantoms, human prostate, and skeletal muscle [109–112]. See Fig. 7 of [113] for image examples. The frequency ω can be varied to acquire information necessary for viscoelastic characterization.

B. Quasi-Static Elastography

A conceptually simple approach to extracting elasticity information from soft tissues involves acquiring maps of anatomy before and after inducing a small deformation of the tissue. Radiofrequency (RF) echo signals are typically the “maps of anatomy” used and tiny (micron-scale) motion induces a change in the phase of the RF echoes that can be tracked (although generally the deformations used are much larger). The most common methods of tracking motion in RF echo signals are correlation-based which can produce unbiased estimates of displacement with very low variance. Displacement can be tracked in 1D, 2D or 3D, and the gradient of the displacement is displayed as a relative strain image. Many groups around the world have contributed to this form of elasticity imaging, but it is reasonable to attribute early strain image formation to Cespedes and Ophir [34].

Although motorized fixtures in the laboratory environment are convenient for controlled deformation, clinical implementation typically involves freehand scanning. Freehand scanning often induces complex motion which requires real-time implementations for instant feedback to the user to control the direction of deformation [114]. Freehand scanning is usually induced at a rate resulting in nearly completely elastic deformations making interpretation much easier than it otherwise might be. The most common clinical application is breast imaging, but any organ that can be clinically palpated has been investigated including prostate, thyroid, muscle and lymph nodes [115–118]. Direct inversion for elastic modulus estimation is possible with sufficiently accurate and low noise displacement estimates and known boundary conditions. However, iterative reconstruction methods are most common and are generally more reliable. As described above, force information, in addition to the measured displacement field, is required to obtain modulus reconstructions on an absolute scale, but relative modulus distributions, accurate within a scale factor, are possible based on displacement estimates alone.

C. Acoustic Radiation Force Impulse (ARFI) Imaging

A group at Duke University has been studying the use of impulsive acoustic radiation force for mapping mechanical responses of tissue [41]. The impulsive force generates a localized displacement of the tissue. When the force ceases, the tissue relaxes to its original position. A number of parameters can be used to characterize the response of the tissue, including the peak displacement, the time that it takes to reach peak displacement, and the recovery time [119]. Typically, the peak displacement is displayed in an image. The peak displacement has been correlated with the inverse of the modulus of the object under interrogation both in finite element models and experimentally [105, 107]. The excitation is performed at one location and the response is measured, and then the excitation line is translated and the response is measured. The alternations of stimulation and detection are performed to build up images of the tissue response [41]. This process can be parallelized to push and track the tissue displacements simultaneously along multiple lines of sight [120, 121].

ARFI imaging has been utilized in numerous applications such as phantom imaging [105, 119, 122], imaging thermally induced lesions [123, 124], abdominal imaging of lesions [125–127], prostate imaging [128], and imaging of the cardiovascular system including the heart [129–131] and vessels [132–141]. See Figs. 5—9 of [142] for image examples.

D. Transient Elastography (TE)

Transient Elastography (TE) uses an external actuator to provide a single cycle of low-frequency (typically around 50 Hz) vibration and ultrasound methods to track the resulting motion. This type of excitation generates four types of waves including a compressional and shear wave in the medium. The compressional and shear waves are separated in time because the longitudinal wave speed is, in most cases, much faster than the shear wave [143, 144]. Applying a sinusoidal excitation at low frequencies with a mechanical actuator with a small cylindrical footprint can cause biases due to wave diffraction from the cylindrical source. Using a transient excitation avoids these biases so that the shear wave can be separated from the compressional wave and any reflected waves [143, 144].

Ultrasound based motion tracking is an important part of this technique. Like other techniques that use ultrasound imaging to measure the shear wave propagation, motion estimation can be performed using cross-correlation of consecutively acquired radiofrequency data. The location of the maximum of the cross-correlation function of two echo signals is used to find the time shift between the two signals. Using the longitudinal speed of sound, this time shift estimate determines how much motion has occurred. The use of cross-correlation in this application has been studied and optimized [145, 146]. Early measurements of shear waves produced by mechanical actuation were reported by Dutt, et al [147].

TE has been used both as a one-dimensional (1D) measurement technique [148, 149] as well as a two-dimensional (2D) imaging technique [150]. The technique has been developed for measurement of stiffness in the liver in a product called FibroScan® manufactured by EchoSens [151]. TE has also been employed for measuring stiffness in phantoms, skeletal muscle, breast, skin, and blood clots [148, 149, 152–158].

E. Shear Wave Elasticity Imaging (SWEI)

Shear Wave Elasticity Imaging (SWEI) was initially described theoretically by Sarvazyan et al. [38], and investigated experimentally by Nightingale and Trahey [159–162] and their combined work was a catalyst for many investigations and development of other techniques that followed. The use of modulated ultrasound was proposed to produce an acoustic radiation force that would create shear waves that could be detected by optical, acoustic, ultrasound, or MRI methods. The radiation force acts as a “virtual finger” that may be used to palpate the organ from the inside, thereby replacing the physician’s fingers on the surface of the body or organ.

In SWEI, compared to other approaches in elasticity imaging, the induced strain in the tissue can be highly localized since the remotely induced shear waves are fully attenuated within a few wavelengths distance. The very large attenuation of shear waves, as compared with the compressional waves where the attenuation per wavelength is two to three orders of magnitude less, is the main reason that shear waves have been ignored for decades as a possible means of obtaining information on the mechanical properties of tissue. Interestingly, this unfavorable feature of shear waves - their high absorption - is one of the factors providing the feasibility of SWEI. Due to the high attenuation of shear waves it is possible to induce mechanical oscillations within a very limited area of tissue in the vicinity of the focal point of a focused ultrasound beam. Consequently, local evaluation of viscoelastic properties is greatly simplified since, in many cases, trivial boundary conditions can be assumed and an infinite medium model used to reconstruct tissue mechanical properties.

The deformations induced by focused ultrasound radiation force could be very small, even at the sub-micron level. Therefore sophisticated signal processing techniques have been introduced to detect the resulting small motion [101, 146, 163–170].

The group at Duke University has studied using the SWEI for material characterization [162]. Among many applications they have developed is their method for assessing the stiffness of the liver. A shear wave is created and tracked at lateral positions from the focal position using a parallel tracking method [120]. An algorithm called RANSAC [171] is used to find the time at which the peak of the shear wave passes by the tracking location [106]. The elastic version of the shear wave speed equation is used to estimate the shear modulus of the tissue. This method has been used for investigation of phantoms, prostate, liver, and cardiac tissue [106, 172–177].

F. Supersonic Shear Imaging (SSI)

In SWEI and ARFI imaging the radiation force is focused at a single location. An extension of these methods is to focus the radiation force in one location and then change the depth of the focal location so that the shear waves created from multiple focal locations constructively interfere to make a conical shear wave [43]. This method is called supersonic shear imaging (SSI) because the radiation force focal point moves at a rate that is faster than the speed of the shear wave in the medium, providing credence to the “supersonic” nomenclature [178]. The shear wave created forms a kind of Mach cone and the Mach number of the excitation can be adjusted make the shear wave directionally oriented.

A critical element to the performance of this method is the ability to image the shear wave propagation which requires the use of an ultrafast scanner that is capable of 5000 frames/second or more. This high frame rate is achieved by eliminating focusing when transmitting pulses used for motion detection. Instead, one plane wave or a set of plane waves with different angular directions are transmitted for tracking the shear wave propagation [43, 179]. The shear wave propagation is measured over a large field of view and the wave equation inversion is used to assess the shear wave speeds and therefore the viscoelastic moduli. SSI has been used in the assessment of phantoms, liver, breast, and skeletal muscle [180–182]. See Figs. 6—10 of [183] for image examples.

G. Vibro-acoustography (VA)

Vibro-acoustography (VA) is a method that uses the acoustic response (acoustic emission) of an object to the harmonic radiation force of ultrasound for imaging and material characterization [39, 40, 184, 185]. The acoustic emission is generated by focusing two ultrasound beams of slightly different frequencies at the same spatial location and vibrating the tissue as a result of ultrasound radiation force exerted on the object at a frequency equal to the difference between the frequencies of the primary ultrasound beams. The two co-focused ultrasound beams of slightly different frequencies f₁ and f₂ (Δf = f₁−f₂ ≪ f₁, f₂) intersect at their joint focal point. For typical vibro-acoustography applications, f₁ and f₂ are on the order of 2–5 MHz and Δf is typically 10–70 kHz such that there are at least two orders of magnitude in difference insuring that Δf = ≪ f₁, f₂. The radiation force from these two beams has a component at Δf (called dynamic ultrasound radiation force), which vibrates the object. The acoustic response of the object to this force is detected by a hydrophone. The co-focus of the ultrasound beams is raster scanned across the object, and the resulting acoustic signal is recorded. An image of the object is formed by modulating the brightness of each image pixel proportional to the amplitude of the acoustic signal from the excitation point of the object.

Vibro-acoustography images have some unique characteristics that set it apart from traditional ultrasound imaging. This is partly due to the nonlinear phenomenon of frequency conversion in this method. For example, VA images are speckle free, which is a significant advantage over conventional pulse-echo imaging. VA also has the ability to image specular surfaces regardless of the orientation of the transducer with respect to the surface, while B-mode ultrasound imaging can only visualize a specular surface if the transducer is perpendicular to the surface.

VA may be used for a variety of imaging and characterization applications, including medical and industrial applications. In medical imaging, VA has been tested on breast [186–190], prostate [191–194], and thyroid [195, 196]. Vibro-acoustography has been used for imaging mass lesions in excised human liver [197], arteries [198, 199], bone [200, 201], and microbubbles [202, 203].

Although VA is primarily an imaging technique, methods for quantitative estimation of viscoelastic parameters of tissue using inverse problem approaches have been presented [204, 205]. The authors studied several finite-element experiments and solved for the material properties using simulated vibro-acoustic data. Comparisons of vibro-acoustic experiments and finite-element inverse problem solutions have shown good agreement.

H. Harmonic Motion Imaging (HMI)

A technique called harmonic motion imaging (HMI) uses ultrasound modulated at low frequencies (10–300 Hz) to produce oscillatory force [42, 206]. The motion is measured at the vibration center and used for assessing the viscoelastic properties of tissue [207, 208]. The radiation force is typically produced by a very large aperture transducer and the motion is detected by a small phased array transducer placed through a hole in the larger transducer.

The main application of this technique is for monitoring high intensity focused ultrasound (HIFU) therapy. The same transducer that is used for radiation force can also be used for creating thermal lesions. Then, the HMI technique can evaluate if the tissue has stiffened by monitoring the displacement induced by the radiation force [209–214].

I. Shearwave Dispersion Ultrasound Vibrometry (SDUV)

Shearwave Dispersion Ultrasound Vibrometry (SDUV) encompasses a set of techniques which involve creation of a shear wave either by an external actuator or internally using acoustic radiation force [215, 216]. The resulting tissue motion is recorded using ultrasound-based techniques. One of the keys to this method is the emphasis on shear wave speed dispersion and taking advantage of this dispersion to characterize the shear elasticity and viscosity using equation (12). We will focus on the radiation force-based implementation. An early implementation was much like the SWEI method that used modulated ultrasound to excite the tissue [215] and varied the modulation frequency to assess the shear wave speed dispersion.

However, this implementation was not easily compatible for modern ultrasound scanners but it was adapted so that excitation pulses were interleaved with pulses used for motion detection. The advantage of using a sequence of excitation pulses transmitted at a rate of f_p, was that motion was stimulated not only at f_p but at its harmonics, 2f_p, 3f_p, 4f_p, etc. Multiple pushing pulses increase the signal-to-noise (SNR) ratio at known frequency components, and the data is acquired all in one sequence of excitations. With data at several frequencies, the phase gradient method can be utilized to estimate the shear wave speed dispersion in one measurement. Thus far SDUV has been demonstrated in measurement of viscoelasticity in phantoms, skeletal muscle, porcine liver, and human prostate [215–218]}.

J. Magnetic Resonance Elastography (MRE)

A method called Magnetic Resonance Elastography (MRE) was developed to measure the propagation of shear waves in tissue using magnetic resonance imaging (MRI) techniques [49, 219, 220]. A conventional MRI scanner employs a phase-contrast technique to measure the displacement patterns of the induced waves. Typically, an external actuator induces a harmonic shear wave in the tissue with frequencies in the 50–1000 Hz range, but specialized equipment can provide measurements at frequencies 1–10 kHz [221]. A motion-sensitizing gradient is used to measure the motion in a specified direction at a specific frequency. The scanner’s motion-sensitized gradient and the mechanical actuator are synchronized. Cyclic motion of the magnetic spins in the presence of these motion-sensitizing gradients produces a measureable phase shift in the acquired MR signal, which is then used to quantify the displacement. The phase shift caused by harmonic motion can be written as [49, 220]

$$\phi (\overrightarrow{r},\theta )=\frac{\gamma NT({\overrightarrow{G}}_0·{\overrightarrow{\xi }}_0)}{2}cos(\overrightarrow{k}·\overrightarrow{r}+\theta ),$$ (16)

where γ is the gyromagnetic ratio, N is the number of gradient cycles, T is the period of the gradient waveform, G⃗₀ is the motion-sensitizing gradient vector, ξ⃗₀ is the displacement amplitude vector, k⃗ is the wave vector, r⃗ is the spin position vector, and θ is the relative phase of the mechanical and magnetic oscillations. It is important to note that the phase shift is proportional to the dot product of the motion-sensitizing gradient and displacement vectors.

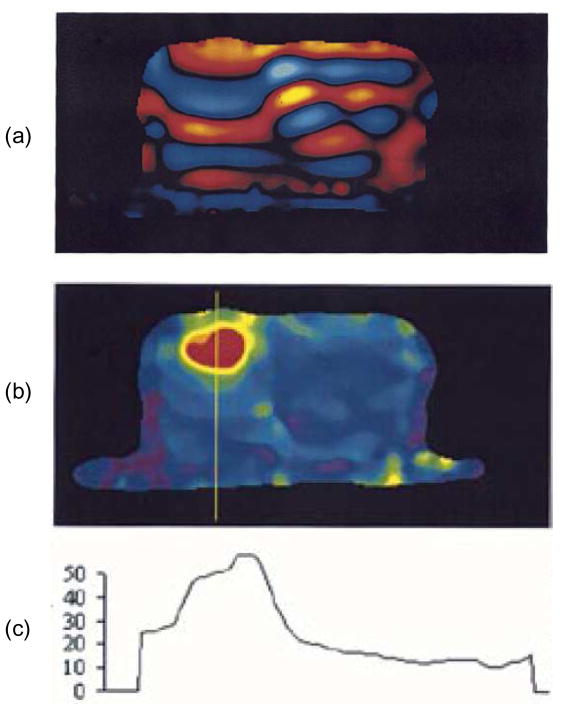
The use of different motion-sensitizing gradients, polarized in different directions, allows for the acquisition of the full three-dimensional (3D) displacement field. The induced shear wave motion can be tracked for amplitudes as small as 100 nm [49]. Each acquisition yields a “wave image” corresponding to the displacement of the magnetic spins. The phase offset, θ, is adjusted to obtain multiple wave images, such that the harmonic component at the mechanical driving frequency can be extracted. In practice, 4 or 8 phase offsets are used [220]. A wave image and the corresponding elastogram from an MRE experiment are shown in Fig. 7 where the scale of the elastogram is in kPa.

Figure 7.

(a) MRE wave image from prostate phantom. Note the long wavelength on the left side of the phantom with respect to the wavelength on the right. (b) Elastogram showing lesion in red. (c) Profile along yellow line in (b). The scale is shear modulus in kPa. [© 2003 IEEE. Adapted with permission from [185]]

MRE has been applied in a number of clinical areas including elasticity imaging of breast [222–224], liver [225–228], brain [229–233], heart [234–238], lung [239–241], cartilage [221, 242, 243], skeletal muscle [244–249], prostate [250, 251], spleen [252], thyroid [253], and the vasculature [254, 255]. The inherent 3D imaging capabilities make MRE very attractive for elasticity imaging because whole organs can be mapped. This advantage also provides that the field of view can be freely oriented for the user, and no acoustic window is necessary. The MRE technique is operator independent, which provides for better reproducibility. Additionally, body habitus is less of an issue than with ultrasound-based techniques as long as sufficient motion can be induced into the organ of interest.

K. Endogenous Motion Imaging

Endogenous motion in the body can be used as the excitation for elasticity imaging. The pumping action of the heart provides an excitation that can be used within the heart and the vascular system. The electromechanical stimulation of the heart muscle generates waves in the cardiac tissue that have been measured [256–260]. The speed of the waves can be used to characterize the material properties of the cardiac tissue. The pulse wave velocity due to a pressure wave of the pumped blood has been measured in arterial vessels for characterization of the elastic properties [258, 261–263]. High-frame rate ultrasound imaging is required to perform these measurements.

L. Mechanical Imaging (MI)

Mechanical Imaging (a.k.a. Stress Imaging or Tactile Imaging) is a branch of Elasticity Imaging which visualizes internal structures of tissue by measuring stress patterns on the surface of tissue compressed by a probe with a pressure sensor array mounted on its contact surface [65]. Temporal and spatial changes in the stress pattern provide information on the tissue internal structures with different elastic properties. The MI probe acts like human fingertips during clinical examination. MI mimics manual palpation much more directly than other elasticity imaging modalities. Laboratory studies on breast phantoms and excised prostates have shown that computerized palpation is more sensitive than a human finger [63, 67, 264]}.

Surface stress data recorded by MI provide information on the elastic structure of the tissue and allow two-dimensional and three-dimensional reconstruction of tissue structure in terms of elasticity modulus. The data acquired allow the calculation of internal lesions such as size, shape, nodularity, consistency/hardness, and mobility. MI, like nonlinear quasi-static elastography and manual palpation, provides high local deformations of tissue (up to 30–40%). This feature is important for quantitative assessment of tissue nonlinear elasticity, one of the mechanical characteristics most sensitive to structural changes in tissue accompanying cancer development [265]. Most of the other elasticity imaging methods, especially those based on the use of acoustic radiation force, do not employ a sufficiently high level of deformation necessary for nonlinear elasticity imaging.

Different MI systems have been created for imaging of the breast [266, 267], prostate [268–270], and vagina [271]. It is shown that the potential of MI is not limited only to cancer detection but also may provide the differentiation between malignant and benign lesions [267].

For many of the applications, where tissue abnormalities are located within a few centimeters under the accessible tissue surface, the sensitivity and specificity of MI may be comparable to those of MR and ultrasonic elasticity imaging devices. Obviously, MI cannot be used for imaging tissue structures located well below the limit of manual palpability.

VI. ADVANTAGES AND LIMITATIONS OF VARIOUS ELASTICITY IMAGING METHODS

The methods detailed in this article are all aimed at the same objective, to quantify the elasticity or viscoelasticity of tissue. However, each method has its own nuances in reaching that goal and it is important to understand that, because of the frequency dependency of elasticity properties of tissue, great care and consideration must be used when comparing quantitative results among these techniques. The excitation is either an external mechanical force, an internal ultrasound radiation force, or an internal endogenous force. The excitation is also differentiated by its frequency content varying from (nearly) static to dynamic with frequency content up to 100 kHz. Measurement techniques are based mostly on ultrasound or MR imaging techniques, but other techniques are used in VA and MI. Lastly, six of the methods detailed in this review use shear waves. Most of the differences for the shear wave methods lie in either the method by which shear waves are created or measured, and the inversion method used to estimate the elastic modulus. A table summarizing the excitation and measurement methods and some advantages of each elasticity imaging method are listed in Table 1.

Table 1.

Comparison of different shear wave-based elasticity measurement and imaging methods.

Method	Excitation		Measurement	Advantages
	Time Course	Physical Stress
Elastography	Quasi-Static	Mechanical	Ultrasound	Full strain and modulus images Estimate elastic nonlinearity Conventional US scanner
ARFI	Dynamic	Radiation Force	Ultrasound	Viscoelastic characterization Conventional US scanner
HMI	Dynamic	Radiation Force	Ultrasound	Viscoelastic characterization
VA	Dynamic	Radiation Force	Acoustic	High spatial resolution
Mechanical Imaging	Static/Dynamic	Mechanical	Pressure	Simple, inexpensive Estimate elastic nonlinearity
Endogenous Motion Imaging	Dynamic	Endogenous	Ultrasound	Mechanical wave imaging High-frame rates
MRE	Dynamic	Mechanical	MRI	3D displacement Large organ imaging
TE	Dynamic	Mechanical	Ultrasound	Simple, inexpensive Compact package
Sonoelastography	Dynamic	Mechanical	Ultrasound	Full elasticity images Conventional US scanner
SWEI	Dynamic	Radiation Force	Ultrasound/MRI	Remote palpation
SSI	Dynamic	Radiation Force	Ultrasound	Full elasticity images Viscoelastic characterization
SDUV	Dynamic	Radiation Force	Ultrasound	Viscoelastic characterization High SNR in frequency components

Sonoelastography, elastography, TE, MRE, and MI all use a mechanical actuation. The advantage of using external mechanical actuators is that large motion amplitudes can be generated, making the displacement or strain measurement process easier, facilitating assessment of tissue elastic nonlinearity and the data is typically less error prone. However, in some instances, mechanical actuation also means that additional hardware is required. The exceptions are elastography and MI wherein the same transducer (the ultrasound transducer and pressure sensor array, respectively) is used for probing and measurement. In the case of MRE, the actuator is separate from the MRI scanner. In TE, particularly in the commercial implementation of FibroScan® (EchoSens, Paris, France), the actuator and the ultrasound measurement device are coupled together in one package, which makes the measurement less awkward. For sonoelastography crawling waves, two separate drivers are required which may be troublesome for some clinical applications of the technology.

ARFI, SWEI, SSI, VA, HMI, and SDUV all create displacement or shear waves using ultrasound radiation force. The advantage of this method is that typically only one ultrasound transducer is necessary to create the vibration and measure the resulting displacement and wave propagation as opposed to some methods that need external mechanical actuation and a separate device to measure the motion. However, because of limits on the intensity used to avoid both mechanical and thermal bioeffects [38, 43, 106, 216], the resulting motion amplitude of the shear waves is usually below 20μm. A disadvantage of radiation force methods is that it is difficult to induce sufficient deformations beyond about 6 cm with current imaging systems. Also, the shear wave attenuation is very high so the waves do not propagate very far. This is an advantage because the shear waves induced by radiation force are less prone to artifacts from reflections and interactions with other tissue boundaries [38]. Therefore, more localized elasticity measurements can be performed with less dependence on boundary conditions.

The main difference between MRE and the other methods mentioned in this article is the use of MRI instead of ultrasound for measurement of the tissue deformation. MRI has the advantage of providing 3D displacement data at millimeter to sub-millimeter resolution at the cost of acquisition time, which can be on the order of seconds to minutes. MRE is also limited because MRI scans are expensive and MR scanners are less widely available than ultrasound scanners.

Using ultrasound for elasticity measurement generally provides a two-dimensional (2D) mapping of the elasticity unless the ultrasound transducer is physically moved or a 2D array transducer is used to obtain 3D displacement data. The spatial resolution of the resulting images is typically in the millimeter to sub-millimeter range and can be improved by using higher frequency ultrasound to perform detection. To measure shear wave or endogenous mechanical wave propagation, high frame rates are necessary, except in the case of crawling waves with sonoelastography. In practice, this is accomplished in one of three ways. In the TE, SWEI, and SDUV methods, only one or a few lines are used for the shear wave propagation measurement. In this case, the pulse repetition frequency (PRF) for each tracking line can be in the kilohertz range. SSI is predicated on a dedicated ultrafast imaging system that can acquire 5,000–20,000 frames/s. This is accomplished by only transmitting a plane wave [43]. Focusing is performed only in receive. However, it has been shown that with such high frame rates, angular compounding can be performed to improve the signal-to-noise ratio (SNR) of the detection process [179]. These high frame rates allow for the investigation of dynamically moving tissues such as the heart and vasculature. Lastly, in sonoelastography crawling waves have been employed so that standard ultrasound scanners can capture the wave motion. The shear waves in this case have been “slowed” down so that measurements can be performed using all lines but with conventional systems.

The spatial resolution of the MR- and ultrasound-based methods is modulated by the processing and inversion techniques utilized. If maximal spatial resolution of the imaging system is used, the images can contain significant levels of noise. Filtering techniques often are used to smooth these images, but spatial resolution and elasticity contrast can be reduced by these methods. The reconstruction speed of the elasticity measurements or images depends on the amount of data and the complexities of the processing techniques. The strain-based elastography methods have been implemented to operate in real-time on clinical ultrasound scanners. Other methods provide measurement results within seconds while others require extensive offline analysis.

Methods based on measuring displacement or strain can be used for elasticity assessment, but true quantitative results can be difficult because of the need to know the stress distribution to solve for the elasticity. Shear wave-based methods have an advantage because they do not require the stress distribution for inversion of the underlying elastic properties because shear wave velocity, under limited conditions, is a simple function of the shear elasticity modulus.

However, as usual in imaging, improved resolution, minimum bias and variance errors and high speed image formation are always desirable. Determining which methods are “best” for a specific application or whether any particular image quality descriptor is of primary importance when analyzing and comparing methods and approaches is always a task-specific study. Such an analysis is beyond the scope of this overview.

VII. CLINICAL APPLICATIONS

For most of the past two decades, since the first papers were published, Elastography has remained largely a research method used by a few select institutions having the special equipment needed to perform the studies. Since 2005 however, increasing numbers of mainstream manufacturers have added Elastography to their ultrasound systems so that today the majority of manufacturers offer some sort of Elastography or tissue stiffness imaging on their clinical systems. This vastly increased availability of Elastography has enabled large numbers of new users to try it on all sorts of tissues and lesions that were not envisioned as candidates initially. Now it is safe to say that some sort of elasticity imaging may be performed on virtually all types of focal and diffuse disease. Most of the new applications are still in the early stages of research, but a few are becoming common applications in clinical practice.

A. Breast

Breast mass evaluation was the first application of Elastography to be studied systematically. The initial clinical work in this field appeared in 1997 and demonstrated that elastographic imaging was feasible, could be performed on a supine patient by compression against the chest wall, and showed that cancers generally appeared stiffer (darker) than benign lesions and surrounding breast tissue [115]. Also, it was noted that cancerous lesions almost invariably appeared larger on the elastogram than they did on the corresponding sonogram (Fig. 8). The combination of lesion stiffness and size relative to the sonogram were used to demonstrate good separability of benign from malignant lesions. Later papers confirmed these findings in larger numbers of patients with reported area under the receiver operating characteristic curve (A_z) values ranging from 0.89 to 0.95 for distinguishing benign from malignant solid nodules [114, 272–275]. Other authors demonstrated the use of color maps to depict tissue stiffness [276, 277] and a standard method of grading lesions was developed for those using Hitachi systems with color display [277]. The initial papers focused on qualitative evaluation of relative hardness but more recently methods for quantitative or semi-quantitative assessment of nodule stiffness have become available. These methods include the measurement of strain ratios between the nodule and some adjacent reference tissue [278] and the assessment of shear wave velocity within nodules [156] which provides an assessment of shear modulus which is related to overall tissue stiffness. Clinical studies using these quantitative methods are only just now appearing in the literature [180, 279, 280].

Figure 8.

Sonogram (left side image) and elastogram (right side image) of an invasive ductal carcinoma showing a stiff lesion (dark) on the elastogram that is somewhat larger than the hypoechoic lesion seen on the sonogram (white arrows).

As breast Elastography becomes a mainstream application, attempts to standardize technique and diagnostic criteria are beginning to appear. As already noted, a set of diagnostic criteria have been developed for Hitachi systems, but criteria for other systems are newer and just beginning to see widespread application. A set of BIRADS criteria for Elastography are reportedly being developed which should help to improve the consistency of Elastography for breast mass diagnosis.

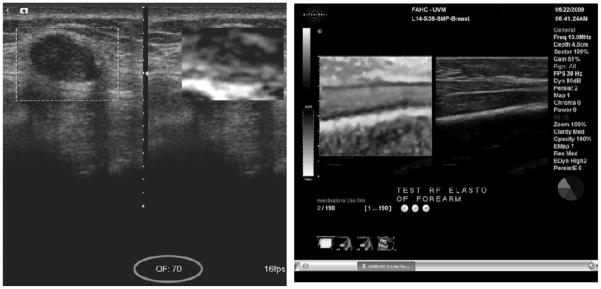
Criteria for distinguishing high quality from low quality elastographic images are also important since many of the images generated during a clinical elastogram acquisition may be of low quality and using these images for diagnosis could lead to incorrect classification of breast lesions. It is not always obvious which images are the best in any sequence of elastograms, especially since lesion visibility does not always correlate well with overall image quality. For example, an image with a high correlation coefficient (a measure of elastogram quality) may not show a lesion if the displacements and strain values are very small throughout the image and an image with a low average correlation coefficient may show a lesion as a low strain region surrounded by decorrelation “noise” (Fig. 9). Most manufacturers have incorporated some sort of visual feedback on the image to help users determine if the elastogram is of diagnostic quality or not (Fig. 10). The methods used to determine the quality of images varies widely but as the technology matures further, a standard method of determining quality will likely be developed and adopted.

Figure 9.

Sonogram (left image), 1% compression elastogram (middle) and 4% compression elastogram (right) of a fibroadenoma (arrows on sonogram). Note that the fibroadenoma is not really visible on the 1% compression elastogram but is visible as an area without decorrelation noise on the 4% compression elastogram. The 1% elastogram has less decorrelation noise than the 4% elastogram but a lesion may be more visible on the “noisier” elastogram.

Figure 10.

On-screen quality indicators. Left image shows a numerical quality indicator (circled) at the bottom of the image. The closer the number to 100 the better. The right hand image shows a pie chart quality indicator--more pie segments in green means better quality.

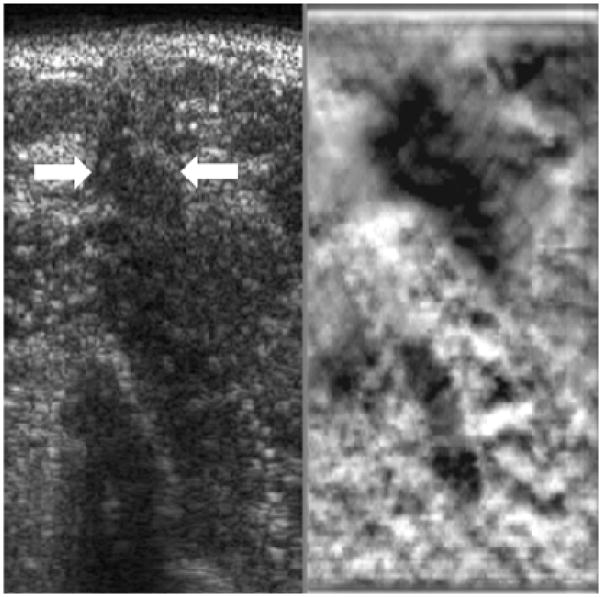
Breast ultrasound has always found a role in the identification of cysts, but in recent years the identification of cysts has become more difficult. One reason is classical acoustic enhancement posterior to cysts is harder to see on current systems due to smaller lesion size (with less fluid path to cause increased transmission), spatial compounding, and multiple transmit focal zones with automatic amplitude matching of layers. All these tend to suppress increased through-transmission. Cysts produce decorrelated RF lines and this can be seen in the strain image as an artifact inside cystic lesions (Fig. 11). The presence of a decorrelation artifact within a lesion can be used as an indication that the lesion is cystic. Unfortunately, the exact nature of the artifact and its appearance depends on the way in which each manufacturer chooses to display decorrelation. So the appearance of a cyst on an elastogram will vary depending on the scanner used. Still, with standardization, the elastogram may be used to identify small debris containing cysts so that biopsy can be avoided. Comparison of correlation coefficients from within cystic lesions to the values in surrounding tissues is a more quantitative way to identify cysts [281].

Figure 11.

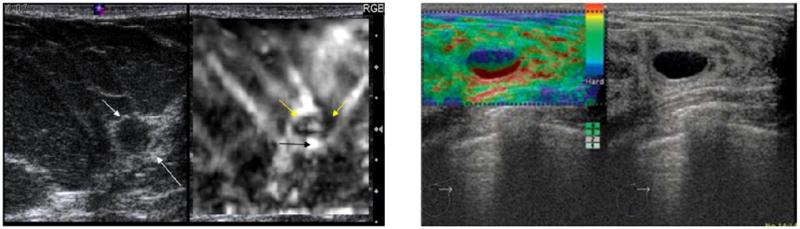
Cyst appearance. Cyst may display as a dark area with a central brighter area (4a). Another common pattern is layered blue, green and red colors with in the lesion as shown in the color overlay image of figure 4b. (Images courtesy of Siemens and from Chiorean et al, Med Ultrasonography 2008;10(2): 73–82.

B. Liver

The second most common application of elasticity imaging is for the evaluation of hepatic cirrhosis and fibrosis [282, 283]. MRE was used for pioneering studies in examining hepatic stiffness [225–228]. These studies demonstrated liver stiffness and viscosity increased with the degree of fibrosis up to the level of cirrhosis. In later studies with more test subjects, it was found that MRE could provide areas under the ROC curves ranging from 0.95–0.99 for distinguishing healthy subjects from patients with fibrosis [284]. Because of its high negative predictive value, MRE is currently being used at the Mayo Clinic to determine which patients would benefit most from biopsy referral [285]. This development is one example of how elasticity imaging has served to change medical practice. Despite this encouraging seminal work, MRE may not be widely available for evaluating liver stiffness, and its use as a screening tool may be cost-prohibitive compared to ultrasound-based techniques.

Hepatic stiffness measurements are most commonly performed using a non-imaging device, the FibroScan® from Echosens (Fig. 12). This device briefly compresses the liver to produce a shear wave that travels through the liver. Ultrasound pulses are next used to track the minute tissue displacements caused by the shear wave and liver stiffness is estimated from the velocity of the shear wave. Area under the ROC curves of 0.84—0.89 for liver fibrosis have been achieved by this method with the best performance on moderate to severe fibrosis. Some of the newer ultrasound systems (i.e. from Siemens and Supersonic Imagine) can also estimate shear wave velocity at various locations in the liver making local estimates of liver stiffness possible with the promise of improved performance [172, 173] (ROC areas of 0.90 or higher) since the effects of overlying tissue can be reduced or eliminated. Since increased liver stiffness correlates well with cirrhosis, such estimates will likely become a routine part of hepatic ultrasound when surveillance scans for hepatocellular carcinoma are performed. With the current high prevalence of chronic hepatitis [286] and a climbing HCC rate that has tripled since 1975 [287], this application of elasticity imaging may become the most common of all.

Figure 12.

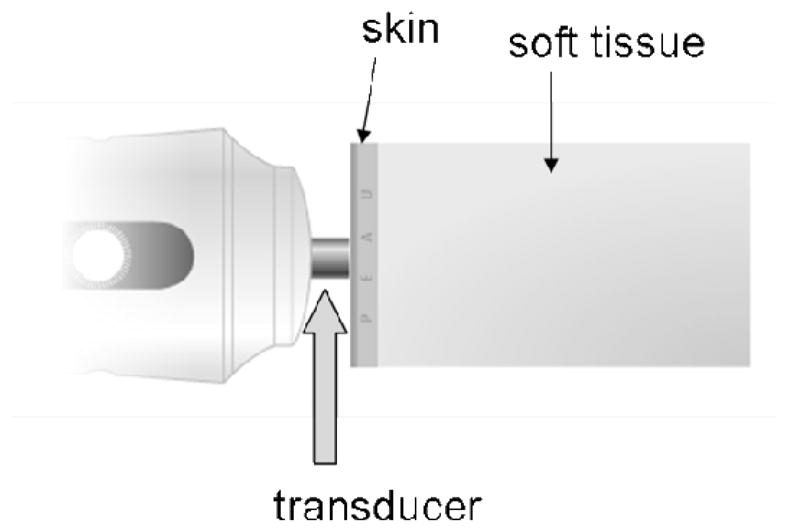
Drawing of the Fibroscan transducer. The piston like transducer rapidly indents the skin producing a compressional wave and shear waves. Ultrasound is emitted from the transducer to track tissue displacement caused by the shear wave to estimate shear wave speed. (Drawing from the Echosens web site)

Elasticity imaging has also been used to evaluate focal liver lesions. Hepatocellular carcinoma (HCC) detection and differentiation from other lesions has been the focus of much of this work. HCC lesions are typically stiffer than normal liver but the difference may be less pronounced when compared to cirrhotic liver in which the tumors typically occur [127]. Preliminary studies are promising for the identification of HCC with A_z values as high as 0.94 [126, 288]. Recent work has also suggested that HCC may be distinguished from other malignancies such as cholangiocarcinoma and metastatic disease with reasonable accuracy using elasticity estimates [289].

C. Prostate

Prostate gland evaluation for detection of cancer is commonly thought of as a logical application of elastography, and was the first potential application that was considered when elastography was originally developed. It was also the application proposed by early proponents of Sonoelasticity imaging [33]. Prostatic cancers are frequently not visible on standard B-mode ultrasonography so use of elasticity imaging to classify nodules already discovered (as is the case for breast elastography) is not possible. This means that to be clinically useful, elasticity imaging must detect cancers reliably – a task quite different from characterization of an already visible mass. Several articles have been published showing prostate elastograms [116, 290] (Fig. 13) but obtaining quality stiffness images of the prostate gland has proved to be more difficult than in the breast [291]. This is in part due to problems with tissue lateral motion caused by compressing with the tightly curved array transducer and to the small amounts of tissue compression that can be achieved at depths beyond 1 cm when using such a transducer. Systems that use shear wave imaging (e.g., ARFI or an external vibration device) may be more successful. Compression of the prostate with a balloon surrounding the transducer has also been tried with some success [292]. Another problem in the prostate gland is the very small size of many cancer foci (often < 1 mm) making detection with a relatively low resolution elasticity imaging system difficult or impossible with current technology. It is also unknown whether such small foci are actually stiffer than normal prostatic tissue or benign prostatic nodules. On the other hand, there is controversy regarding the significance of small cancer foci with many small foci corresponding to clinically insignificant cancers [293–295]. At any rate, even if prostatic elasticity imaging proves insensitive for very small cancer foci, it still may be useful as a biopsy guidance tool for detection of larger suspicious foci that can be biopsied during US guided extended pattern biopsy [116, 296] so that additional cores can be taken from areas deemed suspicious on elasticity imaging. This will hopefully improve the positive biopsy rate so that the number of painful and time consuming transperineal or transrectal saturation biopsies may be decreased.

Figure 13.

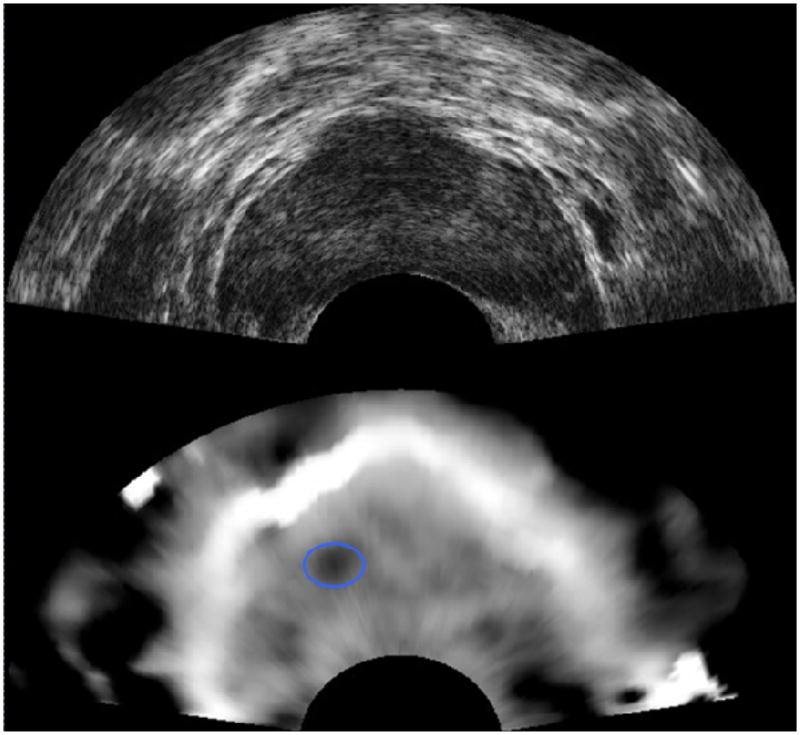
Prostate B-mode sonogram (upper image) and corresponding elastogram (lower image) showing a small dark area (circled) corresponding to a malignancy. This focus is not visible on the sonogram. Images courtesy of Kaisar Alam, Riverside Research Institute.

One application in the prostate gland that may be widely used in the near future is ablation treatment monitoring [297]. Most tumor ablation methods result in increased tissue stiffness [298, 299] that is readily detected using elasticity imaging. This allows documentation of the size of the zone of treated tissue which is useful since B-mode ultrasound cannot easily distinguish between ablated and non-ablated tissue once the microbubbles caused by the actual ablation process disappear. Examples of monitoring of prostatic and liver tumor ablation have appeared in the literature [300–302] (Fig. 14). For this application to become widespread, more work correlating the zone of cell death and injury with the zone of increased tissue stiffness must be performed.

Figure 14.

Prostate sonogram (left image) showing somewhat increased echogenicity due to bubble formation during HIFU. Elastogram on right shows the ablated area as a clear dark (stiff) region. Images courtesy of Remi Souchon.

D. Thyroid

Evaluation of thyroid nodules is a logical potential application for elasticity imaging because the ultrasound and nuclear medicine criteria for distinguishing benign from malignant nodules (size, mural nodularity, echogenicity, activity on scintigraphy) are not reliable. The presence of microcalcifications increases the risk of malignancy but is certainly not an absolute indicator [303]. Several papers have appeared in the literature, demonstrating the potential utility of lesion stiffness for classifying a nodule as malignant [117, 304]. As with other lesions, malignant thyroid nodules tend to be stiffer than benign nodules. Elastographic imaging of the thyroid can be challenging with present equipment due to pulsations from the adjacent carotid artery and due to the steeply sloping neck contour which promotes lateral movement of the thyroid (and decorrelation) when applying compression with the ultrasound transducer. Even if the performance of elastography degrades as more results are reported, it should be possible to use elasticity imaging as a tool to help decide which nodules to biopsy when many are present [305].

Little work has been performed on the evaluation of diffuse thyroid diseases so far. Since chronic thyroiditis is known to increase the firmness of the thyroid on palpation, changes are likely to be observable on quantitative or semi-quantitative elasticity imaging. Results of shear wave velocity analysis using MRE have confirmed this notion showing increased stiffness of the thyroid in Hashimoto’s thyroiditis [253]. As quantitative elasticity imaging becomes more widespread and more experience is gained, stiffness estimates may become useful for helping to confirm thyroiditis though it is not yet clear whether all types of thyroiditis can be detected with this method nor is it likely that elasticity imaging alone will be able to distinguish between various types of thyroiditis. Other elasticity based methods such as poroelastography may be helpful here.

E. Lymph Nodes

Enlarged or palpable lymph nodes represent a common diagnostic problem. Nodes may be enlarged due to infection or inflammation either local or remote and may be involved with or replaced by malignancy. A method for determining whether an enlarged lymph node is likely to be involved with cancer or not would be extremely helpful for selection of lymph nodes for biopsy in patients with suspected malignancy. At least six papers have appeared which discuss elasticity imaging of lymph nodes [118, 306–310]. Evaluation of lymph nodes, using both relative strain values and the subjective Hitachi criteria, have been performed. As with other malignancies, cancerous lymph nodes appear stiffer on elastograms than do benign reactive lymph nodes.

Several studies have shown that elastographic analysis is highly specific for malignancy. Using the strain index (Fig. 15) Lyshchik, et al. found a specificity of 98% whereas Saftoiu, et al. reported 91.7%, and Alam, et al. achieved a specificity of 100% using pattern analysis. ROC analysis was performed in the Alam study yielding A_z values of 0.87 and 0.90, for elastography alone and B-mode sonography alone. For combined B-mode and elastography the A_z value was an outstanding 0.97. Most of the studies have looked at neck lymph nodes and some other superficial lymph nodes, but one study has looked at nodes seen by endoscopic US. Further work using real-time elastography is needed since several of the studies were conducted off line using previously acquired data, but the results so far indicated that elastography combined with B-mode ultrasound will be a useful tool for detection of malignancy in nodes and for selecting nodes for biopsy.

Figure 15.

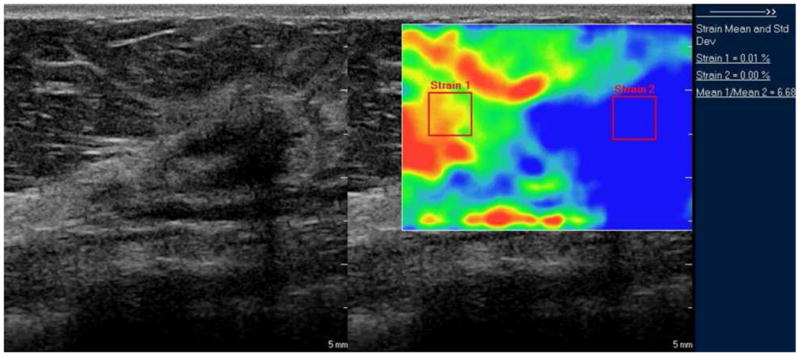
Strain ratio computation. Sonogram of breast lesion on left with color elastogram on right. The ratio of strain within the lesion (strain 2) and adjacent to the lesion (strain 1) is computed as 6.68

F. Arterial Wall/Atheromatous Plaque Characterization

Work on the use of elasticity imaging for evaluation of atheromatous plaque has been underway for more than a decade. Atheromatous plaques may lead to arterial thrombosis when they become filled with soft lipid laden macrophages and subsequently rupture releasing the lipid containing central material causing sudden thrombosis of the vessel. Such plaques are called vulnerable plaques and their detection is important for risk assessment and medical therapy [311, 312]. Elasticity imaging has the potential to detect such plaques by being able to detect the soft lipid laden center [313]. Elastography using intravascular ultrasound (IVUS) has been shown to be able to demonstrate vulnerable plaques [314] but as IVUS is invasive and requires expensive single use catheter mounted ultrasound transducers, it has not become widespread. Some attempts to image atheromatous plaque using transcutaneous ultrasound have been made [315], but the method is still in the developmental stage. More recently, investigations of actual arterial wall elasticity have been attempted [316, 317] and there are indications that increased wall stiffness is a marker of impending atheromatous disease even prior to the development of increased intimal medial thickening on B-mode ultrasound. Use of the transcutaneous method for therapy monitoring has also been reported with promising results [318]. Further investigations are continuing [319] and this area has promise but faces significant technical hurdles before widespread clinical use becomes practical.

G. Thrombosis

When a venous thrombosis is found using ultrasound, estimation of the age of the thrombus is important. Older thrombi are adherent to the vessel wall and do not pose a risk of pulmonary embolus, whereas acute thrombi pose a significant risk of pulmonary embolus but are treatable with anticoagulants. Often the age of a thrombus can be inferred by clinical history and/or symptoms. Gray scale ultrasound signs of an acute thrombus include an enlarged vein and hypoechoic thrombus but when the thrombus is moderately echogenic and the vein is normal sized, the differentiation of acute, subacute and chronic becomes more difficult. Since the stiffness of thrombi increases with increasing age [320], elasticity imaging promises to be helpful with thrombus age determination. An initial study was successful at correctly distinguishing acute from chronic thrombus using normalized strain magnitude [321] (Fig. 16) but some difficulties have also been encountered in early clinical use [322]. Using a combination of backscatter parameters and elastography has shown promise for increasing thrombus classification accuracy [323]. Elastography has also been used experimentally to estimate the stiffness of arterial thrombus in aneurysms created in a dog model at various stages to determine if the method might be useful for pre and post endograft evaluation [324].

Figure 16.

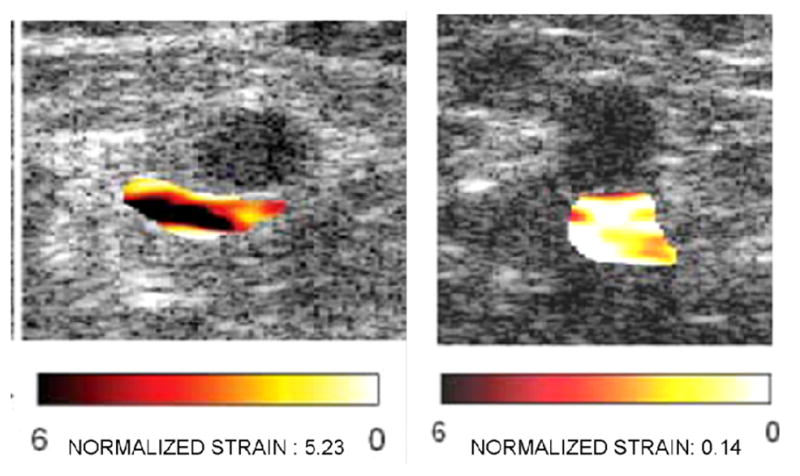
Normalized strain in venous thrombosis. The strain in the vein with chronic thrombosis (right hand image) is much lower than the strain in the more acute thrombosis (left hand image). The echogenicity of the thrombi are nearly identical in grayscale intensity. Images from Rubin JM, et al. J Ultrasound Med 2003;22:443–448.

H. Other tumors

Tumors of almost all major organs have been studied using elastography. For pancreatic cancer, initial reports using endoscopic ultrasound elastography are promising [325, 326], and at least one report of successful cancer imaging using transcutaneous elastography has been reported [327]. There are few reports of testicular elastography, but the use of the method for fertility assessment is promising [328]. Use of elastography for tumor assessment has been reported at meetings [329] but more studies with a larger number of tumors of various types need to be studied since histology of the different neoplasms varies widely. In the skin, elastography has been used to evaluate scleroderma [330], abscesses and decubitus ulcers [331] and appears promising for the evaluation of melanoma and other skin cancers [332]. One report of use of elasticity imaging for salivary gland tumors has appeared but results were not promising [333].

I. Graft Rejection

Since transplant graft rejection involves both inflammation and fibrotic change, both of which increase tissue stiffness, elasticity imaging is a logical method to evaluate the physical status of transplanted organs. Liver transplant fibrosis has been shown to be correlated with transient elastography fibrosis scores using the FibroScan® device [334]. A_z values of approximately 0.90 were obtained for diagnosis of advanced transplant fibrosis (fibrosis score ≥ 3) using this device in line with the performance of the FibroScan® device for fibrosis of native livers. The same device has also been used to evaluate renal allografts with a high rate of technical success (96.5%) with a correlation of stiffness to interstitial fibrosis. A significant difference in stiffness values was seen in patients with low estimated glomerular filtration rate (GFR) compared to those with more normal GFR values above 50 ml/min [335]. Case reports of shear wave imaging of renal transplants are also beginning to appear and pancreatic transplant evaluation using elastography is being discussed even though papers on the subject have not yet appeared.

J. Heart

Unlike most organs, the beating heart is composed of rapidly contracting and relaxing muscle whose stiffness is constantly changing throughout the cardiac cycle. So a system useful for strain or stiffness estimates must acquire data at a very high frame rate. Existing cardiac systems can estimate strain rate from acquired Doppler data which depicts areas of myocardial infarction well [336], but few systems can currently acquire the RF data needed for strain and stiffness estimation. Strain imaging may be helpful for evaluation of localized disorders of myocardial contractility such as might occur after myocardial infarction and ischemia. Studies using ultrasound elasticity estimation have shown promise [337, 338] although multiple methods are available for characterization of myocardial function making widespread clinical application less certain. Considerable work on MRE is also underway [235, 238].

K. Musculoskeletal

Extensive work on elastography of muscle has been performed using MRE [245, 248]. Stiffness in skeletal muscle increases with increased muscle contraction and tension. The method may be useful for quantifying muscle status during treatment. Tendon [339] and ligament [340] elastography has also been accomplished and elastography is even being attempted as an aid to proper massage therapy [341].

Elastography is also being used as a research tool to study hyaline cartilage properties under loading [342]. This work may have clinical applicability in the future as a tool for non-invasively studying articular cartilage prior to arthroscopy and as a tool for studying effects of drug and supplement therapy on cartilage.

L. Lymphedema

Preliminary work has been published on the use of a variant of elastography, called poroelastography, for the diagnosis and grading of lymphedema [343]. Poroelastography evaluates the change in Poisson’s ratio (the lateral to axial strain ratio) over time to get an estimate of the rate of fluid flow from one tissue compartment to another [70–77, 344]. Initial work shows that normal tissues exhibit a Poisson’s ratio of near 0.5 whereas edematous tissues exhibit a declining Poisson’s ratio over time as edema fluid leaves the region being examined. Information regarding the fluid content and movement of tissue is useful to determine the stage of lymphedema (higher stages have less fluid and more fibrosis) as well as an objective way to monitor therapy (a type of massage called manual lymphatic drainage). MRI may also be able to accomplish this task but would probably be more expensive and less available.

M. Brain

The material properties of the brain have been explored in numerous studies using MRE [229–233]. The skull poses a serious obstacle for ultrasound-based elasticity imaging methods because of the lack of appropriate acoustic windows. However, one recent study using SSI has reported shear elasticity in the brains of rats after craniotomy [345]. For MRE studies, wave motion is induced from a vibrating bite bar that the subject puts between his/her teeth or a device that vibrates the head from left to right. The studies using MRE have demonstrated that the brain viscoelasticity can be characterized. A recent study has shown that the viscoelastic parameters decrease in patients with multiple sclerosis compared to normal subjects [346].

N. Other Applications/Summary

New applications of elasticity imaging are appearing weekly in the medical literature. An example of a novel application would be the unsuccessful attempt to use EUS based elastography to evaluate the anal sphincter [70, 347]. Some applications will likely never work but others simply require a different approach or further advances in technology to be successful. From the explosion of applications over the past few years, it is certain that many new applications both diagnostic and therapeutic will soon appear as these powerful techniques become established tools for visualization and diagnosis.

VIII. CONCLUDING REMARKS

Viscoelastic characterization of tissue obtained by the elasticity imaging methods reported here provide efficient indicators identifying diseased tissue versus normal tissue. Elasticity imaging methods are emerging as commercial applications, a true testament to the progress and importance of the field. MRE has been reported using both a General Electric (GE) and Philips 1.5T MRI scanners. Quasi-static elastography has been implemented on many systems including those produced by Siemens, Philips, GE, Hitachi, Toshiba, Aloka and Ultrasonix. Transient elastography has been implemented in the FibroScan® product manufactured by EchoSens (Paris, France) in an effort to quantify liver stiffness for diagnosis of liver fibrosis. Numerous clinical studies have been reported in the literature. A search using the ISI Web of Knowledge yielded 139 original articles when using the search terms “transient elastography and FibroScan®” during the time span 2003–2010. The ARFI imaging has been implemented as the Virtual Touch imaging and Tissue Quantification, respectively, in the Siemens S2000 (Berlin, Germany) ultrasound scanner. Lastly, SWEI and SSI have been implemented on the Aixplorer® manufactured by SuperSonic Imagine (Aix-en-Provence, France). As shear-wave based elasticity methods become a part of standard imaging systems, the number of clinically relevant studies will expand greatly.

As stated above, it is important to recognize that the elastic properties measured with these techniques are part of a continuum of the mechanical response of tissue the deformation stimulus. As such, the elastic modulus measured at low frequency (as in quasi-static elastography) will be predictably lower than the elastic modulus measured with radiation force techniques. Care must be taken in quantitative comparisons.

It should also be noted that there are other approaches for estimating the viscoelastic properties of tissue that are not included here. For example, there is a growing body of literature on optical coherence tomography techniques for elasticity imaging. Further, there are recent developments of techniques using phase contrast techniques in X-ray imaging and X-ray computed tomography for elasticity imaging [348]. In time we will find the significance of these developments.

In summary, the viscoelastic material properties of soft tissue can be characterized using elasticity imaging methods. These viscoelastic properties vary between normal and diseased tissue which provides a unique contrast mechanism for diagnosis of different pathologies. Numerous elasticity measurement and imaging methods have been developed, and the following manuscripts review the advantages and limitations of those methods. The future for this imaging modality holds great potential for many different applications to assist in detection of disease and improving patient outcomes.