Abstract
We characterized the three-dimensional angular vestibulo-ocular reflex (3D aVOR) of adult C57BL6 mice during static tilt testing, sinusoidal and high-acceleration rotations and compared it with that of another lateral-eyed mammal with afoveate retinae (chinchilla) and two primate species with forward eye orientation and retinal foveae (human and squirrel monkey). Noting that visual acuity in mice is poor compared to chinchillas and even worse compared to primates, we hypothesized that the mouse 3D aVOR would be relatively low in gain (eye-velocity/head-velocity) compared to other species and would fall off for combinations of head rotation velocity and frequency for which peak-to-peak position changes fall below the minimum visual angle resolvable by mice. We also predicted that as in chinchilla, the mouse 3D aVOR would be more isotropic (eye/head velocity gain independent of head rotation axis) and better aligned with the axis of head rotation than the 3D aVOR of primates.
In 12 adult C57BL6 mice, binocular 3D eye movements were measured in darkness during whole-body static tilts, 20-100°/s whole-body sinusoidal rotations (0.02-10 Hz) and acceleration steps of 3000°/s2 to a 150°/s plateau (dominant spectral content 8-12 Hz). Our results show that the mouse has a robust static tilt counter-roll response gain of ~0.35 (eye-position Δ / head-position Δ) and mid-frequency aVOR gain (~0.6-0.8), but relatively low aVOR gain for high frequency sinusoidal head rotations and for steps of head rotation acceleration (~0.5). Due to comparatively poor static visual acuity in the mouse, a perfectly compensatory 3D aVOR would confer relatively little benefit during high-frequency, low amplitude movements. Therefore our data suggest that the adaptive drive for maintaining a compensatory 3D aVOR depends on the static visual acuity in different species.
Like chinchillas, mice have a much more nearly isotropic 3D aVOR than do the primates for which comparable data are available. Relatively greater isotropy in lateral-eyed species without retinal foveae (e.g., mice and chinchillas in the present study) compared to forward-eyed species with retinal foveae (e.g., squirrel monkeys and humans) suggests that the parallel resting optic axes and/or radially symmetric retinal foveae of primates underlie their characteristically low 3D aVOR gain for roll head rotations.
Keywords: vestibulo-ocular reflex, visual acuity, mouse, 3D video-oculography
Introduction
C57BL6 mice are widely used in studies of inner ear function and as a background inbred strain from which genetically modified mouse models of human disease are generated. For example, C57BL6 mice and mutants derived from them are used as models for early adult-onset progressive sensorineural hearing loss (Spongr et al., 1997; Hequenbourg and Liberman, 2001; McFadden et al., 2001; Bartolome et al., 2002) and various causes of vestibular dysfunction (e.g., Lurcher mutant: Aleisa et al., 2007; P/Q-type calcium channel mutants: Stahl et al., 2004, Katoh et al., 2007; Head tilt (het) mutant: Harrod and Baker, 2003; Gravity receptor function examined in 25 mouse types, 13 of which had the C57Bl6 as the background strain: Jones et al., 2005). Responses of C57BL6 vestibular nerve afferents and secondary neurons to head rotation have been characterized (Beraneck and Cullen, 2007; Lasker et al., 2008), and C57BL6 angular vestibulo-ocular reflex (aVOR) responses have been described using video oculography (Stahl et al., 2000) and the scleral search coil technique (Harrod and Baker, 2003; van Alphen and De Zeeuw, 2002).
Prior investigations of the aVOR in mice have been limited to study of horizontal and/or vertical eye movement components, due in part to the technical difficulty of obtaining accurate, simultaneous measurement of all components of 3-dimensional (3D) eye rotations in mice. Prior studies have also been limited to head rotations at relatively modest frequencies (<2Hz) and/or accelerations (<2000°/s2) that do not cover the full range of head movements experienced during normal behavior, which extends up to ~4 Hz, ~400°/s and ~5000 °/s2 (Beraneck et al., 2008).
In the present study, we extended characterization of the C57BL6 mouse aVOR to three dimensions and to a wide range of head motion, including static tilts, sinusoidal rotations at 20-100°/s peak velocity over 0.02-10 Hz, and 3000°/s2 transient whole-body rotations about each of five anatomic axes. We then compared the 3D aVOR in mice to that of humans, squirrel monkeys, and chinchillas in order to examine the correlation between 3D aVOR gain and static visual acuity, which varies widely among these four mammalian species. Reasoning that there is little benefit in stabilizing gaze to a greater precision than the minimum angle resolvable by one’s retinae, we hypothesized that species with poorer maximum visual acuity would have lower aVOR gains, particularly at high frequencies (which for a given peak velocity correspond to a smaller peak positional displacement of a target’s image on the retina when aVOR gain is less than ideal). Finally, we compared the degree of 3D aVOR misalignment and anisotropy (gain dependence on rotation axis) between mice, humans, squirrel monkeys and chinchillas. We hypothesized that both of the lateral-eyed species without retinal foveae (mice and chinchillas) would have relatively isotropic, well-aligned 3D aVOR compared to both primate species, which have forward eye orientation, round retinal foveae, parallel optic axes for the two eyes in resting position, and a highly anisotropic 3D aVOR due to a relatively low gain for roll head rotations (Migliaccio et al., 2010).
Methods
We simultaneously measured eye movements of both eyes mediated by the 3D aVOR in response to whole-body head rotations in 12 female adult C57BL6 mice. All procedures were performed in accordance with a protocol approved by the Animal Care and Use Committee of the Johns Hopkins University School of Medicine.
Animal Preparation
To facilitate restraint during eye movement testing, a head bolt was placed with the animal under general (sevoflurane 3-5%) and local (1% lidocaine with 1:100K epinephrine, ≤0.2 cc) anesthesia. The dorsal surface of the skull was exposed and four stainless steel screws (M1×l.5 mm, Small Parts Inc., Miami Lakes, FL) were implanted in the calvarium in square formation. A lightweight metal screw with a flat head was positioned in the center of the square formation and on the skull in the midline. The screw was embedded in a dental acrylic cap engulfing the four screws. The post was oriented so that when the animal was placed into a restraining device within a Fick gimbal mounted atop a servo-controlled, Earth-vertical-axis rotating motor, the plane tangent to the flat part of the dorsal skull (and the occlusal plane of the molars) was pitched 30° ‘nose-down’ from Earth horizontal. With the animal in this position, the axes of the animal’s horizontal semicircular canals (SCC) aligned to within 10° of the rotating table’s Earth-vertical axis (Calabrese and Hullar, 2006). In this position, the left anterior (LA) and right posterior (RP) canals lie approximately parallel to a cardinal LARP plane perpendicular to the horizontal plane and 45° off the midsagittal plane, while the RA and LP canal lie close to a cardinal RALP plane that is the mirror image of the LARP plane across the midline. The gimbal could be reoriented to align any of the canal axes with the Earth-vertical axis of the rotator (model 130-80/ACT2000; Acutronic USA, Inc, Pittsburgh, Pa) with the rotator’s axis passing through the stereotactic origin of the animal’s skull. Animals were allowed to recover completely from anesthesia before aVOR testing, as indicated by response to ambient sounds and light touch to the paw or tail. Although all tilt and aVOR tests were performed with vision occluded, animals were housed between test sessions in cages with normal diurnal lighting.
Tilt testing
Eye position response to static tilts was determined by slowly reorienting the whole animal about the anterior-posterior (AP: roll), interaural (IA: pitch) and superior-inferior (SI: yaw) axes in steps of ±30° from 0° to 180°, then passing back through 0° to -180°, then back to 0°. The zero position of the animal for tilts about the AP and IA axes was neutral (i.e., with the horizontal SCCs aligned in an Earth horizontal plane). The zero position for tilts about the SI axis was nose up with the horizontal SCCs in an Earth vertical plane. At each orientation, the animal’s body remained fixed until 3D eye position no longer changed (~10 seconds) before eye position tabulation. We averaged eye position measurements for all stops at each head orientation.
Rotational Testing
Each animal’s aVOR responses were measured during rotations about each of 5 axes. Yaw/horizontal aVOR was tested with the gimbal in its reference position, with the animal prone and its horizontal SCC axes approximately Earth-vertical. For the other 4 axes, each animal was tested in both orientations that aligned the axis of interest with the Earth-vertical motor axis: roll with nose up [NU] and nose down [ND]; pitch with left ear down [LED] and right ear down [RED]; left-anterior/right-posterior (LARP) with LED-NU and RED-ND; and right-anterior/left-posterior (RALP) with RED-NU and LED-ND. LARP and RALP axes were approximated as being 45° off the midline and in the plane of the horizontal SCCs.
Sinusoidal stimuli included rotations at 0.02, 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 8 and 10 Hz at peak velocity 20°/s and 50°/s and 0.02-5 Hz for peak velocity 100°/s. Stimulus duration was sufficient to include at least 3 cycles at 0.02 Hz and 10 cycles at each other frequency. Transient acceleration stimuli were 3000°/s2 rotations for 50 ms to a 150°/s velocity plateau lasting ~0.9 s, followed by a 3000°/s2 deceleration for 50 ms to rest at 90° from the starting position.
Eye movement recording
The 3D video-oculography (VOG) technique we employed has been described in detail elsewhere (Migliaccio et al., 2005, 2010). This technique was initially developed for use in larger rodents, so modifications described here were made to adapt the approach for mouse eye movement recordings. With this technique, a video camera is used to track a marker array attached to each eye. We assume that if the camera’s optic axis is aligned with the pupil and the center of corneal curvature, then it is also aligned with the center of rotation of the marker array. We also assume that the center of rotation of the eye is not translating with respect to the camera, so that when the eye rotates the marker is traveling on the surface of an imaginary sphere with radius equal to the mean axial radius of an adult (100 day old) C57BL6 mouse eye (1.67 ± 0.18 mm; Schmucker and Schaeffel, 2004).
We fabricated fluorescent marker arrays using the veneer surface of photo paper saturated with fluorescent yellow ink. Arrays were opaque except for 3 fluorescent 200 × 200 μm windows separated by 200 μm and arranged in a 45° right triangle. Before applying the marker array, each cornea was treated with topical anesthetic (0.5% proparacaine) and a miotic agent (1% pilocarpine). After marker array removal, 0.3% ofloxacin was applied to prevent infection.
The imaging system had a resolution of 263 pixels/mm at the eye surface. The camera’s optic axis was aligned with the center of corneal curvature to within 72 μm using the technique described previously (Migliaccio et al. 2005). One camera for each eye (SCOR-1281M-BW, Point Grey Research, Canada) was used to acquire 500 × 400 pixel 8-bit monochrome images with a 1 ms electronic shutter time, transferred asynchronously to a PC at ~130 frame/s per eye. Each camera was retrofitted with a ½” format 16.0 mm focal length, f/2.0 C-mount board lens (BL160, Allthings Inc., Australia) and a 20 mm lens extension barrel to focus on a 1.9 × 1.5 mm region of the eye surface ~30 mm from the lens. At 500 × 400 pixel image size, the absolute resolution of the system (a 1 pixel shift) is <0.3°. Asynchronously acquired image data were aligned to a common time base using a 20MHz timer/counter. A National Instruments PCI-MIO-16×E-10 board acquired analog data from the position and rate encoder of the motorized turntable at 1kHz. VOG data were interpolated on this 1 kHz time base using a nonlinear running spline filter (LabVIEW Spline module; smoothness parameter adjusted so the correlation coefficient between the raw and filtered data was >0.80).
To rule out artifactual eye movements due to movement of the head with respect to the cameras or movement of the marker with respect to the eye, we measured apparent responses in two dead mice using the same stimulus paradigm described above. No artifactual eye movements exceeded the ~3°/s baseline noise level of the measuring system, indicating that the camera was not translating with respect to the eye and that the marker did not shift on the eye during high velocity/acceleration head movements.
Data analysis
Binocular 3D eye rotation data were displayed in real time in eye coordinates during acquisition and converted to rotation vectors in head coordinates during subsequent analysis. Unless stated otherwise, eye and head data are reported in a right-hand-rule head coordinate system centered on the skull stereotactic origin, with the yaw axis (+Z) dorsal and perpendicular to the mean horizontal SCC axis, the pitch axis (+Y) leftward on the interaural axis, and the roll axis (+X) anterior and orthogonal to +Y and +Z. LARP and RALP components were derived from yaw, pitch and roll components computed as rotation vectors. In eye coordinates, each eye’s 3D position has horizontal, vertical and torsional components, with torsion denoting eye rotation about the resting optic axis. The methods of analysis are similar to those that have been described previously (Migliaccio and Todd, 1999; Migliaccio et al., 2004, 2005, 2010). Trials for which the starting head orientation elicited sufficient ocular counter-rotation to cause impingement of marker arrays on the eye lids were not included in the aVOR gain analyses. Head and eye position and velocity data were passed through a 50-point, zero-phase finite-impulse-response filter with a corner frequency of 100 Hz (to calculate latency of transients) or 40 Hz (to assess dynamics of low frequency sinusoidal data) (Minor et al., 1999). Eye velocity data were inverted prior to calculation of gains and phases, so that an ideal VOR would yield a gain of +1 and phase of 0°. Positive phase lead denotes eye velocity leading head velocity.
Analysis of Transient Acceleration Steps
Data from 4–20 stimulus trials in each direction were averaged after removal of quick phases. This process leaves some response trials with gaps in slow phase data, so cycle-averaged responses were computed point by point for each relative time point in the response, ignoring missing data at any given time point. The start and end of quick phases were defined as the points at which eye acceleration fell outside manually estimated maximum slow phase eye acceleration. For each acceleration step trial, response latency was computed as the time difference between the zero-velocity-intercept times for the eye and head velocities, which were measured using an iterative linear fit method (Migliaccio et al., 2005).
For comparison to studies in other species for which the same analysis convention has been applied (e.g., Minor et al., 1999; Migliaccio et al., 2004, 2010), we parameterized aVOR responses during steps of acceleration by computing the ratio of eye/head acceleration during the constant-head-acceleration segment (GA) and the ratio of eye/head velocity during the velocity plateau (GV) when such a plateau was evident. GA and GV were calculated only for the largest component (e.g., the yaw components of eye and head velocity during yaw stimuli). GA was calculated using the ratio of slopes of the two best-fit lines approximating eye and head velocity versus time during the constant-acceleration segment for each trial. GV was defined as the ratio of the mean eye and head velocity 200-400ms after the onset of head movement.
Axis deviation was defined as the angle in 3D space between the axes of eye and head rotation, with the former defined as the instantaneous velocity vector at the time of peak slow phase 3D eye velocity magnitude prior to the first quick phase (usually during the constant acceleration portion of the transient stimulus).
Analysis of Sinusoidal Rotations
Quick phases were removed from each trace and cycles were overlaid and averaged (10-20 cycles for stimuli >0.05 Hz, 3-5 cycles for lower frequencies) on a point-by-point basis as described above. Quick phases occurring at stimulus frequencies >2Hz were infrequent but distorted most of a cycle, so affected cycles were excluded from the analysis. Gain and phase were computed using the component of eye velocity about the axis of head rotation, with response parameters computed separately for excitatory and inhibitory half-cycles of head rotation. Gain was defined as the eye/head quotient of amplitudes for least-squares best-fit pure sinusoids approximating the eye and head velocity mean traces. Gain and phase were expressed with the convention that unity gain and zero phase imply a perfectly compensatory aVOR, and positive phase implies that eye movements lead head movements.
To evaluate the linearity of the aVOR, we compared mean steady state sinusoidal response aVOR gains at different stimulus amplitudes. At any given frequency, unequal gains at different stimulus amplitudes imply system nonlinearity.
Statistical analysis
We used multiway analysis of variance (ANOVA) with two-factor interactions to analyze the data (Diggle et al., 1994). Independent variables included: animal identifier, eye measured (left or right), rotation plane (yaw, pitch-LED, pitch-RED, roll-NU, roll-ND, LARP-LEDNU, LARP-REDND, RALP-REDNU, RALP-LEDND), and direction of rotation (e.g. positive = leftward for yaw). Additional independent variables for sinusoidal rotations were peak velocity and frequency. Dependent variables were gain and phase for analysis of responses to sinusoids and misalignment angle (between eye and head rotation axes), GA, GV and latency for the analysis of responses to steps of acceleration. All variables were included in the ANOVA initially, and those found insignificant were subsequently removed. Only the interaction affects found to be significant are included in the results. Results are described as mean ± 1 SD.
Results
Static ocular tilt response to changes in head orientation with respect to gravity
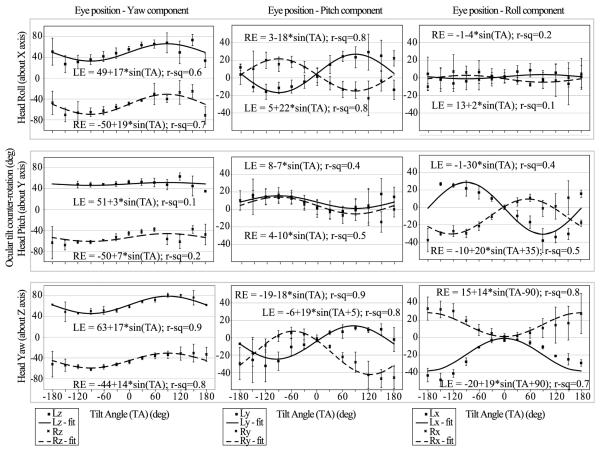
Figure 1 shows the static 3D eye rotational position in head coordinates during head tilts about the roll (AP: X axis), pitch (IA: Y axis) and yaw (SI: Z axis) axes. Tilt responses were not conjugate in eye or head coordinates. Figure 1 includes a regression fit to sinusoidal equations for each component of eye position and the R2 value of the fit. During roll head tilt the eyes move in yaw (in phase with each other) and in pitch (in anti-phase) and both are sinusoidal functions of the tilt angle, whereas the roll component does not change with tilt angle. During pitch head tilt the eyes move in pitch (in phase) and in roll (in anti-phase). (In eye coordinates when the left eye is rotating clockwise the right eye is rotating counter-clockwise and vice versa.) The yaw component of eye position, however, does not change with tilt angle. During yaw head tilt all three components of eye position are a sinusoidal function of tilt angle. The yaw components are in phase, whereas the pitch and roll components are in anti-phase. There is a 90° phase difference between corresponding pitch/yaw and roll eye components, so that when the animal’s nose is pointing directly downwards (at 180° head tilt), the magnitude of the roll eye component is maximal, whereas the magnitudes of the other two components are similar to their starting position magnitudes.
Figure 1.
Static 3D eye rotation during head tilt about the roll (X axis), pitch (Y axis) and yaw (X axis) axes. Both eyes were plotted in head coordinates. Included are regression fits to sinusoidal equations for each component of eye position and the R2 (r-sq) value of the fit. For rotations about all three planes tested the eye movements were disconjugate. The largest tilt response occurred during yaw tilt. The counter-roll gain (eye position Δ / head position Δ) calculated from the component of eye position affected by tilt was maximal in the -30° to +30°, -150° to -180° and 150° to 180° ranges, peaking at ~0.35, and minimal in the 30° to 150° and -30° to -150° ranges, dipping to ~0.22. The only exception to this trend was for the torsional eye component during yaw tilt where counter-roll was maximal (~0.18) in the -120° to -150° and 120° to 150° ranges.
Dependence of aVOR on eye, sense of rotation and head orientation
Before pooling aVOR results measured under different conditions for each axis (e.g., different eyes, senses of rotation, and orientation), we first examined dependence of aVOR response parameters on each of these independent variables.
Conjugacy (aVOR dependence on eye examined)
During yaw, pitch and roll sinusoidal rotations, mean right and left eye responses were conjugate when analyzed in head coordinates (Table 1). During LARP and RALP head rotations, however, responses were disconjugate. The disconjugacy was present at low (0.02-0.1Hz), mid (0.2-1Hz) and high (2-10Hz) frequencies. In a lateral eyed animal, LARP and RALP head rotations result in one eye rotating predominantly about the eye’s torsional axis (i.e., the pupil twists about its line of sight) and the other eye rotating vertically in eye coordinates (i.e., the pupil travels up and down). During LARP and RALP rotations, the eye moving about its torsional axis had ~40% smaller gain than the eye moving about the vertical axis; however, there was no phase difference between left and right eyes.
Table 1.
P values from multiway ANOVA of the VOR gain and phase during sinusoidal rotations. Conjugacy compares gains and phases for left and right eyes. Direction compares gains and phases for positive and negative stimulus half-cycles. Orientation compares gains and phases for nose-up and nose-down starting orientations of the animal. Stimulus frequency is divided into 3 ranges: low (0.02–0.1 Hz), medium (0.2–1 Hz) and high (2–10 Hz). Velocity data, i.e., 20, 50 and 100°/s peak sinusoids, are pooled. Gains were disconjugate during LARP and RALP rotations because the eye rotating torsionally in eye coordinates had a smaller gain than the eye rotating vertically in eye coordinates. Orientation affected the gain and phase probably because during nose-down orientations (LARP–REDND and RALP-LEDND) the quality of eye movement data was low due to lacrimation and a tendency of eyelids to partly close. Bold P values denote a statistically significant difference. LARP=left-anterior/right-posterior; RALP=right-anterior/left-posterior; LED/RED = left/right ear down; ND = nose down.
| Frequency range, Hz |
YAW | LARP | RALP | PITCH | ROLL | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Gain | Phase | Gain | Phase | Gain | Phase | Gain | Phase | Gain | Phase | ||
| Conjugacy | 0.02–0.1 | 0.56 | 0.70 | <0.01 | 0.55 | <0.01 | 0.14 | 0.49 | 0.21 | 0.76 | 0.56 |
| 0.2–1 | 0.15 | 0.37 | <0.01 | 0.79 | <0.01 | 0.09 | 0.18 | 0.60 | 0.33 | 0.11 | |
| 2–10 | 0.16 | 0.13 | <0.01 | 0.12 | <0.01 | 0.16 | 0.12 | 0.58 | 0.63 | 0.47 | |
| Direction | 0.02–0.1 | 0.55 | 0.31 | 0.21 | 0.13 | 0.34 | 0.25 | 0.16 | 0.06 | 0.41 | 0.98 |
| 0.2–1 | 0.30 | 0.31 | 0.32 | 0.12 | 0.25 | 0.04 | <0.01 | <0.01 | 0.23 | 0.09 | |
| 2–10 | 0.70 | 0.13 | 0.68 | 0.75 | 0.68 | 0.02 | 0.86 | 0.55 | 0.31 | 0.42 | |
| Orientation | 0.02–0.1 | -- | -- | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | 0.94 | 0.03 | <0.01 |
| 0.2–1 | -- | -- | 0.04 | <0.01 | <0.01 | <0.01 | <0.01 | 0.60 | 0.50 | 0.18 | |
| 2–10 | -- | -- | <0.01 | 0.05 | <0.01 | 0.32 | 0.98 | 0.81 | 0.40 | 0.32 | |
During steps of acceleration, left and right eye responses were generally conjugate (Table 2), except that during pitch rotations, GA and latency were ~40% smaller for the right eye than for the left eye.
Table 2.
P values from multiway ANOVA of the GA, GV and latency during steps of acceleration to a velocity plateau. In contrast to sinusoidal rotations, GA, GV and latency had no significant dependence on left vs right eye, or (for a given axis) the sense of rotation or head orientation. GA is the ratio of eye and head acceleration about a common axis during the constant-acceleration part of the stimulus after the onset of head rotation. GV is the ratio of eye and head velocity during the plateau of the head velocity 200-400 ms after onset of head rotation. Bold P values denote a statistically significant difference.
| YAW | LARP | RALP | PITCH | ROLL | ||
|---|---|---|---|---|---|---|
| Conjugacy | GA | 0.70 | 0.04 | 0.47 | 0.02 | 0.17 |
| GV | 0.22 | 0.36 | 0.50 | 0.86 | 0.56 | |
| Latency | 0.19 | 0.59 | 0.58 | 0.02 | 0.63 | |
| Direction | GA | 0.67 | 1.00 | 0.38 | 0.70 | 0.27 |
| GV | 0.46 | 0.47 | 0.20 | 0.06 | 0.64 | |
| Latency | 0.36 | <0.01 | 0.76 | 0.16 | 0.77 | |
| Orientatio | GA | -- | 0.68 | 0.39 | 0.32 | 0.58 |
| GV | -- | 0.08 | 0.08 | 0.10 | 0.42 | |
| Latency | -- | 0.71 | 0.25 | 0.25 | 0.39 | |
Directional asymmetry (aVOR dependence on rotation sense about a given axis)
During sinusoidal and transient rotations about any given axis, direction of rotation did not significantly affect aVOR parameters (gain, phase, GA, GV and latency). The two exceptions to this finding occurred during 0.2–1 Hz sinusoidal rotations in the pitch plane (gain and phase) and during transient rotations in the LARP plane (latency) (See Tables 1 and 2).
There was a naso-temporal asymmetry during 0.2-1 Hz sinusoidal rotations in the yaw plane (ANOVA: eye*direction interaction effect on gain: P=0.04), such that the eye moving nasally (adducting) had ~8% higher gain than the eye moving temporally (abducting). This interaction effect was largest during high peak-velocity (100°/s) sinusoids (gain: P=0.02). There was a similar naso- temporal asymmetry during transient yaw rotations on the constant velocity gain GV (P = 0.02).
During 0.2-1 Hz sinusoidal rotations in the LARP, RALP and roll planes, there was a supero-inferior eye movement asymmetry (ANOVA: eye*direction interaction effect on gain: P <0.01, P =0.02, P < 0.01, for LARP, RALP and roll, respectively), such that the eye moving inferiorly (downward in eye coordinates) had a 3-14% higher gain than the eye moving superiorly (upward in eye coordinates).
aVOR dependence on head orientation
During LARP, RALP and pitch sinusoidal rotations, the animal’s orientation affected the aVOR gain and phase across all frequencies (Table 1). For LARP head rotations, aVOR gain and phase was respectively 14.6% higher and 22.54% higher for LEDNU than for the REDND orientation. For RALP head rotations, aVOR gain and phase was respectively 6.4% higher and 20.2% higher for REDNU than for the LEDND orientation and for pitch head rotations, aVOR gain and phase was respectively 8.4% higher and 6.3% higher for LED than for the RED orientation. Whenever the animal was in the ND orientation, eye position data were generally noisier (due to accumulation of tears and relative intolerance of the animal for inverted positioning), so gains and phases were calculated on fewer data points and across fewer cycles. Consequently, we did not pool the sinusoidal LARP-REDND and RALP-LEDND data into our summary data. Orientation had no significant effect during transient rotations (Table 2), probably because the time to complete those sessions was relatively brief.
aVOR responses to steps of head rotational acceleration
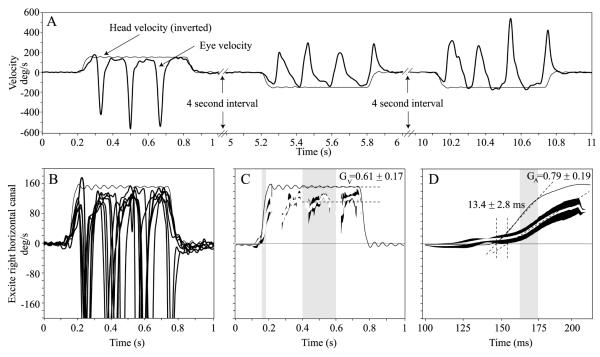
Figure 2A shows raw responses for leftward and rightward steps of yaw rotational acceleration (3000°/s2 to plateau velocity of 150°/s). In figure 2B eye velocity responses from 6 rightward stimulus repetitions are displayed as superimposed traces. The initial response consisted of an eye movement partly compensatory for head velocity (i.e., opposite the direction of head movement at less than the same acceleration) followed by a quick phase that reset the eye toward the centre of the oculomotor range. Successive slow and quick phases of nystagmus followed. Figure 2B and 2C show responses after quick phases have been removed, along with best-fit lines used to compute GA, GV and latency.
Figure 2.
(A) Raw traces of horizontal eye velocity (thick black trace) during leftward and rightward yaw head rotation impulses (accelerations at 3000°/s2 reaching a peak velocity of 150°/s). The head stimuli (thin black trace) were delivered semi-randomly. The head velocity trace was inverted for comparison to eye velocity. (B) Horizontal component of 3D eye and head rotational velocity during multiple rightward yaw head rotation impulses in one mouse. The slow phase eye velocity response is almost perfectly compensatory (opposite in direction to head velocity) during the first ~60 ms after head rotation onset. Once the eye reaches the end of its oculomotor range, a quick phase, which is opposite in direction to the slow phase, brings the eye back to the centre of the oculomotor range. This cycle repeats for the duration of the transient. (C) Quick phases have been removed from the leftmost panel data leaving only the slow phases for analysis. Mean slow phase eye and head velocity traces (Mean ± 1SE) are shown. The velocity gain, GV, is calculated by dividing the mean slow phase eye velocity by the mean head velocity during 200 ms of the velocity plateau shown in grey. (D) The first 200ms of the middle panel data are used to calculate the acceleration gain, GA, which is the ratio of the eye to head velocity trace slopes during the linear part of the acceleration portion of the transient (gray region). Intersections of the line fits used to calculate GA with the zero velocity axis are used to calculate latency.
Table 3 summarizes GA, GV and latency during yaw, pitch, roll, LARP and RALP rotations. GA values were similar for all planes of rotation (ANOVA: P = 0.26) and directions (ANOVA: P = 0.35). GV values during pitch, roll, LARP and RALP head rotations were similar (ANOVA: P = 0.10); however, GV was larger during yaw head rotations (0.76) than for all other axes (ANOVA: P<0.01). To obtain the values in Table 3, eye movement data were pooled between the left and right eye after conversion to head coordinates. This was straightforward for yaw head rotations, because we only performed measurements with the animal upright. We converted each eye’s data into head coordinates, then pooled both eyes for leftward head rotations (and separately pooled both eyes for rightward head rotations). After finding these two pooled sets insignificantly different, we pooled all yaw responses. We analyzed LARP and RALP data analogously. For pitch and roll head rotations, the picture was more complex, because we tested with the head in two orientations (pitch-LED and pitch-RED, roll-NU and roll-ND). We pooled responses in head coordinates for stimuli that excited the same canals (e.g. responses to all positive pitch stimuli moving the nose toward the chin were pooled). Finding no significant difference between the two eyes, we then pooled across eyes before subsequent analysis.
Table 3.
Response characteristics (mean ± SD) for steps of acceleration about each axis, pooled across both eyes, head orientation, and rotation direction about the specified axis. See Table 2 caption for definitions. Asterisk denotes significant difference for yaw GV and latency compared to all other axes of head rotation; no other significant difference was noted.
| Axis | GA | GV | Latency, ms |
|---|---|---|---|
| YAW | 0.47 ± 0.03 | 0.76 ± 0.08* | 10.1 ± 4.1* |
| PITCH | 0.40 ± 0.13 | 0.48 ± 0.12 | 16.0 ± 6.7 |
| ROLL | 0.42 ± 0.12 | 0.48 ± 0.08 | 17.2 ± 5.3 |
| LARP | 0.52 ± 0.15 | 0.53 ± 0.14 | 13.2 ± 9.9 |
| RALP | 0.46 ± 0.14 | 0.53 ± 0.09 | 14.4 ± 4.4 |
The latency of aVOR responses to 3000°/s2 steps of acceleration in the yaw, pitch, roll, LARP and RALP planes was measured in all animals (Table 3). Latencies for pitch, roll, LARP and RALP head rotations were similar (ANOVA: P = 0.26); however, latency was shorter during yaw head rotations (10.1 ms) than for all other axes (ANOVA: P<0.01). Latency data were pooled across animals, yielding a mean ± SD of 14.2 ± 2.7 ms.
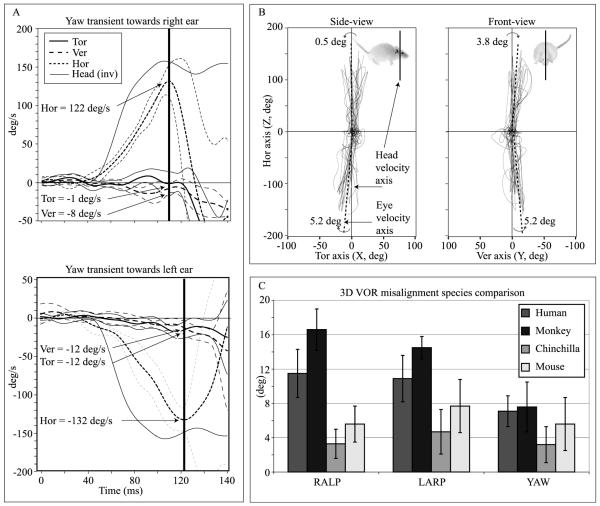
Figure 3 illustrates the extent of misalignment for responses to steps of yaw acceleration for one mouse, along with mean axis deviation for 12 mice and comparison data for chinchillas (Migliaccio et al., 2010), squirrel monkeys (Migliaccio et al., 2004) and humans (Cremer et al., 1998). There was no significant difference in misalignment between animals (ANOVA: P=0.07) or between head rotation axes (ANOVA: P=0.27). The mean misalignment pooled across animals, eyes and senses of rotation was 5.4 ± 2.2°, 7.7 ± 3.3°, 5.6 ± 3.2°, 5.5 ± 2.1° and 6.5 ± 3.9°, for yaw, LARP, RALP, pitch and roll transient rotations, respectively. Pooled across all axes of rotation, the mean misalignment was 6.1 ± 3.1°. Compared to the 3D aVOR of primates, the mouse 3D aVOR maintained better eye-head alignment for all stimuli. However, compared to the chinchilla, the mouse 3D aVOR misalignment was ~60% larger. There were differences in alignment between the four species we compared (ANOVA: monkey versus human, P = 0.02; mouse versus chinchilla, P = 0.005), which became more significant when we compared the pooled human and monkey data versus the pooled chinchilla and mouse data (ANOVA: P<0.0001).
Figure 3.
(A) Calculation of misalignment angle for rightward and leftward yaw head rotations. Each component of the mean peak eye velocity vector prior to the first quick phase was used to calculate the angle between the eye and head velocity vectors. (B) Side- and front-views of the instantaneous eye velocity vectors, which are plotted as 3D points (with horizontal, vertical and torsional components) in head coordinate space. (C) Mean ± 1SD axis of eye rotation for the mouse (n=12), chinchilla (n=11, Migliaccio et al., 2010), squirrel monkey (n=3, unpublished data from Migliaccio et al., 2004) and human (n=7, Cremer et al., 1998). The mouse rotational stimulus was the same as the chinchilla and squirrel monkey stimulus and similar to the human stimulus. Compared to primates, the mouse 3D aVOR maintained better alignment of the eye and head rotation axes for all stimuli, but it was larger than misalignment reported for chinchillas.
aVOR responses to sinusoidal head rotations
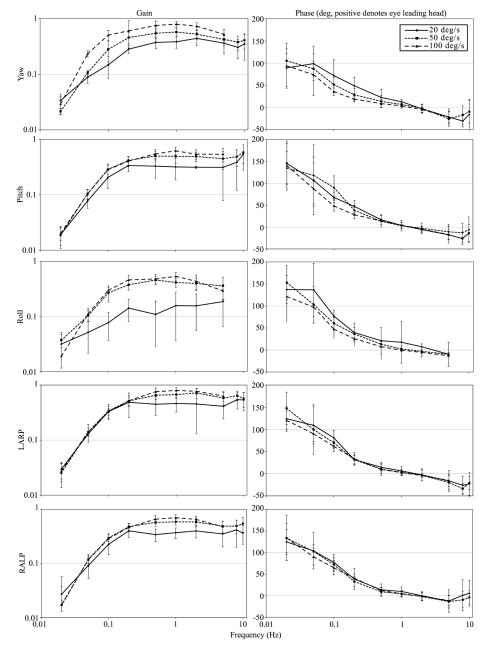
Figure 4 shows mean gain and phase for responses to sinusoidal rotations at 0.02-10Hz, and peak velocity 20, 50 and 100°/s in the yaw, pitch, roll, LARP and RALP planes for all animals. The gain of the aVOR increased with stimulus velocity (ANOVA: P<0.05), indicating nonlinearity in the system. The aVOR gain also increased with stimulus frequency (ANOVA: P<0.05). During yaw rotations the aVOR gain peaked at 2 Hz and then decreased by ~20% at higher frequencies. No such decrease was apparent for pitch, roll, LARP and RALP rotations. The aVOR phase became more negative (the eye leading head less) with increasing stimulus frequency (ANOVA: P<0.05).
Figure 4.
Gain and phase plots of responses to 0.02-10 Hz rotations given with vision occluded, for ± 20, 50 and 100°/s peak, pooled across all mice tested. Data were pooled separately for yaw, pitch, roll, LARP and RALP axes. Error bars indicate 1 SD.
Discussion
The aims of this study were (1) to characterize the 3D aVOR of C57BL6 mice during static tilt testing, sinusoidal and high-acceleration rotations and (2) to compare the 3D aVOR of this species with that of another lateral-eyed mammal with afoveate retinae (chinchilla) and two primate species with forward eye orientation and retinal foveae (human and squirrel monkey). Noting that visual acuity in mice is poor compared to chinchillas and even worse compared to primates, we hypothesized that the mouse 3D aVOR would be relatively low in gain (eye-velocity/head-velocity) compared to other species and would fall off for combinations of head rotation peak velocity and frequency for which peak-to-peak position changes fall below the minimum resolvable angle by mice. We also predicted that, like the lateral-eyed chinchilla, eye rotations generated by the mouse 3D aVOR would be conjugate, isotropic (aVOR gain independent of head rotation axis) and better aligned with the axis of head rotation than the 3D aVOR or primates (Migliaccio, et al., 2010). We also sought to determine whether aVOR gain varies significantly with stimulus amplitude, as noted in squirrel monkeys (Minor et al., 1999; Migliaccio et al., 2004) and chinchillas (Migliaccio et al., 2010) but not in humans (Aw et al., 1996).
Angular vestibulo-ocular reflex gain changes with frequency and velocity in C57BL6 mice
Like the aVOR in all mammalian species examined so far (Ramprashad et al., 1984), mice exhibit a high-pass frequency response with respect to head rotational velocity, as shown in Figure 4. However, the mouse aVOR’s performance at different frequencies relative to other species is interesting, because it supports the notion that differences in aVOR gain and frequency dependence across species depend on static visual acuity.
During static tilt testing the counter-roll response of the mouse was robust with counter-roll gain peaking to ~0.35. The counter-roll range was large, typically ~40°. A previous study that measured 2D eye position during ± 180° pitch and roll tilts in C57BL6 mice reported counter-roll ranges for tilts of ~40° during pitch and 40-60° during roll (Oommen and Stahl, 2007). This is in contrast to chinchillas (which like mice are lateral-eyed and have afoveate retinae), which exhibit a maximal counter-roll gain of ~0.16 and typical range of ~20° (Migliaccio et al., 2010). These results also contrast with monkey (Cabungcal et al., 2001) and human studies (Bockisch et al., 2001), which report maximal counter-roll gains of ~ 0.12 with typical ranges of ~13° and ~10°, respectively.
During sinusoidal rotations with peak velocity 100°/s, aVOR gain increased from ~0 at 0.02 Hz to ~0.8 at 2 Hz for all planes of rotation tested. From 2–10 Hz, aVOR gain remained unchanged or decreased. A decrease in aVOR gain above 2 Hz was also observed for the 20°/s and 50°/s sinusoidal data; however, the decrease was most prominent for 100°/s peak stimuli. The decrease in gain above 2 Hz was especially evident during yaw rotations. The greatest quantity and best quality of sinusoidal data was obtained during yaw rotations, because in this orientation both eyes were in the primary/neutral position (no counter-roll); were in full view for the entire cycle (no eye lid interference with marker imaging); and had minimal tearing. For these reasons, yaw data are particularly of interest.
The horizontal sinusoidal gains that we measured were within the lower end of the range compared to other mouse VOR studies (Stahl et al., 2004; Beraneck et al., 2008). A direct comparison with gains from Stahl et al. (2004) are problematic because of large differences in the stimulus parameters, however, we can compare our data during sinusoidal horizontal rotations with peak velocity 50°/s with those from Beraneck et al., (2008) collected at 0.2, 0.5, 1 and 2 Hz at peak velocity 40°/s. There were no significant differences in gain between the two studies at 0.2, 0.5 and 1 Hz (P = 0.49, P = 0.09, P = 0.08), however, there was a difference at 2 Hz (P = 0.02). At higher velocities (100°/s and 1 Hz) our mean VOR gains ranged from 0.63 - 0.82, which was similar to that reported previously (Stahl et al., 2004; Beraneck et al., 2008).
During transient steps of acceleration, the acceleration gain GA was ~0.5 for all planes of rotation tested. This is in contrast to the gains observed in chinchillas (Migliaccio et al., 2010), squirrel monkeys (Migliaccio et al., 2004) and humans (Cremer et al., 1998), which all have GA ≈ 1. The velocity gain GV was ~0.5 and is similar to that observed in chinchillas (Migliaccio et al., 2010) and squirrel monkeys (Migliaccio et al., 2004).
In summary, the C57BL6 mouse has a robust static counter-roll that is about twice as large in gain and range than that reported in primates and chinchillas, a strong optokinetic response at low frequencies and velocities (<1 Hz and <10°/s, e.g., van Alphen et al., 2001), a medium frequency (0.02–10 Hz sinusoids) aVOR with gain comparable to that found in those other species, and a high frequency aVOR (during steps of acceleration, which have spectral frequency content up to 20 Hz) with gain that is about half as large as that reported in both primates and chinchillas. Yaw sinusoidal data reveal a decrease in gain for stimulus frequencies above ~2 Hz. Taken together, the static, sinusoidal and transient data suggest that the mouse aVOR performs relatively well (compared to other species) for low-frequency, high-amplitude head movements and relatively poorly for high-frequency, low-amplitude head movements.
During periods of exploratory activity, mice produce head movements with frequency contents up 20 Hz, velocities up to 400°/s and accelerations up to 10,000°/s2. However, the majority of head movements are below 5 Hz, 200°/s and 5,000°/s2 (Beraneck et al., 2008). During high-velocity, high-acceleration head rotations the other (than VOR) vision / head stabilizing mechanism is the vestibulo-collic reflex (VCR), which has a gain of 0.1-0.2 (during high-acceleration, 200°/s velocity steps, Takemura and King, 2005). So if the mouse head naturally moves at high-frequencies enough to develop a robust VCR, then why does the VOR become less compensatory at higher frequencies?
Visual acuity is one notable difference between mice and primates that could change the characteristics of the mouse 3D aVOR. Humans and monkeys possess high visual acuity surpassed only by large raptors such as eagles. Behavioral tests have shown that the maximum visual acuity is 50-77 cycle/deg in humans and 40-53 cycle/deg in macaques and squirrel monkeys (Kirk and Kay, 2004). In contrast, mice have very poor visual acuity (0.3-0.6 cycles/deg; Gianfranceschi et al., 1999; Prusky et al., 2000; Wong and Brown, 2006; Prusky and Douglas, 2004) nearly two orders of magnitude worse than primates and also worse than that of rabbits (3.4 cycle/deg; Van, 1967) and rats (1.3 cycle/deg; Hughes, 1979). Several studies in the C57Bl6 mouse have shown that various factors control visual acuity, such as visual contrast (Tabata et al., 2010), luminance (Schmucker et al., 2005) and input from the visual cortex (during Visual Water Tracking, but not Optokinetic testing; see Prusky and Douglas, 2004; Douglas et al., 2005; Prusky et al., 2006). Acuity estimates from the Visual Water Tracking task in the C57Bl6 range from 0.375 to 0.6 cycle/deg (Wong and Brown, 2004; Prusky et al., 2000). Acuity estimates from optokinetic testing peak at ~0.4 cycle/deg (Prusky et al., 2004) and motion coherence thresholds (which is another measure of acuity: 0 to 100% threshold indicates good to poor visual motion discrimination) are ~25% in mice (and rats), which is about 2-3 times higher than in humans (Douglas et al., 2006). Lower visual acuity could lead to a greater tolerance for retinal image position error and slip, because only large changes in retinal image position can be detected. Analogously, lower static visual acuity probably results in reduced adaptive drive to maintain a perfectly compensatory 3D aVOR, particularly for high frequency, low peak velocity sinusoidal head rotations for which the peak to peak travel of retinal image position without any aVOR would fall below the mouse’s minimum resolvable angle. (For example, the peak-to-peak positional amplitude of a 20°/s peak, 5 Hz movement is only 1.3°.) In mice, visual feedback is essential for VOR adaptation and compensation after peripheral vestibular injury (Stahl et al., 2006; Beraneck et al., 2008). While static visual acuity is only one characteristic by which mice differ from chinchillas, monkeys and humans, our findings support an association between static visual acuity and aVOR gain, particularly for high frequency stimuli.
VOR isotropy and 3D alignment of eye and head rotation axes
We found that the 3D aVOR in C57BL6 mice is essentially isotropic (i.e., similar in gain for every direction of head rotation), much like chinchillas, which are also lateral-eyed mammals without retinal foveae (Migliaccio, et al., 2010). Accordingly, both of these lateral-eyed species have well-aligned 3D aVOR (overall mean misalignment pooled across all axes of 6.1 ± 1.0° in mice and 3.8 ± 0.7° in chinchillas). This result is consistent with a previous C57BL6 study showing that the optokinetic response during sinusoidal rotations (0.1-1Hz, amplitude 5°) of a virtual sphere was isotropic (van Alphen et al., 2010). In addition, it has been shown that the spatial distribution of optokinetic sensitivity is also isotropic (although it varies with distance away from ocular primary position) (Shimizu et al., 2010). In contrast, the 3D aVOR of primates is markedly anisotropic, with gain during roll head rotations significantly lower than responses for any other direction of head movement (Cremer et al., 1998, Migliaccio et al., 2004, 2006; Aw et al. 1996; Crawford & Vilis 1991b). This leads to aVOR misalignment in primates for any head rotation other than a pure yaw, pitch or roll. For example, 10-15° of eye-head axis misalignment accrues during LARP and RALP head rotations in squirrel monkeys and humans (Cremer et al., 1998, Migliaccio et al., 2004, 2006, 2010).
The reasons for primates’ relatively low roll gain and large misalignment compared to chinchillas and mice are not clear, but they might include (1) a reduced adaptive drive (due to the fact that a deficient roll aVOR would not move a distant target’s image off either eye’s fovea when the eyes are near their resting position); (2) limitations imposed by extraocular muscle mechanics; or (3) a compromise to avoid diplopia during stereopsis of a nearby target such as a tool in one’s hands (Migliaccio, et al., 2010).
Conclusion
The mouse 3D aVOR is partially compensatory, isotropic (similar gain in all directions) and nonlinear (increasing gain with increasing stimulus amplitude). Although it exhibits the high-pass characteristic typical of aVOR dynamics in all other mammals tested so far, its frequency dependence also includes a modest drop at high frequencies, most notably for yaw head rotations. This fall-off could be due in part to the mouse’s relatively poor static visual acuity, since maintaining a perfect 3D aVOR should be unnecessary for head movements that, in the absence of any aVOR, would not displace a target’s retinal image more than the minimum amount the animal could possibly detect. Relatively greater 3D gain isotropy in lateral-eyed species without retinal foveae (e.g., mice and chinchillas in the present study) compared to forward-eyed species with retinal foveae (e.g., squirrel monkeys and humans) suggests that the parallel resting optic axes and/or radially symmetric retinal foveae of primates underlie their characteristically low 3D aVOR gain for roll head rotations.
Acknowledgements
We are grateful to Dr. Hamish G. MacDougall (Sydney University), who helped create the large rodent version of the VOG system. Supported by a National Health and Medical Research Council (Australia) Biomedical Career Development Award and a University of New South Wales (Australia) Faculty Research Grant to A.A. Migliaccio. Supported by the National Institute on Deafness and other Communication Disorders (USA): RO3-DC007346 to A.A. Migliaccio; R01-DC002390, R01-DC009255 and K08-DC006216 to C.C. Della Santina.
References
- 1.Aleisa M, Zeitouni AG, Cullen KE. Vestibular compensation after unilateral labyrinthectomy: normal versus cerebellar dysfunctional mice. J Otolaryngol. 2007;36:315–21. [PubMed] [Google Scholar]
- 2.Bartolome MV, del CE, Lopez LM, Carricondo F, Poch-Broto J, Gil-Loyzaga P. Effects of aging on C57BL6J mice: An electrophysiological and morphological study. Adv Otorhinolaryngol. 2002;59:106–111. doi: 10.1159/000059247. [DOI] [PubMed] [Google Scholar]
- 3.Beraneck M, Cullen KE. Activity of vestibular nuclei neurons during vestibular and optokinetic stimulation in the alert mouse. J Neurophysiol. 2007;98:1549–65. doi: 10.1152/jn.00590.2007. [DOI] [PubMed] [Google Scholar]
- 4.Beraneck M, McKee JL, Aleisa M, Cullen KE. Asymmetric recovery in cerebellar-deficient mice following unilateral labyrinthectomy. J Neurophysiol. 2008;100:945–58. doi: 10.1152/jn.90319.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bockisch CJ, Haslwanter T. Three-dimensional eye position during static roll and pitch in humans. Vision Res. 2001;41:2127–37. doi: 10.1016/s0042-6989(01)00094-3. [DOI] [PubMed] [Google Scholar]
- 6.Cabungcal JH, Misslisch H, Scherberger H, Hepp K, Hess BJM. Effect of light sleep on three-dimensional eye position in static roll and pitch. Vision Research. 2001;41:495–505. doi: 10.1016/s0042-6989(00)00279-0. [DOI] [PubMed] [Google Scholar]
- 7.Calabrese DR, Hullar TE. Planar relationships of the semicircular canals in two strains of mice. JARO. 2006;7:151–9. doi: 10.1007/s10162-006-0031-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cremer PD, Halmagyi GM, Aw ST, Curthoys IS, McGarvie LA, Todd MJ, Black RA, Hannigan IP. Semicircular canal plane head impulses detect absent function of individual semicircular canals. Brain. 1998;121:699–716. doi: 10.1093/brain/121.4.699. [DOI] [PubMed] [Google Scholar]
- 9.Diggle PJ, Liang KY, Zeger SL. Analysis of Longitudinal Data. Oxford University Press; New York: 1994. [Google Scholar]
- 10.Douglas RM, Alam NM, Silver BD, McGill TJ, Tschetter WW, Prusky GT. Independent visual threshold measurements in the two eyes of freely moving rats and mice using a virtual-reality optokinetic system. Vis Neurosci. 2005;22:677–84. doi: 10.1017/S0952523805225166. [DOI] [PubMed] [Google Scholar]
- 11.Douglas RM, Neve A, Quittenbaum JP, Alam NM, Prusky GT. Perception of visual motion coherence by rats and mice. Vision Res. 2006;46:2842–7. doi: 10.1016/j.visres.2006.02.025. [DOI] [PubMed] [Google Scholar]
- 12.Gianfranceschi L, Fiorentini A, Maffei L. Behavioral visual acuity of wild type and bcl2 transgenic mouse. Vision Res. 1999;39:569–574. doi: 10.1016/s0042-6989(98)00169-2. [DOI] [PubMed] [Google Scholar]
- 13.Heesy CP. On the relationship between orbit orientation and binocular visual field overlap in mammals. The Anatomical Record Part A: Discoveries in Molecular, Cellular, and Evolutionary Biology. 2004;281A:1104–1110. doi: 10.1002/ar.a.20116. [DOI] [PubMed] [Google Scholar]
- 14.Jones SM, Johnson KR, Yu H, Erway LC, Alagramam KN, Pollak N, Jones TA. A quantitative survey of gravity receptor function in mutant mouse strains. JARO. 2005;6:297–310. doi: 10.1007/s10162-005-0009-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Katoh A, Kitazawa H, Itohara S, Nagao S. Dynamic characteristics and adaptability of mouse vestibulo-ocular and optokinetic response eye movements and the role of the flocculo-olivary system revealed by chemical lesions. Proc. Natl. Acad. Sci. 1998;95:7705–7710. doi: 10.1073/pnas.95.13.7705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Katoh A, Jindal JA, Raymond JL. Motor deficits in homozygous and heterozygous p/q-type calcium channel mutants. J Neurophysiol. 2007;97:1280–7. doi: 10.1152/jn.00322.2006. [DOI] [PubMed] [Google Scholar]
- 17.Kaufman GD. Video-oculography in the gerbil. Brain Res. 2002;958:472–87. doi: 10.1016/s0006-8993(02)03557-6. [DOI] [PubMed] [Google Scholar]
- 18.Harrod CG, Baker JF. The vestibulo ocular reflex (VOR) in otoconia deficient head tilt (het) mutant mice versus wild type C57BL6 mice. Brain Res. 2003;972:75–83. doi: 10.1016/s0006-8993(03)02505-8. [DOI] [PubMed] [Google Scholar]
- 19.Hequembourg S, Liberman MC. Spiral ligament pathology: A major aspect of age-related cochlear degeneration in C57BL6 mice. JARO. 2001;2:118–129. doi: 10.1007/s101620010075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mangini N, Vanable JJ, Williams M, Pinto L. The optokinetic nystagmus and ocular pigmentation of hypopigmented mouse mutants. J. Comp. Neurol. 1985;241:191–209. doi: 10.1002/cne.902410207. [DOI] [PubMed] [Google Scholar]
- 21.McFadden SL, Ding D, Salvi R. Anatomical, metabolic and genetic aspects of age-related hearing loss in mice. Audiology. 2001;40:313–321. [PubMed] [Google Scholar]
- 22.Migliaccio AA, Schubert MC, Jiradejvong P, Lasker DM, Clendaniel RA, Minor LB. The three-dimensional vestibulo-ocular reflex evoked by high-acceleration rotations in the squirrel monkey. Exp Brain Res. 2004;159:433–46. doi: 10.1007/s00221-004-1974-2. [DOI] [PubMed] [Google Scholar]
- 23.Migliaccio AA, Macdougall HG, Minor LB, Della Santina CC. Inexpensive system for real-time 3-dimensional video-oculography using a fluorescent marker array. J Neurosci Methods. 2005;143:141–50. doi: 10.1016/j.jneumeth.2004.09.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Migliaccio AA, Minor LB, Della Santina CC. Adaptation of the vestibulo-ocular reflex for forward-eyed foveate vision. J Physiol. 2010;588:3855–67. doi: 10.1113/jphysiol.2010.196287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Oommen BS, Stahl JS. Eye orientation during static tilts and its relationship to spontaneous head pitch in the laboratory mouse. Brain Res. 2008;1193:57–66. doi: 10.1016/j.brainres.2007.11.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Prusky GT, West PWR, Douglas RM. Behavioral assessment of visual acuity in mice and rats. Vision Res. 2000;40:2201–2209. doi: 10.1016/s0042-6989(00)00081-x. [DOI] [PubMed] [Google Scholar]
- 27.Prusky GT, Alam NM, Beekman S, Douglas RM. Rapid quantification of adult and developing mouse spatial vision using a virtual optomotor system. Invest Ophthalmol Vis Sci. 2004;45:4611–6. doi: 10.1167/iovs.04-0541. [DOI] [PubMed] [Google Scholar]
- 28.Prusky GT, Douglas RM. Characterization of mouse cortical spatial vision. Vision Res. 2004;44:3411–8. doi: 10.1016/j.visres.2004.09.001. [DOI] [PubMed] [Google Scholar]
- 29.Prusky GT, Alam NM, Douglas RM. Enhancement of vision by monocular deprivation in adult mice. J Neurosci. 2006;26:11554–61. doi: 10.1523/JNEUROSCI.3396-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ramprashad F, Landolt JP, Money KE, Laufer J. Dimensional analysis and dynamic response characterization of mammalian peripheral vestibular structures. Am J Anat. 1984;169:295–313. doi: 10.1002/aja.1001690306. [DOI] [PubMed] [Google Scholar]
- 31.Schmucker C, Schaeffel F. A paraxial schematic eye model for the growing C57BL6 mouse. Vision Res. 2004;44:1857–67. doi: 10.1016/j.visres.2004.03.011. [DOI] [PubMed] [Google Scholar]
- 32.Schmucker C, Seeliger M, Humphries P, Biel M, Schaeffel F. Grating acuity at different luminances in wild-type mice and in mice lacking rod or cone function. Invest Ophthalmol Vis Sci. 2005;46:398–407. doi: 10.1167/iovs.04-0959. [DOI] [PubMed] [Google Scholar]
- 33.Shimizu N, Tabata H, Wada Y, Sugita Y, Yamanaka T, Hosoi H, Kawano K. Distribution of optokinetic sensitivity across the retina of mice in relation to eye orientation. Neuroscience. 2010;168:200–8. doi: 10.1016/j.neuroscience.2010.03.025. [DOI] [PubMed] [Google Scholar]
- 34.Spongr VP, Flood DG, Frisina RD, Salvi RJ. Quantitative measures of hair cell loss in CBA and C57BL6 mice throughout their life spans. JASA. 1997;101:3546–3553. doi: 10.1121/1.418315. [DOI] [PubMed] [Google Scholar]
- 35.Stahl JS, van Alphen AM, De Zeeuw CI. A comparison of video and magnetic search coil recordings of mouse eye movements. J Neurosci Methods. 2000;99:101–10. doi: 10.1016/s0165-0270(00)00218-1. [DOI] [PubMed] [Google Scholar]
- 36.Stahl JS. Eye movements of the murine P/Q calcium channel mutant rocker, and the impact of aging. J Neurophysiol. 2004;91:2066–78. doi: 10.1152/jn.01068.2003. [DOI] [PubMed] [Google Scholar]
- 37.Stahl JS, James RA, Oommen BS, Hoebeek FE, De Zeeuw CI. Eye movements of the murine P/Q calcium channel mutant tottering, and the impact of aging. J Neurophysiol. 2006;95:1588–607. doi: 10.1152/jn.00318.2005. [DOI] [PubMed] [Google Scholar]
- 38.Tabata H, Shimizu N, Wada Y, Miura K, Kawano K. Initiation of the optokinetic response (OKR) in mice. J Vis. 2010;10:13–1. doi: 10.1167/10.1.13. [DOI] [PubMed] [Google Scholar]
- 39.Takemura K, King WM. Vestibulo-collic reflex (VCR) in mice. Exp Brain Res. 2005;167:103–7. doi: 10.1007/s00221-005-0030-1. [DOI] [PubMed] [Google Scholar]
- 40.van Alphen AM, Stahl JS, De Zeeuw CI. The dynamic characteristics of the mouse horizontal vestibulo-ocular and optokinetic response. Brain Res. 2001;890:296–305. doi: 10.1016/s0006-8993(00)03180-2. [DOI] [PubMed] [Google Scholar]
- 41.van Alphen B, Winkelman BH, Frens MA. Three-dimensional optokinetic eye movements in the C57BL/6J mouse. Invest Ophthalmol Vis Sci. 2010;51:623–30. doi: 10.1167/iovs.09-4072. [DOI] [PubMed] [Google Scholar]
- 42.Walker MF, Zee DS. Rectified cross-axis adaptation of the vestibulo-ocular reflex in rhesus monkey. Ann N Y Acad Sci. 2002;956:543–5. doi: 10.1111/j.1749-6632.2002.tb02877.x. [DOI] [PubMed] [Google Scholar]
- 43.Walker MF, Zee DS. Cerebellar disease alters the axis of the high-acceleration vestibuloocular reflex. J Neurophysiol. 2005;94:3417–29. doi: 10.1152/jn.00375.2005. [DOI] [PubMed] [Google Scholar]
- 44.Walls GL. The Vertebrate Eye and its Adaptive Radiation. Hafner Publishing; New York: 1963. [Google Scholar]
- 45.Wong AA, Brown RE. Visual detection, pattern discrimination and visual acuity in 14 strains of mice. Genes Brain Behav. 2006;5(5):389–403. doi: 10.1111/j.1601-183X.2005.00173.x. [DOI] [PubMed] [Google Scholar]