Virtual Labyrinth model of vestibular afferent excitation via implanted electrodes – Validation and application to design of a multichannel vestibular prosthesis

Abstract

To facilitate design of a multichannel vestibular prosthesis that can restore sensation to individuals with bilateral loss of vestibular hair cell function, we created a virtual labyrinth model. Model geometry was generated through 3-dimensional (3D) reconstruction of microMRI and microCT scans of normal chinchillas (Chinchilla lanigera) acquired with 30–48 μm and 12 μm voxels, respectively. Virtual electrodes were positioned based on anatomic landmarks, and the extracellular potential field during a current pulse was computed using finite element methods. Potential fields then served as inputs to stochastic, nonlinear dynamic models for each of 2415 vestibular afferent axons with spiking dynamics based on a modified Smith and Goldberg model incorporating parameters that varied with fiber location in the neuroepithelium. Action potential propagation was implemented by a well validated model of myelinated fibers.

We tested the model by comparing predicted and actual 3D angular vestibulo-ocular reflex (aVOR) axes of eye rotation elicited by prosthetic stimuli. Actual responses were measured using 3D video-oculography. The model was individualized for each animal by placing virtual electrodes based on microCT localization of real electrodes. 3D eye rotation axes were predicted from the relative proportion of model axons excited within each of the three ampullary nerves.

Multiple features observed empirically were observed as emergent properties of the model, including effects of active and return electrode position, stimulus amplitude and pulse waveform shape on target fiber recruitment and stimulation selectivity. The modeling procedure is partially automated and can be readily adapted to other species, including humans.

Introduction

The vestibular labyrinth provides sensory input that mediates the angular vestibulo-ocular reflex (aVOR), translational VOR (tVOR), vestibulospinal and vestibulocervical reflexes, and perception of head orientation and movement. Failure of gaze stabilizing reflexes due to profound loss of labyrinthine sensation causes a dramatic drop in visual acuity during head movement due to illusory movement of the world. This is especially problematic during high-acceleration transient head rotations, for which vision-dependent mechanisms of gaze stabilization fail. Loss of vestibular sensation also causes chronic disequilibrium and postural instability (Grunbauer et al 1998; Minor 1998; Gillespie and Minor 1999). The only treatment with demonstrated clinical success in reducing these symptoms is vestibular rehabilitation; individuals who fail to improve with rehabilitative exercises remain disabled.

The success of cochlear implants in restoring auditory nerve input after loss of cochlear hair cells suggests that analogous benefits should be achieved using a multichannel vestibular prosthesis (MVP) that comprises 3 gyros aligned with the labyrinth’s semicircular canals (SCCs) to measure 3 dimensional (3D) head rotation, a processor to generate pulse-frequency-modulated biphasic pulse stimuli, and electrodes implanted near the corresponding ampullary nerves. Drawing on studies by Cohen and Suzuki (Cohen et al 1964; Suzuki and Cohen 1964; Suzuki et al 1969a b) and complementing work on a single-channel head-mounted prosthesis prototype created by Gong, Merfeld and colleagues (Gong and Merfeld 2000, 2002; Merfeld et al 2006, 2007; Lewis et al 2010), we developed an MVP and demonstrated it its ability to partly restore the 3D aVOR in rodents and monkeys rendered insensitive to head movement via gentamicin ototoxicity (Della Santina et al 2005a, 2007; Fridman et al 2010; Della Santina et al 2010; Davidovics et al 2010; Chiang et al 2010; Dai et al 2011).

Despite promising results, misalignment between actual and perceived 3D head motion (the latter being approximated by the inverse of the 3D aVOR response) remains a challenge, because current spread and imprecision of electrode placement result in spurious activation of vestibular afferents in nontarget nerve branches (Della Santina et al 2007; Fridman et al 2010; Davidovics et al 2010). Misalignment can be reduced by keeping stimulus currents low, but that strategy constrains the MVP to elicit only small response magnitudes (Davidovics et al. 2010).

It seems likely that electrode position, size and orientation; choice of reference electrode; use of multipolar electrode configurations; choice of stimulus waveform amplitude and shape; encapsulation of electrode arrays in insulating carrier materials; and other controllable features of MVP design can be optimized to improve electrode-nerve coupling with a target nerve branch while minimizing current spread to nontarget afferents. However, study of these parameters in vivo is difficult and costly in time and in number of animals required. Systematic comparison across animals is limited by individual variations in electrode position, and precise variation in electrode position is difficult to accomplish with conventional surgical techniques. To facilitate design of electrodes and stimulus protocols for a MVP, we created a virtual labyrinth model of vestibular nerve excitation by prosthetic electrical currents. Here we describe development and details of the model, underlying assumptions, model evaluation/validation by comparison to empiric data, and a series of virtual experiments performed to better understand the biophysics of current flow and afferent activation in the implanted labyrinth.

Model Description

Model Overview

The model was created with a goal of accurately predicting the pattern of vestibular nerve activity evoked by prosthetic electrical stimuli delivered via electrodes implanted in the vestibular labyrinth. We used chinchillas for this study, because extensive data on their morphology, normal physiology, and response to ototoxic medications and electrical stimuli already exist (Baird et al 1988; Fernández et al 1988, 1990; Goldberg et al 1990a b; Lysakowski and Goldberg 1997; Hirvonen et al 2005; Della Santina et al 2005a b, 2007; Hullar and Williams 2006; Lyford-Pike et al 2007). A standard labyrinthine geometry was first defined based on 3D reconstructions of micro-resolution computed tomography (CT) and micro-magnetic resonance imaging (MRI) data sets for one normal chinchilla. Subsequently, each implanted chinchilla under study was imaged using CT, its labyrinth was coregistered with the standard labyrinth, and virtual representations of its implanted electrodes were positioned within the standard model labyrinth relative to anatomic landmarks. Finite element analysis was performed upon the resulting data sets to estimate the electrical potential field throughout the inner ear when one or more electrodes were active. Field values were then used as the extracellular potential inputs for stochastic, nonlinear dynamic models of action potential initiation and conduction along virtual vestibular afferents whose location and behavior were specified to reflect morphophysiologic correlations established by empiric studies (Fernández et al 1988, 1990; Baird et al. 1988; Goldberg et al. 1990a b; Lysakowski and Goldberg 1997). Afferents were modeled using adaptations of extensively validated computational models for vestibular afferent spike initiation (Goldberg et al. 1984; Smith and Goldberg 1986) and action potential propagation (Frijns and ten Kate 1994; Frijns et al 1994). Eye movement response axes were estimated from the relative proportions of afferents activated in each model ampullary nerve.

Finite Element Model of the Labyrinth

Solving for the potential field throughout a complex 3D anatomy with regions of different conductivity is difficult and often impossible to accomplish analytically. Finite element analysis allows for a comparatively quick and accurate solution. This technique involves three steps: (1) definition of model geometry and generation of a 3D mesh, (2) assignment of tissue conductivities and boundary conditions, and (3) solving the corresponding system of simultaneous equations either directly or iteratively.

Definition of 3D Model Anatomy using MicroCT and MicroMRI

Model geometry was generated through 3D reconstruction of ultra-high resolution microCT and microMRI data sets. To generate the model’s standard labyrinth geometry, we coregistered a CT scan acquired at 12 μm voxel size with MRIs acquired at 30 and 48 μm voxel size. Achieving this voxel size with adequate signal-to-noise for the MRI required 26 hours of acquisition in an 11.7 Tesla magnet. CT and MRI are complementary in that the former provides better detail of bone anatomy, while the latter provides better differentiation between fluid, brain, nerve and neuroepithelium.

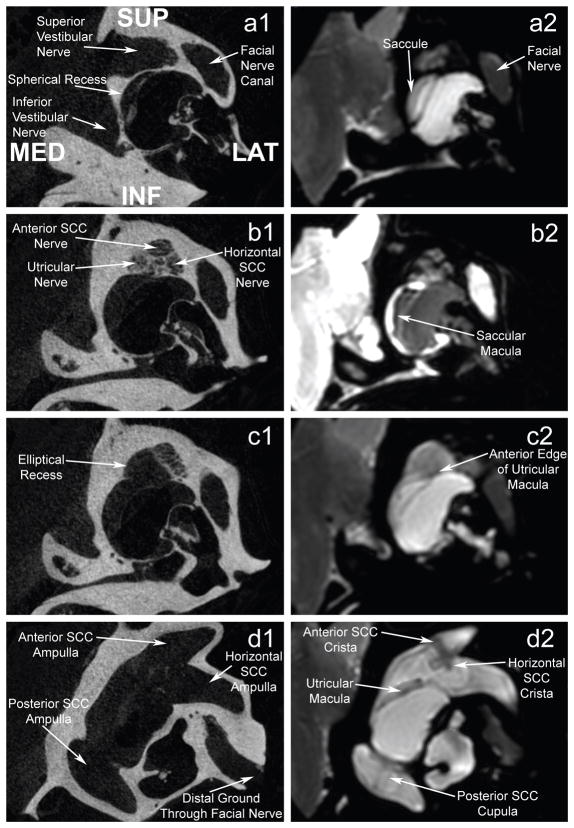
Figure 1 shows representative coregistered slices of the CT and MRI data sets, illustrating key anatomic landmarks. It is clear from this figure that the chinchilla inner ear is a complex, multi-compartmental volume conductor. Close proximity of different vestibular nerve branches is also apparent, particularly for the anterior SCC ampullary nerve, horizontal SCC ampullary nerve, utricular nerve and facial nerve. The limited clearance between these neural structures makes each a challenging target for selective stimulation. As shown in Figs 1b1 and 1c1, the vestibular nerves travel through perforations of the temporal bone before entering the inner ear and contacting neuroepithelium. As the axonal processes of vestibular afferents travel through these openings, the anisotropic conductivity of the neural tissue changes unpredictably. Finally, Figure 1c1 reveals that a long segment of an ampullary nerve can border the fluid filled vestibule separated only by a thin layer of bone. The conductive fluid in the vestibule will affect the local electric field within these portions of the nerve.

Figure 1.

MicroCT (12 μm voxel size, a1–d1) coregistered with a microMRI (48 μm voxel size, a2–d2) of a normal chinchilla labyrinth. Top image pair (a) is the most anterior slice; others are progressively further posterior. MicroCT reveals individual pores in the cribriform plate through which the superior vestibular nerve enters the labyrinth as it breaks into its three branches (b1). Note the close mutual proximity of these three superior vestibular nerve branches in this region. To achieve adequate signal to noise ratio and voxel density to clearly define endorgan neuroepitheilia, the MRI was acquired in a 12 Tesla magnet for 26 hours.

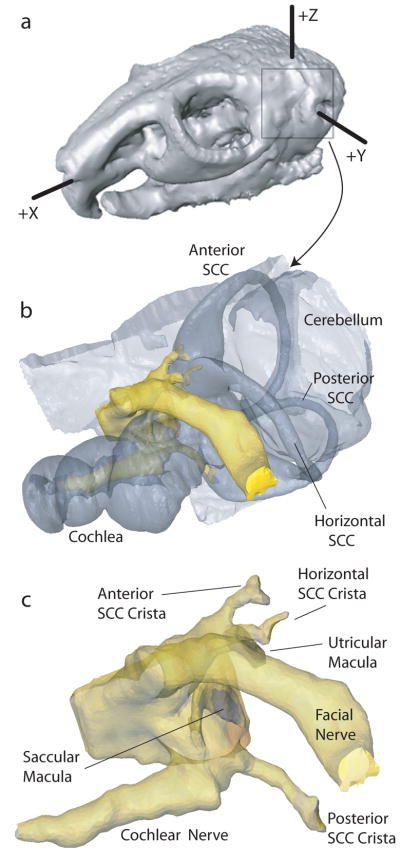
We used Amira software (Mercury Computer Systems, Chelmsford, MA) to coregister and segment the CT and MRI image data sets into tissue volume domains of different conductivity (Figure 2), including nerves with anisotropic conductivity as described below. To individualize the model for a given chinchilla, we acquired post-mortem micro-CT scans to measure electrode locations in that animal’s labyrinth (Figure 3a). We then placed virtual electrodes into the model geometry at the appropriate locations relative to anatomic landmarks, representing them as conductive spheres with surface area similar to that of actual electrode dimensions. The segmented data set was then meshed (i.e., parceled into small, nonoverlapping, tetrahedral volumes). Mesh density was made greatest where the electrical potential gradients were likely to be steepest, such as the region immediately around an electrode or nerve (Figure 3b). Typical meshes included 1.2 to 4 million elements.

Figure 2.

3D reconstructions of chinchilla skull (a), labyrinth (b), and 7^th/8^th nerve complex (c).

Figure 3.

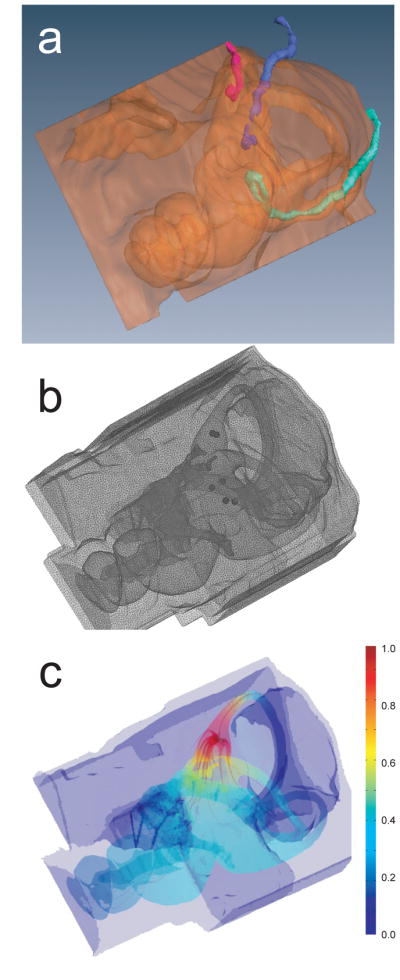
(a) Left anterolateral view of microCT showing 3D reconstruction of electrode trajectories for chinchilla CH050506A. Color scheme: bone/air interface orange; anterior SCC electrode red; horizontal SCC electrode blue; posterior SCC electrode in green. Anatomic features are as labeled in Fig 2b. Note that the posterior SCC electrode pair was overinserted, so that its tips rest in the vestibule rather than the poster SCC ampulla. (b) Tetrahedral mesh of same case. Note the increased mesh densities near the electrodes (dark spheres). (c) Potential field and current density field output by finite element solution. Color scale: electric potential normalized to unity near active electrode and zero at far end of body.

Tissue Conductivities and Boundary Conditions

Each tetrahedral element is assumed to have a single conductivity. Conductivities listed in Table 1 were drawn from existing literature (Tasaki 1964; Geddes and Baker 1967; Kosterich et al. 1983; Suesserman and Spelman 1993; Dow Corning 2005). All fluid spaces within the labyrinth were lumped into one contiguous volume denoted the vestibular lumen. A single conductivity was used to describe the vestibular lumen, since both endolymphatic fluid and perilymph possess similar electrical characteristics. The membranous labyrinth was not considered to represent a barrier to current flow, because (1) it is too thin to represent as a volume of different conductivity without compromising solvability of the finite element equations and (2) it would represent negligible impedance to biphasic current pulses of the durations typically used in a vestibular prosthesis.

Table 1.

Tissue conductivities used in the model

Tissue Domain	Conductivity (Ω−1/m)	Resistivity (Ω-cm)
Vestibular Lumen	2.0	50
Bone	0.0139	7,200
Brain	0.3333	300
Nerve (Longitudinal)	0.3333	300
Nerve (Transverse)	0.0143	7,000
Body	0.1721	581
Silicone	~0	2×1015
Air	~0	~infinite

Cranial nerves were considered anisotropic, with axial conductivity 23x greater than transverse conductivity. Each nerve’s anisotropic conductivity was implemented by subdividing the nerve volume into tissue domains paralleling the nerve’s axis, with each tetrahedron being assigned an anisotropic conductivity tensor with maximum conductivity parallel to the nerve axis in that region.

Brainstem and cerebellum were modeled as isotropic, homogenous conductors, using the average value of conductivity between white and grey matter. A “body” domain lined the model volume’s medial edges to allow for simulation of monopolar stimulation (i.e., injection of current by a single intralabyrinthine electrode with respect to a reference outside of the temporal bone).

Calculation of Extracellular Potential Field and Current Field

Each mesh was imported into COMSOL Multiphysics (COMSOL Inc, Burlington, MA) for finite element analysis using COMSOL’s DC Conductive Media Module. Each simulation was solved iteratively on a 64-bit multicore processor using the conjugate gradients method. The resulting solution, defining the potential and current density at each mesh vertex for a unit stimulus current, was sampled at points in space corresponding to points along model axons in each vestibular nerve branch (Figure 3c).

Quasistatic conditions were assumed, implying an approximation that all tissues are purely conductive without any reactance. Since dielectric relaxation times measured for biological tissues are much shorter than the time scale of stimulus pulses we use, this is a well justified assumption (Malmivuo and Plonsey 1995; Spelman et al 1982). Under quasistatic conditions, no temporal dynamics arise between mesh elements. Therefore, to simulate the time course of potential changes throughout the meshed volume during a current stimulus with a given temporal waveform, one need only compute the potential at each vertex for a unit current injected through the electrode (or electrodes) of interest to determine the relative potential at every vertex in the mesh. Interpolation between mesh vertices can determine the potential at any point in the volume. The potential at that point then rises and falls as a scaled version of the stimulus waveform. (This does not mean that the model lacks realistic temporal dynamics or stochastic behaviors. They accrue from the neuromorphic model elements described below.)

Neuromorphic Model

Model vestibular afferent geometry and physiology

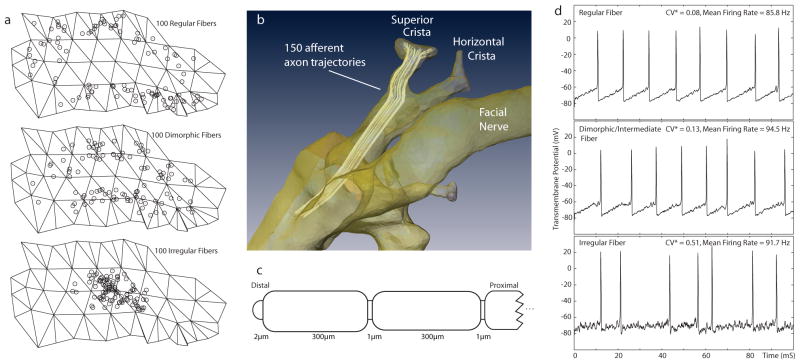
Each ampullary nerve was represented by 505 model afferents, and each macular nerve comprised 450 afferents. We randomly chose the starting location of fibers in each of three concentric zones (central, intermediate and peripheral) on the model neuroepithelial surface, using a distribution for each zone that was uniform over most of that zone but then tapered near the zone’s border with an adjacent zone (Figure 4a). For each fiber, we then randomly chose fiber diameter from Gaussian distributions for which the means and variances were determined by the zone of fiber origin using previously published data (Fernández et al, 1988). For each afferent, a trajectory through the “nerve” domain of the finite element model volume was defined by a polyline (i.e., end-to-end line segments tracing a course through 3D space) that started at a randomly assigned location on the neurosensory epithelial surface and then “grew” medially through the internal auditory canal under control of a semi-automatic, stochastic algorithm that generally maintained relative positions of neighboring fibers as model nerve branches merged en route to the brainstem (Figure 4b) (Hayden 2007). Current vectors and extracellular potential field values extracted from the COMSOL solution at uniformly spaced points along each polyline formed the inputs for each afferent’s individualized neuromorphic model.

Figure 4.

(a) Locations in central, intermediate and peripheral crista zones corresponding to origins of 300 virtual afferent fibers (b) 150 model afferents in the anterior SCC ampullary nerve. (c) Schematic morphology of one model vestibular afferent. (d) Spontaneous activity of three model afferents with different degrees of regularity typical of model fibers from the corresponding zones in (a).

A general neuromorphic model for chinchilla vestibular afferents was adapted from the spatially extended nonlinear node (SENN) axon model previously used in models of prosthetic cochlear stimulation (Frijns and ten Kate 1994; Frijns et al 1994; McIntyre et al 2002). The full modified SENN model (which is described in detail in the Appendix) is summarized here and schematized in Figure 4. Each active model node (representing a node of Ranvier) comprised two nonlinear channels (voltage-gated Na⁺ and voltage-gated K⁺), a leakage channel and a membrane capacitance. Myelinated internodes were considered to be insulated from the extracellular space. Na⁺, K⁺ and leakage channel dynamics were based on parameters reported for rat myelinated axons (Schwarz and Eikhof 1987). Fiber diameters were chosen from published data for chinchilla vestibular afferents (Fernández et al 1988; Lysakowski and Goldberg 1997). Internode length was varied randomly about a mean of 300 μm, nodes of Ranvier were 1 μm, and each heminode (within a crista or macula) was 2 μm (Fig. 4b).

Empiric studies have revealed that vestibular afferent physiology depends strongly on each afferent’s site of origin (e.g., within the central, intermediate or peripheral zones of a crista), spontaneous discharge regularity, and fiber diameter (Fernández et al 1988, 1990; Baird et al. 1988; Goldberg et al. 1990a b; Lysakowski and Goldberg 1997). To reflect these morphophysiologic correlations, the modified SENN model was further modified by inclusion of a stochastic afterhyperpolarization (AHP) model of the spike initiator zone of each model afferent’s distal heminode, based on the model devised and extensively validated by Smith and Goldberg (Goldberg et al. 1984; Smith and Goldberg 1986). Heminodes endowing model afferents with regular, irregular or intermediate spontaneous discharge rates were created by addition of a Smith-Goldberg model channel representing a voltage-independent K⁺ conductance with exponential AHP decay dynamics. To ensure spontaneous activity, heminodes also included stochastic Na⁺ channels governed by a Poisson process with event rate and amplitude based upon Smith and Goldberg’s original model but modified as previously described (Rubinstein and Della Santina 2002; McIntyre et al 2002; Hayden 2007) to create a self-initiating axon despite using the morphologic parameters of Schwarz and Eikhof (1987).

Three prototypical afferents were defined using SENN and Smith-Goldberg models to create virtual afferents with regular, intermediate and irregular spontaneous firing characteristics like those described by Goldberg, Fernández et al. Figure 4c shows a representative time segment of model output for a model of each type. From these standard forms, different classes of ampullary and macular nerve afferents were created by stochastically varying fiber diameter depending on the randomly assigned starting location of each afferent in a neuroepithelium (Figure 4d). Type A afferents modeled regularly firing afferents; types B1, B2 and B3 modeled dimorphic afferents with intermediate behavior; and type C modeled irregularly firing afferents. Table A1 lists the relative number and properties of each type of model afferent, which were based on distributions measured in chinchilla by Fernandez et al (1988, 1990).

Table A1. Model afferent classes.

All model parameters were based on histologic data for chinchilla neuroepithelium by Fernandez et al (1988, 1990).

Fiber Type	Firing Regularity	Number of Fibers	% of Nerve Branch	Diameter (μm)	Zone Within Neuroepithelium	Conduction Velocity (m/s)
SCC-A	Regular	100	20.0	1.40	Peripheral	13.4
SCC-B1	Intermediate	150	29.6	2.21	Intermediate	17.4
SCC-B2		150	29.6	2.23		17.4
SCC-B3		50	10.0	2.49		18.5
SCC-C	Irregular	55	10.8	2.81	Central	19.9
OTO-A	Regular	100	22.2	1.40	Extrastriolar	13.4
OTO-B1	Intermediate	150	33.4	2.21	Intermediate	17.4
OTO-B2		100	22.2	2.23		17.4
OTO-B3		50	11.1	2.49		18.5
OTO-C	Irregular	50	11.1	2.81	Striolar	19.9

SCC: semicircular canal ampullary nerve afferents. OTO: saccular and utricular macular nerve afferents.

Time Series Simulation

To compute the behavior of each model afferent as the ‘virtual labyrinth’ responded to a given electrode current waveform, the potential field value at each node along each afferent polyline was first computed for a unit electrode current by interpolating between nearby mesh vertices using the finite element model results. Responses to a given stimulus current waveform were then modeled by setting the extracellular potential time course at each model node (and the heminode of each afferent) equal to a scaled version of the stimulus current waveform.

Vestibular afferent fibers in a real labyrinth are intrinsically stochastic. At any given moment prior to application of a stimulus, each afferent is in its own state, dependent on recent inputs and on random intra- and extracellular events. To reflect this variability, the initial conditions of each model afferent’s transmembrane potentials, channel states, etc. were set randomly according to distributions determined by that afferent’s type. This was achieved by simulating each axon without electrode current input for a random period of time and then capturing its internal state.

With all parameters, inputs and initial conditions specified, each afferent’s subthreshold, spiking and action potential conduction behavior were computed using a forward Euler method implemented with 0.1 μS time steps in Matlab (Mathworks, Natick, MA). During any time interval, a model afferent was considered active if it conducted an action potential to its medial end during that interval. Electrode-nerve coupling was quantified by the percentage of activated afferents in a given nerve branch. Selectivity was assessed based on the relative fraction of afferents activated in each nerve branch. Because model parameters and initial conditions were randomized over a large number of model afferent fibers, the overall model essentially implemented a Monte Carlo simulation and thus was relatively insensitive to behavior of any single model afferent (Metropolis and Ulam, 1949).

Each model afferent simulation included a binary search for the threshold stimulus intensity that resulted in neural activation. The current amplitude of a standard stimulus waveform (typically a 200 μS/phase symmetric biphasic pulse comprising a constant-current cathodic pulse at the electrode being studied immediately followed by an equal amplitude and equal duration anodic pulse) was varied until converging on two values, one that caused spike initiation and one that did not. Convergence was met when both values resolved within 1% of each other. An analogous approach has been used in models of the cochlea, with good correlation to psychophysical and field potential data recorded from human cochlear implant users (Whiten 2003, 2007).

Prediction of 3D aVOR Eye Movement Responses from Model Afferent Activity

The 3D aVOR of normal chinchillas provides an especially convenient animal model in which to study the effects of prosthetic electrical stimulation of the labyrinth. Like humans, chinchillas exhibit aVOR-mediated eye movements in darkness that are partly compensatory for head rotations over ~0.1–10 Hz and conjugate in 3D (Migliaccio et al 2010). When considered in head coordinates, the chinchilla aVOR is nearly isotropic (i.e., the gain is about the same for head rotations about any axis) and approximately obeys linear vector superposition for stimuli delivered to different ampullary nerves (Migliaccio et al. 2010; Fridman et al. 2010). Since activation of any subset of vestibular afferents within one ampullary nerve causes conjugate binocular eye movements about the axis of that nerve’s SCC (e.g., Cohen, Suzuki and Bender 1964; Cremer et al. 2000), one can approximate the relative level of excitation for each ampullary nerve in a labyrinth by back-projecting the observed 3D eye rotation axis back on to the axis of each SCC. Conversely, one can approximate the 3D axis of aVOR eye rotation knowing the relative levels of excitation in each ampullary nerve. We used this latter approach to predict 3D aVOR responses to different patterns of electrode activation in the virtual experiments described below.

In contrast to the nearly one-to-one mapping between the pattern of ampullary nerve activation and the 3D axis of aVOR-mediated eye movements, the macular nerves are more complex. Dense packing of hair cells and afferents with widely varying directional sensitivities in the utricular and saccular maculae and their nerves makes the relationship between electrically-evoked macular nerve stimulation and aVOR/tVOR-mediated eye movements less predictable (Suzuki et al. 1969a, 1969b; Fluur and Mellström 1970a, 1970b, 1971; Goto et al. 2003, 2004; Curthoys 1987). Existing evidence suggests that eye movement responses to natural stimulation of macular nerves are modest compared to aVOR responses to SCC input during natural head rotation (Baarsma and Collewijn 1975); therefore, we neglected the effects of macular nerve activity when predicting 3D eye movement axes from the pattern of vestibular nerve activity reported by the model.

Experimental methods

All animal experiments were conducted in accordance with protocols approved by the Johns Hopkins Animal Care and Use Committee. Four adult chinchillas (C. laniger, 450–650g) were anesthetized with ketamine/xylazine IM and then treated bilaterally with 0.5cc intratympanic injections of 26.7 mg/mL gentamicin buffered with sodium bicarbonate to pH 7.0. This regimen ablates 3D aVOR responses to head rotation by destroying Type I vestibular hair cells and denuding Type II vestibular hair cells of their stereocilia while leaving a viable population of Type II hair cell bodies and spontaneously firing ampullary and macular nerve fibers subjacent to the endorgan neuroepithelium (Hirvonen et al 2005; Della Santina et al 2005b, 2007b, 2010; Lyford-Pike et al 2007; Fridman et al 2010).

For animal restraint during testing, a post was affixed to the animal’s skull using dental cement. For prosthetic electrical stimulation, each chinchilla was implanted with four pairs of electrodes. One pair was placed within or near each of the three semicircular canal ampullae, while the last pair served as reference electrodes and was implanted in the neck musculature. Electrodes consisted of Teflon^™ coated 10% iridium/90% platinum wires of diameters ranging from 25um to 125um (Medwire, Sigmund Cohn Corp, Mount Vernon, NY). Distal ends of each wire were stripped 200 μm from the end. Electrode wires of 25 μm diameter were flamed to form a ball on the distal end in order to increase the contact area of the electrode-perilymph interface. This was necessary to avoid electrode corrosion and nerve injury that would otherwise occur during passage of stimulus currents (Robblee and Rose 1990).

Measurement of aVOR responses to head rotation

3D aVOR responses to head rotation were studied in darkness starting 3 weeks after treatment. By that time, gentamicin-treated animals exhibited a total or near-total loss of sensitivity to head rotation without prosthetic electrical stimulation. Each animal was secured in a Fick gimbal mounted on a servo motor (Model 130-80/ACT2000, Acutronic USA) and initially rotated without prosthetic electrical stimulation to ensure the absence of compensatory eye movements. Procedures for animal restraint and surgical technique have been described in detail previously (Della Santina et al 2007; Migliaccio et al 2005; Migliaccio et al 2010).

Eye movement data were recorded using a 3D video-oculography (3D VOG) system that tracked markers that were opaque (occluding the pupils) and affixed to each cornea. The VOG equipment and data analysis techniques employed in this study have been described in detail previously (Migliaccio et al 2005, 2010; Della Santina et al 2007; Fridman et al 2010). Recordings from each eye were converted to 3D angular position in rotation vector form in a right-hand-rule canal-referenced head coordinate system. Angular velocity vectors of eye with respect to head were calculated from rotation vectors. For responses to sinusoidal stimuli, three eye movement components about mean SCC axes (horizontal [Z], left-anterior/right-posterior [LARP], and right-anterior/left-posterior [RALP]) were separately averaged for >5 cycles free of saccades and blinks. LARP and RALP axes were approximated as being 45° off the midline and in the mean plane of the horizontal SCCs as estimated from skull landmarks (Hullar and Williams 2006) and direct observation during electrode implantation. During each testing session, eye movements were recorded during sinusoidal head rotations at 0.5 and 2 Hz with peak velocity 50°/s about the horizontal, LARP and RALP axes.

Measurement of aVOR responses to prosthetic electrical stimulation

Electrical stimuli consisted of pulse-frequency-modulated trains of charge-balanced biphasic pulses at the active electrode delivered using a DC-isolated constant current stimulator. Each biphasic pulse comprised (1) a constant-current, constant-duration cathodic phase (typically 200 μS, range 100–230 μS); (2) a zero-current, constant-duration “interphase gap” (typically 30 μS, range 0–50 μS); and (3) a constant-current, constant-duration anodic phase (typically equal in duration and opposite in current direction versus the cathodic phase). The analog signal modulating pulse frequency (intended to represent head angular velocity about the axis of the target SCC), was a sinusoid at either 0.5 or 2 Hz. Parameters for each of the 26 different animal/stimulus combinations tested empirically and modeled are shown in Table 2. In monopolar stimulation, one active electrode implanted near a target ampullary nerve delivers current with respect to a distant reference electrode in neck musculature. For bipolar stimulation, both electrodes are close to the target ampullary nerve (and to each other). In bipolar stimulation, the electrode closest to the target nerve was considered to be the active electrode.

Table 2.

Electrical stimulation parameters for each of 26 cases tested and modeled.

Animal	Target Ampulla	Electrode Arrangement	Stimulus Current (μA)	Phase Duration (μs)	Modulation Frequency (Hz)	Modulation Limits (pulse/s)
CH050506A	LA	Monopolar	140	200	0.5	40 – 300
	LH	Bipolar	290	230	2	40 – 300
	LP	Monopolar	100	200	2	40 – 300
CH050506B	LA	Bipolar	280	200	2	30 – 300
		Monopolar	50, 100, 120, 140, 210	200	2	30 – 300
	LH	Bipolar	230	200	2	30 – 300
		Monopolar	75, 100, 110, 120, 160, 175	200	2	30 – 300
	LP	Monopolar	20, 50, 100, 120, 150, 200	200	2	30 – 300
CH071105	LA	Monopolar	250	200	2	50 – 270
	LH	Monopolar	250	200	2	50 – 270
	LP	Monopolar	250	200	2	50 – 270
CH072106	LP	Monopolar	260	100	2	20 – 300

LA, LH, LP: Left anterior, horizontal and posterior semicircular canals, respectively.

Results

Model Evaluation

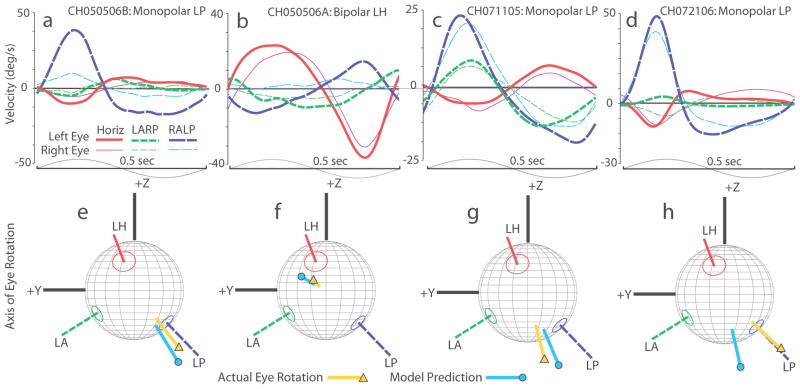
Figure 5 compares measured 3D VOG eye rotation axes for four different vestibular nerve stimulation experiments with simulation results from individualized models. In each case, pulse frequency was modulated by a 2 Hz sinusoidal waveform about a nonzero baseline rate using stimulation parameters summarized in Table 2. (Stimuli used for each of the cases in Figure 5 were equivalent to those an MVP would deliver during a 50°/S peak, 2 Hz sinusoidal head rotation about the target SCC’s axis.) As shown in Figures 5a–d, the largest component of the 3D aVOR response in each case is the one about the axis of the target SCC; however, misalignment (indicated by components about the other SCC’s axes) and disconjugacy (indicated by differences between the left and right eyes) are evident, consistent with spurious stimulation of nontarget ampullary and macular nerves. The mean 3D aVOR axis for measured aVOR responses is depicted in Figures 5e–h, mapped on a spherical polar plot showing the anatomic axis of each of the three SCCs in the implanted left labyrinth. These results show that while the measured 3D aVOR axis does not always align with the desired single-SCC axis, model predictions align to the measured axis within about 20°, or about 10° more than the error inherent in estimating SCC axes from accessible skull landmarks (Hullar and Williams 2006).

Figure 5.

(a–d) Four empiric data sets illustrating 3D angular vestibulo-ocular reflex (aVOR) responses to 2 Hz sinusoidally pulse-frequency-modulated, symmetric biphasic cathodic-first 200 uS/phase stimuli delivered via various electrode configurations to each of 4 animals. In each case, mean eye movement velocity components about the axes of the mean left horizontal (red/solid), left-anterior/right-posterior (LARP, green short-dashed) and right-anterior/left-posterior (RALP, blue long-dash) semicircular canal axes are shown for each eye (thick lines = left eye, thin lines = right eye). Upper bounds of standard deviation at any point along any trace is 6, 14, 13 and 15°/s for Panels a, b, c and d, respectively. Sinusoids at bottom illustrate modulating signal controlling pulse frequency; + denotes half-cycle excitatory for left labyrinth. (e–h) Comparison of measured mean 3D aVOR axes and axes estimated by virtual labyrinth model for the cases shown in Panels a–d. Both are mapped on canal axis coordinate system indicated: LH, LA, LP = axes of left horizontal, left anterior and left posterior semicircular canals, respectively. +Z and +Y correspond to axes shown in Fig 2a. Absolute values of response components were used to facilitate visual comparison. Note that although the actual axis of eye rotation (▲) does not always align well with the axis of the ampullary nerve being targeted (likely due to current spread causing spurious stimulation of other nerve branches), the model’s axis estimate (●) replicates empiric data to within ~20°.

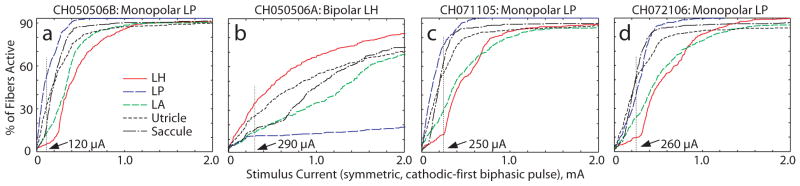
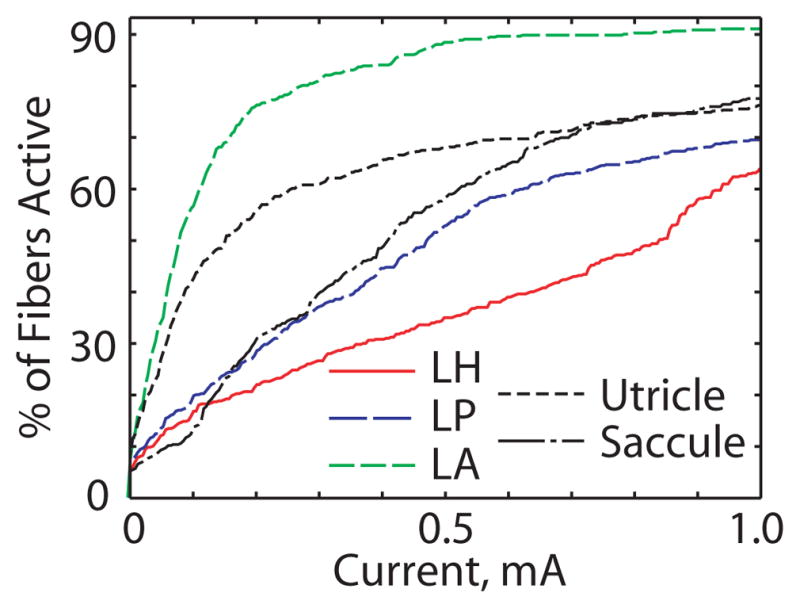
Figures 6a–d show model predictions for vestibular afferent population recruitment curves for each of the five nerve branches as current pulse amplitude increases from 0 to 2 mA during 200 μS/phase, cathodic-first, symmetric biphasic pulses. Four features are evident in these simulation results. First, simulations indicate that every case elicits significant excitation of saccular and utricular afferents, as might be expected from the proximity of these nerves to the target ampullary nerves. (All nerve branches coalesce in the internal auditory canal, where the anodic phase of high stimulus current pulses launched action potentials by direct stimulation of nodes of Ranvier.) Second, macular nerve stimulation is especially great for the monopolar cases, for which nearly all stimulus current courses medially due to the insulating effects of air that surrounds the chinchilla labyrinth laterally. Third, all three of the monopolar cases exhibit greater electrode-nerve coupling but lower target-nontarget selectivity than the bipolar case. Finally, the fiber recruitment curve in each case is typically a saturating nonlinear function of stimulus current. At stimulus currents above about 1 mA, nearly every vestibular afferent is excited in monopolar cases, while the bipolar case still exhibits some selectivity.

Figure 6.

Model-predicted fiber recruitment curves showing fraction of fibers activated in each nerve branch for the cases simulated for Figure 5. Vertical lines show the current level at which each case was simulated. Note that all monopolar cases (a, c, d) show greater electrode-nerve coupling and poorer selectivity than the bipolar case (b).

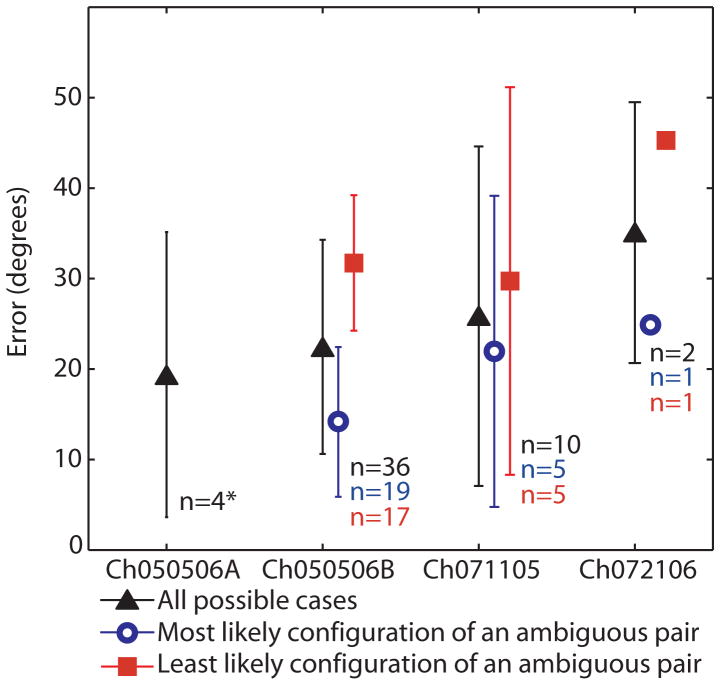
Figure 7 summarizes the mean ± SD misalignment between measured and simulated 3D aVOR response axes for 52 different cathode/anode/stimulus current conditions examined in 4 animals. Twisting of bipolar wire pairs during fabrication and surgical placement made it impossible for post-implantation CT to distinguish the two electrodes of a bipolar pair. Therefore, every possible scenario was simulated and included in Figure 6. In each case, the model discriminated between the two possible active/reference scenarios of a given experiment, yielding good predictions for one configuration and poor predictions for the other. (In the case of chinchilla Ch050506A, all electrode identities were fully known.) Blue triangles in the figure indicate errors calculated for the electrode configuration considered most likely based on operative notes and simulation results.

Figure 7.

Mean ± SD of error between model predictions and actual 3D axis of aVOR eye rotation response for all cases tested empirically and simulated. When the active/reference electrodes could not be discerned from each another with certainty due to twisting of paired wires and limits of CT resolution, both possible scenarios were simulated and included (▲). When only the electrode configurations that were most likely the actual arrangement based on operative notes and fits of the NM model are included, apparent errors are lower (○). *All electrode configurations were known for Ch050506A.

Responses to Monophasic and Biphasic Stimuli

For monophasic current pulse stimuli delivered by an active ‘monopolar’ electrode in the vestibule versus a distant reference, the model accurately reflected empirical findings reported by Goldberg et al (1982, 1984) for analogous studies in monkeys. Cathodic currents delivered to perilymph versus a distant reference usually excited model afferents at the heminode but occasionally launched an action potential from one of the distalmost 3 nodes of Ranvier. Model irregular afferents, which recover quickly from afterhyperpolarization, were stimulated almost exclusively at the heminode by cathodic pulses. In contrast, anodic monophasic pulses acted exclusively on the proximal axon and only at high stimulus currents. At these high currents, spike initiation during anodal spike initiation did not depend much on a model afferent’s afterhyperpolarization status, but it still had a slight bias toward irregular afferents, whose larger calibers make them slightly more sensitive to excitation by exogenous current.

For symmetric 200 μS biphasic pulse stimuli delivered by the same monopolar electrode, the nodal sites at which currents acted were more variable. The first phase of the biphasic pulse always produced spike initiation similar to that observed empirically by Goldberg et al (1982, 1984) for monophasic pulses. For cathodic-first biphasic pulses delivered by a perilymphatic active electrode versus a distant reference, all excited model afferents initiated their spikes at the heminode in response to the cathodic phase. Anodic-first biphasic pulses launched spikes at the proximal axon in response to the anodic current of the first phase. However, the second phase for both of these instances elicited variable responses due to residual effects of the initial phase of the stimulus. Generally, zones of spike initiation formed a bimodal spatial distribution, with afferents being excited at either the heminode or at the proximal axon near the porus acusticus, with little to no spike initiation at sites in between.

Model Applications and Predictions

Having confirmed that model predictions reasonably approximate available empiric data, we set about using the model to evaluate electrode designs and pulse waveforms.

Evaluation of Idealized Electrode Array Designs

Historically, analytic solutions to lumped parameter models of a straight, cylindrical axon in a semi-infinite homogenous volume conductor have yielded useful general rules regarding excitation of axons by extracellular electrodes. For example, such models predict that the likelihood of action potential generation due to a nearby monopolar electrode should scale with the second spatial derivative of electric potential along the axon’s axis (Malmivuo and Plonsey 1995). However, analytic models become intractable as model geometry is progressively made more complex to account for multiple electrodes, nerves with realistic geometry, and regions of different conductivity.

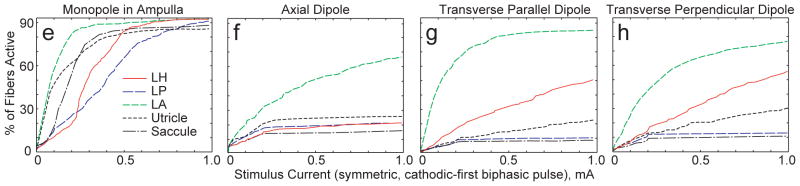
To guide electrode array design for a subsequent generation of MVP, we constructed virtual labyrinth models of four idealized electrode array geometries, comparing fiber recruitment curves for each to identify arrangements that perform best with respect to electrode-nerve coupling and selectivity. Four arrangements were considered for each of the SCC ampullae, resulting in 12 different configurations per labyrinth. Figures 8a–d illustrate cases studied for the anterior and horizontal ampullae. In the simplest case, a monopolar electrode was positioned within the ampulla, roughly coincident with the cupula’s center of mass. Three bipolar electrode configurations were named based upon the orientation of the dipole moment, with the center of each bipolar pair fixed at the position of the ideal monopole. In the axial dipole arrangement, the bipolar electrode’s dipole moment was along a tangent to the SCC at its junction with the ampulla. In the transverse parallel dipole arrangement, the dipole moment was perpendicular to a tangent to the SCC at its junction with the ampulla and parallel to the distalmost portion of the target ampullary nerve. In the transverse perpendicular dipole arrangement, the dipole moment was perpendicular to a tangent to the SCC at its junction with the ampulla and perpendicular to the distalmost portion of the target ampullary nerve.

Figure 8.

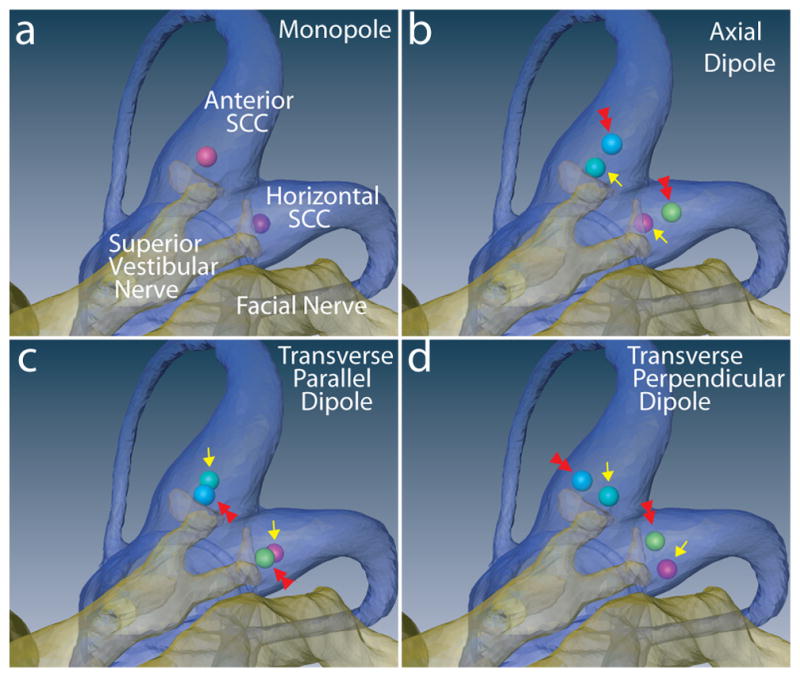
Figure 8a–d: Four idealized electrode configurations as applied in the anterior and horizontal semicircular canal ampullae. (a) Monopolar (active electrodes shown; distant reference electrodes not shown). (b) Axial dipole. (c) Transverse/Parallel dipole. (d) Transverse/Perpendicular dipole. Double red arrows in b–d indicate the active electrode, which is cathodic during the first phase of a symmetric, charge-balanced, biphasic constant-current pulse. e–h: Simulated fiber recruitment plots for each anterior canal case. Transverse/Parallel dipole outperforms other configurations with regard to selectivity.

Figures 8e–h show fiber recruitment curves for models corresponding to each of the electrode arrangements shown in Figure 8a–d. In each case simulated, the target was the anterior SCC ampullary nerve, and the anterior SCC active electrode indicated in Figures 8a–d was cathodic first for a 200 μS/phase symmetric biphasic current pulse.

Of the four electrode configurations considered, the monopolar configuration exhibited the lowest threshold and the poorest selectivity. The model predicted that the anterior ampullary nerve and utricular nerve are excited to about the same extent up to ~50 μA pulse amplitude, while all other branches are still relatively quiescent. As pulse amplitude rises above ~50 μA, model utricular afferent recruitment rises less steeply than recruitment of the target anterior ampullary nerve, while saccular, horizontal ampullary and posterior ampullary model nerves are recruited in sequence as pulse amplitude rises.

According to the model, all bipolar configurations exhibit lower electrode-target coupling but greater selectivity than the monopolar configuration. Of the three bipolar arrays simulated, the transverse parallel dipole (Figures 8c and 8g) performed the best: for a 250 μA/phase symmetric biphasic pulse stimulus, the model predicted that 69% of afferents in the target anterior ampullary nerve are excited and that these make up 70% of all afferents excited by the stimulus. The transverse parallel dipole exhibited similarly advantageous performance when applied to models of electrodes in the horizontal and posterior ampullae. In contrast, the same stimulus current applied via a monopolar configuration excited 86% of model afferents in the target nerve, but this made up only a third of the total afferent activation, since nearly 65% of model macular nerve fibers and 30% of model nontarget ampullary nerve fibers were also excited.

Given uncertainty regarding how different degrees of utricular and saccular excitation affect eye movements, 3D aVOR data are corroborative but insufficient alone to definitively confirm or disprove the model’s predictions for electrode-nerve coupling strengths, sequence of recruitment and other behaviors depending on electrode geometry. If technical hurdles related to stimulus artifact can be overcome, then single unit recordings from the proximal vestibular nerve could directly test the hypotheses generated by virtual labyrinth model results. Efforts toward that aim have been recently described (Phillips 2010).

Evaluation of Different Stimulus Waveforms

An MVP can deliver almost any stimulus waveform that adheres to charge-transfer safety limits (Della Santina et al 2007; Robblee and Rose 1990), and changes in stimulus pulse shape can change spike initiation thresholds, electrode-nerve coupling and selectivity. Cathodic first pseudomonophasic pulses (i.e., a brief high-amplitude cathodic phase followed by a longer duration but lower amplitude anodic charge-recovery phase) are of special interest because they appear to be effective in improving cochlear implant performance (Rubinstein et al 2001; Macherey et al 2006).

We used the 12 models described above to study differences in responses to cathodic- and anodic-first symmetric and pseudomonophasic biphasic pulses. In each case, the active electrode was as illustrated in Figure 8. Simulation parameters and results for a monopolar electrode case are summarized in Table 3. Notably, while the standard cathodic-first symmetric 200 μS biphasic waveform predominantly elicited responses from the target nerve branch’s distal heminode during the cathodic phase, the anodic phase also initiated action potentials. Those anodic-phase spikes mostly arose at nodes of Ranvier in the proximal vestibular nerve, where confluence of all nerve branches precludes selective stimulation of fibers from any one branch. Anodic-first symmetric pulses elicited similar results.

Table 3.

Dependence of model electrode-nerve coupling and selectivity on stimulus pulse shape

Stimulus delivered via monopolar electrode in anterior SCC ampulla	Current waveform at active electrode (1st phase 200 μS, 200 μA; gap 30 μS)	Fraction of afferents excited in target nerve branch (of 505 total)		Fraction of afferents excited in nontarget branches (of 1910 total)
		During Cathodic Phase	During Anodic Phase	During Cathodic Phase	During Anodic Phase
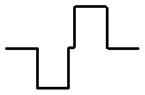
Cathodic-first symmetric biphasic		67%	11%	40%	35%
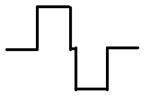
Anodic-first symmetric biphasic		69%	7%	45%	28%
Cathodic-first pseudomonophasic		64%	3%	43%	5%
Anodic-first pseudomonophasic		10%	19%	6%	41%

Considering the tendency of anodic phase excitation to occur in the proximal nerve as opposed to cathodic phases that semi-selectively excite spikes at the distal heminode, stimulation selectivity should improve when the anodic phase is minimized. Although the need to balance charge flow across the electrode-saline interface precludes using truly monophasic cathodic stimuli, a cathodic-first pseudomonophasic pulse can approximate this ideal. As shown in Table 3, cathodic-first pseudomonophasic pulses did indeed yield a marked reduction in anodic-phase excitation of model afferents and a net boost in selectivity. This improvement was evident across all stimulus intensities modeled. Figure 9 shows the model’s fiber recruitment curve for cathodic-first pseudomonophasic pulses delivered via the same monopolar arrangement described in Figures 8a and 8e.

Figure 9.

Model recruitment curve for monopolar anterior canal electrode case shown in Fig. 8a but using cathodic-first pseudomonophasic stimuli. Improved selectivity is apparent compared to standard symmetric biphasic pulse stimulus (Fig. 8e).

For bipolar electrode configurations, pseudomonophasic stimuli offered no performance gain over the standard symmetric biphasic waveform. Similarly, inverting the standard symmetric waveform to be anodic-first yielded no benefit in the model or during empiric 3D aVOR measurements.

Discussion

Previous Models of the Inner Ear

Given the small size of the inner ear and the fragility of its contents, direct measurement of currents induced by a vestibular prosthesis electrode in each of the ampullary and macular nerves is probably impossible without disturbing the system enough to invalidate the measurements. However, the inner ear comprises only a few compartments with known conductivities and geometry that can be precisely measured, so it is a good system to model using finite element analysis. When coupled with computational models of action potential initiation, finite element models of the cochlea have provided helpful guidance for design of cochlear implant electrodes, stimulus protocols and implantation techniques (Spelman et al 1982, 1995; Suesserman and Spelman 1993; Finley et al 1990; Frijns et al 1995; Hanekom 2001, 2005; Whiten 2007). Such models can emulate real systems with impressive fidelity. For example, patient-specific models created from 3D reconstructions of histologic sections through three temporal bones of deceased cochlear implant users yielded results that agreed quantitatively with an extensive archive of measured intracochlear potentials, psychophysical thresholds and electrically-evoked compound action potential recordings recorded from each subject (Whiten 2007). While no computational model can exactly replicate a real system, models such as these allow one to rapidly generate testable hypotheses and perform ‘virtual experiments’ using different designs and pathologic scenarios prior to implantation of animals or patients.

In contrast to the growing body of literature on modeling cochlear implants, no comparable model of the labyrinth has yet been described. Fortunately, conductivity data can be adapted from cochlear models, labyrinthine anatomy can be extracted from 3D imaging data, computational tools are available for finite element analysis on inexpensive computers, and well validated models of vestibular afferent action potential initiation, repolarization and conduction already exist (Smith and Goldberg 1986; Frijns JH and ten Kate 1994; Rubinstein et al. 2001, 2002; McIntyre et al 2002). Conditions are therefore excellent for development of an anatomically precise model describing the biophysics of electrode-nerve interaction in the labyrinth.

Potential Sources of Error: Model Assumptions and Simplifications

Simplifying assumptions are required to create a practical model of the implanted labyrinth. For the current model, these included simplifications of anatomical detail, volume conductor biophysics, and physiology.

Anatomical Simplifications

While the model we report here is the most precise and accurate model of labyrinthine current flow yet described, it includes several anatomic simplifications. One weakness of the finite element method is its difficulty in handling thin structures like periosteum, dura and the membranous labyrinth. Lumping perilymphatic and endolymphatic spaces into a single homogeneous volume conductor is probably justified for the brief current pulses typically used in an MVP (for which capacitive currents readily cross the membranous labyrinth walls). We neglected dura and endosteum for analogous reasons. These assumptions could lead to errors if applied to DC or low frequency current stimuli.

Placement of virtual electrodes in the model mesh relied on coregistration of an animal’s microCT with the ‘standard labyrinth’ created from another animal’s MRI and CT. Although labyrinthine anatomy is highly conserved within animals of a given species, there is still some variation (e.g., the location of the midpoint of a semicircular canal with respect to the skull stereotaxic origin varies with standard deviation up to ~0.5 mm in chinchilla [Hullar and Williams 2006] and ~4 mm in humans [Della Santina et al 2005C]), so this process is imperfect.

Biophysical Simplifications

Models of biological volume conductors usually assume quasistatic conditions, for which reactive components of biological tissue impedance are negligible and each finite element can be considered purely resistive. Since measured dielectric relaxation times for biological tissues are much shorter than the stimulus pulses we used, this simplification is well justified. Spelman et al (1982) found that quasistatic assumptions hold for stimuli up to 12.5 kHz in the cochlea. For symmetric 200 μS/phase biphasic pulses with 30 μS interphase gap, 95% of the spectral energy lies below 10 kHz. Pseudomonophasic pulses we modeled had even more of their energy below 10 kHz. Therefore, the quasistatic assumption probably caused negligible error. Errors would be greater when this model is applied to pulses <50 μS/phase.

In general, tissue conductivity is frequency dependent. Fortunately, conductivities have been described for several species and tissue types; however, many tissues have only been characterized for frequencies outside of our region of interest (Geddes and Baker 1967). In such cases, we used values measured at lower frequency.

Most models of the implanted cochlea have assumed isotropic neural tissue (Finley et al 1990; Frijns et al 1995; Whiten 2003, 2007). However, peripheral and cranial nerves and other fiber tracts are best approximated as anisotropic media, with axial conductivity much greater than transverse conductivity (Tasaki 1964; Ranck and Bement 1965; Hanekom 2001, 2005). Absent data for chinchilla, we used nerve conductivities measured by Tasaki for myelinated frog peripheral nerves (Table 1). A parameter sensitivity analysis studying transverse conductivities ranging from 0.0143 Ω⁻¹/m (the value we used) up to 0.333 (our value for axial conductivity) revealed that fiber activation thresholds were quite sensitive to transverse conductivity, with larger conductivity resulting in greater selectivity of stimulation. When transverse conductivity was set equal to 0.333 Ω⁻¹/m (making the nerves isotropic), the model predicted a wide spread in activation thresholds for different nerve branches, with nearly all fibers in the target branch activating at stimulus currents below the threshold for the next nearest nerve branch, which in turn had thresholds lower than the next nearest nerve branch. This effect should have been manifest by discrete jumps in 3D aVOR axis with increasing stimulus current amplitude. Since we have not observed this effect, we conclude that modeling nerve conductivity as anisotropic better reflects reality.

Bone conductivity is a key parameter in numerical models of the inner ear. Unfortunately, existing literature includes a wide range of values for bone conductivity, from 0.0063–0.16 Ω⁻¹/m (Geddes and Baker 1967; Girzon 1987; Finley et al 1990; Frijns et al 1995; Suesserman and Spelman 1993; Hanekom 2001, 2005; Whiten 2007; Haueisen et al 1995). Absent a clear literature consensus regarding the value of bone conductivity, we chose a relatively low value (0.0139 Ω⁻¹/m) based on a parameter sensitivity analysis (Hayden 2007). Since bone conductivity remains low and relatively constant for stimulus frequencies below about ~25 kHz (Kosterich et al 1983), we did not include a frequency dependence for bone in the model. For stimulus pulses shorter than ~20 μS/phase, bone conductivity should rise and stimulus currents required to activate afferents should also rise (i.e., electrode-nerve-coupling to the target nerve branch is weaker), but the net effect on relative activation of target versus nontarget branches (i.e., selectivity) is small (Hayden 2007).

Physiological Simplifications

Even after gentamicin treatment sufficient to ablate the aVOR to head rotation, Type II hair cell bodies are still present. Although denuded of stereocilia, they may still modulate neurotransmitter release in response to exogenous currents. Errors due to excluding these from the model were probably small for suprathreshold stimuli, since available evidence suggests that currents delivered by MVP electrodes mainly act at the vestibular afferent heminode (Goldberg et al 1984). We also ignored effects of synapse type (i.e., calyceal versus bouton), dendritic tree complexity, vestibular afferent somata and efferent fibers in the vestibular nerve. All of these could be added as refinements to the model framework.

We neglected effects of macular nerve activity when predicting 3D eye movement axes from the pattern of vestibular nerve activity reported by the model. Existing evidence suggests that responses to activation of a single focal region on a single macula (or any small bundle of axons within the utricular or saccular nerve) are relatively small compared to ampullary nerve responses and often disconjugate, with direction and speed that depend not only on which afferents are activated but also on the temporal dynamics of the stimulus, visual target distance and eccentricity, and the pattern of simultaneous activity in ampullary nerves (Fluur and Mellström 1970a, 1970b, 1971; Goto et al. 2003, 2004; Curthoys 1987; Meng and Angelaki 2006). Absent clear guidance from the literature regarding the relationship between macular stimulation patterns and the 3D axis of aVOR/tVOR responses, we assumed that macula-mediated responses were negligible.

This could be improved in future model version. For example, it seems reasonable to assume that disconjugacy between 3D rotation axes of the two eyes during prosthetic stimulation represents an electrically-evoked tVOR driven by inadvertent macular nerve stimulation. Absence of disconjugacy could therefore indicate absence of spurious macular nerve stimulation. Unfortunately, any finite amount of disconjugacy cannot be uniquely mapped back to infer the pattern of macular nerve activity, so refinement of this aspect of the model will require direct electrophysiology measurements of vestibular nerve afferent activity. Efforts toward obtaining such data have begun recently (Phillips et al 2010).

Finally, we assumed a direct mapping from relative activation levels of one labyrinth’s three ampullary nerves to the 3D aVOR components about the axes’ of the corresponding SCCs. Prior studies suggest that this is a reasonable approximation for the acute stimulation paradigms we used (Fridman et al 2010), but it ignores contributions of central nervous system circuitry to the 3D aVOR response. Dai et al (2011) recently demonstrated adaptive changes in 3D aVOR responses of chinchillas allowed to wear a head mounted MVP continuously for 1 week, supporting the conclusion that the central nervous system rapidly intervenes to reduce 3D aVOR misalignment causing abnormal slip of retinal images. While that effect is welcome news to those developing an MVP for clinical application, it also means that only acute VOR responses measured in darkness (or direct nerve recordings) should be used for virtual labyrinth model refinement.

Opportunities for Model Refinement and Application

Each of the assumptions described above represents an opportunity for model refinement. Key priorities include (1) adjustment of model parameters based on single-unit vestibular afferent recordings that empirically measure data corresponding to the model’s fiber recruitment curves; (2) addition of model cochlear afferents; (3) incorporating effects of neurotransmitter release engendered by stimulus currents traversing hair cell somata; and (4) extension of the approach to geometry of monkeys and humans.

Conclusion

Evaluation of different electrode designs and stimulus protocols for a multichannel vestibular prosthesis using 3D oculography or electrophysiologic experiments is costly in terms of investigator time, animals and other research resources. Individual variation in exact electrode location, central adaptation and other factors varying from one implanted animal to the next can preclude drawing solid general conclusions without performing a large number of experiments. Inability to methodically displace electrodes in situ by precisely controlled distances prevents systematic in vivo study of how electrode location affects coupling and sensitivity. Lack of clarity regarding eye movements evoked by excitation of different macular nerve regions complicates the use of 3D aVOR as an assay of electrode-nerve coupling and selectivity, and attempts to directly record from vestibular afferents during prosthetic electrical stimulation can be complicated or confounded by stimulus artifacts and other interactions between stimulating and recording electrodes (Phillips 2010).

Developed in response to analogous challenges, anatomically realistic models of cochlear implants have become valuable tools to aid design of scala tympani arrays (e.g., Spelman et al 1982, 1995; Suesserman and Spelman 1993; Frijns et al 1995; Hanekom 2001, 2005; Whiten 2007). Comparably complex models of semicircular fluid dynamics have provided a clearer understanding of mechanisms underlying head motion transduction, cupular deflection, and benign paroxysmal positional vertigo (Rajguru et al 2004, 2007; Ifediba et al 2007; Rabbitt et al 2009). While no computational model can capture all aspects of a complex system like the labyrinth with sufficient accuracy and precision to obviate empiric experiments, the model we have described provides an anatomically precise, flexible and efficient tool to guide refinement of prosthetic electrode arrays and stimulus waveforms. As for other models, the virtual labyrinth’s simulation results are only useful to the extent that they accurately reflect the real system’s behavior. However, an iterative process of model prediction, empiric testing and model refinement should reach a point at which results of ‘virtual experiments’ can stand alone as valuable indicators of a new electrode design’s performance relative to alternate designs. Created to be readily modifiable, the virtual labyrinth model can be rapidly adapted to different electrode array geometries and stimulus waveforms, and it can be readily adapted for other species, including humans.