Statistical significance in genetic association studies

Clinical & Investigative Medicine (CIM) is receiving an increasing number of reports of candidate-based association studies. The track record of such studies in the past was poor. Numerous genetic associations reported by candidate gene studies was not replicated by later studies[1]. The rise of Genome wide association studies (GWAS) is changing this situation. A well-designed GWAS study may identify a number of candidate loci unbiasedly by screening the whole human genome. Validating and fine-mapping the candidate loci from GWAS are required to clarify the genetic mechanisms. Candidate-based association study is becoming a well-directed effort, instead of searching for a needle in a haystack like before. In the post-GWAS era, we are expecting exponential growth of candidate-based genetic association studies. A pressing issue accompanying this new trend is the assessment of the validity of an association study. By this editorial, we manifest the major cause of false positive association from random sampling bias by an empirical example, and emphasize the application of the probability theory in assessing the validity of a genetic association study.

For the majority of human common diseases, the etiology has not been understood sufficiently. The lack of knowledge impeded the development of effective strategies to prevent or cure the diseases. The effort to understand the molecular mechanisms of common diseases has been complicated by the fact that a common disease usually involves multiple etiological pathways mediated by many of the approximately 20,000 to 25,000 protein-coding genes encoded in the human genome[2]. With the completion of the Human Genome Project in 2003, human genetics has become an indispensable approach to understand the molecular basis of common diseases, and has penetrated into every branch of biomedical science. The theme of human genetics is genes and genetic variations in the highly polymorphic human genome. There are >11 million common DNA variants with frequencies ≥1%, i.e. DNA polymorphisms, in the human genome (the NCBI dbSNP database, http://www.ncbi.nlm.nih.gov/projects/SNP; the 1000 genome project, http://www.1000genomes.org). Except for identical (monozygotic) twins, no two individual’s genomes are identical, although the difference is less than 0.1% of the whole genome between any two persons across the world. Because of the wide-spread of DNA polymorphisms, different individuals may have different susceptibility to a common disease[3]. The diversity of genetic susceptibility to common diseases in the human population enables researchers to understand the molecular mechanisms of common diseases by the method of genetic association study, which examines the coexistence of genetic markers with a disease.

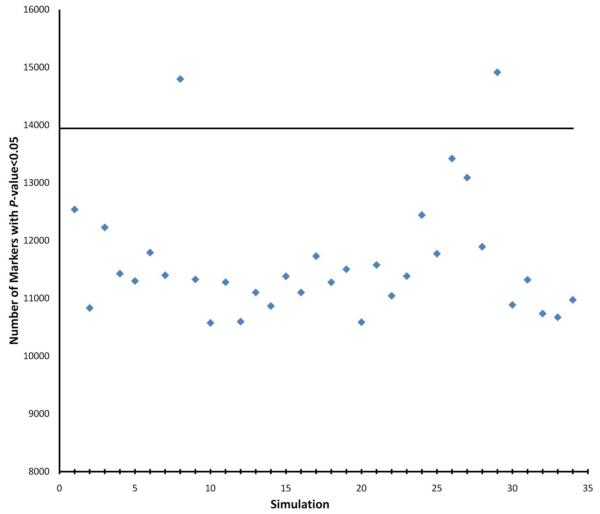
In the analysis of genetic association studies, a parameter of statistical significance, a P-value, is used to determine the certainty of an association. A P-value provides the probability that a given result from a test is due to chance. A common cutoff for each test, such as an α=0.05, claims a 95% certainty that the result is not a coincidence. However, a genetic association study usually tests multiple genetic markers, therefore false positives by chance will accumulate. If each test has 95% certainty, the certainty of n tests to be true will lower to (95%)ⁿ. A GWAS study implements robust genomic technologies and involves an extraordinary number of hypotheses and statistical tests. They are robust examples of the accumulated errors from multiple tests. To demonstrate the accumulated errors empirically, we performed an experiment using a GWAS dataset, the Gene Environment Association Studies initiative (GENEVA, http://www.genevastudy.org) in type 2 diabetes (T2D), involving 3,148 cases and 2,745 controls[4]. From the 871,166 autosome single-nucleotide polymorphisms (SNP) genotyped in this study, we removed all the SNPs with possible disease association in this cohort (56,103 SNPs with P≤0.05). Further, from the remaining 815,063 SNPs, we kept only 278,869 SNPs with low linkage disequilibrium (LD), by pruning out all the other SNPs with r²≥0.5 with these SNPs, to assure that genotyping the retained 278,869 SNPs represented independent tests. Consequently, we performed a resampling experiment, i.e. 500 cases and 500 controls were randomly sampled from the GENEVA T2D cohort, while T2D associations were tested in the resampling cohort. We repeated the resampling experiment for 34 times. A large number of SNPs showed P≤0.05 in each resampling cohort (Fig.1, $\stackrel{‒}{x}\pm s=11,641\pm 1,059$). As we have removed all the SNPs with P≤0.05 in the original cohort, we can assume all these P≤0.05 in the resampling cohort as false positives due to random sampling bias. The average false positive rate is 4.17%±0.38%. Although we pruned out all the other SNPs with r²≥0.5 with these SNPs, the remnant LD among SNPs explains the lower false positive rate from the smaller number of independent hypotheses. The false positives from random sampling bias also explain the transient positives that are commonly seen in low throughput genetic association studies, and disappear with the genotyping of more DNA samples.

Fig.1.

Number of false positive associations in the resampling experiment. X-axis represents 34 times of resampling; Y-axis represents the number of tests with P≤0.05. The horizontal line corresponds to 13,943 false positives (i.e. 5% of 278,869 independent hypotheses by chance alone). The average false positive rate of 4.17% suggests that the 278,869 SNPs across human genome are not completely independent because of LD (~232,577 independent hypotheses).

To address the accumulated errors from multiple tests, desiring a valid statistical evidence will require a corrected significance cutoff. Two methods are commonly used to determine the corrected cutoff, i.e. the Bonferroni correction and the false discovery rate (FDR) correction. The Bonferroni correction is a stringent method, which adjusts p-values by multiplying each p-value with the total number of tests[5]. Only the adjusted p-values ≤0.05 are taken as statistical significant. The False discovery rate (FDR) correction was introduced by Benjamini and Hochberg[6]. The FDR method first ranks all p-values from the smallest to the largest, and then adjusts each p-value accordingly:

$$FDRcorrectedp=\frac{Numberoftests}{pRank}\times p$$

FDR corrections is less stringent and tolerates more false positives, i.e. a FDR=0.05 allows 5% of reported positives are false positives, while the Bonferroni correction α=0.05 requires the whole family of positives to be true positives with the certainty of 95%. However, for the smallest p-value in one study, the Bonferroni corrected p-value is equal to the FDR corrected p-value.

In our resampling experiment, both the Bonferroni correction and the FDR correction addressed the false positive issue. No p-value from the random sampling bias has cleared either correction. The median of the minium p-value of each of the 34 resamplings is 8.75×10⁻⁶, while the smallest p-value of the 34 resamplings is 3.89×10⁻⁷. In our experiment, to get at least one p-value with significance by either Bonferroni correction or FDR correction, the smallest p-value should be less than α=0.05/278,869=1.79×10⁻⁷.

Statistical analysis based on probability theory provides the most critical criterion to assess the validity of the results of a biomedical research. GWAS studies are the perfect examples of the rigorous usage of probability theory to claim the significance of the results. Multiple testing corrections are indispensable to identify true positives and sift out false positives. The large number of false positives in GWAS studies highlights the importance of duly adjusting for multiple tests in the smaller scale and candidate-based genetic association studies. Because of the availability of inexpensive and high-throughput genotyping technology, the cost of DNA genotyping has been much lower than the cost of sample recruitment. A candidate-based genetic association study usually tests multiple loci and markers. Yet, most association studies on candidate gene still published nowadays (and those submitted to CIM) make no mention of the multiple genes that were tested and found not to be significant, only presenting those with p < 0.05. Although it is conceivable that hundreds or thousands of DNA samples were really collected to test a single candidate gene and then destroyed, this is a totally implausible scenario that certainly does not apply in the majority of these reports.

In summary, to ensure the validity of a genetic association article, we require that a study with a definite number of hypotheses (e.g. a GWAS study) should be supported by the statistical significance after correction for multiple testing comparisons. In such a case, the total number of hypotheses used for statistical correction should be justified in the article. Attention is needed for the data interpretation of such studies: if a GWAS study is reporting a number of positive loci (and the related molecular pathways), statistical significance after the less stringent FDR correction would be sufficient; however, for any conclusion on a specific genetic locus, statistical significance after Bonferroni correction is required. For a candidate-based study that the total number of hypotheses cannot be justified indubitably, the association needs to be validated. An independent cohort that has a definite number of hypotheses to be validated can usually offer sufficient statistical evidence. Published GWAS studies on the same phenotype can be a precious resource for the validation purpose. To date, a large number of GWAS data are publicly available in two major GWAS databases, i.e. the NCBI database of Genotypes and Phenotypes (dbGaP, http://www.ncbi.nlm.nih.gov/gap), and the European Genome-phenome Archive (EGA, http://www.ebi.ac.uk/ega). The replication of an association in a public GWAS dataset may be limited by the coverage of the GWAS SNP genotyping arrays. In this case, in silico replication of the association can be done in the GWAS cohort. Depending on the ethnic background of the GWAS subjects, one of the 11 populations genotyped in the HapMap study (phase 2 and phase 3, Feb 09 Release, http://www.hapmap.org) can be used as the reference population. Interesting DNA polymorphisms need to be genotyped in the reference population if not genotyped by the HapMap project. DNA samples of different populations can be acquired from the Human Population Collections of the Coriell Cell Repositories (http://ccr.coriell.org). Consequently, the genotypes and association in the GWAS study can be imputed by the hidden Markov Chain based algorithm, e.g. the MACH software (http://www.sph.umich.edu/csg/abecasis/MaCH/index.html).

Limited by the low throughput genotyping technology, previous association studies had to focus on genes with candidate functions, which had little value in helping us to understand the unknown aspects of a disease. Because a GWAS is hypothesis-free, it has turned out to be a great success in understanding unknown aspects of many human common diseases by examining hundreds of thousands of genetic markers across human genome unbiasedly for disease association[3]. On the other hand, a GWAS has still a limited statistical power and a limited coverage of human genomics. A GWAS may suggest many interesting loci, whereas to be conclusive on novel molecular mechanisms in a disease, association of the candidate loci needs to be validated and fine-mapped. The method of genetic association study is getting more efficient in helping us understand human diseases. The probability theory is a critical fundament of modern biomedical research, which has been strictly applied in GWAS studies, and should not be neglected in candidate gene studies.