Cooperative Responses of Multiple Kinesins to Variable and Constant Loads

Background: Multiple kinesin function is central to intracellular transport.

Results: Unlike single-motor molecules, two kinesin velocities can depend on whether loads vary spatially or temporally.

Conclusion: Kinesin cooperation is influenced appreciably by spatially dependent changes in load.

Significance: Factors governing the force-time history and spatial dependence of loads must be examined to understand mechanisms regulating intracellular transport.

Abstract

Microtubule-dependent transport is most often driven by collections of kinesins and dyneins that function in either a concerted fashion or antagonistically. Several lines of evidence suggest that cargo transport may not be influenced appreciably by the combined action of multiple kinesins. Yet, as in previous optical trapping experiments, the forces imposed on cargos will vary spatially and temporally in cells depending on a number of local environmental factors, and the influence of these conditions has been largely overlooked. Here, we characterize the dynamics of structurally defined complexes containing multiple kinesins under the controlled loads of an optical force clamp. While demonstrating that there are generic kinetic barriers that restrict the ability of multiple kinesins to cooperate productively, the spatial and temporal properties of applied loads is found to play an important role in the collective dynamics of multiple motor systems. We propose this dependence has implications for intracellular transport processes, especially for bidirectional transport.

Introduction

Many subcellular commodities are transported within the cytoplasm by groups of interacting microtubule motors, and there is evidence that such behavior is central to mechanisms that regulate and maintain the internal organization of eukaryotic cells (1, 2). The combined function of motors may allow some cargos to be transported over longer distances and against higher opposing forces than single motor molecules can produce on their own (3). Additionally, many cargos are transported by multiple oppositely directed kinesin and dynein motors and move bidirectionally along microtubule filaments (4, 5). While this competition between antagonistic motors likely contributes to a number of intracellular trafficking processes, bidirectional transport has also been proposed to help disperse cargos throughout the cytoplasm (6), and, similarly, to allow cargos to avoid specific obstructions that would otherwise restrict their motion (4, 7).

Recently, mechanisms governing bidirectional cargo transport have received increased attention (8, 9, 10). In particular, many efforts have focused on determining whether different motor teams coordinate their activities, or whether motors simply compete in a potentially slower game of tug-of-war where the strongest motor team wins and therefore determines the net direction of cargo motion. Observations of how fast cargos reverse their transport direction are often used to choose between these mechanisms (11). However, a new theoretical model also suggests that, provided motor teams possess certain mechanochemical properties, cargos can still switch rapidly between plus- and minus-directed motions even if they are engaged in a tug-of-war (8). This behavior is believed to occur since the unbinding of a motor within one of the teams can cause the remaining motors in that team to experience higher forces, which, in turn, can promote an unbinding reaction cascade where all of the motors in the losing team release from the filament.

Given the differences between the candidate mechanisms described above, understanding the principles underlying bidirectional transport requires more detailed characterization of how loads are distributed between different motors on a cargo, and particularly, whether they can cooperate productively via sharing their total applied load, an issue that has proved to be fairly complicated in its own right. Recent experimental and theoretical studies have shown that multiple kinesins can produce larger run lengths and forces than single kinesin molecules (12, 13). However, when cargos are transported by small groups of kinesins, average cargo-filament detachment forces and velocities have been reported to be remarkably similar to those produced by single kinesin molecules, indicating multiple kinesin deviate from load-sharing behaviors (14).

We have proposed that these results stem from the fact that a group of kinesins can bind to a filament in many different configurations that are not only distinguished by the number of bound motors, but also the distance between the lattice sites positions of each motor along the microtubule (14, 15). The geometry of a multiple motor system's bound configuration dictates how loads on a cargo are distributed between its filament-bound motors (14). For spherical cargos, the front (leading) motor of a complex will bear the majority of a cargo's total applied load if its motors are spaced more than a few lattice sites apart from one another. Cooperative motor behaviors are therefore dependent on the amount of time motor complexes spend bound in these configurations compared with those where motors are spaced closely on the microtubule and can share their load more equitably. Yet, recent theoretical studies indicate there are several kinetic barriers that reduce the abilities of multiple-kinesin complexes to transition from single load-bearing motor configurations to those where each motor can assume a significant portion of the applied load (15). Overall, such behavior indicates that variation in the number of kinesins on a cargo beyond the simple presence or absence of motors will not have a large influence over their competition with other motor types, such as dynein.

Many of the above analyses were made possible by new methods to create multiple motor complexes that have defined compositions, structural organization, and elastic properties. However, to date, the transport properties of these types of complexes have only been investigated in either the absence of applied loads (13, 16), or using a static optical trap where applied loads vary both spatially and temporally (14). There is new theoretical evidence suggesting that multiple motor velocities can be influenced by temporal changes in the applied load and that cargo velocities can even be hysteretic if applied loads change rapidly in time (17). Such behavior could occur if the rate that applied loads change is faster than the rate that a complex can remodel its bound configurations in response to a changing load. Thus, cargo transport by multiple kinesins may be influenced by the loading conditions produced in a static optical trap in ways that diminish their ability to produce large forces and move cargo with higher velocities. Nevertheless, even if these extrinsic factors dominate the dynamics of multiple motors in these types of assays, understanding the impact of these effects is still important since applied loads stem from various sources in cells, and accordingly, motors will experience a wide range of loads with different spatial and temporal dependences (e.g. loads will vary spatially and in time when antagonistic motors stretch their cargos during a tug-of-war). Here, we assess the role of such effects by examining the transport behaviors of organized multiple motor complexes containing two coupled kinesin-1 motor molecules under the controlled loads provided by an automated optical force clamp.

EXPERIMENTAL PROCEDURES

Two Kinesin Trapping Assays

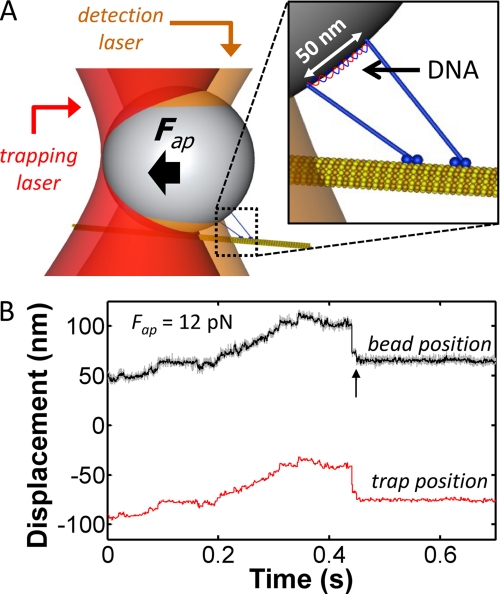
Force clamp assays were performed using multiple motor complexes composed of two recombinant human kinesin-1 motors that are coupled by a single DNA duplex (50 nm in length) that functions as a molecular scaffold (Fig. 1A) (13, 14). The kinesins are linked to each end of the scaffold via engineered, DNA-conjugated protein polymers (18). Biotin molecules are also incorporated into each end of the scaffold to allow the motor assemblies to be anchored to the surface of streptavidin-coated beads (500 nm diameter).

FIGURE 1.

Bead transport by two kinesins in an optical force clamp: A, schematic diagram of the two-kinesin complex shown anchored to a 500 nm bead. The DNA scaffold is labeled in the inset. B, position-time trace for the bead (black) and trap center position (red) where the applied load was held constant at 12 pN.

Motor preparations and other assay conditions were identical to those used in our previous optical trapping experiments (14). In this procedure, two-kinesin complexes are first preformed in solution and then bound to bead surfaces using scaffold/bead concentration ratios where <30% of the beads interrogated, move along microtubules. Under these conditions, ∼93% of beads should possess no more than one surface-bound kinesin assembly. The probability that two assemblies on a bead are positioned close enough such that both can bind a microtubule simultaneously is <2%. To further ensure beads possessed two functional kinesins in the force clamp, beads were interrogated to verify their ability to advance forward continuously under an applied load of 10 pN. Afterward, the same bead was examined at lower applied loads. Force clamp assays were performed using similar procedures to those reported for single kinesin molecules (19). A description of these methods is provided in the supporting information.

Data Analyses

Force clamp data were anti-alias filtered at 10 kHz and then digitized at 30 kHz. Average bead velocities were determined using a linear regression procedure that is similar to those presented in prior reports (14, 24). In this procedure, velocity segments are determined via a linear regression/chi-squared optimization procedure that both partitions traces into segments where beads moved with approximately constant velocities and determines bead velocities during these segments. Average bead velocities were weighted by the time they spent moving with a persistent velocity within a trace segment. While analogous to previous single kinesin analyses where motor velocities are weighted by bead run lengths, this treatment is necessary for analyses of multiple motor behaviors since bead velocities will change depending on the number of load bearing motors in the complex, and the time a complex will spend in these conformations factors into a cargo net average velocity.

Relaxation time constants (τ) describing how rapidly two-kinesin velocities relax to a steady-state value were analyzed by fitting the time-dependent bead velocities to an exponential function: v(t) = v(0)exp(t/τ). Run lengths are taken as the total distance beads were transported forward in the optical trap.

Pairwise distributions of bead displacements or step sizes were generated using established methods. Cargo displacement amplitudes were also analyzed using an objective step-finding algorithm (20). Noise levels in traces were near-identical to those of our static trapping report (14). Predicted dependences of bead displacement sizes on the spacing between the kinesins on the microtubule are also provided in that report.

Modeling

The illustrations of multiple motor complexes in Figs. 1, 4, and 7 were generated with a mechanical model that uses measurements of single motor elasticity along with an energy minimization procedure to determine the distribution of loads within a complex and the position of the bead when both kinesins are bound to the microtubule at specified locations (14). The use of this procedure to calculate the rates motors will bind to, detach from, and step along the microtubule is described in Ref. 15. During these calculations, we assume the vectorial forces experienced by the motors will reach their equilibrium values rapidly compared with the rates motors step, bind, and detach. With this assumption, configuration-dependent transition rates are determined by the change in a complex's strain energy due to the stretching/relaxation of motor-bead linkages (see supplemental data). For the present analyses, these calculations were used to estimate the lattice positions along a microtubule that the trailing kinesin would bind most often and how rapidly a complex transitions from single-load bearing motor to load sharing configurations via motor stepping. The full form of our transition rate model described in Ref. 15 was also used to predict how the distributions of complex's bound geometry evolve in time when applied loads are changed upon activation of the force clamp. A summary of these procedures is provided in the supplemental data.

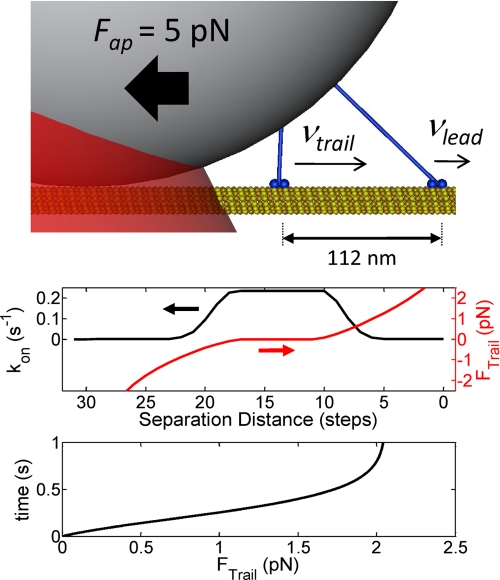
FIGURE 4.

The time required for two-kinesin complexes to develop load-sharing configurations is large. Mechanical modeling of two-kinesin complexes (see Ref. 14) indicates that trailing motors will typically bind at sites positioned well behind their leading partners. When F_ap = 5 pN, this model predicts motors will be separated by 112 nm on the microtubule on average (illustration at top). The plot beneath the illustration shows a predicted dependence of the rate at which the trailing motor will bind to different sites (black line, left axis) and the corresponding load this motor will experience after a binding transition (red line, right axis). The bottom plot shows the rate that the trailing motor's portion of the 5 pN load increases assuming the separation distance between the leading and trailing motor was initially 112 nm.

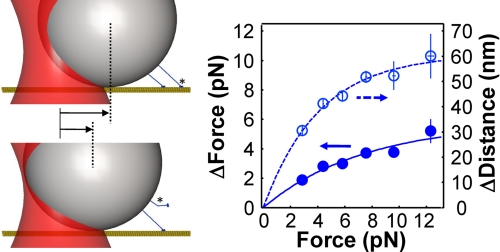
FIGURE 7.

The impact of multistate detachment when applied loads vary spatially. When multiple motors experience spatially dependent applied loads, the partial detachment of a complex leads to rearward cargo displacements that can reduce the load on the bead. Because these displacements are accompanied by changes in the number of bound motors, this process affects the force-dependent probability that a complex will be bound via a single or both motor molecules of a complex. Measurements of reward displacement sizes in a static optical trap (κ_trap = 0.072 pN/nm) indicate that the applied load changes by 4–5 pN on average upon partial bead detachment if it exceeds kinesin's 7 pN stalling force. Such large changes in load can result in a significant reduction in the probability that a two-kinesin complex will be bound via a single motor within this force regime, and therefore result in higher cargo velocities, on average, relative to cases where the applied load remains constant or varies weakly as a function of cargo position. The lines in the plot depict exponential fits to the static trapping data.

RESULTS

Signatures of Two-Kinesin Function

Using the synthetic methods and assay conditions reported in Ref. 14 and “Experimental Procedures,” bead trajectories produced by two-kinesin complexes in the force clamp contained several signatures of multiple-motor dynamics found in our previous optical trapping study (Figs. 1 and 2). Among these signatures is the ability to transport beads forward against loads that exceed the stalling force of a single kinesin motor (7.6 pN for our kinesin construct). An example of this behavior is provided in Fig. 1B, where a two-kinesin complex is shown transporting its bead against an applied load of 12 pN and over a distance of ∼50 nm. This trace also displays an event where the bead retracts backwards by a distance of 40 nm and then dwells at a fixed position prior to complete detachment. Such events were commonly found in our previous static trapping experiments and were attributed to the partial detachment of the complex (14). In both experiments, large rearward displacements will be produced if a complex's leading motor releases from the microtubule and the bead is left tethered to the filament via a single trailing motor linkage.

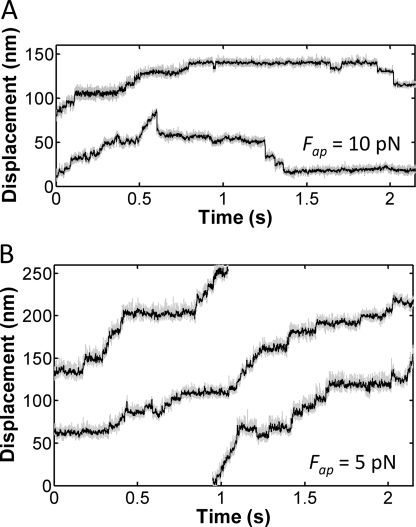
FIGURE 2.

Two-kinesin force clamp traces. A and B, bead position versus time traces are shown for cases where an individual two-kinesin complex transported a bead against a constant load of 10 pN (A), and 5 pN (B). Bead positions were sampled at 30 kHz, after anti-alias filtering at 10 kHz, and then median filtered using a window size of 2 ms. Both the raw (gray) and filtered (black) data are presented.

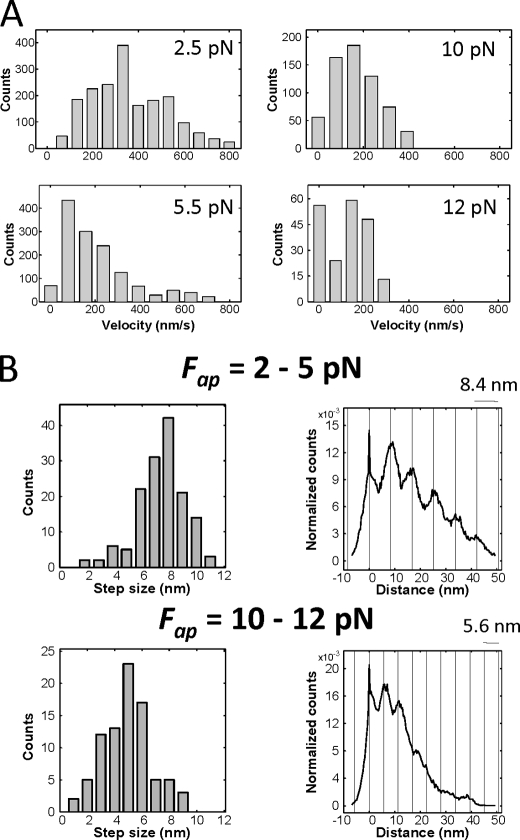
In addition to multistate detachment events, individual bead trajectories were also found to contain mixtures of transport behaviors (Fig. 2). When transporting a bead against a constant 10 pN load, the complexes appear to switch between moments of continuous forward motion and stalling behaviors (Fig. 2A). Similarly, below kinesin's single-motor stalling force, two-kinesin complexes are found to switch between different transport modes where they either moved with high velocities (presumably due to load-sharing between the two motors) or significantly lower velocities (Fig. 2B). In agreement with these observations, histograms of bead velocities for loads of 2.5 and 5.5 pN contain two peaks, one corresponding to the velocities expected if bead transport were driven by only one kinesin within the complex, and a second peak at higher velocities (Fig. 3A). The larger amplitudes of the low velocity peaks shows that, as in our prior optical trapping study (14), bead transport by two kinesins is dominated by the action of a single load-bearing motor and that load sharing makes a relatively small contribution to cargo transport when the applied load is beneath kinesin's stalling force.

FIGURE 3.

Two-kinesin velocity and step-size distributions against constant loads. A, velocity distribution histograms for two-kinesin complexes at applied loads ranging between 2.5 and 12 pN. The load maintained by the force clamp is indicated in each panel. Bead velocities were determined via a chi-squared minimization procedure reported in Ref. 24. Each plot is constructed from 7–27 trajectories (3–19 complexes). Bin counts were taken as the number of distinct trace components where beads moved with a velocity within the range of each bin for a period of 16 ms. B, distributions of bead displacement sizes found using a step-finding algorithm and their corresponding pairwise displacement distribution histograms. Bead displacement analyses are presented separately for cases where the force clamp was used to impose either low (2–5 pN; 58 traces included) or high (10–12 pN; 27 traces included) resisting loads.

Cargo Displacement Sizes Depend on the Magnitude of the Applied Load

Analyses of bead displacement amplitudes also reflect the prevalence of single load-bearing motor behaviors at low applied loads. When constructed from traces where the force clamp's load was less than 7 pN (Fig. 3B, upper panels), histograms of two-kinesin bead displacement sizes display a dominant peak centered at 8.1 ± 1.9 nm, single-motor step size of kinesin. The prevalence of such displacements is also found in histograms of pairwise bead displacements, which contain a clear dominant periodicity of 8.4 nm. This stepping behavior is similar to that observed in a static trap and is expected given that our velocity data indicates beads are primarily driven by a single motor molecule. Bead displacements equivalent to the kinesin intrinsic step size should be produced when only one motor within the complex assumes the applied load (14).

Measurements of bead displacement amplitudes at high applied loads (≥10 pN) are indicative of both load-sharing between the two kinesins and the predominance of asynchronous motor stepping (Fig. 3B, lower panels). A histogram of bead displacement sizes at these loads contains an asymmetric peak at 5.5 ± 1.9 nm, while the corresponding pairwise distribution histogram shows somewhat less defined periodicity at 5.6 nm. Bead displacements of this size are signatures of asynchronous motor stepping, where one motor in the complex advances forward while the other remains fixed (14, 21). This stepping mode causes the separation distance between motors on the microtubule and the distribution of forces within the complex to change in time. Motor-bead linkages stretch and relax in response to shifts in load distributions (bead rotations also occur), resulting in smaller, but not necessarily fractional, bead displacement sizes relative to the 8 nm step of a single kinesin molecule (14). Furthermore, displacement sizes also depend on whether a complex's leading or trailing motor advances. Thus, one should not expect distributions of bead displacement sizes to be defined as uniformly as those produced by single motor molecules.

Motor Complexes Transition from Single Load-bearing Motor to Load-sharing Configurations Slowly

The velocity and displacement analyses described above show that two-kinesin complexes transport beads primarily in single load-bearing motor configurations when the applied load is less than kinesin's stalling force. To examine this behavior from a structural perspective, we used the mechanical modeling procedures described in Ref. 14 to estimate how loads are distributed between motors within a complex as the separation distance between their microtubule binding sites changes (Fig. 4). The transition rate modeling procedure in Ref. 15 was then used to estimate the rates that an unattached motor will bind to different microtubule lattice site positions for a case where the applied load on the bead was 5 pN. Overall, the model predicts a preference for an unattached motor to bind to sites far behind the complex's leading motors (80–160 nm, and 112 nm on average). A key to understanding this behavior is that the separation distance between the motors affects the position of the bead, motor stalk angles, and the degree to which each motor-bead linkage is stretched (14). When the complex transitions from a single-motor bound configuration to one where a newly bound trailing motor assumes a portion of the applied load, the bead is pulled forward and all of these mechanical parameters change. The energetic costs associated with these motions reduce the binding rates of motors to different lattices sites along the microtubule (13, 15).

With estimates of the loads motors experience over a range of filament-bound configurations, one can calculate the rates that each motor will advance along the microtubule, and hence, the rates that the trailing motor's load will increase in time (15). Given the initial condition where a complex's trailing motor is positioned 112 nm behind its leading partner and is unloaded, the difference in the velocities of the two motors will naturally be large (v_trail − v_lead ∼250 nm/s). Thus, it is not surprising that our model predicts the on-microtubule separation distance between the motors will decrease rapidly immediately after a binding transition (Fig. 4, bottom panel). For example, the trailing motor is found to advance forward and take on 20% of the 5 pN load within 250 ms. However, from this point on, the leading kinesin accelerates and the trailing kinesin decelerates as the trailing motor assumes a larger portion of the applied load. As a result, the time that both motors must remain filament-bound to benefit from load-sharing is actually quite large. For example, we predict it will take ∼500 ms on average for a trailing motor to assume 2 pN of a 5 pN load (Fig. 4), which is a significant portion of the bead's runtime at an applied load of 5 pN (see Fig. 6B and “Discussion” below). Importantly, the kinetic analyses used to assess these timescales do not account for expected setbacks due to motor detachment during a run, or the time motors spend detached from the microtubule. These factors will only increase the amount of time that cargo transport will be driven by only one load-bearing motor during a run, and hence, decrease the likelihood a complex will adopt a load-sharing configuration.

FIGURE 6.

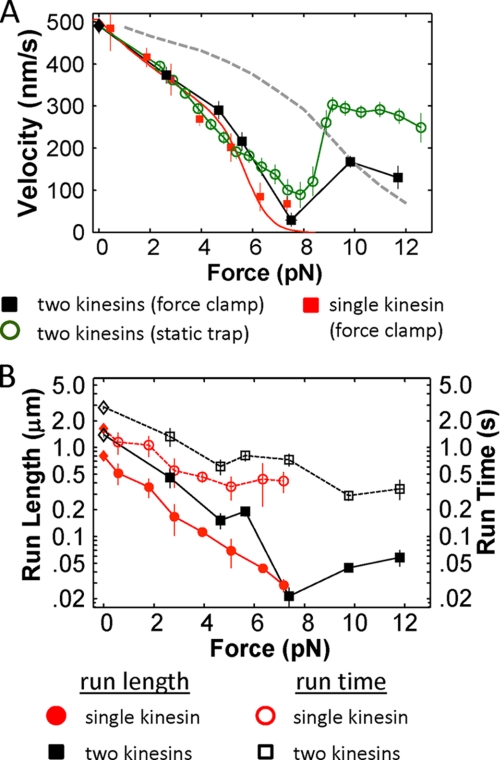
Two-kinesin force-velocity and run time analyses. A, force-velocity (F-V) relationships for two-kinesin complexes (black squares; n_events = 156, range: 4–46; n_complexes = 26, range: 2–18) and single kinesins (red circles; n_events = 125, range: 5–65, n_motor = 21, range: 3–7) measured in a force clamp. In each case, force-feedback was initiated when beads reached a threshold applied load of 2 pN. The load-dependence of two-kinesin velocities in a static trap is presented for comparison (green circles). Velocities are presented as mean ± S.E. The single-kinesin velocity data were fit to the Fisher-Kim model (25). This curve was then used to approximate a trend for two-kinesins if they are assumed to share their applied load equally (gray dashed line). B, average run lengths and run times (mean ± S.E.) measured for single kinesins and two-kinesin complexes are presented as a semi-log plots. The unloaded run lengths and times correspond to previously reported values (13).

Two-kinesin Velocities Relax Rapidly to Their Steady State Values at Low Applied Loads

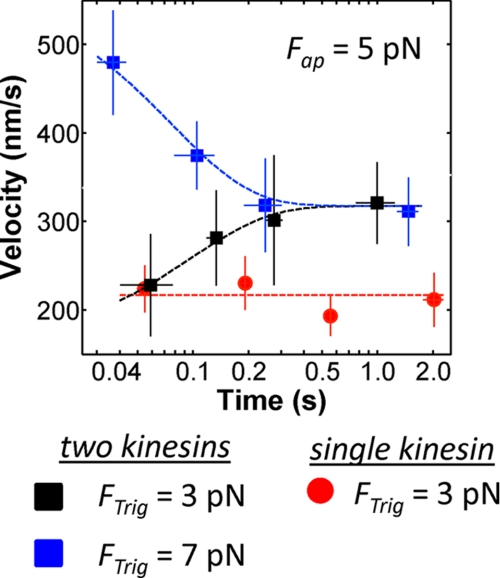
The above analyses support our previous conclusions that there are kinetic barriers that limit a two-kinesin complex's ability to cooperate productively via load sharing when the applied loads are less than the kinesin stalling force (14, 15). The present force-clamp assays also offer the unique ability to examine the extent to which such behavior is affected by the temporal history of an applied load. To test this, we compared the time-dependent responses of bead velocities in experiments where the applied load was maintained at 5 pN by the force clamp, but where the force threshold (F_Trig) used to initiate the feedback mode of the optical trap was set to either 3 or 7 pN (Fig. 5). When force-feedback was triggered at 3 pN, average bead velocities are found to increase in time from a value that is near-equivalent to a single-motor velocity (228 ± 58 nm/s) to an appreciably higher velocity (321 ± 47 nm/s); note, the relatively large standard errors are expected given the mixtures of transport behaviors found in the velocity distribution histograms. Nevertheless, beads only accelerate for a period of ∼200 ms after the force is jumped from 3 to 5 pN (τ = 96 ms; determined via an exponential fit). Over longer time periods, average bead velocities appear to reach a constant (time-invariant) value. On the other hand, when F_Trig = 7 pN, the beads initially moved with high average velocities (497 nm/s ± 77). Yet, in this case, average bead velocities decreased rapidly in time (τ = 77 ms) and eventually converged on a value (311 nm/s ± 39) that is near-equivalent to the velocity measured when F_Trig was set to 3 pN, indicating the two-kinesin system eventually reached the same steady-state velocity in each experiment. Importantly, analogous relaxation behavior is not found for single kinesin molecules (Fig. 5, red).

FIGURE 5.

Two-kinesin velocities relax rapidly in response to abrupt changes in the applied load. Two-kinesin bead velocities were monitored in the force clamp at 5 pN constant load. Bead velocities were characterized separately in experiments where the feedback routine of the force clamp was triggered after the beads reached force thresholds (F_Trig) of either 3 pN or 7 pN (black and blue squares, respectively); transport occurs in a static trap until F_Trig is reached. Exponential fits yielded time constants of 96 and 77 ms for the 3–5 pN and 7–5 pN experiments, respectively. Single kinesin velocities are also presented (F_ap = 5 pN; F_Trig = 3 pN). Velocities are presented as mean ± S.E. Each two-kinesin plot is constructed from at least 54 trajectories generated by 6 different complexes. The blue and black lines correspond to exponential fits to the data.

The relaxation of bead velocities indicates that the force-time history of the load on a cargo can influence multiple-kinesin dynamics. To explore why this behavior occurs, we used the transition rate model in Ref. 15 to predict how bead velocities change in time in the force clamp (supplemental Fig. S1). These calculations produce velocity relaxation behaviors that are qualitatively similar to those in Fig. 5. Although the degree to which velocities change is smaller, bead velocities are found to increase in time when F_trig = 3 pN, and to decrease when F_trig = 7 pN (supplemental Fig. S1A). We also used our model to characterize the distributions of the complex's bound configurations when they reach the F_trig threshold that activates the optical trap in our experiments (supplemental Fig. S1, B–D). These analyses show that configurations where there is a 35–65% or more equal splitting of the load only constitute 10% of the total configurations a complex will adopt when the trap is activated at 3 pN (supplemental Fig. S1B). The corresponding probability at 7 pN is much higher (60%). This behavior is consistent with our velocity and stepping data, which again, suggest that cargo transport by two kinesins is affected by load-sharing to a larger degree at high applied loads. A motor complex will spend more time associated with the microtubule prior to activation of the force clamp if the applied load of the static trap is allowed to reach 7 instead of 3 pN, which provides added time for a second motor to bind. In addition, the kinetic challenges illustrated in Fig. 4 are lessened when a complex experiences a load of 7 pN since the leading motor will stall at this load, allowing the trailing motor to advance more rapidly to a microtubule position where it also bears the load. Both of these circumstances make it easier for a complex to generate load-sharing states prior to the activation of the force clamp.

An important result of the above relaxation experiments is that, when averaged over the entire time course of trajectories, bead velocities are not influenced appreciably by the F_Trig value used to initiate the force clamp. In both experiments, the steady-state velocities of the complex were within 10–20% of the measured average velocities: <v> = 284 ± 31 nm/s and 347 ± 31 nm/s when F_Trig was set to 3 and 7 pN, respectively. Similar behavior is predicted by our transition rate model even when bead velocities are examined over a broader range of F_Trig and F_ap values (supplemental Fig. S2). Here, bead velocities initially depend on F_trig in the force clamp. However, the differences between the force-velocity (F-V)² curves generated using different F_trig values are marginal when the load is small and velocities are averaged over the entire time course of a bead's run. This relatively weak sensitivity to the temporal history of the load appears to stem from the fact that bead relaxation time constants are short (∼100 ms) compared with their average filament-bound lifetime (e.g. 610 ms when measured at F_ap = 5 pN). Thus, beads only spend a relatively small portion of their total time bound to the filament moving with appreciably higher or lower velocities in the force clamp, especially below the kinesin stalling force.

Motor Cooperation Occurs via Transitions between Different Single Load-bearing Motor Configurations

We next examined the load-dependence of two-kinesin velocities, run lengths, and run times under the constant loading conditions of the force clamp (Fig. 6). Because of the low probability of high force production events (>7 pN) in the static optical trap (14), and the short lifetime of the states supporting such behavior, we chose to trigger the force-feedback routine of the trap at 2 pN for these analyses. Furthermore, two-kinesin velocities were averaged over the entire time course of their trajectories for continuity with our run length analyses. As a result, the relaxation behavior found in Fig. 5 will contribute somewhat to our reported velocities. To examine the effects stemming from the spatial and temporal dependence of the applied load, the F-V relationship for the two-kinesin complex measured in a static optical trap is also provided for comparison.

Consistent with the expectation that transport is primarily driven by a single load-bearing kinesin within the complex, two-kinesin F-V relationships measured using a force clamp (constant load) and a static optical trap (spatially and temporally dependent load) both overlap closely with the measured relationship of a single kinesin motor below 7 pN (Fig. 6A). The gray dashed curve in this plot indicates a predicted F-V curve where the fitted single-motor F-V relationship is rescaled assuming F_motor = F_ap/2. As the velocity distributions in Fig. 3 also reflect, the significant deviation from this trend illustrates the dominance of the single load-bearing motor configurations and resultant weak response of bead velocity to the grouping of two motors on a bead.

Despite the negligible changes to cargo velocity, the coupling of two kinesins to a cargo does appear to result in increased run lengths and run times (Fig. 6B). Average run lengths of the two-kinesin complexes in the force clamp are ∼1.6 to 2.7 times larger than their corresponding single-kinesin values. These observations suggest that the average distance cargos travel can be enhanced over single motor run lengths even if the two kinesins are largely unable to adopt microtubule-bound configurations that support motor cooperation via load-sharing.

Loading Conditions Affect Cargo Velocities when Applied Loads Are Large

Our analyses of two-kinesin velocities in a static trap revealed a seemingly unusual, non-monotonic dependence of cargo velocity on the applied load (14, 15). Because bead velocities in this load regime were significantly larger than those predicted if the kinesins are assumed to share their applied load equally, this behavior was attributed, at least in part, to some form of synergistic cooperation between motors that appears to dominate cargo motion at high applied loads (F_ap > 7 pN). Similar behaviors also appear to influence bead velocities at large applied loads in the force clamp (Fig. 6A). As in the static trap, bead velocities are found to increase sharply once the applied load exceeds the kinesin single-motor stalling force. Nevertheless, these new experiments show average bead velocities are appreciably lower in the force clamp than in the static trap in this force regime.

Similar differences between the static trap and force clamp velocities are predicted by our transition rate model (supplemental Fig. S3), which gives us added confidence that the differences between our measured F-V curves are not caused by potential variations between the preparations of the two-kinesin complexes used for these assays. Instead, we attribute these differences to the fact that applied loads vary spatially in the static trap, but are spatially invariant in the force clamp. The significance of these effects is illustrated in Fig. 7. The partial detachment of a complex in a static trap is found to result in large decreases in loads (ΔF_ap = 3–4.5 pN) since these events are accompanied by the retraction of the bead toward the center of the trap. The remaining bound motor is therefore left transporting the bead against a lower applied load. However, as shown in the traces in Fig. 1B, the load remains constant during partial detachment events in the force clamp. Consequently, the total probability that a complex will remain bound above the kinesin stalling force via only one of the complex's motors will be higher in the force clamp than in the static trap.

Finally, beads are still transported with average velocities that are either equivalent to or somewhat higher than the predicted load-sharing trend when the load of the force clamp was set to 10 or 12 pN (Fig. 6A). This observation is significant since transient stalling events within traces due to single load-bearing motor transport behaviors are included in our analyses of bead velocities. As a result, the motors must compensate for single-motor stalling events by moving beads with velocities in excess of the equal load-sharing prediction in order to produce average velocities of these magnitudes (as seen in the velocity distributions of Fig. 3A), implying the two kinesins still functioned synergistically. Alternatively, it is possible that these high average velocities stem from a portion of beads that have more than one motor complex colocalized on their surface, allowing more than two kinesins to interact with the microtubule. Even if this is true, however, it must also be true that these same complexes are producing the single kinesin-like behaviors observed at low applied loads in both our static trapping and current force-feedback experiments. We therefore believe this explanation is still consistent with our conclusion that the number of kinesins on a cargo is relatively inconsequential to cargo transport, if not more so.

DISCUSSION

The collective dynamics of organized complexes containing defined numbers of kinesin-1 motor molecules were investigated under the controlled loading conditions of an optical force clamp for the first time. While analyses of bead velocities and displacement sizes revealed signatures of two-kinesin transport found in our previous static trapping assay (e.g. multi-state detachment, bimodal velocity distributions and attenuated cargo displacement step sizes), the force clamp allowed these behaviors to be characterized without issues surrounding the stretching of motors due to the variable loading conditions of the static trap, which reduce bead velocities and displacement sizes of both single and multiple motor complexes.

The present assays also facilitated new comparisons of multiple-kinesin dynamics under different loading conditions. Overall, these analyses uncovered that collections of two coupled kinesins rarely benefit from load-sharing when they transport beads against applied loads that are smaller than the kinesin single-motor stalling force. In this load regime, velocity enhancements are only found in circumstances where loads decrease rapidly in time (e.g. after the 7–5 pN ramp in Fig. 5), and they only persist for brief time periods. For all other conditions investigated at these loads, the system tended to move with average velocities that are near-equivalent to those produced by a single kinesin motor. Considering that we expect loads imposed on cargos will be less than the stalling force of kinesin during most intracellular transport events, these results indicate that cargo motion will be largely insensitive to changes in kinesin copy number, at least in the small motor number limit.

Our previous and present analyses also indicate the weak response of cargo transport to kinesin number stems from kinetic barriers that lower the average rates that two-kinesin complexes transition via motor binding and stepping from single load-bearing motor configurations to those where both motors share loads on a cargo equally. Nevertheless, the observations in Fig. 6B that two-kinesin run lengths are larger than those produced by single-kinesin molecules indicate cargo transport can still be influenced by collective kinesin function. One possible explanation for this behavior is that a complex can remain bound to its filament for longer periods of time than a single motor by exchanging between different configurations where only one motor in the complex bears the applied load. Yet, it is important to recognize that our measured run length enhancements are appreciably smaller than those predicted from models that assume load-sharing occurs at all times when both kinesins are bound (3, 22). Considering these predictions as a baseline behavior, we still believe the collective dynamics of the two-kinesin complexes are best described as net negative cooperative.

This study also revealed important differences between the behaviors of multiple kinesins in a static trap and the force clamp. Because of the force dependence of the probability that a two-kinesin complex will transport a bead in a load sharing configuration, the load that beads were allowed to reach in the static trap was found to influence the their velocities immediately after the force clamp was activated. However, two-kinesin velocities are found to relax relatively rapidly to their steady-state values in response to changes in the applied load, indicating the motor system remodels its bound configuration quickly through a combination of motor stepping, binding, and detachment. Thus, the temporal history of the load should only influence multiple-kinesin dynamics appreciably if loads change more rapidly than this timescale (∼100 ms).

It is also important to recognize that applied loads also vary spatially in the static trap while they are spatially invariant in the force clamp, and that there are important consequences to this distinction. Beads retract backwards and their load decreases when a primary load-bearing or leading motor detaches from the microtubule in the static trap. The remaining motor will therefore be left transporting the bead against a lower applied load. This behavior reduces the likelihood that a complex will remain bound via a single motor at high loads, giving rise to the differences in bead velocities in the static trapping and force clamp assays. Of note, bead velocities at low applied loads are largely unaffected by this process since, at these loads, the two-kinesin complexes are already most commonly bound in configurations where only one motor bears the applied load.

The observation that the spatial dependence of applied loads can influence the behaviors of multiple kinesins has several important implications. For one, the spatial filtering of a complex's bound configurations described above will accentuate cooperative multiple motor behaviors at high loads (e.g. load sharing and potential synergy between the motors). However, these enhancements come with the expense of diminished motor cooperation at low applied loads since, although cargo velocities are unaffected, motor detachment at high loads can increase the probability that a complex will be bound via a single kinesin molecule at low loads (15). We believe the latter behavior is more significant since the ability for motors to cooperate productively at low applied loads will determine how a complex will transport a cargo against increasing loads, and hence, the probability a multiple motor team will produce high forces. Such effects may also have important consequences for mechanisms of bidirectional transport. Motors will experience spatially dependent loads during tug-of-war competitions with other motors if the cargo they are pulling on is elastic, as is the case of many vesicular cargos (9, 23). The partial detachment of one motor team during this competition may result in an appreciable drop in the load experienced by all of the motors that remain engaged in the tug-of-war competition. If this is the case, directional reversals may be less likely to occur via motor-filament unbinding reaction cascades. In this way, understanding mechanisms of bidirectional transport will not only require general knowledge of how different types of motors function collectively under load, but also, how loads experienced by different competing motor teams vary spatially and temporally as cargos move back and forth along microtubules.