Determination of Axonal and Dendritic Orientation Distributions Within the Developing Cerebral Cortex by Diffusion Tensor Imaging

Abstract

As neurons of the developing brain form functional circuits, they undergo morphological differentiation. In immature cerebral cortex, radially-oriented cellular processes of undifferentiated neurons impede water diffusion parallel, but not perpendicular, to the pial surface, as measured via diffusion-weighted magnetic resonance imaging, and give rise to water diffusion anisotropy. As the cerebral cortex matures, the loss of water diffusion anisotropy accompanies cellular morphological differentiation. A quantitative relationship is proposed here to relate water diffusion anisotropy measurements directly to characteristics of neuronal morphology. This expression incorporates the effects of local diffusion anisotropy within cellular processes, as well as the effects of anisotropy in the orientations of cellular processes. To obtain experimental support for the proposed relationship, tissue from 13 and 31 day-old ferrets was stained using the rapid Golgi technique, and the 3-D orientation distribution of neuronal proceses was characterized using confocal microscopic examination of reflected visible light images. Coregistration of the MRI and Golgi data enables a quantitative evaluation of the proposed theory, and excellent agreement with the theoretical results, as well as agreement with previously published values for locally-induced water diffusion anisotropy and volume fraction of the neuropil, is observed.

I. Introduction

PROPER morphological development of neurons is essential for the formation of functional neural circuits [1], [2]. In the cerebral cortex, pyramidal neurons undergo morphological differentiation after migrating from germinal zones near the lateral ventricles to the cortical plate [3]. Immediately following migration, cell bodies of these neurons are elongated, and their dominant structural feature is a radially-oriented apical dendrite. Subsequently, collaterals branch from the primary apical dendrites, basal dendrites grow from cell bodies at varying orientations relative to the radially-oriented primary apical dendrite, and axons invade the cortex from the subplate. In several experimental models of neurodevelopmental disorders, including examples caused by environmental (e.g., fetal alcohol spectrum disorder [4], [5]) or genetic (e.g., Rett syndrome [6], [7]) factors, the axonal/dendritic arbor complexity is reduced in affected individuals compared to age-matched controls. A noninvasive method to characterize cellular morphology in the developing cerebral cortex could therefore be of value in characterizing neurodevelopmental disorders in humans, and potentially offer a strategy for detecting disease in affected individuals and/or for assessing disease severity.

Magnetic-resonance-based techniques for measuring directional dependence in translational diffusion of water, i.e., diffusion anisotropy [8]–[10], have proven valuable for characterizing the cellular-level microstructure of brain white matter (WM) [11], [12]. In WM of mature individuals, diffusion anisotropy results from the presence of densely packed, coherently oriented axons and myelin sheaths [13]. This is because water displacements due to diffusion are more restricted in directions perpendicular to an axon tract than in directions parallel to the tract. Due to this relationship, diffusion tensor imaging (DTI) measurements provide the basis for several investigations of microstructural changes associated with development and aging [14], [15], and with various neuropathological [16], [17] and neuropsychiatric [18], [19] disorders.

The strategy of utilizing water diffusion anisotropy can also be extended to characterization of the cerebral cortex. Although water diffusion within mature cortical gray matter is only very slightly anisotropic [20], [21], at early stages of morphological development, cortical diffusion anisotropy is comparable in magnitude to that within myelinated WM fiber tracts [22]–[25]. The directional dependence of diffusion in the immature cortex corresponds to the characteristic radial pattern of the undifferentiated neuropil [22]–[26]. Diffusion is relatively unhindered in the direction perpendicular to the pial surface (and thus parallel to elongated cell bodies and apical dendrites), as opposed to diffusion in the parallel direction where membranes of cellular processes impede molecular displacement [24]. In systematic studies of prematurely-delivered human infants [24], [27], postmortem human fetal brains [28], [29], and in several animal model systems [30]–[37], temporal aspects of the transition from high to low cortical diffusion anisotropy have been characterized [38]. This comparative approach has consistently demonstrated that loss in cortical diffusion anisotropy temporally coincides with axonal and dendritic morphological development. Further, a comparison between normally-reared and neonatally enucleated ferrets has shown that cerebral cortical areas with visual-deprivation-induced reductions in axonal/dendritic arbor complexity exhibit elevated anisotropy in water diffusion [39]. These empirical findings suggest that DTI is a potentially sensitive strategy to characterize the developing cerebral cortical neuropil; however, a quantitative understanding of this relationship is lacking. In studies of brain WM, much progress has been made in characterizing heterogeneous distributions of axon orientations by DTI [40]–[47]. Specifically, characterization of multimodal distributions of axonal orientations within individual voxels shows great potential for analyzing diffusion MRI data within areas in which WM fiber pathways intersect [40]–[48]. Within the developing cerebral cortex however, the orientation distribution of axonal and dendritic structures is different. Neighboring axonal and dendritic processes are generally much less aligned in cortical gray matter than axon segments are in WM. In addition, the overall orientation distribution of axonal and dendritic elements within the cerebral cortex is expected to be clustered around a primary (radial) direction, which is in contrast to the multimodal distribution found within regions of crossing WM fibers [49]. Thus, distinct approaches will need to be developed to analyze diffusion MRI data in the cerebral cortex [50]–[52] beyond those used to study WM.

Herein, we propose a theoretical relation between the diffusion tensor and the distribution of structural elements within the developing cerebral cortical neuropil. We have previously derived an expression for the diffusion-attenuated MR signal intensity produced by water diffusing within impermeable cylinders of arbitrary orientational distribution [51]. Here, this expression is used to obtain an analytical relationship between anisotropy in the water diffusion tensor, and anisotropy in the distribution of axonal and dendritic orientations within the cerebral cortical neuropil. This relationship expresses quantitatively how diffusion tensor structure is induced in part by the intrinsic diffusion anisotropy within neuronal processes, and in part by the anisotropy of the orientation distribution of these processes. In order to experimentally evaluate the proposed relation, we compare diffusion tensor measurements to quantitatively analyzed histological preparations. Ideally, DTI and histological comparisons would test the proposed theory using tissue that exhibits a wide range of morphological characteristics. In a recent study of diffusion anisotropy changes in the normally developing ferret cerebral cortex [34], systematic laminar and regional variability in cortical diffusion anisotropy was found to be maximal approximately two weeks after birth. This variability arises from laminar and regional gradients in neuronal birthdates, and is expected to give rise to corresponding variability in anisotropy of the cerebral cortical axonal/dendritic process orientation distributions. Here, 3-D confocal analyses were performed on Golgi-stained brain tissue derived from postnatal day 13 (P13) and P31 ferrets, and the distribution in the anisotropy of axonal and dendritic element orientations was confirmed to be broader at P13 than at P31. Therefore, the P13 cerebral cortical tissue was characterized in multiple histological sections, and image registration procedures were applied to directly compare diffusion anisotropy measurements performed on the post mortem material immediately prior to Golgi staining and analysis.

II. Theory

In this section, an expression is derived to state how the diffusion tensor is influenced by microscopic anisotropy within axonal and dendritic processes, as well as anisotropy in the organization of axonal and dendritic processes within an image voxel. To characterize microscopic diffusion anisotropy in the intracellular compartment, the distinction is made between longitudinal diffusion, parallel to the local axis of the neurite, reflected in the diffusion coefficient D_L, and transverse diffusion, perpendicular to the local axis, reflected in D_T [51]–[53]. To express anisotropy in the organization of cellular elements, the fractional anisotropy in their orientation distribution is defined, as described below.

As published previously [50], [51], the diffusion signal in brain tissue from a Stejskal–Tanner spin echo sequence is described in terms of two nonexchanging components: the signal S_c originating from the volume fraction of a voxel consisting of cylindrically-structured cellular elements such as axons and dendrites, herein termed the neuropil, ν, and the signal accounting for diffusion in the remaining extra-cylindrical volume fraction, S_e

$$S(\mathbf{q},\Delta )=(1-\nu )S_e(\mathbf{q},\Delta )+\nu S_c(\mathbf{q},\Delta )$$ (1)

in which Δ is the time interval separating the two diffusion-sensitizing magnetic field gradient pulse onsets, q = γgδ ≡ qn̂ is the diffusion wave vector in the arbitrary direction of the unit vector n̂, γ is the gyromagnetic ratio of the nucleus under study, δ is the magnetic field gradient duration, and g is the magnetic field gradient strength and direction. Diffusion outside of the neuropil is assumed to be approximately Gaussian, characterized by an effective diffusion tensor D [50], [51], which yields S_e = exp(–bn̂^TDn̂), in which the diffusion weighting (b-factor) is defined as b = (Δ – δ/3)q². Others have similarly utilized a diffusion tensor expression to account for diffusion anisotropy within cell soma and extracellular space in WM [50], [54], [55].

The term S_c accounts for signal originating in the neuropil, and is modeled using expressions for diffusion within cylindrical structures of varying orientations [51]. The diffusion-weighted MR signal is therefore influenced by both intrinsic diffusion anisotropy within the cylindrically-shaped axons and dendrites, and by anisotropy in the fiber orientation distribution. For notational convenience, we define the anisotropic diffusivity D_A as the difference D_L – D_T ≥ 0. We assume that axons and dendrites can be approximated as linear segments in which the diffusion signal can be computed as if arising from an infinite cylinder. This is valid as long as the diffusion length, $\sqrt{D_L\Delta }$, is smaller than the length scale over which the neurites maintain a constant direction and do not branch. Assuming a value for D_L that is half the diffusion coefficient of temperature-matched dilute aqueous solution [51], the diffusion length for the experiments conducted herein is 4 μm, approximately an order of magnitude less than the mean branch length of 55 μm for cerebral cortical pyramidal neurons entered in the NeuroMorpho database¹ measured using the associated querying tool “L-Measure.” The signal from a single cylinder parallel to unit vector û of arbitrary direction, is thus proportional to exp(–b(D_T + (n̂ · û²)D_A)) in the Gaussian approximation, when diffusion weighting b is applied in the direction of n̂. The net signal from the neuropil then arises as a sum of this expression over all neurites. The fiber axonal/dendritic orientation distribution function may be expressed as a function of polar coordinates, f(θ, φ), or equivalently as a function of the vector û, f(û), to quantify the directional distribution of cylindrical structures in the neuropil, such that f(û)dû = f(θ, φ)sin(θ)dθdφ is the probability of a fiber being oriented in a direction û with spherical polar angles θ and φ. Thus, the signal from the neuropil can be written as [50], [51]

$$S_c(\mathbf{q},\Delta )={\int }_{S_2}d\widehat{u}f\left(\widehat{u}\right)e^{-b(D_{\mathrm{T}}+(\widehat{n}\cdot {\widehat{u}}^2)D_A)}$$ (2)

where the domain of integration S₂ refers to the 2-D surface of the unit sphere, i.e., θ ∈ [0; π] and φ ∈ [0; 2π] with dû = sin θdθdφ.

Rather than working with an explicit representation of f(û) as was done in [51] and [56], we show here that it is possible to compute the apparent diffusion and kurtosis tensors directly from the second and fourth moments of f(û). Using angular brackets to signify an average over the orientation distribution of neurites, i.e., for any function of g(û) of û

$$\langle g\left(\widehat{u}\right)\rangle \equiv {\int }_{S_2}d\widehat{u}f\left(\widehat{u}\right)g\left(\widehat{u}\right)$$ (3)

a Taylor series expansion of the exponential function in the integrand of (2) yields

$$S_c\approx 1-b(D_A\langle {(\widehat{u}\cdot \widehat{n})}^2\rangle +D_T)+\frac{1}{2}{b}^2(D_A^2\langle {(\widehat{u}\cdot \widehat{n})}^4\rangle +D_T^2+2D_T{D}_A\langle {(\widehat{u}\cdot \widehat{n})}^2\rangle )+O\left(b^4\right).$$ (4)

Adding to (4) the Taylor expansion of S_e in (1), we have

$$S\approx 1-b((1-\nu ){\widehat{n}}^T\mathrm{D}\widehat{n}+\nu (D_A\langle {(\widehat{u}\cdot \widehat{n})}^2\rangle +D_T))+\frac{1}{2}{b}^2\left((1-\nu ){\left({\widehat{n}}^T\mathrm{D}\widehat{n}\right)}^2+\nu (D_A^2\langle {(\widehat{u}\cdot \widehat{n})}^4\rangle +D_T^2+2D_T{D}_A\langle {(\widehat{u}\cdot \widehat{n})}^2\rangle \right)+O\left(b^4\right).$$ (5)

Equation (5) depends on the shape of the fiber orientation distribution function through its second and fourth moments. For example, the second moment of the orientational distribution is the orientation matrix or scatter matrix T [57] with Cartesian components

$$T_{ij}=\langle u_i{u}_j\rangle ={\int }_{S_2}d\widehat{u}{u}_i{u}_{j}f\left(\widehat{u}\right).$$ (6)

The apparent diffusivity D_app(n̂) ≡ n̂^TD_appn̂ in the direction n̂ is the coefficient of the linear part of the signal in (5) with respect to b, i.e.,

$$\begin{array}{cc}\hfill D_{\text{app}}\left(\widehat{n}\right)& =(1-\nu ){\widehat{n}}^T\mathrm{D}\widehat{n}+\nu (D_T+D_A\langle {(\widehat{u}\cdot \widehat{n})}^2\rangle )\hfill \\ \hfill & =(1-\nu ){\widehat{n}}^T\mathrm{D}\widehat{n}+\nu (D_T{\widehat{n}}^T\mathrm{I}\widehat{n}+D_A{\widehat{n}}^T\mathrm{T}\widehat{n})\hfill \end{array}$$ (7)

where I is the identity matrix. Since this equation holds for any n̂, and since diffusion tensors and scatter matrices are symmetrical, it follows that the identity can be re-expressed as an equality of tensors

$${\mathrm{D}}_{\text{app}}=(1-\nu )\mathrm{D}+\nu (D_T\mathrm{I}+D_A\mathrm{T}).$$ (8)

This equation states concisely how the apparent diffusion tensor is influenced by the microscopic parameters D_L, D_T, and D, and the morphology of axons and dendrites of the developing cerebral cortex, expressed in terms of the scatter matrix T of the fiber orientation distribution.

If the extra cylindrical space is assumed to be isotropic, D = D_effI, then it follows from (8) that the apparent diffusion tensor is a displaced and scaled version of the orientation matrix

$$\nu D_A(\mathrm{T}-\mathrm{Tr}\left(\mathrm{T}\right)\mathrm{I}∕3)={\mathrm{D}}_{\text{app}}-\mathrm{Tr}\left({\mathrm{D}}_{\text{app}}\right)\mathrm{I}∕3.$$ (9)

This equation, which is a special case of (8), expresses how the anisotropic part of the diffusion tensor is induced in part by intrinsic diffusion anisotropy of the neurites, and in part by anisotropy in the orientation distribution of cellular processes. From the equation above it follows that

$${\lambda }_i-\overline{\lambda }=\nu D_A({\tau }_i-\overline{\tau })$$ (10)

where λ_i and τ_i denote the eigenvalues of the diffusion tensor and the orientation matrix, respectively, and where the overbar signifies an average over the three eigenvalues. Note that $\overline{\tau }=\mathrm{Tr}\left(\mathrm{T}\right)∕3=1∕3$ always, as follows from the definition in (6). We henceforth refer to the combinations ${\lambda }_i-\overline{\lambda }$ and ${\tau }_i-\overline{\tau }$ as the centralized eigenvalues λ_c,i and τ_c,i. Similarly, according to (9), the orientation matrix and the diffusion tensor have simultaneous eigenvectors.

A fractional anisotropy of the orientation matrix, FA_T, can be defined analogously to the diffusion tensor FA_D

$$\begin{array}{cc}\hfill {\mathrm{FA}}_D& =\sqrt{\frac{3}{2}\frac{{({\lambda }_1-\overline{\lambda })}^2+{({\lambda }_2-\overline{\lambda })}^2+{({\lambda }_3-\overline{\lambda })}^2}{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}}\hfill \\ \hfill {\mathrm{FA}}_T& =\sqrt{\frac{3}{2}\frac{{({\tau }_1-\overline{\tau })}^2+{({\tau }_2-\overline{\tau })}^2+{({\tau }_3-\overline{\tau })}^2}{{\tau }_1^2+{\tau }_2^2+{\tau }_3^2}}\hfill \end{array}$$ (11)

and these two measures of anisotropy are related, using (10)

$${\mathrm{FA}}_D\sqrt{\sum _i{\lambda }_i^2}=\nu D_A{\mathrm{FA}}_T\sqrt{\sum _i{\tau }_i^2}.$$ (12)

It is straightforward to continue the analysis for higher order tensors, and in Appendix I we compute the kurtosis [58] of the diffusion signal relating it to the axon/dendrite orientation distribution.

Note that (8) holds generally for models in which the signal originates from two nonexchanging components, a Gaussian diffusion pool and a pool residing in cylindrically symmetric structures with an arbitrary orientation distribution. A straightforward modification would be to use an explicit representation of the orientation distribution, for example assuming an axially symmetric distribution of cylindrical cellular processes. Such an assumption, which can be considered a special case of the present framework, would lead to an approach similar to a recent study of WM [59], where a Watson distribution [57]

$$f\left(\widehat{u}\right)\propto e^{\kappa {(\widehat{u}\cdot \widehat{c})}^2}$$ (13)

was used. Here ĉ is the “average” direction of the orientation distribution and κ, the concentration parameter. The Watson distribution is cylindrically symmetric about the main direction ĉ, with κ describing the “width” of the distribution—lower κ corresponds to greater dispersion of directions. For the extracellular space, a Gaussian description is used in [59], with a diffusion tensor related explicitly to the cylinder orientation distribution. This means that in the style of our notation, the extracellular diffusion tensor D in (8) becomes

$$\mathrm{D}=(d_L-d_T)\mathrm{T}+d_T\mathrm{I}$$ (14)

where d_L and d_T = d_L(1 – ν) are the extracellular diffusion coefficients parallel and perpendicular to axons with a single orientation [59]. For the scatter matrix, we find

$$\mathrm{T}=({\tau }_1-{\tau }_2)\widehat{c}{\widehat{c}}^{\mathrm{T}}+{\tau }_2\mathrm{I}$$ (15)

in which τ₂ = (1 – τ₁)/2 and

$${\tau }_1={\int }_0^1{u}^2{e}^{\kappa u^2}du∕{\int }_0^1{e}^{\kappa u^2}du$$ (16)

which can be written in terms of Dawson's integral [60], to obtain expressions equivalent to those presented in [59]. For the Watson model, FA_T can be related to the concentration parameter κ using (11) and τ₃ = τ₂ = (1 – τ₁)/2. For our purposes, it is unnecessary to assume a particular form for f(û), and therefore the subsequent analysis presented here uses the general relation in (9) to avoid the potentially confounding assumption of an axially symmetric distribution of cellular processes.

III. Methods

A. Tissue Preparation

The left hemispheres of brains from one P13 and one P31 female ferret were prepared as described in [34] (the corresponding right hemispheres were subjects P13b and P31b, respectively, in [34]). Procedures were approved by local Institutional Animal Care and Use Committees, and carried out in accordance with the NIH “Guide for the Care and Use of Laboratory Animals” [77].

B. Diffusion Tensor Imaging

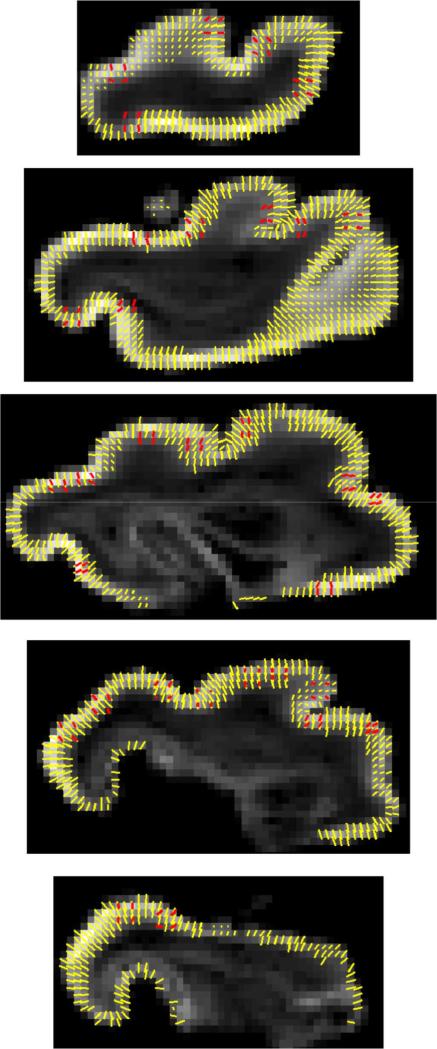
Imaging was carried out on the P13 hemisphere with the tissue immersed in perfluorinated media following previously described procedures [34] using a horizontal 30 cm clear-bore 11.7T magnet interfaced with a 9-cm inner diameter magnetic field gradient coil (Bruker, Rheinstetten, Germany). Diffusion sensitization scheme B in [34] was implemented, in which icosahedral 25-direction sampling [61] was incorporated into a Stejskal–Tanner multislice spin echo pulse sequence utilizing a single b-value of 2.5 ms/μm², in addition to two images in which b = 0 were collected. Pulse sequence parameters were δ = 12 ms, Δ = 21 ms, and g = 11.6 G/cm, TE = 42 ms, TR = 12.5 s, and image resolution was isotropic with 250-μm-sided voxels. The total image acquisition time was approximately 6 h, and the voxel-wise signal-to-noise ratio, determined following previously described procedures [34], was found to be 80. Representative images used to measure water diffusion are shown in Fig. 1. Diffusion tensor calculations were performed for each voxel in the image after co-registration to histology (see below), and fractional anisotropy (FA_D) was calculated from diffusion tensor eigenvalues using the standard formula [10].

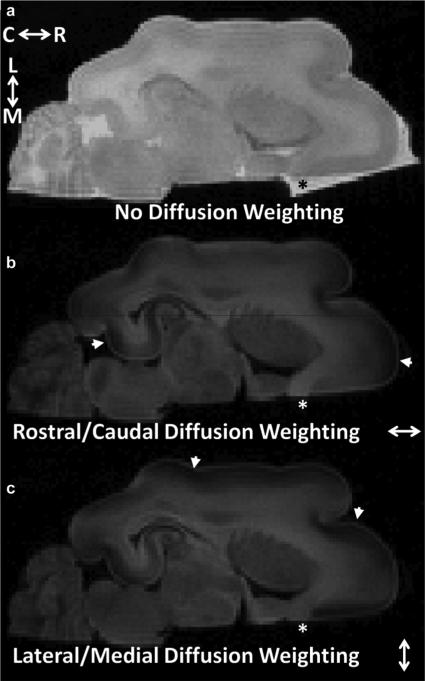
Fig. 1.

Data used to measure water diffusion in cerebral cortex of a P13 brain. All panels are shown on a common intensity scale. The b-value for the axial image in (a) was 0, and for (b) and (c) was 2.5 ms/μm². The diffusion-sensitizing gradients were approximately parallel to the brain rostral/caudal axis in (b) and lateral/medial axis in (c). Due to the larger water diffusion coefficient in aqueous solution than in tissue, image intensity for phosphate-buffered saline surrounding the brain that was not displaced by perfluorinated media is observable in the absence of diffusion weighting [(a) black asterisk], but is dramatically attenuated in images in which b = 2.5 ms/μm² [white asterisks in (b), (c)]. Water diffusion anisotropy in the cerebral cortex is manifest in reduced signal intensity for regions in (b), (c) in which neuronal processes are parallel to the applied diffusion-sensitization gradients (arrowheads). Abbreviations—C: caudal; L: lateral; M: medial; R: rostral.

C. Golgi Staining and Histological Processing

After acquisition of DTI data, Golgi–Cox staining procedures were followed using the Rapid GolgiStain kit (FD NeuroTechnologies, Inc., Catonsville, MD). Hemispheres were impregnated with potassium dichromate, mercuric chloride and potassium chromate solutions (Rapid GolgiStain Solutions A and B) for 21 days according to manufacturer's recommendation. Subsequently, hemispheres were frozen using an isopentane and dry-ice slurry and embedded in Tissue Tek OCT (Optimal Cutting Temperature) compound (Ted Pella, Inc., Redding, CA). For the entire P13 hemisphere, and for regularly-spaced intervals of a portion of the P31 hemisphere, 150-μm-thick axial slices were cut using a cryostat, and tissue was mounted onto Gelatin subbed slides. Staining was performed according to kit instructions.

Light microscope montage images (2.5× magnification, Zeiss 510 META NLO, Carl Zeiss AG, Oberkochen, Germany) were acquired of each section. These montages were used to guide the co-registration of Golgi and DTI images of the P13 brain (described below). For the P13 brain, 32 775 × 775× ~ 100 μm fields were identified within five equally-spaced axial sections, at approximately equally-spaced positions along the rostral/caudal extent of the isocortex for further quantitative characterization. For the P31 brain, 14 fields were characterized within one axial section.

In order to construct 3-D images of cortical fields, 3-D images of the Golgi-stained tissue were acquired in reflected light mode using a 20× PLAPO NA 0.7 objective (633-nm light and a Leica SP5 AOBS microscope, Leica Microsystems, Bannockburn, IL) [62], [63]. Due to an approximately linear reduction in reflected light intensity with depth from the surface on the side proximal to the light source, it is only possible to collect data from an approximately 100-μm-thick slab. Throughout the 150-μm-thick sections, approximately 200 optical sections of reflected light, spaced by 0.5 μm, were obtained at 1.52 μm² pixel resolution (512 × 512 data points per plane) for each cortical field. The detector gain was linearly scaled with depth from the tissue surface to minimize intensity variation throughout the serial image set that arises from the aforementioned linear reduction in intensity. Transmitted light images were also acquired at each focal plane. After assembling serial reflected light images into 3-D datasets, fields were down-sampled along the “through-plane” dimension to provide 1.52 μm × 1.52 μm × 1.52 μm isotropic voxel resolution; and the fields were subdivided into four 387.5 μm × 387.5 μm “in-plane” quadrants, to provide an approximate match between the volume of a Golgi quadrant (387.5 μm × 387.5 μm× ~ 100 μm = 15.0 nL) and a single voxel in the DTI data (250 μm × 250 μm × 250 μm = 15.6 nL).

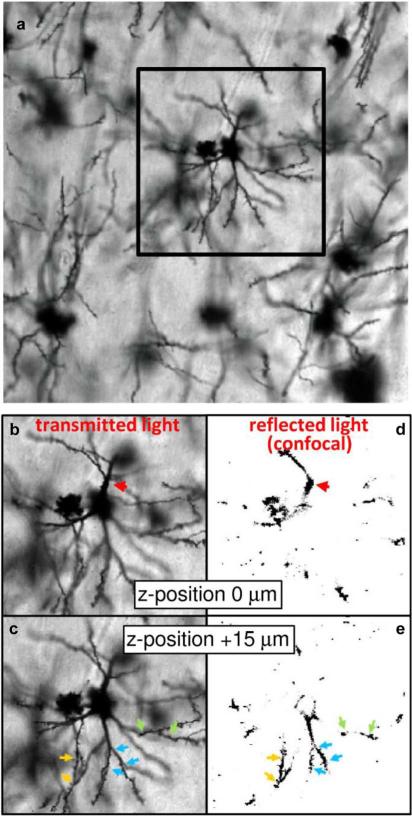
Fig. 2 provides a comparison of standard transmitted light images and confocal images of reflected light to demonstrate that through-plane resolution is achievable by applying the confocal technique to reflected light of Golgi-stained brain tissue. Fig. 2(a) shows an example Golgi field. In Fig. 2(b) and (c), different parts of one neuron are brought into focus in the two transmitted light focal planes separated by 15 μm. The region of the apical dendrite proximal to the cell body is shown in (b) (red arrow), and more of the basal arbor can be seen (c). However, these images are not readily usable to construct 3-D models of neurons, due to significant interference from out-of-plane structures. Confocal images of back-scattered visible light [62], [63] shown in Fig. 2(d) and (e) demonstrate how the confocal technique can provide substantially improved through-plane image resolution, suitable for 3-D reconstruction procedures. Color-coded arrowheads indicate corresponding structures between transmitted and back-scattered light images of (b)–(e). Discontinuities in dendritic structures in (d) and (e) are places where dendrites leave the plane of focus.

Fig. 2.

Comparison of standard transmitted visible light images and confocal images of reflected visible light to demonstrate the through-plane resolution achievable by applying the confocal technique to back-scattered light of Golgi-stained brain tissue. (a) A transmitted light image of a Golgi field within cerebral cortex is shown. Panels (b)–(e) show side-by-side comparisons of the indicated subregion of (a) obtained from transmitted (b), (c) and confocal microscopy of reflected (d), (e) visible light. The focal plane of image pairs (b), (d) is offset relative to (c), (e) by 15 μm. Confocal microscopy of reflected light enables sufficient through-plane resolution to be achieved to construct 3-D models of cellular structures, whereas out-of-plane structures in transmitted light images observable in (b), (c) would interfere with subsequent steps of the 3-D analysis.

D. Registration of Golgi and DTI Data

For the P13 brain, the Golgi and DTI data were directly compared to each other. The overall strategy to register the two sets of images was to perform five separate landmark-based linear registration transformations [64] to the DTI data to obtain slices that are coplanar to each of the five Golgi-stained sections analyzed. In order to generate landmarks to guide the five registrations, 3-D surface models of the cerebral cortical surface were first constructed from the Golgi and DTI data, and these surfaces were registered to one another. From the registered 3-D surface models, it was possible to utilize a set of points that outline the cerebral cortex in a given Golgi section to determine the corresponding plane in the DTI data.

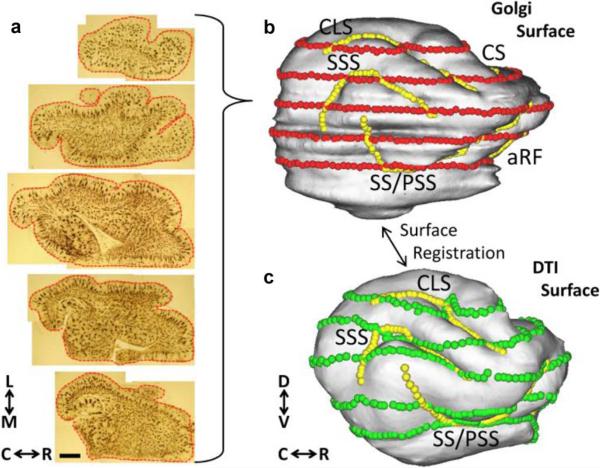
To construct the 3-D surface model from the Golgi data, montages of 2.5× magnification images were assembled for the 70 adjacent 150 μm axial sections making up the P13 left hemisphere. The outline of the cortical surface was manually traced on each montage, and each contour trace was recorded as an ordered set of 2-D points [red dots, Fig. 3(a)]. The 70 contour traces were then used to construct a model of the cortical surface, using functionalities of the Computerized Anatomical Reconstruction Toolkit (CARET)² [65], following procedures described in the software documentation. In the Golgi-based cortical surface model [Fig. 3(b)], surface nodes closest to each of the contour trace points in Fig. 3(a) are shown as red spheres. The operations used to generate a 3-D cortical surface model from the DTI data [Fig. 3(c)] also utilized functionalities of CARET software, and have been described previously [34].

Fig. 3.

Surface models of the P13 cerebral cortex facilitate co-registration of the Golgi and DTI data. Montages of the five axial Golgi-stained sections used for comparisons with DTI data are shown in (a). Manually-traced contour outlines were drawn for each of 70 montages, as illustrated with red lines/points for the five sections in (a). The Golgi-based model of the cortical surface (b) is generated from the 70 adjacent contour outlines using CARET software (see text for details). Surface model coordinates corresponding to the contour outline points are displayed as red spheres in (b). A surface model of the cerebral cortex is also generated from the DTI data, shown in (c) (see text for details). Sulcal landmarks were used to constrain surface-based registration procedures implemented using CARET software. Sulcal landmarks that are visible on the lateral views of (b) and (c) are indicated with yellow spheres. Surface nodes corresponding to red spheres on the DTI-based model are shown as green spheres in (c). Abbreviations—aRF: anterior rhinal fissure; C: caudal; CLS: coronolateral sulcus; CS: cruciate sulcus; D: dorsal; L: lateral; M: medial; PSS: presylvian sulcus; R: rostral; SSS: suprasylvian sulcus; SS: sylvian sulcus: V ventral. Scale bar = 2 mm.

Next, a surface-based registration of the Golgi and DTI models of the cerebral cortex was performed. This step was implemented using CARET software following previously-described procedures [34]. A set of six sulcal landmarks [coronolateral sulcus (CLS), sylvian sulcus/presylvian sulcus (SS/PSS), suprasylvian sulcus (SSS), splenial sulcus (Sps), and cruciate sulcus (CS), and the anterior rhinal fissure (aRF); shown as yellow spheres, Fig. 3(b), (c)] were used to constrain the surface-based registration. The result of the surface registration procedure is to establish a one-to-one correspondence between nodes of the Golgi surface model and nodes of the DTI surface model. Surface nodes on the DTI model that correspond to the five contour traces [red spheres, Fig. 3(b)] are shown as green spheres in Fig. 3(c).

Linear transformations that specify each of the five P13 Golgi slices in the DTI frame were obtained following the method described in [64] using the set of planar contour trace points [e.g., the set of red points for a given section in Fig. 3(a)] and their associated nodes on the DTI-derived cerebral cortical surface model [green spheres for the corresponding section, Fig. 3(c)]. Parameters that specify a rotation matrix R, a scaling parameter c, and the translation vector t, were determined that operate on an arbitrary point i in the DTI frame, $P_i^{\mathrm{DTI}}$, to give the corresponding point in the Golgi frame, $P_i^{\text{Golgi}}$ according to the expression

$$P_i^{\text{Golgi}}=c\mathrm{R}{P}_i^{\mathrm{DTI}}+\mathit{t}.$$ (17)

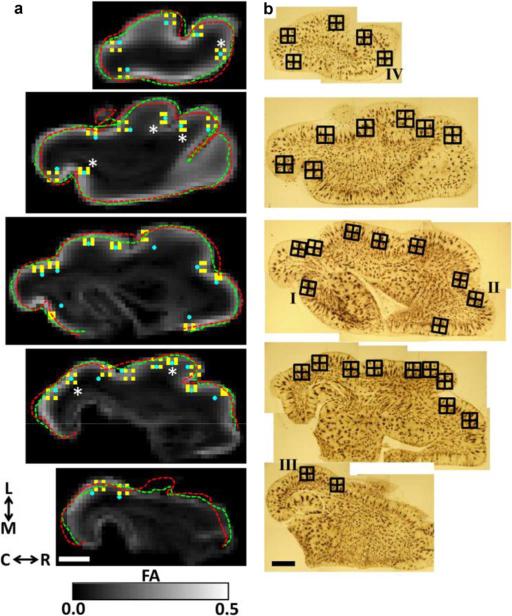
The above expression contains four adjustable parameters; a rotation angle θ specifies the elements of the 2 × 2 rotation matrix R, c is a scalar, and t contains two adjustable parameters in a 2 × 1 column vector. Vector quantities, such as the diffusion sensitization, q, can be transformed from the DTI frame to the Golgi frame according to q^Golgi = Rq^DTI. Diffusion data was expressed in each of the five P13 Golgi slice frames by re-sampling the diffusion-weighted images, and recalculating diffusion tensors for each voxel. For the three most ventral slices analyzed, there was a subset of contour trace points along the medial boundary that overlap noncortical tissue. These points were not included in the set of points used to determine linear registrations because the medial boundary for these slices is not easily recognized in the MRI data. The regions of contour traces used for registrations to the DTI data are overlaid on FA parameter maps for the five slices in Fig. 4(a) (red dashed curves). Traces connecting the set of points in the DTI frame used to determine the linear registration parameters are also projected onto the Fig. 4(a) FA maps (green dashed curves). To provide an estimate of the precision in the linear registration, the distance between Golgi and DTI landmark pairs was determined. The average inter-landmark distance within the Fig. 4(a) planes is 0.36 mm. However, as described below, manual adjustments were made to minimize in-plane misregistration effects. An estimate of the misregistration effects that cannot be corrected by manual adjustment is the average distance for each of the DTI landmarks [green spheres, Fig. 3(c)] to the corresponding plane in Fig. 4(a), which is 0.20 mm.

Fig. 4.

Co-registration results for DTI and Golgi images. In (a), five FA parameter maps that result from resampling diffusion weighted images to be co-planar with each of the sets of surface nodes corresponding to each set of green spheres in Fig. 3(c) are shown. The outline of these points are projected onto each FA map, and overlaid as the green dashed traces. For comparison, contour outline points derived from the Golgi data are displayed as red dashed traces. For the bottom three planes, contour outline points along the medial wall were not included in the registration and are therefore not included in the dashed green and red traces (see text for details). Panels in (b) show the corresponding montages of Golgi-stained tissue sections. The boundaries of each Golgi field, with its four quadrants, are shown as an overlay. Each Golgi field center was projected onto the FA parameter maps in (a), and is illustrated as a blue filled circle. For six Golgi fields [astrisks in (a)], no manual adjustment was needed to provide a match between Golgi and DTI locations. For the remaining fields, manual adjustments were necessary to ensure the field center specified in the FA maps was consistent with the center shown in the Golgi images, relative to gyral and sulcal landmarks. 128 DTI voxels [shown in yellow in (a)] were chosen based on distance from the Golgi field center for comparisons between the DTI data and each Golgi quadrant. Fields labeled I–IV in (b) are shown in more detail in Fig. 9. Abbreviations are as in Fig. 3. Scale bars = 2 mm.

The locations of the 32 Golgi fields used for axonal/dendritic orientation distribution determinations are indicated in Fig. 4(b). As mentioned above and illustrated in Fig. 4(b), each Golgi field was subdivided into four quadrants so that the volumes of the quadrants approximately match the volume of a single DTI voxel. The center of each Golgi field, which is known in the Golgi reference frame common to the set of points $P_i^{\text{Golgi}}$, was transformed to the DTI frame using the equation (17) parameters [blue dots, Fig. 4(a)]. For 26 of the 32 Golgi fields, small manual adjustments to the location of the Golgi field in the DTI frame were necessary to ensure the neighborhood of DTI voxels was located in cerebral cortex that most closely corresponds to the location of the Golgi field center. For the remaining six Golgi fields [asterisks, Fig. 4(a)], no manual adjustment was necessary. For each Golgi field, DTI voxels corresponding to each quadrant were identified by adding/subtracting 387.5 μm to/from the Golgi field center position in the DTI frame. Each set of four DTI voxels is color-coded yellow in Fig. 4(a).

E. Determination of Scatter Matrices

A procedure for estimating the axonal/dendritic scatter matrix, T, from the Golgi data is outlined in Fig. 5. Each of the operations are summarized in the following paragraphs, and the details of how each step was implemented are given as pseudocode in Appendix II. Italicized text refers to specific data structures that are input and/or output for steps in the Fig. 5 procedure. The input to the procedure is a 3-D image of the Golgi-stained tissue, image_stack, and a threshold intensity value to distinguish foreground stained objects from background. The output is a 3 × 3 matrix T, corresponding to the scatter matrix T of the region of Golgi-stained tissue.

Fig. 5.

Schematic illustrating the procedure for estimating axonal/dendritic orientation distributions from serial confocal images of reflected visible light.

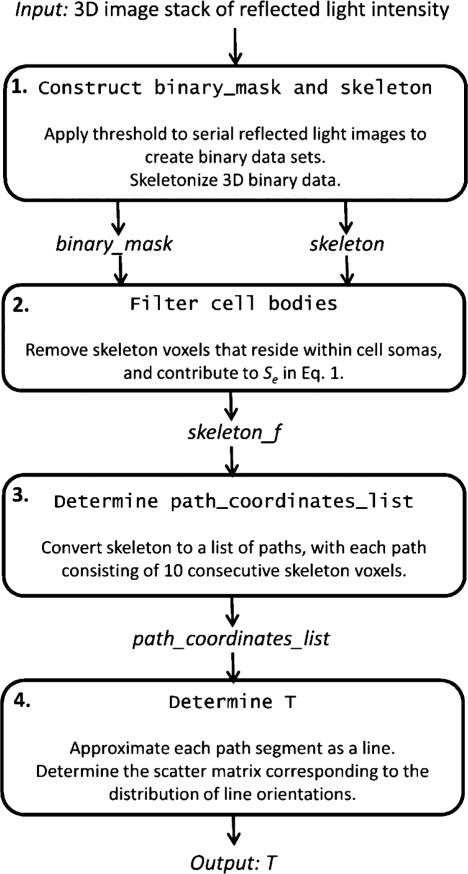
The first step of the Fig. 5 procedure is to produce skeleton representations of the Golgi-stained cellular elements. A binary image distinguishing foreground Golgi-stained objects from the background image voxels, is also produced in this step. This is accomplished by specifying a threshold value, assigning voxels of value lower than the threshold to background, and assigning the remaining voxels to foreground objects. Fig. 6(a) and (b) are a 2-D projection, and a 3-D surface model, respectively, of the dominant foreground object in Fig. 2, which consists of a single pyramidal neuron cell body, and part of its apical (“a” red arrow, with an oblique collateral “o” blue-green arrow) and basal (“b” blue arrows) dendritic arbors. The remaining steps of the procedure will be illustrated using the Fig. 6 neuron. Subsequently, 3-D skeletonization operations are performed on each of the foreground objects within the image produced in step 1. Herein, the algorithm described by Palagyi et al. [66], [67] was implemented in Matlab (The MathWorks Inc., Natick, MA). Pseudocode of our implementation of these operations is given in “Construct binary_mask and skeleton” in Appendix II. It is noted that the surfaces of dendrites are highly irregular due to the presence of dendritic spines (see Fig. 2), therefore, the skeletonization operation produces structures with several short branches emanating from the dendrites and cell bodies. These structures are filtered from the images in the following steps of the analysis because they do not represent the longitudinal orientation of a neurite.

Fig. 6.

Two-dimensional projection (a) and 3-D surface model (b) of the dominant foreground object identified in Fig. 2. Oblique collateral branches (o, green arrow) off apical dendrites (a, red arrow), as well as basilar dendrites (b, blue arrows) are indicated on this pyramidal neuron.

As described above, water molecules within cell bodies are not expected to contribute to S_c, but rather to the extra-cylindrical term S_e in (1). Therefore, the second step in the Fig. 5 procedure is to filter voxels that reside within cell bodies from subsequent analysis. Herein, cell bodies are defined as objects with a radius larger than 6 μm, which corresponds to a diameter of approximately three diffusion lengths, $3\sqrt{D_L\Delta }$. To identify cell bodies, the Euclidean distance from each foreground object voxel to a voxel outside of the object was calculated. Voxels within 6 μm of a voxel that is more than 6 μm from a background voxel were excluded from subsequent analysis. The operations used to perform this step are outlined in the “Filter cell bodies” procedure in Appendix II, which takes the matrices binary_mask and skeleton as input, and produces the filtered skeleton matrix skeleton_f.

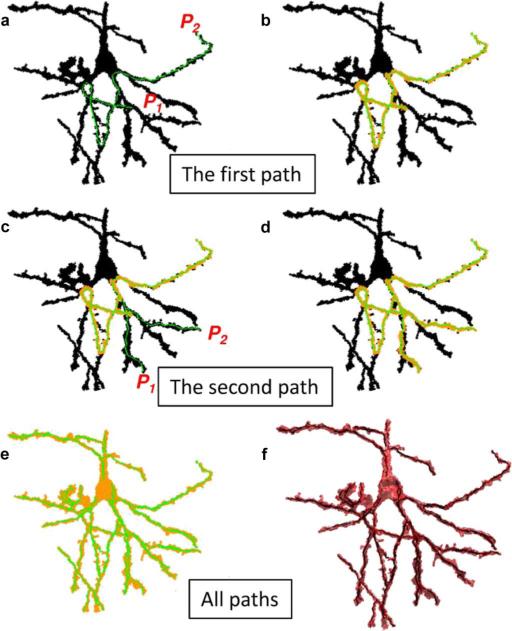
The third step in the procedure converts the filtered 3-D skeleton to a list of paths that span each foreground object. To accomplish this, the following operations are repeated until each voxel in the filtered 3-D skeleton has been assigned either to a path spanning a foreground object, or to a minor branch, defined as a path of less than 10 voxels. First, an arbitrary seed point is selected from the set of voxels with a value of 1 in the filtered 3-D skeleton, and Dijkstra's algorithm [68] is used to determine the shortest path to all other connected points on the 3-D skeleton that are also labeled with a value of 1. The point , which has the maximum shortest path to the seed point, is said to be furthest from the seed point. This is one extreme position of the 3-D skeleton. Dijkstra's algorithm is then utilized a second time to determine the point P₂, which is furthest from P₁. Fig. 7(a) illustrates a 2-D projection of the first pair of points P₁ and P₂, identified in the object shown in Fig. 6. The path connecting P₁ and P₂ (Fig. 7(a), green voxels) is overlaid on a 2-D projection of binary_mask (Fig. 7(a), black voxels). To remove short segments in the skeleton that arise from irregularities such as dendritic spines, the next operation within the loop is to set all skeleton voxels within a Euclidean distance of 5 μm from any point along the path connecting P₁ and P₂ to a value of 0, as illustrated by orange voxels in Fig. 7(b). Next, it is determined whether the path connecting P₁ and P₂ traverses a threshold distance of at least 10 voxels. If so, the path is considered to be within a major axonal/dendritic fiber, and the ordered set of coordinates connecting points P₁ and P₂, is stored to memory. If not, the path is not considered to be a major fiber segment, but instead arises from image “speckles” or from dendritic spines, and it is not stored to memory. Fig. 7(c) and (d) shows the result of the second iteration of this loop. This is repeated for each object included in the filtered 3-D skeleton. Fig. 7(e) shows the complete set of paths (green voxels) identified for the foreground object. In Fig. 7(f), the paths are displayed as black voxels. Pseudocode for these operations are given in Appendix II, “Determine path_coordinates_list.” This step in the Fig. 5 procedure converts the input matrix skeleton_f to the list of paths path_coordinates_list.

Fig. 7.

Extraction of major axonal and dendritic neuronal elements from a skeletonized object. Initially, each voxel within the foreground object pictured in Fig. 2 is labeled with a value of 1, color-coded black in the 2-D projections in panels (a)–(d), and the following operations are repeated until all foreground object voxels are labeled with a value of 0, color-coded orange in (b)–(e). First, the longest minimum path length along the 3-D skeleton that connects two points within the object is determined as described in the text [green path connecting points P₁ and P₂ in (a)]. Next, if the path length is greater than 10 μm, the ordered set of voxel coordinates intersected by the path is stored to memory. Last, regardless of the length of the path, all foreground object voxels within a Euclidian distance of 5 μm from any point along the path are relabeled with a value of 0 [orange voxels, (b)]. Subsequent paths are identified within connected subsets of voxels within the object that are labeled with a value of 1. Panels (c), (d) illustrate the second iteration of the sequence. Panel (e) shows the paths stored to memory at the end of the sequence. Paths within a 3-D model of the object are shown in (f).

In the final step of the Fig. 5 procedure, each of the paths defined in step 3 is approximated as a set of line segments, and the orientation distribution of these line segments is used to determine the scatter matrix T. This is accomplished by separating each path in path_coordinates_list into groups of 10 consecutive coordinates. Each group of 10 coordinates is thus represented as a 10 × 3 matrix, C, in which each of the 10 rows specifies the x, y, and z component of a coordinate, c₁ = (c_1,x, c_1,y, c_1,z), . . ., c₁₀. This group of 10 coordinates approximates a line segment by 3-D orthogonal distance regression. The point m = (m_x, m_y, m_z) is defined as the mean of the x, y, and z components (i.e., the mean of the columns of C). A 10 × 3 matrix, B, is defined as consisting of the difference between each row of C and m: d_i,x, d_i,y, d_i,z = c_i – m, and

$$\mathrm{B}\equiv \left[\begin{array}{ccc}\hfill d_{1,x}\hfill & \hfill d_{1,y}\hfill & \hfill d_{1,z}\hfill \\ \hfill \hfill & \hfill ⋮\hfill & \hfill \hfill \\ \hfill d_{10,x}\hfill & \hfill d_{10,y}\hfill & \hfill d_{10,z}\hfill \end{array}\right].$$ (18)

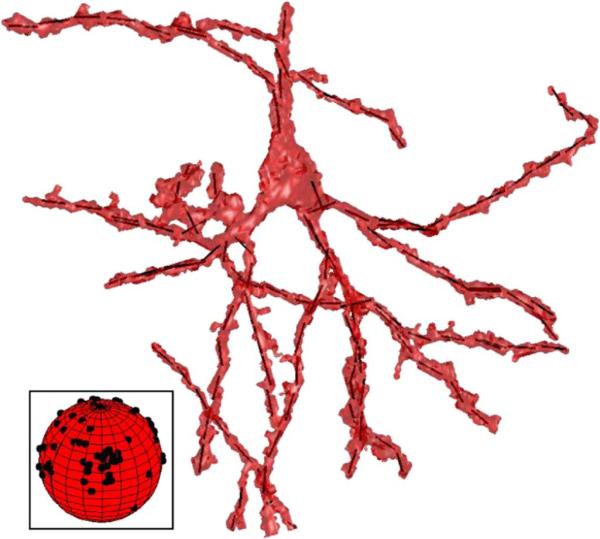
The direction of the 3-D orthogonal distance regression line is the primary eigenvector of the matrix B^TB. Line segments derived from the example foreground object are shown in Fig. 8. The set of primary eigenvectors derived from this analysis are projected onto a unit sphere in the Fig. 8 inset.

Fig. 8.

The set of orthogonal distance regression line segments used to approximate the object, and estimate the orientation distribution of neuronal processes are shown within the foreground object surface model. In the inset, the distribution of line segment orientations are shown on a unit sphere.

For a given Golgi-stained region, this procedure will give orientations of N line segments. In order to compute the scatter matrix, T, representing the second moment of the orientation distribution of the N line segments, an N × 3 matrix S, having the N primary eigenvector x, y, and z components as its rows, is constructed. The scatter matrix T is then T = S^TS/N, c.f. (6). Its tensor properties such as fractional anisotropy (FA_T) may be derived from the tensor eigenvalues, τ, as given in (11). Pseudocode to compute the output T from the input path_coordinates_list according to the fourth step of the Fig. 5 procedure is given in “Determine T” of Appendix II.

IV. Results

It has previously been shown in ferrets that reductions in cerebral cortical diffusion anisotropy associated with brain development take place primarily between the first and fourth weeks of life [34]. It was therefore expected that anisotropy in scatter matrices in the cerebral cortex from a P31 animal would be lower, on average, than anisotropy observed within cerebral cortex of a P13 animal. However, the reduction in cortical diffusion anisotropy takes place according to an inside-out laminar gradient, such that deep cortical layers exhibit lower diffusion anisotropy than superficial layers; and a rostral-caudal regional gradient, such that rostral cortical regions exhibit lower diffusion anisotropy than caudal regions. Due to the presence of these gradients, it was also expected that more variability in anisotropy of scatter matrices would be observed in the P13 brain than in the P31 brain. To experimentally test these predictions, the 32 sites (containing a total of 128 sub-ROIs) within five axial sections of the P13 brain were compared to a set of 14 sites (56 sub-ROIs) characterized within a single axial section of the P31 brain. Mean and standard deviations of the distributions of FA_T values were 0.46 ± 0.15 and 0.34 ± 0.12 for the P13 and P31 sections, respectively, which confirms the expectation that FA_T is higher and more variable at P13 than at P31. Subsequent analysis was therefore focused on the P13 brain, to determine whether variability in the FA_T values is reflected in variability of cerebral cortical diffusion anisotropy, as predicted by (12).

To provide a visual comparison of Golgi and DTI data, and to evaluate the hypothesis that neurite orientation anisotropy is a major determinant of diffusion anisotropy, a model independent comparison of anisotropy in diffusion and axon/dendrite orientation distributions was made. An intuitive approach is based on comparing the behavior of the diffusion signal S(n̂) and the neurite orientation density f(n̂) as functions on the unit sphere. We use spherical interpolation such that both may be evaluated at any point on the sphere. This can be done e.g., on the basis of an expansion in spherical harmonics Y_lm(θ, φ), As described for example in [50], [51], [69], any sufficiently smooth function f(θ, φ) on the sphere can be represented as a Laplace series

$$f(\theta ,\phi )=\sum _{l=0}^{\infty }\sum _{m=-l}^l{f}_{lm}{Y}_{lm}(\theta ,\phi )$$ (19)

with coefficients f_lm determined by

$$f_{lm}=\int d\Omega Y_{lm}^{\ast }(\theta ,\phi )f(\theta ,\phi )$$ (20)

where the asterisk denotes complex conjugation. When used to represent the axon/dendrite segment orientation distribution f(û), we see from the equation above that the coefficients f_lm are the average value of the corresponding complex conjugated spherical harmonic. This average is estimated empirically by using the observed neurite directions

$$f_{lm}=\frac{1}{N}\sum _i{Y}_{lm}^{\ast }\left({\widehat{u}}_i\right)$$ (21)

where N is the number of neurites and û_i is a unit vector in the direction of the i′th neurite³. Similarly, coefficients S_lm are used to represent the normalized diffusion-weighted MRI signal intensity and were estimated by the linear least squares solution of

$$S\left({\widehat{n}}_i\right)∕S_0=\sum _{l,m}{S}_{lm}{Y}_{lm}\left({\widehat{n}}_i\right)$$ (22)

see e.g., [70], where here n̂_i is the ith diffusion weighting direction. In our implementation, we keep terms up to and including l = 4.

Data from four pairs of neuronal process orientation distributions and diffusion tensors are shown in detail in Fig. 9. For fields labeled I–IV in Fig. 4(b), transmitted light images are shown in the left column of Fig. 9. The set of line segments used to estimate the scatter matrix for cellular processes within one quadrant for each of the four fields is displayed as 3-D surface models in the adjacent column of Fig. 9. The right two columns of Fig. 9 show Schmidt plots, an equal area stereographic projection [57] method, of the neuronal process orientation distribution and diffusion MRI data. Each Schmidt plot is shown in the Golgi reference frame (e.g., the azimuthal angle for each Schmidt plot corresponds to the in-plane direction in the Golgi images). The orientation distribution plots reflect the probability that a neuronal process is oriented according to polar and azimuthal angles shown, whereas the diffusion MRI plots (Fig. 9, right plots showing the negative log of the diffusion signal) reflect the apparent diffusion coefficient measured along a direction specified by a given set of polar and azimuthal angles. These plots display qualitatively similar features. In each row, peak intensities for orientation distributions and diffusion-weighted MRI signal intensity are observed for similar polar and azimuthal angles. In addition, Golgi quadrants in which the neuronal process orientation distribution peak is narrow (within fields I and II) generally correspond to narrow peaks in the diffusion-weighted signal, whereas broad orientation distribution peaks (quadrants within fields III and IV) are generally matched with broad peaks in the diffusion weighted signal. For comparison, fractional anisotropy values FA_D (third column) or FA_T (fourth column), are given in the upper left corner of each Schmidt plot. Overall, the Golgi peaks appear sharper than the DTI peaks, and we believe there are two main reasons for this. First, diffusion anisotropy is affected also by water in the extracellular space which is arguably less anisotropic than the intracellular space. Second, even for a single neurite direction, the diffusion peak would be blurred since the diffusion direction (the diffusion wave vector) has a component parallel to the neurite for most directions.

Fig. 9.

Model independent comparison of the angular dependencies of the neuronal process orientation distribution and negative log of the diffusion signal for four quadrants. Images in rows I–IV are taken from corresponding fields labeled I–IV in Fig. 4(b). From left to right, the first column shows transmitted light images for each field. The quadrant shown in the remaining three columns is outlined with a black box. The second column shows 3-D surface models of the set of line segments used to estimate the scatter matrix for the stained cellular processes. Images are rotated slightly to show the boundaries of the quadrants. An equal area stereographic projection method (Schmidt plot) has been used to render the 3-D probability density distributions in a manner that is suitable for 2-D graphs in the third and fourth columns. In each plot, the polar angle θ ranges from 0° (center of plot) to 90° (outer perimeter of the circle). Concentric circles within the outer perimeter of each plot correspond to polar angles of 30° and 60°. The azimuthal angles for each plot are aligned with the first and second columns of the figure. Orientation distributions are expressed using (19) in the third column, and the negative log of the diffusion signal intensity is expressed using (22) in the fourth column. Numbers in upper left corners of the third and fourth columns are FA_T and FA_D, respectively, as defined in (11).

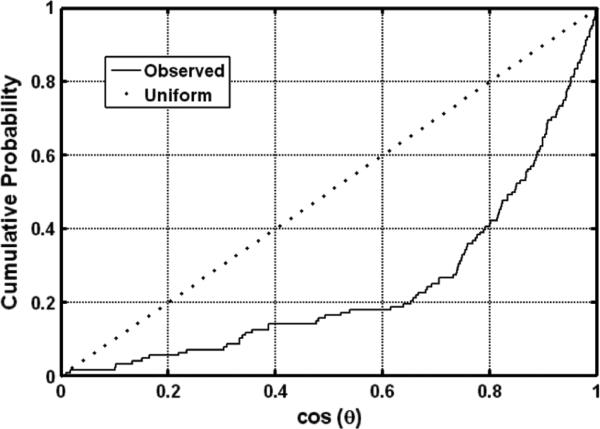
The degree of agreement between the principal DTI and scatter matrix eigenvectors was used as one way to quantitatively assess whether the prediction of (9) was upheld in our data. Fig. 10 provides a graphical comparison of primary eigenvectors of the DTI data for voxels within the cerebral cortex, expressed in the Golgi frame (yellow vectors), with primary eigenvectors of the 128 Golgi field quadrants (red vectors). As expected, the orientations of the two sets of vectors generally coincide. The distribution of relative angles θ ∈ [0, π/2] between the corresponding directions was examined to determine whether a statistically significant correlation exists between the two sets of tensor eigenvectors. The null hypothesis is that no correlation between these directions exists. Under conditions of the null hypothesis, cos(θ), which is the z-component of the primary DTI eigenvector in a coordinate system in which the Golgi primary eigenvector defines the z-axis, would be uniformly distributed between zero and one. Fig. 11 shows the cumulative distribution of cos(θ), compared to the uniform distribution. The actual distribution is clearly different from the uniform, in particular there is a tendency for the relative angles to be close to zero, indicating general alignment between the principal directions of the diffusion tensor and the scatter matrix. Indeed, the Kolmogorov–Smirnov test rejects the null hypothesis (p < 10^–6). The average angle between the diffusion principal direction and scatter matrix principal direction is approximately 36°, and the scatter characterized by the length of the resultant vector $\mathbf{R}=1∕128{\sum }_{i=1}^{128}(\text{cos}{\theta }_i,\text{sin}{\theta }_i)$ is 0.93. Note that |R| = 0 would correspond to maximal scattering over the unit circle, whereas |R| = 1 would correspond to maximal coherence.

Fig. 10.

Overlay of diffusion tensor (yellow) and axon/dendrite scatter matrix (red) primary eigenvectors on FA parameter maps for each of the five P13 Golgi sections.

Fig. 11.

Estimated cumulative distribution of the length of the projection of the DTI principal direction onto the main direction of the scatter matrix. If the two directions were unrelated, this variable would be uniformly distributed between zero and one, and resemble the dotted line. Deflection of the solid line below the dotted line indicates diffusion tensor and scatter matrices are correlated, which is statistically significant according to a Kolmogorov–Smirnov test (p < 10^–6).

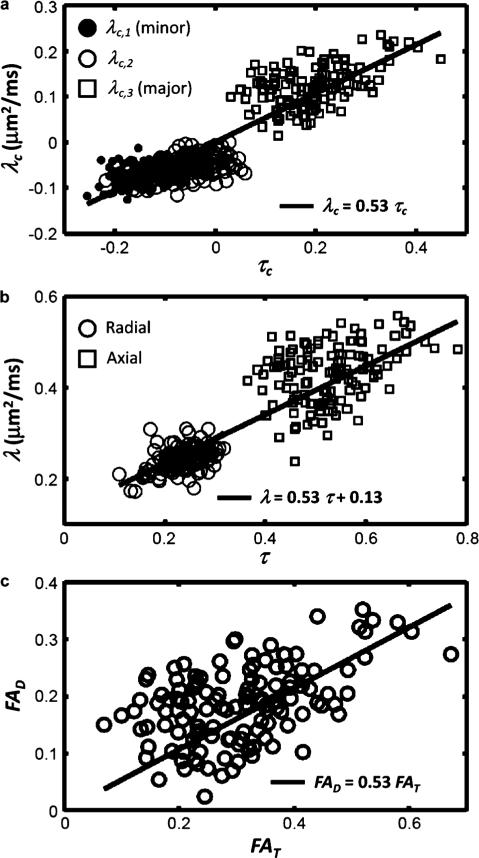
To test the prediction in (10) of a linear relationship between the eigenvalues of the two matrices, the centralized eigenvalues of the scatter matrix were matched pairwise to the centralized eigenvalues of the DTI matrix according to rank. These pairs are plotted in the Fig. 12 upper panel where a clear linear relationship is observed, as predicted by the theory, corresponding to a significant Spearman correlation using either the largest (ρ = 0.30, p < 6 × 10^–4) or smallest (ρ = 0.37, p < 3 × 10^–5) eigenvalues. The best linear fit (using the robust fitting function “robustfit” in Matlab), resulted in a slope of νD_A = 0.53. A second analysis was performed in which the diffusion eigenvalues were represented as radial diffusivity, defined to be the average of the two smallest diffusion eigenvalues, and axial diffusivity, defined to be the largest diffusion eigenvalue. Similarly, radial and axial eigenvalues were defined for the scatter matrix, and the resulting 2 × 128 pairs of points were plotted against each other in the Fig. 12 middle panel. Given that the mean diffusivity $\overline{\lambda }$ across the voxels is relatively constant (average $\overline{\lambda }=0.30$, standard deviation 0.027), (10) predicts a linear relationship between this set of numbers, with slope νD_A and y-axis intercept $\overline{\lambda }-\nu D_A\overline{\tau }=\overline{\lambda }-\nu D_A∕3$. This is shown as a solid line in the middle panel, using the values obtained from the fit above (νD_A = 0.53 and intercept 0.13). An independent fit gave similar values (νD_A = 0.58 and intercept 0.11). In the Fig. 12 lower panel, fractional diffusion anisotropy FA_D is plotted against the fractional orientation anisotropy FA_T, cf. (12), and again a significant linear correlation is found (p < 10^–5) with a correlation coefficient of ρ = 0.40, and an estimate of νD_A = 0.57.

Fig. 12.

(a) The centralized eigenvalues of the diffusion tensor versus the centralized eigenvalues of the scatter matrix, along with the best robust fit (line). The slope of the lines shown for all panels corresponds to the product νD_A, as described in the text, and is set to a value of 0.53, determined from the data shown in (a). In (b), radial and axial diffusivities versus corresponding numbers using the scatter matrix eigenvalues are plotted, and the solid line is the predicted linear relationship using the fit from (a) and the observed mean diffusivity $\overline{\lambda }=0.30$ μm²/ms. In (c), fractional anisotropy of water diffusion (FA_D) is plotted against fractional anisotropy of the axon/dendrite scatter matrix (FA_T), and the line corresponds to the fit determined in panel (a).

V. Discussion

In this work we have investigated the structural origins of diffusion anisotropy in the immature ferret cerebral cortex by comparing DTI measurements to quantitative analyses of Golgi-stained tissue. The early postnatal ferret brain is suitable for this comparison because it exhibits a high degree of similarity to fetal human cerebral cortex, including the development of sulcal and gyral structures at a developmental stage that is temporally coincident with the loss of cortical diffusion anisotropy. Additionally, the trajectory of DTI changes with development has been extensively characterized in this species [31], [34]. We derived a direct mathematical relation between the diffusion tensor and the axonal and dendritic architecture in the neuropil, expressing quantitatively how diffusion anisotropy is induced by intrinsic diffusion anisotropy within axons and dendrites and anisotropy in their orientation distribution. A methodological framework for quantitative characterization of histologically-prepared tissue was described, and applied to tissue from a P13 and a P31 ferret. In accordance with predictions based on previous studies of cortical diffusion anisotropy, a larger amount of variance in FA_T was observed at P13 than at P31. Therefore, to assess the veracity of the proposed theoretical relationship in (9), scatter matrices were measured throughout the P13 cerebral cortex, and these were demonstrated to be significantly correlated to diffusion tensor measurements performed on the same brain as predicted by (9).

To experimentally determine cortical orientation distributions of neuronal processes, it was necessary to choose a staining technique that enables visualization of dendritic and axonal structures. An ideal technique for providing comparisons to cortical DTI measurements stains cortical cells in an unbiased manner, provides data from several cells within each MRI voxel, and will stain cells in a manner that will enable individual axonal and dendritic processes to be resolved. The Golgi technique is one of very few methods that meet these criteria. By staining a small, random subset (~1%) of cells in a complete manner [71], the Golgi technique enables an overall representation of cellular architecture to be characterized, but the staining is not so dense that it is impossible to resolve neighboring fibers. For these reasons, the Golgi method has been in use for over a century as a general method for characterizing neuronal morphology (e.g., see [72] and references cited therein), and has previously been used to document dendritic development in pyramidal neurons of ferret cerebral cortex [73]. For these reasons, the Golgi technique was selected here for comparisons to DTI measurements. However, it is also noted that the procedures described here can be extended to other methods for visualization of cellular processes in the future.

There was a strong mutual alignment between the directions of the principal eigenvectors of the scatter and DTI matrices, in agreement with theory. The theoretical relationship was further supported by comparing centralized eigenvalues of the neurite orientation and water diffusion tensors to one another, as well as measures of fractional anisotropy. The straight line which best fit the pairs of centralized eigenvalues had a slope corresponding to νD_A of 0.53 μm²/ms, according to (10) and (12). Typical values of D_A = 0.7 μm²/ms were previously reported in measurements of water diffusion within post mortem baboon cerebral cortex [52] resulting in an estimate of neurite density on the order of ν ≈ 0.7–0.8, consistent with literature values of the neuropil volume fraction of 0.7 (rat, [74]) and 0.8 (rhesus macaque, [75]). Thus the observed slope estimated using (10) to the data is in excellent agreement with previous measurements by us and others.

Several factors potentially contribute to the variance in the Fig. 12 plots. Variations in neurite volume fraction ν or intrinsic diffusion anisotropy D_A among the different Golgi fields were not taken into account, which likely explains some of the scatter in the data points around the straight lines in Fig. 12. Additionally, slight misregistration of the Golgi and DTI reference frames is also expected to contribute to scatter in the Fig. 12 plots. Specifically, histological preparation procedures introduce nonlinear deformations of the tissue that are not fully accounted for by the linear registration approach described in Section III-D. However, efforts were made to minimize these effects, such as manual in-plane adjustments to match each Golgi ROI to a specific DTI voxel. Although nonlinear methods could in principle improve the registration procedures, we found the adopted approach to provide considerable accuracy (the mean distance between DTI-frame landmarks and the corresponding planes in Fig. 4(a) was found to be 0.20 mm). Due to the lack of similarity in image contrast patterns between the Golgi and DTI data, nonlinear registration strategies were not pursued here. Last, although the volumes of the Golgi regions were nearly matched to the volume of a single DTI voxel, the shapes of the Golgi regions (387.5 μm × 387.5 μm × ~ 100 μm) differed from DTI voxels (250-μm-sided cubes) due to constraints of the Golgi imaging technique. This distinction could lead to differences in the manner in which the two methods sample cerebral cortical neuronal morphology. Despite these potential complications, a highly statistically significant correlation between DTI derived parameters and neurite orientation matrix was observed, in agreement with the proposed theory.

In addition to factors expected to contribute to variance in Fig. 12, systematic effects related to simplifying assumptions of the (1) model may also influence the relationship between the measured diffusion tensor and the orientation distribution in neuronal processes. Several of these factors have been discussed in previous studies [39], [50], [51]. For example, only neuronal processes were accounted for in the histological measurements, whereas vasculature, glial processes and anisotropy of the extracellular space could, in principle, contribute to diffusion anisotropy. It should be noted, however, that the volume fraction of capillaries and glial cells are each estimated to be less than 5% [74], and the contribution of these components to diffusion anisotropy is thus expected to be minor. In addition, since intra- and extracellular spaces are complementary to one another, the anisotropy of the extracellular space will very likely mimic the variation in the neuritic anisotropy, and the net effect may thus amount to a rescaling of the proportionality constant ν in (9). In the future, experiments with other histological or immunohistochemical stains will be of value to specifically determine the extent that e.g., glial processes contribute to the observed measurements, and to separate the axonal and dendritic contributions.

Recent investigations have shown that diffusion MRI is sufficiently sensitive to detect differences between cortical areas within an individual [50] and between cerebral cortices of different treatment groups, such as visually-deprived and control animal subjects within visual cortex [39]. Despite the obstacles encountered in characterizing the link between MRI measurements on intact tissue and measurements performed on the same tissue following histological processing, the work presented here demonstrates it is possible to interpret directionally-dependent diffusion MRI measurements in terms of the 3-D orientation distribution function of cellular processes in the developing neuropil. This capability is particularly significant in the contexts of neurodevelopmental disorders, in which affected individuals exhibit simplified dendritic arbors within the developing brain [4]–[7], as well as for studies of the relationship between environmental factors and neuronal morphology, such as the effect of stress on hippocampal pyramidal dendrite structure [76]. Therefore, it is anticipated that measurements of diffusion anisotropy within the cerebral cortex will be of increasing value for extending the diagnostic capabilities of MRI in studies of neuropsychiatric disorders in the future.

VI. Conclusion

An experimental framework based on confocal microscopy for quantitative comparisons of histology to MRI was described, and used to evaluate a novel relation between the MR diffusion tensor and axonal/dendritic architecture. This relation was a mathematical expression of how microstructural anisotropy in gray matter shapes the diffusion tensor. The proposed microstructural underpinnings of the diffusion tensor were experimentally validated on a fixed ferret brain by confocal microsocopy using reflected visible light of Golgi-stained tissue following diffusion tensor imaging. Quantitative comparisons following coregistration of the Golgi and DTI data support the proposed theoretical relationship between the water diffusion tensor and the orientation tensor of neuronal processes. These results provide a framework for interpreting DTI measurements of the cerebral cortex in terms of cellular morphological properties that can be influenced by environmental experience, or perturbed in neurodevelopmental disorders.

Appendix I

In this section, we focus on the kurtosis to illustrate how to extend the procedure to relate higher-order cumulants of the diffusion signal to corresponding moments of the neurite orientation distribution function. Reverting (5) to an expansion of log(S)

$$\ln S∕S_0\approx -b{\widehat{n}}^T{\mathrm{D}}_{\text{app}}\widehat{n}+\frac{1}{6}{b}^2\mathrm{Tr}{({\mathrm{D}}_{\text{app}}∕3)}^2\widehat{n}{\widehat{n}}^T{\mathrm{K}}_{\text{app}}\widehat{n}{\widehat{n}}^T$$ (23)

we find for the apparent kurtosis

$${\mathrm{K}}_{\text{app}}=[\nu D_A^2\mathrm{W}+(1-\nu )\nu {(\mathrm{D}-\mathrm{I}{D}_T-D_A\mathrm{T})}^{\otimes 2}]∕\mathrm{Tr}{({\mathrm{D}}_{\text{app}}∕3)}^2.$$ (24)

Here, we have defined the centralized fourth moment W (a rank 4 tensor) of the neurite orientation distribution

$${\mathrm{W}}_{ijkl}=3\langle u_i{u}_j{u}_k{u}_l\rangle -\langle u_i{u}_j\rangle \langle u_k{u}_l\rangle -\langle u_i{u}_k\rangle \langle u_j{u}_l\rangle -\langle u_i{u}_l\rangle \langle u_k{u}_j\rangle$$ (25)

and used the tensor product notation ⊗: e.g., for two second rank tensors A and B, the tensor product $\mathrm{A}\otimes \mathrm{B}$ is a rank four tensor with Cartesian components ${(\mathrm{A}\otimes \mathrm{B})}_{ijkl}={\mathrm{A}}_{ij}{\mathrm{B}}_{kl}$, and ${\mathrm{A}}^{\otimes 2}\equiv \mathrm{A}\otimes \mathrm{A}$. The second term in (24) is a cross term of the two compartments, and vanishes if either ν = 1 or 0. The first term reflects the fourth moment of the neurite orientation distribution. This result reflects the general property that the n^th order cumulant tensor contains information about the neuronal process orientation distribution moments of order less than or equal to n. Since the higher-order cumulants affect the diffusion signal only for sufficiently high diffusion weighting, this in turn implies that increased information about small-scale angular variations in the microstructure requires higher b values, in addition to better directional sampling.

Appendix II

This section gives pseudocode routines for the data processing procedures shown in Fig. 5.

Construct binary_mask and skeleton
Input. A 3-D (e.g., 128 × 128 × 100) matrix, image_stack, of reflected light intensity values, and a threshold intensity to distinguish foreground and background objects.
Output. Two binary 3-D matrices; a thresholded image of stained cellular elements, binary_mask, and a 3-D skeleton of the thresholded image, skeleton.
1.	Construct 3-D matrices binary_mask and skeleton of size equal to image_stack; Set all voxel values of both matrices to 0.
2.	For each voxel in image_stack with intensity greater than threshold, assign the corresponding voxel of binary_mask a value of 2
3.	while the maximum voxel value of binary_mask is 2
4.	Choose an arbitrary voxel, V0, in binary_mask that has a value of 2.
5.	Determine the set S voxels in binary_mask that are connected to V0 by a path that traverses only voxels of value equal to 2.
6.	Set binary_mask voxels in S to a value of 1.
7.	Determine the 3-D skeleton of S; assign voxels a value of 1 in skeleton.
8.	end while

Filter cell bodies
Input. binary_mask and skeleton from “Construct binary_mask and skeleton.”
Output. A filtered binary 3-D matrix of skeletonized foreground objects, skeleton_f, in which voxels within cell bodies of radius greater than 6 μm are assigned a value of 0.
1.	Construct the matrix skeleton_f by duplicating skeleton.
2.	for each voxel vi with a value of 1 in binary_mask
3.	if the Euclidean distance between vi center and the center of the nearest voxel of value 0 in binary_mask is greater than 6 μm
4.	Determine the set of voxels N that are within 6 μm of vi.
5.	Set the connected set of voxels within N that contains vi and are of value 1 in binary_mask to a value of 0 in skeleton_f.
6.	end if
7.	end for

Determine path_coordinates_list
Input. skeleton_f from “Filter cell bodies.”
Output. A list of skeleton paths spanning axons and dendrites, path_coordinates_list.
1.	Construct the matrix M = skeleton_f.
2.	Initialize counting variable i = 1.
3.	while the maximum voxel value of M is 1
4.	Choose an arbitrary voxel, P0, in M that has a value of 1.
5.	Use Dijkstra's algorithm to find P1, the voxel with the maximum shortest path to P0 within the connected set S of voxels of value 1 in M containing P0. P1 is said to be the furthest voxel from P0.
6.	Find P2, the furthest voxel in S from P1.
7.	Use Dijkstra's algorithm to determine the shortest path between P1 and P2; Define {P1P2} as the list of coordinates connecting P1 and P2.
8.	Set voxel values for coordinates within a 5 μm Euclidean distance of any {P1P2} coordinate to 0.
9.	if the length of {P1P2} consists of 10 or more voxels
10.	Assign voxel coordinates on {P1P2} to path_coordinates_list(i).
11.	Increment i.
12.	end if
13.	end while

Determine T
Input. path_coordinates_list from “Determine path_coordinates_list.”
Output. 3 × 3 scatter matrix T defined in (6).
1.	Initialize counting variable n.
2.	for1 each of the i paths in path_coordinates_list
3.	Initialize counting variable j = 1.
4.	while j is less than or equal to floor(0.1 * (number of coordinates in path_coordinates_list(i)))
5.	initialize counting variable k = 1.
6.	for2 coordinates 10 * (i – 1) + 1 to 10 * i in path path_coordinates_list(i)
7.	Assign the x, y, and z components of coordinate 10 * (i – 1) + k to the kth row of the 10 × 3 matrix C.
8.	Increment k.
9.	end for2
10.	Define the 1 × 3 vector m as the mean values of the 3 columns of C.
11.	Construct the 10 × 3 matrix B by setting each of its rows equal to the difference between m and the corresponding row of C.
12.	Assign to row n of matrix S the primary eigenvector of the matrix BTB.
13.	Increment n and j.
14.	end while
15.	end for1
16.	Define N = n – 1.
17.	Determine T = STS/N.