Entropic Intermediates and Hidden Rate-Limiting Steps in Seemingly Concerted Cycloadditions. Observation, Prediction, and Origin of an Isotope Effect on Recrossing

Abstract

An unusual intramolecular kinetic isotope effect (KIE) in the reaction of dichloroketene with cis-2-butene does not fit with a simple asynchronous cycloaddition transition state, but it can be predicted from trajectory studies on a bifurcating energy surface. The origin of the KIE is related to a high propensity for transition state recrossing in this system, with heavier masses recrossing less. The KIE can also be predicted by a statistical model that treats the cycloaddition as a stepwise mechanism, the rate-limiting second step being associated with an entropic barrier for formation of the second carbon-carbon bond. The relevance of this stepwise mechanism to other asynchronous but seemingly concerted cycloadditions is suggested by examination of organocatalytic Diels-Alder reactions.

Conventional transition state theory (TST) assumes that molecular systems passing through a dividing surface (the TS) in the direction of products do not turn back and reform reactants. It was recognized from the beginning that this “no-recrossing assumption” is an approximation, and this led to the incorporation of transmission coefficients into TST.¹ The inaccuracy in TST engendered by recrossing can be minimized by a sagacious choice of the dividing surface, and this is the central idea in variational TST.² Some recrossing occurs that is not yet predictable by statistical methods,^3,4,5 and we have observed its impact on experimental observations.⁶ Recrossing in general remains largely a hidden phenomenon; little is known about its importance in ordinary organic reactions and there are no general experimental probes for its occurrence.

We describe here the observation of an unusual heavy-atom kinetic isotope effect (KIE) in a simple organic cycloaddition. This cycloaddition traverses a single potential energy saddle point, but neither the saddle point nor its closely associated variational TS dictate the rate of the reaction or its experimental KIE. However, this KIE can be predicted from trajectory studies, which find that heavier isotopes are less likely to recross the TS. We also describe a statistical procedure that successfully predicts the KIE, though within a statistical view this simple cycloaddition involves a short-lived intermediate entrapped between entropic barriers. Finally, we find that the same mechanistic complications apply to an organocatalytic Diels-Alder reaction. The results provide insight into structural effects on recrossing and complicate the mechanistic understanding of cycloadditions.

Our previous work suggested that asynchronous cycloadditions are often subject to substantial recrossing of the conventional or variational TS.⁶ Because suprafacial [2 + 2] cycloadditions are formally forbidden pericyclic processes, the [2 + 2] cycloadditions of ketenes with alkenes are intrinsically highly asynchronous, and we chose the facile reaction of cis-2-butene (1) with dichloroketene (2) for experimental study. This reaction was probed by the determination of the intramolecular KIEs for the cis-2-butene carbons in the reaction. When a ¹³C is present in 1, the otherwise equivalent cyclobutanone products 3 and 3' become isotopomeric. The ratio of the products constitutes an intramolecular KIE, and two such KIEs may be observed depending on whether the ¹³C was in the olefinic or methyl carbons of 1. These KIEs were readily determined at natural abundance by NMR methodology.⁷ A total of 24 KIE measurements were made on samples of 3 obtained from three independent reactions at 25 °C. The methyl-carbon KIE was 1.000 ± 0.001. The olefinic-carbon result, 0.993 ± 0.001, is rather more interesting.

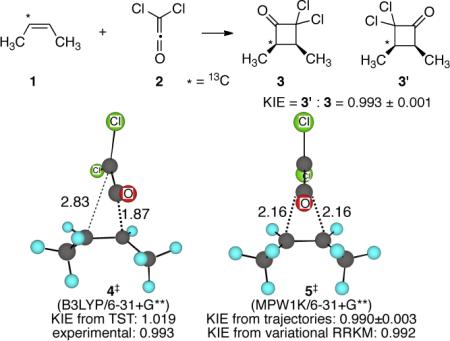
The unusual observation here is that more ¹³C is found in the methine position adjacent to the carbonyl (as in 3) than in the methine distal from the carbonyl (as in 3'). If the cycloaddition is viewed in qualitative terms as an electrophilic attack of the carbonyl carbon of the ketene on the olefinic carbons, then one would generally expect that the carbonyl carbon would preferentially end up attached to ¹²C. In keeping with this idea, KIEs (defined as 3'/3) calculated based on ordinary asynchronous transition structures such as the B3LYP/6–31+G** structure 4^‡ (see the Supporting Information (SI) for examples using other methods) are in the 1.01 to 1.02 range. The experimental “inverse”⁸ intramolecular KIE shows that such calculated structures are qualitatively incorrect.

Other calculational methods support a different picture of the reaction. In M06, MPW1K, and MP2 calculations, the lowest-energy approach of the two molecules places the axis of the ketene orthogonal to the π-bond of the alkene and the cycloaddition transition structure has C_s-symmetry, e.g. the MPW1K/6–31+G** structure 5^‡.⁹ The C_s-symmetry is supported by CCSD(T)/6–311++G**/PCM(CH₂Cl₂) single-point energies on a grid of M06–2×/6–31+G** geometries (see the SI). The qualitative picture of the energy surface obtained in these calculations is shown in Figure 1. This is a “bifurcating energy surface” in which there are continual downhill paths from the transition structure to two product wells. On this surface, the formation of the second new C–C bond in the cycloaddition is not set up to occur by a continuation of motion through the TS. Rather, trajectories crossing the saddle point must make a sharp “turn” to get to 3 or 3'. Notably, trajectories that do not make this turn rapidly encounter a potential energy wall associated with a high-energy cyclopropanoid structure. A second saddle point on this surface, 6^‡, is formally the transition structure for the interconversion of the two products.

Figure 1.

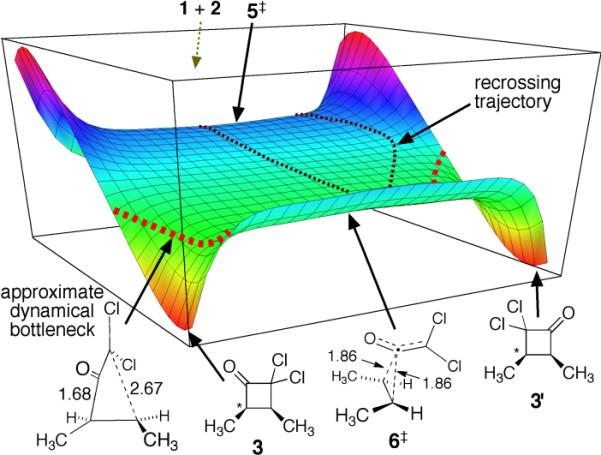
A qualitative depiction of the energy surface (M06, MPW1K, or MP2) for the [2 + 2] cycloaddition of dichloroketene with cis-2-butene.

Conventional TST provides no prediction of the intramolecular KIE on such bifurcating surfaces, and we turned to trajectories to gain insight into the unusual KIE. Due to the impractical number of trajectories required for statistically significant predictions of small KIEs, we applied our previously described trick of using, in silico, superheavy isotopes of carbon.¹⁰ Quasiclassical direct-dynamics¹¹ trajectories on an MPW1K/6–31G* energy surface (chosen because it models well the CCSD(T)/6–311++G**/PCM(CH₂Cl₂) surface) were initiated from isotopologues of 5^‡ containing a single ²⁸C, ⁴⁴C, ⁷⁶C, or ¹⁴⁰C (12 + 2^N amu, N=4, 5, 6, or 7). Each normal mode in 5^‡ was given its zero-point energy (ZPE) plus a Boltzmann sampling of additional energy appropriate for 25 °C, with a random phase and sign for its initial velocity. As will be discussed, the sign of the velocity in a particular normal mode, “mode 3,” has a dominant effect on the trajectory outcome, and an equal number of trajectories were started with the sign of the mode-3 velocity being positive versus negative. The transition vector was given a Boltzmann sampling of energy `forward' from the col. The trajectories were integrated in 1-fs steps until either the product was formed or separate starting materials were reformed.

The trajectories results (Table 1) provide a number of interesting observations. The first is that they account for the experimentally observed KIE. Superheavy olefinic carbons in 1 preferentially end up adjacent to the carbonyl carbon in the product (3' < 3), and the preference increases with increasing mass. Extrapolation of the results to ¹³C (see the SI) leads to a predicted KIE of 0.990 ±0.003. The consistency with the unusual experimental KIE supports the idea that the underlying physics leading to the KIEs with the superheavy carbons is the same as with ¹³C experimentally.

Table 1.

Trajectories started from 5^‡employing superheavy carbons.

isotope	total runs	mode 3 positive 3': 3 : recrossec	mode 3 negative 3': 3 : recrossed	3'/ 3
140C	11092	39.3 : 1.3 : 59.5	1.3 : 48.2 : 50.5	0.820
76C	7112	40.5 : 1.0 : 58.5	0.6 : 47.3 : 52.1	0.852
44C	5860	40.2 : 0.6 : 59.1	0.7 : 45.3 : 54.1	0.889
28C	10366	40.1 : 0.8 : 59.1	0.8 : 43.4: 56.1	0.915
			extrapolated to 13C:	0.990(3)
			exoerimental:	0.993m

The second observation is that the product outcome of the trajectories is essentially completely predetermined by the sign of the velocity of a normal mode at the TS. Motion in the low-energy (74 cm⁻¹) mode 3, depicted in Figure 2, desymmetrizes the transition structure in such a way that the combination of motion in this mode and motion along the transition vector morphs the structure toward the product geometries. When the trajectories have an initial positive sign for the mode-3 velocity (defining positive as in Figure 2), then ≈98% of the product formed is 3'. When mode 3 is negative, ≈98% of the product formed is 3. The scant crossover process occurs equally in each direction. This correspondence of selectivity to motion through an initial TS is a form of dynamic matching.^6b The mode-3 motion defines a “ridge” in the TS hypersurface. Trajectories cross the ridge at diverse positions but neither the crossing point nor the phase of any other mode affects which product is formed. Since the sign of mode 3 determines the product and since this sign is random, how is it possible for product selectivity to occur in the reaction?

Figure 2.

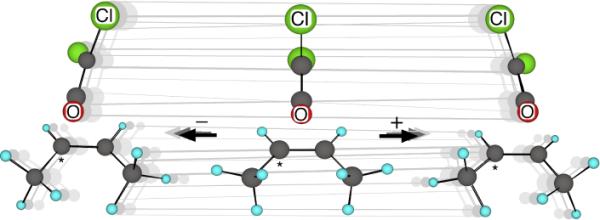
Motion associated with “mode 3” in the cycloaddition saddle point. With “*” designating a heavier isotope, a positive velocity is defined as motion toward the right.

The answer lies in the two most interesting observations from the trajectories: most trajectories recross the TS and reform the starting materials, and the propensity for recrossing depends on isotopic mass. The trajectories that recross the conventional TS are not associated with the canonical variational TS near 5^‡ (see the SI). Rather, the recrossing trajectories proceed into the area of 6^‡ and beyond; the average closest approach of the carbonyl carbon to the olefinic carbons was 1.69 Å. In the parent isotopologue (all carbons ¹²C), only 39% of the trajectories crossing the conventional TS proceed to products, while 61% recross, and the average time from crossing the TS to recrossing it (defined by C–C distances > 2.2 Å) is 183 fs. When the mass of both of the olefinic carbons is increased to ¹⁴⁰C, the recrossing is decreased to 51%. With singly-labeled alkene, the recrossing depends on the sign of the mode 3 velocity; when it is positive, mass has no effect on the recrossing, but when it is negative, the trajectories recross less as the mass is increased. This leads to the observed KIE.

We analyzed the origin of this mass effect on recrossing from both a dynamical perspective and a statistical perspective. From a dynamical perspective, a number of observations appear to be pertinent. First, the major product is not correctly predicted by the intrinsic reaction coordinate (IRC); that is, the steepest-descent path in mass-weighted coordinates starting from 5^‡ leads to 3', not the major 3. This suggests that the observed KIE is not analogous to the “Newtonian” KIEs that we have previously described.¹⁰ Second, when fully classical trajectories are employed in place of the quasiclassical trajectories above, the experimental isotope effect is still accounted for (the extrapolated KIE is 0.992). The suggestion from this observation is that ZPE effects are at most a minor contributor to the isotope effect. Third, increasing isotopic mass increases the time required for both product-forming and recrossing trajectories. With all carbons as ¹²C, the average times for product formation and recrossing were 195 fs and 163 fs,¹² respectively, while with both olefinic carbons as ¹⁴⁰C, these times were increased to 245 fs and 238 fs, respectively. With singly-labeled alkene, the trajectory times depend on whether mode 3 is positive or negative. When mode 3 is negative, with the carbonyl carbon approaching the heavy olefinic carbon, the longer-lived trajectories that might have recrossed get “pruned” by relatively fast product formation (which requires little motion of the heavy isotope). Because of this pruning, the average lifetime of the mode-3-negative recrossing trajectories (203 fs) is increased less (versus all ¹²C) than that of mode-3-positive trajectories (218 fs), and fewer trajectories recross. This picture, summarized in Figure 3, is a gross simplification of the effect of mass on the complex ensemble of trajectories but it qualitatively accounts for the trajectory and experimental observations.

Figure 3.

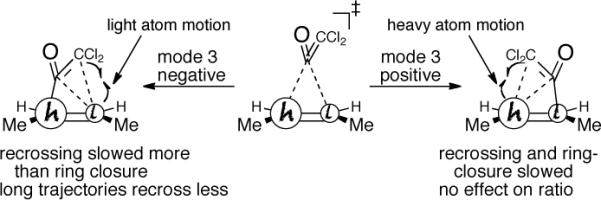
A cartoon depicting the effect of a heavy isotope on trajectories. Fewer trajectories recross at left because the ring closure, involving mainly light-atom motion, is slowed less than the recrossing is by the presence of a heavy isotope.

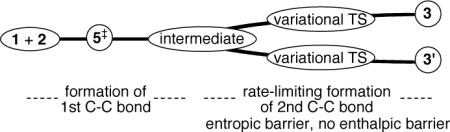
A statistical approach to predicting the KIE is made possible by the presence of “hidden”¹³ dynamical bottlenecks for product formation. These bottlenecks may be understood by viewing the asynchronous cycloaddition process as occurring in two stages, corresponding to the formation of a first C–C bond (between the carbonyl and an olefinic carbon) and a second C–C bond (between the CCl₂ carbon and the other olefinic carbon). As the second stage starts, the atoms involved in the bond formation are restricted in their motions and the vibrational frequencies increase. This causes an increase in the zero-point energy and a more consequential decrease in the entropy. The formal consideration of these effects requires defined reaction paths between 5^‡ and the two products, and we adopted the procedure of Lluch for defining such paths on bifurcating energy surfaces.¹⁴ On these paths there is no barrier between 5^‡ and the products. However, above 100 K there is a significant barrier in the free-energy (if the energy distribution were a canonical Boltzmann distribution) and at 298 K this later barrier is 1.2 kcal/mol above that of 5^‡! In other words, trajectories must pass through two TSs to afford the products, the first being associated with 5^‡ and the second being a rate-limiting variational TS associated with forming the second C–C bond. The short-lived species in between the TSs would, perforce, be an intermediate. In this statistical view the cycloaddition is a stepwise process, and this has an experimental consequence in the isotope effect. The intermediate itself is delineated by an entropic barrier and it has no focal structure.

In predicting a KIE from this statistical perspective, a problem is that the energy distribution after passing through the first TS would not be canonical. To allow for this, we have extended the canonical variational TST procedure employed by Lluch to a microcanonical variational RRKM procedure. The key assumptions in our model are that the total molecular energy is conserved over the time course of the reaction coordinate past the initial TS, and that the energy is statistically distributed. For each energy slice out of a canonical energy distribution for 25 °C in 5^‡ (including one ¹³C in an olefinic position), the RRKM rate constant was calculated at each point along the paths to 3 and 3'. At each energy, two RRKM TSs (one near 5^‡, another after the intermediate) were defined by points at which the RRKM rate constant was a minimum, and a unified statistical¹⁵ rate constant was calculated. The total rate constants were obtained by integrating over the initial energy distribution. The predicted KIE, calculated from the ratio of the total rate constants for formation of 3' versus 3, is 0.992. This fits strikingly well with the experimental observation, and it is the first accurate statistical prediction of a KIE on a bifurcating energy surface.

The success of the statistical model in predicting the KIE is at once enlightening and perplexing. It is enlightening in that it suggests that the observed selectivity arises ultimately from the normal factors considered by statistical rate theory, i.e. in thermodynamic parlance the enthalpy and entropy associated with dynamic bottlenecks. The success is perplexing because it is difficult to completely reconcile the statistical picture with the trajectory observations. Most notably, the intermediate in the statistical model is presumed to partition statistically between product formation and recrossing, but the predetermination of the product by the sign of mode 3 shows that the intermediate in no way partitions statistically between the two product-forming pathways. It is also notable that the amount of recrossing in the statistical model (84%) is significantly higher than that seen in the trajectories,¹⁶ suggesting that the formation of product, as opposed to recrossing, may be favored by non-statistical dynamics in the system. This intriguing trend is seen again in the example below.

Despite our incomplete understanding of them, the mechanistic complications of recrossing, entropically delineated intermediates and hidden TSs may be broadly relevant to asynchronous cycloadditions. A suggestive example is the Diels-Alder reaction of the vinyliminium ion 7 with cyclopentadiene. This example was the first organocatalyzed Diels-Alder reaction studied by MacMillan,¹⁷ and a standard computational study of this class of reactions on a B3LYP/6–31G* surface has been reported by Houk.¹⁸ As Houk found in his examples, we have found that these reactions exhibit a single potential energy saddle point, e.g. 8^‡, along each stereochemical mode of approach of the addends. The potential energy surface thus gives the appearance of a simple concerted cycloaddition.

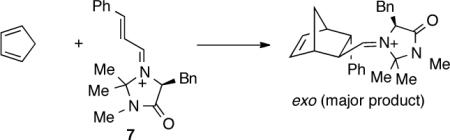
This misses much. When quasiclassical trajectories are started from the cycloaddition saddle point 8^‡, 46% (90 out of 196) fully form one C–C bond (with an average C–C minimum distance of 1.65 Å) before recrossing to starting materials. An even greater amount of recrossing (63%, 50 out of 79 trajectories) occurs when starting from the lowest-energy transition structure leading to the minor enantiomer (see the SI). This difference in recrossing increases the enantiomeric ratio by a factor of 1.5. Treating the energy distribution as canonical for 25 °C, there are two variational TSs along the IRC the first being associated with 8^‡ and the second, 9^‡, near the start of a stage forming the second C–C bond (Figure 4). The latter is highest in free energy and represents a hidden rate-limiting step in the reaction. For the pathway affording the minor enantiomer, the late variational TS is 0.6 kcal/mol above the saddle point in free energy, and the enantiomeric ratio would be increased by a factor of 2.5 with these hidden TSs taken into account. Within this statistical model, the cycloaddition is stepwise and its reactivity, selectivity, substituent effects, solvent effects, isotope effects, and activation parameters would be mainly determined at a geometry that is far from the conventional TS.

Figure 4.

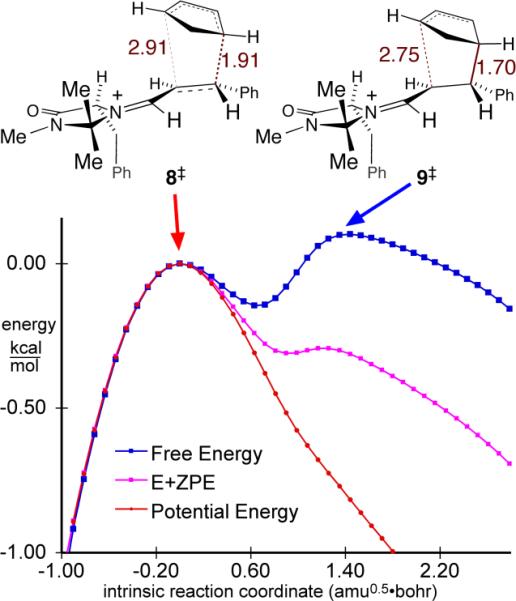
Energy profiles along the IRC through TS 8^‡, with the saddle point taken as the zero of energy. The free-energy profile is based on generalized free energies of activation obtained from GAUSSRATE.¹⁹

The results here are disconcerting with regard to the conventional consideration of stepwise versus concerted cycloaddition mechanisms, but they are not so surprising. It is of course well understood that conventional TST is an approximation. Due to the complications of recrossing and tunneling, the understanding of the rates and selectivities of reactions using conventional TST is subject to some inaccuracy. That inaccuracy is often negligible, but in pernicious examples such as barrierless reactions and high-tunneling regimes, TST can fail at a qualitative level. In this regard the results here have simply demonstrated another, arguably relatively minor, inaccuracy. However, our results demonstrate that hidden dynamical bottlenecks in cycloadditions can affect experimental observations and affect the qualitative understanding of their mechanism. In turn, the unusual experimentally observed isotope effects arising from recrossing should be useful as probes of hidden intermediates and TSs in seemingly simple reactions.