A Differential Geometric Approach to Automated Segmentation of Human Airway Tree

Abstract

Airway diseases are frequently associated with morphological changes that may affect the physiology of the lungs. Accurate characterization of airways may be useful for quantitatively assessing prognosis and for monitoring therapeutic efficacy. The information gained may also provide insight into the underlying mechanisms of various lung diseases. We developed a computerized scheme to automatically segment the three-dimensional human airway tree depicted on CT images. The method takes advantage of both principal curvatures and principal directions in differentiating airways from other tissues in geometric space. A “puzzle game” procedure is used to identify false negative regions and reduce false positive regions that do not meet the shape analysis criteria. The negative impact of partial volume effects on small airway detection is partially alleviated by repeating the developed differential geometric analysis on lung anatomical structures modeled at multiple iso-values (thresholds). In addition to having advantages, such as full automation, easy implementation and relative insensitivity to image noise and/or artifacts, this scheme has virtually no leakage issues and can be easily extended to the extraction or the segmentation of other tubular type structures (e.g., vascular tree). The performance of this scheme was assessed quantitatively using 75 chest CT examinations acquired on 45 subjects with different slice thicknesses and using 20 publicly available test cases that were originally designed for evaluating the performance of different airway tree segmentation algorithms.

I. INTRODUCTION

Appearing as an upside-down bifurcating tree, human airways are susceptible to a wide variety of diseases as a result of direct exposure to airborne pathogens. Airway related diseases such as asthma and chronic obstructive pulmonary disease (COPD) are the most prevalent diseases associated with high morbidity and mortality [1]. Studies have shown that airway diseases are frequently associated with damage and/or obstruction of the airway anatomical structures that generally correlate with pulmonary function [2–4]. Hence, accurate segmentation and quantitative assessment of airway morphology and related features (e.g., airway wall thickness) are useful in routine clinical practice for assessing the existence and/or severity of specific diseases and for monitoring responses to therapies. Although advanced CT imaging techniques enable visualization of three-dimensional (3D) lung structures in significant detail, it is extremely time consuming to manually segment the airways due to the complexity of the bronchial structure and the involvement of a large number of CT images in a single examination. There are typically large errors associated with subjective assessments in terms of inter- and intra-observer variability [5–6]. Therefore, the availability of an automated, reliable, and accurate computerized segmentation tool for this purpose could be of great value.

Leakage and obstruction are the two primary challenging problems associated with automated computerized segmentation of the airway tree. Both are frequently caused by partial volume effects that reduce the contrast between the airway wall and the lumen [7]. Leakage typically leads to the fusion of airways with surrounding lung tissues (e.g., parenchyma) and obstruction typically results in broken or discontinuous segmented airways. These problems occur frequently in the segmentation of small airways where image artifacts and/or noise have a relatively high impact on the detectability of small airways. These problems are magnified in the presence of lung diseases such as chronic obstructive pulmonary disease (COPD) or interstitial lung disease (ILD). Attempts to “smear out” image artifacts or to reduce noise using a smoothing operation (e.g., Gaussian filters) actually decreases the contrast between the airway wall and the lumen due to the incurred blurring.

In an attempt to robustly segment airway trees, a large number of computerized schemes have been developed [8–31]. To take advantage of the relatively large contrast between the air (airway lumen) and the surrounding soft tissue (airway wall), an intuitive approach to this problem is frequently based on automatically or interactively locating one or multiple seeds in large airway regions (e.g., trachea) and then performing a three-dimensional (3D) region growing operation under either a fixed or an adaptive threshold [8–14]. However, region-growing methods are frequently associated with leakage and therefore this approach often fails to identify small airways. Regardless, due to its simplicity and efficiency, this approach has been used in the majority of available schemes as an initial step and it is primarily used for the detection of large airways [15]. To extract more airway generations, additional operations that exploit intrinsic information and/or knowledge about the airway tree structure are needed. These methods can be generally classified into five categories: (1) knowledge or rule based methods, (2) morphological methods, (3) template matching methods, (4) shape analysis methods, and (5) hybrid methods. The knowledge or rule based approaches typically include prior anatomical relationships between airways and vessels in space [16], airway topology [17], local image appearance [18], fuzzy logic [19], and connectivity [20]. Template matching methods [21–22] use a set of predefined masks or structures (templates), which are based on some prior knowledge of the airways, to facilitate a search of highly correlated regions in 2D or 3D space. For example, Mayer et al. [22] defined a set of oval rings with different radii as templates and used these to identify airways by searching consecutive image slices. Kaftan et al. [23] used a tree-path structure as a template for airway identification. To refine the initially detected airway tree, different morphological operations [17, 24–27] have been used to connect (merge) disconnected 2D/3D regions. For example, Aykac et al. [25] developed a scheme that identified airways on single slices followed by a dilation operation to connect identified regions on consecutive slices. Fetita et al. [26] described a connection-cost based mathematical morphological procedure to detect airway regions. Since airways generally appear as tubular shapes, eigenvalue analysis of the Hessian matrix of CT images has also been used to enhance and track tubular structures in image space by analyzing the second derivatives of airway boundaries [28–31]. In a recent study, Graham et al. [15] identified small airways by analyzing the elliptical shape of the airways cross sections following the application of a region growing operation. In practice, many schemes [17, 29, 32] combine region growing with two or more of the above strategies in order to improve performance. For example, Bartz et al. [21] introduced a hybrid method consisting of three stages, namely a 3D region growing stage, a 2D wave propagation stage, and a 2D template matching stage.

In this study, we present a fully automated airway tree segmentation scheme that operates by analyzing both the principal curvatures and the principal directions of lung anatomical structures in geometric space followed by a “puzzle game” procedure. We deal with the wide intensity range associated with airway walls using a progressively adjusted threshold based modeling strategy. The underlying idea is to take advantage of the fact that: (1) the minimum curvatures of tubular regions are close to zero and (2) the principal directions associated with minimum curvatures of tubular regions are parallel to the axes of these regions. The performance of this scheme was tested on 95 chest CT examinations comprising of two independent datasets. A detailed description of the scheme and a preliminary assessment of performance follow.

II. METHODS

A. Scheme Overview

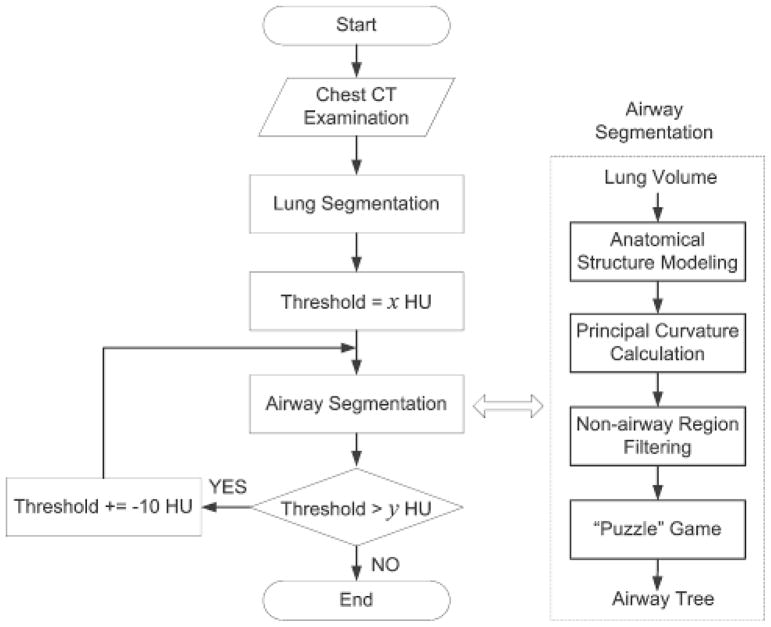
The proposed airway tree segmentation algorithm has four basic steps (Fig. 1): (1) anatomical structure modeling; (2) principal curvature computation; (3) non-airway region filtering; and (4) a “puzzle game” procedure acting as a “correction” operation for filtering false identifications. Before the airway segmentation procedure commences, a lung volume segmentation operation is applied to limit the computation space, thereby improving the scheme’s efficiency and eliminating the possibility of erroneous identifications outside the lung. As intensity levels of inner airway walls depicted on CT images are not fixed in value, we used a multi-threshold (or iso-value) strategy when modeling lung anatomical structures and repeated the airway segmentation steps at each iso-value. The union of the airways identified at different iso-values forms the final segmented airway tree. The implementation of these steps is presented in the following sections.

Fig. 1.

Schematic flowchart of the airway segmentation algorithm

B. Lung Volume Segmentation

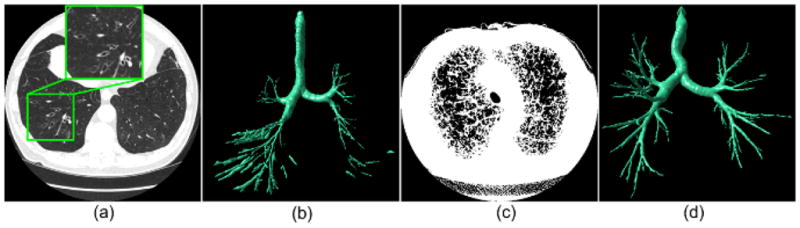
Due to the low intensity values of lung parenchyma regions and the high contrast with surrounding tissue, we used a well-established and computationally efficient thresholding operation to extract the lung volume (Fig. 2(a)). The threshold is determined adaptively based on intensity histogram analysis of the CT images [34]. The isolated pockets of air (if any) between the patient and the CT bed as well as image noise or artifact after thresholding are filtered out by applying a simple size based classification rule. Unlike other lung segmentation schemes designed for specific applications [35–37], this thresholding approach cannot assure a smooth lung boundary and/or the inclusion of specific diseases (e.g., the juxtapleural nodule as indicated by the arrow in Fig. 2(b)). However, this simple approach is sufficient for our specific application because the airway regions are retained due to their relatively low intensities.

Fig. 2.

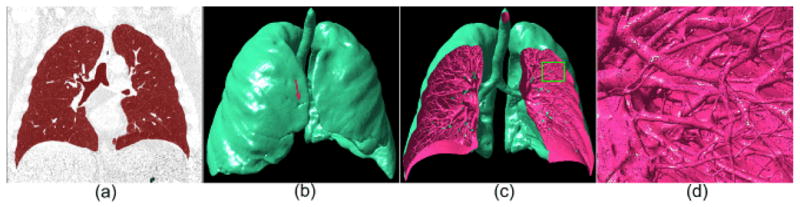
An example of the lung volume segmentation using the adaptive thresholding operation and its three-dimensional surface model: (a) shows the segmented lung volume in overlay (red), (b) shows the three-dimensional model of (a) at an iso-value of −650 HU, (c) is a “cut-out” version of (b), and (d) shows an local enlarged region indicated by the box in (c). The arrow in (b) indicates a juxtapleural nodule.

C. Lung Anatomical Structure Modeling

Applying the Marching Cubes Algorithm (MCA) [33] to the segmented lung volume results in three-dimensional lung anatomical structures in the form of a triangle mesh surface (Fig. 2(b)–(d)). In this study, the front faces of a surface model, whose normal vectors point to the outside of an object (i.e., from high intensity to low intensity), are displayed in pink and the back faces, whose normal vectors point to the inside of an object (i.e., from low intensity to high intensity), are displayed in green. Such a lung model generally contains an extremely large number of triangles (e.g., the model in Fig. 2(b) consists of 12,747,562 triangles). The MCA treats eight neighboring voxels in the scalar field of the lung volume as a logical cube and determines the isosurface along each edge of the cube by linearly interpolating the scalar values of the voxels that form the edges. If a cube has one or more voxels with higher or lower intensity than a predefined iso-value, this cube contributes a set of triangles. After traversing all voxels, a triangular surface is constructed. A detailed description of the MCA has been described elsewhere [33]. The linear interpolation property of the MCA enables CT examinations with different in-plane or through-plane resolutions to be processed directly without the need for an additional reconstruction.

When applying the MCA to a scalar field, an intensity threshold (an iso-value) has to be specified in order to define the surface boundary of interest. An example in Fig. 3 is used to demonstrate the impact of the selected iso-value on lung anatomical structure modeling. As the iso-value is adjusted from −950 HU to −450 HU for the same local region enclosed by the bounding box as shown in Fig. 3(a), the inner and outer airway walls as well as other structures (such as vessels) vary in appearance. In Fig. 3(c), the inner airway wall is visible while vessels are not modeled due to the relatively low iso-value selected and the relatively high intensity of the vessels. In Fig. 3(h), on the other hand, portions of the airway wall are fused with vessels due to their similar intensity in relationship to the selected iso-value. Since intensity levels between the airway lumen and the airway wall vary over a wide range of values, it is impossible to pre-determine a fixed optimal iso-value for all airways. Therefore, we used a multiple iso-value strategy (e.g., an iso-value ranging from −800 HU to −900 HU) to fully model the airway structure.

Fig. 3.

An example demonstrating the impact of the iso-value (threshold) on the lung anatomical structure modeling: (a) shows a CT examination, (b) shows the enlarged version of the region indicated by a box in (a), and (c)–(h) show the anatomical structures within the indicated region in (b) as modeled at different iso-values, i.e., −950 HU, −850HU, −750 HU, −650 HU, −550 HU, and −450 HU, respectively. The tubular regions in (c) indicate the inner airway wall regions depicted on the image in (b).

D. Principal Curvature Computation

As a concept describing a shape in differential geometry, curvature is a measure of how a surface or a curve “bends” at a given point and is defined in terms of the amount of bending and the bending direction. The principal curvatures k₁ and k₂ are defined here as the maximum and minimum values of the normal curvatures at a given point p, and the principal directions e₁ and e₂ are defined as the directions in which the normal curvatures reach maximum and minimum values. Given a point with a normal vector n, a local coordinate system (u, v) perpendicular to n (or tangent to the local surface) is generated. The normal curvature k at this point can then be expressed in a fundamental form:

$$k=\left(\begin{array}{cc}s& t\end{array}\right)\left(\begin{array}{cc}\frac{\partial \mathit{n}}{\partial u}u& \frac{\partial \mathit{n}}{\partial v}u\\ \frac{\partial \mathit{n}}{\partial u}v& \frac{\partial \mathit{n}}{\partial v}v\end{array}\right)\left(\begin{array}{c}s\\ t\end{array}\right)=\left(\begin{array}{cc}s& t\end{array}\right)\mathrm{\Pi }\left(\begin{array}{c}s\\ t\end{array}\right)=\left(\begin{array}{cc}{\mathit{e}}_{\mathit{1}}& {\mathit{e}}_{\mathit{2}}\end{array}\right)\left(\begin{array}{cc}{k}_1& 0\\ 0& k_2\end{array}\right)\left(\begin{array}{c}{\mathit{e}}_{\mathit{1}}\\ {\mathit{e}}_{\mathit{2}}\end{array}\right)$$ (1)

where Π denotes the second fundamental tensor. The principal curvatures k₁ and k₂ and the principal directions e₁ and e₂ can be determined by diagonalizing the symmetric matrix in Eq. (1). A number of investigations [28–31, 38] used curvature analysis to identify lesions and/or structures with specific shapes (e.g., airway and nodules), where the curvatures were typically derived from the eigenvalue calculation of the Hessian matrix in image space. Due to their discrete voxel-based representation, CT images are frequently convolved prior to setting up the Hessian matrix with Gaussian filters that frequently suppress valuable anatomic information as well as image artifacts or noise. In this study, we estimated the curvatures of the anatomical structures in geometric space and exploited both the principal curvatures and the principal directions in order to identify the airway tree and remove non-airway regions. The MCA can faithfully model anatomical structures as geometric surfaces, where image noise/artifacts are also included as a part of the modeling. However, proper geometric processing can remove the latter (noise and/or artifact) without changing the anatomical structures and their associated topology.

A number of computational geometry based methods to accurately estimate the principal curvature at a given point on a surface have been developed [39–42]. These can be classified into two broad categories: (1) local surface fitting [39–40], and (2) finite difference analysis of normal vectors [41–42]. The former estimates the curvatures at a point analytically by fitting (or parameterizing) a mathematical surface (e.g., z= ax² + bxy + cy² + dx + ey) using neighboring vertices of the point of interest. The latter estimates surface curvatures based on a differential analysis of the relative positions of neighboring vertices. As compared with the local surface fitting method, the finite difference method frequently exhibits inferior accuracy, but it has high computational efficiency. Considering the large number of triangles involved in the modeling of lung anatomical structures, we used the finite-difference approach developed by Rusinkiewicz [41] to estimate principal curvatures and principal directions. This method offers reasonable accuracy with a linear computational complexity in space and time (i.e., O(N), where N is the number of vertices). Here we offer but a brief description of our implementation.

To generate the second fundamental form in Eq. (1), Rusinkiewicz used Eq. 2, in which finite differences of the normal vectors at each vertex are computed along the three edges of a triangle (Fig. 4(a)), as an approximation of Eq. (1):

$$\{\begin{array}{c}{\mathbf{k}}_{i,j}=\mathrm{\Pi }\left(\begin{array}{c}{s}_1·u\\ s_1·v\end{array}\right)=\left(\begin{array}{c}({\mathbf{n}}_j-{\mathbf{n}}_i)·u\\ ({\mathbf{n}}_j-{\mathbf{n}}_i)·v\end{array}\right)\\ {\mathbf{k}}_{j+1,i}=\mathrm{\Pi }\left(\begin{array}{c}{s}_2·u\\ s_2·v\end{array}\right)=\left(\begin{array}{c}({\mathbf{n}}_i-{\mathbf{n}}_{j+1})·u\\ ({\mathbf{n}}_i-{\mathbf{n}}_{j+1})·v\end{array}\right)\\ {\mathbf{k}}_{j,j+1}=\mathrm{\Pi }\left(\begin{array}{c}{s}_3·u\\ s_3·v\end{array}\right)=\left(\begin{array}{c}({\mathbf{n}}_{j+1}-{\mathbf{n}}_j)·u\\ ({\mathbf{n}}_{j+1}-{\mathbf{n}}_j)·v\end{array}\right)\end{array}$$ (2)

Fig. 4.

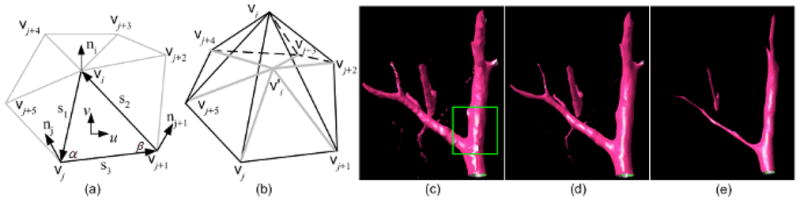
An illustration of the Rusinkiewicz curvature estimation (a) and the Laplacian smoothing (b) using a 1-ring mesh. In (a), (u, v) is the local coordinate system of the triangle in bold; in (b), the vertex $v_i^{\prime }$ is the centroid for the 1-ring triangles around v_i. The smoothing and shrinking effects after applying the Laplacian operation to the structure in (c) 5 and 20 times are shown in (d) and (e), respectively.

The normal vector n_o at a vertex is usually estimated as a weighted average of the normal vectors of the m triangles adjacent to that vertex:

$${\mathbf{n}}_o=\frac{{\displaystyle \sum _{i=0}^m}{A}_i{\mathbf{n}}_i}{\Vert {\displaystyle \sum _{i=0}^m}{A}_i{\mathbf{n}}_i\Vert }$$ (3)

where n is the face normal vector of the i^th adjacent triangle, and A_i is the area of the i^th adjacent triangle.

Thereafter, a least square solution is applied to solve for the resulting second fundamental form (Eq. (2)). We used the LDL factorization to obtain a numerical solution to the above linear equations. Since A is symmetric and positive, we solved for AX = B by computing the LDL factorization A = LL^T, then solved LY = B for Y, and finally L^TX=Y for X. Finally, with consideration for the contributions of the neighboring vertices to the curvatures at a given vertex, the curvature tensor at each vertex was adjusted by averaging the curvature tensors of its 1-ring neighboring triangles (Fig. 4). The average weights are determined by the “Voronoi areas” rather than the geometric areas of the neighboring triangles as detailed in [41]. Given a triangle (e.g., the v_i v_j v_j+1 in Fig. 4), its Voronoi area is computed as:

$$A_{\mathit{Voronoi}}=\frac{1}{8}\left(\Vert v_i-v_j\Vert cot\alpha +\Vert v_i-v_{j+1}\Vert cot\beta \right)$$ (4)

where α represents the angle between s₁ and s₃, and β represents the angle between s₂ and s₃.

To assure an accurate estimation of curvatures, we first smoothed the triangle mesh of the modeled anatomical structures using Laplacian smoothing [43] before applying the above curvature estimation approach. As illustrated in Fig. 4(b), Laplacian smoothing adjusts the location of each mesh vertex v_i to the geometric center $v_i^{\prime }$ of its neighboring vertices v_j (j∈[0,5]) without any modification of the topology of the triangle mesh itself:

$$v_i^{\prime }=\frac{{\displaystyle \sum _{j=1}^n}{A}_j{v}_j}{{\displaystyle \sum _{j=1}^n}{A}_j}$$ (5)

where A_j denotes the area of the j^th adjacent triangle of the vertex v_i. The computational complexity of Laplacian smoothing is linear to the number of triangles. This smoothing operation is often performed iteratively and tends to progressively shrink the size of an object and flatten its surface. Thus, small isolated artifacts tend to degenerate into points after iterations, spherical surfaces (e.g., nodules) tend to become more “spherical”, and tubular surfaces (e.g., vessels) along the axial direction tend to become flatter (Fig. 4(c)–(d)). Unlike Gaussian filtering, which is performed in image space and may “smooth out” anatomic information and image artifacts, Laplacian smoothing does not meaningfully change the number of triangles or the topology of a triangle mesh. Therefore, the shape information of lung structures is well persevered while artifacts and image noise tend to be reduced as a result of Laplacian smoothing. The example in Fig. 5 demonstrates the performance of the Rusinkiewicz’s method in estimating principal curvatures and principal directions. In the field of computer graphics, there have been a number of algorithms developed for this purpose such as curvature flow [44] or bilateral de-noising [45]. These approaches may achieve better performance than the Laplacian smoothing approach in terms of surface smoothing. However, due to the very large number of triangles involved in lung modeling, the Laplacian smoothing operation offers higher efficiency as compared with other smoothing algorithms, and it provides a sufficiently robust performance for our purpose.

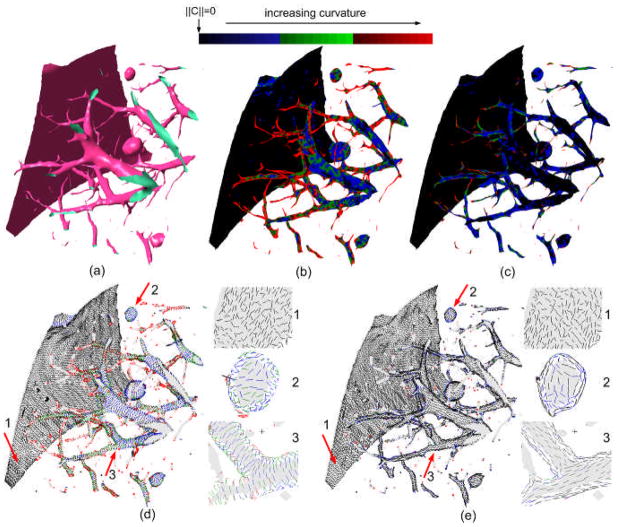
Fig. 5.

An example demonstrating the performance of the Rusinkiewicz’s method in estimating the principal curvatures and the principal directions: (a) shows local lung anatomical structures with three basic shapes, namely planar, spherical, and cylindrical, (b) and (c) show color-coded visualizations of the maximum and the minimum curvatures respectively, (d) and (e) depict the maximum and the minimum curvature directions respectively for local regions with typical shapes.

E. Non-Airway Region Filtering

The general shapes of the soft tissues in human lungs can be reasonably represented by three basic categories, namely spheres (e.g., nodules), planes (e.g., fissures), and cylinders (e.g., vessels and airways). The basic properties of the principal curvatures and the principal directions associated with these three general shapes are summarized in Table 1. In general, the minimum curvature at any point on a plane or a cylinder is zero but it has non-zero values at any point on a sphere. For concave cylinders or spheres, the maximum curvatures have negative values, while for convex cylinders and spheres the maximum curvatures have positive values. Therefore, knowledge of curvatures should be useful in differentiating these basic shapes. Unfortunately, these properties are quite sensitive to local surface perturbations due to the second derivatives involved. Hence, to reliably identify airways that appear as concave cylinders, we explore both the principal curvatures and the principal directions at each point on a given surface. As the example in Fig. 5 shows, the principal directions in the neighborhood of a point on a cylinder are typically parallel to each other, while those on a sphere or a plane are randomly distributed.

Table I.

Basic shapes and associated characteristics of principal curvatures

Basic Shapes	Examples	Cmax	Cmin	Dmax	Dmin
plane	fissures	0	0	random	random
convex cylinder	vascular tree	1/r	0	orthogonal to axis	parallel to axis
concave cylinder	inner airway wall	−1/r	0	orthogonal to axis	parallel to axis
convex sphere	nodules	1/r	1/r	random	random
concave sphere	n/a	−1/r	−1/r	random	random

C_max: the maximum curvature;

C_mix: the minimum curvature;

r: the radius of a cylinder or a sphere;

D_max: the principal direction associated C_max;

D_min: the principal direction associated C_min;

n/a: no example available.

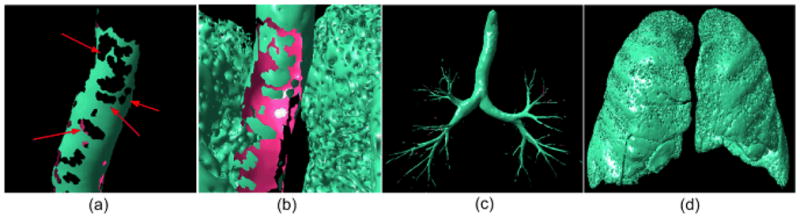
Non-airway regions were removed in our implementation through the identification of vertices that meet one of the following empirically predetermined criteria: (1) C_max≥−0.05 (unit: 1/mm); (2) |C_max| ≥ 0.2 (unit: 1/mm); and (3) A_max > 30°, where A_max is the largest angle difference in the minimum principal directions among the 1-ring vertices. The first criterion filters out convex regions as well as plane regions. The second and the third criteria assure that remaining regions have cylindrical shapes. The primary intent behind the above parameter selection is to identify as many as possible concave cylindrical regions of interest (airways) while maintaining a reasonable number of false positive identifications. The example in Fig. 6(b) shows the results after applying the three criteria to a three-dimensional lung model of a chest CT examination displayed in Fig. 6(a). It can be seen that, as intended, the majority of non-airway regions were discarded.

Fig. 6.

The lung surface model (a) at an iso-value of −850 HU is subdivided into an “airway” component (b) and a non-airway component (c), following the application of the set of curvature filtering criteria.

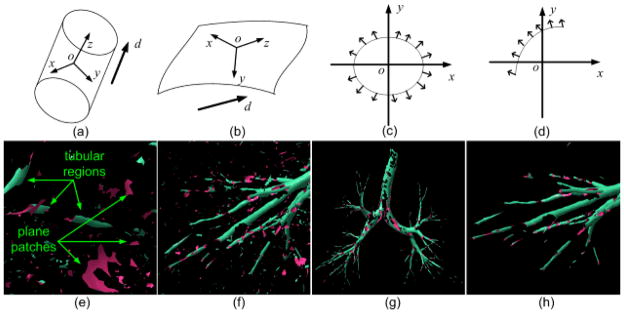
Curvature-based filtering will result in a number of false positive identifications that typically appear as small regions (Fig. 6(b)) due to the existence of surface perturbations. Although the application of a simple size criterion would likely filter out many of these regions, there is no unique fixed threshold for robust filtering of non-airway regions. As airway regions of interest are cylindrical in shape they appear as circles when projected along the axis and other non-airway regions could be treated as small plane patches due to their small size (Fig. 7(e)–(f)). Therefore, we developed a normal vector distribution based method to retain regions with a tubular shape and discard all other regions. Given an isolated surface patch that could be any shape, a direction d is determined by the average of the minimum curvature directions e_2i of all vertices of the surface patch in question:

$$d=\frac{{\displaystyle \sum _{i=0}^n}{\mathit{e}}_{2i}}{\Vert {\displaystyle \sum _{i=0}^n}{\mathit{e}}_{2i}\Vert }$$ (6)

where n represents the number of vertices that a surface patch contains. This surface is then transformed in a manner that d is aligned with the z-axis of the global coordinate system (Fig. 7). Following this transformation a tubular region, as shown in Fig. 7(a), typically has a normal vector distribution (not vertex distribution) in all the four octants (Fig. 7(c)), while a plane surface does not (Fig. 7(d)). Hence, the normal vector distribution can be used to differentiate tubular regions from planar patches. Shown in Fig. 7(g)–(h) are the results after applying a normal distribution based filtering operation to the initially identified airways in Fig. 6(b) and the locally enlarged region in Fig. 7(f).

Fig. 7.

Illustration of the small planar region filtering procedure: (a) shows a cylindrical shape, (b) shows a plane like surface patch, (c) and (d) show the normal vector distributions of a cylindrical shape and the plane like patch in (a) after aligning their averaged minimum curvature directions with the z-axis, (e) shows tubular regions and surface patch regions using the locally enlarged region in Fig. 6(b), (f) shows the local region identified by the arrow in Fig. 6(b), (g) shows the airway after the application of the filtering operation, and (h) shows the “cleaned up” result for the region shown in (f).

F. False Positive /Negative Reduction Using a “Puzzle Game”

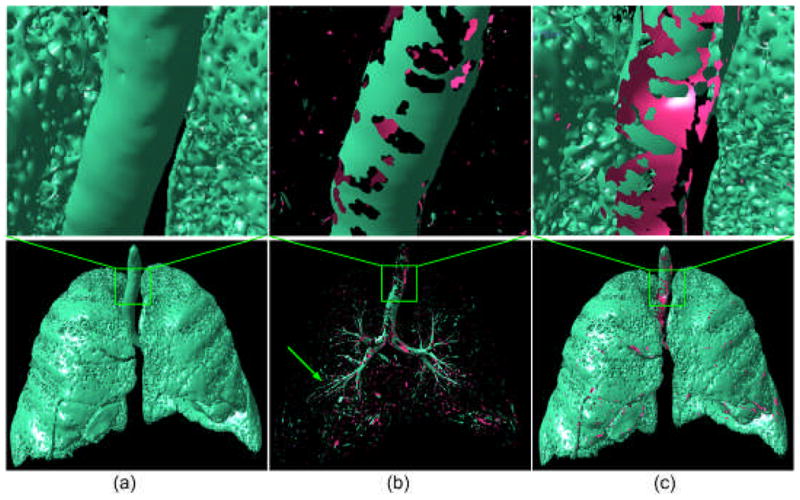
The initial non-airway filtering divides the lung model denoted as S (Fig. 6(a)) into two sets, namely the “airway” set A (Fig. 6(b)) and the “non-airway” set B (Fig. 6(c)). For brevity, we show in figure 8 results of Fig. 6(b) and Fig. 6(c) after normal vector distribution based filtering for the trachea regions. In both sets, there are regions that could be misclassified. As demonstrated by the local enlargement in Fig. 6(a), the “holes” appearing on the trachea indicate the existence of false negative regions. These are primarily caused by the fact that airways are not exactly cylindrical in shape everywhere. Therefore, local regions as indicated by the “holes” are actually incorrectly removed from the “airway” set. These missing regions (holes) in the airway set typically appear as isolated matching regions in the non-airway set B shown in Fig. 8(b). Similarly, some non-airway regions with local shapes that are similar to a concave cylinder could be incorrectly classified as airways (i.e., false positive identifications). Because the initially modeled lung anatomical structure (Fig. 6(a)) is represented by a completely enclosed surface, the misclassified isolated regions in either set (A or B) would have corresponding holes in the other set. Hence, by investigating the “matched” regions between the sets using a “puzzle game” we can reduce the false positive and false negative identifications.

Fig. 8.

(a) and (b) show local enlargements of trachea regions after applying the normal vector distribution based filtering to regions shown in Fig. 6(b) and Fig. 6(c); (c) and (d) show the airway set (A) and non-airway set (B) after applying the “puzzle game” operation to the regions in Fig. 6(b) and Fig. 6(c). The arrows indicate the “holes” or missing airway regions.

This “puzzle game” consists of a forward operation and a backward operation. The forward operation reduces the false negative identifications by determining which isolated regions in the non-airway set (B) “match” holes in the airway set (A). First, we ranked all isolated regions by the size of surface area and identified the two largest regions in A and B, and these two regions were excluded from the game. The remaining regions in set B were tested one by one in a surface area size decreasing order. Given an isolated region in set B, it is assumed to belong in set A if two criteria (both) are met: (1) it actually shares edges with a region in set A and (2) it has a smaller geometric area than the connected region in set A. The backward operation reduces the false positive identifications by determining which isolated regions in the airway set (A) actually belong in the non-airway set (B). In the backward operation, we filtered out isolated regions located on the lung boundary, since it is assumed to be an impossibility for regions located inside the lung volume that appear as concave cylindrical shapes to represent non-airway regions. Shown in Fig. 8(c) and 8(d) are the updated results after applying the “puzzle” game to the airway set (A) and the non-airway set (B) in Fig. 6.

G. Airway Region Mapping from Geometric Space to Image Space

After a round of airway identification was completed at a specific iso-value (e.g., −850 HU), the resulting airway tree was represented as a geometric surface in a triangle mesh. Before repeating the above steps at different iso-values, we mapped the identified airway tree from the geometric space to the CT image space. The motivation for this mapping arises from the technical difficulty in computing the union of airway trees identified at different thresholds in geometric space because different iso-values may lead to different airway tree boundaries as a result of the different lung anatomical structure models. When segmented airway trees at different iso-values are mapped onto the CT image space, their union can be computed by a simple summation of the mapped airway voxels. In addition, this mapping enables a direct visualization of the performance of the airway tree segmentation superimposed on the corresponding CT images.

Although there are a number of algorithms developed for “voxelization” of a triangle mesh object, many of them require a water-tight (or continuous) surface and these algorithms often have a high computational cost in time and space. Since the identified airway trees in this scheme frequently had holes that needed to be filled in, the mapping operation was relatively complicated. Considering that airways appear as concave cylindrical shapes, we took advantage of the shrinking effect of the Laplacian smoothing operation. Repeating the Laplacian operation on the identified airways progressively shrinks their size (Fig. 4(c)–(e)). However, the Laplacian operation does not change the topology or the number of triangles in a triangle mesh surface; hence, this repetitious process progressively increases the “triangle density” in the triangle mesh and thereby slowing the shrinking process. To accelerate the process, we adaptively adjusted the “triangle density” by performing a simple “ring-collapse” operation on the triangle mesh, after each Laplacian operation. The ring-collapse operation merges the 1-ring vertices of a vertex v_i onto a single vertex v_i (Fig. 9) under the condition that the distance between a vertex v_i and the centroid $v_i^{\prime }$ of its 1-ring, is smaller than a predefined value (threshold). The threshold in this case should be smaller than the size of a voxel so that this sweeping operation does not “jump over” any voxel within the airway volume. In this study, we empirically set the threshold as one fourth of the size of a voxel. The computational complexities in time and space of both the Laplacian operation and the edge-collapse operation are linear with respect to the number of the vertices contained in an airway tree. Hence, the mapping of airways from the geometric space onto the CT image space is relatively efficient. Shown in Fig. 10 are the results of mapping the identified airway tree onto the CT images.

Fig. 9.

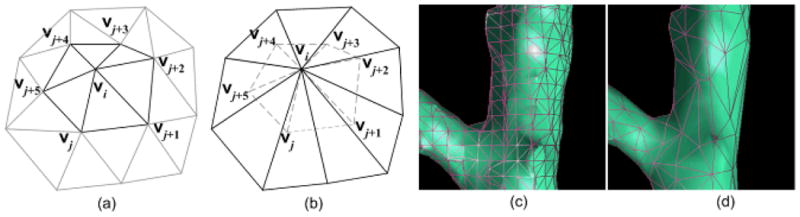
Illustration of the ring-collapse operation: (a) shows a 2-ring triangle mesh, (b) shows the collapsed triangle mesh of (a) where the dashed edges in (b) are removed from the triangle mesh, and (c) and (d) show the local region indicated by the box in Fig. 4(c) before and after the ring-collapse operation.

Fig. 10.

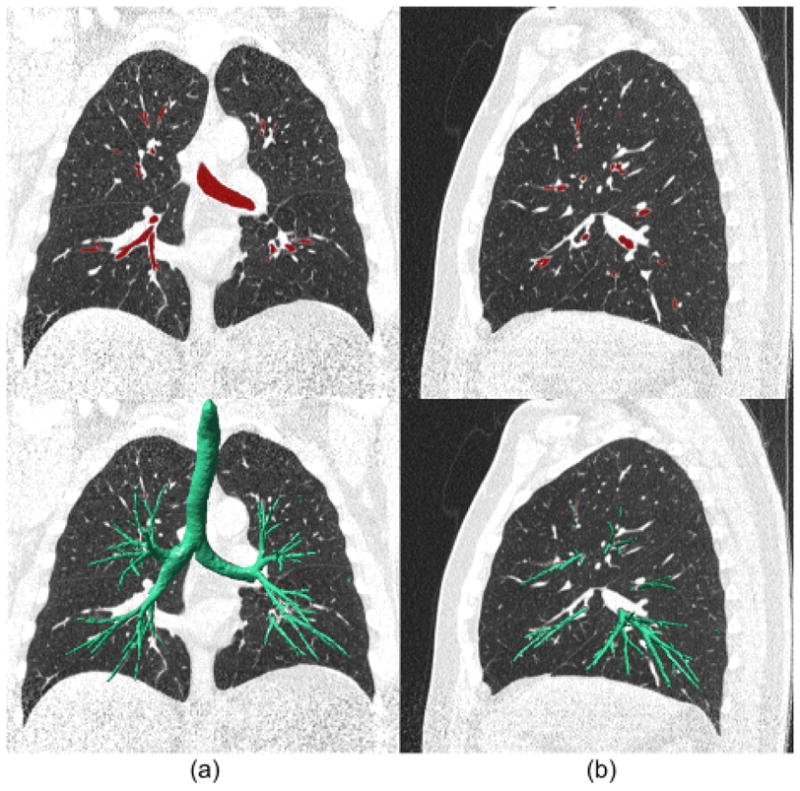
An example of the mapping of the identified airway tree from the geometric space onto the CT image space: (a) and (b) shows a coronal view and a sagittal view of the mapped results and the superimposed geometric airway tree, respectively.

H. Iterative Airway Identification Based On Multiple Thresholds

As explained previously, there is a need to overcome the negative impact of the selected iso-values on the lung anatomical structure modeling (Fig. 3). This is important in particular in regard to airway regions where partial volume effects may cause fusion with other non-airway regions. Therefore, we repeated the airway identification process at different iso-values. The examples in Fig. 11 show the impact of different iso-values on the identification of an airway tree. When the iso-value is set at a high value, surfaces of larger airways (e.g. trachea) become less smooth and curvature analysis may remove some of these regions, ultimately causing an incomplete identification of these “easier” airways. Similarly, the example in Fig. 3 shows the possible effect of the iso-values on modeling of small airways. These demonstrate that a lower iso-value typically results in the identification of smaller airways as shown in Fig. 11. The union of these airway trees in image space is shown in Fig. 12(a) with a set of empirically set threshold values ranging from −800 HU to −900 HU at 10HU increments.

Fig. 11.

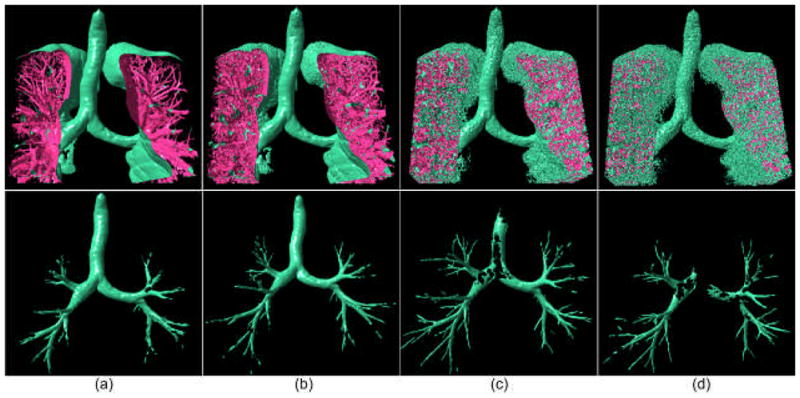
Airway trees are shown (bottom row) after performing the segmentation algorithm on the three-dimensional lung anatomical structures modeled at different iso-values: (a) −750HU, (b) −800 HU, (c) −880 HU, and (d) −900 HU. The airway tree identified at an iso-value of −850 HU is shown in Fig. 10. For better visualization, only a fraction of the lung anatomical structures are displayed.

Fig. 12.

Airway centerline extraction and labeling: (a) shows the segmented airways; (b) shows the centerline and branch points of (a); and, (c) shows a mixed rendering of (a) and (b) at different locations and from different perspectives. The regions in light green in (c) indicate centerlines and regions in green represent inner airway walls.

I. Performance Measures

It is extremely difficult if not impossible to manually and accurately trace and mark the three-dimensional airway trees depicted on CT images and use these as a gold standard for evaluation purposes. As important, there are no datasets that are accepted as a gold standard for this purpose. Therefore, as summary performance measures we provide objectively determined performance measures obtained on a defined dataset, namely the total tree length (excluding the trachea), the branch number, and the generation number. To enable computation of the summary measures, we used a skeletonization algorithm developed by Cornea et al. [46] to automatically extract the centerlines and identify the branch points of segmented airway trees. The example in Fig. 12 shows the results after applying this algorithm to an identified airway tree in a form proposed for application in virtual bronchoscopy. The detailed description of this algorithm was reported elsewhere [46]. Given that human airways typically appear as a bifurcating tree, we defined a generation as a continuous region starting and ending at two distinct bifurcations and used the dichotomic representation to count the airway generation number. Unlike other approaches, we did not compute measures related to leakage (e.g., leakage volume) as there is no leakage issue per se associated with our proposed methodology. Three measures were computed automatically using the airway tree centerline extraction scheme [46] with mean values and standard deviations calculated for all test cases. We also investigated the impact of CT image slice thickness on performance measures reported here. To do so, we computed all performance measures on clinically ascertained CT examinations that had been reconstructed with different slice thicknesses at 0.625 mm, 1.25 mm, and 2.5 mm.

III. EXPERIMENTS AND RESULTS

A. Testing CT Dataset

We selected a dataset of 75 chest CT examinations acquired on 45 participants in a COPD (chronic obstructive pulmonary disease) screening cohort at the University of Pittsburgh Medical Center. All subjects had relatively low levels of airflow obstruction and/or visually depicted emphysema noted during interpretations of their CT examinations. These examinations were performed under an Institutional Review Board (IRB) approved protocol using a LightSpeed VCT 64-detector scanner (GE Healthcare, Waukesha, WI) with subjects holding their breath at end inspiration. CT data were acquired using a helical technique at a pitch of 0.969, 120 kVp, 0.4 sec gantry rotation, and 250 mAs (or 100 mAs). The CT images were represented using a 512 × 512 pixel matrix with a pixel dimension ranging from 0.549 to 0.738 mm, depending on the participant’s body size. The detector configuration was 32 × 0.625 mm. We note that our primary objective is not to comprehensively assess the quality of segmentation as a function of slice thickness. However, lower resolution CT examinations with slice thicknesses of 1.25 mm and 2.5 mm are widely used in routine clinical practice. In addition, as a part of other unrelated studies we had acquired examinations reconstructed at different slice thicknesses for other purposes. Therefore we included these examinations in the performance assessment and investigated preliminarily the impact of CT slice thickness on the performance of our scheme. The examinations in our dataset were divided into two groups. The first group included 30 examinations (on 30 participants, i.e., Case #1 - Case #30 in Table II) that were reconstructed to encompass the entire lung field using the GE “standard” kernel at 0.625 mm slice thickness and at 0.625 mm increments (namely, no slice overlapping). The second group includes 45 examinations (15 participants, i.e., Case #31 - Case #45 in Table II) that were reconstructed using the “bone” kernel with two additional slice thicknesses: (1) 1.25 mm slice thicknesses with 1.25 mm increments and (2) 2.5 mm slice thickness with 2.5 mm increments. We note that none of the examinations in the testing dataset had been used in any intermediate assessments and/or visual evaluations of the scheme during development.

Table II.

Summary of airway segmneation performance levels for 45 chest ct examination recontructed with a slice thicknesses of 0.625 mm, 1.25 mm, and 2.5 mm

Case	Total Tree Length (cm)			Number of Generations			Number of Branches (Isolated Branches)
	0.625 mm	1.25 mm	2.5 mm	0.625 mm	1.25 mm	2.5 mm	0.625 mm	1.25 mm	2.5 mm
1	264.0	–	–	9 (0–8)	–	–	178 (6)	–	–
2	297.2	–	–	8 (0–7)	–	–	204 (3)	–	–
3	165.9	–	–	7 (0–6)	–	–	130 (7)	–	–
4	253.7	–	–	9 (0–8)	–	–	168 (3)	–	–
5	238.5	–	–	9 (0–8)	–	–	154 (6)	–	–
6	315.2	–	–	9 (0–8)	–	–	203 (3)	–	–
7	416.7	–	–	9 (0–8)	–	–	246 (5)	–	–
8	132.8	–	–	8 (0–7)	–	–	90 (8)	–	–
9	186.2	–	–	9 (0–8)	–	–	139 (8)	–	–
10	175.3	–	–	10 (0–9)	–	–	117 (2)	–	–
11	291.0	–	–	9 (0–8)	–	–	207 (4)	–	–
12	111.5	–	–	8 (0–7)	–	–	82 (4)	–	–
13	242.7	–	–	8 (0–7)	–	–	174 (7)	–	–
14	230.2	–	–	8 (0–7)	–	–	177 (3)	–	–
15	391.5	–	–	10 (0–9)	–	–	275 (3)	–	–
16	387.9	–	–	11 (0–10)	–	–	269 (20)	–	–
17	241.1	–	–	8 (0–7)	–	–	155 (6)	–	–
18	246.3	–	–	9 (0–8)	–	–	164 (6)	–	–
19	249.6	–	–	8 (0–7)	–	–	172 (3)	–	–
20	125.6	–	–	9 (0–8)	–	–	104 (5)	–	–
21	233.8	–	–	10 (0–9)	–	–	154 (5)	–	–
22	212.1	–	–	11 (0–10)	–	–	155 (4)	–	–
23	455.7	–	–	9 (0–8)	–	–	295 (10)	–	–
24	274.1	–	–	10 (0–9)	–	–	207 (5)	–	–
25	272.5	–	–	9 (0–8)	–	–	227 (15)	–	–
26	243.8	–	–	9 (0–8)	–	–	172 (7)	–	–
27	395.2	–	–	11 (0–10)	–	–	278 (8)	–	–
28	145.7	–	–	10 (0–9)	–	–	106 (7)	–	–
29	188.7	–	–	9 (0–8)	–	–	132 (5)	–	–
30	228.2	–	–	9 (0–8)	–	–	161 (3)	–	–
MS1	253.8±87.5	–	–	9.1±1.0	–	–	176.5±58.4 (6.0±3.7)	–	–
31	255.0	210.3	98.1	10 (0–9)	10 (0–9)	7 (0–6)	170 (7)	144 (2)	63 (5)
32	371.8	294.5	127.5	9 (0–8)	9 (0–8)	8 (0–7)	261 (10)	184 (9)	81 (0)
33	222.1	178.2	75.9	9 (0–8)	8 (0–7)	6 (0–5)	157 (12)	129 (19)	43 (2)
34	258.0	224.1	142.6	9 (0–8)	9 (0–8)	8 (0–7)	178 (6)	157 (6)	101 (2)
35	281.7	224.7	99.0	9 (0–8)	9 (0–8)	7 (0–6)	187 (9)	148 (6)	56 (6)
36	177.9	134.4	70.0	9 (0–8)	9 (0–8)	8 (0–7)	121 (7)	86 (5)	38 (1)
37	141.1	116.3	59.4	8 (0–7)	8 (0–7)	7 (0–6)	121 (2)	98 (4)	40 (2)
38	421.9	374.6	179.0	10 (0–9)	9 (0–8)	8 (0–7)	251(7)	204 (7)	100 (2)
39	111.7	90.7	42.4	8 (0–7)	8 (0–7)	5 (0–4)	78 (5)	57 (2)	27 (0)
40	220.3	169.0	76.1	10 (0–9)	9 (0–8)	6 (0–5)	154 (7)	118 (3)	56 (2)
41	119.6	95.6	34.9	11 (0–10)	11 (0–10)	5 (0–4)	79 (6)	66 (8)	23 (1)
42	160.1	145.5	61.6	11 (0–10)	10 (0–9)	9 (0–8)	108 (3)	93 (2)	34 (1)
43	279.3	235.7	75.2	10 (0–9)	9 (0–8)	7 (0–6)	187 (6)	146 (9)	33 (0)
44	249.4	206.0	102.5	10 (0–9)	9 (0–8)	6 (0–5)	158 (4)	140 (5)	63 (1)
45	467.0	371.8	175.7	9 (0–8)	9 (0–8)	8 (0–7)	291 (10)	219 (10)	114 (2)
MS2	249.1±105.7	204.8±88.5	94.7±44.3	9.5±0.9	9.1±0.8	7.0±1.2	166.7±63.2 (6.5±2.4)	132.6±47.6 (6.5±4.4)	58.1±28.9 (1.8±1.7)
TMS	252.2±92.7	–	–	9.2±1.0	–	–	173.2±58.1	–	–

MS1: the means and standard derivations of the measures for the first group of examinations;

MS2: the means and standard derivations of the measures for the second group of examinations;

TMS: the means and standard derivations of the measures for all examinations with a slice thickness of 0.625 mm in the two groups.

We are aware of the fact that our dataset is unique and our results, when the scheme is applied to our own dataset, can not be directly compared with other methods. Therefore, we applied the developed scheme to the publicly available dataset of 20 test cases that were originally designed to compare performance of different segmentation algorithms (http://image.diku.dk/exact/index.php) [47] and provide the same summary measures for these cases. A detail description of these cases was presented in [47].

B. Experimental Results

The three performance measures in terms of total tree lengths (excluding the trachea), generation numbers, and branch numbers resulting from the application of our segmentation scheme to each of the 75 chest CT examinations are summarized in Table II. As the segmentation results may include disconnected airways (Fig. 12-Fig. 13), we also calculated the number of “isolated” branches for each examination. For all examinations with a slice thickness of 0.625 mm (45 examinations), the average total airways length of the segmented airway trees per examination was 261.8±92.9 cm, the average number of airway tree generations per examination was 9.2±1.0, and the average number of segmented airway tree branches per examination was 173.2±58.1. Among these airway branches, the number of isolated (non-connected) branches was 6.1±4.0 per examination. As compared to examinations with a slice thickness of 0.625 mm, the performance of airway segmentation decreased somewhat in examinations with a slice thickness of 1.25 mm. The average airways total length per examination decreased in the subset of 15 examinations from 259.2±106.1 cm to 214.8±88.9 cm. When the slice thickness was increased to 2.5 mm, the segmentation performance deteriorated significantly, namely the average airways total length decreased to 104.7±44.6 cm. The average airway total length per examination in the two subsets of cases reconstructed with different kernels, namely 263.2±87.5 cm and 259.2±106.1 cm, suggest that there was but a small difference in performance between segmentation of examinations reconstructed with a “standard” kernel and those reconstructed with a “bone” kernel. There was no simple direct relationship between the generation numbers and the average total airway lengths, and the average total length and branch number in an airway tree seemed to reflect the quality of segmentation performance more accurately and directly than did the generation number. To visually demonstrate the performance of the scheme, we listed a set of segmentation results from each group with the “high”, “average”, and “poor” levels of performance. Several examples are also presented to illustrate the impact of slice thickness on the performance of our airway tree segmentation scheme.

Fig. 13.

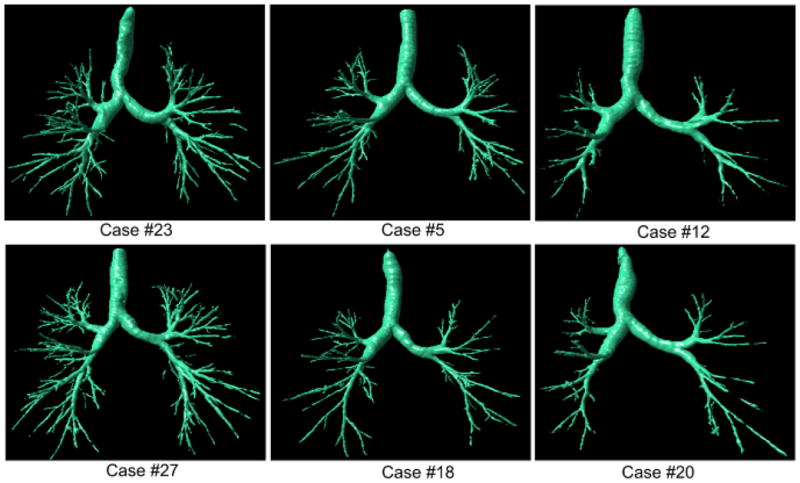
Examples of airway tree segmentations selected from the first group (i.e., Case #1 - Case #30) with the better performance (the left column: Cases #23 and #27), mid-level performance (the middle column: Cases #5 and #18), and worst performance (the right column: Cases #12 and #20). All examinations have a slice thickness of 0.625 mm and were reconstructed with a “standard” kernel.

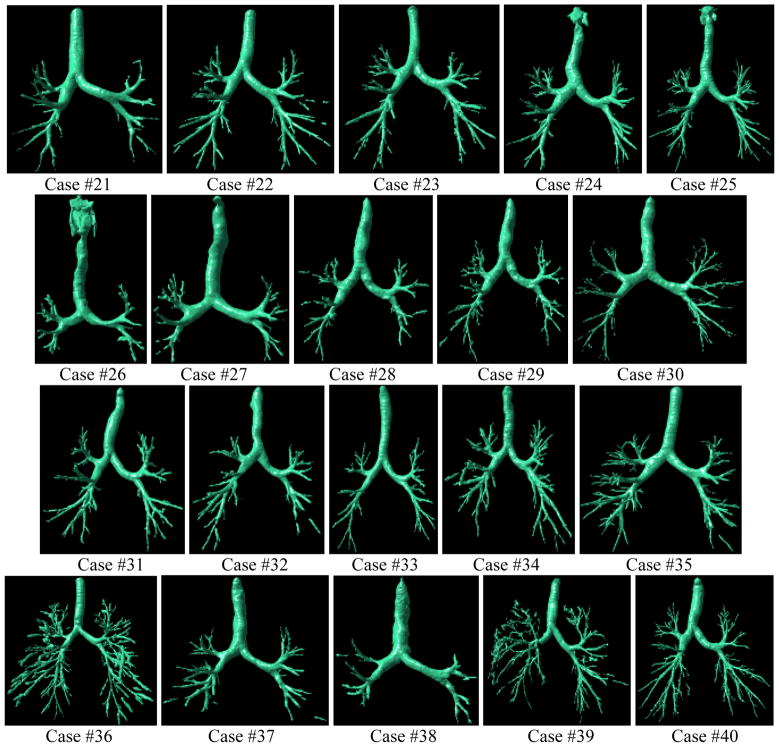
When the scheme was applied “as is” to the publicly available test dataset of 20 cases our average airways total length, average number of airway tree generations per examination and the average number of segmented airway tree branches per examination were 188.5±102.5 cm, 8.2±1.2 generations, and 120.1±67.4 segmented branches, respectively (Table III). The screenshots of the segmentation results are shown in Appendix.

Table III.

Summary of airway segmneation performance levels for the 20 test cases in exact’09 (http://http://image.diku.dk/exact/)

Case	Total Tree Length (cm)	Number of Generations	Number of Branches (Isolated Branches)
21	99.3	8 (0–7)	70 (4)
22	220.9	9 (0–8)	152 (5)
23	151.4	8 (0–7)	96 (5)
24	206.2	8 (0–7)	123 (3)
25	252.0	8 (0–7)	147 (3)
26	110.8	5 (0–4)	70 (0)
27	83.8	7 (0–6)	54 (3)
28	106.0	8 (0–7)	71 (4)
29	143.6	9 (0–8)	108 (2)
30	106.2	8 (0–7)	66 (6)
31	155.8	8 (0–7)	93 (2)
32	136.4	10 (0–9)	75 (5)
33	123.3	8 (0–7)	85 (0)
34	260.5	9 (0–8)	164 (3)
35	264.8	9 (0–8)	176 (2)
36	471.7	10 (0–9)	314 (11)
37	165.9	7 (0–6)	87 (3)
38	65.5	7 (0–6)	40 (1)
39	349.4	10 (0–9)	221 (7)
40	296.7	9 (0–8)	190 (4)
Mean	188.5±102.5	8.2±1.2	120.1±67.4 (3.7±2.5)

IV. DISCUSSION

We developed a computerized scheme to automatically segment the airway tree in the human lungs as depicted on chest CT examinations and tested its performance on 75 chest CT examinations with different slice thicknesses as well as on a small publicly available dataset consisting of 20 examinations. This scheme has a number of advantages and unique characteristics: 1) unlike previous approaches, this scheme does not trace the paths of airways; hence, there are no leakage related issues; 2) with but limited changes this scheme can be easily generalized to extract other tubular type structures. As shown in Fig. 14, simply changing the signs of the curvatures used for filtering purposes and adjusting the intensities of swept voxels could lead to the identification of the vascular tree; 3) the three-dimensional surface representation of the identified airways makes it reasonably intuitive and enables an automated, objective measurement of the geometric properties of segmented airways (e.g. airway volume, lumen area, etc.). Most important, the surface representation used here makes it possible to use a “puzzle game” to partially correct for false negative regions. Our analysis showed that isolated regions were typically caused by either partial volume effect or airway obstruction. Although several previously developed morphological operations [17, 24–27] could be used to “bridge” isolated regions, these approaches may not always depict correctly the morphological properties of the “bridged” airways.

Fig. 14.

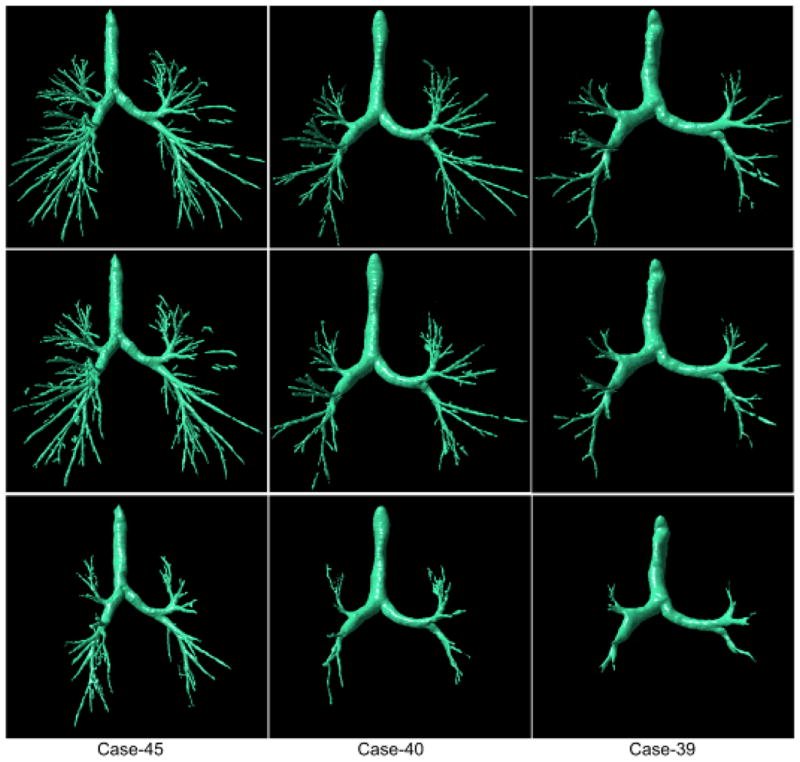
Examples of airway tree segmentations selected from the second group (i.e., Case #31 - Case #45) with the better (“high”) performance (the left column: Cases #45), mid-level (“average”) performance (the middle column: Case #40), and “poor” performance (the right column: Case #39). These examinations were reconstructed with “bone” kernel and have three different slice thickness of 0.625 mm (the top row), 1.25 mm (the mid row), and 2.5 mm (the bottom row), respectively.

The unavailability of the “truth” makes it difficult to assess the performance of an airway segmentation scheme. Several studies [16, 22, 25, 26] evaluated performance of their own airway segmentation schemes by comparing scheme results with the number of bronchial sections manually traced by one or multiple radiologists. However, this is an extremely time-consuming task that is prone to observer/rater errors, in particular in examinations that may include as many as 400–600 slices per case. Lo et al. [47] assembled a “reference standard” by computing the union of the airway segmentations obtained from multiple schemes developed by different teams with a visual verification by an expert observer. Seven measures were computed in [47] to assess the performance of an airway segmentation scheme. When applied to the publicly available test dataset (EXACT’09), we found that our results were competitive and quite satisfactory. We note that the overall average performance of the scheme on the EXACT dataset is somewhat lower in terms of summary measures, than that when applied to our own dataset. This stems primarily from the fact that the EXACT set includes lower dose (higher noise) examinations and includes a different of case mix depicting abnormalities at different severity levels. We summarize the performance of several methods developed previously in Table IV as an indirect way to compare the performance of our scheme with other approaches. The size of the testing datasets used for this purpose ranged from 8 examinations to 44 examinations and the evaluation methods used varied significantly among these studies. As compared with these methods, our scheme tended to be comparable to or better than most in terms of airway lengths and the number of branches, albeit we emphasize that our results are based on a different testing dataset.

Table IV.

Summary and comparison of some typical airway segmentation methods

Studies	Case#	Slice Thickness	Method	2D/3D	Auto	Performance
Aykac et al. [25]	8	3 mm	morphological reconstruction	2D+3D	fully	sensitivity: 73% total 364 branches
Bartz et al. [21]	22	1.0 mm	3D region growing, 2D wave propagation, and 2D template matching	2D+3D	semi	2)7th generation 2)20~100 seconds
Fabija ska [8]	10	0.625 mm	region growing and morphological operation	3D	fully	~9th generation ~10 minutes
Fetita et al. [26]	30	0.6 mm	energy based reconstruction	3D	fully	sensitivity is ~91%
Graham et al. [32]	23	N/A	3D Region growing and graph optimization	3D	fully	~3 minutes > 7th generations
Kiraly et al. [27]	30	0.6 mm	3D region growing and mathematical morphology	3D	fully	2~25 minutes 12 generations per case 182 branches per case
Mayer et al. [22]	22	1.25 mm	3D region growing, 2D wave propagation, 2D template matching	2D+3D	fully	sensitivity: 86%~ 94% 27 seconds
Sonka et al. [16]	44	3.0 mm	3D region growing, rules, anatomical knowledge	2D+3D	fully	sensitivity: 69%~87%
Tschirren et al. [20]	22	0.6 mm	Fuzzy connectivity	3D	fully	27.0±4.4 segments

We recognize that the scheme described in this study has a relatively higher computational cost in both absolute time and space, requiring approximately 30 minutes and 1.5 GB memory for a desktop PC (AMD Athlon^™ 64×2 Dual 2.11 GHZ central process and 4 GB RAM) to identify a complete airway tree depicted in a typical high resolution chest CT examination. Fortunately, with the exception of real time bronchoscopy related applications, currently airway identification is typically performed offline. However, the computational complexities in space and time of the primary steps involved in the airway segmentation, namely (1) anatomical structure modeling, (2) principal curvature calculation, (3) non-airway region filtering, and (4) “puzzle game” execution, are linear (O(n)) in terms of the number n of the triangles in the lung model. The absolute high computational cost is attributed to the huge number of triangles in the lung model (more than 10 millions triangles) and the repetition of the whole procedure at multiple thresholds. Hence, potential for improving efficiency lies in reducing the number of triangles forming the lung model without changing the geometric shape. We are investigating ways to improve efficiency of this scheme using triangle mesh simplification. In addition, as the scheme identifies airways in the same manner at different iso-values, efficiency of the algorithm could be improved significantly when using more modern computers with multiple processors. Although our dataset included cases that were selected from a COPD screening cohort and some of the examinations depicted airway disease, such as bronchiectasis (Fig. 16), we did not perform a comprehensive quantitative assessment of the impact of the presence of different lung diseases with varying severity levels on segmentation performance. This is the focus of a future study but at this time is beyond the scope of the current study. Finally, at the bifurcating regions where the next generation of airways originates and the airways are close to each other, the scheme may produce small junctions due to partial volume effects and the use of the multiple iso-values when modeling the airways.

Fig. 16.

Two examples of the airways segmentations results is severely diseased cases: (a) shows an examination (Case #25) with bronchiectasis, (b) shows the segmented airway tree of the examination in (a); (c) shows an examination (Case #2) with severe COPD displayed at a threshold of −950 HU, and (d) shows the airway tree as segmented from the examination in (c).

V. CONCLUSION

A fully automated computerized scheme was described in this study to segment the airway tree depicted on CT images. The identification process was primarily achieved by applying a computational differential geometry method to the entire lung region/volume at multiple thresholds or iso-values. The proposed approach has several advantages such as generalizability, simplicity, reliability, and it is relatively insensitive to image noise or artifacts. A preliminary study using a set of clinical chest CT examinations acquired from a COPD screening cohort has verified its feasibility and robustness in both normal and pathological cases.

Fig. 15.

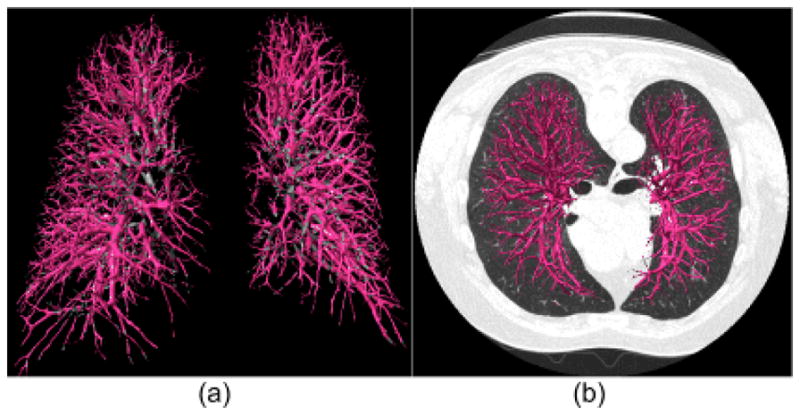
An example of the use of the developed scheme to segment vascular tree depicted on CT images: (a) shows the segmented three-dimensional vascular tree, and (b) shows a mixed rendering of (a) superimposed on the corresponding CT images.

APPENDIX

Fig. 17.

Screenshots of the segmentation results on the 20 publicly available test cases from EXACT’09.