The Quantum Workings of the Rotating 64-Grid Genetic Code

Abstract

In this article, the pattern learned from the classic or conventional rotating circular genetic code is transferred to a 64-grid model. In this non-static representation, the codons for the same amino acid within each quadrant could be exchanged, wobbling or rotating in a quantic way similar to the electrons within an atomic orbit. Represented in this 64-grid format are the three rules of variation encompassing 4, 2, or 1 quadrant, respectively: 1) same position in four quadrants for the essential hydrophobic amino acids that have U at the center, 2) same or contiguous position for the same or related amino acids in two quadrants, and 3) equivalent amino acids within one quadrant. Also represented is the mathematical balance of the odd and even codons, and the most used codons per amino acid in humans compared to one diametrically opposed organism: the plant Arabidopsis thaliana, a comparison that depicts the difference in third nucleotide preferences: a C/U exchange for 11 amino acids, a G/A and a G/U exchange for 2 amino acids, respectively, and a C/A exchange for one amino acid; by studying these codon usage preferences per amino acid we present our two hypotheses: 1) A slower translation in vertebrates and 2) a faster translation in invertebrates, possibly due to the aqueous environments where they live. These codon usage preferences may also be able to determine genomic compatibility by comparing individual mRNAs and their functional third dimensional structure, transport and translation within cells and organisms. These observations are aimed to the design of bioinformatics computational tools to compare human genomes and to determine the exchange between compatible codons and amino acids, to preserve and/or to bring back extinct biodiversity, and for the early detection of incompatible changes that lead to genetic diseases.

Introduction

How many ways exist to reach a specific mathematical result? Certainly numerous; however, some of them are more practical or logical for use than others. For example, to reach 64 as a result by multiplying only, we have the briefer and more straightforward way, which is 8 × 8 = 64, or the strategy we found directly in the genetic code, based on all possible combinations of the four nucleotides in codons, which are the nucleotides grouped by threes, which mathematically written is 4 × 4 × 4 = 64.

In the same way that we can reach the result of 64 in at least two ways, the total number of codons based on the best representations of the genetic code, can be reached in at least two information-filled ways. The minimal way to validate anything experimentally or mathematically is by having at least two ways to reach the same result; in this case, a circular genetic code and its non-circular equivalent.

The word “workings” used in the title of this article is to pay homage to Richard Grantham and to his excellent earlier research on codon usage among organisms (Grantham, 1980).

I’m searching here for a non-circular equivalent of the rotating classic circular genetic code capable to provide at least the same informational content.

My view of the quantic theory as applied to the processes of the brain is that we can reach any result by using at least two different strategies, as exemplified before. The theoretical representation I seek to reach should have, not only collective, but individual rotating components. This will be a representation with more flexibility allowed to it, as in the orbits of the electrons. The natural world teaches to us about this inherent flexibility inside atoms, proteins, molecules, organelles, cells, tissues, organisms, ecosystems and planets (Fig. 1).

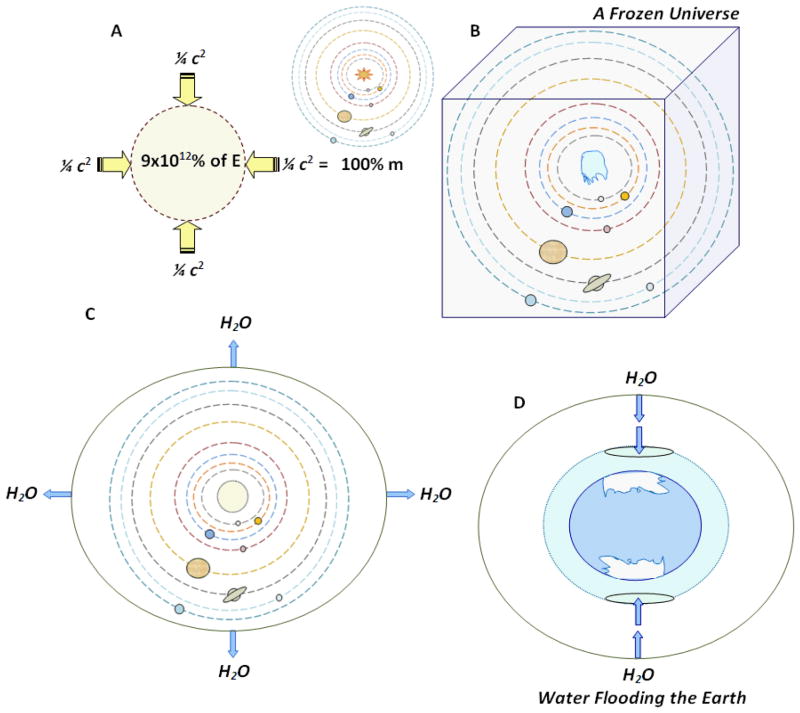
Figure 1.

Past events endured by the universe, the planets, and by our Earth. A) The mass or matter (100% of m) could be obtained by compressing or condensing Energy (9×10¹²%E) through the pressure of the speed of light (3×10⁵ km/sec) at the square (c²), according to the constructive transforming equation of Einstein (1905). B) First glacial age in which the whole universe was frozen (only the solar system is represented), when dinosaurs and their contemporaries died. C) The light of the first day melted the frozen universe. Such light was different to the light of the sun, which was frozen. The resulting waters exited to the outside of an expanding and circumscribed universe possibly through the black holes. D) Second glacial age, when most of the gigantic mammals of the Earth died, and in which water entered to the Earth from the outside of the Universe mostly through the atmospheric ozone holes.

Fig. 1A represents Einstein’s equation as it was written by him in his initial papers, in the constructive or edifying way: E/c²=m (Einstein, 1905), indicating that mass or matter was obtained by compressing energy at least with the force of the speed of light at the square (Genesis 1:1)http://www.webcitation.org/63YujQxF9 [p. 3; Appendix 2, 3]. The common way in which this formula is currently and universally known is E=mc², which represents its destructive side; i.e., if you project a pencil (m=mass) with the speed of light (186,000 miles/sec.) at the square (c²), the pencil disintegrates, transforming itself into energy (E) like an atomic bomb. Light is both energy and mass, as the photons attracted by planetary gravities in their interstellar travel demonstrate.

Fig. 1B and 1D presents the two encompassing or massive glacial ages the earth has experienced in its existence, being the first a global or universal event, while the second was a partial one, localized mostly on both poles of the Earth’s Pangaea. In the first glacial age, the Solar System was drowned by the waters, freezing its “nucleation centers” (sun and planets), and “paralyzing” their orbital movements and rotation. This event evidently extinguished the dinosaurs and all their contemporaries. Evidence of gigantic showers of ice-meteorites is been found worldwide, even on the surface of the moon! A terrestrial and lunar “cratering” (Schulte et al, 2010; Bottke et al, 2007; Becker et al, 2004, etc.) originated in the first glacial age. All the animals that breathe were drowned and died under those waters and under those freezing conditions.

Fig. 1C depicts the resolution of the first ice age by the removal of the waters and/or melted ice from the dark space outside the Earth’s atmosphere, taking them to the thick monolayer of water present in the exterior of the universe. Einstein advanced some initial mathematical considerations for a circumscribed universe (Einstein, 1917), something further supported by Lemaitre/Hubble’s discovery that the universe is expanding like a spherical or elliptical balloon (Block, 2011; van den Bergh, 2011; Smith, 1982). Einstein used the concept of quantum and the quanta of energy (Einstein, 1911); before Einstein, Max Planck worked on it, and after him, Niels Bohr (Carson, 2000) developed it further than them, i.e., to represent the orbital flow of electrons within the atom.

The light of the first day after the first and global glacial age, being different to the absent lights of the sun and the stars turned-off by the waters, was a light that was warm enough to melt the universal ice in preparation for its removal, taking those waters, as mentioned before, from the dark space to the outside of the universe. After this removal of waters, planet Earth was left as a 100% blue planet filled all over with water, with only waters on its surface but not dry land. The one-continent piece of land called Pangea (Whiteside et al, 2011) emerged later with every conceivable plant also emerging from it. The DNA was saved and preserved from the first glacial age, mostly through the seeds of plants (McLoughlin et al, 2008), microorganisms, and phytoplankton (Ribeiro et al, 2011).

Even if the current conditions are not the optimal original conditions of the first humanity or the first blood, they are good enough for us to track the workings of the genetic code (Fig. 2).

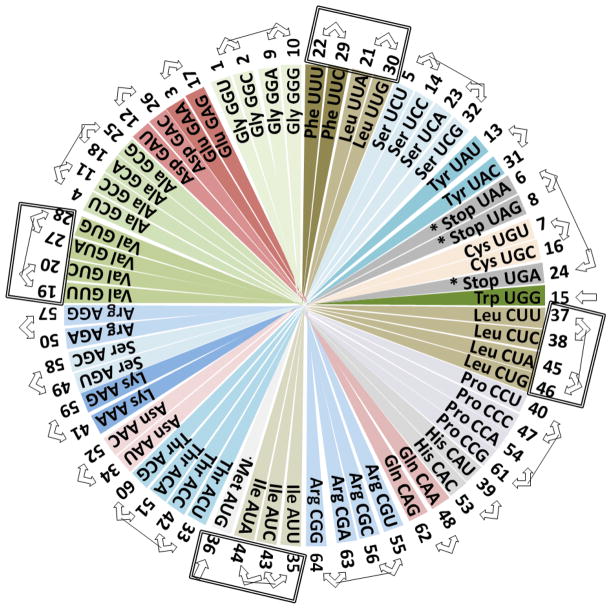
Figure 2.

The colored rotating classic circular genetic code. Quadrant one starts at Phe UUU and ends at Trp UGG, quadrant two starts at Leu CUU and ends at Arg CGG, quadrant three starts at Ile AUU and ends at Arg AGG, and quadrant four starts at Val GUU and ends at Gly GGG. The numbers outside of each codon indicate their position in the rotating 64-grid genetic code (Fig. 3). The arrows on the outside indicate that the position of those linked codons may be exchanged in a wobble-like quantic movement, except for Trp UGG and Met AUG. Codons with U at the center codifying for essential hydrophobic amino acids fall at a distance of 90 degrees in all quadrants (emphasized with a rectangle outside of them).

Here, I will translate the positional resonances (Fig. 2) and homologies found in the classic rotating circular genetic code (Castro-Chavez, 2010), into a rotating 64-grid representation (Fig. 3) of the genetic code. The main difference is that in the original conventional or classic circular genetic code, the order of codons is fixed in a sequential pattern of UCAG ² for the first, second and third concentric circles, while the 64-grid representation will be more ‘quantic’, because positions can be exchanged between related codons within the quadrants.

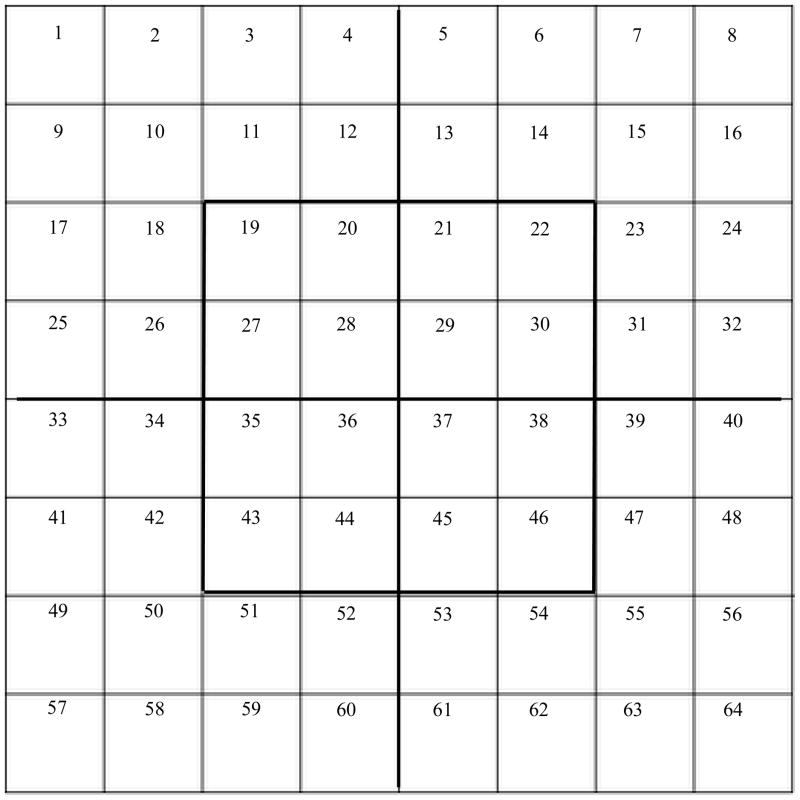
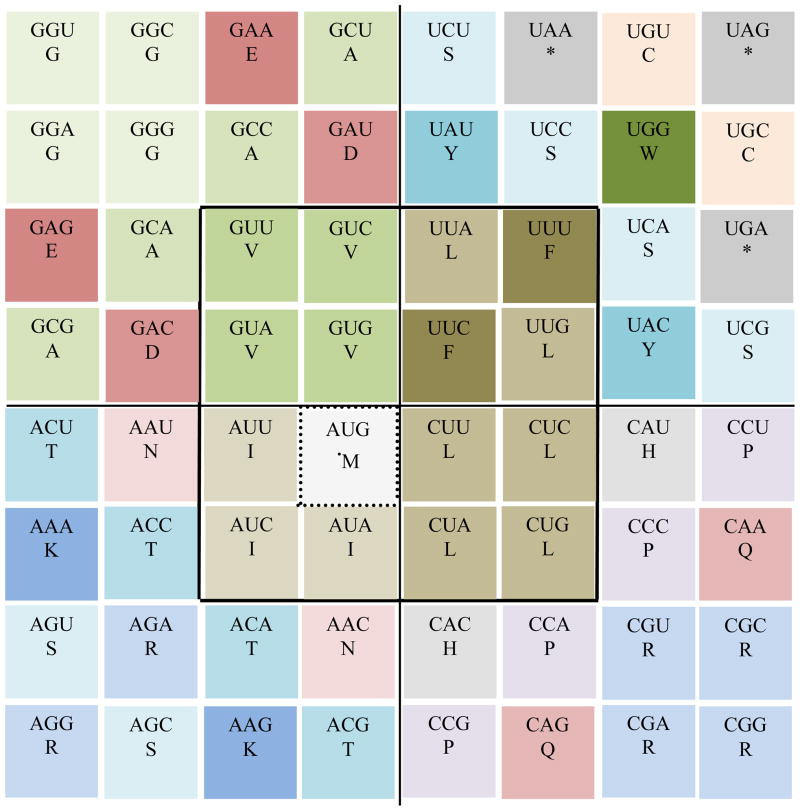
Figure 3.

The 64-grid template that will be adopted as a model to represent the rotating genetic code whose foundation is the rotating classic circular genetic code (Castro-Chavez, 2010). The codon logic of the circular genetic code will be transferred to this novel 64-grid conformation.

I did choose a 64-grid representation because there are 64 codons, and because this is the chessboard number of the most clever table games, such as chess and checkers (Schaeffer, 2009);other related factoid is that one mile is equivalent to eight furlongs, a term still used in horse races (Staszkow, 2003);in India, a classic religious drawing of a man is a representation encased by 8 × 8 squares consisting of 64 grid cells only used for sacred buildings (Rao, 1988). A theoretical puzzle to determine the minimal number of moves required to get a stack of 64 successively sized disks from one pin to another (the 64-disk monks’ version of the “Tower of Hanoi”), having a total of three pins: 1) the one containing the 64 disks, 2) the second empty one where all the 64 disks need to be positioned orderly as they appeared initially in the first pin, and 3) a third empty pin to help with the moves, moving one disk at a time while never placing a larger disk over a smaller one. The result of this puzzle is ≥5.8×10¹¹, obtained by solving the problem of (2⁶⁴)-1 (Brumbaugh and Rock, 2001).

In this number of NeuroQuantology, Petoukhov (2011) uses the 64-grid structure in special Hadamard (8x8)-genomatrices, in Punnett’s matrices of dyadic shifts, in Kronecker multiplication of matrices, and in Rademacher and Walsh functions; however, the credit for presenting for the first time the full Fu-Xi (Fu Hsi) genetic code pattern of 8x8=64 hexagrams made by 0’s and 1’s based on the ancient Chinese ‘Book of Changes’ (I Ching), combined with our current knowledge of molecular biology, was Stent (1969), followed by Schonberger (1992), Yan (1993), Walter (1996), Petoukhov (1999), and most recently, Sepulveda-Lopez (2008), among others; having each small differences in reasoning, and/or in the coupling of nucleotides to the Chinese binary symbols, assigning the 0 for the broken horizontal line, and the 1 for the continuous horizontal line (Leibnitz, 1703). Here, it may as well be true the fact that “the order of factors does not affect the product”.

My biomedical colleague Raul Cruz-Mireles (Cruz-Mireles and Ortega-Blake, 1991)³ did bring to my attention the fact that Semitic languages have “triliteral roots” (‘triplets’), and that the variation between words with similar or related meaning occurs by changing the third letter. The first and the second Hebrew letters remain, in general, constant like the “invariants”, which is similar to what happens in the codons of the genetic code. Both the third Hebrew letter and the third codon nucleotide are the “variable”. The next excerpts from Edkins (1889) should raise the interest on this important language similarity: “Hebrew roots may be compared to tripods” (p. 68); “The third radical of triliteral roots is often a pronoun… the marks for gender, number, and case…” (p. 74); here, it seems that masculine and singular are the two invariable roots (as in Adam first being alone), while the modifiers feminine and plural were understood by adding the third radical (as in Eve [Ishshah] being originated from and after Adam [Ish] in Genesis 2:23; in the old Reina-Valera Spanish (1569-1960), this was also the case: "varón" for the man and "varona" for the woman, which also persists, though backwards, in the current English language as "man" and "woman") http://www.webcitation.org/63YujQxF9 [p. 6, Appendix 14]; “Biliteral roots are made triliteral by inserting a letter” (p. 75), “throughout the Semitic area the triliteral root prevailed” (p. 134); “The triliteral vocabulary and grammar seem to have reached their fullest development soon after the time of Moses” (p. 136), as if given directly to Moses from above.

The previous observations are also a reminder that, similar to the Hebrew language, for women to produce their hormones (estrogens), they need to produce them in their ovaries first as male hormones (androgens), further modifying them in order to obtain their own hormones (estrogens). The pathway for the formation of estrogens starts in the same way as for the formation of androgens, after the cholesterol, in both cases with its derivative pregnenolone, to produce progesterone, being progesterone transformed into 17α-hydroxyprogesterone both in males and females. The molecule 17α-hydroxyprogesterone is transformed into androstenedione both in males and females, being androstenedione then transformed into testosterone which is predominant in men, both in males and females. The female pathway branches further modifying androstenedione to produce their estrone, while modifying testosterone to obtain their estradiol (Berg et al., 2007).

The bio-mathematical balance between codons per amino acid will be preserved in this novel 64-grid representation of the genetic code (Fig. 3). Such balance for odd and even codons in the genetic code was previously demonstrated, and is: 2[1(1)+1(3)+1(4)+4(2)]=2[2(2)+3(4)] (Castro-Chavez, 2011; here in Fig. 7).

Figure 7.

Mathematical balance of the genetic code as learned by the rotating circular genetic code (Castro-Chavez, 2011): 2[1(1)+1(3)+1(4)+4(2)]=2[2(2)+3(4)]. The left side of the equation represents quadrants one and three, while the right side of the equation represents quadrants two and four. Only the odd numbered codons present in quadrants 1 and 3 are colored, as well as the codons only present by pairs in quadrants 2 and 4. Notice that in this image the subject is not exchangeability but the abstract numerical equilibrium of odd codons and of even codons, being the even codons grouped both by pairs and by tetrads.

Through the use of biomathematics (Stewart, 2011), we will add the ingredient of mathematics in the simplest way as possible, to the already complex reality of the genetic code, a code composed of biology, chemistry, physics and information (Jimenez-Montano, 2009; Barbieri, 2008). By making the individual codon-rectangles, inside the 64-grid representation, that are codifying for the same amino acid to alternate positions within their quadrants, we will represent the wobble effect, making this representation, with the help of quantum thinking, one step closer to reality (Crick, 1966; Siegfried et al., 2010). However, the third position of the codons may be more important than previously imagined, similarly to the informational richness of what previously was considered “junk DNA” (Wells, 2011), or the important role of the previously despised “pseudogenes” (Pink et al, 2011), including the regulatory function of micro RNAs and their transport (Vickers et al., 2011).

Experimental Section

The rotating circular genetic code (Castro-Chavez, 2010 and 2011; here in Fig. 2) was ‘translated’ to a 64-grid “chessboard” representation (Fig. 3), while keeping the logic of its relative positions. The three rules of variation previously described (Castro-Chavez, 2010) were adapted to this new structure (Figs. 4–6), as well as the mathematical balance of codons (Fig. 7), and the most used codons per amino acid in humans compared to the plant Arabidopsis thaliana (Fig. 8), using the useful database developed by Nakamura et al (2000). The ratio of codons analyzed between H. sapiens and A. thaliana, was: 40,662,582 versus 31,098,475.

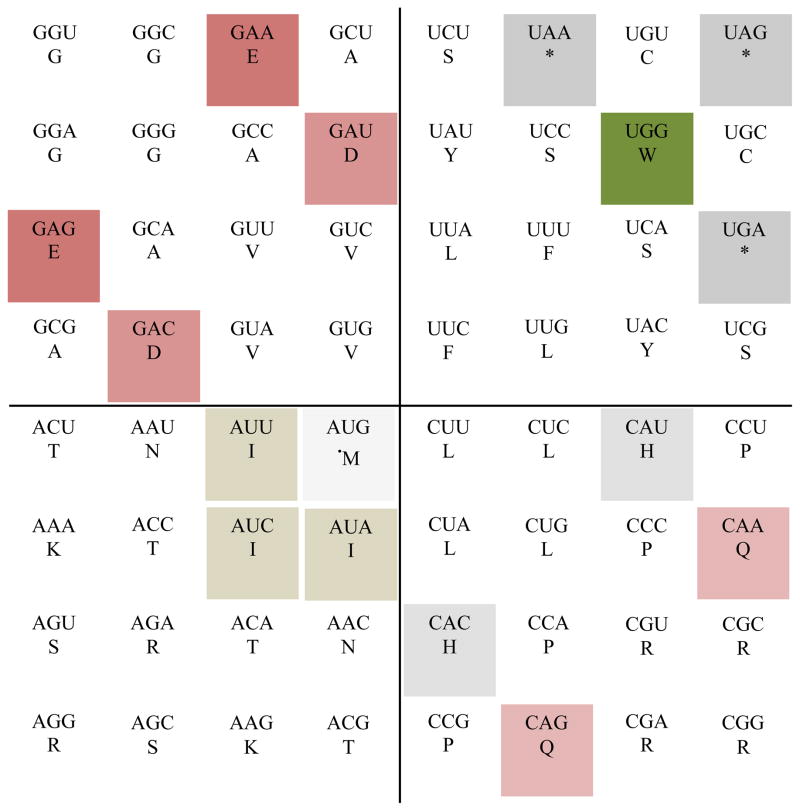
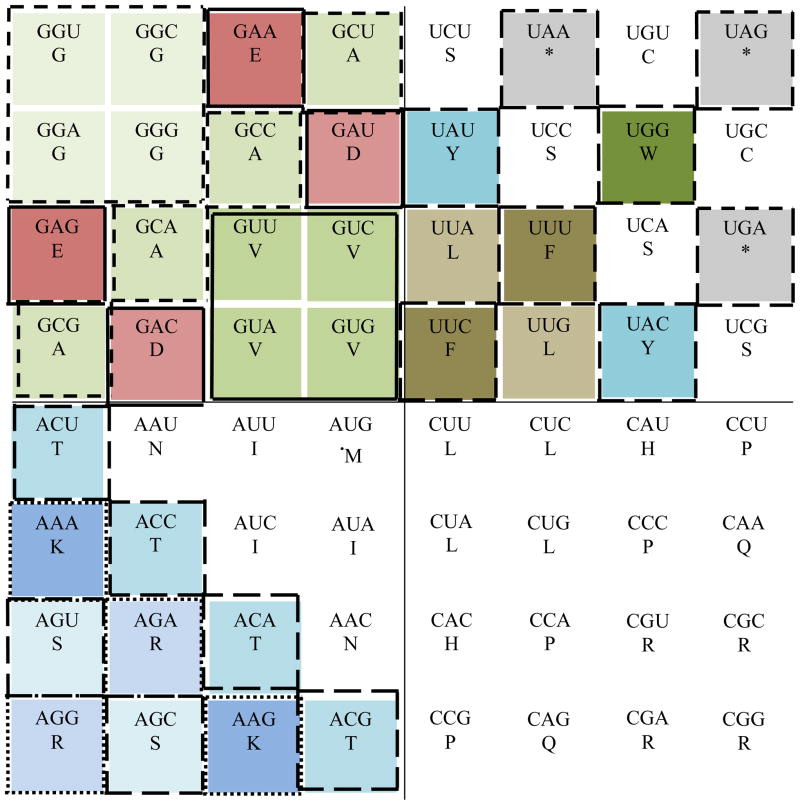
Figure 4.

Rule 1 of variation translated from the classic circular genetic code to the 64-grid genetic code. This image represents the rule number 1 which emphasizes the codon exchangeability in the four quadrants between essential hydrophobic codons (Castro-Chavez, 2010). At the center of the image we find the 16 codons for the essential hydrophobic amino acids with U at their center, considered to be the ‘engines of variation’. In a quantic fashion, all the codons for Valine (V), Leucine (L), Isoleucine (I) or Phenilalanine (F) can rotate, occupying any cell within their own amino acid per quadrant. Clockwise, quadrant 1 is at the top right, quadrant 2 at the bottom right, quadrant 3 at the bottom left and quadrant four at the top left. The starting codon M is noticed by a dotted cell near the center of the 64-grid.

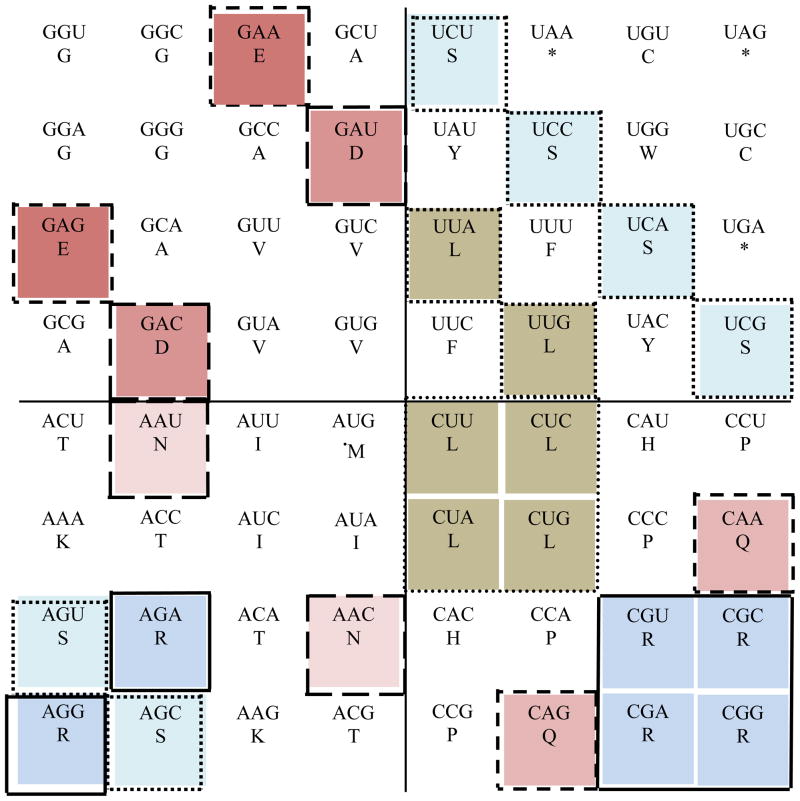
Figure 6.

Rule 3 of variation translated from the classic circular genetic code to the 64- grid genetic code. This image represents the rule number 3 that establishes codon exchangeability within one quadrant between codons for equivalent amino acids (Arginine (R) and Lysine (K); Serine (S) and Theronine (T); Glutamate (E) and Aspartate (D); Glycine (G) and Alanine (A); Tryptophan (W), Phenylalanine (F) and Tyrosine (Y), etc.) (Castro-Chavez, 2010). In a quantic fashion, all the mentioned codons can rotate, exchanging places among themselves in their assigned spaces per amino acid within each quadrant.

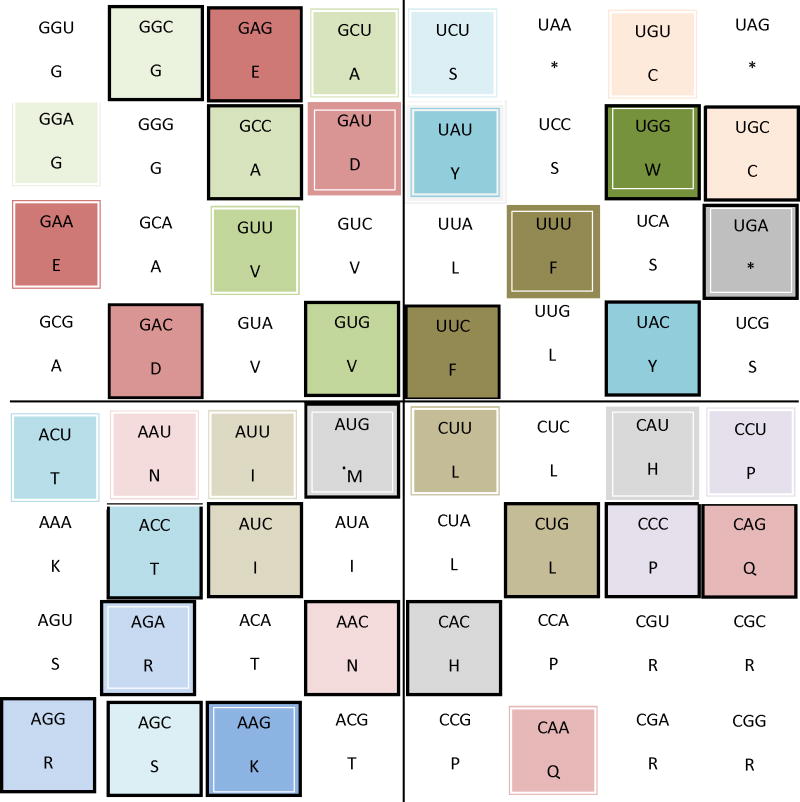
Figure 8.

Most used codons per amino acid in humans [in black rectangles] compared to a plant Arabidopsis thaliana [in white smaller rectangles]. The codons that are the most used by both organisms [in double rectangle, external black for man and inner white for the plant], are the unique codons for amino acid Met (M), and for Trp (W), respectively, plus the basics: one Arg (R) AGA and one Lys AAG, and the stop codon UGA. Humans use equally two codons for one amino acid: Arg AGA and Arg AGG. The color for the rest of the codons has been removed to make comparisons easier (database used: Nakamura et al., 2000).

Fig. 2 and/or Fig. 4 (or the same images without words in Appendix A1 and/or A2), can be printed twice, then pasting looking outward these identical duplicates at both sides of a solid cardboard or metallic cap of a can, while making a strong cord to cross through two small holes made near the center of the rotating genetic code (i.e., near the center, where cell 29 is, and where cell 36 is); then, knotting the cord at its extremes, to make the code to rotate with the use of the fingers of our hands, while noticing how the colors, when they rotate at full speed (like in a “disco zumbador”), blend themselves producing the white color (Newton, 1730).

An identical coloring pattern was used for both representations: the circular and the 64-grid, according to Microsoft Office^™ 2007.

Results and Discussion

The 64-grid genetic code will be presented next. We need to remember that the drawings of the rotating 64-grid genetic code presented here are a reflection of the classic circular genetic code previously analyzed (Castro-Chavez, 2010; 2011).

Figures 4 to 6 demonstrate that the 64-grid representation can keep the same positional order and resonance for the three rules of variation discovered within the rotating circular genetic code (Castro-Chavez, 2010). The codons per amino acid within each quadrant can ‘rotate’ in a quantic way, which means that each and every one of the codons for the same amino acid within quadrants may be capable to exchange positions.

The exchange of positions can be more easily described by referring to the cell numbers present in Fig. 3, and will be indicated below for each rule of variation.

For the rule number 1 presented in Fig. 4, next are the ‘quantic’ cells that can rotate or be exchanged among them: For V in quadrant 4: cells 19, 20, 27 and 28; the V codons can occupy any of those cells. In quadrant 1, for F: cells 22 and 29; and for L: cells 21 and 30. In quadrant 2, for L: cells 37, 38, 45 and 46. In quadrant 3, for I: cells 35, 43, and 44 (see in Fig. 3 the respective numbers per cell).

In Fig. 4, I was capable to represent at the center the 16 essential hydrophobic codons, including the one and unique starting codon for Met, while keeping the stop codons in the outer corner of quadrant 1. We need to remember that the stop codons within the genes are positioned strictly in a non-random way, being the less used codons of all; if the positioning of the stop codons were random, we should be expecting some 30 stop codons per mRNA, when only one stop codon is present and necessary (Strachan and Read, 1999).

Next, for the rule number 2 presented in Fig. 5, the cells that can be exchanged or that can rotate occupying each one the space of the other and vice versa, are, including the cells for L previously mentioned for rule number 1, in quadrant 1 we can exchange for S: cells 4, 14, 23 and 32; in quadrant 2, for Q: cells 48 and 62; for R: cells 55, 56, 63 and 64; in quadrant 3, for S: cells 49 and 58; for R: cells 50 and 57; and for N: 34 and 52; in quadrant 4, for E: cells 3 and 17; and for D: cells 12 and 26 (see in Fig. 3 the respective numbers per cell; the same for the next related Figs. 6 to 8).

Figure 5.

Rule 2 of variation translated from the classic circular genetic code to the 64- grid genetic code. This image represents the rule number 2 that establishes codon exchangeability in two quadrants between codons for identical amino acids (Arginine (R), Leucine (L), or Serine (S)), or related amino acids (Glutamate (E) and Glutamine (Q), Aspartate (D) and Asparagine (N), and for Q and N among themselves) (Castro-Chavez, 2010). In a quantic fashion, all the mentioned codons per amino acid can rotate exchanging places within each quadrant. Clockwise: quadrant 1 is at the top right, quadrant 2 at the bottom right, quadrant 3 at the bottom left and quadrant four at the top left. The color for the rest of the codons has been removed to make easier the comparisons.

Fig. 5 was able to keep the same rotational and relative positions for Arg at the corners of quadrants 2 and 3, while keeping in a contiguous rotational ladder-like configuration the codons for Ser between quadrants 1 and 3, while Leu again remained in the same 90 degree rotational position in both quadrants 1 and 2 as seen in the circular genetic code. The same can be said for the rotational position of the acidic amino acids and their respective amides.

Notice that in Fig. 6, only quadrant 2 lacks of any representative codon for rule number 3.

For Fig. 6, representing rule number 3, adding to the previously mentioned for F, L, S, R, V, E, and D, the next ones are the rotationally compatible codons, starting with quadrant 1: the stop codons (*): cells 6, 8 and 24; for Y: cells 13 and 31; for quadrant 3: T: cells 33, 42, 51 and 60; for K: cells 41 and 59; and for quadrant 4: G: cells 1, 2, 9 and 10; and for A: cells 4, 11, 18 and 25(see in Fig. 3 the respective numbers per cell).

Another mathematical ‘quanta’, easy to find on the internet, is the “Knight’s Tour”, “originally proposed by mathematician Euler. The question is this: Can the chess piece called the knight move around an empty chessboard and touch each of the 64 squares once and only once?” (Rajeevan, 2011).

The heuristic “Warnsdorff’s algorithm” was used to solve the problem posted in the previous paragraph; however, to follow such ‘algorithm’ does not always lead to a solution when only a single next square is chosen at each step (Roscoe, 2010).

Euler himself did a special 8 × 8 “order eight magic square” that not only had equal row and column sums (260), but each successive number was a chess horse “L” step (a knight’s step) from the preceding number.

More recently, software written by J. D. Meyrignac (widely distributed by Guenter Stertenbrink), found 140 distinct ‘magic’ knight’s tours with ‘magic’ row and column sums!

The classic 8 × 8 “order eight magic square” drawn by Benjamin Franklin had many interesting patterns, in addition to the sum of all rows and columns (260); i.e., if we divide the full square into its four quadrants (4 × 4), each of them provides equal row and column sums of 130; diagonals from left to right sum 268, while diagonals from right to left sum 252, etc. (Schumer, 2004).

As written elsewhere: “Euclid’s elegant icosahedron, devoid of practical application for more than 2,000 years, turned out to be just the right shape for making a virus. The big question was: why? Part of the answer is energy”, and also: “the paradox of the plankton: the niches are few, yet the diversity is enormous… The solution to the paradox comes from chaos theory” (Stewart, 2011).

One of those 140 Knight’s strategies or other strategies not necessarily chess-related may be used as quantic ways to track the timing and/or the paths followed by the first 64 amino acids of any given protein.

We can start to explore the 64-grid protein or peptide strategies by focusing on proteins that are composed by 64 amino acids:

1. the basic DNA-binding protein of Bombyx mori nuclear polyhedrosis virus (BmNPV), with an estimated molecular weight of 7947 Da; here, “the amino acid sequence determined by direct peptide sequencing was identical with the deduced amino acid sequence” (Maeda et al., 1991),

2. CI2 (Chymotrypsin Inhibitor type 2), a small (MW of 7.1 kDa), compact, α/β protein for which both crystal and solution structures have already been determined (Koharudin et al, 2003),

3. 3) Glycomacropeptide (GMP), a single peptide of 6755 Da (Furlanetti and Prata, 2003), etc.

Fig. 7 represents the bi-dimensional or ‘tetradic equation’ for the rotating genetic code, being it circular (Castro-Chavez, 2011) or ‘chessboard like’ (64 grids, rectangles or squares), as presented here.

In Fig. 8 we can see that the codon preferences per amino acid between humans and plants differ in the third nucleotide: eleven times the human C in the codons’ third position has been replaced by U (the C/U exchange), two times the replacement has been G/U and also two times G/A, and one time the replacement has been C/A, while four amino acids, and the stop codon, as described in the image, experienced no change. The analysis presented in this figure may be an example to help as a shortcut, for the study of multiple closely compatible genomes between organisms, which is a possible way to demonstrate my fourth rule of variation on compatible genomics (Castro-Chavez, 2011). The comparison of the human genome to the squid genome (squid pattern for its 3^rd nucleotide: _ _U/A, 13-6-3 U-A-G), will be presented elsewhere in this number (Castro-Chavez, 2011b), where it will be shown visually why is it that I prefer the circular genetic code representation for this kind of most used codons per genomic population comparisons.

Fig. 8 also shows that the distribution of most used codons in their third nucleotide position for humans is: 12-8-2 C-G-A, while the distribution in A. thaliana follows a pattern of 13-5-3 U-A-G. These definite patterns are helping in the establishment of at least two hypotheses:

1. Human and vertebrate genes are slower in their translation to proteins due to their preference for three hydrogen bonds in the third position of their codons;

2. Invertebrate (or plant) genes are faster in their translation to proteins due to their preference of two hydrogen bonds in the third position of their codons.

The third nucleotide usage biases in the codons of amino acids that differ within and between genomes may be helping in the regulation of the rate of protein synthesis.

We read: “if the transfer RNA that matches a codon is rare, then transcription of genes including that codon will be slowed. For some proteins there is evidence that such pace-setting codons help ensure correct folding of the amino acid chain” (Hayes, 2004), “slow translation rate correlates with the high content of rare codons” (Pedersen, 1984).

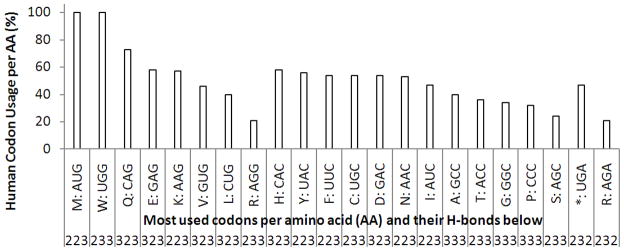
Figure 9 is a visual representation of the human codon usage taken from Fig. 8 using a graphic, where we can see the most used human codons per amino acid and their hydrogen bonds ordered according to their most used third nucleotide, being it G, C or A, respectively.

Figure 9.

Most used codons per amino acid (AA) and their hydrogen bonds (H-bonds, at the bottom) in humans. The first eight correspond to the codons that end in G. The amino acids that have only one codon correspond to this category: M: AUG and W: UGG; then we have the next twelve codons that end in C, this category includes three with a saturated 333 H-bond (i.e., with 3 × 3 = 9 hydrogen bonds or bridges): A: GCC, G: GGC and P: CCC; finally, we have the two most used codons that end in A, one corresponds to the stop (*) function: UGA, while the other corresponds to the equally used codon for R: AGA [the other equally used Arg is R: AGG]. The H-bond numbers at the bottom of the graphic also correspond to those presented in Table 1 (below).

If we group the human codons according to the hydrogen bonding of their three nucleotides, the most used codons per amino acid in humans fell within four groups (Table 1).

Table 1.

The most used human codons per amino acid according to their hydrogen bonding (in bold). In parenthesis is the one letter code for each amino acid. An asterisk indicates the presence of the stop codons.

223	323	233	333	232	222	322	332
AUG (M)	CAG (Q)	UGG (W)	GCC (A)	UGA (*)	UUU (F)	CUU (L)	CCU (P)
AAG (K)	GAG (E)	UGC (C)	GGC (G)	AGA (R)	UUA (L)	CUA (L)	CCA (P)
UAC (Y)	CAC (H)	ACC (T)	CCC (P)	UCU (S)	UAU (Y)	CAU (H)	CGU (R)
UUC (F)	GAC (D)	AGC (S)	CCG (P)	UCA (S)	UAA (*)	CAA (Q)	CGA (R)
AAC (N)	GUG (V)	AGG (R)	CGC (R)	UGU (C)	AUU (I)	GUU (V)	GCU (A)
AUC (I)	CUG (L)	UCC (S)	CGG (R)	ACU (T)	AUA (I)	GUA (V)	GCA (A)
UUG (L)	CUC (L)	UCG (S)	GCG (A)	ACA (T)	AAU (N)	GAU (D)	GGU (G)
UAG (*)	GUC (V)	ACG (T)	GGG (G)	AGU (S)	AAA (K)	GAA (E)	GGA (G)

In Table 1, the three-digit numbers in bold italics will represent the hydrogen bonding for each of the three nucleotides per codon: 223 ⁴ (6 codons: 4 with C at the end and 2 with G), 323 (6 codons: 4 with G at the end and 2 with C), 233 (5 codons: 3 with C at the end and 2 with G), 333 (3 codons, all with C at the end). Only two of the most used codons had H-bonding of the type 232 ending with A (Table 1). The H-bond human categories that have no codons represented in the “most used codons” list are 222, 322 and 332, all of them ending in weaker two H-bonds.

The additional rules of variation that I reported recently are: 4) compatible genomes, 5) homologous recombination and 6) production of a healthy and fertile offspring (Castro-Chavez, 2011).

The basic conceptual equations expanded for the rule of variation number six are:

$$\text{Genes}+\text{Environment}=\text{Natural}\text{Variation}$$ 1)

Notice here that the genomic variation to adapt to a changing environment is a slow process that starts working selflessly for at least two generations before the inheritance of a more adaptively advantageous polymorphism; those polymorphisms can experience a non-random reversion by a process barely understood (Castro-Chavez, 2011).

$$\text{P}1+\text{P}2=\text{F}1\text{f}$$ 2)

If P1 + P2 = F1f (F1 Fertile), then P1 and P2 are varieties of the same theme, no matter how morphologically different they may appear; v.gr., Chihuahua dog and Saint Bernard dog.

$$\text{P}1+\text{P}2=\text{F}1\text{s}$$ 3)

If P1 + P2 = F1s (F1 Sterile), then P1 and P2 are members of a different theme, no matter how morphologically similar they may appear, v.gr., horse and donkey (Castro-Chavez, 2011). The exceptional “fertile” female mules that interbreed by natural means produce 100% horses, depending on their resulting chromosomal random pool.

Since my earlier bibliographic search entitled “Putting Limits on the Diversity of Life” (Castro-Chavez, 2004) I discovered that variation is strongly related to homologous recombination for the generation of healthy and fertile offspring; I also submitted an earlier article where these observations were used for practical purposes (Castro-Chavez, 2005).

In my conversation with other biologists,⁵ I noticed that by studying the genomic compatibility of organisms we cannot only help in solving the innumerable misclassifications of the past; we can also help to reduce the currently inflated number of “phenotypic species” by seeking organisms that are genetically compatible, to prevent their extinction and/or to generate new varieties, a fact that has been corroborated time after time in the animal sciences, crop production, and in new domestic varieties such as dog breeds (Doberman, Shar-Pei), new colorful singing birds, new semi-docile rodents, new gold-fishes, new cichlid flowerhorns (http://www.google.com/images?rlz=1T4DMUS_enUS318&q=flowerhorns), etc.

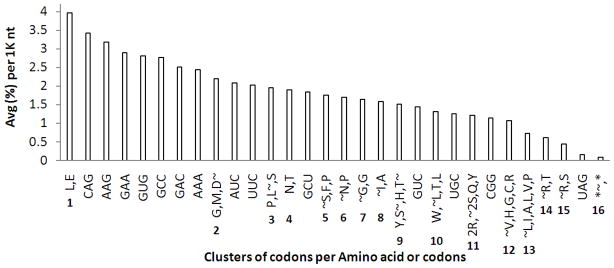
In Figure 10, the 16 human clusters of global codon usage are presented and grouped together if two contiguous members in the cluster are separated by 0.02% from each other. A heterogeneous visual amino acid/codon representation has been chosen to reduce space.

Figure 10.

Graphic representation of most used codons in humans in their genome, in percent per averaged sequences of 1,000 nucleotides (1K) in length. Symbols: ~, at right side of letter indicates that the codon is not the most used; ~, at left side of a group of letters indicates that the whole group of codons in that line is not the most used. Codon correspondence for the 16 clusters of amino acids abbreviated by one letter: 1) L, Leu: CUG; E, Glu: GAG. 2) G, Gly: GGC; M, Met: AUG; D, Asp: GAU. 3) P, Pro: CCC; L, Leu: CUC; S, Ser: AGC. 4) N, Asn: AAC; T, Thr: ACC. 5) S, Ser: UCC; F, Phe: UUU; P, Pro: CCU. 6) N, Asn: AAU; P, Pro: CCA. 7) G, Gly: GGA; G, Gly: GGG. 8) I, Ile: AUU; A, Ala: GCA. 9) Y, Tyr: UAC; S, Ser: UCU; H, His: CAC; T, Thr: ACA. 10) W, Trp: UGG; L, Leu: CUU; T, Thr: ACU; L, Leu: UUG. 11) 2R, 2 Arg: AGA, AGG; 2S, 2 Ser: UCA, AGU; Q, Gln: CAA; Y, Tyr: UAU. 12) V, Val: GUU; H, His: CAU; G, Gly: GGU; C, Cys: UGU; R, Arg: CGC. 13) L, Leu: UUA; I, Ile: AUA; A, Ala: GCG; L, Leu: CUA; V, Val: GUA; P, Pro: CCG. 14) R, Arg: CGA; T, Thr: ACG. 15) R, Arg: CGU; S, Ser: UCG. 16) *~, Stop: UAA; *. Stop: UGA. The reverse Amino acid correspondence for the 14 codons is: CAG: Gln, Q; AAG: Lys, K; GAA: Glu, E; GUG: Val, V; GCC: Ala, A; GAC: Asp, D; AAA: Lys, K; AUC: Ile, I; UUC: Phe, F; GCU: Ala, A; GUC: Val, V; UGC: Cys, C; CGG: Arg, R; UAG: Stop, *.

In Fig. 10 there are at least 16 clusters of expression, fulfilling the 0.02% separation specifications, for groups of codons that are expressed with a similar intensity, ranging from two to six; i.e., Leu CUG and Glu GAG, both at the top of the list have an identical frequency of 3.96%, while in the last (13^th) of the two biggest clusters (the other is the 11^th), Leu UUA, Ile AUA, Ala GCG, Leu CUA, Val GUA and Pro CCG, range from 0.69% to 0.77%.

To see once more the potential vastness of this new field of research (my previous, briefer list is included in Castro-Chavez, 2011), let’s read some additional examples found in the literature and use them to support a compatible genomics approach and its viability to generate biodiversity, while helping to preserve from extinction endangered organisms, starting with some of those cichlids.

Fishes

We read: “we have produced intergeneric hybrids of Lake Victoria cichlids (Pundamilia x Platytaeniodus) that have not shown any evidence of loss of viability or fertility up to the 5th generation… species that do not interbreed in nature will sometimes hybridize under ‘no choice’ (NC) conditions in the laboratory” (Turner et al., 2001), “Cichlid fish species of Lake Victoria can interbreed without loss of fertility… Lake Victoria… had …at least 500 species of haplochromine cichlids… [Derived] from a single ancestral species” (Seehausen et al., 1997); among three-spined sticklebacks: “Complete viability and fertility of hybrids is the norm… given the ease with which various hybrid crosses can be raised in the laboratory” (Schluter, 2001).

Birds

“Among our sample more than half the crosses between species in the same genus produce fertile hybrids… viable hybrids have been produced between taxa…” (Price and Bouvier, 2002); and shorebirds: Black-necked Stilt (Himantopus mexicanus) × American Avocet (Recurvirostra americana) found by Principe (1977), American Oystercatcher (Haematopus palliatus) × Black Oystercatcher (Haematopus bachmani) found by Jehl (1985), Little Stint (Calidris minuta) × Temminck’s Stint (Calidris temminckii), found by Jonsson (1996), Dunlin × White-rumped Sandpiper (Calidris alpina × Calidris fuscicollis), found by McLaughlin (2000), Curlew Sandpiper (Calidris ferruginea) × Pectoral Sandpiper (Calidris melanotus) = “Cox’s Sandpiper” (“Calidris paramelanotos”), studied by Christidis et al. (1996), Curlew Sandpiper (Calidris ferruginea) × Sharp-tailed Sandpiper (Calidris acuminata) = “Cooper’s Sandpiper” (“Calidris cooperi”), studied by Cox (1990a, 1990b), New Zealand Black Stilt × Pied Stilt (Himantopus novaezelandiae × Himantopus leucocephalus), studied by Pierce (1984), White Rumped Sandpiper (Calidris fuscicollis) × Buff-Breasted Sandpiper (Tryngites subruficollis), Baird’s Sandpiper (Calidris bairdii) × Buff-Breasted Sandpiper (Tryngites subruficollis), Dunlin (Calidris alpina) × Purple Sandpiper (Calidris maritima), White Rumped Sandpiper (Calidris fuscicollis) × Pectoral Sandpiper (Calidris melanotus), Common Sandpiper × Green Sandpiper (Tringa hypoleucos × Tringa ochropus), the last examples found in the book by Paulson (2005). I published this list in Dec., 2005: http://fdocc.blogspot.com/2005/12/interbreeding-in-shorebirds.html

Insects

Laupala crickets: “Matings between L. paranigra and L. kohalensis result in viable and fertile offspring, and the second generation of hybrids (F2) provide a genetic and phenotypic mosaic of parental types” (Mendelson and Shaw, 2006); flies, three varieties of maggots, Rhagoletis, including the blueberry fly and “…the apple and hawthorn flies… were interbreeding with one another… they can mate and produce viable offspring when brought together in the lab … Population genetics models show that it takes very little interbreeding to erase differences between two populations, such as the apple maggots and hawthorn flies” (Gibbons, 1996).

Crustaceans

Crayfish: “Orconectes rusticus, or the rusty crayfish, and a native crayfish, O. propinquus (the blue crayfish), are indeed fertile” (Roush, 1997).

Amphibians

Toads: B. americanus and B. fowleri, “…both species are closely related, and that they possibly interbreed occasionally, these forms with the characteristic marks, etc., of both species representing the hybrids” (Deckert, 1917); the fire-bellied toad Bombina bombina and the yellow-bellied toad B. variegata “interbreed within the region of overlap and produce viable, fertile hybrids resulting in a stable hybrid zone” (Kruuk and Gilchrist, 1997).

Flowers

“Two sister species of monkey-flowers (Mimulus lewisii and M. cardinalis) in the lab easily produce fertile hybrids” (Morell, 1996).

Mammals

Wallabies: “in the north of its range, there is a narrow hybrid zone in which there is interbreeding between Petrogale penicillata and the neighbouring species, Petrogale herbertii” (Hutchins, 2002), etc., etc.

Elsewhere, I also mentioned that the list is too long, that these additional examples will suffice, to demonstrate that a solid and compatible interbreeding already takes place in nature.

The rotating genetic code, either circular (Castro-Chavez, 2010 and 2011) or in this novel 64-grid format presented here, is proposed as a tool for the comparison of compatible genomes because its capability to discriminate differences and similarities, not only within human populations and their polymorphisms, but also for the general study of compatible genomics in nature, with the potential advantage of allowing to observe side by side the changes of nucleotides in exons, and their corresponding changes in amino acids, not only inside gametes, but also for the early detection of somatic changes within hazard-exposed cells to prevent cancers and other diseases (Castro-Chavez, 2011). Table 2 exemplifies the spectrum of possible changes.

Table 2.

Amino acid replacement dependent on nucleotide replacement. The replacement goes from identical to incompatible (nucleotide replacement in bold). Abbreviations used here: Nucleotides: C: cytosine, A: adenine, G: guanine, T: thymine. Amino acids: V: valine (Val), I: isoleucine (Ile), L: leucine (Leu), F: phenylalanine (Phe), D: aspartic acid (Asp), E: glutamic acid (Glu), Q: glutamine (Gln), R: arginine (Arg), K: lysine (Lys), S: serine (Ser), P: proline (Pro), C: cysteine (Cys), Y: tyrosine (Tyr). Sbjct: Subject.

Identical	Equivalent	Borderline	Incompatible
Query: AGT	Query: GAG	Query: TCT	Query: GAG
Sbjct: TCT	Sbjct: GAC	Sbjct: TAT	Sbjct: GTG
Query: S	Query: E	Query: S	Query: E
Sbjct: S	Sbjct: D	Sbjct: Y	Sbjct: V
Query: AGG	Query: AGG	Query: CAA	Query: TAC
Sbjct: CGG	Sbjct: AAG	Sbjct: AAA	Sbjct: TGC
Query: R	Query: R	Query: Q	Query: Y
Sbjct: R	Sbjct: K	Sbjct: K	Sbjct: C
Query: CTG	Query: ATT	Query: TTC	Query: CGG
Sbjct: TTG	Sbjct: CTT	Sbjct: TGC	Sbjct: CCG
Query: L	Query: I	Query: F	Query: R
Sbjct: L	Sbjct: L	Sbjct: C	Sbjct: P

After studying codon usage in the mRNA database, Grantham (1980) proposed his “genome hypothesis” by declaring that: “all genes in a genome, or more loosely genome type, tend to have the same coding strategy”; “The optimization of secondary structure by choices between possible third bases might also affect coding strategy… Unfortunately, progress has been slow in determining mRNA conformation in the cell experimentally,” “third base choice could regulate the expression of mRNA at the translation level”, and that “the picture is increasingly one of manifold constraints and adaptations, of both structural and functional natures.” More than 30 years later, we could not be more in agreement with Grantham’s observations.

Recently, I learned that the classic circular representation of the genetic code is also called, since at least 1995, “the rising sun” (“el sol naciente” in Spanish, as seen in Luque-Cabrera, 2001); the co-author of this beautiful circular genetic code design calls it the code sun (Hausmann, 2002, or even earlier).

Conclusions and Outlook

This article demonstrates that it was possible the ‘translation’ from the conventional or classic rotating circular genetic code (Castro-Chavez, 2010) to the 64-grid new representation of the genetic code. By using ‘quantic’ ways of thinking we may be able to reach faster heuristic solutions impossible to be obtained otherwise.

The third nucleotide position of the codons may be more important than previously imagined, as demonstrated by the radically different preferences exhibited by humans when compared to A. thaliana.

The codon usage preferences per amino acid are leading us to at least two hypotheses, the possibility of: 1) a slower translation in vertebrates, contrasted to 2) a faster translation in invertebrates due possibly to the aqueous environments where these invertebrates live (squid, octopus), or are indwelled with (plants).

By studying the codon usage preferences per amino acid we may be able to easily determine the closest compatible genomes, which was one of the earliest attempts done by Grantham with his “genome hypothesis” (1980), as well as to compare these preferences with the ones of individual proteins within the same organism, to learn about the structural and functional third dimensional aspects of their mRNA, and its transport and translation within different cells and organisms.

The 64-grid representation is used here for the first time as a rotating image of the classic rotating circular genetic code, a quantic model to represent the 64-codon genetic code. This is different to the classic square representation of the genetic code (Khorana, 1965), which, as demonstrated elsewhere, falls short providing molecular information (Castro-Chavez, 2010).

By the use of this 64-grid representation, similar advantages to the ones reported elsewhere for the circular genetic code can be achieved, to evaluate compatible variation in nature, and for the early detection of hereditary genetic diseases (Castro-Chavez, 2010; 2011). A slight improvement over the invariable conventional circular genetic code was introduced here in this 64-grid representation, which is the ‘quantic’ concept of mobility within quadrants for equivalent codons, and maybe among quadrants by the codons for the same amino acids, an aspect in need of further study to experimentally define the relative mobility within less used or secondary codons, in function of the fixed primary or most used codon per amino acid.

The next step will be to design a precise, still elusive, 3D representation of the genetic code (my first working article is: "The Tetrahedron of 16x4 equilateral triangular grids is the minimal third dimensional representation of the 64 triplets present in the genetic code"). The same features applied to the first and original human language (the so-called “mother tongue”), can also be found in the genetic code. Somebody wrote: “language is an engineered miracle” (Mozeson, 2011), and, as we have seen, the same can be said about the genetic code. By studying the codon usage preferences per amino acid we may be able to determine the genomic compatibilities, and to compare them to individual mRNAs, to learn about their structural and functional third dimensional aspects, and about their 3D transport and translation within cells and organisms. The global codon usage per organism may be compared to the particular, or individual, codon usage per protein within the same organism to learn about the preferred environments for those proteins.

The 64-grid genetic code can also be made to rotate clockwise, either by the use of cords as indicated above, by putting at its center a pin with a fixed outer reference pointing towards the start codon (Met AUG), or by adding a virtual, size-adjusting clock’s arm or, even better, a trail-less cell-walking dot (i.e., Rajeevan, 2011).

In this number of NeuroQuantology, Negadi takes a “quantum-like” approach to find relational patterns in the number of atoms and nucleons within codons, their amino acids and precursors, as well as their water-interactions and the symmetrical importance of serine (Negadi, 2011); these studies, added to my upcoming research on the reciprocal folding(Castro-Chavez, 2011c) of complementary codons within the 64-grid genetic code, will certainly inject novelty to future strategies for better ‘information-rich’ comparisons of genes and sequences in bioinformatics (my second working article is: "The three binary annealing representations of the genetic code as seen in the primeval I Ching of Fu-Xi and the directionality of its resulting Yin/Yang components").

My studies on the genetic code are aimed at the design of computational tools to compare human genomes, and to determine the exchangeability between compatible codons and amino acids to generate, to preserve, and/or to retrieve extinct biodiversity, and for the early detection of incompatible changes that are leading to genetic diseases, while using the genetic code itself as the best engine of choice to compare compatible sequences.

Appendix A1

The two rotating models of the genetic code, for you to make them rotate without words, only with colors:

Appendix A2

The novel 64-grid representation introduced in this article.