Nonlinear structured-illumination microscopy with a photoswitchable protein reveals cellular structures at 50-nm resolution

Abstract

Using ultralow light intensities that are well suited for investigating biological samples, we demonstrate whole-cell superresolution imaging by nonlinear structured-illumination microscopy. Structured-illumination microscopy can increase the spatial resolution of a wide-field light microscope by a factor of two, with greater resolution extension possible if the emission rate of the sample responds nonlinearly to the illumination intensity. Saturating the fluorophore excited state is one such nonlinear response, and a realization of this idea, saturated structured-illumination microscopy, has achieved approximately 50-nm resolution on dye-filled polystyrene beads. Unfortunately, because saturation requires extremely high light intensities that are likely to accelerate photobleaching and damage even fixed tissue, this implementation is of limited use for studying biological samples. Here, reversible photoswitching of a fluorescent protein provides the required nonlinearity at light intensities six orders of magnitude lower than those needed for saturation. We experimentally demonstrate approximately 40-nm resolution on purified microtubules labeled with the fluorescent photoswitchable protein Dronpa, and we visualize cellular structures by imaging the mammalian nuclear pore and actin cytoskeleton. As a result, nonlinear structured-illumination microscopy is now a biologically compatible superresolution imaging method.

Recent years have seen many advances in fluorescence light microscopy, and it has become clear that diffraction—once thought of as an insurmountable physical limit—is no longer the barrier to obtaining high-resolution information on a biological specimen. Several methods are now capable of resolving structures well below the classical Abbe diffraction limit, which states that the resolution of a microscope is limited to about half the wavelength of light. Each of these subdiffraction methods can be traced to one of two ideas: localizing individual fluorophores in the sample to subdiffraction precision, or structuring the illumination light to yield small, subdiffraction regions of fluorophores in the emitting or nonemitting state. Localization-based techniques like PALM, STORM, and others (1–6) need thousands to tens of thousands of raw images to achieve the best resolution, whereas light-structuring techniques like stimulated-emission depletion (STED) (7) and saturated structured-illumination microscopy (SSIM) (8) typically use extremely high light intensities from either a focused laser beam or an illumination pattern in wide field, respectively, to generate a high-resolution image. These and other requirements impose unfortunate practical limitations that prevent subdiffraction imaging from taking full advantage of the benefits that light microscopy has to offer. Namely, fluorescence microscopy excels at studying biological samples because it can be minimally invasive, acquire data rapidly, and target molecules of interest with specific labeling strategies. Consequently, there is a need to continue to advance subdiffraction—or superresolution—microscopy such that it realizes ultrahigh resolutions while retaining those qualities of a light microscope that make it an invaluable resource for cell biology. In this article, we present a biologically compatible superresolution method based on structured illumination with a reversibly photoswitchable protein; our technique uses 10- to 1,000-fold fewer images than localization-based techniques, and many orders of magnitude lower light intensities than other light-structuring techniques.

The first set of techniques introduced above treats the sample as a collection of individual fluorophores. Various implementations of this localization-based idea—PALM (1), STORM (2), F-PALM (3), and others (4–6)—have achieved resolution down to 10–20 nm by relying on the precision to which a light distribution from a single molecule can be mathematically determined. An image is reconstructed by combining hundreds to tens of thousands of raw frames, each containing only a few single molecules. There is a fundamental trade-off between resolution and quantity of images, and, although there have been published reports on slowly moving, living samples (9, 10), ultimately, such high numbers of raw images limit the speed at which data can be taken and, by consequence, the temporal resolution that can be achieved.

The method presented in this article is an example of the second set of techniques introduced above. In general, these methods treat the sample as a continuous fluorescent object and gather high-resolution data about that object by structuring the incoming illumination light (11). This can be done in either a scanning configuration as in confocal microscopy or in a wide-field configuration as in linear structured-illumination microscopy (SIM). By choosing an appropriately small pinhole in confocal microscopy (12), or an appropriately fine line spacing in linear SIM (13), structures at roughly √2 or 2 times the conventional diffraction limit can be resolved, respectively. However, in their most basic form (i.e., under conditions of linear fluorescence), these methods are still fundamentally diffraction-limited because the same physical laws that govern the resolution of the detected structure also determine the resolution of the illumination pattern.

If appropriate nonlinear fluorescence phenomena are introduced, then an effective illumination pattern can be generated that is of theoretically unlimited resolution (8, 14). This idea applies to a point-scanning configuration called STED microscopy and has shown resolution down to 5.8 nm on nonbiological structures by using a donut-shaped beam tuned to stimulate the emission from excited fluorophores and decrease the effective focal spot of a laser beam (15). Because of the low cross-section for stimulated emission, such high resolution requires extreme peak intensities from the depletion laser—on the order of GW/cm². High peak light intensities are known to accelerate the photobleaching of fluorescent molecules (16), and fluorescent proteins may be especially sensitive to this phenomenon (17). Despite this, STED has reached 50- to 70-nm resolution using fluorescent proteins depleted with more modest, yet still high, peak intensities of approximately 400–800 MW/cm² (18, 19). Similarly, SSIM, an implementation of nonlinear SIM (NL-SIM), has achieved a resolution of approximately 50 nm in a wide-field configuration on dye-filled polystyrene beads by exploiting saturation of the excited state of a molecule (8, 14). Although the peak intensities of approximately 10 MW/cm² used for saturation were a few orders of magnitude lower than those required for stimulated emission, to our knowledge there have been no published results of improved resolution by SSIM of biological structures due to the poor photostability of most fluorescent molecules under such excitation intensities.

Photoswitching is an inherently nonlinear process and has been proposed as an alternative to saturation or stimulated emission for resolution enhancement purposes because of the genetically encoded photoswitchable molecules (20, 21) available, and the low light intensity needed to switch the molecules. In general, photoswitchable fluorescent molecules can be reversibly switched between two spectrally distinct states using light; saturating either of these population states results in a nonlinear relationship between the fluorescence emission and the illumination intensity. This method has been implemented on purified protein adsorbed to nonbiological structures and protein-filled bacteria in one dimension with a wide-field configuration (22, 23) or in two dimensions with a point-scanning, donut-mode configuration (24), but, to our knowledge, has never demonstrated improved resolution of cellular structures.

Here, we use the photoswitchable fluorescent protein Dronpa (21) to generate a nonlinear response from the sample using light intensities on the order of 1–10 W/cm². Taking 63 raw images with a wide-field total internal reflection fluorescence (TIRF) structured-illumination setup, we resolve information in two dimensions at four times the conventional diffraction limit. To verify the enhanced resolution we look at purified microtubules labeled with Dronpa, the nuclear pore complex in purified mammalian nuclei, and the actin cytoskeleton in fixed mammalian cells.

Method Concept

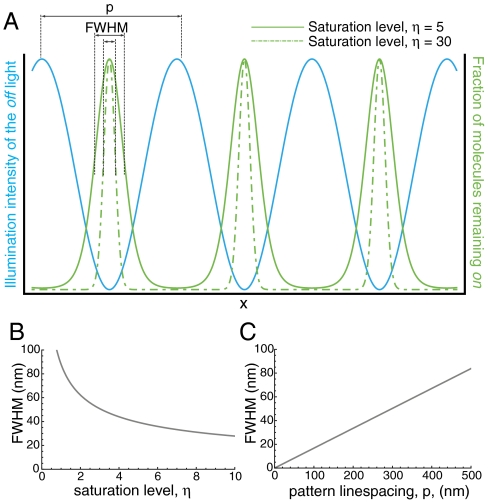
Dronpa can be reversibly switched between a fluorescent on state with an excitation peak at 503 nm and a nonfluorescent off state with an absorption peak at 390 nm using light (21). In principle, either of these states can be saturated, producing a nonlinear relationship between the illumination intensity and the fluorescence emission from the sample. Saturating the off state should result in cleaner minima of the illumination pattern leading to higher signal-to-noise ratio of the higher-order harmonics (22); for this reason we have chosen to saturate the off state. Dronpa decays to its dark state under blue-light (488-nm) illumination with a characteristic timescale, τ_off, dependent on the illumination intensity of the light (Fig. S1). We define the “saturation level” η, as the ratio of the exposure time to τ_off. If the sample is illuminated with a sinusoidal pattern of light that drives the molecules to their off state, only molecules at the minima of the pattern will remain on (Fig. 1A; SI Discussion). As the exposure time and, by consequence, η, increases, the region of molecules left on will become more confined, its size far smaller than the conventional diffraction limit (Fig. 1B). Importantly, the final NL-SIM resolution is not only a function of this saturation factor but also of this pattern line spacing (Fig. 1C).

Fig. 1.

Real-space representation. (A) Spatially patterned off light (blue) is used to drive the molecules to the off state. In a small region surrounding the zeros of this pattern, a fraction of the molecules will remain in the on state (green). At high saturation level (dashed green) only those molecules that fall directly in the zero of the pattern will remain fluorescent. This region can be approximated as a Gaussian with a FWHM, which depends on both the saturation level (B) and the line spacing of the pattern (C). At high saturation levels and fine line spacings of the pattern, the FWHM of these peaks, and consequently the resolution of the microscope, can be much higher than conventional diffraction-limited resolution.

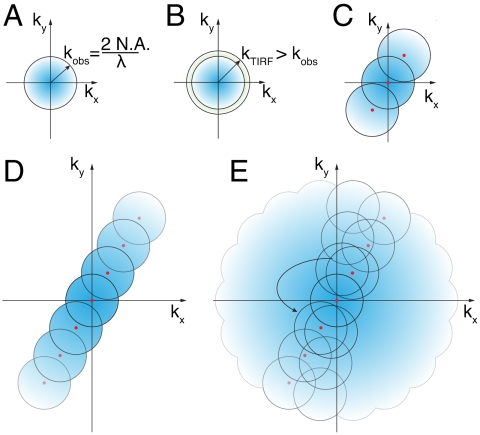
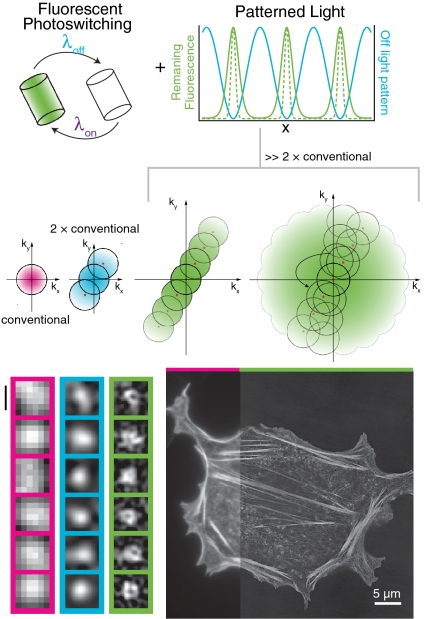
This process alone does not affect the resolution of the microscope because the collected fluorescence will be blurred by diffraction; additional processing must be done to reconstruct a high-resolution image. As in our earlier studies (8, 13, 25–27), we have chosen to reconstruct the data in frequency space. In frequency space, the resolution of a microscope is represented by the support, or the nonzero region, of the optical transfer function (OTF) (Fig. 2A). The radius of the OTF support (i.e., the highest spatial frequency at which the OTF reaches zero) is a function of the wavelength of detected light, and the numerical aperture (N.A.) of the objective. In general, the illumination OTF support can be slightly larger than the detection OTF support because of the shorter excitation wavelength used in fluorescence microscopy (due to the Stokes shift), but this is especially true in objective-style TIRF microscopy: The detection OTF can fall to zero within the N.A. required to produce TIRF (Fig. 2B and Fig. S2). In two-dimensional SIM, the sample is illuminated by a sinusoidally varying pattern of light with a spatial frequency at the edges of the illumination OTF support (13) (Fig. 2C). This spatial frequency mixes with the underlying spatial frequencies in the sample, some of which fall outside the normal OTF support, and moves this information into the conventional detection OTF support in the form of moiré fringes. Linear SIM requires that at least three different images are collected at different phases of the illumination pattern so that the information can be properly unmixed. In NL-SIM, the effective illumination pattern, as represented by the green curve in Fig. 1A, contains more than one spatial frequency. In fact, if the nonlinear phenomenon used is nonpolynomial, like photoswitching, then the effective illumination pattern theoretically contains an infinite number of higher-order harmonics with spatial frequencies that are integer multiples of the fundamental illumination spatial frequency (8). Consequently, the final NL-SIM resolution depends linearly on the spatial frequency of the illumination pattern as described in Fig. 1C; for this reason, we chose an illumination pattern with a spatial frequency close to the resolution limit itself. Likewise, although the number of higher-order harmonics, and by consequence the number of contributing information components, is in principle infinite, there will only be a finite number that are detectable above the noise. The saturation level affects the number of these detectable higher-order harmonics and this in turn determines the final NL-SIM resolution (Fig. 2D and Fig. S3A). To unmix the high-resolution sample information that these higher-order harmonics shift into the conventional OTF support, more images must be taken at finer phase steps as compared to linear SIM. The number of contributing higher-order information components that need to be separated establishes the number of images needed in each pattern orientation (Fig. S3A), and the one-dimensional pattern can be rotated in a sufficient number of orientations to achieve nearly isotropic resolution enhancement in two dimensions (Fig. 2E and Fig. S3 B and C). Moreover, when using photoswitching, each image corresponds to a photoswitching cycle, and thus a photoswitchable molecule able to withstand multiple rounds of cycling before photobleaching is needed.

Fig. 2.

Frequency-space representation. The reconstruction of the data was done in frequency space. (A) The support, or nonzero region, of the OTF is a frequency-space-based representation of the resolution limit of a microscope. In a conventional microscope, the radius of the OTF support is the inverse of the Abbe diffraction limit. (B) Using TIRF illumination, the spatial frequency of the excitation pattern can be slightly outside the detection OTF support. (C) In linear SIM, the illumination pattern has a single spatial frequency, in addition to the DC component at the origin (red dots), which mixes with frequencies in the sample itself, some of which are too fine to resolve normally. The sample information centered at the nonzero spatial frequency of the illumination pattern is shifted into the OTF support where it can be resolved by the microscope. When reconstructed, this high-resolution sample information is shifted back to its proper place in frequency space and the resolution becomes approximately twice that of a conventional microscope. (D) In NL-SIM, the effective illumination pattern contains spatial frequencies that are integer multiples of the illumination pattern. Similar to linear SIM, these mix with the underlying sample information and when reconstructed can extend the resolution even further. (E) By rotating the one-dimensional pattern, the entire two-dimensional space can be sampled.

Results

Dronpa.

The photophysical properties of Dronpa were evaluated to determine its suitability as a photoswitchable molecule for our purposes. Two parameters were tested: the emission intensity of Dronpa in its on state as compared to the intensity in its off state, and the overall photobleaching rate of the molecules. The first parameter affects the signal-to-noise ratio of the higher-order harmonics: Higher fluorescence background in the off state increases the contribution of the conventional component to the NL-SIM image, which in turn lowers the relative contribution of the higher-order harmonics (Fig. S4). The second parameter determines how many images can be taken without a significant loss in fluorescence signal.

Dronpa was illuminated with 488-nm laser light, which both excites the molecule to fluoresce and drives the transition from the on to the off state (21). The off to on state transition was driven with 405-nm laser light. The emission fluorescence intensity of the on state was found to be roughly 50 times greater than that of the off state at η = 5 (Fig. S1C). Although Dronpa molecules are efficiently driven to their reversible dark state with 488-nm light, there is a nonzero probability of the molecules being driven to an irreversible dark state (28). After each round of cycling, fewer molecules can be converted to their fluorescent state, contributing to an overall photobleaching rate of the sample. This rate was determined for Dronpa molecules in buffer at pH 6.9, and it was observed that after roughly 15 cycles the fluorescence dropped to 1/e of the initial value (Fig. S1 B and C). We were able to increase the number of switching cycles before photobleaching in two ways. First, a known antifade reagent—p-phenylenediamine (PPD)—was added to the sample (Fig. S1 B and C). Second, the intensity of the laser was decreased while simultaneously increasing the exposure time, so that the dose of photons (defined as the illumination intensity multiplied by exposure time) remained constant (Fig. S1B). This was seen to have a dramatic effect on the photobleaching rate of the molecules. With the addition of 5 mM PPD under an illumination light intensity of 5 W/cm², we observed Dronpa switch 60–70 times. Although this number of switching cycles would not allow us to extend our technique to three dimensions as has been done for linear SIM (25, 26), and could be potentially improved with a more exhaustive search for an optimal mounting condition, it was sufficient for resolution enhancement in two dimensions. Subsequently, we decided to implement our technique in TIRF. With TIRF microscopy we were able to use our inherently wide-field technique to enhance the resolution in two dimensions over large fields of view.

Resolution Test.

Microtubules conjugated to Dronpa by a biotin-streptavidin interaction were used as a resolution test (Movie S1). Unlabeled microtubules are 25 nm in diameter; biotin-PEG4 has a length of 2.9 nm; streptavidin tetramers are reported to have dimensions of 5.4 × 5.8 × 4.8 nm (29); Dronpa itself has a similar fold to GFP, which has dimensions 2.4 × 4.2 nm (30, 31). Therefore, we estimate that coated tubules will have diameters no larger than 50 nm, which is equal to or smaller than the resolution we expect given the number of photoswitching cycles we were able to obtain from Dronpa. The linear microtubules display a strong feature in frequency space, which provided us a metric by which to determine if we were indeed able to detect superresolution information centered around the spatial frequencies of the higher-order harmonics.

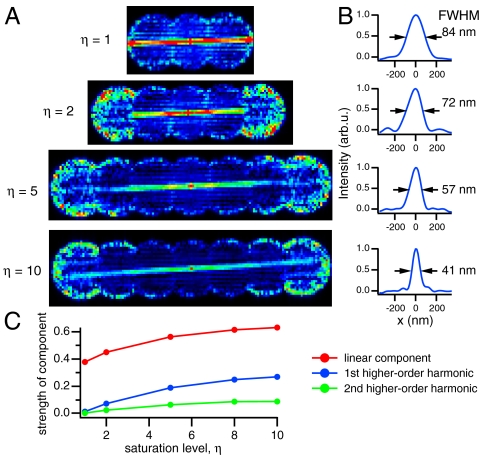
We first wanted to verify the dependence of resolution on saturation level. To this end, we took four structured-illumination datasets on the same region of Dronpa-coated microtubules, each with seven phases in one dimension. We increased the saturation level in each subsequent dataset, from η = 1 to η = 10, by increasing the time used to drive the molecules to the off state. Taking the Fourier transform of a region containing an isolated microtubule, which happened to align nearly perpendicular to the pattern vector, we saw the feature in frequency space become more prominent in the higher orders as the saturation level increased (Fig. 3A). In real space, this corresponds to a full width at half maximum (FWHM) through the microtubule from 84 nm with a saturation level of 1 (approximating linear structured illumination) to 41 nm with a saturation level of 10 and two higher-order harmonics (Fig. 3B). By comparing the individual orders in the region of frequency space where they overlap, we determined the strength of each information component, compared to the conventional component, as a function of saturation level. As we expected, the strengths of each component increased with saturation level (Fig. 3C).

Fig. 3.

Saturation versus resolution. To understand how the saturation level, η, affected the resolution of the system, we took four datasets each comprising seven phases along one pattern orientation on the same region of microtubules. In each subsequent dataset, we increased the saturation level by increasing the time used to drive the molecules to the off state. (A) Fourier transforming an isolated microtubule, which happened to align perpendicular to the pattern vector, we see the feature in frequency space appear in the higher-order information components as the saturation level is increased. The feature is most clearly visible in the highest order at η = 10. (B) By taking line profiles through the microtubule, we find that the resolution is enhanced from 84 nm with η = 1 (simulating linear SIM) to 41 nm with η = 10. (C) By comparing the orders in the region of frequency space where they overlap, we were able to determine the strength of the higher orders compared to the conventional component.

We next imaged the microtubules with our nonlinear structured-illumination microscope in two dimensions using η = 10, subsequently processed the data, and Fourier transformed the result. As we expected, the signal-to-noise ratio of the features in frequency space, which represent coated microtubules not much smaller than the predicted resolution, decreased in each subsequent higher-order information component. Nevertheless, we detected features in frequency space that extended into the second higher-order information component in multiple orientations of the pattern (Fig. 4). Averaging line profiles of 10 microtubules, we measured a resolution of 42 nm (Fig. 4C), or four times the resolution of a conventional microscope. Interestingly, because there were a few sparse single Dronpa molecules in the background, these samples were useful for understanding how the stochastic nature of these single molecules affected our images. The binary on → off transition of single molecules is a highly nonlinear process, yet the stochasticity of this process means that the molecules will not be reliably on or reliably off during imaging. In a few directions the single molecules are very narrow, whereas in other directions the molecules appear much broader, giving them a “streak”-like appearance (Fig. S5). This effect can also be seen on the microtubules themselves at the highest resolution because there are fewer Dronpa molecules per pixel as the resolution improves and the pixel area decreases. To understand how this stochasticity affected the reproducibility of our images, we took NL-SIM datasets in which we repeated the phase series for each orientation of the pattern (η = 5; five phases; seven orientations). After acquisition we separated the interleaved datasets and processed each set individually. To simulate low and high labeling densities, we did this experiment on microtubules coated with 0.2 mg/mL streptavidin (Fig. S6 A–F) and 1 mg/mL streptavidin, respectively (Fig. S6 G–L). As expected, at low labeling densities the effect of the stochastic single molecules was more apparent than at high densities. However, at low labeling density this phenomenon was slightly mitigated by processing the data using the images resulting from the off exposure in addition to the on exposure images as described in the Materials and Methods (Fig. S6 D–F); this processing step seemed to have little to no effect on the final processed image at high labeling densities (Fig. S6 J–L). Although this phenomenon does not affect the overall resolution of the microtubules, which are well labeled along their width and thus the direction of the resolution enhancement we measured, it does contribute to the qualitative nature of the images and should be taken into account when interpreting nonlinear structured-illumination data.

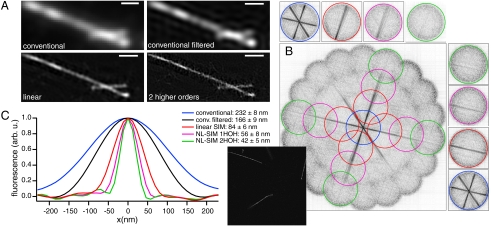
Fig. 4.

Comparison of conventional TIRF, linear SIM-TIRF, and NL-SIM-TIRF. (A) Two Dronpa-coated microtubules imaged by conventional TIRF, conventional filtered TIRF, linear SIM-TIRF, and NL-SIM-TIRF with two higher-order harmonics. Scale bar, 500 nm. (B) Fourier transforming a different subset of the data (Inset) reveals strong features in frequency space. Two microtubules display features that are visible in the second higher-order information component, which is most obvious when the orders are separted above and to the right. The contrast in B was inverted for clarity. (C) Line profiles were taken through 10 microtubules and subsequently aligned and averaged. The filtered conventional image and associated profile were generated by processing the data and then discarding all orders except for the conventional component and as such represents the conventional Wiener filtered data. As expected, the final resolution of the NL-SIM data with two additional higher-order harmonics (2HOH) is 4 times that of conventional microscopy, or 42 nm.

Biological Structures in Cells.

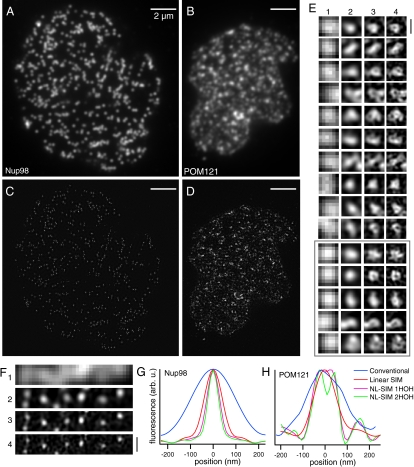
We next looked at the nuclear pore complex in human HEK293 cells transiently transfected with a nuclear pore protein—either Nup98 (32) or POM121 (33)—genetically fused to Dronpa. The nuclei were purified to ensure that the nuclear membrane resided in the TIRF zone. They were fixed in 2% paraformaldehyde (PFA), adsorbed to a poly-lysine coated coverslip, mounted in PPD, and imaged with 5 W/cm² of 488-nm light and saturated by a factor of η = 8–10. The localization patterns of the two proteins were strikingly different especially as the resolution increased (Fig. 5 E and F). Nup98, which is known to associate with both the nucleoplasmic and cytoplasmic side of the pore (34), was found in tightly localized spots with an average FWHM of 55 nm (Fig. 5 A, C, F, and G). In contrast, POM121, an integral membrane protein, displayed a wide range of structures, many of them resembling rings with a diameter of 40–70 nm (Fig. 5 B, D, E, and H and Fig. S7). These observations are consistent with the locations of the yeast homologues of these proteins in the yeast nuclear pore complex (35).

Fig. 5.

Nuclear pores in a mammalian nucleus. Human HEK293 cells were transiently transfected with either (A and C) Dronpa-Nup98 or with (B and D) POM121-Dronpa, both of which are associated with the nuclear pore complex. We extracted the nuclei to ensure that the nuclear membranes resided in the TIRF zone. Entire nuclei were imaged by (A and B) conventional TIRF microscopy and (C and D) by NL-SIM-TIRF microscopy using two additional higher-order harmonics (HOH). (E and F) The two proteins showed different localization patterns, which was especially apparent at the highest resolution in enlarged subsets of the data: (1) conventional, (2) linear-SIM, (3) NL-SIM with 1 HOH, and (4) NL-SIM with 2 HOH. (F) Dronpa-Nup98 localized to small uniform punctae, whereas (E) POM121-Dronpa, an integral membrane protein, showed a variety of different structures, many of which resemble rings with an inner diameter between 40–70 nm. We repeated these observations in another nucleus on the same coverslip (gray box and Fig. S7). (G) The average FWHM of 90 nuclear pores in the Dronpa-Nup98 expressing cells decreased from 223 ± 12 nm using conventional microscopy (blue) to 55 ± 8 nm using NL-SIM-TIRF with 2HOH (green). (H) Simply taking a line profile through one nuclear pore in the POM121-Dronpa expressing cells confirms that a ring structure is only resolved using NL-SIM. Scale bars, 2 μm (A–D) and 200 nm (E–F).

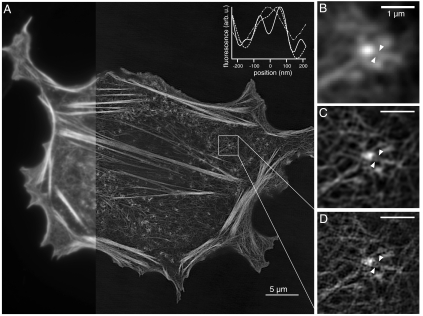
In order to verify that our technique works on more complicated structures, we next imaged the actin cytoskeleton in mammalian cells expressing the Lifeact peptide (36) genetically fused to Dronpa (Fig. 6). The cells were fixed in 1% PFA, mounted in PPD, illuminated by 5 W/cm² of 488-nm light and saturated by a factor of 10. We detected and reconstructed one higher-order harmonic corresponding to a resolution of approximately 60 nm over a field of view that is roughly the size of an entire mammalian cell (Fig 6A). Enlarging a subset of the data revealed a closely packed network of f-actin bundles, the structure of which is most clearly resolved with nonlinear structured illumination (Fig. 6 B–D and Inset).

Fig. 6.

Dronpa–Lifeact in a mammalian CHO cell imaged with NL-SIM. (A) Because SIM is a wide-field technique, high-resolution data over a large field of view is possible. On the left, a portion of the entire image is shown with conventional microscopy. The image is displayed using a nonlinear intensity scale (gamma = 0.65) to highlight the small filaments in the background over the thick and bright stress fibers. A subset of the data is enlarged and shown with (B) conventional TIRF microscopy, (C) linear SIM-TIRF, and (D) nonlinear SIM-TIRF. Lifeact marks the actin network, the structure of which is most clearly resolved with nonlinear SIM-TIRF as demonstrated by the normalized intensity profiles (Inset) taken between the white triangles in B–D). Two filaments are clearly resolved with NL-SIM (solid), but are not resolved with either conventional microscopy (dot dashed) or linear SIM (dashed). Scale bars, 5 μm (A) and 1 μm (B–D).

Discussion

We have used a photoswitchable protein to enhance the resolution of biological structures at extremely low light intensities using NL-SIM. In the future, NL-SIM should be a capable technique for addressing a wide range of fundamental biological questions. For example, the nuclear pore is a highly conserved and complex macromolecular structure consisting of at least 400 individual protein molecules (37). The most detailed knowledge of the yeast nuclear pore complex has been gained through a set of groundbreaking, yet technically challenging, studies using both experimental and computational techniques (35, 38). NL-SIM, on the other hand, may be able to provide knowledge of this protein structure simply using light microscopy and all the benefits it affords—genetically targetable probes, multiple colors, etc. Likewise, there is much we do not understand about the actin cytoskeleton and all its molecular components. A superresolution light microscope capable of rapid live-cell imaging—like NL-SIM could be with further technical developments—may prove critical for visualizing the actin network’s various structures and dynamics with the spatial and temporal resolution such a biological system demands (39).

We consider the processing method used in this paper to be advantageous over similar methods (22, 23). The processing algorithm described in ref. 23 requires that the illumination pattern be easily resolvable—i.e., the spatial frequency of the pattern must fall well within the support of the conventional OTF—a requirement that our algorithm does not impose. Such a requirement means that the spatial frequency of the pattern used in ref. 23 was ∼0.4 k_max, where k_max is the highest detectable spatial frequency. In this article, we used a spatial frequency k₀ that lies on the very edges of the illumination OTF support and falls outside the support of the detection OTF (i.e., k₀ > k_max) rendering it irresolvable in the fluorescence image. Even at this high spatial frequency, however, our coherent and s-polarized illumination source produced a pattern with almost perfect modulation contrast (95–96.5%). Such an illumination pattern does not sacrifice the signal strength of the high-resolution information present in the raw data. Our algorithm was designed to (I) unmix this raw data into information components representing different regions of frequency space, (ii) estimate the contribution of each component, and (iii) reassemble them in their proper frequency-space locations. This processing method allowed us to take advantage of an illumination pattern with the highest possible diffraction-limited line spacing. As described in Fig. 1C, the resolution of the microscope is linearly proportional to the line spacing of the pattern (1/k). In this way, given the same saturation level, structured-illumination methods used in this article allowed for an improvement in resolution by a factor of approximately 1/0.4, or approximately 2.5 over methods used in ref 23; or, equivalently, for the same resolution, the methods we describe require approximately 2.5 fewer images and less saturation.

Although we have demonstrated NL-SIM is possible in fixed mammalian cells, in general, SIM is well suited for live-cell superresolution imaging (27) because significantly fewer images are needed to reconstruct a high-resolution image than are needed for localization-based methods. Furthermore, SIM’s wide-field nature permits data on large fields of view, without a significant cost in acquisition time, in contrast to scanning methods, for which acquisition time is proportional to the scanned area. What obstacles must be overcome for live-cell NL-SIM? The most obvious is motion blur. This concern is the same for all microscopy: To prevent motion blurring, the acquisition time for a single time point must be short enough such that the sample moves less than an amount close to the final resolution. For superresolution techniques, the acquisition time requirements become more stringent because the resolution length scale is much smaller, underscoring the need for development of both faster hardware and more photostable photoswitchable probes. To address the former concern, in recent years we and others (27, 40) have developed methods for electronic pattern generation based on spatial light modulators. As yet, this technology has been used only for live-cell linear SIM, but similar technology could be applied toward live-cell NL-SIM. Therefore, for live-cell NL-SIM to be feasible the most needed development is that of a better photoswitchable probe.

In principle, any nonlinear phenomenon can be used for resolution enhancement; however, in practice, we believe photoswitching to be the most applicable for biological imaging because photoswitchable molecules typically need low light intensities—a crucial requirement for live-cell microscopy. We were initially encouraged by published reports of high numbers of switching cycles on single Dronpa proteins (41), but ultimately we were unable to obtain such high numbers of cycles in ensemble without the addition of toxic antibleaching chemicals and long exposure times that drastically increased the total acquisition time. For live-cell NL-SIM to be possible, another, more photostable, photoswitchable protein must be developed. We note that this has been possible for other proteins—notably, EosFP was engineered to be a better probe for PALM (42). Our requirements are different than those of the localization microscopies, however. First, localization microscopies favor photoactivatable proteins that emit all their photons in a single activation step; our technique needs photoswitchable molecules that are able to emit their photon budgets over 50 to a few hundred cycles (depending on the desired resolution and dimension), without a significant decrease in photon output. Second, localization microscopies typically need probes with very high contrast ratios of thousands or tens of thousands to detect signals from the activated single molecules, whereas NL-SIM may be able to tolerate contrast ratios of 50–100, depending on the resolution desired. Another option is to employ small-molecule organic dyes or dye pairs that STORM and similar techniques use and that have been shown to switch hundreds of times as single molecules or pairs of molecules (2). But, like the photoswitchable proteins, how they behave in ensemble remains to be fully explored. Furthermore, to photoswitch, many of these dyes or dye pairs require oxygen scavengers and thiol-containing compounds and higher light intensities that may be incompatible with live-cell imaging. Nevertheless, small-molecule organic dyes may be useful now for NL-SIM imaging on fixed tissue, and with further development could prove very useful for detecting proteins in living samples.

With technological advances in fast pattern generation and a photoswitchable probe that is able to tolerate short exposure times, a 60-nm resolution full-frame NL-SIM image consisting of 25 raw-data exposures could be acquired on a timescale faster than other superresolution techniques. For example, mEos2, a photoactivatable protein, has been able to withstand multiple PALM time points—each comprised of 1,500 40-ms raw-data exposures—resulting in a Nyquist-limited resolution of 60 nm (9). With a similarly photostable, photoswitchable protein, we see no technological reasons that NL-SIM could not take data at similar frame rates. This would allow for an improvement in time resolution by a factor proportional to the number of raw-data exposures. Moreover, NL-SIM’s wide-field nature may permit larger area or volume rates than a point-scanning method like live-cell STED, which has demonstrated a 62 nm resolution at 28 frames per second on a small region of 2.5 × 1.8 μm² (43).

Perhaps even more than live-cell imaging, NL-SIM could excel at studying three-dimensional structures. Linear SIM has been implemented in three dimensions, providing optical sectioning and doubling of the resolution in all three dimensions with one objective (25) or isotropic resolution in all three dimensions with two objectives (26). NL-SIM could be extended in similar ways, but the photostability requirements of the dyes dramatically increase. With such a probe, though, 3D NL-SIM represents a way for sub-100-nm resolution imaging of three-dimensional structures at volumes of cubic microns. Extending other superresolution techniques to three-dimensions is possible but is typically limited to thicknesses of less than a micron near the coverslip (44) or near the focal spot of a laser (45).

Although there is much room for improvement, we believe NL-SIM to be a powerful approach, among others, in the exciting new field of superresolution light microscopy. All superresolution techniques excel in certain aspects and fail in others—the best technique will be determined by the demands of the application. We believe NL-SIM to be best for those applications that require low light intensity and few exposures, at a resolution of approximately 40 nm in two dimensions with currently available photoswitchable fluorescent probes.

Materials and Methods

Microscope.

A custom SIM-TIRF microscope (Fig. S8) was built similar to those previously described (13, 25, 27). Both 405-nm and 488-nm continuous-wave laser light were directly coupled into one single mode, polarization-maintaining PC/APC fiber (Thorlabs P5-488PM-FC-2), using an achromatic lens (f = 10 mm). The output light was collimated and circularly polarized (Meadowlark AQ-050-0545) and then passed through a custom phase grating with a period of 33.5 μm that was translated and rotated to achieve the necessary pattern phases and orientations (8). The polarization of the light was linearized and corotated with the grating to maintain s-polarized light and maximum pattern contrast at each orientation as described in ref. 13. All diffraction orders except the +1 and -1 were blocked at a secondary pupil plane; these orders were focused at the edges of the back focal plane of a 100×, 1.46 N.A. Zeiss TIRF objective lens. Intermediate lens focal lengths were chosen to produce a maximum illumination N.A. of the two side orders of 1.46, resulting in a projected pattern period on the sample of 166 nm. To produce a consistent light intensity across the field of view—and thus a consistent saturation factor—we chose a collimation lens in front of the fiber such that the excitation light distribution dropped by approximately 20% at the edges of the field of view corresponding to the full CCD chip. The fluorescence was collected by the same objective, passed through a Zeiss 1× tube lens, separated by a custom dichroic setup described elsewhere (27), filtered using stacked emission filters (Semrock 525/40), and finally imaged onto a cooled back-illuminated 1,024 × 1,024 Andor iXon EMCCD running in conventional 16-bit mode. The 13-μm pixels on the camera mapped to 46-nm pixels in sample space. A metric for determining the optimal focus was designed by calculating the ratio (|S_HF|² - |S_var|²)/(|S_LF|² - |S_var|²), where S_HF is the high-frequency signal within the OTF support, S_LF is the low-frequency signal within the OTF support, and S_var is the variance of each as determined by measuring the noise outside of the OTF support. We created immersion oil from Cargille laser liquids with an index of refraction different than the one supplied with the Zeiss objective to optimize the 2D OTF. With the optimized immersion oil of 1.505, we observed that the detection OTF went to zero at an N.A. of 1.2–1.3 (Fig. S2).

To maintain optimal focus, we designed a custom sample stage. A single-ended capacitive sensor (Physik Instrumente part no. D-510) was mounted directly to the sample holder and in closed-loop with a piezoelectric stage (Physik Instrumente part no. P-611) that controlled the sample stage’s height above the objective. The axial position of the sensor was stable relative to a polished steel plate that directly mounted to a floating optical table. The microscope and sample stage were enclosed in a custom box to maximize thermal stability. Using this setup, minimal sample drift (< 50 nm) in the axial direction was observed for up to 45 min as determined by the focus metric described above.

Image Acquisition and Reconstruction.

Custom image acquisition software was written using LabVIEW. Each subimage was a result of three exposures: (i) First, the molecules were uniformly and completely turned on with 405-nm light; (ii) second, using a sinusoidal pattern of 488-nm light, the molecules were turned off to a given saturation level as described in Fig. 1A; (iii) third, the phase of the pattern was shifted by π to collect the fluorescence from the molecules remaining on. This process was repeated for a predetermined number of phases and orientations of the pattern. To account for phase errors resulting from lateral sample drift, online phase correction was done. Successive conventional images—generated from the sum of the images resulting from (ii) and (iii) above—within a phase series were cross-correlated to determine the amount of sample drift between them in the direction of the pattern vector. This calculated number was fed back to the diffraction grating, and the diffraction grating was translated to compensate the next image. Ideally, such an algorithm would generate equally spaced phases of the illumination pattern after drift correcting the raw images. However, in practice, because the estimated phase correction for an image was generated by comparing the two previous images, there may still have been residual phase errors if this correction did not accurately reflect the true sample drift for the image.

The data were processed and reconstructed similarly to previously described methods (8, 13). In brief, the images within a phase series (i.e., a pattern orientation) were drift corrected and registered. These images were Fourier transformed and separated into the 2N + 1 information components, where N is the number of orders, including the conventional component. Instead of assuming equal phase steps of 2π/(2N + 1), and thus accounting for any residual phase errors, the online drift estimation was compared with the postacquisition drift estimation; the differences between the two were used to modify the ideal matrix for separating the raw data. The separated conventional orders for each pattern orientation were cross-correlated, and the result was used to correct for any drift between orientations of the pattern. The starting phase, pattern vector, and modulation amplitudes of each information component were determined by comparing successive information components within each pattern orientation in the region of frequency space where they overlap. As described in ref. 8, we typically found it desirable to manually enter the modulation amplitudes empirically because the signal-to-noise ratio of the highest information components was often too low for an accurate computational determination; this was especially true at the orientations acquired last and thus of the lowest signal due to photobleaching. The different components were then combined through a generalized Weiner filter (25). Rather than being rotationally averaged as in our earlier studies, instead the measured OTF represented the true two-dimensional transfer function. To maintain high signal-to-noise ratio of the nonrotationally averaged 2D OTF, we averaged many isolated point sources (Invitrogen Yellow-Green 100-nm beads, catalog no. F8803) to obtain the final OTF used during processing. Finally, the enlarged, effective OTF support of the processed image was apodized at the edges to prevent ringing and Fourier transformed back to real space.

To detect two higher-order harmonics, we observed that 63 images—seven phases, nine orientations—were sufficient for nearly isotropic resolution in two dimensions isotropically. The final NL-SIM images on the purified microtubules took advantage of all 63 images. Under similar imaging conditions, we were unable to detect the second higher-order harmonic on the mammalian cells transfected with Dronpa–Lifeact. In this case, we simply discarded the second higher-order harmonic. In theory, only 25 images—five phases, five orientations—would be enough to detect one higher order in two dimensions. Moreover, the nuclear pore and Lifeact data taken on mammalian cells were processed in a slightly different manner. As mentioned above, each image processed by the reconstruction software is a result of three laser exposures. If imaging speed is of concern, only the last needs to be captured by the camera. However, to increase the signal-to-noise ratio of the higher-order harmonics, we chose to acquire the image resulting from the off exposure, (ii) above. Although most of the information contained in this exposure is the same information contained in the conventional and linear structured-illumination components, there is also a slight nonlinear component. We added this component in a noise optimal way to the nonlinear components that were separated from the data collected in (iii) above; that is, we combined the separated components through a weighted sum in which the weights were the inverse variance of the noise for each component.

The conventional images we have displayed in this article were generated by summing the images resulting from (ii) and (iii) above.

Sample Preparation and Light Intensity Calibration.

All other methods can be found in the SI Materials and Methods accompanying this manuscript.