Quantum coherence spectroscopy reveals complex dynamics in bacterial light-harvesting complex 2 (LH2)

Abstract

Light-harvesting antenna complexes transfer energy from sunlight to photosynthetic reaction centers where charge separation drives cellular metabolism. The process through which pigments transfer excitation energy involves a complex choreography of coherent and incoherent processes mediated by the surrounding protein and solvent environment. The recent discovery of coherent dynamics in photosynthetic light-harvesting antennae has motivated many theoretical models exploring effects of interference in energy transfer phenomena. In this work, we provide experimental evidence of long-lived quantum coherence between the spectrally separated B800 and B850 rings of the light-harvesting complex 2 (LH2) of purple bacteria. Spectrally resolved maps of the detuning, dephasing, and the amplitude of electronic coupling between excitons reveal that different relaxation pathways act in concert for optimal transfer efficiency. Furthermore, maps of the phase of the signal suggest that quantum mechanical interference between different energy transfer pathways may be important even at ambient temperature. Such interference at a product state has already been shown to enhance the quantum efficiency of transfer in theoretical models of closed loop systems such as LH2.

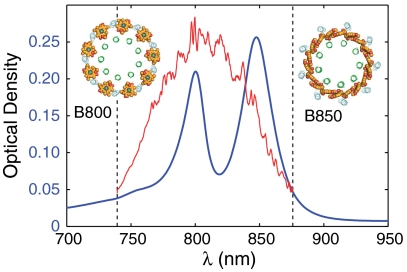
Light-harvesting complex 2 (LH2) is the peripheral antenna pigment-protein complex of purple non-sulfur bacteria. LH2 contains two rings of BChl a pigments known as the B800 and B850 rings according to their respective room-temperature absorption bands in the infrared region of the spectrum (Fig. 1). These pigments are held in place by noncovalent interactions with pairs of low-molecular weight apoproteins. In most bacterial species, the LH2 complex consists of eight or nine of these protein heterodimers (αβ) organized in a highly symmetric ring (1). LH2 increases the effective cross-section for photon absorption from the solar spectrum in the membrane of purple bacteria. The energy absorbed by LH2 passes to another light-harvesting complex (LH1) tightly associated with the photosynthetic reaction center (2), wherein a stable charge separated state forms that ultimately drives the production of ATP.

Fig. 1.

LH2 linear absorption spectrum at room temperature. B800 and B850 bands from the light-harvesting complex of the photosynthetic bacterium Rhodobacter sphaeroides at room temperature. Continuum-generated pulse spectrum is shown in red. Dashed lines correspond to limits of detection for the grating and CCD combination used in these experiments.

The energy transfer dynamics in LH2 has been studied for many years. Numerous time-resolved experiments have measured energy transfer from the B800 ring to the B850 ring in under a picosecond at room temperature (3–7). Förster resonance energy transfer (FRET) theory (8) estimates a slower transfer time by approximately a factor of five (9–13). Close examination of electronic coupling between pigments within each ring reveals, in part, the origin of this discrepancy. Studies on the excitation of the B850 ring (14–17) indicate the existence of Frenkel excitons (18, 19), delocalized excitations that persist across several pigment molecules depending on the degree of structural symmetry present. In one limiting case, excitation is delocalized across the entire ring, invalidating a fundamental assumption in FRET theory: that the distance between donor and acceptor is large with respect to their size. A large number of theoretical works have modified Förster theory to treat the multichromophoric nature of the pigments in LH2 (20–23). These works identify the importance of system–bath coupling in optimizing the transfer efficiency. Simply interpreted, the system–bath coupling modulates the spectral overlap of donor and acceptor states. Ambiguities in the source of spectral broadening arise because different types of disorder (e.g., diagonal and off-diagonal) are consistent with the experimentally determined spectra. In a recent work, Jang and Sibley (22) claim that the spectral position of the B800 and B850 bands is optimized for irreversible and rapid energy transfer. These theoretical works show the importance of quantum coherence within each of the two rings but ignore coherent coupling between the rings. While such effects could, in principle, be incorporated into the models, experimental evidence for such coherence has until now remained elusive. That several strikingly different models of energy transfer in LH2 can reproduce the transfer rate demonstrates the need for new experimental data to discern between the models.

In this work, we directly observe long-lived electronic coherence after femtosecond excitation between the B800 and B850 rings of LH2 at room temperature using single-shot two-dimensional electronic spectroscopy. We find that the strength of coupling between excitons on each ring shows strong correlation to its rate of decoherence. The phase relationship among the quantum-beating signals suggests that relaxation pathways between the rings in LH2 carry different phase. Taken together with the high symmetry of the complex, such phase patterns are indicative of a complicated mechanism that avoids destructive interference at the trap state—a quintessential quantum mechanical effect.

Results

We utilize a variant of two-dimensional photon echo spectroscopy (2D PES) to probe the electronic structure and dynamics of isolated LH2 complexes at room temperature. Two-dimensional PES spectrally resolves the third-order nonlinear system response originating from the multiple Feynman pathways that contribute to the echo signal (24–26). The spectra reveal both coherent and incoherent contributions to energy transfer dynamics. This spectroscopic tool has been used previously to discover and probe quantum coherence in photosynthetic complexes (27–30).

Probing LH2 demands more bandwidth than is available from rengeneratively amplified titanium sapphire (Ti:Saph) lasers. We therefore employ continuum generation in argon gas to gain sufficient bandwidth to excite and probe the B800 and B850 bands simultaneously. Arising from a highly nonlinear process, such white light continuum sources are inherently less stable than the Ti:Saph pump laser. This instability poses a challenging problem for traditional 2D electronic spectrometers. The shot-to-shot fluctuations introduce noise in the indirect domain, some of which survives Fourier filtering and contaminates the spectra. To circumvent this issue, we couple our continuum source to a single-shot version of 2D PES called gradient-assisted photon echo spectroscopy (GRAPES).

The single-shot nature of GRAPES permits integration of unstable light sources because each laser shot contributes to every point in the indirect domain. Details of GRAPES are described elsewhere (31–33). In short, GRAPES maps coherence time delays onto a spatial axis of the sample, resulting in a parallel acquisition of all coherence time delays at once. GRAPES therefore offers a speedup in acquisition time by two to three orders of magnitude while making the technique compatible with supercontinuum-generated white light excitation (32). This critical advantage of capturing the 2D spectrum in a single shot results in sufficient signal-to-noise ratio to permit observation of small amplitude beating signals.

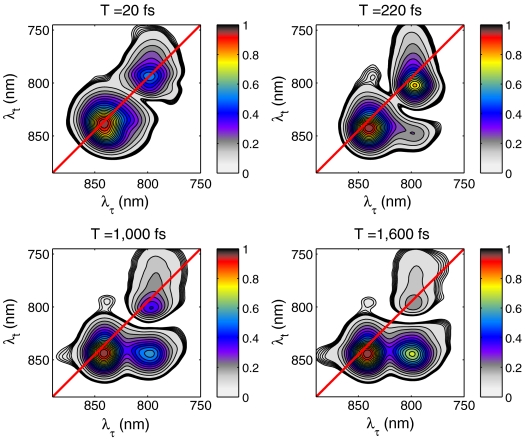
Two-dimensional rephasing spectra of LH2 showing the absolute value of the third-order nonlinear response at different waiting times (T) are shown in Fig. 2A. At all waiting times measured, the B800 and B850 bands are clearly visible along the diagonal of the spectra. At early times, features above and below the diagonal become visible, indicating coupling and energy transfer.

Fig. 2.

Two-dimensional power spectra of LH2 at select waiting times. The acquisition time for each spectrum is 200 ms and is displayed normalized to its highest peak value for ease of visualization. The contour lines are displayed in increments of 0.5% from 7.5% to 9.5% and in increments of 5% from 10% to 100% of the signal maximum for each waiting time. Only the absolute value of the 2D spectra is shown even though the complex third-order nonlinear signal is measured owing to ambiguity in the global phase term. This term does not affect the analysis because it is uniform across the 2D spectrum. From previous transient absorption measurements, the large tail of the 800-nm diagonal peak toward the blue edge of the spectrum arises from excited-state absorption. The deviation of the peak maximum near the diagonal of the spectrum is a result of an ultrafast Stokes shift due to solvent reorganization.

Examining first the dynamics evident in the lower cross-peak, we observe that, concomitant with the appearance of the cross-peak below the diagonal, the B800 band diminishes relative to the B850 band. This change in amplitude and emergence of the cross-peak indicates downhill energy transfer between the rings. The time scale of this relaxation is just less than one picosecond and is consistent with prior time-resolved measurements on energy transfer in LH2 at room temperature (see SI Text).

The dynamics of the cross-peak above the main diagonal are more complex and will be the primary focus of this study. The source of this cross-peak could be either incoherent (uphill) energy transfer or exciton delocalization. We first eliminate the possibility of incoherent energy transfer. While the Boltzmann distribution does allow for some uphill transfer for states split by > 3 kT, such a signal should show a rise on the picosecond time scale. No such growth is observed. We therefore conclude that the presence of the upper diagonal cross-peak lends strong support to direct electronic coupling between states, absorbing at 800 nm and 850 nm.

Supporting this notion that a cross-peak can arise from direct electronic coupling rather than energy transfer dynamics, we look to a simple model system. For a dimeric system, the cross-peak above the diagonal is related to the magnitude of the local transition dipoles, the angle between them, and the degree of delocalization of the excited state, defined as κ ≡ cos θ sin θ where

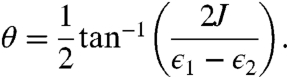J is the electronic coupling strength between the two chromophores with energies ϵ₁ and ϵ₂. In the limit of zero electronic coupling, the cross-peak above the diagonal exactly vanishes. In the presence of non-zero coupling, this same phenomenon gives rise to a static contribution to the upper diagonal cross-peak in LH2 and can explain the appearance of the cross-peak at early times.

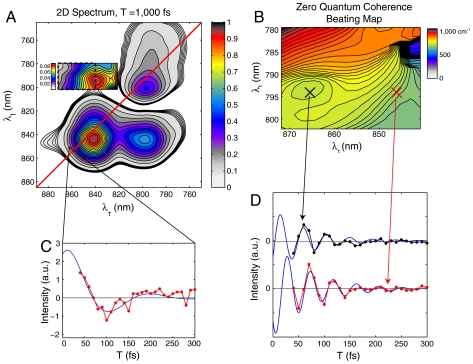
Next, we inspect the upper cross-peak for quantum beating signals that might indicate coherent dynamics. Even in the absolute-value spectra, quantum beating signals will be visible as a rotating coherence interferes with the static contribution explained above. A closer look at the upper cross-peak on a different color scale is shown in Fig. 3. Contour lines are reliable to below the 1% value of the maximum signal in the spectrum. Analysis of only a subsection (dotted box in Fig. 3A) of the cross-peak above the diagonal is shown because the large amplitude of the tails from the diagonal peaks swamps any beating signals on the right and lower portions of the upper cross-peak. Analysis of this subsection of the cross-peak shows strong amplitude beating after subtraction of a single exponential decay. The beating fits well to the product of a sinusoidal and an exponentially decaying function (see SI Text for error bar map):

where A(λ_τ,λ_t), Ω(λ_τ,λ_t), Φ(λ_τ,λ_t), and Γ(λ_τ,λ_t) are the amplitude, detuning, phase, and dephasing maps, respectively. The beat frequency map, Ω(λ_τ,λ_t), is shown in Fig. 3B. The amplitude, phase and dephasing maps are shown in Fig. 4. Some regions of the upper cross-peak fit slightly better to a sum of two exponentially decaying sinusoidal functions (see SI Text), but we have not pursued this point further in the analysis below. The frequency of the beating signal (Fig. 3B) at each point in the map matches well with the detuning (within approximately 75%, not including the uncertainty in the carrier frequency of excitation), 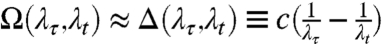. Traces from two different points within the region are shown to oscillate with different phase and frequency (Fig. 3D). These two points correspond to two states in the B850 band that themselves beat with the expected energy difference (Fig. 3C), indicating that multiple low-lying B850 states are coupled to the B800 band.

Fig. 3.

Quantum-beating signal. (A) Two-dimensional spectrum at T = 1,000 fs normalized to its maximum value. The cross-peak above the diagonal is displayed on a different color scale to highlight features. (B) Each region inside the dashed box of A is fit to an exponentially decaying sinusoidal function. The single frequency value of the fit is displayed as a zero-quantum coherence (ZQC) beating map. This map matches the theoretical prediction based on the detuning between coherence and rephasing frequencies to within experimental error. (C) The signal as a function of the waiting time is shown for the (860 nm, 852 nm) voxel along with a fit to an exponentially decaying sinusoidal function. See SI Text for more information. (D) Residual signal (black and red dots and blue fit) is plotted after subtraction of an exponential decay for two points in the region of B (x marks).

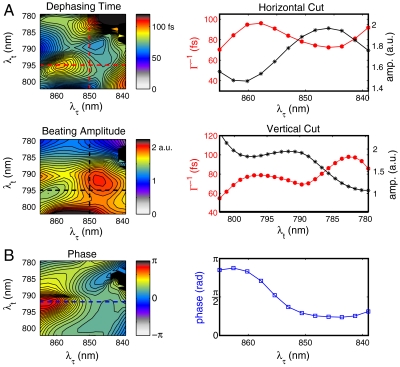
Fig. 4.

Primary factors controlling energy transfer optimization in LH2. (A) Dephasing and beating maps in the upper left cross-peak of the 2D spectrum. Maps are derived from fitting each pixel in the 2D spectrum to the functional form described in the text. The dephasing map is a measure of the extent of system–bath interactions during the waiting period. The amplitude map is proportional to the strength of electronic coupling between excitons on each of the two subunits of LH2. Cuts through the dephasing time (red dashed lines) and amplitude (black dashed lines) maps showing strong anticorrelation. (B) The phase map modulates the quantum mechanical interference between different energy transfer pathways. Cut through a fixed value of the rephasing frequency at 794 nm is shown to the right.

Such quantum beating signals arise from either electronic or vibrational quantum coherences. In this case, the vibrations would correspond to a vibrational manifold on the first electronic excited state of the individual BChl a molecules within LH2. However, the influence on the beating signal at such large values of the detuning is expected to be negligible at room temperature (see SI Text for a detailed analysis and discussion of vibrational coherence). We therefore conclude that the observed beating signals arise from electronic coherence consistent with prior analysis of other photosynthetic complexes. In determining which electronic states participate in the coherence, we explore two possibilities: coherence between excited electronic states on the B850 ring and coherence between B850 and B800. The cross-peak and beating signals could, in principle, arise from higher excited states (e.g., k =  ± 3, ± 4,…) of the B850 ring because these states can interact strongly with the lower k =  ± 1 states. According to the theoretical model of Kruger, Scholes, and Fleming (9) and calculations by Jang and Silbey (34), the upper band states match the energy level differences consistent with the beating frequencies (800–1,000 cm^-1) observed in the cross-peak region. However, experimental and theoretical work on LH2 to date indicates that these states have negligible oscillator strength (see, for example, refs. 35 and 36). Because the 2D photon echo signal is proportional to the product of four transition dipole moment elements (37), these higher excited states cannot give rise to a cross-peak with approximately 5% of the diagonal peak amplitude. We therefore assign the upper cross-peak and associated beating signal to electronic coupling and coherence between B850 and B800 states.

Despite the increased resolution of 2D spectroscopy, states within the B800 and B850 bands cannot be resolved at room temperature. However, quantum beating signals permit resolution beneath the features because of interference effects. In Fig. 4A, maps of the dephasing time (Γ^-1), amplitude, and phase of the fits are shown for the same region of the cross-peak above the diagonal as in Fig. 3B. We observe surprising structure in the dephasing and amplitude map, each showing multiple local extrema (Fig. 4A). Comparing the maps of amplitude and dephasing time, we find near-perfect anticorrelation in the signals. The small deviation on the red end of the coherence axis reflects the contribution from the phase term in this region of the spectrum. Two prominent extrema are visible along the coherence frequency axis (λ_τ) at 845 nm and 860 nm. Although definitive assignment is not possible, these energies closely match the k^a =  ± 1 excitons of the B850 unit observed by polarization-dependent single-molecule fluorescence excitation spectra at 4.2 K in Rh. Acidophila (38). Supporting this assignment, we observe two distinct regions in the phase map shown in Fig. 4B indicating that the two features represent coupling to two different states. Several peaks are also evident along the rephasing direction although we cannot confidently assign these peaks to features observed in the B800 band of single LH2 complexes because of the very short coherence times present at room temperature compared to 4.2 K. Future work at low temperature may help to resolve these bands.

Discussion

The upper cross-peak in the 2D spectra (Fig. 2) indicates electronic coupling between B850 and B800 states. This upper cross-peak signal arises from interference between two Feynman response pathways, one representing ground-state bleach and the other representing excited-state absorption. These pathways carry opposite signs. In the absence of coupling, the pathways exactly cancel. At early times, the 2D spectra therefore provide a relative mapping of the electronic coupling terms between excitons at a given frequency weighted by the dipolar interactions with the fields. The absolute coupling strength, however, cannot be extracted from these spectra. Previous theoretical work suggests that these values lie in the range of tens of wavenumbers (10, 39).

Although the presence of the cross-peak above the diagonal is evidence only of an electrostatic coupling that gives rise to B800-B850 coherence at room temperature, the beating signals observed provide much more information. For example, external perturbations lead to modulations of the coupling strength and consequently to energetic detuning. This detuning gives rise to a unique pattern of dephasing. This pattern not only allows resolution beneath the cross-peak, but it also helps to illustrate how the bath modulates different couplings in different ways.

The beating signal also permits extraction of a phase map (Fig. 4B). This map shows that the relaxation pathways that couple the states carry different phase. Initially excited exciton states may reach the trap state through multiple pathways each carrying a different cumulative phase owing to differing external perturbations. While we cannot definitively assign the origin of this phase difference, one possibility is that it arises from the system–bath coupling. For example, dynamic Stokes shifts will influence the relative phase of coherences. While the laser fields themselves can induce such phase differences, we rule out the laser field as the dominant source of such phase contributions to the signal because the phase map does not display a linear correlation between the coherence and rephasing frequencies as expected when employing identical pulses for excitation.

By examining a cut through the phase map of Fig. 4B, we measure a phase change of approximately 95° ± 5° from the λ_τ = 850 nm region to the λ_τ = 860 nm region at a fixed value of the rephasing frequency near 800 nm (individual traces shown in Fig. 3D). Based on tentative spectral assignments, we interpret this data to mean that relaxation through the energy transfer pathway to the k^a = +1 exciton is acquires approximately π/2 radians of phase relative to relaxation through the energy transfer pathway involving the k^a = -1 exciton. While these two states have mutually orthogonal transition dipole moments, such orientation contributions to the signal should give rise only to a change in amplitude, not phase in the beating signal. We should note that although we only analyze the absolute value of the signal, rather than the complex-valued signal, this procedure only results in loss of a absolute phase terms, thereby it does not affect our conclusions based on the relative phase of the signal. While eliminating errors from a pump–probe phasing process, which can be oscillatory due heterodyned scatter, this analysis strategy does allow phase differences to appear based on the underlying constant background. Such a background signal cannot be completely excluded, but at short times we see no sharp features that could account for a π/2 radians phase shift, and we do not see phase evolution during the beating from population dynamics. Supporting this assumption, prior works on LH3 and other similar photosynthetic complexes consistently show broad, featureless excited state absorption in the upper diagonal region of the spectra (40–42). We also observe beating between the two states in the B850 band at the expected difference frequency as shown in Fig. 3C, indicating both coupling and long-lived coherence between these two states. The relative phase of this pathway is equal within the margin of error to that between the 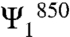and Ψ⁸⁰⁰ states.

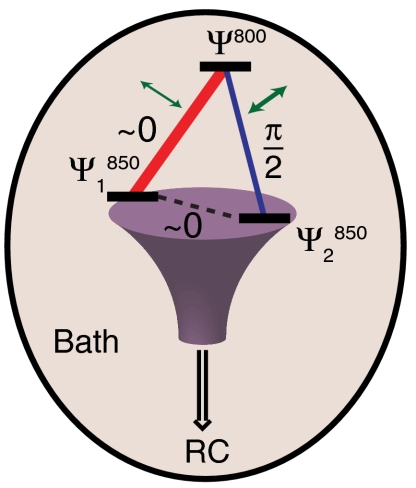
The system–bath interaction, in addition to inducing electronic coupling between excitons, also causes the system to decohere. The dephasing map, therefore, is a direct measure of the degree of decoherence between excitons arising from these interactions. The dephasing and amplitude map show strong anticorrelation, meaning that system–bath interactions that link particular excitons on each ring are also likely responsible for rapid decoherence. Simply interpreted, bath fluctuations increase the coupling, which causes increased energetic splitting between the excitons and therefore induces dephasing. The environment can, in fact, assist in the efficiency of transport through an interplay of coherent effects and dephasing—an idea supported by recent theoretical work (43–46). Microscopically, the protein fluctuation either brings regions of BChl a pigments on each ring close together, promoting exciton coupling, or alternately gives rise to a change in the dielectric environment, which promotes stronger coupling. A schematic model of the supermolecular complex is shown in Fig. 5 that captures the interplay between pathway interference, decoherence, electronic coupling, and detuning in funneling energy to the trap state.

Fig. 5.

Schematic representation of quantum phase interferometry. In LH2, we observe three states coupled together in a loop configuration. Relaxation through different pathways (red and blue) can lead to interference at the lowest energy B850 state in an isolated LH2 complex devoid of the photosynthetic reaction center (RC). The strength of the coupling as determined by the amplitude of the beating signal is represented by the thickness of the line connecting the states (blue and red line segments). The green arrows indicate the extent of system-bath interactions determined by the dephasing rates. The experimentally determined phase terms are indicated to within 0.1 radians of the values measured.

The effect of pathway interference in excitonic networks has been modeled by Cao and Sibley (47). In particular, they examined the effect relative phase of mutual coupling terms of a three-site model in a closed loop configuration in detail. In one particular case, Cao and Silbey consider a single high lying state coupling to two coupled low-lying states (large negative detuning in their formalism) (47). This situation is analogous to LH2, in which the B800 state couples to two coupled states in the B850 ring. Performing a global search in parameter states, they found that the minimal trapping time occurs when the phase of the coupling is between the low-lying states is 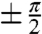and dephasing is slow. The proof by Cao and Silbey (47) is identical within a unitary transformation of the Hamiltonian to the LH2 case. However, while our data demonstrates the phase relationship predicted by Cao and Silbey (47), our data is unable to definitively identify any functional role of interference between the pathways.

In summary, the LH2 complex demonstrates a complex interplay of inter- and intramolecular interactions in linking the B800 to B850 rings (see Fig. 5). This relationship is in general agreement with recent models that explored the optimal conditions in simple closed loop network topologies. Owing to the high structural symmetry of LH2, state delocalization creates multiple relaxation pathways to the acceptor states due to the spatial extent of the states. Multiple relaxation paths to the same state provide the opportunity for quantum interference. This interference is controlled by the magnitude of system–bath coupling terms that act to provide wave function overlap with the trap state, leading to a particular pattern of constructively and destructively interfering transfer pathways. Cao and Silbey (47) and, separately, Plenio and coworkers (44, 45) recognized the importance of the relative phase between pathways in simple model systems of closed loops and linear chains of coupled excitons. In particular, they found that systems incorporating closed loops require quantum mechanical pathway interference for maximum efficiency of trapping.

The results presented here represent direct experimental evidence that LH2 capitalizes on both the phase and amplitude of coupling, on dephasing rate, and on detuning between the two subunits to facilitate efficient energy transfer. The phase map of quantum beating signals within LH2 identifies the relationship between various energy transfer pathways that result in efficient trapping at the B850 ring. This quantum mechanical interference represents a previously undescribed strategy for control of excitonic dynamics.

Methods

Optical Apparatus.

Details of our experimental setup have been published previously (31). Briefly, the output of the regenerative amplifier (40 fs, 5 kHz, 800 nm) is focused into a flowing stream of Argon gas to generate a high-power continuum pulse. Using low GVD dielectric mirrors, the 750–870 nm region of the white light spectrum is selected. After collimation, the pulse is compressed by two pairs of chirped mirrors (total GVD is -360 fs²). Single-shot nonresonant transient grating measurements in an optical flat estimate the pulse duration at fewer than 40 fs with a slight degree of positive chirp. Chirp affects the line shapes of the 2D spectrum only slightly for population times less than the pulse duration (48). To minimize the effects of chirp during the coherence time, we discarded the first 25 fs of the spatially encoded τ points.

After compression, the ultrabroadband pulse is split by a 50∶50 beam splitter, and the delay between the two beams, corresponding to the population time, T, is controlled by a motorized translation stage. Using Fresnel reflections from the front and back surfaces of an uncoated wedged optic, we further split each pulse into a pair of pulses. Optical flats are employed to balance the dispersion in each path. These four parallel polarized beams are then incident on a mirror assembly to form a distorted boxcar geometry. The LO beam is attenuated by approximately three orders of magnitude and delayed, so as to arrive approximately 1.5 ps prior to the signal. After focusing in the horizontal direction using a cylindrical lens, the four beams are vertically aligned such that the overlap at the sample generates tilted wavefronts that spatially encode the temporal delays across the sample and permit acquisition of the echo signal in the rotating frame. An imaging spectrometer resolves the resulting heterodyned signal onto a 2,048 × 2,048 pixel thermoelectrically cooled CCD camera. The resulting interference pattern allows the determination of the phase and magnitude of the third-order rephasing signal. The timings between pulses were determined using spectral interferometry as described by Joffre and coworkers (49). Our data analysis uses a modified procedure of that used for multiscan two-dimensional spectroscopy as described in detail by Brixner et al. (50). However, without adequate pump–probe data or another external reference, we cannot assign absolute phase to the 2D spectrum. Due to the sensitivity of the third-order response to the laser fluence, we can only present absolute-value spectra with confidence. We also note that an inherent uncertainty exists in the absorption frequency axis using GRAPE spectroscopy because tilting the wave fronts to create the pulse delays results in phase evolution in the rotating frame, meaning that the frequencies appearing during the coherence period are measured relative to the carrier frequency of the excitation. While the carrier frequency is straightforward to measure for well-characterized pulses, it has proven difficult to measure for continuum pulses. Nonetheless, we have estimated its value from other measurements on well-characterized systems (e.g., IR144 in methanol) with a negligible or known Stokes shift and assumed no change between measurements.

Sample Preparation.

LH2 was isolated from Rhodobacter sphaeroides cultures as described by Frank et al. (51). Sufficiently pure samples suitable for spectroscopic investigation required two sequential runs through a DEAE-Sephacel column and eluted between 500–600 mM NaCl. Samples were subsequently concentrated down to 0.2 OD at 850 nm in a 200-μm cuvette.